Abstract
The present study examined the neural substrate of two classes of quantifiers: Numerical quantifiers like “at least three” which require magnitude processing, and logical quantifiers like “some” which can be satisfied using a simple form of perceptual logic. We assessed these distinct classes of quantifiers with converging observations from two sources: functional imaging data from healthy adults, and behavioral and structural data from patients with corticobasal degeneration, who have acalculia. Our findings are consistent with the claim that numerical quantifier comprehension depends on a parietal-dorsolateral prefrontal network, but logical quantifier comprehension depends instead on a rostral medial prefrontal-posterior cingulate network. These observations emphasize the important contribution of abstract number knowledge to the meaning of numerical quantifiers in semantic memory and the potential role of a logic-based evaluation in the service of non-numerical quantifiers.
Keywords: fmri, number, semantic memory, comprehension
INTRODUCTION
Numerical knowledge and language are intricately related. We use language to refer to numerical concepts, including cardinal number words (i.e. “one”) and also using certain quantifier terms, such as “most”. However, the exact nature of this relationship is a matter of much debate. Most previous analyses have investigated concepts of magnitude, and examined the extent to which language faculties are necessary for precise numerical understanding. In this study, we adopt an alternate approach; that is, we examine words whose conceptual representation depends on knowledge of magnitude.
The processes underlying numerical comprehension have received increased attention recently (Ansari & Dhital, 2006; Cantlon & Brannon, 2006; Cohen Kadosh, Cohen Kadosh, Kaas, Henik, & Goebel, 2007; Piazza, Pinel, Le Bihan, & Dehaene, 2007). Although regions near the intraparietal sulcus are associated with simple magnitude judgments and mathematical computation (Dehaene, Piazza, Pinel, & Cohen, 2003), some complex numerical manipulations appear to depend in part on linguistic mediation, as suggested by their reliance on perisylvian language regions (Baldo & Dronkers, 2007; Dehaene et al., 2003). However, language abilities are not necessary for all aspects of number meaning; other aspects of number knowledge, such as the appreciation of quantity, or magnitude comprehension, can be demonstrated in preverbal infants and primates, who lack advanced language abilities (Cantlon & Brannon, 2007; Xu, Spelke, & Goddard, 2005).
Quantifier terms are noun phrases which we believe may also rely in part on a magnitude comprehension system. These terms are common in daily speech, yet we know little about their neural basis. A quantifier is a noun phrase that asserts a property from a set and maps this to a truth-value (Clark & Grossman, 2007; Frege & van Heijenoort, 2000). There are several distinct classes of quantifiers defined in formal linguistics (Keenan & Stavi, 1986; van Benthem, 1986), and we focus on two in the current study: Cardinal and Aristotelian. Cardinal quantifiers, which we refer to as “numerical quantifiers” from this point forward, are based in part on knowledge of magnitude. Consider the sentence “At least three scientists drink coffee.” The comprehension of this sentence relies on the magnitude expressed by “three”. If only two coffee-drinking scientists can be identified, then the statement is false. This can be contrasted with Aristotelian quantifiers, which we will refer to as “logical quantifiers”, which do not depend on quantity. Logical quantifiers like “some” and “all” are based instead on an elementary logic system that detects the presence of a unique feature. In the sentence “Some scientists drink coffee,” evaluation involves the detection of a single scientist drinking coffee; knowledge regarding precise numerosity is not required. This is equally true for statements such as “All scientists drink tea,” in which identification of a single non-tea drinking scientist falsifies the statement. These differences in task requirements between numerical and logical quantifiers suggest that they may be supported by dissociable cognitive mechanisms.
Evidence consistent with the hypothesis that two distinct cognitive systems support separate classes of quantifiers would come from the identification of a distinct neural network associated with each class of quantifier. As noted above, numerical quantifiers appear to depend on a quantity-based system to determine their conceptual accuracy. Much evidence from patient observations (Cipolotti, Butterworth, & Denes, 1991; Cohen, Dehaene, Chochon, Lehericy, & Naccache, 2000; C. H. Halpern et al., 2004) and fMRI studies (Dehaene et al., 2003; Simon, Mangin, Cohen, Le Bihan, & Dehaene, 2002) associates magnitude knowledge with the intraparietal sulcus (IPS). Although the exact function of the IPS in assessing numerical information has not been fully clarified, previous neuroimaging studies have demonstrated that this region responds in a ratio-dependent manner to magnitude judgments. Thus, for a quantified statement containing “at least three” to be true, IPS is important for evaluation of the magnitude information present in this statement. Because the criterion (“three” in the example) must be kept in mind while perceptual information is evaluated, comprehension of numerical quantifiers may also depend on dorsolateral prefrontal (dlPFC) brain regions to support working memory. This demand might be particularly high when numeric computations require serial maintenance (Botvinick & Watanabe, 2007).
Logical quantifiers appear to require a simple decision-making mechanism adapted to interpret relatively constrained alternatives and support of a selective attentional system. Logical quantifiers thus may depend in part on rostral medial prefrontal cortex (rmPFC), which plays a role in simple decision-making about dichotomous events in the environment (Gilbert, Spengler, Simons, Frith, & Burgess, 2006) such as attending to and interpreting the occurrence of exceptional events. This area may work together with an attentional mechanism in posterior cingulate cortex (PCC) that involves selective attention to visual-perceptual stimuli (Dana M. Small et al., 2005; D. M. Small et al., 2003). To determine that a quantified statement containing “some” is true, for example, the set of items must be attended, and a dichotomous decision about seeing at least one of the specified targets must be made.
To assess the neural networks supporting numerical and logical quantifiers, we designed a task in which participants viewed serial arrays of familiar objects and then judged the accuracy of a simple statement containing a quantifier. We used a serial presentation for several reasons: This design most appropriately allows us to model the processes involved in quantifier meaning, without confounds presented by potential differences in making decisions about the stimuli. Additionally, a serial presentation minimizes potential visual processing associated with parietal cortex (Hubbard, Piazza, Pinel, & Dehaene, 2005). Statements included logical quantifiers like “some” and “all,” such as “Some of the balls are blue.” Other statements featured numerical quantifiers like “at least three,” such as “At least three of the flowers are red.”
Converging evidence to support two distinct classes of quantifiers was obtained from two sources. First, we monitored regional brain activity with BOLD fMRI while healthy young adults performed this task. We expected distinct patterns of activation for each class of quantifiers. This included rmPFC and PCC activation for logical quantifiers, and IPS and dlPFC activation for numerical quantifiers. Secondly, we collected behavioral data from patients with focal cortical neurodegenerative disease, and we examined the neuroanatomic distribution of disease with voxel-based morphometry (VBM) analyses of high resolution structural MRI scans. Corticobasal degeneration (CBD) is a rare neurodegenerative condition that causes parietal lobe disease (Murray et al., 2007). This results in deficits on tasks assessing number knowledge (C. Halpern et al., 2004; C. H. Halpern et al., 2004). Even though these patients do not have aphasia, we hypothesized that numerical quantifiers would be selectively impaired in these patients due to their parietal disease. If we are correct about the distinct nature of the two quantifier systems, we would expect that their comprehension of numerical quantifiers would be worse than their comprehension of logical quantifiers.
METHODS
Participants
We assessed 14 healthy adult participants from the University of Pennsylvania community in the fMRI study. Participants ranged in age from 20–28 years (M = 24.4, SD = 2.70) and had an average of 15.6 years of education. All were right-handed native English speakers, in good health, and none were taking any medication known to affect cognitive function or brain activity.
We also examined 13 patients diagnosed with CBD (mean ±S.D. age = 64.1 ±9.6 years; mean ±S.D. education = 14.3 ±3.3 years; mean ±S.D. disease duration = 49.0 ±26.1 months; mean ±S.D. MMSE = 22.9 ±3.3). All patients were identified in the outpatient clinic of the Department of Neurology at the University of Pennsylvania Medical Center. The clinical diagnosis was made by a board-certified neurologist with expertise in the diagnosis of dementing conditions (MG). We are unaware of any published consensus criteria for the clinical diagnosis of CBD, although experts have suggested specific clinical features that may be important in diagnosing CBD (Litvan et al., 2003; Riley & Lang, 2000). The criteria we developed, based on a review of literature concerned with clinical–pathological diagnosis of CBD and our own autopsy series (Murray et al., 2007), include the insidious onset and gradual progression of: apraxia, cortical sensory deficit, gait instability and axial rigidity, and/or asymmetric extrapyramidal features such as myoclonus, dystonia, and limb rigidity, but little resting tremor. These patients did not have aphasia as determined by clinical evaluation. To assess regional cortical atrophy in these patients, we compared the gray matter images of a subset of CBD patients (n=8) who had volumetric MRI scans to 8 healthy adults (mean ±S.D. age = 70.9 ±6.0 years; mean ±S.D. education = 16.0±2.1 years). Participants were paid for their participation. Informed consent was obtained from all individuals according to a protocol approved by the Institutional Review Board at the University of Pennsylvania.
Procedure
Subjects and patients determined the accuracy of grammatically simple, written propositions containing a quantifier (e.g. “Some of the balls are blue”) that probed a color feature of a familiar object (e.g. balls, flowers, cars, shirts, hats, stars) in a serially presented visual array (Figure 1). Stimuli were presented serially to minimize the potential visual-spatial confound associated with scanning a single array consisting of many objects presented at one time (Hubbard et al., 2005). An event-related design was used, and 144 statements containing one of six different quantifiers were presented in a fixed pseudorandom order where no more than three stimuli of a particular type occurred consecutively in the stimulus series. Statements contained quantifiers that were either logical (some, all), or numerical (consisting of the quantifiers at least three, more than two, even, and odd). We included parity quantifiers (even, odd) because we wanted to test a range of numerical quantifiers. Parity judgment tasks are frequently used in numerical discrimination tasks, and consistently show automatic access to numerical magnitude (Dehaene, 1997). For the purpose of this experiment, parity quantifiers provided an additional numerical stimulus without an increase of working memory demands beyond those of counting. To ensure that these were an acceptable stimulus to include as numerical, we directly contrasted the main effects of parity and cardinal quantifiers. There were no activation differences between these two subtypes.
Figure 1.
Schematic of Stimulus Presentation
Each trial began with a 3 s presentation of the proposition containing a quantifier. Pictures of the objects were then displayed, one at a time, for 1.5 s each. The number of stimuli in the array varied between 4, 6, or 8 objects. We used small numerosities in the numerical quantifiers and small numbers of total objects to minimize the risk that CBD patients would not be able to perform the task due to their number limitations. Following the serial array, the initial statement was again presented concurrently with a “Yes or No” probe. This remained on the screen for a maximum of 3- s or until subjects responded using a keypad. Between each trial, an inter-trial interval of 3, 6, 9, or 12 seconds was used, during which a white, blank screen was displayed. Participants were trained ahead of time on the experimental method with several practice items, and all participants appeared to understand the task and the procedure for indicating their judgments during the practice session prior to the experiment.
Functional imaging procedure and analysis
The experiment was carried out at 3T on a Siemens Trio scanner (Siemens Medical Systems, Erlangen, Germany). Each imaging study began with a 3D MPRAGE protocol (TR=1620 msec, TE=30 msec, 192 × 256 matrix), acquiring 1 mm isotropic voxels to determine regional anatomy. BOLD fMRI images were then acquired to detect alterations in blood oxygenation accompanying increased mental activity. All images were acquired with fat saturation, 3 mm isotropic voxels, flip angle of 15°, TR=3000 msec, TEeff= 30 msec, and a 64 × 64 matrix, acquiring 45 contiguous axial slices through the entire brain every 3 sec.
Individual subject data were then prepared for analysis using SPM5, developed by the Wellcome Trust Centre for Neuroimaging (http://www.fil.ion.ucl.ac.uk/spm/software/spm5). The images in each subject’s time series were registered to the initial image in the series. The images were then aligned to a standard coordinate system using the MNI152 average brain template. The data were spatially smoothed with an 8 mm FWHM isotropic Gaussian kernel to facilitate statistical analyses and to account for local variations in activation and sulcal anatomy across participants. Low-pass temporal filtering was implemented by controlling auto-correlation with a first-order auto-regressive method.
After eliminating judgment errors (mean ±S.D. accuracy = 93.6% ±3% correct), a random-effects model was used to analyze neural activation for each type of quantifier. We modeled each object as an event beginning with the first object after the quantified statement, and ending when the statement had been satisfied. For example, for the statement “At least three stars are yellow,” we modeled all object presentations as events from the first star until the third yellow star). We used this analysis method because multiple stimuli contribute to the ability to make the final judgment. Additionally, the point of decision does not necessarily occur at the time of response, but, when the final object necessary to assess the statement’s validity is presented. For example, “some of the stars are yellow” can be verified at the occurrence of the first yellow star, while “an even number of stars are red” can only be assessed after all stimuli are presented. Event onsets times were convolved with a canonical hemodynamic response function to estimate their potential contribution to the fMRI data. We then contrasted the main effects associated with the two quantifier classes with each other. These analyses were performed in each individual, and these contrasts were then entered into a second-level analysis to assess group effects. We used a voxel-wise threshold of p < .001. To control for false positives, we required the peak voxel in a cluster to pass a threshold of p < 0.05 with a false discovery rate (FDR) correction for multiple comparisons. Using this procedure, all clusters also had a cluster-level significance of p < 0.001.
Regions of interest (ROIs) were identified using the significant clusters identified in the contrasts summarized in Table 1. They were extracted using the MarsBaR toolbox in SPM5 (Brett, Anton, Valabregue, & Poline, 2002). This averages the time series across the cluster, and uses information about conditions in order to extract a parameter estimate for each condition. After ROIs were determined, the time series information was extracted from the main effect analysis.
Table 1.
Activation peaks for Functional MRI Study in Healthy Adults
| Contrast | Coordinates | Z Score | Cortical Region | ||
|---|---|---|---|---|---|
| x | y | z | |||
| Numerical > Aristotelian | −54 | −36 | 40 | 5.59 | Right parietal |
| 52 | −36 | 50 | 5.37 | Left parietal | |
| 40 | 42 | 24 | 4.74 | Right superior frontal | |
| 50 | 20 | 2 | 4.13 | Right dorsolateral frontal | |
| −24 | 2 | 60 | 5.36 | Precentral gyrus | |
| −36 | −56 | −36 | 5.19 | Left cerebellum | |
| Aristotelian > Numerical | −2 | 60 | 8 | 4.81 | Medial frontal |
| −2 | −24 | 46 | 4.54 | Posterior Cingulate | |
To examine the degree to which the activated regions worked together, we analyzed intersubject correlations in activation. We assume that if active regions are working in a coordinate fashion, they will covary across participants. For each ROI we extracted the mean level of activity expressed by the mean beta value from our model. We performed pairwise bivariate correlations on these values between the two networks we identified.
Structural imaging procedure and analysis
Analysis of patients’ structural images was performed using voxel-based morphometry (Ashburner & Friston, 2000). We compared regional gray matter intensity in CBD patients to that of age-matched control subjects. Each imaging study involved a high resolution, 3D MPRAGE protocol (TR=1620 msec, TE=30 msec, 192 × 256 matrix), acquiring 1 mm isotropic voxels. Preprocessing of the images was performed using a generative model that combines tissue segmentation, bias correction, and normalization using tissue probability maps (Ashburner & Friston, 2005). Total gray matter signal was preserved by scaling the intensity of each voxel by its change in volume during the normalization process (Good et al., 2001). The resulting gray matter images for each subject were visually inspected to ensure they were free from obvious defect. Each image was smoothed with an isotropic Gaussian kernel of 12 mm FWHM. We used a voxel-wise threshold of p < 0.01. We accepted clusters in which the maximum voxel had a Z-score of > 3.14 (equivalent to p < .001 uncorrected), with an extent criterion of 50 voxels.
RESULTS
fMRI Studies in Healthy Adults
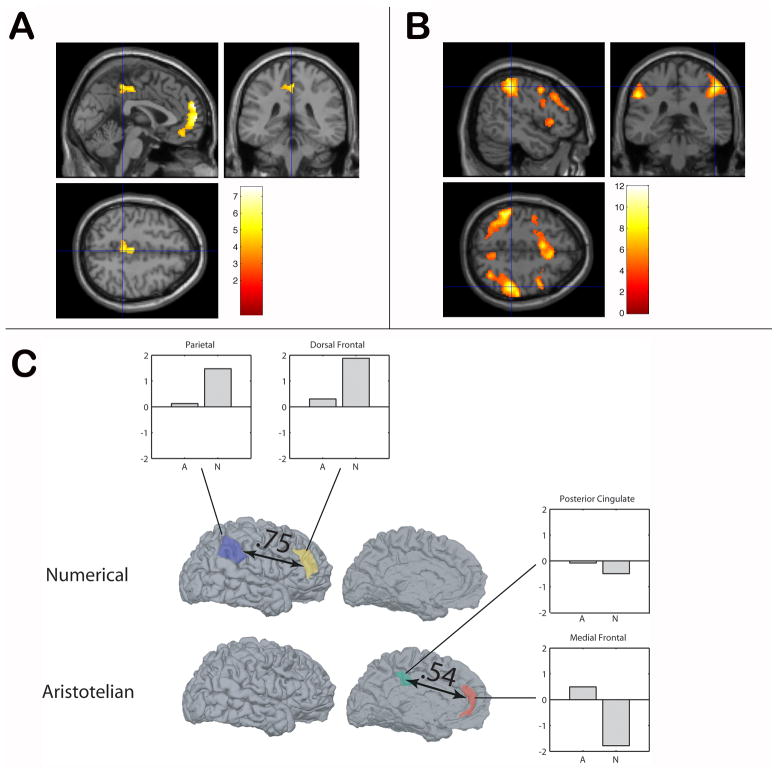
Participants were significantly faster at judging the accuracy of logical quantifiers (t(13) = 4.86 p < 0.001); mean r.t. ±S.D. logical = 869 ±320 msecs; mean r.t. ±S.D. numerical = 1110 ±461 msecs. Comparisons of activation between numerical and logical quantifiers are shown in Figure 2, and listed in Table 1. Figure 2, Panel A shows that logical quantifiers significantly activated rmPFC and PCC relative to numerical quantifiers. By comparison, we observed significant bilateral activation of the intraparietal sulcus, right dlPFC, and left precentral regions for numerical quantifiers relative to logical quantifiers.
Figure 2. Functional Activation during Judgments of Quantifiers.
Panel A: Activation for Aristotelian quantifiers; Panel B: Activation for numerical quantifiers. Panel C: Network correlation analysis of classes of quantifiers, with significant correlation values, and parameter estimates for activations in each anatomic region for Aristotelian (A) and numerical (N) quantifiers.
We confirmed these dissociated activation patterns by creating a region of interest (ROI) for each significantly activated area and examining the parameter estimates associated with each class of quantifier for each region. Parameter estimates are illustrated in the subviews of Figure 2, Panel C. The IPC ROI was recruited for numerical quantifiers, but this region was not activated for logical quantifiers. The ROI in rmPFC was positive only for logical quantifiers but not numerical quantifiers.
We then correlated the activations seen during the time series associated with logical and numerical quantifiers. These correlations were based on the mean beta value extracted from the ROIs as described in the Methods. Results of this analysis are displayed schematically in Figure 2C and listed in Table 2. In Figure 2C, a line between two regions indicates a significant correlation, and the number next to the line is the Pearson r value from the bivariate correlation. During judgments of logical quantifiers, we observed a significant correlation in activation between rmPFC and PCC. However, neither of these regions correlated significantly with IPC or dlPFC. Likewise, we observed a significant correlation between IPC and dlPFC during judgments of numerical quantifiers, but these areas did not correlate with rmPFC or PCC. These observations emphasize the double dissociation between the networks activated for numerical quantifiers and logical quantifiers.
Table 2.
Correlations of Activations in Clusters during Judgments of Aristotelian and Numerical Quantifiers
| ARISTOTELIAN QUANTIFIERS | ||
|---|---|---|
| rMPFC | PCC | |
| rMPFC | - | .537** |
| PCC | .537** | - |
| DLPFC | .254 | −.148 |
| IPS | .408 | .054 |
| NUMERICAL QUANTIFIERS | ||
| DLPFC | IPS | |
| rMPFC | −.066 | −.295 |
| PCC | .144 | .009 |
| DLPFC | - | .787** |
| IPS | .787** | - |
Results in Patients with Corticobasal Degeneration
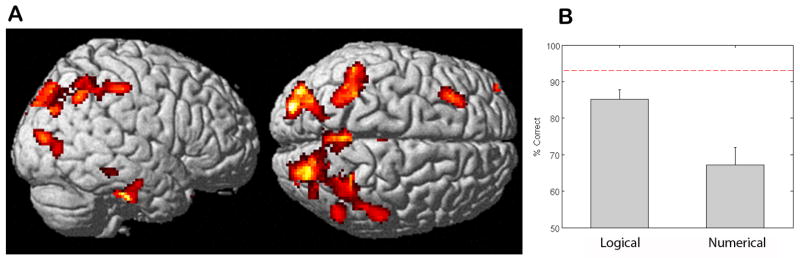
The distribution of cortical atrophy in these CBD patients is illustrated in Figure 3, and Table 3 summarizes the coordinates of the peak voxels in these atrophied clusters relative to the group of age-matched healthy seniors. CBD patients have parietal disease involving the intraparietal sulcus, but they do not have medial prefrontal disease. This is consistent with their impairment on quantifiers that rely on number knowledge, and their spared comprehension of logical quantifiers that depend on a form of simple perceptual logic.
Figure 3.
Behavioral Performance and Cortical Atrophy in Corticobasal Degeneration. Panel A: Cortical atrophy of corticobasal degeneration patients as compared to healthy age-matched seniors; Panel B: Histogram illustrating behavioral accuracy for each class of quantifier. Dashed line represents mean accuracy of Parkinson’s disease patients;
Table 3.
Regions of Cortical Atrophy in Patients with Corticobasal Degeneration
| Coordinates | Z Score | Cortical Region | ||
|---|---|---|---|---|
| x | y | z | ||
| 24 | −52 | 50 | 4.30 | Right inferior parietal |
| 40 | −74 | 2 | 3.24 | Right occipital |
| 18 | −44 | −12 | 3.21 | Right parahippocampal gyrus |
| 44 | −34 | −14 | 3.18 | Right fusiform gyrus |
| 14 | 10 | 26 | 3.89 | Right anterior cingulate |
| −76 | −44 | 46 | 3.47 | Left inferior parietal |
| −46 | −46 | −6 | 3.58 | Left posterior temporal |
| −42 | 22 | −30 | 4.12 | Left inferior temporal |
| −28 | −20 | −28 | 3.37 | Left parahippocampal gyrus |
| −42 | 66 | 12 | 3.66 | Left frontal |
| −36 | 26 | 64 | 3.12 | Left superior frontal |
| −16 | 18 | 22 | 3.13 | Left anterior cingulate |
| −14 | −36 | 42 | 3.52 | Left posterior cingulate |
The same task was administered by computer to patients with CBD. Non-demented patients with idiopathic Parkinson’s disease (PD) served as a brain-damaged control group (n = 8; mean ±S.D. age = 62.6 ±10.6 years; mean ±S.D. education = 15.1±3.4 years)). CBD patients were impaired on both conditions relative to the PD control group ((logical: t(19) =3.51 p<.01; numerical: t(19) =4.24 p<.001). As summarized in Figure 3, CBD patients were significantly impaired on numerical quantifiers relative to their comprehension of logical quantifiers (t(12) = 4.86 p < 0.001); mean accuracy ±S.D. logical = 85.1 ±9.9; mean accuracy ±S.D. numerical = 67.2 ±17.3. There were no accuracy differences between the two conditions for the PD control group (t(7) = 1.59 p=.155); mean accuracy ±S.D. logical = 97.8 ±2.3; mean accuracy ±S.D. numerical = 96.6 ±3.9.
DISCUSSION
Our findings demonstrate that two dissociable neural networks contribute to quantifier meaning. Numerical quantifiers are supported by a parietal-dorsolateral prefrontal network that depends on quantity-based or numerical processing. Logical quantifiers are associated with rostral medial prefrontal cortex that plays a crucial role in a form of elementary logic, supported by a selective visual-spatial attention mechanism in posterior cingulate cortex. Converging evidence supporting this double dissociation comes from fMRI studies of healthy adults and patients with CBD. We discuss each of these quantifier networks below.
Role of parietal regions in numerical quantifier comprehension
The role of the IPC, and the intraparietal sulcus in particular, is well known in magnitude and number processing (Dehaene et al., 2003; Simon et al., 2002). Precise concepts of larger numbers are thought to be mediated in large part by their representation in language (Dehaene, 1997; Dehaene et al., 2003). However, the extent to which certain segments of the lexicon depend on number representation has not been critically examined. In the present study, we found IPC activation in the area of the intraparietal sulcus in association with comprehension of numerical quantifiers. This resembles a previous fMRI study assessing quantifier comprehension (McMillan, Clark, Moore, Devita, & Grossman, 2005). In this previous report using materials similar to the current study, the authors demonstrated activation in right IPC during the comprehension of numerical quantifiers. One potential confound in this previous assessment of quantifier comprehension was that the object arrays under evaluation were presented as a single set of stimuli distributed in space. It could not be definitively stated that performance on the task was not due to spatial processing that is also supported in part by IPC (Simon et al., 2002). The serial presentation design used in the present study minimized this problem since each stimulus was presented in a series in a central location in space.
Converging evidence for the role of IPC in numerical quantifier comprehension comes from the observation that CBD patients have difficulty understanding this class of quantifiers, despite the absence of aphasia or comprehension difficulty. Moreover, patients with CBD have significant IPC atrophy, encompassing the intraparietal sulcus. This parietal disease in these patients is associated with compromised number knowledge (C. Halpern et al., 2004; C. H. Halpern et al., 2004; Murray et al., 2007).
In addition to difficulty with magnitude comprehension, patients with CBD are impaired in their comprehension of quantifiers. Previously, it has been reported that their comprehension of numerical quantifiers is significantly greater than in patients with other neurodegenerative diseases such as frontotemporal lobar degeneration (McMillan, Clark, Moore, & Grossman, 2006). Further support for a separation of cortical support for number knowledge as compared to other domains of semantic knowledge comes from a recent case study of a patient with semantic dementia who had relatively preserved comprehension of quantifiers such as “couple” and “dozen” despite impaired knowledge of objects (Cappelletti, Butterworth, & Kopelman, 2006).
Magnitude knowledge by itself may not be sufficient to convey the meaning associated with a numeric quantifier. Consistent with this notion we also found dlPFC activation for the numerical quantifiers in the current study. This prefrontal region may contribute to serial processing resources needed to maintain the numerosity of an ordered series of the stimuli (Botvinick & Watanabe, 2007; Marshuetz, Reuter-Lorenz, Smith, Jonides, & Noll, 2006) or a general working memory resource necessary to maintain quantities in an active mental state over the period of time needed to evaluate the quantified statement (Smith & Jonides, 1999). Previous studies of quantifier comprehension, including fMRI work (McMillan et al., 2005) and assessments of patients with focal cortical neurodegenerative diseases (McMillan et al., 2006), have not demonstrated reliance on a dlPFC network for numerical quantifiers. However, both of these studies involved judgments about spatially-arrayed objects, which may not require the working memory maintenance of a serial array employed in the current study. Although a serial design allowed us to minimize the potential confound of spatial processing components of object array perception, future work involving a direct comparison of spatial and serial presentations is needed to resolve possible task-related differences between these fMRI studies.
These findings also lend interesting perspective to the dissociable concepts of language and number. Typical tests contrasting language and number rely on tasks manipulating concrete object knowledge. It is difficult to reconcile the current results with this dichotomy, because quantifier terms are, by definition, linguistic. A study by Butterworth et al. (2001) suggests that preservation of quantifiers may be supported by parietal cortex. Our results are consistent with this interpretation for quantifier terms relying explicitly on magnitude, such as numerical quantifiers. While it seems these terms do not require left temporal cortex typically associated with semantic comprehension, this is not to say that other language processes serve full comprehension of these terms.
Rostral Medial Prefrontal Cortex and an Elementary Logic Network
One elementary form of logic is known as perceptual logic, which can be supported by a simple attention-orienting system that detects whether at least one element in an array has a specified property. Evidence from animal models (Watanabe & Huber, 2006) and developmental studies (Piaget, 1970) is consistent with the remarkable conservation of this primitive but powerful form of logic. Logical quantifiers appear to depend in large part on this form of simple logic. These quantifiers require attentional control and interpretation during relatively simple, dichotomous decision-making, such as attending to the presence of a single instance of a stimulus set. For example, the truth value of the statement “Some of the balls are blue” is satisfied with the occurrence of a single blue ball; “All of the balls are blue” is falsified with the occurrence of a single non-blue ball.
Our observations implicate rmPFC and PCC regions in the comprehension of logical quantifiers. We observed activation of these areas during the fMRI study while participants were evaluating sentences containing quantifiers like “some” and “all.” Because participants’ response times were significantly faster for logical quantifiers, it may seem that these stimuli were just easier. However, we do not believe this difference is enough to explain the differential patterns of activations we observed in light of several considerations. Namely, the reaction time data is collected at the point of response for each statement, which does not necessarily correspond to the time at which the meaning and relative accuracy of each statement is assessed. For example, “some” can be verified as soon as a single instance is seen, while “an even number of” can only be evaluated after all objects in an array are viewed. Subjects thus have considerable preparation time prior to a request for a response for the former class of stimuli, but the latter class of stimuli requires additional processing time since the decision can be made only at a point that is immediately prior to the request for a response. Because we are interested in the neural basis for quantifiers and not other processes involved in the final judgment of stimuli, we believe that response times do not accurately reflect the relative difficulty of these stimuli. In order to confirm that these separable networks were not due to item difficulty, we correlated reaction time from logical quantifiers with main effect activations. If activation associated with these stimuli was determined by difficulty, one might expect that more difficult stimuli (reflected by a longer reaction time) would recruit regions of the frontal-parietal network associated with numerical quantifiers. We did not find responses to be correlated with any activity observed in the main effect. These data lend additional support to the idea that the observed reaction time differences are less than ideal measures for assessing task difficulty in this paradigm, and these observations are consistent with a separable network for logical quantifier comprehension. It remains a possibility that the observed dissociation between logical and numerical quantifiers is due to more general differences in attention, object individuation, or working memory demands. We cannot rule out this possibility with the current design, but believe that a future study would serve to verify our hypothesis that these quantifier types differ in the underlying cognitive algorithms necessary for assessment and comprehension (i.e. examining differences between “some” and “at least one”). Because this dissociation is supported by linguistic theory (Keenan & Stavi, 1986; van Benthem, 1986), we believe that the observed differences are indeed due to distinctions in the contributing cognitive mechanisms, and not merely disparities related to difficulty.
Rostral medial prefrontal and posterior cingulate cortices are associated with biasing spatial attention towards areas where significant events are expected to occur (Dana M. Small et al., 2005; D. M. Small et al., 2003). Rostral medial prefrontal cortex has also been implicated in previous functional imaging studies involving simple decision-making about attended features in the environment, particularly when the experimental condition does not require extensive internal processing (Burgess, Dumontheil, & Gilbert, 2007; Gilbert et al., 2006). These observations are consistent with an elementary logical network capable of interpreting the results of dichotomous decisions.
Offering additional support to this notion is the finding that patients with CBD were significantly better with these quantifiers relative to numerical quantifiers, consistent with the absence of extensive cortical atrophy in rmPFC. While CBD patients were impaired with both numerical and logical quantifiers compared to PD patients, their performance with logical quantifiers was significantly better than their own performance with numerical quantifiers. We interpret this relative preservation as a difference between this patient population’s extensive parietal atrophy in contrast to their modest posterior cingulate atrophy.
We note that several previous studies have defined a role for angular gyrus in tasks requiring precise numerical comprehension, possibly related to the verbal mediation needed for precise number knowledge. From this perspective, since all quantifiers require language processing, it is difficult to assess the role of the angular gyrus in a specific class of quantifiers.
The Representation of Quantifier Meaning in Semantic Memory
Our observations are consistent with an abstract coding of number knowledge in the intraparietal sulcus portion of IPC that contributes to numerical quantifier meaning, regardless of the form of input (Piazza et al., 2007). We suggest that this abstract sense of numerosity plays a fundamental role in the comprehension of numerical quantifiers such as “at least three” (Clark & Grossman, 2007). This parallels the way in which perceptual feature representations contribute to object knowledge and the meaning of words like “cup” in sensory-motor theories of semantic memory (Martin, 2007). From this perspective, the meaning of a word that depends in part on a numerical property appears to depend in part on brain regions near where abstract number knowledge is processed. The distinct nature of this quantity-based set of quantifiers is emphasized by its difference from the class of logical quantifiers that depend in part on an attention-mediated feature processing mechanism supported by regions important for simple logical computations.
This may also clarify the basis for the successful use of a subset of quantifier concepts in children and subhuman primates. It has been observed that the child’s acquisition of precise number words is neither necessary nor sufficient to support the comprehension of logical quantifiers like “some” that do not depend on number concepts (Halberda, Taing, & Lidz, 2008). The acquisition of logical quantifiers in children and correct judgments of logical quantifiers in animals thus may be independent of number knowledge and counting ability since logical quantifiers like “some” do not appear to require number knowledge. This is consistent with several developmental studies indicating a grasp of certain quantifier words without full counting ability (Hurewitz, Papafragou, Gleitman, & Gelman, 2006; Papafragou & Schwarz, 2005).
Conclusions
We propose a model of quantifier comprehension that involves two dissociable neural networks. One network involves brain regions important in the representation of abstract number knowledge in the intraparietal sulcus portion of IPC. Together with dlPFC, this network appears to be capable of supporting the comprehension of numerical quantifiers. This is distinct from a second, fundamentally distinct network that involves a form of simple, attention-mediated, perceptual logic that can detect and interpret the occurrence or absence of single properties of sets. This network is capable of verifying logical quantifiers and is supported in part by rmPFC, with input from PCC.
Acknowledgments
This work was supported in part by grants from NIH (NS44266, NS53488, AG15116, AG17586, and NS54575).
Footnotes
Portions of this work were presented at the Academy of Aphasia Annual Meeting, Washington, D.C., 2007 and the Society for Neuroscience Annual Meeting, San Diego, 2007.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ansari D, Dhital B. Age-related Changes in the Activation of the Intraparietal Sulcus during Nonsymbolic Magnitude Processing: An Event-related Functional Magnetic Resonance Imaging Study. J Cogn Neurosci. 2006;18(11):1820–1828. doi: 10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Voxel-based morphometry-The methods. NeuroImage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Unified Segmentation. NeuroImage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Baldo JV, Dronkers NF. Neural correlates of arithmetic and language comprehension: A common substrate? Neuropsychologia. 2007;45(2):229–235. doi: 10.1016/j.neuropsychologia.2006.07.014. [DOI] [PubMed] [Google Scholar]
- Botvinick M, Watanabe T. From Numerosity to Ordinal Rank: A Gain-Field Model of Serial Order Representation in Cortical Working Memory. J Neurosci. 2007;27(32):8636–8642. doi: 10.1523/JNEUROSCI.2110-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brett M, Anton J-L, Valabregue R, Poline J-B. Region of interest analysis using an SPM toolbox; Paper presented at the 8th International Conference on Functional Mapping of the Human Brain. from marsbar.sourceforge.net.2002. [Google Scholar]
- Burgess PW, Dumontheil I, Gilbert SJ. The gateway hypothesis of rostral prefrontal cortex (area 10) function. Trends in Cognitive Sciences. 2007;11(7):290–298. doi: 10.1016/j.tics.2007.05.004. [DOI] [PubMed] [Google Scholar]
- Butterworth B, Cappelletti M, Kopelman M. Category specificity in reading and writing: the case of number words. Nature Neuroscience. 2001;4(8):784–786. doi: 10.1038/90484. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Shared System for Ordering Small and Large Numbers in Monkeys and Humans. Psychological Science. 2006;17(5):401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Basic Math in Monkeys and College Students. PLoS Biology. 2007;5(12):e328. doi: 10.1371/journal.pbio.0050328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cappelletti M, Butterworth B, Kopelman M. The understanding of quantifiers in semantic dementia: A single-case study. Neurocase. 2006;12:136–145. doi: 10.1080/13554790600598782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cipolotti L, Butterworth B, Denes G. A specific deficit for numbers in a case of dense acalculia. Brain. 1991;114(6):2619–2637. doi: 10.1093/brain/114.6.2619. [DOI] [PubMed] [Google Scholar]
- Clark R, Grossman M. Number sense and quantifier interpretation. Topoi. 2007;26(1):51–62. [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh K, Kaas A, Henik A, Goebel R. Notation-Dependent and -Independent Representations of Numbers in the Parietal Lobes. Neuron. 2007;53(2):307–314. doi: 10.1016/j.neuron.2006.12.025. [DOI] [PubMed] [Google Scholar]
- Cohen L, Dehaene S, Chochon F, Lehericy S, Naccache L. Language and calculation within the parietal lobe: a combined cognitive, anatomical and fMRI study. Neuropsychologia. 2000;38(10):1426–1440. doi: 10.1016/s0028-3932(00)00038-5. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The number sense. New York: Oxford University Press; 1997. [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cognitive Neuropsychology. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Frege G, van Heijenoort J. Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought. From Frege to G\"(o)del: A Source Book in Mathematical Logic; San Jose, CA: toExcel; 2000. pp. 1879–1931.pp. 1–82. [Google Scholar]
- Gilbert SJ, Spengler S, Simons JS, Frith CD, Burgess PW. Differential Functions of Lateral and Medial Rostral Prefrontal Cortex (Area 10) Revealed by Brain-Behavior Associations. Cereb Cortex. 2006;16(12):1783–1789. doi: 10.1093/cercor/bhj113. [DOI] [PubMed] [Google Scholar]
- Good CD, Johnsrude IS, Ashburner J, Henson RNA, Friston KJ, Frackowiak RSJ. A voxel-based morphometric study of aging in 465 normal adult human brains. NeuroImage. 2001;14:21–36. doi: 10.1006/nimg.2001.0786. [DOI] [PubMed] [Google Scholar]
- Halberda J, Taing L, Lidz J. The age of onset of ‘most’ comprehension and its potential dependence on counting abilities in preschoolers 2008 [Google Scholar]
- Halpern C, Clark R, Moore P, Antani S, Colcher A, Grossman M. Verbal mediation of number knowledge: Evidence from semantic dementia and corticobasal degeneration. Brain and Cognition. 2004;56(1):107–115. doi: 10.1016/j.bandc.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Halpern CH, Glosser G, Clark R, Gee J, Moore P, Dennis K, et al. Dissociation of numbers and objects in corticobasal degeneration and semantic dementia. Neurology. 2004;62(7):1163–1169. doi: 10.1212/01.wnl.0000118209.95423.96. [DOI] [PubMed] [Google Scholar]
- Hubbard EM, Piazza M, Pinel P, Dehaene S. Interactions between number and space in parietal cortex. Nature Reviews Neuroscience. 2005;6(6):435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Hurewitz F, Papafragou A, Gleitman L, Gelman R. Asymmetries in the acquisition of numbers and quantifiers. Language Learning and Development. 2006;2:77–96. [Google Scholar]
- Keenan EL, Stavi J. A semantic characterization of natural language determiners. Linguistics and Philosophy. 1986;9:253–326. [Google Scholar]
- Litvan I, Bahatia KP, Burn DJ, Goetz C, Lang AE, McKeith IG. SIC Task Force appraisal of clinical diagnostic criteria for parkinsonian disorders. Movement Disorders. 2003;18(5):467–486. doi: 10.1002/mds.10459. [DOI] [PubMed] [Google Scholar]
- Marshuetz C, Reuter-Lorenz PA, Smith EE, Jonides J, Noll DC. Working memory for order and the parietal cortex: An event-related functional magnetic resonance imaging study. Neuroscience. 2006;139(1):311–316. doi: 10.1016/j.neuroscience.2005.04.071. [DOI] [PubMed] [Google Scholar]
- Martin A. The representation of object concepts in the brain. Annual Review of Psychology. 2007;58:25–45. doi: 10.1146/annurev.psych.57.102904.190143. [DOI] [PubMed] [Google Scholar]
- McMillan CT, Clark R, Moore P, Devita C, Grossman M. Neural basis for generalized quantifier comprehension. Neuropsychologia. 2005;43(12):1729–1737. doi: 10.1016/j.neuropsychologia.2005.02.012. [DOI] [PubMed] [Google Scholar]
- McMillan CT, Clark R, Moore P, Grossman M. Quantifier comprehension in corticobasal degeneration. Brain and Cognition. 2006;62(3):250–260. doi: 10.1016/j.bandc.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Murray R, Neumann M, Forman MS, Farmer J, Massimo L, Rice A, et al. Cognitive and motor assessment in autopsy-proven corticobasal degeneration. Neurology. 2007;68(16):1274–1283. doi: 10.1212/01.wnl.0000259519.78480.c3. [DOI] [PubMed] [Google Scholar]
- Papafragou A, Schwarz N. Most wanted. Language Acquisition. 2005;13:207–251. [Google Scholar]
- Piaget J. Genetic epistemology. New York: Columbia University Press; 1970. [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A Magnitude Code Common to Numerosities and Number Symbols in Human Intraparietal Cortex. Neuron. 2007;53(2):293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Riley DE, Lang AE. Clinical diagnostic criteria. Philadelphia: Lippincott, Williams, and Wilkins; 2000. [Google Scholar]
- Simon O, Mangin JF, Cohen L, Le Bihan D, Dehaene S. Topographical Layout of Hand, Eye, Calculation, and Language-Related Areas in the Human Parietal Lobe. Neuron. 2002;33(3):475–487. doi: 10.1016/s0896-6273(02)00575-5. [DOI] [PubMed] [Google Scholar]
- Small DM, Gitelman D, Simmons K, Bloise SM, Parrish T, Mesulam MM. Monetary Incentives Enhance Processing in Brain Regions Mediating Top-down Control of Attention. Cereb Cortex. 2005;15(12):1855–1865. doi: 10.1093/cercor/bhi063. [DOI] [PubMed] [Google Scholar]
- Small DM, Gitelman DR, Gregory MD, Nobre AC, Parrish TB, Mesulam MM. The posterior cingulate and medial prefrontal cortex mediate the anticipatory allocation of spatial attention. NeuroImage. 2003;18(3):633–641. doi: 10.1016/s1053-8119(02)00012-5. [DOI] [PubMed] [Google Scholar]
- Smith EE, Jonides J. Storage and executive processes in the frontal lobes. Science. 1999;283:1657–1661. doi: 10.1126/science.283.5408.1657. [DOI] [PubMed] [Google Scholar]
- van Benthem J. Essays in Logical Semantics. Dordrecht, the Netherlands: D. Reidel Publishing Company; 1986. [Google Scholar]
- Watanabe D, Huber L. Animal logics: Decision in the absence of human language. Animal Cognition. 2006;9:235–245. doi: 10.1007/s10071-006-0043-6. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES, Goddard S. Number sense in human infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]