Probabilistic models in human sensorimotor control

Abstract

Sensory and motor uncertainty form a fundamental constraint on human sensorimotor control. Bayesian decision theory (BDT) has emerged as a unifying framework to understand how the central nervous system performs optimal estimation and control in the face of such uncertainty. BDT has two components: Bayesian statistics and decision theory. Here we review Bayesian statistics and show how it applies to estimating the state of the world and our own body. Recent results suggest that when learning novel tasks we are able to learn the statistical properties of both the world and our own sensory apparatus so as to perform estimation using Bayesian statistics. We review studies which suggest that humans can combine multiple sources of information to form maximum likelihood estimates, can incorporate prior beliefs about possible states of the world so as to generate maximum a posteriori estimates and can use Kalman filter-based processes to estimate time-varying states. Finally, we review Bayesian decision theory in motor control and how the central nervous system processes errors to determine loss functions and optimal actions. We review results that suggest we plan movements based on statistics of our actions that result from signal-dependent noise on our motor outputs. Taken together these studies provide a statistical framework for how the motor system performs in the presence of uncertainty.

1. Introduction

With over a century of intensive research on the control of human movement it is illuminating to ask how well we are doing elucidating the principles that govern movement. One way to assess progress is to examine how well we can build machines that emulate human skills. Taking the game of chess, we can pit a grandmaster against the best chess computers in the world and usually the computer will win. In fact, if the computer were to play the entire population of the world perhaps only a handful of people would be able to ever win a single game. Therefore, when compared to the majority of players this problem is effectively solved. However, if we consider the skills of piece dexterously manipulating a chess it is clear that if we pit the best robots of today against the skills of a young child, there is no competition. The child exhibits manipulation skills that outstrip any robot. Why is choosing where to move a chess piece so much easier than actually moving it? The answer may lie in the algorithms required to achieve each task. In the case of determining which piece to move where, the algorithm is obvious even to a child - look at all possible moves to the end of the game and choose the one that ensures you win. While the algorithm is clear its implementation is far from straightforward. The number of moves clearly exceeds the ability of any computer to enumerate. However, with the dramatic increases in computer speed and some shortcuts it has been possible to approximate such an algorithm. However, when it comes to the problem of skilled movement the algorithm is simply not known. Unlike the game of chess where the state of the board and the consequences of each move are known, the control of movement requires interaction with a variable and ever-changing world.

The signals which the brain has access to when perceiving the world and acting upon it are not discrete signals such as the location of a pawn on the chess board, but analogue signals which the brain represents with its digital code. This transformation from analogue to a digital code limits resolution and, in addition, many of the properties of neural transduction and synaptic interaction add a great deal of noise to these signals (Barlow, Kaushal, Hawken, & Parker, 1987). This noise, that is unwanted disturbance on the signal, makes the problems of perception and action computationally difficult. For example, if we bought a motor for a robot with the noise properties of our motor system - coefficient of variance of around 6% (Hamilton, Jones, & Wolpert, 2004) - we would send it back saying it is too noisy for our use. To what extent will solution to robotics come from hardware or from software? We would argue that it will be software. For example, on the sensory side even people who have lost all their proprioceptive sense, while being far from as skilled as normal participants, are nevertheless able to control movements in a feedforward manner better than robotic devices (Cole, 1995).

While there are many factors that make motor control hard in a noise-free system, such as nonlinearities and long time delays, noise is one area in which there have been significant advances in our understanding of how the brain may deal with noise and underlying principles have recently begun to emerge. In this review we will focus on the issue of how the brain may minimize the negative features of noise within the framework of Bayesian decision theory.

Bayesian theory is named after an 18th century English Presbyterian minister named Thomas Bayes. During his lifetime he published two works, of which only one dealt with mathematics in which he defended the logical foundation of Isaac Newton’s methods. However, after Bayes death, his friend Richard Price found a mathematical proof among Bayes’ papers and sent it to the Editor of the Philosophical Transactions of the Royal Society stating “I now send you an essay which I have found among the papers of our deceased friend Mr. Bayes, and which, in my opinion, has great merit. . ..”. The paper was published posthumously in 1764 as “Essay towards solving a problem in the doctrine of chances.” In the latter half of the 20th century Bayesian approaches have become a mainstay of statistics and a more general framework has now emerged, termed Bayesian decision theory (BDT) (Cox, 1946; Freedman, 1995; Jaynes, 1995; MacKay, 2003).

The application of BDT to neuroscience has provided a framework for how the brain deals with noise and ambiguity. It is important to distinguish two different forms of uncertainty. The first is inherent ambiguity that arises not because of noise but because often there are situations in the world which truly can have different interpretations. For example, the world has a three dimensional structure yet the first stage of vision is to project the three-dimensional image onto a two-dimensional retina. A two-dimensional image is consistent with an infinite number of three-dimensional worlds and therefore the stimulus is inherently ambiguous (Yuille & Kersten, 2006). The second form of uncertainty is signal imprecision. This comes about through structural constraints such as the limit in receptor density and the analogue-to-digital conversion necessary to code stimuli in neurons that spike. In addition, noise at various processing stages limits the precision of perception and noise in the motor outputs limits the precision with which we can control our limbs. BDT provides a framework to deal with both sources of uncertainty.

BDT consists of two components. The first, Bayesian statistics, is a process of making inferences based on uncertain information. Within this framework probabilities are used to represent the degree of belief in different propositions. Therefore, P(A) would be our belief in proposition A and the strength of the belief is assigned a value between 0 and 1, with 0 being a proposition we are certain is untrue and 1 being a belief we are convinced about. For example, P(all ravens are black) might be assigned a value of 0.95. The second part of BDT is decision theory that aims to select optimal actions based on our inferences. In this review we will consider these two parts of BDT in turn.

2. Bayesian statistics

In Bayesian statistics there are two important quantities, unobserved parameters (θ) and observed data (s). For example, when we fit a line to data in linear regression, the parameters of our system are assumed to be the intercept, slope and variance (noise). The observed data is the pairs of (x, y) we are given as data points. In vision the parameters might be the object identity, whether it is an apple or orange, and the observed data might be the activity of the ganglion cells taking information from the retina. In terms of localizing our hand in space, the parameters are the hand’s actual location and the observed data would be the relevant sensory input from proprioception and vision. An important concept is that the brain never has direct access to the true parameter values but only has access to the data from which it makes inferences.

A natural question is: how are the unobserved parameters and observed data related? The key idea is that the latter depends on the former and in fact there are generative models which will allow us to produce (generate) artificial data given a particular setting of the parameters. For example, in linear regression if we have specified the parameters (slope, intercept and variance) we can generate data y for any point x by using the intercept and slope to calculate the mean response and then drawing data from the Gaussian distribution with specified variance around that point. Importantly, this is a probabilistic model which will not just generate data on the line (that would not look like the data we used to fit the model) but would generate data probabilistically. Similarly, we can think of a generative model which generates ganglion cell activity based on a visual image, or generates sensory inputs based on our outgoing motor command.

2.1. Maximum likelihood estimation (MLE)

Assuming we have a generative model, we can ask how probable is it that we observe a particular data set. Therefore, we can calculate the probability of generating the entire data set that we have observed for a particular parameter setting. This is given by P(s|θ), which is the probability of the data given (the vertical line “|” is shorthand for “given”) a particular parameter setting. This is termed the Likelihood. Given such a model we could choose to believe the parameters that makes the data the most likely. This is termed maximum likelihood estimation (MLE), choosing the parameters which make the observed data most likely. In recent years is has been shown that in several situations humans generate such a MLE estimate when confronted with several sources of information (Ernst & Banks, 2002; Jacobs, 1999).

To understand how to apply such a model we can consider a case in which there is a true parameter setting for some attribute such as the location of an object, θ, and we get two sensory inputs s₁ and s₂ from two different modalities (such as the location of an object given by vision and by proprioception). We would like to find the MLE parameter setting of θ, that is the setting that maximizes the probability of getting the two sensory inputs P(s₁, s₂|θ). If we assume that the two modalities are independent, then this corresponds to the product of the probability of each modality alone P(s₁|θ)P(s₂|θ). We can consider each sensory modality as representing the true value of the stimulus θ corrupted by noise: s₁ = θ + ε₁ where ε₁ is normally (Gaussian) distributed with zero-mean and variance ${\sigma }_1^2$ (similarly for s₂). We can then derive a simple analytic solution to the optimal integration of the two inputs given the variances of each: ${\sigma }_1^2$ and ${\sigma }_2^2$. Specifically the optimal estimate of θ is a weighted average of the two sensory inputs ws₁ + (1 - w)s₂ where $w={\sigma }_2^2∕({\sigma }_1^2+{\sigma }_2^2)$. The variance of this estimate is given by ${\sigma }_1^2{\sigma }_2^2∕({\sigma }_1^2+{\sigma }_2^2)$, which is always less than the variance of either modality in isolation - therefore combining is always less modalities or cues is always beneficial. This says that we should optimally combine two sources of information about a single parameter based on their relative reliabilities.

To test this model of optimal integration several studies have examined how we estimate properties of the world based on single modalities and how we estimate the same parameter when we have multiple modalities available (for a review see Ernst & Bulthoff, 2004). For example, we can estimate the size of an object based on vision alone, touch alone or if we can simultaneously see and touch the object, based on a combination of vision and touch. By examining touch and vision in isolation it is possible to estimate the variability of the estimation process based on a single modality. This variability can be used to estimate the variance of the noise in each modality (${\sigma }_1^2$ and ${\sigma }_2^2$ described above). Based on the estimates of the noise in the visual and touch modalities it is possible to predict the optimal weighting (w) of the two modalities when they are presented simultaneously. In addition to the weighting, the variability of the combined estimates can also be predicted. This can then be compared to the empirically estimated weighting and variance. In just such a visual-haptic size estimation task it has been shown that the empirical weighting and variability is very close to those predicted by an optimal integration model (Ernst & Banks, 2002). Moreover, in a wide range of tasks it has been found that humans demonstrate such optimal combination of cues. For example, recent studies have shown that we are close to optimal when we combine visual and auditory information to estimate the position of a stimulus (Alais & Burr, 2004), combine visual texture and motion or stereo cues into a single depth estimate (Hillis, Watt, Landy, & Banks, 2004; Jacobs, 1999; Knill & Saunders, 2003), combine proprioceptive information about the location of our hand with visual information of the hand itself (Van Beers, Sittig, & Denier van der Gon, 1996; Van Beers, Sittig, & Gon, 1999), or estimate the position of our hand and the configuration of their joints (Sober & Sabes, 2005). Moreover, it has recently been shown that the optimal use of unaligned sensory information can explain movement drift in the absence of vision (Smeets, Van den Dobbelsteen, De Grave, Van Beers, & Brenner, 2006). All these results suggest that we have knowledge about the variability in our different sensory modalities and can thereby combine different modalities together in a statistically optimal fashion.

While the above studies have mainly examined estimating a single dimensional parameter, such as the width of an object, other studies have examined multi-dimensional estimation. For example, when visual-proprioceptive integration for hand localization in two-dimensions was investigated it was found that vision is more precise for discriminations along the azimuth compared with depth. By contrast, proprioception (for some configurations of the arm) is more reliable for depth than azimuth (Scott & Loeb, 1994). The prediction from this asymmetric reliability is that the MLE should lie on a curved path between a visually and proprioceptively specified location of the hand and not, as one might naively assume, on a straight path, a prediction that has been confirmed (Van Beers et al., 1999). Moreover, this difference in precision plays into learning, in that if a discrepancy is introduced between vision and proprioception we would expect the less precise modality to adapt more. When a discrepancy is introduced in azimuth (e.g., by wearing prism glasses) vision dominated proprioception and the proprioceptive map changes more than the visual map. However, when a discrepancy is introduced in depth it was the visual map that moved more than the proprioceptive map as proprioception is more precise than vision in depth (Van Beers, Wolpert, & Haggard, 2002).

2.2. Maximum a posteriori (MAP) estimates

Maximum likelihood estimation aims to increase the likelihood P(s|θ), that is the probability of seeing the data given the parameters. However it is clearly the parameter θ we are interested in and we can ask instead what the most probable setting of the parameter given the data, that is what setting of the parameter maximizes P(θ|s), which is termed the posterior. How are the likelihood and posterior related? The answer to this is that they are related by a simple probabilistic relationship termed Bayes rule:

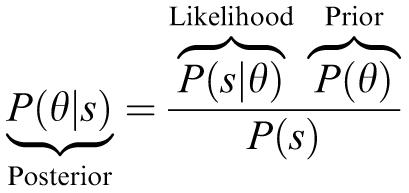This says that the posterior is proportional to the product of the likelihood and P(θ), which is termed the prior. The prior reflects how probable different parameter settings are a priori, independent of the observed data. The denominator P(s) is simply a normalization factor and does not change the relative probabilities of different parameter settings. In its most general sense there is nothing mystical about Bayes rule, it is simply a consistency relationship between probabilities that can be derived straightforwardly. For any setting of the data and parameters we can ask what is the probability that both settings occur, which is written as P(θ, s) where the comma is shorthand for “and”. This can be written in two alternative forms, that is the probability of one of the settings happening, e.g., P(θ), multiplied by the probability of the second setting given that the first has happened P(s|θ). This gives three expressions which are all identical: P(θ, s)= P(θ|s)P(s) = P(s|θ)P(θ). By discarding the left hand term and dividing both the others by P(s) we obtain Bayes rule as above. Although the form of Bayes rule may be intuitive, its implications are extensive and often counter-intuitive.

In the previous section we considered the use of MLE that is maximizing the probability of seeing the data given the parameters we wish to estimate. In the absence of prior knowledge (that is if P(θ) is the same for all values of θ) then the maximizing likelihood or the posterior is the same process. However, if we have knowledge about the possible parameters of the world, that is a prior, then we should use Bayes rule to estimate the posterior. The maximum of the posterior can be used to find the most probable parameter settings, at the peak of the posterior distribution, and this is termed the maximum a posteriori estimator (MAP).

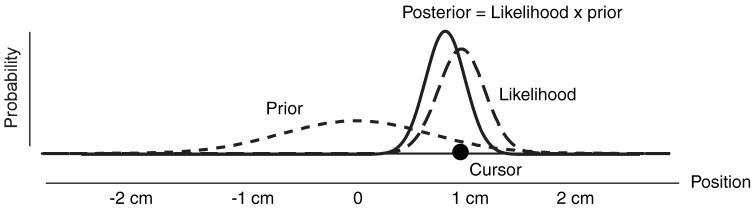
To provide some intuition for the Bayesian estimation process we can A experiment. cursor appears very briefly at a location along a straight line and a participant’s task is to point accurately to the location. Because the cursor presentation is very brief there is uncertainty from the visual system which we can consider noise. Therefore, if the cursor appears at location 1 cm (Fig. 1), then this is the most probable location at which it will be seen. But because of noise there is some probability that the participant will see it at 0.9 or 1.1 cm. If we assume Gaussian noise, the probability of the cursor being at different locations given it is seen at 1 cm (the likelihood) is represented by the thick dashed curve and therefore the MLE estimate is for the participant to report the location at which the cursor is seen. However, consider that over many trials the cursor does not appear uniformly across the line but has some distribution of locations, such as Gaussian centred on 0 with standard deviation 1.0 cm (thin dashed curve). Should that change the participant’s strategy? Bayes rule is clear on this in that this will change the posterior and therefore the location estimate. Consider the situation in which the participant sees the cursor at 1 cm. As there is noise in the visual system it is possible that the true location is 0.9 cm with a visual error due to noise of 0.1 cm or it could be that the true location is 1.1 cm with a visual noise of -0.1 cm. A visual error of +0.1 or -0.1 cm is equally likely. However, because the prior distribution (thin dashed line) of the cursor locations is Gaussian, a true location of 0.9 is more likely than 1.1 cm. Therefore it is more probable that the visual appearance of 1 cm is made of a 0.9 cm true location with a 0.1 cm error than a 1.1 cm true location with a -0.1 cm error. In fact the most probable location is found by multiplying the prior curve point-wise with the likelihood curve (and normalizing so that the area is 1.0). The peak of this posterior curve (solid line) is the MAP which will be biased towards the mean of the prior distribution. We can now consider the distribution of estimates under this strategy. If we were to look at all trials in which the true cursor location was at 1 cm, the Bayesian strategy would lead to an estimate that is biased towards the prior that is perhaps participants pointing to 0.9 cm. That means that participants on average miss the target which seems counter-intuitive. How can the optimal behaviour miss the target? The reason is that if the MLE estimate is used then participants will be on average on the target but their spread due to noise will be large. However, in the Bayes optimal solution, although participants show some bias, they will reduce their variance. In fact the Bayes solution reduces participants mean squared error, which can be decomposed into the sum of the bias-squared and variance. Therefore the Bayesian estimate optimally trades off bias for variance. This means that if you see someone perform a task and they miss the target on average it does not mean that they are not optimal. It may just mean they are optimal for statistics of the task you do not know about. Therefore response bias towards the mean of conditions in experiments (Poulton, 1979) may reflect optimal behaviour rather than some form of sub-optimal behaviour.

Fig. 1.

Bayesian estimation. A cursor appears briefly at locations on each trial defined by the prior probability (thin dashed line). Because of sensory noise the likelihood of the visual location is given by the thick dashed line. The application of Bayes rule leads to a posterior (solid line) whose peak is located between the peak of the prior and the peak of the likelihood. Note that the posterior is the likelihood multiplied point-wise by the prior and then normalised to have area 1.

Do participants perform in such a way in tasks which have prior statistics? Several studies have shown that this is the case. For example, in a task very similar to the cursor task described above participants indeed showed biases appropriate for MAP estimation when the cursor location had an underlying Gaussian distribution (Kording & Wolpert, 2004a). Moreover, when the noise was artificially increased in the visual feedback participants biased their reposes more to the prior as predicted. More recently it has been shown that such behaviour can be seen in force estimation tasks (Kording, Ku, & Wolpert, 2004), timing tasks (Miyazaki, Nozaki, & Nakajima, 2005) and pointing tasks in which independent measures of the likelihood and prior are possible (Tassinari, Hudson, & Landy, 2006). These results suggest that when people learn new tasks they learn not only the statistics of the task but also know about noise in their own sensory apparatus and can then combine the two in a Bayesian manner.

One question is to what extent all priors about the word are adaptable. In vision, it has long been realized that to interpret visual scenes priors are used. For example, when interpreting shape from shading, our prior is to assume that light comes from above (Ramachandran, 1988). However, even this prior has been shown to be adaptable after a period of feeling objects with the light shining from below (Adams, Graf, & Ernst, 2004). Moreover, several visual illusions, rather than being the result of some faulty neural processing may be Bayesian optimal interpretations of the world under uncertainty (Geisler & Kersten, 2002; Weiss, Simoncelli, & Adelson, 2002).

2.3. Dynamics Bayesian estimation: Kalman filter

The estimation processes in the previous sections have focussed on integration either of multiple modalities or of a prior with a modality at one point in time. However, it is often the case that we need to estimate parameters that evolve over time. For example, to control our body we need an estimate of the current state of the body, that is it configuration. As we move, the configuration changes continuously and we would like to have an estimate that is as accurate as possible. Two things make this estimation task particularly challenging. First, the transduction and transport of sensory signals to the CNS involve considerable delays. Second, the CNS must estimate the system’s state from sensory signals that may be contaminated by noise and may only provide partial information about the state.

To gain insight into how a state estimate of our body can be made, consider moving our arm and trying to estimate its state (configuration). If we simply relied on sensory inputs from our spindles, joint receptors and skin to estimate our arm’s configuration, our estimate would be delayed by around 100 ms. In addition, because the sensory signals are contaminated by noise, a single sensory snapshot would not be accurate. Averaging the sensory signals over a time window would make sense if the arm was not moving. However, if the arm moves then there is a trade-off between averaging to remove noise and keeping the time-window narrow enough that we do not include sensory inputs which are out of date. However, there is an additional valuable source of information, that is knowing the motor commands that have been applied to the arm. To use the motor command we must know the effect the motor command might have on the state of the arm. To do this requires an internal forward (predictive) model of the arm’s dynamics. Moreover, this predictive model can compensate for time delays by predicting ahead. This combination, using sensory feedback and forward models to estimate the current state, is known as an ‘observer’, an example of which is the Kalman filter (Goodwin & Sin, 1984). The major objectives of the observer are to compensate for sensorimotor delays and to reduce the uncertainty in the state estimate that arises because of noise inherent in both sensory and motor signals. For a linear system, the Kalman filter is the optimal observer in that it estimates the state with the least squared error. The Kalman filter is a recursive filter that maintains an estimate of the current state and updates this based on both the sensory feedback and motor commands. The Kalman filter is in fact a Bayesian estimator for time varying systems. Such a model has been supported by empirical studies examining estimation of hand position (Wolpert, Ghahramani, & Jordan, 1995), posture (Kuo, 1995) and head orientation (Merfeld, Zupan, & Peterka, 1999).

It may seem surprising that the motor command is used in state estimation. In fact the first demonstration of a forward model used a system which relies only on motor command to estimate state, that is the position of the eye within the orbit. The concept of motor prediction was first considered by Helmholtz when trying to understand how we localize visual objects (Helmholtz, 1867). To calculate the location of an object relative to the head, the central nervous system (CNS) must take account of both the retinal location of the object and also the gaze position of the eye within the orbit. Helmholtz’s ingenious suggestion was that the brain, rather than sensing the gaze position of the eye, predicted the gaze position based on a copy of the motor command acting on the eye muscles, termed efference copy. He used a simple experiment on himself to demonstrate this. When the eye is moved without using the eye muscles (cover one eye and gently press with your finger on your open eye through the eyelid), the retinal locations of visual objects change, but the predicted eye position is not updated, leading to the false perception that the world is moving.

3. Decision theory

In the sections above, in determining MLE and MAP estimates we have made it sound like the output of a Bayesian estimation process is the location of a target or identity of a visual object. However, that is not the case. In general the output of the Bayesian estimation process is the posterior probability, that is the probability of all possible states of the world (parameters) given the sensory input (observed data). Therefore, if we have estimated the probability for a target being at different possible locations, where should we choose to point? This is not a well-posed question unless we have some means of knowing how we will penalize errors. In different fields this has different names such as loss, cost, utility or reward. Here we will use loss, which represents how we will penalise errors of different magnitudes.

In the most general case decision theory deals with the problem of selecting the decision or action based on our current beliefs. The essence is to minimize the expected loss (or to maximize expected reward/utility) given our beliefs. This loss function quantifies the value of taking each possible action for each possible state (θ) of the world, L(action, θ). To choose the best action one simply calculates the expected loss for a given action, that is the loss averaged across the possible states weighted by the degree of belief in the state.

$$\sum _{\theta }L(\text{action},\theta )P(\theta \mid S)$$

where Σ denotes a summation over all possible states. We can then choose the action which has the smallest expected loss. The challenge in recent years has been to develop efficient and accurate approximations to the optimal solution. Recently, a new field of neuroeconomics (Glimcher, 2003) has emerged which considers neural processing within the framework of Bayesian decision theory.

3.1. Motor control loss functions

We can ask what the loss function is for motor control. In statistics, for example, when we fit a line to some data using linear regression we are choosing the loss as the sum of the squared vertical deviations of the data points from the line. Therefore this penalises the sum of squared error over all the data points. In statistics and machine learning it is typical to penalise squared errors, sometimes for good reasons but often because it is simple to solve for squared errors such as error² because this loss is differentiable whereas absolute error is not. However there is no a priori reason to believe that the brain will penalise the errors it makes in a similar way. To assess the brain’s loss function we need to give a choice of errors and examine which it prefers. For example, which is preferable when pointing to a target twice: a 2 cm error followed by a 2 cm error or a 1 cm followed by a 3 cm error? If the loss function is error² then the first scenario has total loss of 2² + 2² = 8 and the second has total loss 1² + 3² = 10 and the first scenario is better. If the loss function is absolute error then the first scenario has total loss of 2 + 2 = 4 and the second has total loss 1+3=4 and both scenarios are equally good. If the loss function is the square root of error $\left(\sqrt{\text{error}}\right)$ then the first scenario has total loss of $\sqrt{2}+\sqrt{2}\approx 2.8$ and the second has total loss $\sqrt{1}+\sqrt{3}\approx 2.7$ and the second scenario is better. So depending on the loss function we would want to distribute our errors differently.

Using this logic a recent experiment asked participants to operate a virtual pea shooter which spit out virtual peas at the rate of 10 per second (Kording & Wolpert, 2004b). However, although the participant could choose how to aim the pea-shooter at the target the distribution of peas was controlled by the experimenter. On each trial a new distribution was chosen and the way participants lined up the distribution with the target so as to be “on average as accurate as possible” was used to infer the loss function. This showed that for small errors participants penalised errors quadratically, that is as the square of error. However, for larger errors the loss function was less than quadratic and almost linear. These suggest that the many models of motor control which assume squared errors are a good approximation to the true loss. But unlike quadratic loss (such as in linear regression) humans are more robust to outliers.

Although when we point to a simple target we use an intrinsic loss function that is quadratic for small losses we can also learn to minimize losses that are externally specified. For example, when pointing to target configurations that have different reward and penalty regions (such as overlapping circular regions, one of which represents a numerical reward and the other a numerical penalty), it has been shown that subjects are able to choose their average pointing location so as to minimize the loss that accrues through the variability of pointing (Trommershauser, Maloney, & Landy, 2003).

3.2. Optimal actions

Finally, having focussed on using Bayesian estimation to make optimal inferences about the world in the face of uncertainty the final step is to choose an action based on these inferences. We have suggested that the final loss will be the squared error (for small errors) but this loss is not sufficient to specify how to move. This arises as tasks are usually specified at a symbolic level: I want to pick up a glass, dance or have lunch. However movement specification requires a detailed determination of the temporal sequence of action of the 600 or so muscles in the human body. There is clearly a gap between the task specification and the muscle activations. For example, if we consider perhaps the simplest of all tasks, reaching from one point in space to another, it becomes clear that this is a highly redundant task that can be achieved in infinitely many different ways. The duration of the movement can be freely selected from a very wide range and given a particular choice of duration the path and speed profile of the hand along the path can take on infinitely many patterns. Even selecting one trajectory still allows for infinitely many joint configurations to hold the hand on any given point of the path. Finally, even holding the arm in a fixed posture can be achieved with a wide range of co-contraction levels. Therefore there is a huge choice to be made for any movement.

Do we all choose to move in our own way? The answer is clearly no. Hundreds of studies have documented that we show very stereotypical behaviour both between repetitions within an individual and also between individuals (e.g., Morasso, 1981; Soechting & Lacquaniti, 1981; Viviani & Flash, 1995). This suggests that the end result of motor evolution or motor learning leads to stereotypical patterns of behaviour. How do these invariant patters relate to Bayesian decision theory? BDT is about being optimal and many theories for why these invariance patterns emerge rely on optimal control theory (which can be though a subset of BDT). In optimal control a cost is postulated that has to be minimized over a movement. For example, to model walking an energy cost has been shown to reproduce normal walking patterns (Pandy, 2001; Srinivasan & Ruina, 2006). However, for goal-directed movement of the eye, head and arm such energy costs have not been able to reproduce natural movements. Several deterministic costs have been proposed that depend on the kinematics (Flash & Hogan, 1985; Hogan, 1984) or dynamics of movement (Uno, Kawato, & Suzuki, 1989) and these have been successful in modelling some aspects of movements. These costs all have a common underlying cost in that they all penalize lack of smoothness in movement. However, these costs are somewhat arbitrary in that it is not clear why the brain should care about measures such as jerk or torque-change and they cannot generalise to different tasks or effectors, such as the eye.

What constraints are there on motor performance which could act on an evolutionary and learning timescale? One proposal is that it is noise in the motor output which is a fundamental limitation (Harris & Wolpert, 1998). When a desired temporal sequence of motor commands is produced the actual motor commands are a corrupted version of this, corrupted by noise (Clamann, 1969; Matthews, 1996). However, the level of noise depends on the size of the motor command. In this model it is assumed that the standard deviation of the noise increases linearly with the average level of the command giving signal-dependent noise (SDN) with a constant coefficient of variation (SD/mean) (Schmidt, Zelaznik, Hawkins, Frank, & Quinn, 1979; Schmidt, Zelaznik, & Frank, 1978). Therefore for large forces there will be large variability and for small forces there will be little variability. In examining isometric task this SDN has been observed and also modelled (Hamilton et al., 2004; Jones, Hamilton, & Wolpert, 2002) with recent results suggesting that there are both random and deterministic contributions to the changes in force variability with change in force level (Frank, Friedrich, & Beek, 2006). Given a particular sequence of motor commands, the actual commands still carry SDN and each time the same desired command is produced a different realization will be achieved. Therefore over repeated applications of the same desired commands the actual motor commands, and hence movement, will be different. As a result, a sequence of motor commands will lead to a probability distribution of movements in terms of final position, velocity, configuration, force, etc. However, as we have already discussed there are different ways to move, each with some specified desired motor command, and each of these different ways will have a different probability distribution of movement associated with it. Turning this logic around, it is apparent that the statistics of action can be controlled by choosing different ways to move. This provides a very general framework for motor planning. Given a particular task, such as reaching from one location to another or serving at tennis, the brain can specify which statistics of the task are important. For example, in a reaching movement it may be that we wish to minimize the mean squared error at the end of the movement. The problem of planning is then to choose a sequence of motor commands which optimizes these statistics pertinent to SDN. That is, the CNS finds the best way to move to minimize the negative consequences of SDN. For saccadic eyes movement (Harris & Wolpert, 2006), arm movement (Harris & Wolpert, 1998) and wrist movements (Haruno & Wolpert, 2005) it has been shown that this model reproduces many key features of the trajectory, duration and muscle activations.

Why were models based on smoothness so good at reproducing behaviour for limb movements? One reason is that in a low-pass inertial system such as the arm, if you want to be non-smooth it requires large motor commands to abruptly change velocity. However, such large commands inject an appreciable amount of SDN and therefore have a deleterious consequence in terms of accuracy. Therefore, to be accurate you need to be smooth but you do not need to measure smoothness. All that is needed is an adaptive system to update control parameters so as to minimize error and in the presence of SDN you will end up making movements which show stereotypical patterns of behaviour. The stereotype between individuals is likely to reflect similar dynamic properties of our bodies and similar noise processes.

In general movements are made up of a combination of feedback and feedback control. Therefore a new framework of optimal feedback control has been developed in which a cost based on both statistics and energy was considered in the presence of SDN (Scott, 2004; Todorov, 2004, 2005). Optimal feedback control can model a wide variety of movement behaviours and provide a framework for very general and flexible control.

4. Conclusions and future

The resolution of uncertainty plays a key part in both perception and action. As reviewed above, Bayesian decision theory BDT provides a framework to understand some unifying principle of the control of movement, from state estimation, through planning and error processing. The concept of optimally estimating states of the world and our own bodies and then determining optimal actions has had a wide-ranging impact on our understanding of empirical data. Although human behaviour in many instances seems to fit well with predictions made by BDT, the mechanisms which allow the nervous system to manipulate probabilities and learn the optimal estimates and behaviour is still far from clear. In coming years a key question will be how the brain represents and computes with statistical distributions, and indeed how rigorous these computations are or whether subtle approximations are employed. Moreover, although for simple systems we can simulate the optimal solutions, when it comes to nonlinear systems such as the human body we cannot yet solve optimal control problems which our brains seem to have solved. Understanding the computational mechanism that the brain uses in determining optimal control will be a major challenge.