Multi-finger ab- and adduction strength and coordination

Abstract

Simultaneous ab- and adduction of the fingers (finger spreading and finger squeezing) are fundamental to many prehension tasks. This is the first study to describe all finger forces during multi-finger ab-/adduction. Twenty one healthy subjects (12 female) produced maximal ab-/ adduction efforts against a stationary apparatus equipped with four independent multi-axis force transducers. Total force was computed as the sum of the absolute values of individual finger forces. The males were significantly stronger than the females, and adduction (squeezing) forces (42.4 N) were significantly greater than abduction forces (32.6 N). The relative contributions of individual fingers to the total force were consistent across the genders, implying that strength did not affect coordination. Ab-/adduction were coordinated symmetrically and multi-finger performance was not predictable from single finger strengths. The latter finding, in particular, indicates that multi-finger spreading/squeezing force measurements can provide information about hand function that cannot be derived from other tests.

Introduction

Finger ab- and adduction are used in almost all daily activities involving the hand. Reaching for a glass of water, the fingers abduct to facilitate a controlled grip (e.g. Santello et al. 1998). When people exert supination efforts on a vertically oriented object the index/middle and ring/little pairs of fingers generate oppositely directed tangential forces, i.e. the fingers are ‘squeezed’ (Zatsiorsky et al., 2003). While typing, fingers sequentially ab- and adduct to locate the correct keys (e.g. Soechting and Flanders 1997). Playing musical instruments (piano, guitar, etc.) also requires large abduction movements. The importance of finger ab-/adduction (AbAd) is further demonstrated in the clinical literature: compromised strength or coordination of the intrinsic hand muscles, common to a variety of pathologies including myelopathy hand (Ono et al. 1987), hand-arm vibration syndrome (Necking et al. 2003), etc., can cause an “awesome decrease” in overall hand function (Ketchum et al. 1978).

Current AbAd functional assessment protocols either manually test finger strength (e.g. Buschbacher 1997), measure individual finger strength separately (e.g. Matheson et al. 1970; Schreuders et al. 2000; Li et al. 2003), or examine only kinematic quality (e.g. Sandqvist and Eklund 2000). Instrumented measurement of multi-finger AbAd has, to our knowledge, not yet been performed. Simultaneous measurement of all finger forces can provide information that single-finger and kinematic studies cannot. For example, we know a priori that the ‘peripheral’ (Index and Little) fingers should produce force in opposite directions, but how do the ‘central’ (Middle and Ring) fingers behave?

Using a device recently developed specifically for multi-finger radial/deviation force testing (Pataky et al. 2007b), we herein quantify the strength of multi-finger ab-/adduction in healthy female and male subjects. Using various indices derived from the force data, we also describe finger coordination in the context of previous studies. We had no a priori hypotheses; this is a descriptive study of a novel task that addresses the context of the data post hoc using standard techniques from the finger biomechanics literature.

Methods

Design

Twenty-three right-handed subjects (12 females, age: 23.0 ± 4.2 years; 9 males, 25.0 ± 5.3 years) gave informed consent to participate in the study. Normal (F_n) and tangential (F_t) finger forces were measured at 50 Hz using multi-component force transducers (Nano-17; ATI Industrial Automation, Garner, NC, USA) and an apparatus designed for quasi-static AbAd tasks (Figure 1; Pataky et al. 2007b). Subjects pressed against finger ‘slot’ walls that were spaced 2 cm apart in the X direction. Y positions were set uniquely for each subject such that finger pad apexes were coincident with the center of the force transducers. Finger position relative to the slots was controlled by thick padding that also provided subject comfort. The whole device was fixed to a table with a vise and the subjects’ upper arm posture was fixed with their forearms parallel to the slot openings by an arm restraint (Figure 1b).

Figure 1.

Experimental apparatus, following Pataky et al. (2007). (a) The transducers, with 1.8×2×2 cm slots attached, were spaced 2 cm apart in the X direction, and their Y positioning was determined according to subjects' finger lengths (which were obtained from a photocopy of their right hand). The positive sense of normal (F_n) and tangential (F_t) forces are indicated. (b) Experimental hand posture and arm rest restraint. The arm padding was molded for a generic subject and a Velcro strap prevented lateral arm movements. Clamps were used to restrain the arm rest and apparatus (not pictured for clarity).

The two experimental AbAd tasks were to produce maximal voluntary contractions (MVC) by (a) “squeezing together” or (b) “spreading apart” the fingers against the slot walls. In addition to these multi-finger AbAd tasks, subjects also performed eight single finger AbAd tasks by producing MVCs with one finger in one direction (positive or negative X direction) while ignoring the other fingers. These single finger data are published elsewhere (Pataky et al. 2007a); we separated the data because of the unique nature of the current AbAd data which have not been previously reported. Two trials of each task were performed. The multi-and single-finger tasks were interspersed and trials were completely randomized.

Each trial lasted five seconds. Similar to other MVC experiments (e.g. Li et al. 2003) subjects were free to choose the manner in which they produced MVC; they tended to either ramp slowly to MVC or to generate MVC in a brief thrust. Post hoc analysis revealed that maximum force was not dependent on the time taken to generate that force (linear regression yielded a correlation coefficient of r² = 0.0025). No performance feedback was given. A mandatory 30 second rest period separated trials, and although longer rest periods were permitted, no subject exercised this option. No subject complained of pain or fatigue at any point during the experiment.

Of the two repetitions performed by each subject, the better trial was selected for analysis and the other trial was discarded. For the single-finger tasks, the better trial was the one associated with greater single-finger force in the required direction. For multi-finger squeezing and spreading tasks, the better trial was the one associated with greater strength as defined by Equation 1 (see below). Note that such single trial analysis is common for strength studies (e.g. Grant et al. 1996).

Two males (of originally 11 male subjects) were discarded from the current analyses because all fingers produced forces in the same direction. Specifically, subjects were rejected if the Index finger produced force in the same direction as the Little finger at the moment of peak force. In total, 42 trials were analyzed (the best spreading and squeezing trials for each the 21 subjects).

Performance indices

The following variables were calculated to characterize various strength and coordination phenomena: strength, force sharing, recruitment, force deficit, and functional hand center. Fingers are referred to here and throughout as: Index (I), Middle (M), Ring (R), and Little (L). All performance indices were computed only at the instant of maximum performance (as defined by Equation 1).

AbAd strength was determined at the instant at which the sum of absolute finger forces was maximal:

$$\mathit{strength}=\text{max}{\displaystyle \sum _{i=1}^4|}{(F_t)}_i|$$ (1)

where i indexes the four fingers. Although we acknowledge various difficulties with strength measurements for multi-finger AbAd (see Discussion), this strength measure was selected because it is most congruous with the task.

Force sharing was computed as the ratio between an individual finger force and the sum of all absolute forces:

$$\mathit{force}\mathit{sharing}=\frac{|{(F_q)}_i|}{{\displaystyle \sum _{i=1}^4|{(F_q)}_i|}}\times 100\%$$ (2)

where q is an arbitrary direction and i is an arbitrary finger. Absolute values are necessary in Equation (2) because the sum of signed forces may be zero in the tangential direction. Force sharing is typically calculated for pressing tasks (e.g. Li et al. 1998b) and reflects the distribution of force amongst the fingers. Rather than indicating relative finger strength, force sharing reflects biomechanical and neurophysiological interdependence in redundant effectors. Use of the term ‘sharing’ for ab-/adduction is somewhat obscure because fingers do not produce forces in the same direction. We nevertheless retain this terminology because in the tangential direction it can still refer to the total amount of force produced.

Recruitment reflects the proportion of a given finger’s strength capacity that was used during the multi-finger finger tasks:

$$\mathit{recruitment}=\frac{{(F_q)}_i}{{\left[{(F_q)}_i\right]}_{\mathit{MVC}}}\times 100\%$$ (3)

where [(F_q)_i]_MVC is the direction-dependent single-finger strength.

Force deficit (originally described by Ohtsuki 1981) is the complement to recruitment (recruitment + deficit = 1):

$$\mathit{deficit}=\frac{{\lfloor {(F_q)}_i\rfloor }_{\mathit{MVC}}-{(F_q)}_i}{{\left[{(F_q)}_i\right]}_{\mathit{MVC}}}\times 100\%$$ (4)

Force deficit indicates the strength capacity reserve of a given finger. Negative force deficit, or force ‘facilitation’, is possible if a finger produces more force in a multi-finger task than in its single finger task.

Note that even though Equation (2– Equation 4) are all percentages, their denominators are different. Force sharing (2) is expressed in terms of total multi-finger strength, while recruitment (3) and deficit (4) are expressed in terms of single finger strength.

In addition to force sharing, a second (and final) variable: ‘functional hand center’ was computed to further describe force distribution. It was calculated to be the real solution x of the polynomial:

$$\mathit{f}(\mathit{x})={\mathit{a}}_3{\mathit{x}}^3+{\mathit{a}}_2{\mathit{x}}^2+{\mathit{a}}_1\mathit{x}+{\mathit{a}}_0$$ (5)

where a_i are fitted coefficients, and x is the horizontal position (Figure 1) from which the given finger force originates. The positions are assumed to be constant at: x = 1, 2, 3, and 4 for the I, M, R, and L fingers, respectively. A third order polynomial is necessary to capture the arbitrary variations of the four data points.

The functional hand center represents an imaginary point of zero force from which the tangential finger forces ‘originate’. A value of 2.5, for example, would imply that the functional hand center is located in the center of the M-R inter-digit interval. A value of 2.6 indicates that the functional hand center lies 60% of the distance between the Middle and Ring fingers, and also a bias toward the Ring finger of 20% (0.1 is 20% of the distance from 2.5 to 3). Although we could have selected the actual experimental positions of the fingers (e.g. x = 2, 4, 6, and 8 cm), the dimensionless values of 1 through 4 permit a more immediate interpretation of the functional hand center’s position with respect to the hand.

Statistics

ANOVA, linear regression, and multiple linear regression were used to make statistical inferences (α= 0.05) regarding the main results. ANOVA employed the factors: GENDER (2 levels: female, male), DIRECTION (2 levels: abduction, adduction), and FINGER (4 levels: I, M, R, L). Only three levels of FINGER (I, M, R) were used for force sharing (Equation 2) because there are only three independent values. Note that ANOVA results for force sharing would be identical irrespective of the three finger levels chosen. Tests incorporated only main effect and two-factor interaction terms; due to the exploratory nature of this study we did not include three-way interactions. To allow for meaningful statistical comparisons across the two DIRECTIONS, individual finger force data for the adduction task were negated such that all data appeared to be abduction.

For tests involving variables that combined individual finger data (Equation 1 and Equation 5), only GENDER and DIRECTION were used as factors. A fourth factor: COMPONENT (2 levels: normal, tangential) was added to the model for recruitment and deficit analyses which compared F_n to F_t. All statistical analyses were conducted using the Statistics Toolbox of MATLAB 7.3 (The MathWorks Inc., Natick, MA, USA).

Results

Strength

Example data (Figure 2) show the typical time course of force development. F_t increased over an interval of 1.1 s (2.4 ± 1.3 s across subjects), and then ramped back down to zero force within the allotted 5 s. The I finger tended to produce force in the opposite direction to the other three fingers throughout the trial. There was close to zero net F_t, showing that the subject nearly balanced forces even though this was not a mechanical requirement. Substantial F_n was observed, and the peripheral (IL) fingers dominated the central (MR) fingers in both F_n and F_t magnitude. Statistical analyses of these and other trends appear in the paragraphs that follow.

Figure 2.

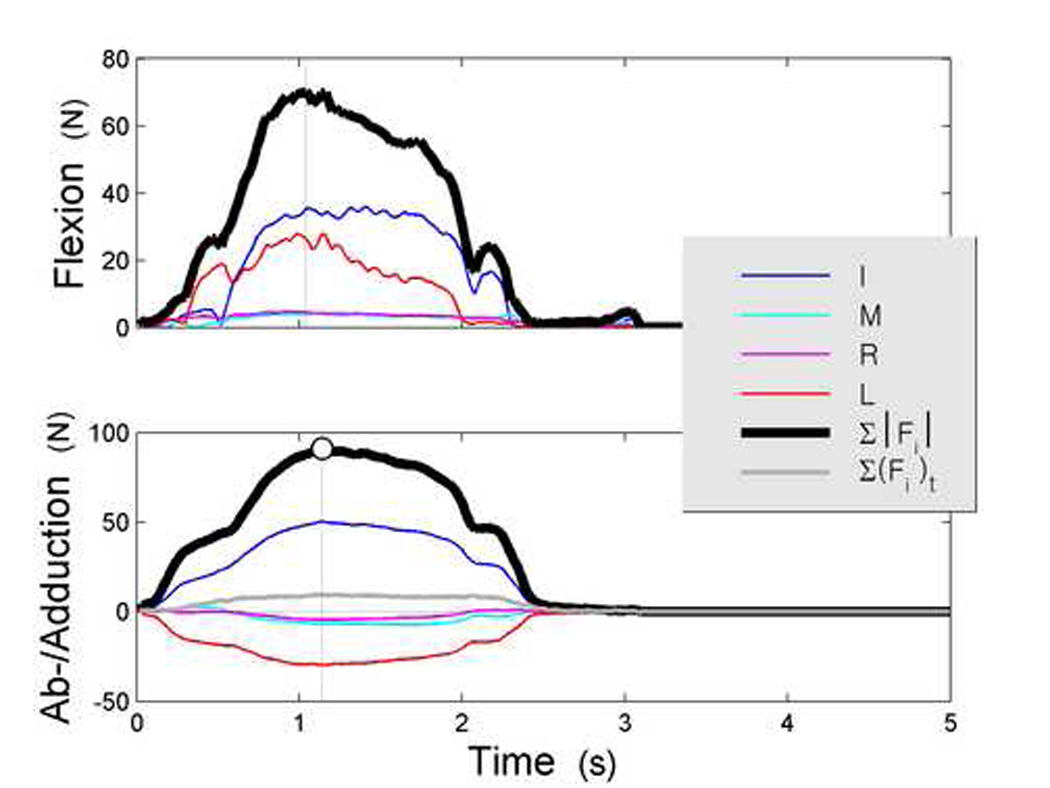
Typical trial (adduction). The top and bottom panels respectively illustrate normal (F_n) and tangential (F_t) force time series. Presented are the four fingers: Index (I), Middle (M), Ring (R), and Little (L), as well as the sum of the absolute finger forces (∑|F_i|) and the net tangential force (∑(F_i)_t). Tangential force signs correspond to the global X direction (see Figure 1a); the data above show that the the MRL forces opposed the I force throughout. Since normal forces can act in only one direction net force is not plotted in the top panel (i.e. ∑|F_i|_n = ∑(F_i)_n). The instant of strength measurement, maximum absolute F_t, is indicated by a large marker and a vertical line.

AbAd strength was measured to be on the order of 40 N (Table 1). Adduction was stronger than abduction by an average factor of 1.3, and the males were, on average, 1.5 times stronger than the females. These trends were confirmed by ANOVA, which found significant effects of both GENDER (p<0.001) and DIRECTION (p=0.018). No interaction was found (p=0.693).

Table 1.

Multi-finger ab-/adduction strength; the sum of the absolute finger forces (units: N). Flexion (F_n) and Ab-/Adduction forces (F_t) are presented separately. Here and elsewhere parentheses indicate standard deviations.

	Abduction		Adduction
	Fn	Ft	Fn	Ft
♀	11.7 (7.7)	26.6 (4.8)	16.3	35.0 (9.6)
♂	14.8 (21.8)	40.7 (14.1)	14.5 (28.0)	52.3 (20.7)

Single finger strength was positively correlated with but generally a poor predictor of AbAd strength; multiple linear regression with finger strengths as independent variables yielded a squared correlation coefficient of r²=0.36 (p<0.001) across all subjects. For this regression analysis, the direction-dependent single finger strength data were sign-paired to the multi-finger AbAd force data. For example, the radial deviation strength of the Index finger was used when the Index finger radially deviated (i.e. the multi-finger abduction task). The four collected independent variables (one per finger) were then used to regress on a single dependent variable: AbAd strength. At the individual finger level, positive but generally poor correlation with AbAd strength was observed (Figure 3). When the regressions were re-performed on GENDER-separated data, males exhibited higher correlation coefficients for the Index and Middle finger strengths with adduction strength (r² = 0.75 and 0.37, respectively) but all other regressions yielded r²<0.20 (Figure 4). Using the absolute values of the residuals from the regressions, ANOVA found main effects of GENDER (p=0.001), but not of DIRECTION (p=0.247) or FINGER (p=0.919). Of the interaction terms, only the GENDER×DIRECTION interaction effect reached significance (p<0.001) and the other terms were greater than p = 0.850. The data imply that ab-/adduction strength is generally not predictable from single finger strength.

Figure 3.

Relation between single finger and AbAd strengths for all 21 subjects; genders pooled. The single finger strength data are unique for each finger (Index – I, Middle – M, Ring – R, and Little – L) and each direction (ab-, adduction). Linear regression lines and squared correlation coefficients (r²) are also shown. All panels have the same scale.

Figure 4.

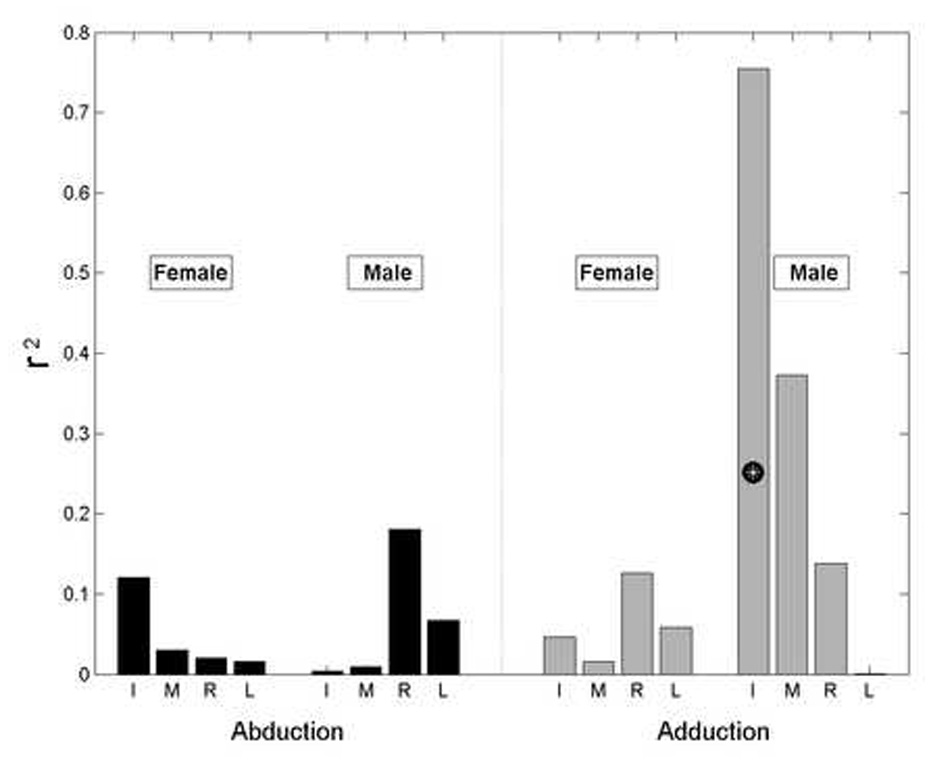
Squared correlation coefficients (r²) between single finger strength and AbAd strength. The r² values were calculated separately for females (N=12 data points) and males (N=9). White asterisks indicate statistical significance (p≤0.05).

Coordination

The finger forces recorded at the instant of maximal performance (Equation 1) are presented in Table 2a. Since relations among finger forces are relevant to coordination but finger forces themselves are not, no statistical tests were performed on these absolute force data. Note that the absolute values of the data in Table 2a do not sum to the values in Table 1; this is because the Table 2a means were computed from signed force magnitudes.

Table 2.

Individual finger forces at the instant of strength measurement.

			Abduction				Adduction
			I	M	R	L	I	M	R	L
(a)		♀	−11.1	2.1	3.8	7.3	16.5	−1.7	−3.8	−10.0
			(4.1)	(5.2)	(1.4)	(2.3)	(7.0)	(5.3)	(2.2)	(3.9)
		♂	−16.4	5.8	7.2	10.2	22.4	−2.3	−6.6	−18.0
			(6.5)	(8.3)	(5.5)	(6.3)	(14.1)	(7.6)	(2.2)	(7.8)
(b)		♀	41.6	17.2	14.3	26.9	46.1	13.9	11.0	28.9
			(12.9)	(12.8)	(4.5)	(5.9)	(12.9)	(7.8)	(6.1)	(10.1)
		♂	44.6	15.1	15.5	24.8	40.8	10.0	14.5	34.6
			(19.9)	(14.0)	(9.8)	(13.2)	(13.2)	(10.3)	(7.9)	(7.5)
(c)		♀	55.7	37.3	53.9	63.3	81.9	25.2	39.3	61.5
			(26.7)	(28.8)	(16.9)	(21.7)	(37.9)	(13.7)	(24.2)	(19.9)
		♂	65.1	27.4	50.5	51.6	63.7	17.3	42.1	80.4
			(47.1)	(27.6)	(32.9)	(41.5)	(28.8)	(20.9)	(18.5)	(19.2)
(d)		♀	13.0	8.2	13.2	19.3	13.2	20.4	28.9	18.2
			(13.8)	(8.4)	(14.9)	(13.3)	(15.5)	(20.4)	(22.2)	(16.8)
		♂	16.2	12.2	12.2	26.6	22.2	12.2	27.6	33.6
			(8.3)	(9.2)	(18.0)	(16.1)	(27.1)	(12.3)	(20.5)	(30.9)

As force magnitude (Table 2a) is relevant to strength, force sharing (Table 2b, Equation 2) is relevant to coordination. The peripheral (I and L) fingers contributed, on average, 72.1 ± 27.9% to the total AbAd force, significantly more than half of the total force (p<0.001) as determined by a single sample t test. ANOVA found a main effect of FINGER (p<0.001), but no main effects of GENDER or DIRECTION (p=0.768, 0.340). No interaction terms reached significance (p>0.531). These results suggest that: (i) different fingers contribute differently to the total AbAd forces, and (ii) force sharing is symmetrical across the two movement directions.

Force recruitment (Table 2c, Equation 3) indicates the proportion of an individual finger’s strength that was used in the multi-finger AbAd tasks. ANOVA found a significant main effect of FINGER (p<0.001), but not of GENDER (p=0.566) or DIRECTION (p=0.851). Neither GENDER-based interaction term was significant (× DIRECTION: p=0.747, × FINGER: p=0.762), but the DIRECTION×FINGER interaction effect did reach significance (p=0.047). These results indicate that: (i) fingers recruited different proportions of their individual strength capacities, (ii) normalizing data by finger strength eliminates performance differences between genders, and (iii) adduction is associated with greater peripheral (IL) recruitment and lower central (MR) recruitment as compared with abduction. The latter result was confirmed with post-hoc two-sample t tests (p=0.031 and 0.017 for the peripheral and central fingers, respectively).

Force deficit is, by definition, the complement of recruitment (Equation 3, Equation 4) and thus statistical results are identical. Deficit data are presented here (Figure 5) to permit comparisons with previous studies. Negative force deficit, or force ‘facilitation’ was not observed in the central (MR) fingers, and was observed only infrequently in the L finger (4.8% of the 42 trials). The I finger, contrastingly, exhibited force facilitation in 14.3% of the abduction trials and 28.6% of the adduction trials.

Figure 5.

Force deficit (Equation 4); complementary to recruitment data (Table 2c). Data are pooled across GENDER because no GENDER-related terms reached significance in the ANOVA model for recruitment (p>0.566; see text). Error bars indicate standard deviations.

Normal force values were large, on the same order as the tangential forces (see Figure 2). Normal force recruitment (Table 2d) was, however, notably lower than tangential force recruitment. This was confirmed by four-way ANOVA with GENDER, DIRECTION, FINGER, and COMPONENT as factors; the only significant main effects were: FINGER and COMPONENT (p<0.001), and the only significant interaction effect was FINGER×COMPONENT (p<0.001). All other ANOVA terms failed to reach significance (p>0.136). Linear regression between normal and tangential forces at the instant of maximal performance reveal an average squared correlation coefficient of r² = 0.282 over eight comparisons (4 FINGERS, 2 DIRECTIONS). The statistical results suggest that: (i) Although normal forces were large, they were not as highly recruited as tangential forces, (ii) Normal forces and tangential forces are only weakly related at the instant of maximal AbAd force exertion.

Net AbAd forces (see Figure 2) were not mechanically required to be zero. Nonetheless subjects produced only small net forces (1.3 ± 11.9 N), indicating that we adequately controlled wrist involvement. Of the 42 observations, 76.2% were less than 10 N, and only 4.7% were greater than 15 N. Despite an apparent trend for males to generate greater net force than the females (Table 3), ANOVA failed to find significant effects of GENDER (p=0.933), DIRECTION (p=0.145), or GENDER×DIRECTION (p=0.172).

Table 3.

Net force exerted on the apparatus in the Ab-/Adduction direction (N). Positive net force is in the ulnar direction (see Figure 1).

	Abduction	Adduction
♀	2.0 (7.1)	0.96 (10.7)
♂	6.8 (15.9)	−4.5 (13.4)

The final variable we analyzed was the ‘functional hand center’; this variable represents the position from which the tangential forces ‘originate’. The average roots of the fitted polynomials (see Methods) were 1.70 (±0.51) and 1.92 (±0.50) for abduction and adduction, respectively, indicating that the functional hand center lay between the I and M fingers, biased toward the M finger by approximately 60% (Figure 6). ANOVA found no significant effect of GENDER (p=0.569), DIRECTION (p=0.143), or GENDER × DIRECTION (p=0.465).

Figure 6.

Functional hand center, genders pooled. Bars indicate average force data across all subjects (N=21); error bars indicate standard deviations. Vertical dashed lines indicate the functional hand center for the two AbAd directions as determined by fitted polynomials (see Methods). The abscissa lists the dimensionless x values used for polynomial fitting. Error bars indicate standard deviations.

Discussion

Strength

The multi-finger AbAd strength data show that males were significantly stronger than females, and that adduction was significantly stronger than abduction. The former result was expected (Matheson et al. 1970; Pataky et al. 2007a). The latter could not be predicted from Index finger anatomy: the Index finger has a radial interosseous with a greater moment arm (An et al. 1983) and greater physiological cross-sectional area (An et al. 1985) than the ulnar interosseous. The results could also not be predicted from the Index finger biomechanics literature. Strength measurements conducted on the Index finger confirm a tendency for greater abduction force (Li et al. 2003, Cruz et al. 2005), but in contrast with the current results Li et al. (2003) show that ab- and adduction forces become similar when also performing flexion.

The literature that reports data from other fingers agrees with the current findings: the non-Index fingers have been shown to be stronger in radial as compared with ulnar deviation (Matheson et al. 1970, Pataky et al. 2007a). We infer that the radial deviation strength of the non-Index fingers drives the difference between ad- and abduction strengths. Since multi-finger adduction is a grasping (as opposed to releasing) pattern it may have evolved to be stronger than abduction in the same way that flexion is stronger than extension (e.g. Li et al. 2003, Cruz et al. 2005).

The final strength-related finding was that there were very low central finger (MR) forces. Since MR recruitment was so low, we conclude that central finger strength does not limit AbAd performance.

Coordination

Despite strength differences between males and females, normalized forces eliminated coordination differences between genders as evidenced by both force sharing and recruitment data. This is non-trivial because it implies that AbAd, like finger flexion (Shinohara et al. 2003), obeys some fundamental control rule that is independent of a healthy individual’s capacity to produce force. It is also interesting that, although not mechanically required, subjects produced close to zero net force and exhibited similar locations of the functional hand center irrespective of strength. This suggests that the central nervous system imposes both constraints, and also strongly points to the existence of a single control scheme common to all individuals.

Considering coordination symmetry between ab- and adduction, the functional hand center was found to be in the same position, between the Index and Middle fingers and biased slightly toward the Middle finger, irrespective of whether the subject was abducting or adducting. We interpret the consistency in the functional hand center across GENDERS and DIRECTIONS to support the implicit hypothesis that ab-/adduction can be controlled using a single control variable. That is, the functional hand center represents a confluence of neural and biomechanical constraints and the controller need specify only the magnitude of ab-/adduction.

Force sharing was similarly unaffected by movement direction and is, importantly, not uniquely determined by the functional hand center. For example, the following two force sharing vectors yield the same functional hand center: [50% 0 0 % 50 ], [25% 25 % 25 % 25 %].

The observed coordination consistencies are reminiscent of the secondary moment hypothesis of Li et al. (1998b). The hypothesis states that finger flexion forces are coordinated to minimize the net moment about a functional hand axis. The close-to-zero net forces observed in the current study agree with this hypothesis: in the previously mentioned 1D vector system (see Methods: Performance indices), the analogy to a balanced moment system is a balanced force field. The current data also promote a second level interpretation of the hypothesis; since the AbAd forces can be summarized as emanating from a single point, the role of the hand axis may not just be a mechanical one. It may also represent a fundamental aspect of finger force control. That is, since the location of the functional hand center is completely unconstrained mechanically, that it is reliably reproduced implies a control constraint.

The one exception to the finding of symmetry across the movement directions was the DIRECTION×FINGER recruitment interaction effect; adduction was associated with greater peripheral (IL) recruitment and lower central (MR) recruitment as compared with abduction (p=0.047), which exhibited more evenly distributed recruitment. We consider this a minor asymmetry, considering especially the symmetry in force sharing, and thus attribute the finding to the difficulties associated with collecting single finger MVC data, particularly for the central fingers (Pataky et al. 2007a).

The current force deficit data are of the same order but show the opposite trend to the deficit data for multi-finger radial/ulnar deviation; when fingers act in the same direction rather than opposing each other (Pataky et al. 2007a). In particular, the central (MR) fingers exhibited high deficit during AbAd tasks, and low deficit during radial/ulnar deviation tasks. This can be explained simply by the much lower central finger forces employed during AbAd. The contrasting force and deficit data provide evidence that the two tasks (AbAd and radial/ulnar deviation) are coordinated differently.

The three encompassing coordination findings were thus that multi-finger AbAd coordination is: (a) independent of muscular strength, (b) symmetric between abduction and adduction directions, and (c) distinct from radial/ulnar deviation coordination.

Digression

Generalization of these findings to everyday submaximal tasks (e.g. holding a glass of water, manipulating tools, opening jars, etc.) should be done with caution since different strategies may be used to optimally solve the force requirements of these tasks. We also acknowledge that the current data set is limited by our strength definition (Equation 1); other strength measures could have been used. Imagine, for example, the case where the fingers are held together by a taut elastic band against which the subject abducts. In this case, a more functional representation of performance is tension in the elastic band. By extension, one could argue that it is only the difference between the Index and Little finger forces that are functionally related to AbAd, not the total force of all fingers as in the present study.

We emphasize, however, that our task, unlike the hypothetical elastic band task, kinematically constrained all fingers. Since all fingers had equal mechanical opportunity to transmit AbAd forces, we believe that our strength definition is appropriate to the current task. The definition should be reconsidered in a different task.

We also acknowledge a second limitation: that we have only assessed coordination at the instant of maximal performance. Attempts to analyze the evolution of our coordination indices through time series cross correlation were unsuccessful, yielding highly variable and non-significant results. The problem was that neither the force ramping style nor the net force was specified, so subjects had too much freedom in regions ‘far’ from the task maximum. It could be informative to examine sub-maximal AbAd coordination during controlled ramping as, for example, was done by Li et al. (1998b).

Finally, it may be useful to study the problem with a free object such that net AbAd force is more tightly constrained to be zero. Although the current net forces were close to zero, reduced variability in net force may reduce the variability of other performance indices and clarify results.

Summary

This study is the first to investigate the forces involved in multi-finger ab-/adduction. We found that multi-finger ab-/adduction is a unique task that reveals strength and coordination information that cannot be derived from other task data. The information derived from this functional task may be helpful to clinically identify and isolate muscle pathology.