Mass Transfer Model for Drug Delivery in Tissue Cells with Reversible Electroporation

Abstract

Reversible electroporation is the temporary permeabilization of the cell membrane through the formation of nano-scale pores that are transient defects in the membrane. These pores are caused by short electrical pulses, typically on the order of a few to several hundred microseconds that are delivered by electroporation electrodes inserted around the treated tissue. Reversible electroporation has become an important technique in molecular medicine. It is used to introduce macromolecules such as genes or anti-cancer drugs, to which the cell membrane is normally not permeable, into the cytosol. For optimal application of molecular medicine, it is important to be able to predict precisely the mass transfer in tissue during reversible electroporation. In this study, we introduce a first attempt at developing a macroscopic mathematical model for analyzing the mass transfer into cells during reversible electroporation of tissue. The model combines a macroscopic model of the electrical fields around electroporation electrodes with a new cells-scale model of electroporation-driven mass transfer and with a macroscopic mass transfer model in tissue. The model is illustrated for a situation typical to that in electrochemotherapy in which cancer is treated with reversible electroporation and a non-cell membrane permeant drug such as bleomycin.

Introduction

Molecular medicine often requires the introduction of specific molecules, such as gene constructs or (macro) molecular drugs, into specifically targeted cells in the body. Often, molecules have difficulty penetrating the cell membrane. These difficulties are caused by the molecule charge, molecular weight, hydrophilicity, or other physio-chemical properties [1]. This makes it impossible for several potentially useful drugs, e.g., bleomycin, to be efficiently used in treatment of cancer. Plasmids and genes are also examples of molecules that cannot enter the cell.

Tissue electroporation is a novel approach to introduce molecules and genes into the cells of specific areas of the body. It employs the ability of certain electrical fields to reversibly permeabilize the cell membrane in a process known as reversible electroporation. Electroporation is a phenomenon that makes cells permeable by exposing them to strong, rapid (microsecond scale) electric pulses [2]. The exact mechanism of this process is not yet fully understood. It is thought that the electrical field changes the electrochemical potential around a cell membrane and induces instabilities in the polarized bilayer lipid membrane of the cell. The unstable membrane then alters its shape, forming aqueous pathways that are possibly nano-scale defects (pores) through the membrane [3]. Mass transfer can now occur through these channels (pores), which in reversible electroporation persist for a period of a few seconds. Typically, in reversible electroporation, the permeabilization pulses are delivered on a time scale of microseconds, and the pores reseal on a time scale of seconds. Macromolecules in the extracellular space can enter the cells by diffusion during the time the pores are open.

Electroporation is commonly used in medicine and biotechnology for the introduction of non-permeable chemical species across the cell membrane, from small molecules such as fluorescent dyes, drugs and radioactive tracers to high molecular weight molecules such as antibodies, enzymes, nucleic acids, high molecular weight dextrans and DNA. The permeabilization state has been shown to persist, which implies that the molecules enter the intracellular space after the application of the electric pulse [4]. Once a cell is permeabilized, small molecules generally enter via diffusion. It should be emphasized that while diffusion probably occurs in small molecules such as anti-cancer drugs, much less is known about how electrically charged genes enter the cells during electroporation.

The study of the effect of electric fields on living cells dates back to the late 1960s [5, 6]. Dielectric breakdown of the cell membrane due to an induced electric field was first observed in the early 1970s [7–9]. The ability of the membrane to reseal was discovered separately during the late 1970s [10–12]. Neumann et al. and Wong and Neumann in 1982 were the first to demonstrate cell transfection in vitro through electroporation [13]. The use of electroporation to increase the permeability of the cell membrane in tissue was introduced by Okino and Mohri in 1987 and Mir et al. in 1991 who independently discovered that combining the electric pulses with an nonpermeant anticancer drug greatly enhanced the effectiveness of the treatment compared to either the electric pulses or the drug alone [14, 15]. Mir et al. soon followed with clinical trials that have shown promising results and coined the treatment electrochemotherapy [16]. Currently, the primary therapeutic in vivo applications of electroporation are; antitumor electrochemotherapy (ECT), which combines a cytotoxic non-permeant drug, bleomycin is the leading example, with permeabilizing electric pulses, electrogenetherapy (EGT) as a form of non-viral gene therapy, and transdermal drug delivery [17]. Bleomycin is a highly cytotoxic drug [18] that is used to kill cells during mitosis, as the cell divides. For this reason, it is used in chemotherapy to treat cancer tumors, whose cells divide much more frequently than benign cells. Bleomycin works by inducing breaks in the DNA which cause the cell cycle to arrest when it reaches mitosis, subsequently killing the cell [19].

The studies on ECT and EGT have been summarized in several publications [17, 20–23]. Most of the studies focus on demonstrating the feasibility of the various tissue electroporation techniques and determining the optimal electrical parameters for the application. Another paper summarized the results from clinical trials performed in five cancer research centers. Basal cell carcinoma (32), malignant melanoma (142), adenocarcinoma (30) and head and neck squamous cell carcinoma (87) were treated for a total of 291 tumors [24]. Electrochemotherapy is a promising method to locally treat tumors regardless of its histological type with minimal adverse side effects and a high response rate [25][21]. In a typical application of electrochemotherapy, bleomycin is injected at a certain concentration in the extracellular space of the tumor. Electroporation pulses are applied through electrodes that surround the malignant tissue and the hope is that the electrical field will permeabilize the cell membrane sufficiently for the drug to enter the cell and ablate the tumor.

Currently, the use of reversible electroporation in molecular medicine in tissue is developed through a methodology that employs systematic parametric studies and experiments. Since only a very narrow range of electrical parameters produce reversible electroporation, there has been a great deal of in vitro cell work to determine the optimal electric parameters required for reversibly electroporation. Researchers use the cell work as a baseline for developing electroporation protocols for in vivo tissue therapeutic applications. The outcome of electroporation protocols in tissue is evaluated either indirectly (i.e. evaluating the success or failure of a particular treatment) or directly (e.g. measuring the uptake of a nonpermeant molecules either non-invasively with DTPA and a gamma-camera [26], or invasively with fluorescent markers or Cr-EDTA), or topologically [17] as a function of the electroporation pulses. These results are than used optimize efficacy for particular clinical procedures. However, in order for tissue electropermeabilization to become routine in molecular medicine, there is a need for mathematical models that can predict the mass transfer process of molecules into cells in tissue during electroporation. Mathematical models have been developed to evaluate the electrical fields that occur during electroporation in tissue and then, to correlate the electrical fields with the outcome of the reversible electroporation procedure, as a measure for the mass transfer process that has occurred [27]. These models have become important in the study and practice of electroporation in tissue. Other models may be used to predict the mass transfer process during electroporation at the single cell level [28]. However, to the best of our knowledge, there are no complete models of the mass transfer during reversible electroporation in cells in tissue. Such models could support the design and analysis of protocols for molecular medicine. The goal of this study is to introduce a first order model for mass transfer during reversible electroporation. The use of bleomycin in electrochemotherapy is considered as a case study to illustrate the model

Methods

With bleomycin and electrochemotherapy in mind, we have developed a macroscopic mass transfer model of reversible electroporation. An important part in the macroscopic model is our use of existing models of formation of pores in the cell membrane during electroporation at the single cell level. In this particular study we use a single cell electroporation model that was recently introduced by Krassowska et al. [28]. The model describes the creation of pores during electroporation as well as their resealing, at a single cell level. In our model, we combine and solve simultaneously: a) a mathematical model of the electrical field in tissue during electroporation, b) the electrical field induced single cell permeabilization model, c) the mass transfer process at the single cell level and d) the macroscopic mass transfer diffusion process in the extracellular space during electroporation. The solution, obtained with the finite element technique, predicts the flux of drug molecules into the cells throughout the treated tissue. In the case of bleomycin, this can be directly translated to the probability of cell death and the optimal use of electrochemotherapy in the treatment of cancer.

In the model we have two electrodes that are used for electroporation. The electrical field that is induced by the electroporation pulse is obtained through the solution of the Laplace equation

$$\nabla ((\sigma +{\epsilon }_0\epsilon )\nabla \phi )=0$$ (1)

where φ is the electric potential, σ, is the extracellular conductivity, ε, is the relative permittivity (dielectric constant) and ε₀ is vacuum permittivity. The boundary conditions are defined on the electroporation electrodes, usually as the applied potential.

In typical applications, the distance between the electrodes is much larger and has a different length scale from the size of a cell. Therefore, even though the electrical field between the electrodes is generally non-uniform, we assume that at the single cell scale length, the field is locally uniform. The transmembrane potential V_m of a spherical cell in a uniform electrical field E, depends on the angle θ between the direction of the field and the normal to the point of interest in the membrane as depicted in Figure 1. Defining r as the radius of the cell modeled as a sphere we have [29]

Figure 1.

A single spherical cell in a uniform electrical field

$$V_m=1.5\mathit{rE}cos(\theta )$$ (2)

The theory of electroporation predicts that the pore formation is a function of the transmembrane potential. At the single cell level, pores are created differently in different parts of the membrane depending on the local transmembrane potential. Most of the pores are created at the poles, (θ =0 or π), where the highest transmembrane potential occurs while near the equator (θ = π/2 or 3π/2) where the transmembrane potential is very small, there are no pores at all. It is interesting to note that the Krassowska model predicts that the largest pores are created not at the poles, but rather near the border between the electroporated and non electroporated areas [28].

The number of pores in each part of the membrane is computed according to the Krassowska model using the pore density N which is following the differential equation:

$$\frac{dN}{dt}=\alpha e^{{(V_m/V_{ep})}^2}(1-\frac{N}{N_0{e}^{q{(V_m/V_{ep})}^2}})$$ (3)

where α is the pore creation rate coefficient (10⁹ m⁻²s⁻¹) V_ep is the characteristic voltage of electroporation (0.258V) N₀ is the equilibrium pore density for the membrane area at V_m=0 (1.5·10⁹ m⁻²) and q is an electroporation constant (q = 2.46).

In our model we assume that for each cell the number of pores in the membrane will determine the cell membrane permeability to the macromolecules. Therefore in our macroscopic model of mass transfer, we attribute to each cell at any location in the tissue a lumped value of permeability to drug which is proportional to the local value of the electrical field and the single cell pore formation model. Consequently, the permeability of the cells to the drug in different parts of the tissue depends on the local electrical field in that area. Typical to how bleomycin works, we assume in this case study that as the membrane becomes permeable to the drug, each cell is modeled as a mass sink. Once a drug molecule passes the membrane and enters the cytoplasm it binds to its target, and will no longer leave the cell, regardless of the extracellular concentration of the drug.

On the single cell level, we examine a spherical cell under a uniform electrical field. The number of pores increases significantly with the increase in the external electrical field. Since the electroporation pulses are in microseconds and several orders of magnitude shorter than the time it takes for the pores to reseal we assume that no molecules enter the cell during the short pulse time and that all of the mass transfer occurs from the end of the pulse until the pores reseal. In the single cell mass transfer analysis, we calculate the total area of the pores, A_p, from the number of pores per cell and the area of each pore:

$$A_p=\pi R_p^2·N_p$$ (4)

where N_p is the number of pores at the end of the electroporation pulse and is computed by integrating the pore density over the entire cell membrane surface:

$$N_p=\oint \mathit{NdS}$$ (5)

Shortly after the electroporation pulse ends, the pores start to reseal and their number decreases exponentially with a time constant of single seconds. Therefore when considering the post pulse mass transfer, we need to add a correction term which makes the area an exponentially decaying function of time:

$$A_p=\pi R_p^2·N_p{e}^{-t/\tau }$$ (6)

To obtain the amount of drug that enters a cell by diffusing through the aqueous pores across the cell membrane, we take the flux per area J times A_p. The concentration outside the cell is taken to be that of the extracellular space and the intracellular concentration is zero (according to our assumption of how bleomycin works). According to Fick’s law:

$$J=-P·(c_{ex}-c_{in})$$ (7)

where P is the permeability of the drug molecule through the membrane pores. There are currently no fully reliable values for the permeability of the electroporated cell membrane. As a first order assumption, for very large pores and very small molecules it could be approximated by the ratio of D, the diffusion coefficient and δ the membrane thickness P=D/δ. However, actual values depend on the size of the molecule and the interaction between the molecule and the pore so this upper limit may be very high compared to realistic scenarios. In this paper we show a parametric study analyzing a range of permeability values and their effect on the uptake of a drug.

The process of mass transfer happens in every cell in the tissue. When developing the model of macroscale mass transport in the tissue, we assume that the cells are infinitesimally small, and that the drug entering the cell can be modeled as a uniformly distributed reaction rate. We further assume, in this first order model, that the cells are uniformly packed in the tissue so that each spherical cell is contained in a cube whose edge is equal to 2r. Therefore the reaction rate for cells contained in a cube with a volume V₀=(2r)³ is:

$$R=J{A}_p/V_0$$ (8)

The concentration throughout the extracellular space is calculated from the diffusion equation

$$\frac{\partial c}{\partial t}-\nabla (D\nabla c)=R$$ (9)

This equation is solved subject to initial conditions, which are the initial concentration in the extracellular space, and boundary conditions, which we modeled as no mass flux.

Results and discussion

While the model developed is general, we implemented it in a particular case study involving the use of bleomycin in electrochemotherapy. In this case study we assume that electroporation is performed with two very long needle electrodes that are inserted into the treated tissue. This makes the problem two dimensional. The needle electrodes have a typical diameter of 1 mm and they are placed 14 mm apart. The electrodes deliver a 1 msec high voltage pulse of 1000 V that generates a large non uniform electrical field throughout the tissue. To calculate the electrical field at each point, we consider that there are no current sources in the tissue and make a first order assumption that the tissue is homogeneous.

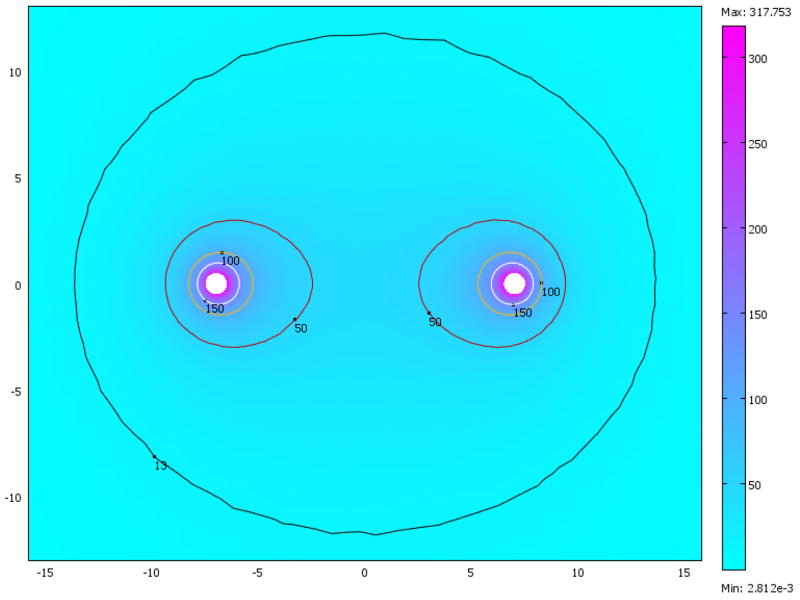
The parameters used to solve equation (1) were: σ = 1.2 S·m⁻¹ is the extracellular conductivity, ε = 72 is the relative permittivity (dielectric constant) and ε₀ is vacuum permittivity [30]. The boundary conditions were defined as a potential of 1000 V on one electrode and ground on the other electrode. The outer edges of the tissue, which are far from the electrodes and the region of interest, are assumed to be electrically insulating. The equation was solved using the finite element method with the code written in Comsol Multiphysics (version 3.3a, www.comsol.com). To verify that the solution converges and is mesh independent, we have tried two different mesh sizes. The solutions for both meshes match. The calculated electrical field for the smaller mesh is shown in Figure 2. It is evident that the highest fields, where the largest changes in electrical potential occur, are around the electrodes. A considerable field also exists between the electrodes and it drops swiftly as we move away from them.

Figure 2.

Magnitude of the electric field at different parts of the tissue in units of kV/m. Contours depict lines of equal field strength.

On the single cell level we examined a spherical cell with a radius of 50 μm, as in the model of Krassowska and Filev [28], under a uniform electrical field that in this case study ranges from 13 kV/m to 100 kV/m. In the model, fields above 100 kV/m are assumed to cause irreversible electroporation, which leads to cell death. Different sizes of pores are created at first as a function of the local transmembrane potential, but 2 μsec after the end of the pulse, all of them shrink to small pores (radius is R_p =0.8 nm) [28]. We assume that no molecules enter the cell during the pulse and that all of the mass transfer occurs from the end of the pulse until the pores reseal. We calculate the total area of the pores, A_p, from the number of pores per cell and the area of each pore with the radius given above. The number of pores, N_p, is calculated by a numerical solution of equations (3) and (5) and for the above mentioned parameters we use the results of [28].

Shortly after the electroporation pulse ends, the pores start to reseal and their number decreases exponentially with a time constant of about 1.5 seconds, as shown in equation (6). The diffusion coefficient D is assumed to be 10⁻⁴ mm² s⁻¹ which is reasonable for the case of bleomycin as well as many other molecules that have similar traits [31]. The initial concentration of the drug is c(t=0) = 5 μM = 5·10⁻¹² mole·mm⁻³.

The solution of Eq. (9) gives the drug concentration at every point in the tissue and how it evolves over time. This analysis was also carried out using Comsol with two different mesh sizes to verify convergence and mesh independence. Again, the solutions for both meshes match. The local concentration changes mostly due to the mass transfer of drug from the extracellular space into the tissue, where we assume that it binds to its target and disappears from the system. A secondary effect is the diffusion of the drug in the extracellular space. Figure 3 shows the changing concentration of a drug with permeability of P = 5·10⁻⁷ m/sec at different time points after the termination of the electroporation pulse. The results indicate which parts of the tissue are affected by the treatment and to what extent. We can also see how long the treatment takes and adjust accordingly parameters such as the electrical fields, initial drug concentration, electrode size and distance and more.

Figure 3.

Drug concentrations for different times after the electroporation pulse. a) t = 0.5 sec. b) t = 2 sec. c) t = 3 sec. d) t = 5 sec. Darker regions depict lower drug concentration.

This analysis also allows us to calculate the amount of drug that enters each cell. If we take bleomycin for example, it is highly toxic and a few hundred molecules that enter the cell are sufficient to cause cell death. As mentioned above, the change in local concentration is mostly due to the drug entering the cells, so at each point we calculate the average number of molecules that enter a cell in that small region, based on the change in concentration from the initial value. The drop in drug concentration in the cube with volume V₀ around a cell, is attributed to molecules flowing inside the cell. Since the concentration is given in moles/mm³, N the number of molecules per cell is

$$N=N_A(c(t=0)-c)V_0$$ (9)

where N_A is Avogadro’s number.

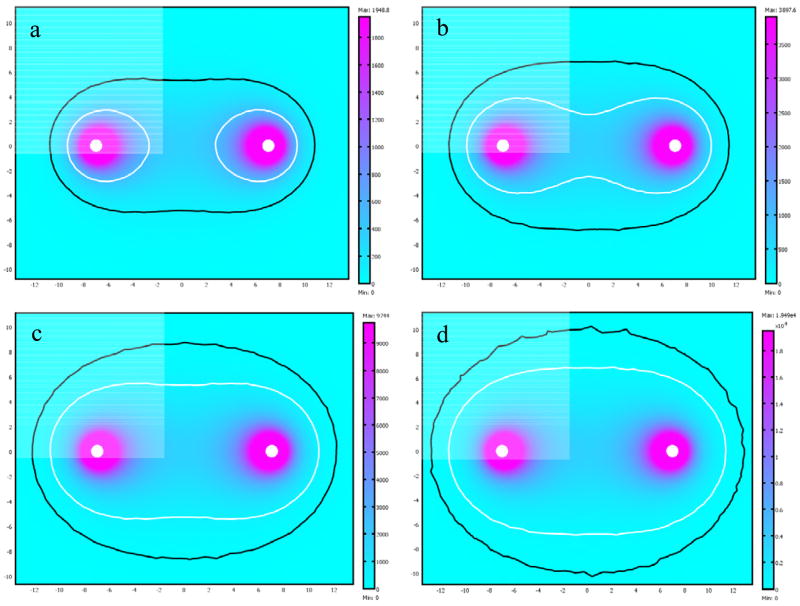
Figure 4 shows the average number of bleomycin molecules that enter the cell at different areas of the tissue five seconds after electroporation. The contours show the regions where cells go through cell cycle arrest and consequently die. The minimal number of molecules that is needed to induce cytotoxicity is 100 [18] and at 500 molecules per cell, around 70% of the cells are expected to die [19].

Figure 4.

Number of molecules that enter the cell in each part of the tissue for different permeability values. The bright line marks the area that will be ablated by bleomycin and the dark line marks the area that will show some effect. a) P = 10⁻⁷ m/sec b) P = 2·10⁻⁷ m/sec c) P = 5·10⁻⁷ m/sec d) P = 10⁻⁶ m/sec

Since the permeability changes for different drugs, due to the size of the molecule and the type of interaction between the drug and the membrane, we give the results for a range of permeability values from 10⁻⁷ m/sec to 10⁻⁶ m/sec. At the high end of the scale where the permeability is 10⁻⁶ m/sec, the affected area is practically the entire electroporated tissue. Even drugs with a higher permeability will not enter cells beyond this part of the tissue, simply because the electrical field there is too low to create pores in the membrane. On the other hand, molecules with permeability lower than 10⁻⁷ m/sec will not be able to enter the cells in significant numbers and would require a different electroporation protocol, such as, higher fields, or additional low voltage pulses that will keep the pores open for a longer time.

Conclusion

This study presents a first-order model of mass transfer during electroporation. The case study illustrates the value of such a model in designing optimal electroporation protocols. It is obvious that much more research and better models need to be developed for this important application. Electroporation is often more complex and the pulses employed are much more complex than in this example. Furthermore mass transfer of electrical species, such as genes may need a different model. Nevertheless, the primary goal of this study is to introduce the need for such studies and to roughly outline a way to develop such models.

Nomenclature

A_p

Area of pores, m²

c

Concentration, mol·m⁻³

D

Diffusion coefficient, m²s⁻¹

E

Electrical Field, V/m

J

Flux, mol·m⁻²s⁻¹

N

Pore density, m⁻²

N₀

Equilibrium pore density, m⁻²

N_p

Number of pores

P

Permeability, m·s⁻¹

q

Electroporation constant

r

Radius of a cell, m

R

Reaction rate, mol·m⁻³s⁻¹

R_p

Radius of pores, m

t

Time, s

V₀

Volume of a cube surrounding a cell, m³

V_ep

Characteristic voltage of electroporation

V_m

Transmembrane potential, V

α

pore creation rate coefficient, m⁻²s⁻¹

ε₀

vacuum permittivity

ε

Dielectric constant

σ

Conductivity, S·m⁻¹

φ

Electric potential, V