Motility of Escherichia coli cells in clusters formed by chemotactic aggregation

Abstract

Cells of Escherichia coli under conditions of certain cellular stresses excrete attractants. Cells of chemotactic strains respond to these excreted signaling molecules by moving up their local concentration gradients and forming different types of stable multicellular structures. Multicellular clusters are the simplest among these structures. Fluorescence microscopy was used to characterize the macroscopic properties of the clusters and to track individual E. coli cells in the clusters in real time. A quantitative analysis reveals that the equilibrium cluster size is only weakly dependent on the total number of cells in the cluster. The tumble frequency of an individual cell strongly depends on the position of the cell within the cluster and its direction of movement. In the central region of the cluster, tumbles are strongly suppressed whereas near the edge of the cluster, the tumble frequency is restored for exiting cells, thereby preventing them from leaving the cluster, resulting in the maintenance of sharp cluster boundaries. A simulation based on a model of the sensory memory of E. coli reproduces the experimental data and indicates that the tumble rate and consequently the morphology of the cluster are determined by the sensory memory of cells.

Motile bacteria are able to interact with their environment by accumulating in regions of high concentrations of certain chemicals called attractants and avoiding others called repellents. Motile behavior, which brings bacteria toward (away) from sources of attractants (repellents), is called chemotaxis. Over the last four decades, different aspects of chemotactic motility, especially for the model organisms Escherichia coli and Salmonella spp., have been studied in great detail (1–3). For our purposes, the following details about the motility and chemotaxis of E. coli are important. E. coli cells have several extracellular helical thread-like structures called flagella. Each flagellum has a rotary motor at its base, which can rotate in a clockwise or counterclockwise direction. When individual flagella rotate counterclockwise, they assemble into a coherent rotating bundle, and this bundle propels the bacterium forward. These smooth runs are terminated by tumbles, which are short episodes of erratic motion without net translation. Tumbles are caused by the disintegration of the flagellar bundle, which results from the reversal in the rotation direction of the individual flagella from counterclockwise to clockwise. After each tumble the bacterium moves in a new, almost random direction. Thus in the absence of gradients of chemoattractants an individual cell performs a random walk. The distribution of run times is always exponential and in an isotropic medium has a mean of ≈1 s (4). Reception of attractants and repellents occurs by binding of their molecules to specialized chemoreceptors on the cell surface. Bacterial cells evaluate changes in signal concentrations by a temporal mechanism, in particular by comparing their average number of bound receptors over the past 1 s with their average number during the previous 3 s (5). An increase in the fraction of occupied receptors transiently raises the probability of counterclockwise rotation, which translates into extended runs (for a review see ref. 6).

For a long time, chemotaxis was viewed only as a behavior that guides individual bacteria toward favorable environments (7). However, we have demonstrated recently that under certain stress-generating conditions, cells of E. coli and S. typhimurium excrete two amino acids attractants, aspartate and glutamate. These cells then become moving sources of attractants and start interacting with each other, by coordinating chemotactic motility over a long spatial range. This interaction leads to different nontrivial collective phenomena such as formation of dense multicellular clusters, moving bands, 3D-moving structures called slugs, and complex stationary patterns (8–10).

High cell density clusters form in a layer of still, uniform liquid culture of chemotactic strains of E. coli or S. typhimurium, after the addition of intermediates of the tricarboxylic acid cycle, within a matter of a few minutes (8, 9). Cell division is not required to generate these multicellular structures because they form on a much shorter time scale than the cell-doubling time. The process leading to formation of multicellular clusters can be qualitatively understood as follows: fluctuations in the local cell density produce local gradients of attractants. Cells respond by moving up these concentration gradients thus amplifying the initial spatial nonuniformities in the cell distribution and forming multicellular clusters. This and similar phenomena where chemotactic motility in gradients of self-excreted signals leads to the generation of multicellular structures and patterns of cell density have also been studied theoretically, and macroscopic models have been proposed for this process (8, 11–14).

In this work, we focus on the mechanism of dynamical maintenance of multicellular clusters. Individual cell behavior inside the clusters at their equilibrium size was explored and was correlated to the macroscopic properties of the cluster. Individual E. coli cells expressing GFP mixed in a culture of nonfluorescent cells were tracked in real time by using fluorescence microscopy. The main result of our study is that the rate of tumbling depends strongly on the position and direction of swimming of individual bacteria in a cluster. If, after tumbling, the cell swims away from the cluster, it tumbles almost immediately, whereas a cell entering the cluster does not tumble and subsequently traverses the cluster. This mechanism is responsible for the maintenance of the sharp cluster boundaries. The steady-state size of clusters is almost independent of the number of cells comprising them and is likely determined by the sensory memory of cells.

Materials and Methods

Reagents, Cell Cultures, and Sample Preparations. All chemicals were purchased from Sigma except for agar and tryptone, which were purchased from Difco. E. coli tsr^- strain RBB1050 (15) was kindly provided by H. Berg. Transformation of the original RBB 1050 tsr^- with the plasmid pGFPmut3.1, purchased from Clontech, was done by conventional methods (16). Cells containing this plasmid exhibit bright green fluorescence even in the absence of inducer (isopropyl β-d-thiogalactoside) because of the high plasmid copy number. Transformed cells were selected for motility similar to that of the original strain by growing individual clones of transformed cells on Petri dishes with semisolid medium containing 0.24% agar, 1% tryptone, and 0.5% NaCl (17). Cells were selected from the periphery of colonies that displayed the same radial growth rate as colonies of the nonlabeled strain. The selected cells also demonstrated chemotactic collapse dynamics similar to the original strain, in liquid medium. The aggregation time and the approximate number of aggregates formed in 1.2 ml of liquid culture after the addition of 12 μl of 5 mM fumarate was found to be very similar to that of the parental strain. To prepare liquid cultures, individual colonies were picked from LB agar plates and grown to stationary phase in M9 glycerol medium as described in ref. 9. For the GFP-expressing cells, 50 μg/ml ampicilin was additionally added. Then 200 μl of this culture was used to inoculate 20 ml of M9 glycerol medium and was grown overnight in flasks at room temperature, without shaking. These cultures were used for experiments when OD₆₀₀ reached 0.05. To prepare the slides, bacterial cultures were first diluted to OD₆₀₀ = 0.025 with fresh growth medium. At this cell density, an optimal number of clusters (≈10) formed on each slide. At higher densities, too many clusters would form thereby reducing the inter-cluster distance leading to interaction between clusters and an unwanted drift of clusters. Culture (800 μl) was mixed in a small Petri dish with 200 μl of 1% hydroxypropylmethylcellulose solution to provide the optimal viscosity for E. coli motility (18). GFP-expressing cells (10 μl) were then added. This volume ratio would give ≈1–2 GFP-expressing cells per cluster, which was found to be optimal for tracking cells. To the above mixture, 10 μl of 0.5 M sodium fumarate was added and the mixture was swirled well by hand for ≈15 s. This mixture (17 μl) was then placed in the middle of a dusted glass slide and covered with an 18 mm × 18 mm glass coverslip (VWR Scientific).

Microscopy and Data Acquisition. To record the motion of individual cells in the clusters, the slides were left undisturbed for ≈20 min on the microscope stage, which was found to be the optimal time required to form tight clusters that did not drift. Images were acquired within the window of 20–40 min because after 40 min many cells lost motility and the clusters had a tendency to disperse. This result is probably caused by exhaustion of oxygen by bacterial respiration. Cells grown in LB medium typically loose motility under a coverslip after ≈20 min. The cluster size in LB medium is comparable to that observed in minimal media (M9 glycerol). Both dark field and fluorescence microscopy were used to characterize the macroscopic cluster properties and the motility of single cells. Images were acquired at 15 frames/s by using a Nikon E800 microscope equipped with a cooled CCD camera (CoolSNAP_HQ, Roper Scientific, Duluth, GA).

Data Analysis. Cells were tracked by using Metamorph (Universal Imaging Systems), which yielded the coordinates of each fluorescent cell for every frame of the video. Cells that left the field of view were not tracked. These data were then analyzed by using a tumble detection algorithm similar to Alon et al. (19) implemented in MATLAB (Mathworks, Natick, MA). Cells that swum at <75% of the mean speed were discarded from the data set. Success of the program was verified by visual examination of recordings and was found to be 90% accurate. The errors were largely due to cells that did not slow down while changing direction. It is possible that these may not in fact be tumble events but instead collisions with other cells or with the slide or coverslip. The center of a cluster was determined by averaging dark field images acquired over 6.5 s. In total, from the trajectories of 32 individual cells expressing GFP found in 28 clusters, 97 tumble events were registered. To determine the cell density profile, 19 clusters consisting only of cells expressing GFP were analyzed. The mean swimming speed of cells was determined to be 27 μm/s, which is the projected 2D speed. The actual speed will be a slightly greater because the system is only quasi-2D; i.e., the height of the system was ≈40 μm, which is approximately one-fifth of the typical cluster diameter.

Results

Experiments. A small number of E. coli cells expressing GFP were mixed with nonfluorescent cells. To initiate chemotactic aggregation, sodium fumarate was added to this suspension (see Materials and Methods for details). Within ≈6 min the bacteria aggregated and formed clusters. Dark field and fluorescence microscopy were used to characterize the macroscopic cluster properties and the motility of single cells. The clusters were typically ≈150–200 μm in diameter. The number of bacteria per cluster varied between ≈70 and 500. Fig. 1A shows a typical dark field image of a cluster. Individual cell motion within the cluster was monitored by fluorescence microscopy as shown in Fig. 1 B–D.

Fig. 1.

(A) A cluster imaged by dark field microscopy. (B–D) Snapshots of green fluorescent bacteria in the same cluster at t = 0, 4, and 8 s. The lines depict the trajectories of the bacteria. The montage shows one cell tumbling at the edge of the cluster (top, right) whereas the other cell that swims toward the center does not tumble. (Scale bar = 100 μm.)

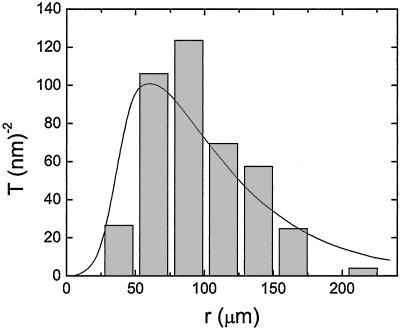
Figs. 2, 3, 4 summarize the properties of single cell motility within the cluster as determined from 32 single-cell trajectories found in 28 different clusters. The tumbling probability density T(r) is azimuthally symmetric with respect to the center of the cluster, where r is the radial distance from the center of the cluster. The tumbling probability density T(r) is shown in Fig. 2. It is clear that in the central region of the cluster, tumbles are strongly suppressed. The data in Fig. 2 have been collected from clusters comprising different total number of cells ranging from 50 to 400. Below we demonstrate that the variation in cluster size is nearly independent of the number of cells in the cluster (see Fig. 5B). Therefore tumble data from different clusters were directly compared in Fig. 2.

Fig. 2.

The tumble probability density T(r) as a function of radial distance from the center of the cluster r. T(r) is computed by normalizing the total number of tumble events between r and (r + Δr) to the area 2πrΔr in which these tumbles occurred. The Δr is the bin-width of the histogram. The solid line denotes T(r) obtained by the theoretical two-state model.

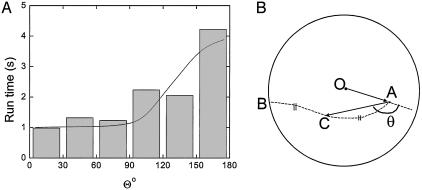
Fig. 3.

(A) Cell run time as a function of the orientation of the cell with respect to the center of the cluster. The angle θ indicates whether a cell is swimming away (θ ≈ 0) or toward the cluster center (θ ≈ π). The solid line denotes the results obtained from the two-state model. (B) A cell tumbles initially at point A, randomizes its direction, and subsequently runs until it tumbles again at point B. The trajectory AB is not straight due to rotational diffusion. Point C is defined as the mid-point of trajectory AB and partitions AB into two equal spatial lengths (denoted by//). The swimming angle θ is the smallest angle between the line OA (connecting the center of the cluster O and the first tumble position A) and the line AC (connecting the first tumbling position and the mid-point of trajectory AB).

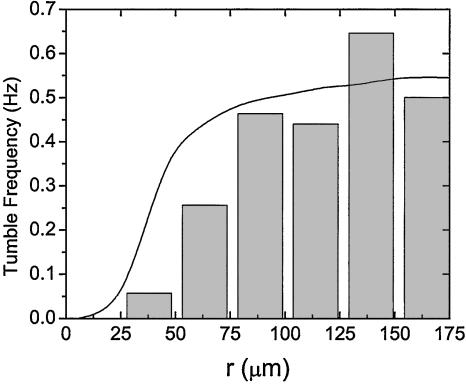
Fig. 4.

The tumble frequency (for an individual cell) as a function of radial distance from the center of the cluster. The data were obtained by dividing the tumble density profile (Fig. 2) by the bacterial density profile (Fig. 4) and normalizing the frequency at large radii to be that obtained by averaging run times over all angles of swimming (Fig. 3). The solid line denote the prediction of the two-state model.

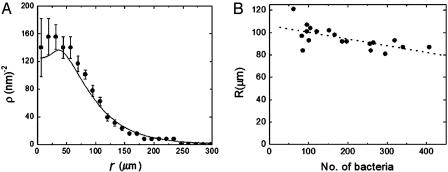
Fig. 5.

(A) The cell density distribution as a function of the radial distance from the center of the cluster ρ(r). The solid line denotes ρ(r) calculated from the two-state model. (B) The cluster radius R as a function of the number of cells comprising the cluster. The dotted line is a guide to the eye and not obtained from the simulations that predict that all clusters should have the same radius.

Data presented in Fig. 3 further support the observation that the tumble frequency is strongly suppressed in the central region of the cluster. The mean run times as a function of the swimming angle θ are shown in Fig. 3A. The swimming angle θ is the angle between the radius vector at the position at which the bacterium tumbles and the line joining this point to the mid-point of the subsequent trajectory (the path traveled between tumbles). This definition is illustrated in Fig. 3B. For bacteria leaving the cluster (small θ, swimming down the attractant concentration gradient), the mean run length is ≈1 s, consistent with values found in aspartate by Berg and Brown (4). For bacteria swimming back into the cluster (θ ≈ 180°, swimming up the attractant concentration gradient), the mean run length is ≈4 s. Bacteria swimming toward the center of the cluster often swim right across the entire cluster and tumble at the opposite edge.

To determine the tumbling density for a single cell as a function of its distance from the center of the cluster, it is necessary to normalize T(r) by the average radial density distribution of bacteria in the cluster. For this measurement, the fluorescence from 19 clusters formed from GFP-expressing cells was monitored. In these measurements all bacteria in the cluster expressed GFP. The averaged cell density distribution of clusters ρ(r) is shown in Fig. 5A. Fig. 5B shows the remarkable result that there is a <15% variation in the size of clusters (the size was determined by fitting to the profile obtained from our simulations) even when the fluorescence (proportional to the number of bacteria and hence the size of the gradient) varies by a more than an order of magnitude. The cluster diameter R is only weakly dependent on the number of cells in comprising the cluster. This observation will be further discussed later.

The tumbling density of an individual cell can now be determined by normalizing the tumble probability density T(r) by the cell density ρ(r). To obtain the tumbling frequency, the saturating value of the tumble density at large radii has been set to be equal to the tumble frequency obtained by averaging run times over all angles (Fig. 3). Fig. 4 shows that the tumble frequency of a single cell is suppressed in the central region of the cluster but is restored to its ambient value at a radial distance of ≈80 μm. The radius at which the tumble frequency is restored coincides with the region where the cell density decreases sharply. Thus, restoration of the tumbling frequency for exiting cells prevents them from leaving the cluster, resulting in the maintenance of sharp cluster boundaries.

Simulations. A simulation was done, based on a model of bacterial chemotaxis as proposed by Segall et al. (5) and Schnitzer (20). In these models, cells compare their average receptor occupancy between 4 and 1 s ago 〈c〉_1–4 to the average receptor occupancy during the last second 〈c〉_0–1. Henceforth we will refer to this difference as the biaser b = 〈c〉_0–1 - 〈c〉_1–4. If b > 0, the cell reduces the tumbling rate Γ_tumble from the ambient value Γ_o by an amount dependent on b: Γ_tumble = Γ_o - γf(b), where f(b) is a monotonically increasing function of b. The parameter γ sets the magnitude of the response of the bacterium to changes in attractant concentration. If b ≤ 0 however, Γ_tumble is retained at the ambient value Γ_o.

In our experiments, it was observed that cells almost never tumble when they are traveling toward the center of the cluster. In terms of the model above this means that when a cell is swimming up the attractant gradient (b > 0) the tumble rate approaches zero. Physically this would happen when the chemotactic response γ and/or the aspartate concentration gradient are large. From both earlier experiments (4) and our experiments, we find that in a spatially uniform or decreasing concentration of attractant, cells tumble on average every 1.0 s, therefore Γ_o = 1.0 s^-1. Based on these experimental facts, the model above reduces to a two-state model in which cells either do not tumble if b > 0, or tumble with a rate Γ_o = 1.0 s^-1 if b ≤ 0. This model was numerically simulated and the results are plotted as solid lines in Figs. 2, 3, 4, 5.

In the simulations, an initial attractant concentration profile was chosen with a maximum attractant concentration at the center of the cluster. The exact functional form of the attractant profile turned out not to be important for the motile behavior of the cells, as long as the profile has a maximum in the center and monotonically decreases from the center. Simulations were performed by using linear, Gaussian, and Lorentzian attractant distributions, and a <1% difference was found among the tumble densities, cell densities, and run times obtained for the different attractant profiles. We note that although Γ_tumble is independent of the magnitude of b, Γ_tumble does depend on the sign of b, which in turn depends on the functional form of the attractant profile. The simulations demonstrate however that this dependence is very weak.

Initially the bacterium starts off at the center of the cluster swimming with constant speed ν in a random direction. After each numerical time step 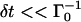(the cell traverse a distance νδt), the biaser b is computed. If b > 0, the cell will not tumble and continues swimming in the same direction. If b ≤ 0, the tumble probability is Γ_oδt. Now a random number r is uniformly drawn from the interval [0,1]. If r < Γ_oδt, the cell tumbles; otherwise it continues in the same direction. The numerical time step δt was chosen such that the results were unchanged upon decreasing δt.

There is a good agreement with the experimental data and the numerical simulations. The only parameter that was used as a fit parameter was the swimming speed ν. After performing a global fit to all experimental values (plotted in Figs. 2, 3, 4, 5), we find ν = 21 μm/s. The fitted speed is slightly less than the experimentally measured speed 27 μm/s. The results of the simulations are shown in Figs. 2, 3, 4, 5 by the bold lines.

Discussion

The mechanism of dynamical maintenance of multicellular clusters of chemotactic E. coli cells was studied. Individual cell behavior inside the clusters at their equilibrium size was explored and was correlated to the macroscopic properties of the cluster. Individual E. coli cells expressing GFP mixed in a culture of nonfluorescent cells were tracked in real time by using fluorescence microscopy. The main result of this study is that the rate of tumbling depends strongly on the position and direction of swimming of individual bacteria in a cluster. In the central region of the cluster, tumbles are strongly suppressed. Near the edge of the cluster, the tumble frequency is restored for exiting cells, thereby preventing them from leaving the cluster. This leads to the maintenance of sharp cluster boundaries. The steady-state size of clusters is almost independent of the number of cells comprising them and our simulations indicate that it is determined by the sensory memory of cells.

The boundary of clusters is sharp because of the restoration of the tumble frequency to its ambient value at a distance r ≈ 75 μm from the center of the cluster (Fig. 4). The decrease in tumble frequency near the center of the cluster can be qualitatively understood in the following manner. In the limit for which the chemotactic gain γ is large, or the attractant gradient generated collectively by the cells is large, i.e., γf(b) ≥ Γ_o, the tumbling rate can only have two values. If b > 0 cells do not tumble and Γ_tumble = 0, whereas if b ≤ 0 cells tumble at a rate Γ_tumble =Γ_o. In this two-state model, bacteria swimming from the periphery toward the center of the cluster rarely tumble, pass through the center, and begin to swim down the gradient. Consider a bacterium swimming toward the center of the cluster from a large distance. After crossing the center (1 s), the biaser b is still positive. Even though the bacterium is swimming down the gradient, it has not “realized” this yet. However, 2 s after crossing the center, the biaser is negative. Therefore somewhere in between 1 and 2 s after swimming through the center, the cell will first realize that it is swimming down the gradient (b goes from positive to negative). For a linear profile, this happens at t = 1.6 s, independent of the slope. However, even when swimming down a gradient, cells typically swim for ≈1 s before tumbling. Thus on average a cell will swim for ≈2.6 s after crossing the center before it begins tumbling independent of the exact shape of the attractant profile. Given a swimming speed of 27 μm/s, the tumble density should saturate at a distance of ≈75 μm from the center, consistent with Fig. 4.

According to the simulations on the two-state model, there is no perceivable difference in the sizes of clusters. This is because the tumble rate only takes binary values: 0 or Γ_o. Therefore the bacterium only measures relative concentrations to determine whether it is moving up or down the gradient, albeit with a delay as described above. Our experiments and numerical simulations demonstrate that the cluster size is set by the duration of the sensory memory of cells. This observation is in contrast to earlier proposed mechanisms that predict that the cluster size is determined by the availability of nutrients and oxygen, nonlinearity's in the bacterial division rates, or volume exclusion (11). The sensory memory is most likely determined by the (de)methylation rates of the Tar receptor. Altering these rates could change the memory and therefore the cluster size.

The feature that the cluster size weakly depends on the number of bacteria in the cluster serves as an extremely simple, yet effective, way of concentrating bacteria in space. Such a mechanism would be extremely advantageous to the bacteria if they need to create a high local cell density on a short time scale, e.g., in response to various xenobiotics, to create high concentrations of detoxifying enzymes. Unlike transcriptionally regulated stress responses, chemotactic aggregation does not depend on production of new proteins and would work even in toxic environments where protein and RNA biosynthesis cannot take place. Clustering by chemotactic aggregation enables bacteria to generate a robust spatial structure and maintain a localized population through the temporal sensing of the concentration of a single species of molecule secreted by them, without a specialized morphogenetic program.

The motility of free-swimming E. coli cells is very well characterized and understood (1–7). The challenge for the future is to explore how single cell motility is altered by the presence of other cells and characterize and understand collective motility. Recently there have been studies on other microorganisms such as Myxococcus xanthus and Dictyostelium discoideum that have characterized repertoire of behaviors of single cells in a community and correlated single-cell motility with the macroscopic properties of the community (21, 22). These types of experiments enable the dissection of mechanisms of community motility that result from the motion of single cells within it.