Trp-cage: Folding free energy landscape in explicit water

Abstract

Trp-cage is a 20-residue miniprotein, which is believed to be the fastest folder known so far. In this study, the folding free energy landscape of Trp-cage has been explored in explicit solvent by using an OPLSAA force field with periodic boundary condition. A highly parallel replica exchange molecular dynamics method is used for the conformation space sampling, with the help of a recently developed efficient molecular dynamics algorithm P3ME/RESPA (particle–particle particle–mesh Ewald/reference system propagator algorithm). A two-step folding mechanism is proposed that involves an intermediate state where two correctly formed partial hydrophobic cores are separated by an essential salt-bridge between residues Asp-9 and Arg-16 near the center of the peptide. This metastable intermediate state provides an explanation for the superfast folding process. The free energy landscape is found to be rugged at low temperatures, and then becomes smooth and funnel-like above 340 K. The lowest free energy structure at 300 K is only 1.50 Å C^α-RMSD (C^α-rms deviation) from the NMR structures. The simulated nuclear Overhauser effect pair distances are in excellent agreement with the raw NMR data. The temperature dependence of the Trp-cage population, however, is found to be significantly different from experiment, with a much higher melting transition temperature above 400 K (experimental 315 K), indicating that the current force fields, parameterized at room temperature, need to be improved to correctly predict the temperature dependence.

Understanding protein folding is critical in molecular biology not only because it is one of the fundamental problems remaining in protein science, but also because several fatal diseases are directly related to protein folding/misfolding, such as the Alzheimer's disease, mad cow disease, and Cystic fibrosis disease (1–4). Despite enormous efforts made by various groups, the problem is still largely unsolved. Experiments that probe proteins at different stages of the folding process have helped elucidate both kinetics and thermodynamics of folding, but many of the details remain unknown. Computer simulations performed at various levels of complexity, ranging from simple lattice models with no solvent to all-atom models with explicit solvent, are used to supplement experiment and fill in some of the gaps in our knowledge about protein folding (1–4). Typical molecular dynamics (MD) simulations using all-atom models are still within the nanosecond to microsecond regime, even with today's supercomputers (2–4), but most of the proteins known fold in the microsecond to millisecond time frame. Both experimentalists and theoreticians keep searching for faster and faster folders to make the two ends meet (there is probably a limit to how fast a protein can fold due to the diffusion rate). A number of rapidly folding proteins have been characterized in recent years to fulfill this need because these fast folding proteins can provide the first direct comparisons between simulations and experiments.

The 20-residue miniprotein Trp-cage (NLYIQ WLKDG GPSSG RPPPS) designed recently by Neidigh et al. (5) is probably one of the best such examples. This protein folds spontaneously and cooperatively into a Trp-cage in ≈4 μs (6), which is by far the fastest folding protein known. The protein was derived from the C terminus of a 39-residue extendin-4 peptide. Several constructs of increasing stability were made by gradually introducing stabilizing features such as helical N-capping residues and a solvent-exposed salt-bridge (5). It contains a short α-helix in residues 2–9, a 3₁₀-helix in residues 11–14, and a C-terminal polyproline II helix to pack against the central tryptophan (Trp-6) (5, 6). The folding seems highly cooperative, with CD, fluorescence, and chemical shift deviations (CSD) generating virtually identical sigmoidal thermal denaturation profiles (5, 6). The small size, high stability, and fast folding time make Trp-cage an ideal choice for protein folding simulations.

There are several simulations published already on this Trp-cage: one by Simmerling et al. (7), who ran a few 20- to 50-ns MD simulations with a modified AMBER99 (assisted model building with energy refinement 99) force field and found a structure very close to the native one from many low potential energy structures; and one by Snow et al. (8), who estimated the folding rate by using thousands of short (nanoseconds) kinetics runs with the united atom OPLS force field; and another by Pitera and Swope (9), who ran replica exchange method and found a <1.0-Å C^α-rms deviation (C^α-RMSD) structure from the simulated ensemble using AMBER94 force field. All three studies used a continuum solvent model, generalized Born (GB) model (10), to save computational cost. Here, we intend to study the Trp-cage folding in explicit solvent using the powerful replica exchange method (REM) (11, 12) with the help of an efficient MD algorithm P3ME/RESPA (particle–particle particle–mesh Ewald/reference system propagator algorithm) (13). It has been shown recently that GB-type continuum solvent models might have deficiencies, such as predicting incorrect lowest free energy structures (14, 15), overly strong salt-bridges (14), and absence of the desolvation free energy barriers (16–18). Thus, we chose the explicit solvent model to study the Trp-cage folding in water.

REM is a powerful tool for efficient sampling of conformation space (11, 12). The free energy landscapes of protein folding in water are believed to be at least partially rugged. At room temperature (RT), protein systems are often trapped in many local potential energy minima. This trapping limits the capacity for effective sampling of the configurational space using normal MD. The high temperature replica in REM can traverse high energy barriers so it provides a mechanism for the low temperature replicas to overcome the quasi-ergodicity they would otherwise encounter. A recently developed MD algorithm P3ME/RESPA (13) is also used to help efficiently explore the free energy landscape. The all-atom OPLSAA (optimized potential for liquid simulation–all atom model) force field and SPC (simple point charge) explicit water model are used with periodic boundary condition. Based on detailed results from the simulation in explicit solvent, a folding mechanism has been proposed for this Trp-cage that involves an intermediate state where the structures show two partially prepacked hydrophobic cores separated by a salt-bridge between residues Asp-9 and Arg-16 near the center of the peptide. This metastable intermediate state might have provided a mechanism for a fast two-step folding process for this miniprotein. The lowest free energy structure at 300 K shows only a 1.50-Å C^α-RMSD from the NMR structures, and the simulated nuclear Overhauser effect (NOE) pair distances are in excellent agreement with the raw NMR data at 300 K. However, the temperature dependence of the native Trp-cage population is found to be significantly different from experiment, which indicates that the current force fields parameterized near RTs need to be improved to correctly predict the temperature dependence.

Method and System

REM has been implemented in the context of the molecular modeling package IMPACT (19) following Okamoto's approach by combining MD with a temperature exchange Monte Carlo process through velocity rescaling (20). Replicas are run in parallel with a sequence of temperatures. Periodically, the configurations of neighboring replicas are exchanged, and acceptance is determined by a Metropolis criterion that guarantees detailed balance. The underlying sampling in each replica can be generated by Monte Carlo, by MD-based Hybrid Monte Carlo, or by MD with velocity rescaling (20). For simplicity, we followed Okamoto's approach, with velocity-rescaling MD. We also used a recently developed MD algorithm that efficiently couples a multiple time step algorithm RESPA with the P3ME method, P3ME/RESPA (13). The P3ME/RESPA method is about one order of magnitude faster than the standard Verlet/Ewald method for a normal size solvated protein system (13). For details of the P3ME/RESPA algorithm, interested readers can consult the ref. 13.

REM (11, 12) can be summarized by the following two-step algorithm: (i) Each replica i (i = 1, 2,..., M) at fixed temperature T_m (m = 1, 2,..., M) is simulated simultaneously and independently for a certain number of Monte Carlo or MD steps. (ii) Pick a pair of replicas, and exchange them with the acceptance probability: T(x → x′) = min[1,exp(-Δ)], where Δ = (β - β′)[U(x′ - U(x)], β and β′ are the two reciprocal temperatures, {x} is the configuration at β and {x′} is the configuration at β′, and U(x) and U(x′) are potential energies of the entire system at these two configurations, respectively. After the exchange, go back to step i. In the present work, MD is used in step i, and all of the replicas are run in parallel on 50 processors; and in step ii, only exchanges between neighboring temperatures are attempted because the acceptance ratio decreases exponentially with the difference of the two βs.

The Trp-cage structure under study is taken from the NMR structure (PDB 1L2Y.pdb, structure 1 of the total 38 NMR structures) (5). The protein is then solvated in a 50 × 50 × 50 ų water box by using the SPC model with a density of 1.0 g/cm³. This procedure results in a total of 12,242 atoms for each replica, with 305 protein atoms and one Cl^- counter ion to neutralize the solvated protein system. All of the MD (canonical ensemble, constant number, volume, and temperature) simulations are carried out with the IMPACT package (19). The long-range electrostatic interactions with periodic boundary condition are evaluated by the P3ME method on a mesh size of 50 × 50 × 50 (grid spacing 1.0 Å). A time step of 4.0 fs (outer time step in RESPA) is used for every replica through the efficient algorithm P3ME/RESPA mentioned above (13). A total of 50 replicas are simulated, with temperatures ranging from 282 K to 598 K. A conjugate gradient minimization is performed first for each replica. Then, a two-stage equilibration, each consisting of 100 ps MD, is followed: in the first stage the protein is frozen in space and only the solvent molecules are equilibrated; and in the second stage all atoms are equilibrated. The final configurations of the above equilibration are then used as the starting points in the 50 replicas. Each replica is run for 5.0 ns for data collection. The replica exchanges were attempted every 0.4 ps, and the protein configurations were saved every 0.08 ps. This process results in a total of ≈3 million configurations and an aggregate MD integration time of 0.25 μs. Block averaging is used to estimate uncertainties in ensemble averages of NOE pair distances and Trp-cage populations, with block size set to be at least twice the correlation time of corresponding autocorrelation functions.

Results and Discussion

The optimal temperature distributions in REM should be roughly exponential and can be obtained by running a few short trial simulations. In this study, we set the acceptance ratio to be ≈20–30%, which resulted in a temperature series of 282, 287, 291,..., 589, and 598 K with gaps from 4 K to 9 K. We observe that the “temperature trajectory” for one replica (e.g., replica 5 starting at 300 K) visits all of the temperatures many times during the 5-ns MD run, and, at a given temperature (e.g., 300 K), all of the replicas are also visited many times during the same MD run, indicating that our temperature series are reasonably optimized. It should be pointed out, however, that a 5-ns MD might not be sufficient to completely equilibrate the system, even with 50 REM replicas (total 250 ns MD). However, we did notice that there are hundreds of “transitions” (exchanges), followed by extensive relaxation between various free energy basins even at the low temperatures. If there were only a few transitions between free energy states, one might worry about the incomplete equilibration; here, the hundreds of transitions and reasonable uncertainties from block averaging indicate that a reasonable equilibration might be achieved. Of course, a more rigorous proof will need two or more simulations starting from different configurations to see whether they converge to the same result (this experiment is probably beyond the current capacity; the 5-ns MD in explicit solvent already takes ≈2.5 mo on 50 IBM SP2 Power3–375-MHz processors, or equivalently ≈10 processor-years).

The free energy landscape is determined by calculating the normalized probability from a histogram analysis (21, 22),

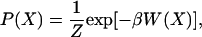[1]

where {X} is any set of reaction coordinates, P(X) is the probability at {X}, and Z is the equipartition function. The relative free energy, or so-called potential of mean force (PMF), can then be easily expressed as

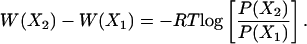[2]

We have tried a number of reaction coordinates in previous studies (23), such as hydrogen bonds, radius of gyration (Rg), fraction of native contacts, RMSD from the native structure, and principal components (24); and searching for better reaction coordinates is still of great interest in protein-folding studies. Here, we will use the fraction of native contacts (ρ) and the Rg to map the free energy landscape.

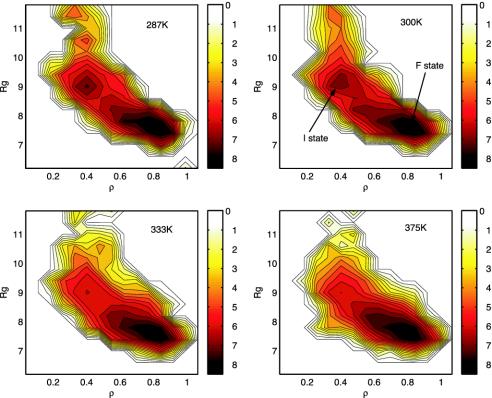
Fig. 1 shows the free energy contour maps (in units of RT) with the two reaction coordinates ρ and Rg at various temperatures, 287 K, 300 K, 333 K, and 375 K. A native contact is defined as a C^α - C^α distance <6.5 Å for nonadjacent residues; and the Rg is based on all heavy atoms with unit mass. The free energy surfaces reveal several interesting features of this Trp-cage folding. (i) The folding free energy landscapes are in general fairly smooth. Above 340 K, the landscape becomes very smooth and funnel-like (25, 26), indicating a very stable two-state folder sliding from the extended state into the folded state. (ii) At low temperatures, however, such as 287 K and 300 K, there exists an intermediate state, I, near reaction coordinates (9.4 Å, 0.42) with ≈15% population at 300 K. The intermediate state structures are found to have two correctly packed partial hydrophobic cores separated by a salt-bridge between residues Asp-9 and Arg-16 near the center of the molecule (more discussion below); the free energy barrier between the intermediate state I and the folded state F is low although, for example, at 300 K, it is only ≈1.2 RT, indicating that it is easy for the peptide to cross over the barrier with thermal fluctuations. (iii) The folded state F has a much lower free energy than the intermediate state, which means that it dominates the population at equilibrium; for example, it is estimated to be ≈70% at 300 K. These results are generally consistent with the NMR, fluorescence, and CD experiment results (5, 6), which also show a stable two-state folder with a very high native state population. Compared with previous free energy contour maps for another fast folder, the β-hairpin from C terminus of protein G (folds in 6 μs) (27), the free energy landscape of Trp-cage seems smoother, indicating that the Trp-cage might be a better two-state folder than the β-hairpin (14, 15, 23). Thus, we agree with the authors of previous studies (5–7) that this Trp-cage is indeed an ideal choice for protein folding simulations. The low free energy barrier between the intermediate state I and the folded state F at 300 K indicates that the intermediate state structures might be short-lived.

Fig. 1.

Free energy contour maps at various temperatures vs. the two reaction coordinates, the Rg and the fraction of the native contacts (ρ). It shows the free energy landscape is rugged at lower temperatures and then becomes smooth at higher temperatures. There is an intermediate state I in addition to the folded state F at low temperatures such as 300 K. See text for more details.

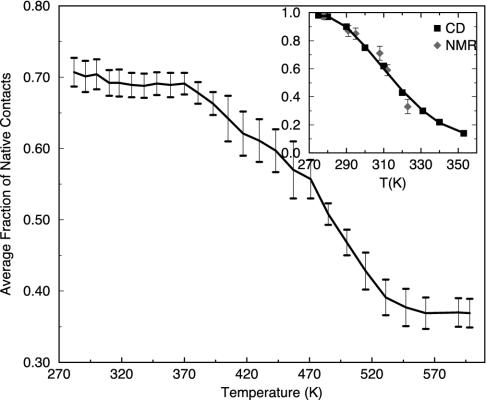
The native population at 300 K from our simulation is somewhat lower than that of the fluorescence or chemical shift deviation experiment. This result might be related to the fact that we estimate the population with a tougher criterion; i.e., all of the native contacts have to be within 6.5 Å to be counted in the simulated ensemble conformations whereas the Trp fluorescence experiment (using residue Trp-6) might collect the fluorescence signal if Trp-6 is buried but not perfectly folded with other residues. In other words, partially folded structures with Trp-6 buried might exhibit the Trp fluorescence as well. The CSD experiment, on the other hand, recalibrates the signal to be 100% folded for the largest values observed for the C-cap and cage formation measures (5). Thus, our lower population at low temperatures might be reasonable (see more data in the temperature dependence study in Fig. 5). Similar results were also found in the β-hairpin population estimation (15, 23).

Fig. 5.

The average fraction of the native contacts (Trp-cage population) as a function of the temperature. The error bars are estimated by block averaging (block size 200 ps). The experimental results (3) from NMR CSD and CD are shown in the Inset for comparison [converted from their unfolded population; the fluorescence data (4), not shown, are basically identical to CD]. Even though both the simulation and experiment show a monotonic decrease in the Trp-cage population with temperature, the melting transition temperature is found to be ≈440 K in simulation, which is much higher than the experimental transition temperature of 315 K, indicating that the temperature dependence of the force field has serious deficiency.

Fig. 2 shows the comparison of the lowest free energy structure from the free energy landscape and the native NMR structure. The lowest free energy structure shows only a 1.50-Å C^α-RMSD from the native structure, with major deviations in residues N1, G10 and S20, which all show a C^α-RMSD larger than 2.2 Å. If one ignores the two terminal residues, which are poorly defined in NMR, the C^α-RMSD is reduced to 1.31 Å (backbone-RMSD 1.62 Å). The noticeable differences between our lowest free energy structure and the NMR structure include: (i) the 3₁₀-helix in residues 11–14 is no longer apparent in the simulated structure; (ii) the sidechain (phenyl ring) in residue Try-3 is not as closely packed to the central Trp-6 as in the native structure, but instead, it extends more into the solvent to fully expose the hydroxyl (^-OH) group. Interestingly, this result is also seen in the best structure in the simulation of Snow et al. (8). This overall 1.50-Å C^α-RMSD seems slightly worse than the best structure from the simulation of Simmerling et al. (0.97-Å C^α-RMSD without two end residues; ref. 7) and the simulation of Pitera and Swope (<1.0-Å C^α-RMSD; ref. 9). However, these best structures are picked either from many low energy structures (7) or from the smallest RMSD in the entire ensemble (9); they are not necessarily the lowest free energy structures. On the other hand, the structure we reported is the lowest free energy structure from the free energy landscape. Even so, it is still noticeably better than the best structure obtained by Snow et al. using mean structure analysis (8). The best structure of Snow et al. shows a >2.1-Å C^α-RMSD, and, most importantly, the central Trp-6 residue is not well packed within the “cage,” but, instead, it sticks out from the “valley” between the N terminus and C terminus (figure 2B in ref. 8). On a separate note, one reason why the best structures of Simmerling et al. and Pitera and Swope from AMBER force fields have a lower RMSD than our lowest free energy structure from OPLSAA might be partially related to the fact that the final NMR structures are minimized with the AMBER force field (5). Furthermore, the potential energy profiles from AMBER or any other force fields are usually very degenerate with respect to RMSD; in other words, very different structures can share the same low potential energy. Therefore, it is difficult to determine the best structure based on the single point potential energy. In the case of Simmerling et al., for Trp-cage, there are also many structures with backbone RMSDs >4 Å but having potential energies comparable with the lowest one (figure 1 in ref. 7).

Fig. 2.

Comparison between the lowest free energy structure (a) and the native NMR structure (b). The key hydrophobic residues packing against the central Trp-6 residue (Tyr-3, Trp-6, Leu-7, Pro-12, Pro-17, Pro-18, and Pro-19) are shown in sticks following previous studies (3, 5, 6), and all other residues are shown in ribbons. The lowest free energy structure shows an overall C^α-RMSD of 1.50 Å from the native structure, with the major differences in the 3₁₀-helix region (residues 11–14) and residue Tyr-3, where the phenyl ring is not as closely packed to the Trp-6 as the native structure.

There are NMR NOE distance constraints available (down-loaded from the Protein Data Bank web site) for this Trp-cage in solution (5); thus, it is of great interest to compare the simulation results directly with the raw NMR data. The NMR measurements by Neidigh et al. (5) have provided 169 NOE distance constraints, of which 43 are for intra-residue constraints, 62 for sequential residues, 36 for i/(i + n) with n = 2–4 residues, and 28 for i/(i + n) with n ≥ 5 residues. The last 28 constraints are the key long-range distance constraints (5) and will be used as the main source for direct comparison in the following. The intra-residue and sequential residue NOE constraints are easily satisfied, even for structures significantly deviated from the native one. The question we try to address here is whether or not the calculated proton pair distances fall within the distance range of the NOEs assigned in the NMR experiment. The distances are calculated by R_AVG = 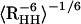and averaged over the entire ensemble at 300 K.

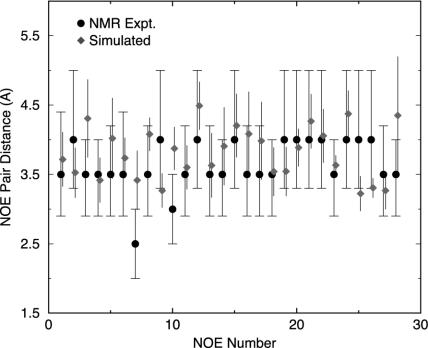
The overall agreement with the NMR NOEs is excellent for the 169 distance constraints at 300 K. If we consider an NOE constraint to be violated if the pair distance is 0.25 Å or more beyond the upper bound or below the lower bound in the NMR distance range, the percentage of violations from simulation is found to be only 8%. In other words, 92% of all NOEs are satisfied in our simulation ensemble. Moreover, of the 8% of violated pairs, only three pairs (namely, HA N1 and HD1^* I4; HD2^* L7 and HN G11; and HA P12 and HN G15) show a >5-Å pair distance, which is the typical distance for observing NMR NOE signals. The first pair (HA N1 and HD1^* I4) involves the flexible N-terminal residue N1, which is not well defined even for the 38 NMR structures (5). The other two are related to the residues in the 3₁₀-helix region, which OPLSAA force field seems not to handle well, consistent with the missing 3₁₀-helix seen in the lowest free energy structure (Fig. 2a). Fig. 3 compares the detailed NOE pair distances from simulation to the NMR data for the 28 key long-range (i/(i + n) with n ≥ 5) pairs. All of the 28 key proton pairs are found to be within 5 Å, the typical NOE signal distance. In fact, none of them exceeds >4.4 Å from simulation. Most of them are within the NOE distance ranges provided by Neidigh et al. (5), with only four exceptions showing >0.25-Å deviations: pair 3, HA Y3 and HD2 P19; pair 7, HZ2 W6 and HA P12; pair 10, HH2 W6 and HD1 P19; and pair 28, HB1 D9 and HB2 S14, as shown in Fig. 3. The largest deviation comes from pair 7, HZ2 W6 and HA P12, which has been assigned an NOE distance of 2.5 Å (2.0–3.0 Å) in NMR. The simulated pair distance is 3.4 ± 0.4 Å, ≈0.9 Å larger than the NMR distance. Interestingly, there is a neighbor pair 9, HH2 W6 and HA P12, which shares the same HA atom of Pro-12 with pair 7, and, in addition, the atom HH2 W6 in pair 9 is near the atom HZ2 W6 in pair 7 on the same indole ring. However, the NOE distance for pair 9 is assigned as 4.0 Å (3.3–5.0 Å) in NMR, 1.5 Å larger than pair 7. Both the NMR structures and the simulated lowest free energy structure show that the W6 indole ring is oriented roughly parallel to the P12 ring (Fig. 2); thus, the distance from HA P12 to the HZ2 and HH2 atoms in W6 might be expected to be roughly the same. Indeed, the simulated distance for this pair 9 is found to be 3.3 ± 0.2 Å, very close to the distance 3.4 ± 0.4 Å for pair 7. Thus, we speculate that this 2.5-Å NOE distance constraint for pair 7, HZ2 W6 and HA P12, the largest deviator in our simulation, might be too small. The other three pairs are all within a deviation of 0.5 Å compared with the NOE distance range. In general, the NOE distance assignments can easily have an error ≈0.5 Å, so these deviations might not be too bad. As mentioned earlier, all of the 28 key long-range proton pairs are within the NOE signal distance (<4.4 Å). Therefore, the overall agreement between the simulation and NMR NOEs is excellent. The slight differences between the simulated structure and the NMR structures might be partly related to the fact that the NMR structures are minimized with the AMBER force field, which favors α-helix structures (15, 18, 28), and/or partly because OPLSAA might not handle 3₁₀-helices well.

Fig. 3.

Comparison of simulated NOE pair distances (represented as diamonds with error bars) with the NMR data [represented as circles with distance ranges (3)]. The simulation data are shifted slightly in x axis to show error bars clearly. The error bars are estimated by block averaging (block size 200 ps). The 28 key long-range (i/(i + n) with n ≥ 5) NOE pairs are shown of the total 169 constraints. They are as follows: 1, HE^* Y3 and HB2 P18; 2, HA Y3 and HB2 P19; 3, HA Y3 and HD2 P19; 4, HA Y3 and HG^* P19; 5, HB2 Y3 and HG^* P19; 6, HD^* Y3 and HA P12; 7, HZ2 W6 and HA P12; 8, HH2 W6 and HG^* P12; 9, HH2 W6 and HA P12; 10, HH2 W6 and HD1 P12; 11, HD1 W6 and HB^* R16; 12, HE1 W6 and HN R16; 13, HE1 W6 and HB^* R16; 14, HE1 W6 and HA P17; 15, HZ2 W6 and HA P17; 16, HD1 W6 and HD^* R16; 17, HD1 W6 and HG^* R16; 18, HZ2 W6 and HD1 P18; 19, HZ2 W6 and HD2 P18; 20, HZ2 W6 and HB1 P18; 21, HZ2 W6 and HG1 P18; 22, HH2 W6 and HB1 P18; 23, HE1 W6 and HA P18; 24, HH2 W6 and HG1 P18; 25, HD1 W6 and HA P18; 26, HD1 W6 and HD2 P19; 27, HD2^* L7 and HD1 P12; 28, HB1 D9 and HB2 S14.

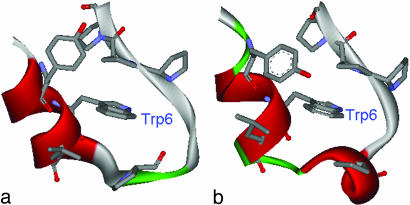
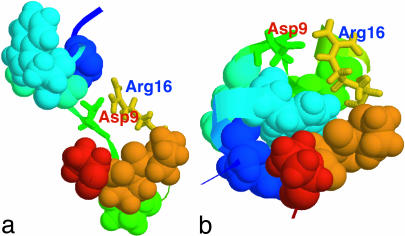
Another interesting point is to take a closer look at the structures in the intermediate state I for a better understanding of the folding mechanism. We select the representative structures from the clustering analysis (14, 15). A distance matrix based on backbone RMSD is first calculated. Then, count number of neighbors with a cutoff 1 Å, take the structure with the largest number of neighbors and all its neighbors as a cluster, and eliminate them from the pool. Repeat this procedure for the remaining structures in the pool until no structures are left. Fig. 4a shows a representative structure, i.e., the most popular structure, from the intermediate state at 300 K. The native structure is also plotted in Fig. 4b for comparison. The intermediate state structure shows two partially formed hydrophobic cores, one by residues Tyr-3, Trp-6, and Leu-7, and the other by the four Pro residues. The two charged residues Asp-9 and Arg-16 form a salt-bridge, which is located near the center of the molecule. In contrast, the native structure (Fig. 4b) shows that the salt-bridge between Asp-9 and Arg-16 is formed outside the central hydrophobic core region and is located on the molecular surface to be exposed to the solvent.

Fig. 4.

Comparison of the most popular structure in the intermediate state I (a) with the native NMR structure (b). The key hydrophobic core residues packing against Trp-6 (Tyr-3, Trp-6, Leu-7, Pro-12, Pro-17, Pro-18, and Pro-19) are shown in space-fill mode whereas the two charged residues Asp-9 and Arg-16 are represented as sticks. The intermediate state shows structures having two partially formed hydrophobic cores separated by a salt-bridge between Asp-9 and Arg-16 near the center of the molecule.

This prematurely formed salt-bridge near the center of the molecule creates a metastable state, the intermediate state I, because it takes energy to break this salt-bridge to make the final hydrophobic core. Breaking a salt-bridge might take up to 3–4 kcal/mol free energy for buried salt-bridges (29) and ≈1.0 kcal/mol for surface salt-bridges (smaller than the buried ones because strong hydrogen bonds with water can make up some differences) (30). In this case, the salt-bridge between Asp-9 and Arg-16 is probably closer to the surface one because it is largely exposed to solvent; hence, a free energy loss of ≈1 kcal/mol might be expected for breaking this prematurely formed salt-bridge. The overall free energy barrier of 1.2 RT (≈0.8 kcal/mol) from the intermediate state to the native state in Fig. 1 is consistent with this analysis. Thus, the folding process seems to involve an intermediate state where the peptide quickly forms two correctly packed partial cores, separated by a salt-bridge between residues Asp-9 and Arg-16. The two prepacked partial cores then collapse into a larger one, and the salt-bridge reforms on the molecular surface to further stabilize the system. It will be interesting to see exactly how the intermediate state structure folds into the final native structure. Preliminary kinetics runs (many 20-ns MD simulations at 300 K) starting from the intermediate state show that the structure can stay with the salt-bridge formed and open and reformed for the whole 20-ns trajectory, and only very few of them see the salt-bridge broken and a hydrophobic core similar to the native one formed (data not shown). We also looked at the folding kinetics starting from the fully extended structure, and preliminary results also show that similar intermediate structures exist with a salt-bridge formed near the center of the molecule (data not shown). Because these are all very demanding simulations, we would like to focus the current article on the free energy landscape and thermodynamics by using the powerful REM. This metastable state might have provided an explanation for the superfast folding rate of this miniprotein because it is easier to form partial hydrophobic cores for subunits. Hence, a superfast two-step folding mechanism emerges. First, the peptide is separated into two regions to form partial cores by forming a metastable salt-bridge near the center; then, the two correctly prepacked partial cores form the final larger one and the salt-bridge is reformed on the molecular surface to gain further stability. This result is slightly different from the experimental two-state folding mechanism even though at higher temperatures the simulation also shows a two-state folder. Of course, one might argue that the salt-bridge-induced metastable state can also act as a trap because it takes energy to break it, thus slowing down the folding rate. We think it depends on the native-like contacts or hydrophobic contacts that the metastable state forms; if the metastable state forms many non-native-like hydrophobic contacts, it might indeed act as a trap rather than a catalyst. We think this is not the case here. Also, from the above analysis, one would expect that the folding rate might decrease if the slat-bridge between Asp-9 and Arg-16 is mutated away. More experiments might be helpful here to study the intermediates and their structural and dynamical properties. In addition, no meaningful α-helix is found in the intermediate state, which indicates that the α-helix is formed at the last stage with the Trp-cage core.

The CSDs, CD, and Trp fluorescence experiments have all determined the temperature dependence of the Trp-cage unfolding/folding population at various temperatures. The melting transition temperature was found to be around 315 K (5, 6). It is of interest to see whether all-atom force field simulations can reproduce this temperature dependence. As we have shown in the previous studies for the β-hairpin of the C terminus of protein G, the temperature dependence of the β-hairpin population deviates significantly from the experimental data (14, 15, 23). All of the three commonly used force fields [OPLSAA, AMBER, and CHARMM (chemistry at Harvard molecular mechanics)] show a similar significantly high melting transition temperature. Here, we would like to study the temperature dependence again for Trp-cage to see whether the problem is specific to the β-hairpin or is more general. We follow the same approach used by Klimov and Thirumalai (31) and ourselves (23) in the β-hairpin work by calculating the average fraction of native contacts to estimate the Trp-cage population. Fig. 5 shows the average fraction of native contacts as a function of temperature. The experimental unfolding molar fractions from NMR CSD and CD spectrums (5) are also shown in the Inset for comparison. The experimental data show that the Trp-cage population decreases monotonically with temperature, with a melting transition temperature around 315 K. Our simulation also shows a monotonic native population decrease with temperature, but the population decays much more slowly than the experiment, with a melting transition temperature around 440 K. This finding is similar to the temperature dependence result for the β-hairpin folding in water where a much higher than experimental melting transition temperature was also found. Interestingly, a very recent simulation by Pitera and Swope (9) with AMBER94 force field and the GBSA continuum solvent model also shows a melting transition temperature >400 K for this Trp-cage. Thus, it seems that this high melting transition temperature is not specific to the β-hairpin, but more general. This finding is probably not too surprising, given that most of the modern force fields are parameterized at RT. Therefore, even though the explicit solvent OPLSAA/SPC model gives very good results near RTs, the temperature dependence results are not quite right. This result is also true in the continuum solvent model simulations (9). Nevertheless, we include the temperature dependence results here to provide data for force field developers to improve the models. It should be pointed out that the population at very high temperatures, such as >500 K, is not zero. This result is because of the way the population is calculated. Even at very high temperatures, the unfolded Trp-cage structures still have some native contacts locally. The non-zero populations at high temperatures are also partly due to the number, volume, and temperature ensemble used. The volume will increase at higher temperatures, which typically favors the unfolding. This favoring of unfolding will decrease the Trp-cage populations at higher temperatures, but the populations near RT, which we care about most, should not be affected much.

Conclusion

The folding free energy landscape of a 20-residue miniprotein Trp-cage has been explored in this study with explicit solvent simulation and periodic boundary condition. A highly parallel replica exchange method consisting of 50 replicas spanning from 282 K to 598 K is used with the help of an efficient MD algorithm P3ME/RESPA. The OPLSAA force field with an SPC water model is adopted for this simulation, and the main conclusions are summarized in the following.

An intermediate state has been identified, and a folding mechanism is proposed for this Trp-cage. At RT 300 K, the Trp-cage quickly undergoes an intermediate state that has two correctly packed partial hydrophobic cores separated by an essential salt-bridge between residues Asp-9 and Arg-16 near the center of the molecule. The free energy barrier (≈1 kcal/mol) to break this prematurely formed salt-bridge makes it a metastable state, which might have provided an explanation for the superfast folding rate of this miniprotein because it is easier to make correct hydrophobic core packing for subunits. Thus, a fast two-step folding mechanism emerges: first the peptide is separated into two regions to form partial cores by forming a metastable salt-bridge near the center; then, the two correctly prepacked hydrophobic cores form the final larger core and also the salt-bridge reforms on the molecular surface to gain further stability. The lowest free energy structure is found to show a 1.5-Å C^α-RMSD from the NMR structures at 300 K. Also, the detailed analysis on NMR NOE distance constraints reveals an excellent agreement between the simulated pair distances with the NOE constraints. No meaningful α-helix is found in the intermediate state, which indicates that the α-helix is formed in the final stage along with the Trp-cage core. The population of the Trp-cage is found to be monotonically decreasing with temperature, from ≈72% at 282 K, with a melting transition temperature ≈440 K, which is significantly higher than the experimental 315 K. This high melting transition temperature seems consistent with the previous findings of β-hairpin folding in explicit water and is also consistent with a recent study on the Trp-cage with a continuum solvent model with AMBER force field. Thus, it shows that there is still more work that needs to be done in the force field parameterization to yield the correct temperature dependence. Future works will include further study of the dynamical properties of the intermediate state (i.e., how the intermediate state structures fold into the native state); working with experimental groups to verify the intermediate state and also investigate the salt-bridge effects on the folding rate by mutagenesis studies; and working with force field developers to help improve the temperature dependence of force field parameterizations by using the large amount of data obtained from the Trp-cage and β-hairpin simulations.