Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Feb 10.
Published in final edited form as: Radiat Phys Chem Oxf Engl 1993. 2008;77(10-12):1213–1217. doi: 10.1016/j.radphyschem.2008.05.046

Electron Emission from Foils and Biological Materials after Proton Impact

Michael Dingfelder 1, Anderson Travia 1, Robert A McLawhorn 1, Jefferson L Shinpaugh 1, Larry H Toburen 1
PMCID: PMC2638064  NIHMSID: NIHMS71481  PMID: 19212448

Abstract

Electron emission spectra from thin metal foils with thin layers of water frozen on them (amorphous solid water) after fast proton impact have been measured and have been simulated in liquid water using the event-by-event track structure code PARTRAC. The electron transport model of PARTRAC has been extended to simulate electron transport down to 1 eV by including low-energy phonon, vibrational and electronic excitations as measured by Michaud et al. (Radiat. Res. 159, 3–22, 2003) for amorphous ice. Simulated liquid water yields follow in general the amorphous solid water measurements at higher energies, but overestimate them significantly at energies below 50 eV.

Keywords: electron transport, liquid water, amorphous solid water

1. Introduction

Electron emission spectra from thin foils (e.g., Al, Cu, Au and those covered by thin layers of frozen gases, like frozen water) provide valuable information on low-energy electron transport properties in condensed phase materials and can be used to validate or update Monte Carlo (MC) track-structure codes. These codes follow the incident particles as well as all secondary electrons event-by-event, from starting or ejection energy to total stopping. These transport models require reliable interaction cross sections for charged particles with atoms and molecules of the material under consideration.

MC track structure simulations play an important role in many radiobiological models employed to develop a quantitative understanding of the mechanisms of radiation damage in biologic material, e.g., the assessment of the role of initial damage patterns on damage to such critical biological targets as cellular DNA. It has been noted that ionization, and the subsequent electron transport along ion tracks, accounts for more than 90% of the biological effectiveness of heavy charged particles ((Schmidt et al. 1987)). Moreover, it is becoming increasingly clear that the spatial patterns of energy deposition at the nanometer-scale following interactions of ionizing radiation with biological targets greatly influence the final biological response (see, e.g., (Goodhead 1987, 1999; Paretzke 1987)). Because these initial damage patterns can affect the efficiency and/or fidelity of biologic repair, the accuracy of the MC transport codes used for radiobiological applications at the molecular level becomes crucial.

The success of MC energy transport codes depends on the accuracy of both, the theoretical model assumptions and the physical input data used. Because of the lack of firm, detailed information on energy transport properties of biological material, many assumptions must be made in developing energy transport codes. Traditionally these codes have relied on theoretical descriptions of condensed-phase interaction probabilities for model systems combined with parameters extrapolated from gas phase studies, or they have relied entirely on gas phase data. The former often require extrapolations of unknown accuracy, whereas the latter fail to account for effects of long-range electronic screening associated with dense media; they ignore potential-energy shifts associated with phase transitions, and more importantly, they fail to properly account for collective modes of energy-loss appropriate to condensed phase material. This last factor could play a critical role at nanometer dimensions associated with the production of clustered damage in DNA; such damage can render biological repair processes inefficient and/or decrease the fidelity of repair that does occur. The measurements provided in this project are the first data available on which to base direct experimental tests of MC energy transport models at the fundamental level of the physics of electron transport in condensed media of biologic importance.

The basic concepts of track structure theory have been reviewed in a number of articles (see, e.g., (Paretzke 1987; Paretzke et al. 1995; Ritchie et al. 1991; Zaider et al. 1994)). The MC approach represents a powerful method to simulate the statistically complete detailed event-by-event history of energy deposition and electron transport in matter. A typical MC code starts with the primary ion, or electron, and follows the history of interactions by the primary and all secondary particles interaction-by-interaction. Monte Carlo simulations have been applied to simulate electron transport in water vapor, and with somewhat greater uncertainties in liquid water and other condensed phase materials. Nikjoo et al. ((Nikjoo et al. 2006; Nikjoo et al. 1998)) provide a summary of some of the most commonly used Monte Carlo codes for both electron and ion transport utilized in a variety of studies. These codes are generally based on a mixture of experimental data and extrapolations using theoretical models. Even those Monte Carlo studies developed specifically for condensed phase media rely heavily on gas phase data for guidance owing to the lack of availability and/or reliability of the equivalent condensed phase data. Another limitation of most current models is their focus on water as the sole component of the stopping medium. This is generally justified on the basis that water is the dominant component of biological tissue; thus most interactions occur with water.

With these limitations in mind we have initiated measurements and calculations of the spectra of electron emission from thin metal foils (e.g., Al, Cu, Au) and from foils with thin layers of gases, like water, frozen on them after fast proton impact. In the following we describe briefly the experimental system and procedures, followed by a description of the Monte Carlo simulations using the track structure code PARTRAC. We discuss and compare our preliminary experimental results with results obtained by simulations and speculate on how we might improve our theoretical cross section models used in PARTRAC.

2. Methods and Results

2.1 Experimental tests and Guidance for Monte Carlo Modeling

Essentially all Monte Carlo models of energy deposition and charged particle track structure rely on theoretical cross sections for the interactions with condensed phase material, and water is generally used as a surrogate for tissue. The use of theoretical cross sections is required because experimental values are either unavailable, or technically unfeasible. The Monte Carlo codes developed in this way are then used to provide detailed information on the spatial patterns of energy deposition and transport with no clear experimental tests of the detailed reliability.

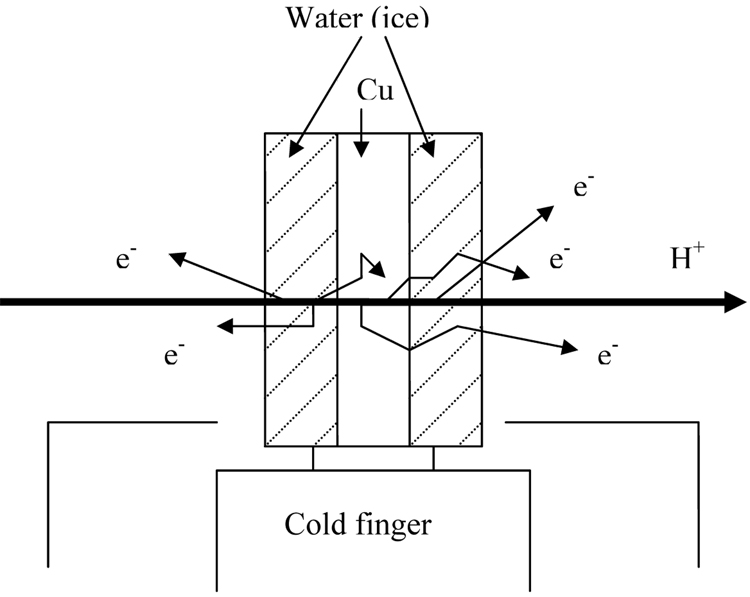
A few years ago, we set out, with the support of the National Cancer Institute, to provide experimental tests of the “physical” process of electron transport in condensed phase materials, i.e., test without involving chemical species formation for detection. We designed a system to produce primary electrons within the bulk of condensed phase material, and to measure the energy and angular distributions of electrons as they escape the surface of a thin foil. To study electron transport in water, we could freeze a thin layer of water on a cryogenically cooled metal substrate. A schematic representation of the target system is shown in Figure 1. Amorphous solid water (ASW) is frozen to a copper substrate held at approximately 40 K. Electrons produced by the protons within the copper and the ASW are detected by a micro-channel detector as a function of time following the pulse of excitation.

Figure 1.

Figure 1

Open in a new tab

Schematic of the experimental target design used for frozen targets. Amorphous solid water (ASW) is frozen to a copper substrate held at approximately 40 K. Electrons produced within the copper and the ASW are detected by a micro-channel detector as a function of time following the excitation by a pulsed high energy proton beam.

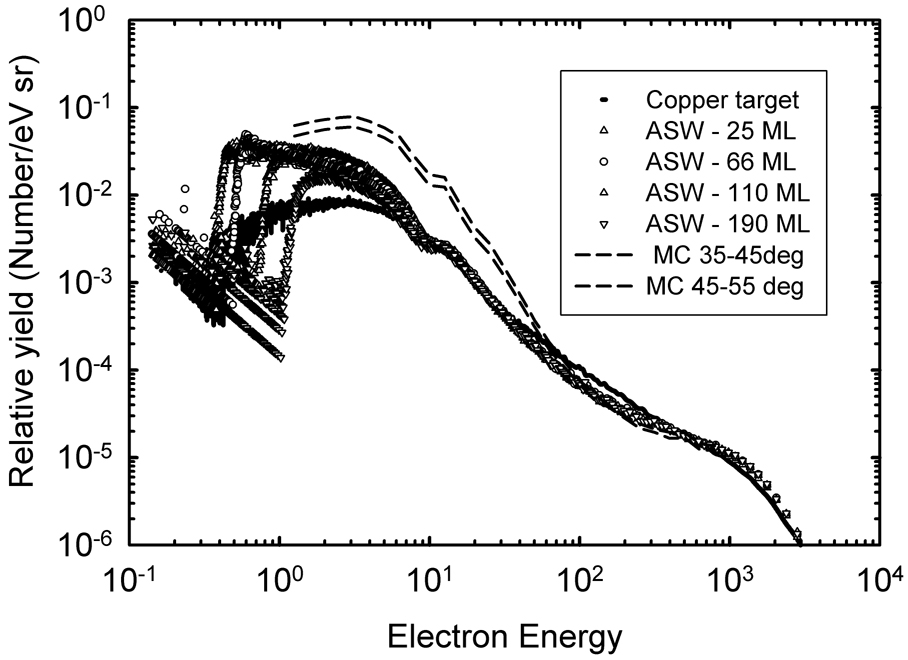
Using this apparatus with a proton beam pulsed at two-megahertz and pulse duration of approximately one nanosecond we can measure the energy spectra of electrons ejected for the surface with energies from a few tenths of an eV to about 1 keV and at emission angles from about 10 degrees with respect to the forward direction of the ion beam to nearly 160 degrees, i.e., electrons are measured for both forward scattering and backward emission. Further details on the experimental apparatus and procedures are described in Ref. (Christou 2004). Data from Christou (2004) are shown in Figure 2 for electron emission at 45 degrees from a sputter cleaned copper substrate and for ASW of several thicknesses frozen to the copper substrate. These data illustrate some of the difficulties associated with the study of water; because water is an insulator it tends to charge when electrons are ejected resulting in a potential barrier effecting the subsequent emission of low energy electrons. The thicker the water layer, the greater the potential barrier seen by the ejected electrons, and the large decrease in low energy electrons observed for large ASW thickness. By a study of electron emission as a function of ASW thickness we can establish the “envelop” of emission characteristics for comparison to the simulation of electron emission by Monte Carlo techniques. Monte Carlo results (described in the next subsection) for electron emission at 40 and 50 degrees are shown in Figure 2 for comparison to the measured 45 degrees spectrum. Note that for ejected electron energies above about 100 eV the shape of the curves measured and calculated are in good agreement, whereas at lower energies the simulation is as much as a factor of five too large.

Figure 2.

Figure 2

Open in a new tab

Electron emission from amorphous solid water of varying thicknesses frozen to a thin copper foil. Also shown are electron emission from the sputter cleaned copper foil and Monte Carlo simulations as described in Section 2.2. Experimental data are taken from the dissertation of Ch. Christou (Christou 2004).

As noted above, water can be a very difficult material to study. In addition to the effects of charging as an insulator is ionized, the actual density and thickness of the amorphous water layer is dependent on the substrate temperature and the dosing method. Fortunately, a great deal of research has been published on the properties of ASW ((Kimmel et al. 2005, 2006; Stevenson et al. 1999)). To produce the water foils we leaked water vapor into the vacuum chamber where it was frozen onto the polycrystalline copper substrate held at about 37 K. This technique should result in a low-density, about 0.6 g/cm3, amorphous solid water ((Stevenson et al. 1999)). We have no direct means of measurement, but believe that the surface should be reasonably smooth and have little effect on the emission spectra. The phenomenon of foil charging also needs further investigation. Questions arising are: What are the actual mechanism of foil charging and how might that charging mechanistically reduces the yield of low-energy electrons in a thickness dependent fashion? Does the ASW trap low-energy electrons in the bulk producing a negative potential barrier for the subsequent electrons to tunnel through to exit the surface? Or does the positive charge left behind from ionization on the ASW form a Coulomb attraction (positive barrier) for the low-energy ejected electrons? The latter could attract low-energy ejected electrons and form an additional negative barrier on the surface, assuming no electron transport within the insulator. This latter effect would produce a sandwich of positive charge in the bulk followed by a negative barrier on the exterior surface – either one of which could reduce the yield of low-energy electrons. Many of these questions are currently under study.

The sizable discrepancies between the results measured for ASW and calculations for liquid water raise several questions. Is the difference related to the charging of the water foil and our methods to interpret the result; do these discrepancies simply reflect a difference between ASW and liquid water; is there an error in the primary electron spectra assumed for the proton collisions; are we seeing a real difference in model relative to calculation; or are there other possibilities? We have initiated new measurements to compare source terms for different ions, and to model electron emission from metal foils in order to try to resolve these questions. The later are easier to measure and to model because of their conductivity and well established characteristics of metals. The first step in this continuing modeling effort will be to calculate the collisional cross sections for electrons and ions in metals.

2.2 Monte Carlo simulations of electron emissions

2.2.1 The PARTRAC simulation code

The Monte Carlo track structure simulation code PARTRAC was developed at the National Research Center for Health and Environment (GSF) in Germany. PARTRAC is currently capable to simulate track structures of electrons in the energy range from 10 eV to 10 MeV, protons (1 keV – 1 GeV) and alpha particles (1 keV – 1 GeV) in liquid water. Inelastic interaction cross sections are calculated within the framework of the plane wave Born approximation (PWBA). In this approximation the doubly differential (in energy and momentum transfer) cross sections factorize into an energy loss function and kinematic factors. The energy loss function is a function of energy and momentum transfer and describes completely the electronic properties of the target. We have modeled the energy loss function and fitted to available optical data of liquid water ((Heller et al. 1974)). Details on the calculations of interaction cross sections and simulation techniques can be found in the following references: for electron transport see (Dingfelder and Friedland 2001; Dingfelder et al. 1998; Dingfelder et al. 2007), for proton transport see (Dingfelder et al. 2000; Friedland et al. 2003), and for alpha transport see (Dingfelder et al. 2005; Friedland et al. 2005).

2.2.2 Low-energy electron transport

As seen in Figure 2 most of the electrons emitted from thin foils have kinetic energies below 10 eV. However, the PARTRAC transport model was designed to stop electron transport at 10 eV which is the ionization threshold for liquid water (Eion = 10.79 eV in our model for liquid water ((Dingfelder et al. 1998))). In order to be able to transport electrons at energies below 10 eV we have extended the electron transport model. We consider additionally to the five ionization shells and five excitation levels (as described in (Dingfelder et al. 1998; Dingfelder et al. 2007)) in total eleven more inelastic phonon, vibrational and electronic excitation states, as described and measured by the Sherbrooke group ((Michaud and Sanche 1987a, 1987b; Michaud et al. 2003)). In detail, we consider two translational phonon states vT,1 and vT,2, two librational phonon states vL,1 and vL,2, three vibrational excitations vV,2 (bending), vV,1–3 (stretching), and vV,3 (asymmetric stretching), two combinations vV,1–3 + vL and 2(vV,1–3), and two additional electronic excitations 2A1 and 2B2, two dissociative attachment anion states. Total cross sections for these additional states are taken directly from (Michaud et al. 2003). Relative energy differential cross sections for each of the additional excitation states are represented by a Lorentzian function, given by L(E) = N/[1 + (E – E0)2 / g2]. Here, E0 is the mean excitation energy, g the full width at half maximum (FWHM) and N a normalization constant. The energy loss E is limited to E0 - 3/2 g ≤ E ≤ E0 + 3/2 g, which leads to N = 1/[2g arctan(3 / 2)]. The advantage of using a Lorentzian instead of a Gaussian is that the Lorentzian can be inverted analytically, i.e., the cumulative energy distribution is obtained analytically. The actual energy loss E is then sampled directly from the cumulative distribution function and given by E = E0 + g tan[R arctan(3 / 2) + (R-1)arctan(E0 / g)], where R is a random number between 0 and 1. The parameter E0 and g used for the eleven additional states are given in Table 1. Angular deviations for phonon and vibrational states are assumed to be the same as for elastic scattering; no angular deviation is considered for dissociative attachment anion states, i.e, they peak strictly in forward direction.

Table 1.

Mean excitation energies E0 and widths g of the Lorentzians used to model the energy loss for the additional eleven low-energy excitation states.

Symbol E0 g Name
1 vT,1 10 meV 1 meV Phonon, translational
2 vT,2 24 meV 25 meV Phonon, translational
3 vL,1 61 meV 30 meV Phonon, librational
4 vL,2 92 meV 40 meV Phonon, librational
5 vV,2 204 meV 16 meV Vibrational: bending
6 vV,1–3 417 meV 50 meV Vibrational: stretching
7 vV,3 460 meV 5 meV Vibrational: asymmetric stretching
8 vV,1-3+vL 500 meV 40 meV Combination
9 2(vV,1–3) 835 meV 75 meV Combination
10 2A1 2 eV 0.5 eV Dissociative attachment anion state
11 2B2 6 eV 1 eV Dissociative attachment anion state
Open in a new tab

2.2.3 The extended electron transport model

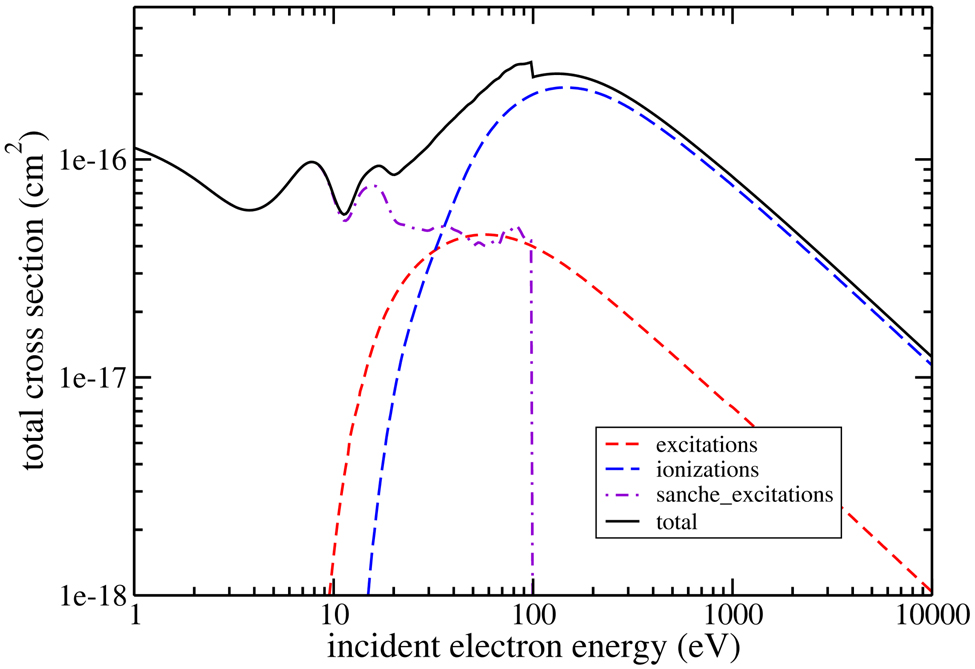
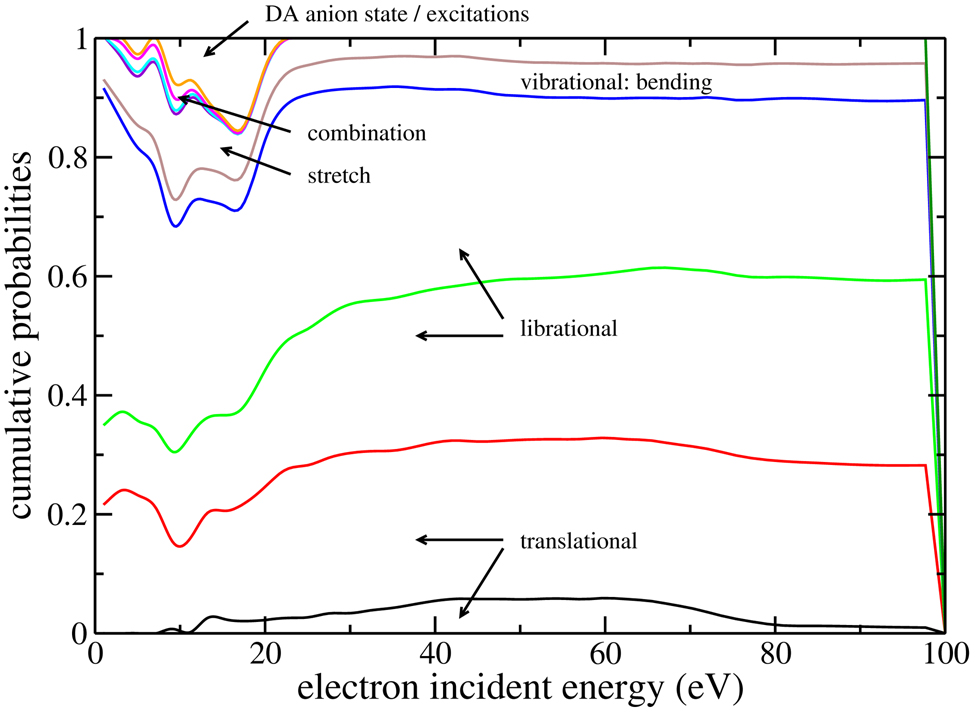
We add the additional eleven low-energy excitations as new excitations on top of our five ionization shells and five electronic excitation levels. Low-energy excitations are only considered in the energy range from 1 eV up to 100 eV, where experimental values are provided. We did not extrapolate these total cross sections to higher energies; theoretically, total cross sections for low-energy electronic excitations should behave as AT−1 ln(BT) as a function of the electron kinetic energy T, where A and B are constants (Bethe theory). However, vibrational modes do not fall rapidly as the energy increases due to the dominance of the quadrupole interaction relative to the dipole one (see e.g., (Itikawa 1974)). Total cross sections for ionizations, excitations, and low-energy excitations are shown in Figure 3. The relative distributions between the different low-energy excitations are shown in Figure 4 as cumulative probabilies; phonon excitations contribute 90% at energies above 20 eV and up to 70% at energies below 20%, where electronic excitations contribute. Vibrational excitations contribute around 10% over the full energy range.

Figure 3.

Figure 3

Open in a new tab

Total inelastic cross sections as used in the extended version of PARTRAC. Shown are the partial cross sections for ionization, electronic excitation, the additional new low-energy excitations, and the total sum.

Figure 4.

Figure 4

Open in a new tab

Cumulative probabilites for the different low-energy excitations.

2.2.4 Simulated electron emission spectra

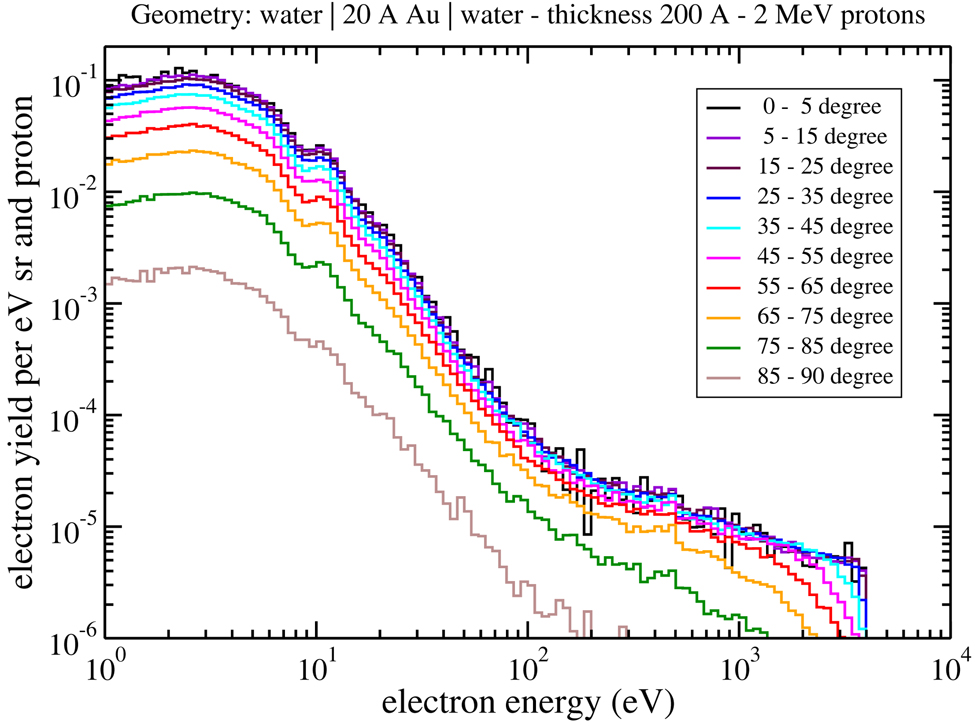
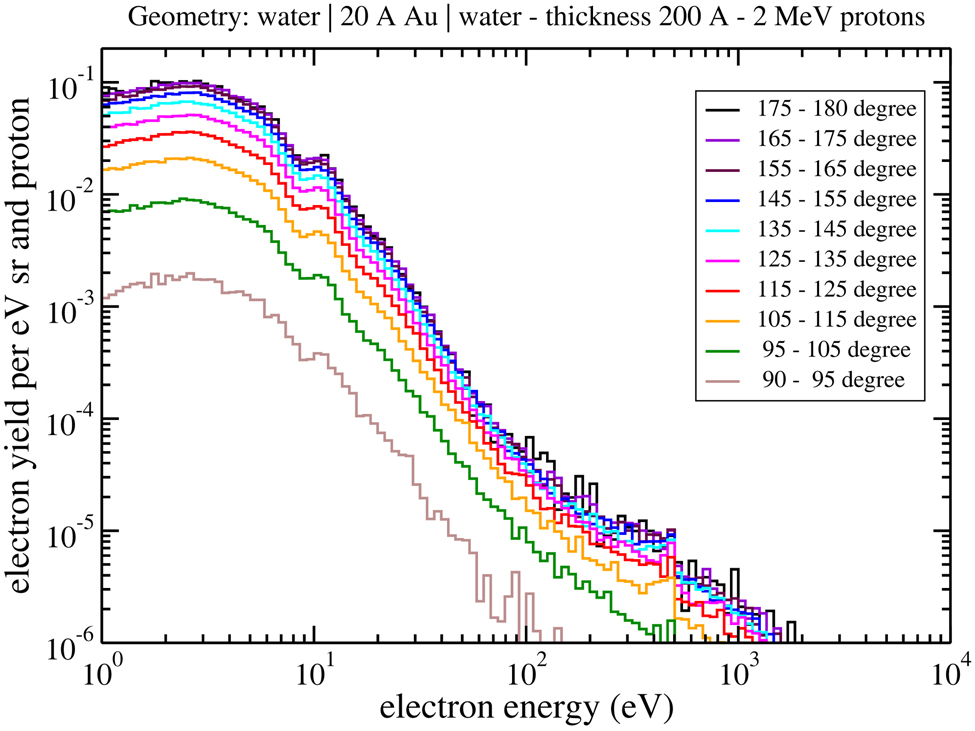
We have simulated electron emission spectra from layers of liquid water after 2 MeV proton impact. The thickness of the water layers was 200 Å, the thickness of the metal foil 20 Å (see schematics in Figure 1). The water layer is thick enough to ensure that almost all electrons emitted were produced within the water layer. We simulated electron emission in the metal foil by using density scaled liquid water. Emitted electrons were analyzed in energy and angle. The theoretical emission spectra are presented in Figure 5. Panel a shows forward angles, while panel b displays backscattering. Forward angles 40 degrees (emission between 35 and 45 degrees) and 50 degrees (emission between 45 and 55 degrees) are also displayed in Figure 2 together with experimentally obtained emission spectra for ASW at 45 degrees. Both data sets are normalized at 500 eV. Simulated liquid water yields in general follow the amorphous solid water measurements at higher energies, but overestimate them significantly at energies below 50 eV. However, these measurements provide guidance for the assessment of the physical parameter (cross sections) of the electron transport model appropriate to the condensed phase

Figure 5.

Figure 5

Figure 5

Open in a new tab

Simulated electron emission spectrum produced by 2 MeV protons passing through a liquid water slab (200 Å) “frozen” on both sides of a gold slab (10 Å; density scaled water). Shown are the emission spectra in forward directions (panel a) and backward directions (panel b).

3. Discussion

3.1 Assessment of liquid water cross sections for electron transport

As mentioned before, the current interaction model implemented in PARTRAC is based on calculations within the PWBA, a first order perturbation theory which is valid if the incoming electron is sufficiently fast. At lower energies electron cross sections are corrected using semi-empirical correction factors derived from theoretical models and gas phase data. Also, exchange corrections have to be considered for electron transport. All this introduces considerable uncertainties into the cross sections. Another source of uncertainty is the energy loss function (ELF). The model used in PARTRAC is based on one optical reflectance measurement performed by Heller et al. in 1974 ((Heller et al. 1974)). In 2000, Hayashi et al. published a new measurement of the optical data of liquid water using inelastic x-ray scattering (synchrotron radiation) ((Hayashi et al. 1998, 2000; Watanabe et al. 1997)). They found significant differences with respect to the older optical reflectance measurements. Emfietzoglou and co-workers ((Emfietzoglou et al. 2005; Emfietzoglou and Nikjoo 2005, 2007)) used the new measurements to model the ELF and obtained significantly smaller inelastic cross sections compared to the optical-reflectance based model.

Another source of uncertainty is elastic scattering. First, PARTRAC uses atomic gas-phase cross sections for elastic scattering obtained by standard phase-shift calculations as published in (Berger et al. 1993). Molecular scattering cross sections are obtained by additivity rules. Also, angular deviations in elastic events are sampled from simplified and averaged angular distributions. Second, Sanche and co-workers ((Michaud et al. 2003)) reported integral elastic cross sections in amorphous solid water to be up to about two orders of magnitude smaller than in the gas phase. However, they state that certain components included in the gas phase measurements were explicitly excluded in the condensed phase measurement.

We therefore plan to update our model of the ELF to include and reflect the new inelastic x-ray scattering measurements by Hayashi and co-workers ((Hayashi et al. 1998, 2000; Watanabe et al. 1997)) and revisit low-energy corrections to the PWBA. Also, the low-energy excitations should be modeled with some more detail and extended to higher energies to provide a smooth transition in the total cross sections. Elastic scattering cross sections will be updated due to the recommendations in the very recently published ICRU Report 77 ((ICRU 2007)).

We have also initiated the measurement and simulation of electron emission spectra from thin metal foils after fast proton impact. Metals are atomic materials and much easier to deal with in both, experiment and theoretical calculations. Comparisons of experimental and theoretical results for metal foils should provide useful insights to understand better the discrepancies found for liquid water vs. amorphous solid water.

Acknowledgments

This work is supported in part by the national Institute of Health, National Cancer Institute Grant No. 2R01CA093351-04A1 and by the National Aeronautics and Space Administration, Grant No. NNJ04HF39G.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Berger MJ, Seltzer SM, Wang R, Schechter A. Gaithersburg, MD: U. S. Department of Commerce; Elastic scattering of electrons and positrons by atoms: Database ELAST. 1993
  2. Christou CI. Department of Physics. Greenville, NC: East Carolina University; 2004. Electron emission from condensed targets by 2-MeV proton impact. [Google Scholar]
  3. Dingfelder M, Friedland W. Basic data for track structure simulations: Electron interaction cross sections in liquid water. In: Kling A, Barão F, Nagagawa M, Távora L, Vaz P, editors. Advanced Monte Carlo for Radiation Physics, particle transport simulations and applications. Berlin: Springer Verlag; 2001. pp. 267–272. [Google Scholar]
  4. Dingfelder M, Hantke D, Inokuti M, Paretzke HG. Electron inelastic-scattering cross sections in liquid water. Radiat. Phys. Chem. 1998;53:1–18. [Google Scholar]
  5. Dingfelder M, Inokuti M, Paretzke HG. Inelastic-collision cross sections of liquid water for interactions of energetic protons. Radiat. Phys. Chem. 2000;59:255–275. [Google Scholar]
  6. Dingfelder M, Ritchie RH, Turner JE, Friedland W, Paretzke HG, Hamm RN. Comparisons of calculations with PARTRAC and NOREC: Transport of electrons in liquid water. Radiat. Res. revised - under review. 2007 doi: 10.1667/RR1099.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dingfelder M, Toburen LH, Paretzke HG. An effective charge scaling model for ionization of partially dressed helium ions with liquid water; Proceedings of the Monte Carlo 2005 Topical Meeting: The Monte Carlo Method: Versatility Unbounded in a Dynamic Computing World. American Nuclear Society; April 17–21; La Grange Park, IL. Chattanooga, TN: 2005. pp. 1–12. CD-ROM (ANS Order No. 700321) [Google Scholar]
  8. Emfietzoglou D, Cucinotta FA, Nikjoo H. A complete dielectric response model for liquid water: A solution of the Bethe ridge problem. Radiat. Res. 2005;164:202–211. doi: 10.1667/rr3399. [DOI] [PubMed] [Google Scholar]
  9. Emfietzoglou D, Nikjoo H. The effect of model approximations on single-collision distributions of low-energy electrons in liquid water. Radiat. Res. 2005;163:98–111. doi: 10.1667/rr3281. [DOI] [PubMed] [Google Scholar]
  10. Emfietzoglou D, Nikjoo H. Accurate electron inelastic cross sections and stopping powers for liquid water over the 0.1 – 10 keV range based on an improved dielectric description of the Bethe surface. Radiat. Res. 2007;167:110–120. doi: 10.1667/RR0551.1. [DOI] [PubMed] [Google Scholar]
  11. Friedland W, Dingfelder M, Jacob P, Paretzke HG. Calculated DNA double-strand break and fragmentation yields after irradiation with He ions. Radiat. Phys. Chem. 2005;72:279–286. [Google Scholar]
  12. Friedland W, Jacob P, Bernhardt P, Paretzke HG, Dingfelder M. Simulation of DNA damage after proton irradiation. Radiat. Res. 2003;159:401–410. doi: 10.1667/0033-7587(2003)159[0401:soddap]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  13. Goodhead DT. Physical basis for biological effects; Nuclear and Atomic Data for Radiotherapy and Related Radiobiology. Vienna: International Atomic Energy Agency; 1987. pp. 37–53. [Google Scholar]
  14. Goodhead DT. Mechanisms for the biological Effectiveness of High-LET radiations. Radiat. Res. 1999;40 Suppl.:1–13. doi: 10.1269/jrr.40.s1. [DOI] [PubMed] [Google Scholar]
  15. Hayashi H, Watanabe N, Udagawa Y, Kao CC. Optical spectra of liquid water in vacuum uv region by means of inelastic x-ray scattering spectroscopy. J. Chem. Phys. 1998;108:823–825. [Google Scholar]
  16. Hayashi H, Watanabe N, Udagawa Y, Kao CC. The complete optical spectrum of liquid water measured by inelastic x-ray scattering. Proc. Natl. Acad. Sci. USA. 2000;97:6264–6266. doi: 10.1073/pnas.110572097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Heller JM, Jr, Hamm RN, Birkhoff RD, Painter LR. Collective oscillations in liquid water. J. Chem. Phys. 1974;60:3483–3486. [Google Scholar]
  18. ICRU. ICRU Report 77: Elastic Scattering of Electrons and Positrons. International Commission on Radiation Units and Measurements. Oxford University Press; 2007. [Google Scholar]
  19. Itikawa Y. Electron-impact vibrational excitation of H2O. J. Phys. Soc. Japan. 1974;36(4):1127–1132. [Google Scholar]
  20. Kimmel GA, Petrik NG, Dohnalek Z, Kay BD. Crystalline ice growth on Pt(111): Observations of a hydrophobic water monolayer. Phys. Rev. Lett. 2005;95:1666102. doi: 10.1103/PhysRevLett.95.166102. [DOI] [PubMed] [Google Scholar]
  21. Kimmel GA, Petrik NG, Dohnalek Z, Kay BD. Layer-by-layer growth of thin amorphous solid films on Pt(111) and Pd(111) J. Chem. Phys. 2006;125:044713. doi: 10.1063/1.2218844. [DOI] [PubMed] [Google Scholar]
  22. Michaud M, Sanche L. Total cross section for slow electrons (1–20 eV) scattering in solid H2O. Phys. Rev. A. 1987a;36:4672–4683. doi: 10.1103/physreva.36.4672. [DOI] [PubMed] [Google Scholar]
  23. Michaud M, Sanche L. Absolute vibrational excitation cross sections for slow electron (1–18 eV) scattering in solid H2O. Phys. Rev. A. 1987b;36:4684–4699. doi: 10.1103/physreva.36.4684. [DOI] [PubMed] [Google Scholar]
  24. Michaud M, Wen A, Sanche L. Cross sections for low-energy (1-100 eV) electron elastic and inelastic scattering in amorphous ice. Radiat. Res. 2003;159:3–22. doi: 10.1667/0033-7587(2003)159[0003:csflee]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  25. Nikjoo H, Uehara S, Emfietzoglou D, Cucinotta FA. Track-structure codes in radiation research. Radiat. Meas. 2006;41:1052–1074. [Google Scholar]
  26. Nikjoo H, Uehara S, Wilson WE, Hoshi MD, D T, G Track structure in radiation biology: theory and applications. Int. J. Radiat. Biol. 1998;73(4):355–364. doi: 10.1080/095530098142176. [DOI] [PubMed] [Google Scholar]
  27. Paretzke HG. Radiation track structure theory. In: Freeman GR, editor. Kinetics of nonhomogeneous processes. New York: John Wiley & Sons; 1987. pp. 89–170. [Google Scholar]
  28. Paretzke HG, Goodhead DT, Kaplan IG, Terrissol M. IAEA-TECDOC-799. Vienna: International Atomic Energy Agency; 1995. Atomic and molecular data for radiotherapy and radiation research. [Google Scholar]
  29. Ritchie RH, Hamm RN, Turner JE, Wright HA, Bolch WE. Radiation interactions and energy transport in the condensed phase. In: Glass WA, Varma MN, editors. Physical and Chemical Mechanisms in Molecular Radiation Biology. New York: Plenum Press; 1991. pp. 99–133. [Google Scholar]
  30. Schmidt S, Schmidt-Böcking H, Kelbch C. The 3rd Workshop on Heavy Charged Particles in Biology and Medicine. Germany: GSI, Darmstadt; 1987. Jul, pp. 13–15. [Google Scholar]
  31. Stevenson KP, Kimmel GA, Dohnalek Z, Smith RS, Kay BD. Controlling the morphology of amorphous solid water. Science. 1999;283:1505–1507. doi: 10.1126/science.283.5407.1505. [DOI] [PubMed] [Google Scholar]
  32. Watanabe N, Hayashi H, Udagawa Y. Bethe surface of liquid water determined by inelastic x-ray scattering spectroscopy and electron correlation effects. Bull. Chem. Soc. Jpn. 1997;70:719–726. [Google Scholar]
  33. Zaider M, Fung A, Dardash M. Charged-particle transport in biomolecular media: the third generation. In: Varma MN, Chatterjee A, editors. Computational Approaches in Molecular Radiation Biology. New York: Plenum Press; 1994. pp. 72–92. [Google Scholar]

RESOURCES