Determination of torque-limits for human and cat lumbar spine specimens during displacement-controlled physiological motions

Abstract

Background Context

Quadruped animal models have been validated and utilized as biomechanical models for the lumbar spine. The biomechanics of the cat lumbar spine has not been well characterized, even though it is a common model used in neuromechanical studies.

Purpose

Compare the physiological ranges of motion and determine torque-limits for cat and human lumbar spine specimens during physiological motions.

Study Design/Setting

Biomechanics study.

Patient Sample

Cat and human lumbar spine specimens.

Outcome measures

Intervertebral angle (IVA), joint moment, yield point, torque-limit, correlation coefficients.

Methods

Cat (L2-sacrum) and human (T12-sacrum) lumbar spine specimens were mechanically tested to failure during displacement-controlled extension, lateral bending, and axial rotation. Single trials consisted of 10 cycles (10mm/s or 5°/s) to a target displacement where the magnitude of the target displacement was increased for subsequent trials until failure occurred. Whole-lumbar stiffness, torque at yield point, and joint stiffness were determined. Scaling relationships were established using equations analogous to those that describe the load response of elliptically-shaped beams.

Results

IVA magnitudes for cat and human lumbar spines were similar during physiological motions. Human whole-lumbar and joint stiffness magnitudes were significantly greater than those for cat spine specimens (p<0.05). Torque-limits were also greater for humans compared to cats. Scaling relationships with high correlation (R²>0.77) were established during later lateral bending and axial rotation.

Conclusions

The current study defined “physiological ranges of movement” for human and cat lumbar spine specimens during displacement-controlled testing, and should be observed in future biomechanical studies conducted under displacement control.

Introduction

Quadruped animals have been used as biomechanical models of the human lumbar spine [1]. Utilizing such models can be advantageous over human cadaveric tissue because it reduces the risk of infection for researchers, and non-human spine specimens are much more readily available. Non-human species are generally chosen based on similarities in size, anatomy, and/or material characteristics. The biomechanics of sheep [2], calf [3,4], dog [5], and deer [6] lumbar spines have been tested for their appropriateness as models for human spines. It was determined that the ranges of motion in these animal species were similar enough to humans to warrant their use as alternative models for the human lumbar spine.

In a cadaveric study on deer lumbar and thoracic spines, it was determined that while ranges of motion were similar between human and deer spines, stiffness of human functional spinal units was much higher than that of deer in some spinal regions [6]. Sheep lumbar spines had similar ranges of motion compared to human lumbar spines during lateral bending, flexion, and extension, but were less during axial rotations; data from human spines often showed high variability, limiting the interpretation of these similarities [2]. By contrast in calf spines, range of motion was less in lumbar functional spinal units compared to humans during flexion and extension, but similar during other motion types; again, large variability in human lumbar spine data make interpretation of these data difficult beyond qualitative assessment [3].

The animal models described above have been recommended for use in mechanical testing of the performance of spinal implants. Other animal models such as the goat [7,8], rabbit [9,10], rat [11,12,13] and cat [14,15,16,17] have been utilized for investigating neurological responses to spinal loading. Physiological mechanisms of spinal afferent responses to mechanical loading are just beginning to become understood via neuromechanical studies conducted in animal models. Even though afferent responses to mechanical loading of feline lumbar spines have been measured [14,15,16,17], the biomechanics of cat lumbar spines have not been studied extensively.

The current study was designed with the long-term goal of establishing a mathematical (or “scaling”) relationship between the biomechanics of cat and human lumbar spine specimens to provide a rational basis for extrapolating cat neurophysiological data to humans. An important first step in establishing a scaling relationship between cat and human lumbar spine biomechanics is to determine the “physiological range of movement” for both species. Accordingly, the aim of the current study was to establish vertebral joint torque limits for human and cat lumbar spines during physiological loading. Preliminary data has been reported in abstract form [18].

Methods

Preparation of spine specimens

Cat and human lumbar spine specimens were mechanically tested to failure during extension, lateral bending, and axial rotation. Intact human, musculo-ligamentous lumbar spine specimens (T12-sacrum) were obtained from National Disease Research Interchange (NDRI; Philadelphia, PA). These specimens were procured within 24 hours post mortem, shipped frozen to our laboratory, and frozen at −80°C until used.

Laboratory bred, adult male cats (~4 kg) were obtained using an IACUC approved protocol. On the day of tissue harvesting, cats were anesthetized using a mixture of oxygen (5 liters/min) and halothane (5%) in a sealed induction chamber. After induction, euthanasia was accomplished by an overdose of anesthetic in accordance with the recommendations of the Panel on Euthanasia of the American Veterinary Medical Association. After verification of death (10 minutes lack of breathing and heartbeat), the intact, musculo-ligamentous lumbar spine (T10-sacrum) was obtained.

Until ready for use, cat and human lumbar spine specimens were kept wrapped in gauze soaked with phosphate buffered saline (PBS, pH = 7.4), wrapped in plastic, and stored at −80°C. The day before dissection, spine specimens were thawed at room temperature (human: ~24 hours; cat: ~12 hours). All superficial tissues were removed using gross and fine dissection while keeping the interspinous, capsular, and the posterior and anterior longitudinal ligaments intact. For cat spines, portions of the spine cephalic to the L2 vertebra were removed by transecting the L1-2 disc and disarticulating the L1-2 joint, resulting in spine specimens complete from L2-sacrum (L2 through L7 lumbar vertebrae + sacrum). For human spine specimens, the T11-12 disc was transected and the T11-12 joint disarticulated, which resulted in human spine specimens complete from T12-sacrum (T12 + L1-L5 lumbar vertebrae + sacrum). During dissection, as well as during mechanical testing, specimens were kept moist by wrapping them in PBS-soaked gauze and periodically misting exposed areas with PBS.

Experimental setup for extension and lateral bending

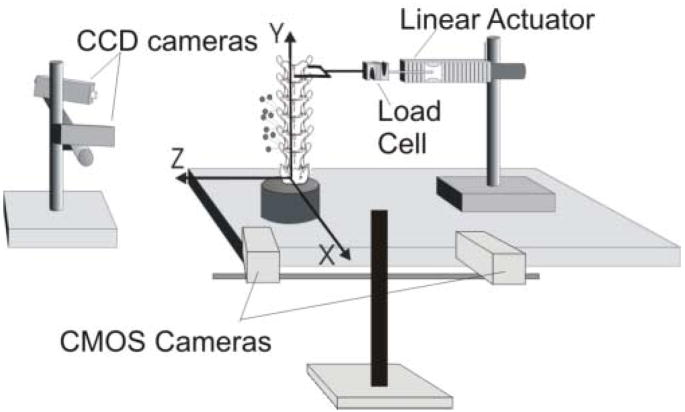
Ligamentous cat and human lumbar spine specimens (extension: n=6 human, n=1 cat; lateral bending: n=3 human, n=6 cat) were prepared and successfully tested using the same experimental setup described previously for the testing of human lumbar spine specimens during displacement-controlled physiological motions [19] (Fig. 1, left). Briefly, spine specimens were potted at the sacrum using a quick-setting epoxy and rigidly fixed to the testing surface. A linear actuator (Model 317, Galil, Inc., CA) was attached to the anterior portion of the most superior vertebral body (human: T12, cat: L2) via a U-shaped coupling such that a torque was not induced at the point of load application. The actuator was attached to the U-coupling using a universal joint and threaded rods that were in-series with a uniaxial force transducer (human: Model 9363-D1-50-20P1, Revere Transducers, CA, Range ±220 N; cat: Model LCF300, Futek, CA, Range ±110 N). The magnitude of peak displacement, displacement rate and number of cycles were controlled using a custom program (Labview V. 7.1, National Instruments, Inc, TX).

Figure 1.

(Left) Schematic of the experimental setup for determining cat and human lumbar spine specimen torque-limit during extension and lateral bending (Left) and axial rotations (Right; cat shown). Vertebral kinematics were measured by optically tracking, with two CCD cameras, the 3D displacements of markers attached to transverse processes.

Multiple trials were conducted until failure as follows. A single trial consisted of 10 displacement cycles to a pre-defined magnitude at a displacement rate of 10 mm/s. Peak displacement for the first trial was 10 mm and was increased by 5 mm for subsequent trials until failure occurred, while observing a three-minute intertrial interval [19]. After failure, specimens were tested to two additional peak displacement magnitudes (incremented by 5mm) to further define the “force-global displacement” relationship. Peak force and displacement magnitudes for all trials contributed to the force-global displacement profile for that specimen, and were used to compute spine stiffness (see Data Analysis).

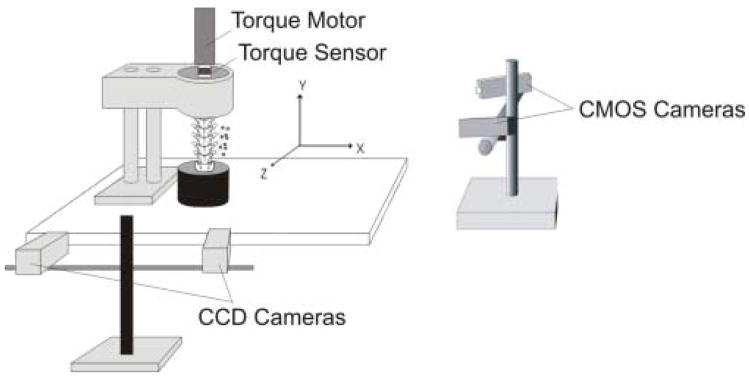
Experimental setup for axial rotation

Prior to mechanical testing, additional specimens (n=1 human, n=6 cat) were potted at the sacrum and the most cephalic vertebra (cat: L2, human: T12). The experimental setup for testing cat and human spines during axial rotation was similar to that previously reported for human spines [20,21]. Briefly, potted spine specimens were prepared for testing by attaching an aluminum plate to the epoxy on the superior end. The plate had a 3 cm high, ¾″ 6-point bolt soldered to its surface, and it was positioned on the epoxy such that the bolt was aligned with the long axis (Y-axis) of the spine (Fig. 1, right). The bolt was coupled to a rotary motor (Model ME2130-198B, Galil, Inc., Rocklin, CA) via a ¾″ socket, which was in-series with a torque sensor (Model TTD400, Futek, Irvine, CA). The motor was suspended over the specimen and aligned along its Y-axis. A PID digital controller with custom-written software (LabVIEW V. 7.1, National Instruments, Inc., TX) was used to control the magnitude and rate of angular displacement.

A single trial consisted of 10 cycles to a peak angular displacement at a rate of 5 deg/s. Peak angular displacement magnitude for the first trial was 5 deg and was increased by 5 deg for subsequent trials until failure occurred. After failure, specimens were tested to two additional peak displacement magnitudes to further define the “torque-global displacement” relationship for the most caudal joint. Peak caudal joint torque and angular displacement magnitudes for all trials contributed to the caudal joint torque-global displacement profile for that specimen, and were used to compute spine stiffness (see Data Analysis).

Data analysis

During extension and lateral bending, peak force for a given trial was taken as the mean peak force for the last five cycles comprising that trial (where load had reached equilibrium). Joint torque at the three most caudal joints (human: L3-4 through L7-S1; cat: L5-6 through L7-S1) was computed as the product of the mean peak force (measured by the force transducer) and the respective moment arm (perpendicular distance between the center of the facet joint and the point of load application). During axial rotation, mean peak torque (measured by the torque sensor) was also taken as the mean peak torque for the last five cycles.

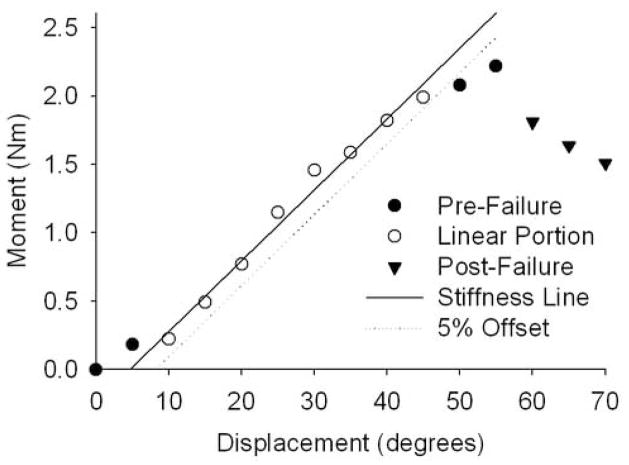
Kinematics of the three most caudal vertebrae (cat: L5 through L7; human: L3 through L5) were measured by optically tracking (at 60 Hz) the displacements of sets of three noncollinear markers, each set attached to the respective transverse processes (Qualysis Track Manager, Innovision Systems, Inc., Columbiaville, MI), and the rigid-body motions (six degrees of freedom [DoF]) were computed [22]. Whole spine stiffness (Fig. 2) was computed as the slope of the linear portion of the developed torque-global displacement relationship (i.e., displacement of the actuator). Similarly, joint stiffness at the three most caudal joints (cat: L5-6 through L7-S1; human: L3-4 through L5-S1) was computed as the slope of the linear portion of joint torque-intervertebral angle relationships. Yield point at 5% offset was determined (Fig. 2) [23]. A conservative torque-limit was defined as the 10th percentile of the torque at yield point (where only 10% of the specimens had a torque at yield smaller in magnitude than the torque-limit).

Figure 2.

Whole-lumbar stiffness during the test to failure was computed as the slope of the linear portion of the moment-displacement relationship. Yield point at 5% offset was determined (cat, axial rotations shown).

The developed caudal joint torque-global displacement relationships (cat: L7-S1; human: L5-S1) were regressed using incremental polynomial regression (IPR). Significant differences in joint stiffness were assessed for a given motion type using 2-way analysis of variance (ANOVA), where the two factors were species (cat versus human) and joint level (cephalic, middle, or caudal). For a given motion type, significant differences in species whole-lumbar stiffness were assessed using unpaired t-tests. To assess differences in torque at yield point across species (cat or human) and/or motion type (lateral bending, axial rotation, or extension), 2-way ANOVA was also performed (factors: species and motion type). If significant main effects or interactions were identified using 2-way ANOVA, multiple comparison tests were conducted to determine which groups were significantly different (Student Newman Keuls Test [SNK]). SigmaStat (V. 3.01) and α = 0.05 were used for all statistical tests.

Mathematical modeling

The bending of a beam, where one end is fixed and a torque is applied at the other end, can be described as: $\rho =\frac{\text{EI}}{\text{M}}$, where ρ is the radius of curvature, E is Young’s modulus, I is the area moment of inertia, and M is the moment (i.e., torque). Young’s modulus (E) would be impossible to measure for lumbar spine specimens, as the spine is comprised of several different types of materials. Hence, caudal joint stiffness (Ê) was used as a proxy for Young’s modulus and used to compute a proxy radius of curvature using linear regression: $\frac{{\text{M}}_{\text{ij}}}{{\widehat{\text{E}}}_{\text{ij}}}=\frac{1}{{\widehat{\rho }}_{\text{ij}}}{\text{I}}_{\text{ij}}$, where M_ij/Ê_ij (torque at yield point divided by caudal joint stiffness) was the dependent variable, I_ij (moment of inertia) was the independent variable, and 1/ρ̂_ij was the slope of the regression line. Similarly, the torsional or axial loading of a beam can be described as: $\phi =\frac{\text{LT}}{\text{GJ}}$, where φ is the angle of twist, L is the length of the beam, T is the torsional torque, G is Young’s modulus during torsional loading, and J is the polar moment of inertia. Caudal joint stiffness (Ĝ) was used as a proxy for Young’s modulus to compute a proxy for angle of twist (φ̂). The following relationship was regressed: $\frac{{\widehat{\text{G}}}_{\text{j}}}{{\text{M}}_{\text{j}}}=\frac{1}{{\widehat{\phi }}_{\text{j}}}\frac{{\text{L}}_{\text{j}}}{{\text{J}}_{\text{j}}}$, where Ĝ_j/M_j (caudal joint stiffness divided by torque at yield point) was the dependent variable, L_j/J_j (specimen length divided by polar moment of inertia) was the independent variable, and 1/φ̂_j was the slope of the regression line.

As defined here, the proxies for angle of twist and radius of curvature do not hold physiological meaning themselves. However, high correlation between structural (i.e., area moment of inertia or polar moment of inertia and specimen length) and material (i.e., caudal joint stiffness and torque at yield point) properties would indicate that a relationship does in fact exist.

Results

A number of logistical constraints prohibited the completion of mechanical testing to failure during certain physiological motions. In preliminary studies when testing cat spine specimens from the neutral (vertical) posture to extension or flexion, these specimens did not fail (i.e., there was no decrease in load with an increase in displacement) until they became completely horizontal. Once horizontal, they became loaded axially in tension until failure occurred. Hence, torque at failure was not indicative of failure during extension or flexion but rather during tensile axial loading. As the results of these tests would not have been indicative of loading during extension, only a single representative specimen was reported. For human spine specimens, a single specimen was successfully tested to failure during axial rotations. Testing was attempted for two additional specimens during axial rotations, but the torque sensor and motor were not powerful enough to achieve the peak angular displacement necessary for failure to occur. The type of statistical test performed was modified as needed to accommodate small sample sizes; specific instances of this are detailed below.

Joint torque

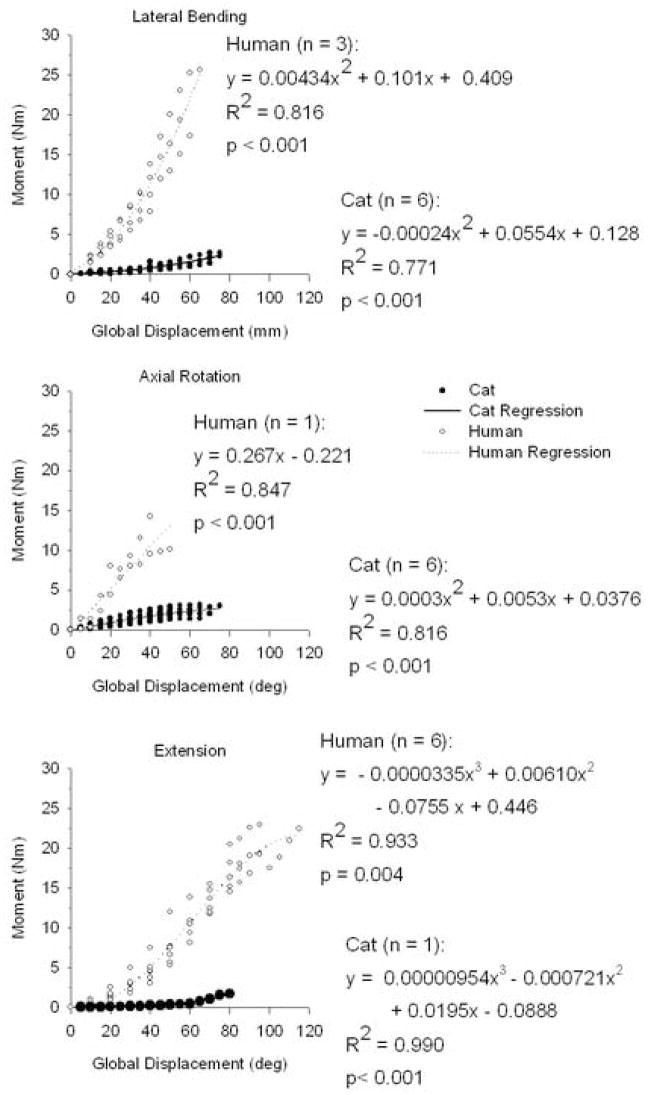
Caudal joint torque-global displacement relationships (as assessed by incremental polynomial regression [IPR]) were highly correlated (R² range = 0.771–0.990), although order of fit depended upon the species and motion type being considered (Fig. 3). During lateral bending for human and cat lumbar spines, developed joint torque-global displacement relationships were second order (IPR; human: R² = 0.816, p < 0.001; cat: R² = 0.771 and p < 0.001). During axial rotation, the order of fit was different for human (IPR: first order: R² = 0.847; p < 0.001) and cat (IPR: second order: R² = 0.816; p < 0.001) lumbar spines. During extension, human and cat lumbar spines were both best fit with third order relationships (IPR; human: R² = 0.933 and p = 0.004; cat: R² = 0.990 and p < 0.001). Developed joint torque magnitudes for human lumbar specimens were larger in magnitude compared to cat lumbar specimens for each motion type.

Figure 3.

Pre-failure, developed moment-global displacement relationships were determined using Incremental polynomial regression (p < 0.005). The order of fit (1st, 2nd, or 3rd) varied depending upon what motion type (lateral bending, axial rotation, or extension) and species (cat or human) was considered.

Intervertebral angle (IVA)

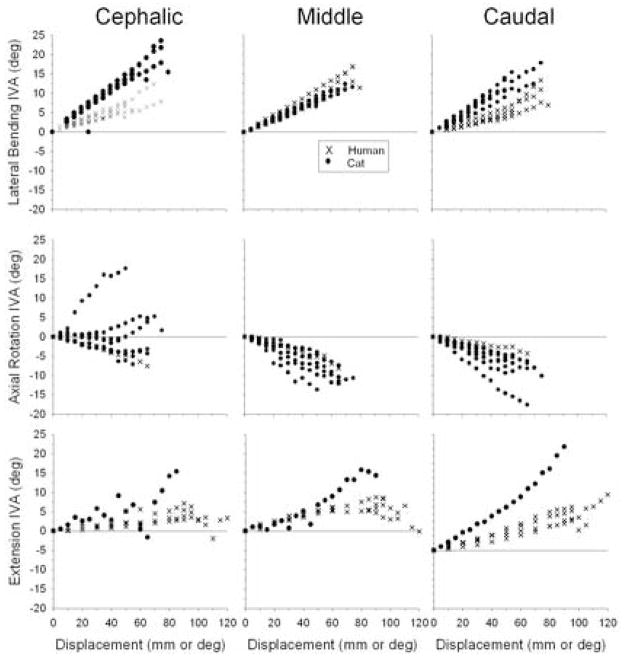
Major-axis IVA for cat and human lumbar spine specimens are shown in Fig. 4. During lateral bending, IVA magnitudes for cat and human lumbar spines were similar at the cephalic, middle, and caudal joint levels, though cat IVA was slightly larger.

Figure 4.

Cat and human intervertebral angle (IVA) versus displacement relationships during lateral bending, axial rotations, and extension.

Stiffness

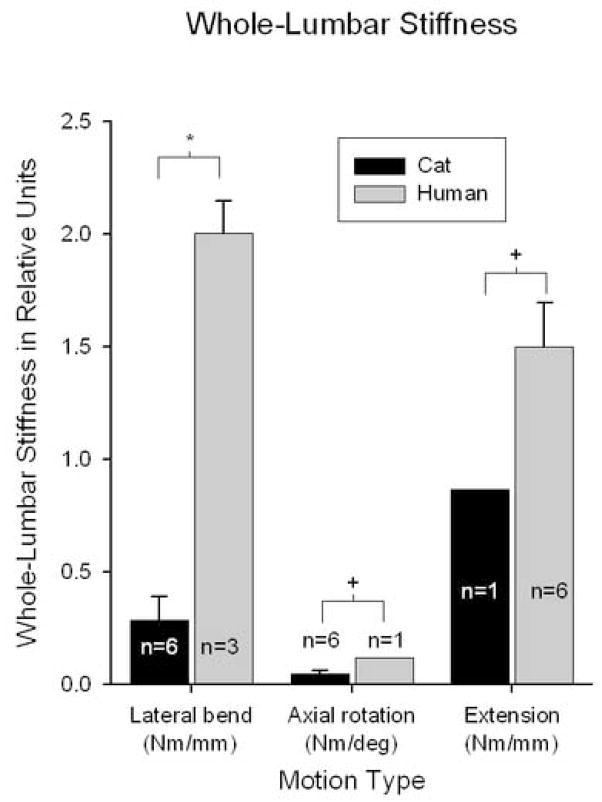
Whole-lumbar stiffness magnitudes were greater for human spines compared to cats (Fig. 5). During lateral bending, mean whole-lumbar stiffness for human spines was seven times greater than for cat spines (t-test; p < 0.001). During axial rotation, it was not possible to perform a t-test because only one human spine specimen was tested successfully. However, whole-lumbar stiffness for the human spine was almost twice the magnitude of the upper-limit of the 95% confidence interval for cat spines (0.117 Nm/deg and 0.061 Nm/deg, respectively). Similarly during extension, whole-lumbar stiffness for the single cat specimen was smaller in magnitude compared to the lower limit of the 95% confidence interval for that of humans (0.866 Nm/mm and 1.297 Nm/mm, respectively).

Figure 5.

Whole-lumbar stiffness magnitudes were significantly greater for human lumbar spine specimens compared to cat lumbar spine specimens (*unpaired t-test, p < 0.001; +Data from n = 1 was outside 95% confidence interval for n=6).

Joint stiffness magnitudes varied depending upon the motion type (Fig. 6). During lateral bending, there were significant interactions between species and joint level (2-way ANOVA, p < 0.001). At all three joint levels, human spine joint stiffness was significantly greater than that for cats (SNK, p < 0.05). Human joint stiffness increased caudally, where joint stiffness at a given joint was significantly greater than that for the respective more cephalic joints (SNK, p < 0.05). During axial rotation, 2-way ANOVA could not be performed to assess differences between species due to the small number of human lumbar spine specimens (n = 1). For cat spine specimens, joint level did not have a significant effect on joint stiffness magnitude (1-way ANOVA; p = 0.957). Analogous to the comparisons of whole spine stiffness, the effect of species on stiffness at a given joint level was investigated by looking at the 95% confidence intervals for the cat spine data. Joint stiffness magnitudes for the single human spine specimen at the cephalic, middle, and caudal joint levels (3.63, 2.07, and 3.55 Nm/deg, respectively) were much greater than the upper limit of the 95% confidence intervals for the same joints of cats (0.53, 0.51, and 0.56 Nm/deg, respectively).

Figure 6.

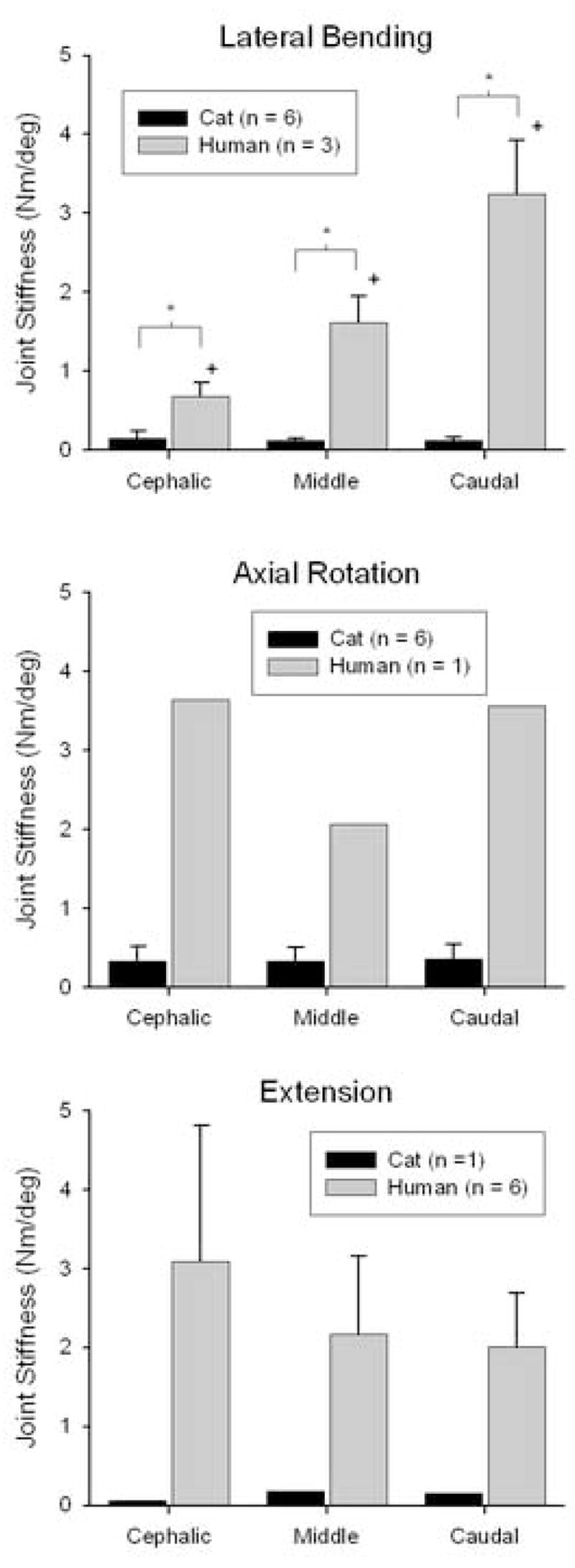
Joint stiffness for cat and human lumbar spine specimens. During lateral bending (top), there were significant interactions between joint level and species (2-way ANOVA, p < 0.001). Interactions and the effect of species type were not tested during axial rotation (middle) or extension (bottom) due to sample size. Joint level did not have a significant effect on cat joint stiffness during axial rotation or on human joint stiffness during extension (ANOVA, p > 0.35).

Similarly, the small number of cat spine specimens during extension (n = 1) precluded investigation of the effects of joint level and species on joint stiffness using 2-way ANOVA (statistical power would have been less than 10%). There were no significant differences in human joint stiffness magnitudes with joint level (1-way ANOVA; p = 0.36). The effect of species on joint stiffness at a given joint level was investigated by looking at the 95% confidence intervals for the human spine data. Joint stiffness magnitudes for the single cat spine specimen at the cephalic, middle, and caudal joint levels (0.05, 0.19, and 0.15 Nm/deg, respectively) were well below the lower limit of the 95% confidence intervals for the same joints of humans (0.97, 0.95, and 0.94 Nm/deg, respectively).

Torque at yield point and torque limit

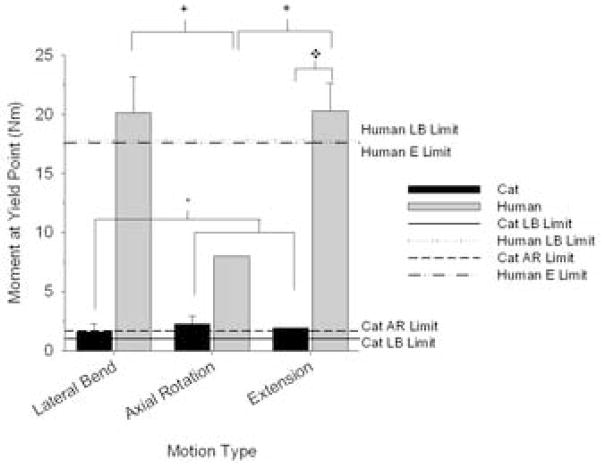
Torque at yield point was significantly associated with interactions between species and motion type (Fig. 7; 2-way ANOVA; p = 0.046). During extension, torque at yield was significantly greater for human spines compared to cat (SNK, p < 0.05). For cat specimens during lateral bending, torque at yield point was significantly less than that during axial rotation or extension (SNK, p < 0.05). For human spine specimens during axial rotation, torque at yield point was significantly smaller in magnitude compared to lateral bending or extension (SNK, p < 0.05). Torque-limit (Fig. 7; 10^th percentile of the yield point) was computed for human specimens during extension and lateral bending (the missing data during axial rotations (n = 1) precluded calculation of torque-limit). For cat spines, torque-limit was computed for axial rotations and lateral bending (missing data during extension (n = 1) precluded calculation of torque-limit). Human lumbar torque limits during lateral bending and extension were 17.8 and 17.6 Nm, respectively. For cat specimens, torque-limits during lateral bending and axial rotation were consistently an order of magnitude lower (1.0 and 1.7 Nm, respectively).

Figure 7.

Moment at yield point and torque limit for cat and human lumbar spine specimens during lateral bending (LB), axial rotation (AR), and extension (E). There were significant interactions between species and motion type (2-way ANOVA, p = 0.046). Multiple comparison tests (Student-Newman-Keuls Test, p < 0.05): *Motion significant within cat; +Motion significant within human; ◆Species significant within motion. Lines show torque-limit, which was computed as the 10th percentile of the moment at yield point. Torque-limits for human lumbar spines were larger in magnitude compared to that of cat spines.

Mathematical modeling

During lateral bending, representations of lumbar spine specimens as elliptical shafts undergoing bending were highly correlated. For cat spine specimens, relating the torque at yield point and L7-S1 stiffness (Ê; proxy for Young’s modulus) to area moment of inertia (I) was highly correlated (R² = 0.831). The result was the proxy for the radius of curvature (ρ̂_cat = 67900). Correlations for human spine specimens during lateral bending were high as well (R² = 0.99), and the proxy for radius of curvature was ρ̂_human = 83300.

During axial rotation, the relationship between cat spine material properties (Ĝ; torsional stiffness of L7-S1 as a proxy for Young’s modulus and torque at yield point) and structural properties (specimen length and polar moment of inertia) was highly correlated (R² = 0.875). The proxy for angle of twist (φ̂) was 0.00949. No proxy for angle of twist could be determined for human spines because data was obtained for a single specimen only (and hence a regression relationship could not be established).

Although no data were obtained from cat spines during extension, ρ̂ was computed for human spine specimens during extension. The relationship was not significant (p = 0.194) and was poorly correlated (R² = 0.480).

Discussion

This is the first report quantifying cat lumbar torque limits during physiological motions and the first report of human lumbar spine specimens (T12-sacrum) during displacement-controlled loading. Cat torque limits were smaller in magnitude compared to that of human for the same type of physiological motion. Torque-limits for cat and human lumbar spine specimens were mathematically modeled as elliptically-shaped beams undergoing bending using equations that related geometric and material properties. The torque limits found in the current study can be used in future studies investigating the biomechanics of cat or human spines within the “physiological range.”

Major-axis IVA magnitudes were similar in cat and human spine specimens during lateral bending. During extension or axial rotation, comparison across the two species using data from the current study was limited due to the small sample sizes, although previous studies from our laboratory indicate that during similarly applied global displacements, cat IVA magnitudes were comparable to those that develop in humans during these motions as well. For example, at 40 mm displacement during extension, IVA magnitudes in human spines were approximately 5.5° at L5-S1 (c.f. Fig. 4 in Ianuzzi et al.[19]), which were similar to cat IVA magnitudes for the same amount of global spine displacement in the current study (Fig. 4). Similarly during axial rotations, human IVA magnitudes were relatively small (e.g., about 3° at L4-5; c.f. Fig. 7 in Ianuzzi and Khalsa [21]) and were in the same range in the cat in the current study (Fig. 4). Human IVA magnitudes approaching the yield point in the current study were greater compared to prior studies (e.g., L4-5 IVA during lateral bending approached 18°). The data also were more variable within that region, which was likely due to the onset of plastic deformation and variability in yield point among the specimens.

The higher torque-limit in cat spines during axial rotation compared to lateral bending (1.7 Nm versus 1.0 Nm, respectively) was likely because while both motion types are restricted by the bony facets and accessory processes, lateral bending is restricted more by soft tissue (e.g., facet joint capsule and intertransverse ligaments) on the contralateral side. Compared to the relatively stronger bony structures that restrict axial rotations, the lower strength of the soft tissues that restrict lateral bending could have resulted in failure at smaller torque magnitudes, which was supported by the significant differences in mean torque at yield point between the two motion types.

During axial rotations and lateral bending, there were high correlations between geometric (i.e., moment of inertia and/or length) and mechanical properties (i.e., stiffness and yield point) of cat lumbar spines. A scaling relationship was determined for cat and human spines during lateral bending. The strength of each relationship demonstrated that there is indeed an association between geometric and mechanical properties in both cat and human lumbar spines. Even though other physiological motions were not examined in this study, the results support the use of the cat as a model for the human lumbar spine.

The cat is a well-established in vivo model that has been used to investigate how spinal afferents respond to spinal loading [14–17]. Such experiments would not be possible to conduct in humans due to ethical and logistic considerations. Neurophysiological data from cat models could be utilized to estimate how human afferents might respond to biomechanically similar motions. The similar ranges of motion measured in cat and human lumbar spines in the current study support the use of the cat as a model to study neuromechanics of the lumbar spine.

During extension in human spines, there was a poor correlation for determination of ρ̂ (proxy for radius of curvature). This may have occurred because during extension, several of the spine specimens failed at the sacrum, as was evidenced by a cracking noise at failure and a prominent fracture that could be seen in the sacrum. Different mechanisms of failure for each spine specimen could have increased variability, accounting for the poor correlation and insignificant relationship. For these specimens, including area moment of inertia and stiffness at L5-S1 in the relationship also probably increased variability, as the point of failure was not at this joint level for these specimens. Human spine specimens were obtained from an aged population (65.0 ± 12.7 years), which increased the likelihood that the sacral bone was weaker (i.e., osteoporotic) compared to if the specimens had come from younger donors.

During static, torque-controlled loading of human spine specimens, Panjabi et al. [24] reported that torque exceeding 15 Nm resulted in load-displacement relationships indicative of soft tissue damage. This is smaller in magnitude compared to the torque-limits established for displacement-controlled testing in the current study (extension: 17.8 Nm; lateral bending: 17.6 Nm). The difference was most likely due to the inherent viscoelasticity of the spine, which creeps under a constant load, but relaxes under constant displacement. Mechanical testing of human spine specimens under torque control has been suggested as a standardized method for evaluating spinal implant performances across different studies [4]. The lumbar spine is viscoelastic [25], and repetitive cyclic or static loading under torque control results in creep of soft paraspinal tissues in human [26] and cat [27]. Under displacement controlled, repetitive cyclic testing, human lumbar spine specimens undergo stress relaxation [19]. The data suggest that under displacement-controlled testing, a higher torque limit, up to 17 Nm, could be utilized with less chance of damage to the paraspinal tissues after repetitive testing.

Torque-limits computed for cat lumbar spines during axial rotation and lateral bending were smaller in magnitude compared to those obtained for human spines. This may have been due to anatomical differences between the two species. In humans, pure axial rotation ceases when the sagittally-oriented facet joints come into contact [28], while the kinematics of lumbar joint segments have not been studied extensively in cats. Lumbar facets in cats have slightly different orientations, with the superior and inferior facets facing medial-posteriorly and lateral-anteriorly, respectively [29]. Cats also have elongated accessory processes lateral to the facets [29], which are not as well developed in humans. Anatomical differences between cat and human lumbar spines may result in different biomechanics during these motions, causing different structures to fail. The difference in torque-limits may also be due to differences in yield strength of the paraspinal tissues that fail. Supraspinous and interspinous ligaments of cat spines have a higher ratio of elastic fibers to collagenous fibers compared to humans [30], which likely resulted in different failure strengths. Although there have not been any studies investigating histological properties of the other lumbar spinal ligaments in cats, observations in our laboratory indicated that other spinal ligaments in cat were also thinner and more delicate than those of humans. This likely translated to differences in ligament material properties between the two species, which also would account for differences in yield point of cat and human lumbar spines. Increased flexibility in cat lumbar spines allows for activities such as galloping and grooming [31].

There are a number of limitations that should be considered when interpreting the results of this study. Inherent limitations of cadaveric models included lack of musculature and surrounding tissue, and possible drying (and perhaps stiffening) of soft tissues over time. Attempts were made to limit drying of tissues by wrapping spine specimens in PBS-soaked gauze and periodically spraying exposed tissue with PBS. Secondly, torque-limits were determined under displacement control and, due to the spine’s inherent viscoelasticity, were likely larger in magnitude compared to those under torque control. Another methodological consideration was that human spine specimens were obtained from a relatively old population, while cat spines in the current study were relatively young adults. If human spine specimens had come from a more controlled source, sample variability and correlation coefficients probably would have been improved and more similar to that observed in the cat specimens (which were laboratory-bred and matched for age, mass, etc.).

In conclusion, the physiological limit was determined for vertebral joint torque of cat and human cadaveric spine specimens. The physiological range of movement for cat lumbar spine specimens was determined for the displacement-controlled testing apparatus described here. Torque-limits determined in this study can aide in the design of future neurophysiological studies using cat spines to ensure that mechanical testing is conducted within the physiological range. Future work will also include scaling biomechanics of cat and human lumbar spine specimens during other motion types (e.g., physiological motions or simulated spinal manipulation).