Abstract
Many problems in computer vision involving recognition and/or classification can be posed in the general framework of supervised learning. There is however one aspect of image datasets, the high-dimensionality of the data points, that makes the direct application of off-the-shelf learning techniques problematic. In this paper, we present a novel concept class and a companion tractable algorithm for learning a suitable classifier from a given labeled dataset, that is particularly suited to high-dimensional sparse datasets. Each member class in the dataset is represented by a prototype conic section in the feature space, and new data points are classified based on a distance measure to each such representative conic section that is parameterized by its focus, directrix and eccentricity. Learning is achieved by altering the parameters of the conic section descriptor for each class, so as to better represent the data. We demonstrate the efficacy of the technique by comparing it to several well known classifiers on multiple public domain datasets.
1. Introduction
Many notable problems in computer vision and related fields, such as automated face recognition from images [11], diagnosis of Epilepsy from MRI scans of the brain [10], and diagnosis of various forms of Cancer from micro-array gene expression data [1], can be posed in the general framework of supervised learning. In such cases, the abstract problem may be posed formally as follows: One is given a dataset of N labeled tuples {〈X1, y1〉, … 〈XN, yN 〉}, where the Xi’s are the data points represented in some feature space  , and the yi’s their associated class labels. For a dataset with K classes, the yi’s take nominal values in the range [1, K].
, and the yi’s their associated class labels. For a dataset with K classes, the yi’s take nominal values in the range [1, K].  in most cases is the Euclidean space ℝM. The goal of learning is to identify a function f:
in most cases is the Euclidean space ℝM. The goal of learning is to identify a function f:  → [1, K] (called the classifier) that minimizes the generalization error.
→ [1, K] (called the classifier) that minimizes the generalization error.
Although Statistical Learning Theory [12] does provide formal bounds for the generalization error of a classifier as a function of the classifier’s empirical error on the given dataset and a formalization of the complexity of the classifier’s concept class, such bounds are often weak. The common practice therefore is to estimate the generalization error via such protocols as cross-validation and bootstrapping. Without detailed prior knowledge regarding the nature of a dataset, it is not possible to predict which of a given set of concept classes will yield the smallest generalization error. Practitioners therefore resort to applying as many classifiers with different concept classes as possible, before choosing the one that yields the least generalization error estimated via one of the above noted protocols. Every new concept class with a corresponding tractable learning algorithm is consequently a potential asset to a practitioner since it expands the set of classifiers that can be applied to a dataset.
The difficulty of learning a classifier becomes particularly acute when the dimensionality of the feature space, M, is far greater than the size of the dataset, N. This situation arises whenever the “natural” description of a data point in the problem domain is very large and the cost of collecting large number of labeled data points is prohibitive. Classification problems that involve images are specifically prone to this issue. In such scenarios, learning even a simple classifier such as a linear discriminant is under-constrained because one has to solve for M + 1 parameters given only N inequalities. Additional objectives, such as maximizing the margin of the discriminant, is usually introduced to fully constrain the problem. The learning problem becomes progressively difficult as the concept class of the classifier becomes richer, since such classifiers require larger number of parameters to be solved for, given the same number of constraints. This leads to over-fitting and the generalization capacity of the classifier suffers. The traditional response to this quandary has been to either restrict oneself to the simplest of concept classes or to reduce the dimensionality of the dataset by projecting onto a subspace through techniques such as PCA; the assumption underlying the second approach being that there is a smaller set of compound features that is sufficient for the purpose of classification.
In this paper, we present a novel concept class that expands the power of the first approach noted above. The concept class, presented in Section 2, is rich and subsumes linear discriminants, and yet is specified with merely twice the number of parameters as a linear discriminant. Each member class in the dataset is represented by a prototype conic section in the feature space, and new data points are classified based on a distance measure to each such representative conic section. In Section 3, we present a tractable algorithm for learning the appropriate conic sections (i.e., their directrices, foci, and eccentricities) for the classes given a labeled dataset. In Section 4, we demonstrate the efficacy of the technique by comparing it to several well known classifiers on multiple artificial as well as public domain datasets.
2. The Concept Class using Conic Sections
A conic section in ℝ2 is defined as the locus of points whose distance from a given point (the focus) and that from a given line (the directrix), form a constant ratio (the eccentricity). Different kinds of conic sections, ellipse, parabola and hyperbola, are obtained by fixing the value of the eccentricity to < 1, = 1, and > 1, respectively. The concept can be generalized to ℝM by making the directrix a hyperplane of codimension 1. Together, the focus and the directrix hyperplane generate an eccentricity function that attributes to each point X ∈ ℝM a scalar valued eccentricity defined as:
| (1) |
where F ∈ ℝM is the focus, and (b + DT X) (assuming DT D = 1) is the orthogonal distance of X from the directrix represented as {b, D}, where b ∈ ℝ is the offset of the directrix from the origin and D ∈ ℝM, DT D = 1, is the unit normal vector to the directrix. Setting ε(X) = ê yields an axially symmetric conic sections in ℝM.
We are now in a position to formally define the concept class. To each class, k, we assign a distinct conic section parameterized by the descriptor set: focus, directrix and eccentricity, as Ck = {Fk, {bk, Dk}, êk}. For any given point X, each class attributes an eccentricity εk(X), as defined in Eqn. 1, in terms of the descriptor set Ck. The conic sections for a set of K classes induce a mapping ε*: ℝM → ℝK, from the feature space to the eccentricity space (ecc-Space) as, ε*(X) = 〈ε1(X), …, εK (X)〉. The point X is assigned to the class whose eccentricity descriptor êk is closest in magnitude to the attributed eccentricity, i.e.,
| (2) |
| (3) |
With an eye towards simplicity, we restrict the rest of the presentation to the binary classification case. The discriminant boundary (Eqn. 3) for this case is the locus of points equidistant to the representative conic sections, in eccentricity. This discriminant corresponds to a rich, non-linear surface in ℝM.
The concept class just described has several notable features. As shown in Fig. 1, different configurations of two conic sections (shown in ℝ2) generate different discriminant boundaries, ranging from simple to complex. Fig. 1(a) corresponds to a configuration where the directrices for the two classes are identical, the foci for the two classes lie symmetrically on the two sides of the directrix, and the class eccentricities are equal. If the foci are moved such that the line joining them is bisected by the directrix, the boundary remains linear (Fig. 1(b)). When the angle between the normals to the directrices, D1, D2, is non-zero, the boundary becomes non-linear (Fig. 1(c)). Further changes in the descriptors produce rich non-linear boundaries (Fig. 1(d)).
Figure 1.
Discriminant boundaries in ℝ2. (See Sec-2)
Regardless of the dimensionality of the feature space, the discriminant is linear when the directrices of the two classes are parallel, the foci are equidistant from the directrices, and the class eccentricities are equal and lie in a particular range. The concept class therefore subsumes linear discriminants. Finally, the number of parameters necessary to specify the conic sections for each class is 2 * (M + 1), which is far less than the M2 parameters necessary to specify a generic quadratic surface. We point out in passing that there is no known kernel for the support vector machine which matches this concept class, and therefore, the concept class is novel.
3. Learning Algorithm - The Two-Class case
In this section, we present a novel incremental algorithm (Algorithm-1) for learning the conic section descriptors, Ck = {Fk, {bk, Dk}, êk} for k = 1, 2, that minimize the empirical error (Eqn. 4). We assume a set of N labeled samples P = {〈X1, y1〉, …, 〈XN, yN 〉}, where Xi ∈ ℝM and the label yi ∈ {1, 2}, and that the data is sparse in a very high dimensional input space, i.e., N ≪ M.
Algorithm 1.
Learning the descriptors C1, C2
| Data: Labeled Samples P |
| Result: Conic Section Descriptors C1, C2 |
| 1: Initialize {F1, b1, D1}, {F2, b2, D2} [Sec. 3.6] |
| 2: Compute 〈ε1(Xi), ε2(Xi)〉 ∀Xi ∈ P |
| 3: Find class-eccentricities 〈ê1, ê2〉 [Sec. 3.1] |
| 4: Compute the desired [Sec. 3.2] |
| 5: Update foci & directrices alternately. [Sec. 3.3, 3.5] |
| 6: Goto (2) until convergence of descriptors. |
Following initialization of the descriptors (Section 3.6), the learning process is comprised of two stages. In the first stage, C1 and C2 are held fixed, and each Xi is mapped into ecc-Space by computing its attributed eccentricities, 〈ε1(Xi), ε2(Xi)〉. The pair of class eccentricities 〈ê1, ê2〉 that minimizes the empirical risk Lerr is then computed.
| (4) |
where  is the indicator function. For each misclassified sample, one can find a desired pair of attributed eccentricities
that would correctly classify that sample.
is the indicator function. For each misclassified sample, one can find a desired pair of attributed eccentricities
that would correctly classify that sample.
In the second stage, the foci {F1, F2} and the directrices {{b1, D1}, {b2, D2}} are updated alternately so as to achieve the desired attributed eccentricities for those misclassified samples, without affecting the attributed eccentricities for those samples that are already correctly classified. The process is repeated until the descriptors converge or there can be no further improvement in classification.
3.1. Finding Class-Eccentricities 〈ê1, ê2〉
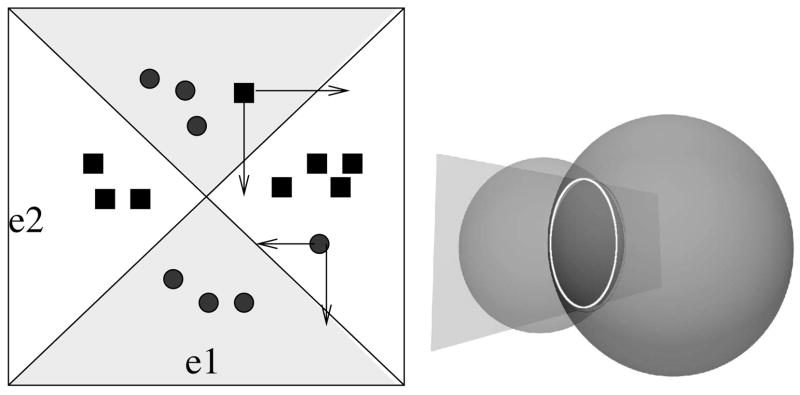
Note that the dimensionality of ecc-Space is the number of classes (2 in our case). For any given choice of class eccentricities, the discriminant boundary (Eqn. 3) in ecc-Space is a pair of orthogonal lines with slopes +1, −1, respectively, as illustrated in Fig. 2(a). The lines intersect at 〈ê1, ê2〉 (referred to hereafter as the cross-hair). The lines divide ecc-space into four quadrants with opposite pairs belonging to the same class. It should be noted that this discriminant corresponds to a non-linear decision boundary in the feature space ℝM.
Figure 2.
(a) Shaded regions in this ecc-space belong to one class. Learning involves shifting misclassified points into desired regions. (b) Intersection of two hyper-sphere Null spaces
We now present an O(N2) algorithm to find the optimal cross-hair. The method begins by rotating ecc-Space around the origin by 45° so that any choice of the discriminants will now be parallel to the new axes. Each axis is divided into (N + 1) intervals by projecting the points in ecc-Space onto that axis. Consequently, ecc-Space is partitioned into (N + 1)2 2D intervals. We now make a crucial observation: within the confines of a given 2D interval, any choice of a cross-hair classifies the set of samples identically. We can therefore enumerate just the (N + 1)2 intervals and choose the one that gives the smallest classification error. The cross-hair is set at the center of this 2D interval. In cases where there are multiple 2D intervals that give the smallest classification error, the larger one is chosen.
3.2. Learning Misclassified Points
Given the attributed eccentricities 〈ε1i, ε2i〉 of a misclassified point, we can compute its desired location in ecc-Space (see Fig. 2(a)) by moving it into the nearest quadrant associated with its class label. This movement can be achieved by updating a focus or directrix in Eqn. 1. In order to keep the learning process simple, we update only one descriptor of a particular class at each iteration. Hence, we move the misclassified points in ecc-Space by changing ε1i or ε2i for the class of the descriptor being updated.
The learning task now reduces to alternately updating the foci and directrices of C1 and C2, so that the misclassified points are mapped into the desired quadrants in ecc-Space, while the correctly classified points remain fixed. Note that with such an update, our learning rate is non-decreasing. We also introduce a margin along the discriminant boundary and require the misclassified points to be shifted beyond this margin into the correct quadrant. In most of our experiments the margin was set to 5% of the range of eccentricity values in ecc-Space.
3.3. Updating The Focus
Our objective here is to achieve the desired attributed eccentricities
for all the samples by changing the focus Fk. For each correctly classified sample, the desired eccentricity
is simply its previous value εki. From Eqn. 1 we can conclude that the εki’s for k = 1 depend only on the class descriptor C1, and likewise for k = 2. Since we update only one focus at a time, we shall hereafter deal with the case k = 1. The update problem may be posed formally as follows. Find a focus F1 that satisfies the following N quadratic constraints. Let || · ||2 be the Euclidean  2 norm.
2 norm.
| (5) |
| (6) |
In effect, each point Xi desires F1 to be at a distance r1i from itself, derived from Eqn. 6. Pc and Pmc are the set of classified and misclassified points respectively. The inequalities above imply that the desired location can lie in an interval along an axis in ecc-Space (See Fig. 2). In order to closely control the learning process, we learn one misclassified point at a time, while holding all the others fixed. This leaves us with only one inequality constraint.
We refer to the set of all feasible solutions to the above quadratic constraints as the Null Space of F1. Further, we have to pick an optimal F1 in this Null Space that maximizes the generalization capacity of the classifier. Although the general Quadratic Programming Problem is known to be NP-hard, the above constraints have a nice geometric structure that can be exploited to construct the Null Space in O(N 2M) time. Note that by assumption, the number of constraints, N ≪ M. The Null Space of F1 with respect to each equality constraint in Eqn. 5 is a hyper-sphere in ℝM. Hence, the Null Space for all the constraints combined is simply the intersection of all the corresponding hyper-spheres in ℝM with centers {X1, …, XN} and radii {r11, …, r1N }. Let XN be the single point being updated in ecc-Space. Then, r1N can take any value within an interval (rmin, rmax) corresponding to the range of desired . The solution to this case is presented next.
3.4. The Intersection of Spheres problem
We present an algorithm that builds the Null Space incrementally. For ease of readability, we drop the reference to class in this section. The Null Space is initialized as the set of feasible solutions for the first equality constraint in Eqn. 5. It can be parameterized as the hyper-sphere S1 = (r1, X1), where r1 is the desired distance of a solution from the sample X1. At the next step, the second equality constraint is introduced, the Null Space for which, considered independently, is the hyper-sphere S2 = (r2, X2). Hence the combined Null Space for the two constraints is the intersection of the two hyper-spheres, S1 ∩ S2.
As illustrated in Fig. 2(b), the intersection of two spheres in ℝ3 is a circle that lies on the plane of intersection of the two spheres. Our technique is based on a generalization of this setting in ℝM. We make two critical observations: the intersection of two hyper-spheres is a hyper-sphere of one lower dimension, and this hyper-sphere lies on the intersecting hyper-plane of the original hyper-spheres. We re-parameterize the combined Null Space, S1 ∩ S2, as a lower-dimensional hyper-sphere S{1,2}, lying in the hyperplane of intersection H{1,2}. Based on the geometry of the problem and the parameterization of S1 and S2, it is trivial to compute, in O(M), the radius and center of the new hyper-sphere S{1,2} = (r{1,2}, X{1,2}), as well as the intersecting hyper-plane H{1,2} represented as (b{1,2}, Q12), the first parameter being the displacement of H{1,2} from the origin and the second being the unit normal to H{1,2}. Q{1,2} lies along the line joining X1 and X2.
We now solve the remainder of the problem on the hyperplane H{1,2}. This is accomplished by intersecting each of the remaining hyper-spheres S3,., SN that correspond to the samples X3,., XN, with H{1,2}, in O(N M) time. Once again, based on the geometry of the problem, it is trivial to compute the new radii and centers of the corresponding hyper-spheres. In short, the intersection of the N hyper-spheres problem is converted into the intersection of (N −1) hyper-spheres and a hyper-plane H{1,2} problem.
| (7) |
| (8) |
The problem is now transparently posed in the lower dimensional hyper-plane H{1,2} as a problem equivalent to the one that we began with, except with one less hyper-sphere constraint. The end result of this iteration for all the (N − 1) equality constraints is a low dimensional linear subspace in which lies the Null Space Se represented as a single hyper-sphere (parameterized as a radius and a center), computed in O(N2M) time. It should be observed that all the intersections thus far are feasible and that the successive Null Spaces have non-zero radii since the equality constraints have a feasible solution apriori.
Let SN be the null space for the inequality constraint with rN ∈(rmin, rmax). If SN intersects with Se, we chose a radius rN that maximally shifts the corresponding misclassified point in ecc-Space. On the resultant final Null Space, we picked a solution that improves the generalization capacity of the classifier. We have found that any choice of the solution that arrives at a configuration close to that in Fig 1(a), results in a simpler discriminant in the input space. If Se does not intersect with SN, this simply means that the chosen misclassified point can not be shifted entirely to the desired location in ecc-Space. In such a case, we picked an appropriate solution on Se that allows the maximum possible shift.
3.5. Updating The Directrix
We demonstrate in this section that the Directrix Update problem is closely related to the Focus Update problem owing to the duality of points and hyper-planes. We begin by once again noting that {b1, D1} may be updated independent of {b2, D2}, and vice versa. The goal here is to update the directrix descriptor {b1, D1} for a given F1 and desired eccentricities . Just as in the focus update, each point Xi desires the directrix to be at a certain orthogonal distance v1i, from itself. The problem reduces to finding a directrix that satisfies the constraints:
| (9) |
| (10) |
This problem appears simpler at first sight since it is comprised of N linear constraints. However, the quadratic constraint requiring D1 to be an unit normal makes the above a Quadratic Programming Problem which is again NP-hard in general. Once again, we exploit the geometric structure inherent in the problem to arrive at the Null Space in O(N2M) time. We first solve for the scalar b1 by translating the origin to the first classified point, X1, so that b1 = v11. In addition, just as in Section 3.3, we learn a single misclassified point, say XN, in each iteration. With a known b1, we translate and scale all remaining points such that the linear constraints become:
| (11) |
| (12) |
| (13) |
Now the null space of D1, for each constraint in Eqn. 11 considered separately, is a hyper-plane Hi ∈ ℝM represented as {−v̂1i, X̂i}. The null space corresponding to the quadratic constraint on D1 is a unit hyper-sphere, S1 ∈ ℝM, centered at the new origin. Hence, the final Null Space for D1 is the intersection of all the Hi’s and S1.
We now make two critical observations. The intersection of a hyper-plane with a hyper-sphere is a lower-dimensional hyper-sphere. Same is the case with the intersection of two hyper-spheres. We can therefore convert this hyperplane-hypersphere intersection problem into a hypersphere-hypersphere intersection problem. In effect, we can replace each hyper-plane Hi with a suitable hyper-sphere Si such that Hi ∩ S1 = Si ∩ S1. Owing to the geometry of the problem, we can compute Si from Hi and S1. The Null Space for all the constraints combined is now the intersection of all the hyper-spheres S1, S2, …, SN. The problem, now reduced to a hyperspheres-intersection problem, is solved as in Section 3.4.
3.6. Initialization
Given a set of labeled samples, we found that there are several ways of initializing the conic section descriptors that led to a solution. Random initializations converged to different conic descriptors each time leading to inconsistent performance. We observed that owing to Eqn. 1, the Null Spaces are small or vanishing if the foci or directrices are very close to the samples. We found the following initialization to be consistently effective in our experiments. The foci were first placed at the sample class means and then pushed apart until they were outside the sample clouds. The normals to the directrices were initialized as the line joining the foci. The directrix planes were then positioned at the center of this line or on either sides of the data.
3.7. Discussion
One of the core characteristics of our algorithm is that after each update any point that is correctly classified by the earlier descriptors is not subsequently misclassified. This is due to two reasons. First, we begin with an initialization that gives a valid set of assignments for the class attributed eccentricities. This implies that the Null Space for the classified points is non-empty. Second, the search for updates in the Null Space always guarantees the feasible solution for the constraints related to the correctly classified points.
A key contribution of our technique is the tracking of the set of all feasible solutions as a compact geometric object. From this Null Space we pick a solution biased towards a linear discriminant so as to improve upon generalization. The size of margin in ecc-space also gives a modicum of control over generalization. The order of samples processed does not affect the final Null Space. The convergence of our learning algorithm depends on data and initialization. However, we found that it converged to a local minima typically within 50 iterations of the focus and directrix updates.
4. Experiments
We evaluated the classifier on two synthetic datasets and four real datasets. The results were compared against several state-of-the-art linear and non-linear classifiers. The classification accuracies based on leave-one-out cross-validation are presented in Table-1.
Table 1.
Classification accuracies for the Conic Section Classifier, (Linear & Kernel) Fisher Discriminants and SVM. (See Sec-4)
| Samples | Data Size (N×M) | CSC | LFD | KFD PLY | KFD RBF | SVM PLY | SVM RBF |
|---|---|---|---|---|---|---|---|
| Synthetic Data1 | 20 × 40 | 100 | 100 | 100 | 100 | 100 | 100 |
| Synthetic Data2 | 32 × 64 | 93.75 | 87.5 | 75 | 75 | 81.25 | 87.5 |
| Epilepsy | 31 × 2286 | 77.42 | 67.74 | 67.74 | 61.29 | 67.74 | 74.19 |
| Colon Tumor | 62 × 2000 | 87.1 | 85.48 | 75.81 | 82.26 | 82.26 | 85.48 |
| UMIST FaceDB | 575 × 10304 | 97.74 | 98.72 | 99.93 | 99.91 | 99.3 | 99.06 |
| Texture Pair1 | 95 × 601 | 100 | 100 | 100 | 100 | 100 | 100 |
| Texture Pair2 | 95 × 601 | 92.63 | 98.94 | 100 | 100 | 90.52 | 82.10 |
Support Vector Machines (SVM) [2] and Kernel Fisher Discriminants (KFD) [7] broadly represented the non-linear category. Both employ the kernel trick of replacing inner products with Mercer kernels. Among the linear classifiers, we chose the Linear Fisher Discriminant (LFD) [4] and linear SVM. We used the OSU SVM toolbox for MATLAB based on libSVM [13]. We considered Polynomial (PLY) and Radial Basis (RBF) Kernels.
The best parameters were empirically explored. Polynomial kernels gave best results with either degree = 1 or 2 and the scale was approximately the sample variance. The RBF kernel performed best when the radius was the sample variance or the mean distance between all sample pairs.
4.1. Results
Synthetic dataset-1 was randomly generated from two well separated Gaussian clusters in ℝ40. The results in Table-1 validate our classifier’s effectiveness on simple, linearly separable data. Synthetic dataset-2 was generated by sampling from two intersecting paraboloids (related to the two classes) in ℝ3 and placing them in ℝ64. This instance shows that our classifier favors data lying on paraboloids. It clearly out-performed the other classifiers.
Epilepsy data [10] consists of displacement vector fields between the left and right hippocampi for 31 epilepsy patients. The displacement vectors are computed at 762 discrete mesh points on each of the hippocampal surfaces, in 3D. This vector field representing the non-rigid registration, captures the asymmetry between the left and right hippocampi. Hence, it can be used to categorize different classes of epilepsy based on the localization of the focus of epilepsy to either the left (LATL) or right temporal lobe (RATL). The LATL vs. RATL classification is a hard problem. As seen in Table-1, our classifier out-performed all the others and with a significant margin, except over SVM-RBF. In fact, our result is better than that reported in [10]. The best RBF kernel parameters for SVM and KFD methods were 600 and 1000, respectively. The best degree for the polynomial kernel was 1 for both of them.
The Colon Tumor data [1] comprises of 2000 gene-expression levels for 22 normal and 40 tumor colon tissues. The normals to directrix descriptors were initialized with the LFD direction in this case. Our classifier yielded 87% accuracy outperforming the other classifiers. Interestingly, most of the other classifiers could not out-perform LFD, implying that they were learning the noise as well. Terrence, et al. [5] were able to correctly classify two more samples with a linear SVM, only after adding a diagonal factor of two to the kernel matrix.
The Sheffield (formerly UMIST) Face Database [6] has 564 pre-cropped face images of 20 individuals with varying pose. Each image has 92 × 112 pixels with 256 gray-levels. Since we only have a binary classifier now, the average classification performance over all possible pairs of subjects is reported. This turned out to be an easier problem. Conic classifier achieved a comparable accuracy of about 98%, while the others were near 100%.
CURET database [3] is a collection of 61 texture classes imaged under 205 illumination and viewing conditions. Varma et al. [9] have built a dictionary of 601 textons and computed texton frequencies in a given sample image. The texton frequency histograms obtained from [8], can be used as the sample feature vectors for classification. About 47 images were chosen from each class, with out a preferential order so as to demonstrate the efficacy of our classifier for high-dimensional sparse data. We report the results for an easy pair and a relatively tougher pair of textures for classification. The two cases are Sand paper vs. Rough paper (Pair1) and Sand paper vs. Polyester (Pair2), respectively. As seen in Table-1, Pair1 turned out to be easier case in deed. KFD out-performed the others for the second pair and our classifier fared comparably.
5. Summary and Conclusions
In this paper, we have introduced a novel concept class based on conic section descriptors, provided a tractable supervised learning algorithm, and have tested the resultant classifier against several state-of-the-art classifiers on many public domain datasets. Our classifier was able to classify tougher datasets better than others in most cases as validated in Table-1. The classifier in its present form uses axially symmetric conic sections. In future work, we intend to extend this technique for multi-class classification and to conic sections that are not necessarily axially symmetric.
Footnotes
This research was in part supported by NIH RO1 NS046812 to BCV.
References
- 1.Alan U, et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. PNAS. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cortes C, Vapnik V. Support-vector networks. Machine Learning. 1995;20(3):273–297. [Google Scholar]
- 3.Dana KJ, et al. Reflectance and texture of real-world surfaces. ACM Transactions on Graphics. 1999;18(1):1–34. [Google Scholar]
- 4.Duda RO, Hart PE, Stork DG. Pattern Classification. Wiley-Interscience; 2001. [Google Scholar]
- 5.Furey T, et al. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics. 2000;16(10):906–914. doi: 10.1093/bioinformatics/16.10.906. [DOI] [PubMed] [Google Scholar]
- 6.Graham D, Allinson N. Characterizing virtual eigen signatures for general purpose face recognition. NATO ASI Series F, Comp & Sys Sci. 1998;163:446–456. [Google Scholar]
- 7.Mika S, et al. Fisher discriminant analysis with kernels. Neural Networks for Signal Processing. 1999;IX:41–48. [Google Scholar]
- 8.Spellman E, Vemuri BC, Rao M. Using the KL-center for efficient and accurate retrieval of distributions arising from texture images. CVPR. 2005:111–116. [Google Scholar]
- 9.Varma M, Zisserman A. Texture classification: Are filter banks necessary? 2003 June;2:691–698. [Google Scholar]
- 10.Vohra N, et al. Kernel fisher for shape based classification in epilepsy. MICCAI. 2002:436–443. [Google Scholar]
- 11.Zhao W, et al. Face recognition: A literature survey. ACM Comput Surv. 2003;35(4):399–458. [Google Scholar]
- 12.Vapnik V. Statistical Learning Theory. John Wiley and Sons; New York: 1999. [Google Scholar]
- 13.Chang C, Lin C. LIBSVM: a Library for Support Vector Machines (Version 2.31) [Google Scholar]