Pentobarbital Produces Activation and Block of α₁β₂γ_2S GABA_A Receptors in Rapidly Perfused Whole Cells and Membrane Patches: Divergent Results Can Be Explained by Pharmacokinetics

Abstract

Millimolar concentrations of the barbiturate pentobarbital (PB) activate γ-aminobutyric acid (GABA) type A receptors (GABARs) and cause blockade reported by a paradoxical current increase or “tail” upon washout. To explore the mechanism of blockade, we investigated PB-triggered currents of recombinant α₁β₂γ_2S GABARs in whole cells and outside-out membrane patches using rapid perfusion. Whole cell currents showed characteristic bell-shaped concentration dependence where high concentrations triggered tail currents with peak amplitudes similar to those during PB application. Tail current time courses could not be described by multi-exponential functions at high concentrations (≥3,000 μM). Deactivation time course decayed over seconds and was slowed by increasing PB concentration and application time. In contrast, macropatch tail currents manifested eightfold greater relative amplitude, were described by multi-exponential functions, and had millisecond rise times; deactivation occurred over fractions of seconds and was insensitive to PB concentration and application time. A parsimonious gating model was constructed that accounts for macropatch results (“patch” model). Lipophilic drug molecules migrate slowly through cells due to avid partitioning into lipophilic subcellular compartments. Inclusion of such a pharmacokinetic compartment into the patch model introduced a slow kinetic component in the extracellular exchange time course, thereby providing recapitulation of divergent whole cell results. GABA co-application potentiated PB blockade. Overall, the results indicate that block is produced by PB concentrations sixfold lower than for activation involving at least three inhibitory PB binding sites, suggest a role of blocked channels in GABA-triggered activity at therapeutic PB concentrations, and raise an important technical question regarding the effective rate of exchange during rapid perfusion of whole cells with PB.

INTRODUCTION

γ-Aminobutyric acid (GABA) is the primary inhibitory neurotransmitter in the vertebrate central nervous system. GABA binds to an ionotropic, heteropentameric receptor (GABA type A receptor [GABAR]) and triggers the activation of an integral chloride channel. This generally results in membrane hyperpolarization via phasic and tonic inhibitory mechanisms leading to suppressed neuronal excitability. GABAR function is subunit dependent, and a wide variety of pharmacologically relevant compounds, including benzodiazepines, intravenous and volatile anesthetics, neurosteroids, and barbiturates, are thought to exert their effects on cellular excitability by altering GABAR activity (for reviews see Macdonald, 1994; Mehta and Ticku, 1999; Thompson and Wafford, 2001).

The barbiturate pentobarbital (PB) modulates GABARs in a complex fashion. At low concentrations (10–100 μM), PB potentiates GABA-gated currents (Macdonald and Barker, 1978; Schulz and Macdonald, 1981; Akaike and Oomura, 1985); at intermediate concentrations (100–1,000 μM), PB directly activates GABARs (Barker and Ransom, 1978; Akaike et al., 1985; Robertson, 1989; Rho et al., 1996); and at high (>1,000 μM) concentrations, there is inhibition (Akaike et al., 1987; Rho et al., 1996). PB washout produces a paradoxical current rebound or “tail” reflecting PB unbinding from a site(s) that produces channel blockade (Akaike et al., 1987; Rho et al., 1996; Thompson et al., 1996; Wooltorton et al., 1997; Serafini et al., 2000; Krampfl et al., 2002).

Tail currents are clearly observed at concentrations exceeding 1,000 μM, which is higher than those that trigger channel activation (Akaike et al., 1987; Rho et al., 1996; Serafini et al., 2000; Krampfl et al., 2002; Feng et al., 2004), suggesting that a binding site(s) mediating block has lower affinity than that for activation (Rho et al., 1996; Thompson et al., 1996; Wooltorton et al., 1997; Dalziel et al., 1999; Krampfl et al., 2002). The concentration dependence of tail currents (Akaike et al., 1987; Rho et al., 1996; Serafini et al., 2000; Krampfl et al., 2002) and PB-triggered single-channel gating (Akk and Steinbach, 2000a) suggest that blockade involves multiple binding sites, but the precise number remains an open question. Single-channel studies indicate the blocking mechanism involves open-channel block (Akk and Steinbach, 2000a; Akk et al., 2004). Finally, tail current deactivation time course is slowed by increasing PB concentration (Rho et al., 1996; Serafini et al., 2000; Feng et al., 2004), and at high concentrations, it appears that it cannot be accounted for by multi-exponential functions (see Akaike et al., 1987, Fig. 6, and Akk et al., 2004, Fig. 5). This deviates from linear kinetic behavior expected under concentration clamp provided by rapid whole cell perfusion. As a result, the objectives of this study were to provide new insight into PB blockade of GABARs, specifically into the number of inhibitory binding sites and the gating underlying the complex modulation of tail current time course by PB.

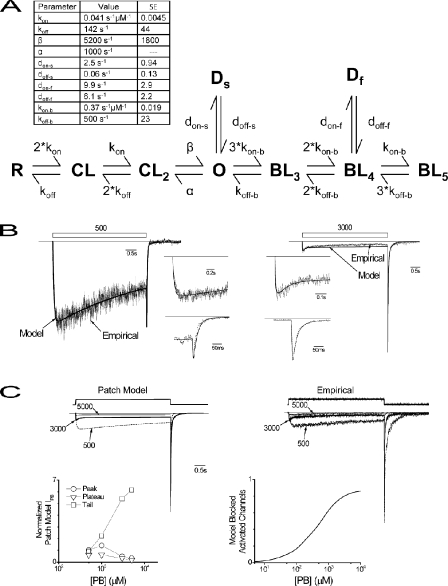
Figure 6.

Patch model reproduces features of gating in macropatches. (A) Patch-gating model that accounts for macropatch currents. Model states are as follows: R, resting closed; CL, singly bound closed, one agonist site; CL₂, doubly bound closed, two agonist sites; O, open; D_s, slow desensitized; D_f, fast desensitized; BL₃, triply bound blocked, two agonist and one inhibitory; BL₄, quadruply occupied, two agonist and two inhibitory; BL₅, pentuply occupied, two agonist and three inhibitory. Model parameter values are given in a table with standard errors (SE). Model fits of empirical macropatch target data used in parameter estimation values are as indicated (B: left, 500 μM; right, 3,000 μM). Open bars above indicate delivery of PB at specified concentration. (Insets) Fits of activation and tail current time course on expanded timescale for clarity. Straight lines indicate baseline. (C, top) Comparison of families of the patch model (left) and empirical (right; reproduced from Fig. 4 A) responses. Individual traces selected for clarity (concentrations indicated) and families were scaled to normalize to the peak of a 3,000-μM response. Upper trace indicates PB application. (Bottom, left) Concentration–response relationships for patch model I_PB peak, plateau, and tail amplitudes in the same fashion as used for the empirical results in Fig. 4 A. (Right) Fraction of activated channels blocked versus PB concentration in patch model. Activated channels represent those that are open (O) or have sojourned through the open state (D_s, D_f, BL₃, BL₄, and BL₅). Blocked activated channels approximates the conditional probability of blocked states, given that the channel is activated and is represented by the expression [P{(BL₃, BL₄, or BL₅) | (O, D_s, D_f, BL₃, BL₄, or BL₅)}] (see Results).

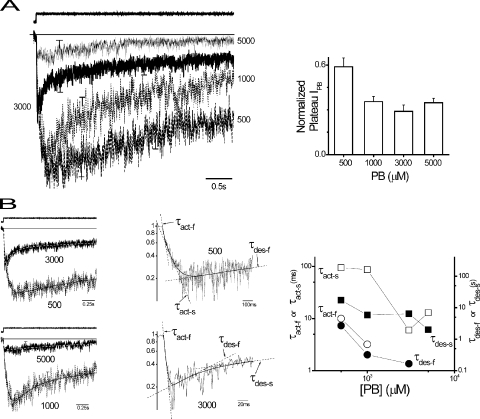
Figure 5.

Kinetic analysis of macropatch currents during PB application. (A, left) Macropatch currents (means ± SEM) during PB application replotted from Fig. 4 A on an expanded timescale at the indicated concentrations (μM). Representative liquid junction potential response (see Materials and methods) representing the time course of the PB pulse is shown above. (Inset) Bar plot of plateau I_PB normalized by peak I_PB taken as a reporter of overall apparent desensitization versus PB concentration. (B, left) Selected responses replotted from above to clearly show the time course and best fit of multi-exponential functions (smooth solid and dashed line). The general multi-exponential fitting involved time constants (fast activation, τ_act-f; slow activation, τ_act-s; fast desensitization, τ_des-f; fast desensitization, τ_des-s) as well associated exponential component amplitudes (not depicted). (Middle) Selected responses replotted on semi-logarithmic axes with fitted multi-exponential functions (smooth solid lines). Exponential components are indicated responses by linear phases marked by dashed straight lines and associated time constants. (Right) Concentration dependence of fitted exponential time constants (see Results).

To this end, we investigated recombinant α₁β₂γ_2S GABARs, thought to be present in the central nervous system (Whiting et al., 1999), in rapidly perfused, whole cell, and single-channel outside-out cell-free membrane patches. Early efforts in whole cells reproduced salient features of PB modulation (Akaike et al., 1987; Feng et al., 2004). We then explored single-channel gating in rapidly perfused outside-out membrane patches. We frequently encountered macroscopic patch currents with tails that manifested eightfold greater relative amplitude and 20-fold faster deactivation relative to whole cells, and that were insensitive to PB concentration and application time. Subsequently, we developed a parsimonious gating model reconciling micro- and macropatch results (patch model). We then considered simple mechanisms that may explain the divergence between whole cell and patch macroscopic currents. Barbiturates manifest low apparent transcellular permeability rates (∼0.4 μm/sec) (Behrens et al., 2001), which may manifest pharmacokinetics (PKs) on a timescale of seconds in HEK-293 cells. This may cause the effective solution exchange of the unstirred layer (Maconochie and Knight, 1989), which bathes membrane-bound GABARs, to be unexpectedly slower than that of whole cell perfusion. We tested this hypothesis through the addition of a lipophilic PK compartment to the “patch” model, which allows it to account for all divergent features of whole cell tail currents.

The major findings of the study derived from macropatch currents include deactivation time course independent of PB concentration and application duration, GABA coapplication potentiation of PB blockade, and channel blockade that is mediated by at least three bindings sites where block is caused by PB concentrations sixfold lower than those for activation. Finally, the divergence in tail current features between whole cells and macropatches can be explained by PB entry into a proposed lipophilic, cellular, PK compartment. Overall, the results advance the understanding of the mechanism underlying PB blockade, point to a role of PB-blocked channels at therapeutic concentrations, previously thought unlikely, and question the effective rate of solution exchange during rapid perfusion of whole cells with PB and perhaps lipophilic agents in general.

MATERIALS AND METHODS

Cell Culture and Transient Transfection

Transformed HEK-293 cells, purchased from American Type Culture Collection, were plated on 18 × 18–mm glass coverslips in 60 × 15–mm Falcon dishes (BD) and cultured in MEM supplemented with 10% FBS and 1% each of penicillin, streptomycin, and glutamine (all from Invitrogen). After incubation in 37°C, 5% CO₂ for 48 h, cells were transiently transfected using a lipofection technique described previously (Gingrich et al., 1995) with cDNAs encoding rat brain α₁, β₂, and γ_2S subunits inserted individually into the plasmid pCDM8 (Invitrogen). In brief, aliquots of lipofection reagent (Lipofectamine; Invitrogen) and appropriate plasmids (1:1:1 by weight, α₁/β₂/γ_2S) were mixed in a modified, serum-free medium (Opti-MEM; Invitrogen) and incubated at room temperature for 10 min. Cells were washed with PBS (Invitrogen), and supplemented MEM was replaced with Opti-MEM, followed by the addition of liposome plasmid–containing solution. After a 6–8-h incubation period (37°C, 5% CO₂), cells were washed with PBS and returned to supplemented MEM for further incubation. Cells were ready for electrophysiological recording 48 h after transfection.

Electrophysiological Recordings

Coverslips with transfected cells were transferred to the lid of a culture dish mounted on the stage of an inverted microscope (IMT-2; Olympus) with Hoffman-modulated optics. The cells were immersed in a modified Tyrode's solution containing (in mM): 135 NaCl, 1 CaCl₂, 5 HEPES, NaOH, pH 7.2. Glass pipettes were prepared from borosilicate glass (Corning) with a multistage puller (Flaming Brown, model P-97; Sutter Instrument Co.) and fire polished (MF-9 Microforge; Narishige). For single-channel recordings, the pipettes were coated with Sylgard (Dow Corning Company). Pipettes were filled with (in mM): 135 CsCl, 1 MgCl₂, 10 HEPES-KOH, 10 EGTA, pH 7.2. Open tip resistances were typically 2–5 MΩ for whole cell recordings and 5–10 MΩ for outside-out patch recordings under these ionic conditions. Currents were recorded with either the whole cell or outside-out configuration of the patch clamp technique (Hamill et al., 1981) using an Axopatch 200A amplifier (Axon CNS; MDS Analytical Technologies). Macropatch currents were those recorded from outside-out membrane patches with sufficient channel number, such that measured currents reflected macroscopic gating. Macroscopic currents were filtered at 1–2 kHz (−3 dB, 4-pole Bessel) and sampled at 12.5 kHz. Single-channel currents were filtered at 2 kHz (−3 dB, 4-pole Bessel) and sampled at 25 kHz. Digitized data were collected and stored on an IBM-compatible (Gateway 2000 4DX-2-66) computer running the Axobasic environment (MDS Analytical Technologies) using software of our own design. Data were collected at room temperature (20–23°C). The chloride potential is 0 mV under these ionic conditions resulting in inward currents (outward Cl⁻ movement) at a holding potential of −60 mV for whole cell recordings and −70 mV for macropatch and single-channel recordings throughout our experiments.

Rapid Solution Changes

PB (Sigma-Aldrich) was prepared fresh daily and diluted to the desired concentrations in Tyrode's solution. Control and test solutions were delivered from syringes mounted on a syringe pump (whole cell experiments; Harvard) or gravity fed (macropatch and single-channel experiments) separately into the lumens of dual-barreled pipettes constructed from pulled borosilicate theta tubing (Sutter Instrument Co.). Pulse application (0.1–10 s) of PB (10–5,000 μM) was achieved by rapid solution changes (rise times: whole cell, <10 ms; patch, <1 ms) through a piezoelectric translator (Gingrich et al., 1995; Burkat et al., 2001). The application period was >30 s. Cells resided on coverslips during whole cell experiments. Outside-out membrane patches were raised to near the middle of the perfusion stream after patch excision. Test solutions containing PB were applied by delivering a filtered (model LPF-100B; 4-pole Bessel, 200 Hz; Warner Instrument Corporation) voltage pulse to a high-voltage amplifier (model P-275.10; Physik Instruments) that drove the macro-block translator, such that a dual-barreled pipette tip moved a short distance. For single-channel recordings, PB pulses were applied every 15 s. At experiment end, the membrane patch was ruptured and open tip junction potential current responses were obtained using half-diluted Tyrode's solution. This response was taken to represent the PB time course during the experiment. Experiments were included only if the time course approximated a pulse with 10–90% rise time <300 μs. In preliminary experiments, the variability of the wash-in latency was <120 μs (SEM). This was reported by the time to reach the half-amplitude point of the junction potential response during repetitive pulsing when the wash-in criterion was satisfied.

Data Analysis

Macroscopic currents during the application of PB and “rebound” currents upon PB washout were fit to multi-exponential functions using a Levenberg-Marquardt algorithm (Origin v7.5; Originlab). The goodness of fit was evaluated by the χ2 value, and adequacy of fit to multi-exponential functions was judged by eye. The number of fitted exponential components was increased until additional functions failed to improve the fit. Normalized concentration–response relationships were fit with the logistic equation [V = A / (1 + (x/x₀)^slope)], where V is the endpoint addressed, A is the maximum value of the fit to V, x is the PB concentration, x₀ is related to the half-blocking concentration, and slope is a slope factor related to the Hill coefficient. Single-channel events were detected by half-height criterion (Sachs et al., 1982) and idealized with custom software running in the Matlab v5.1 environment (Mathworks). The number of active channels in a patch (n) was determined by the stacking of unitary events, which is a good estimator, especially for n ≤ 4 (Horn, 1991). The time-dependent probability (P) of the single-channel open state (O) is P(O). Channel counting was performed at time point when P(O) reached a maximum (peak P(O)), which was taken at the washout of 3,000 μM PB. A typical patch contained two to four active channels. The primary conductance, n-channel patch ensemble current, and n were used to calculate the single-channel P(O) over time. The primary conductance was calculated using primary unitary current and an Ohmic relationship (chloride reversal potential = 0 mV; holding potential = −70 mV). Dwell time histograms were fitted by a maximum likelihood method. Transformed probability density functions were fit to dwell time histograms by only considering durations greater than three times the system dead time (t_d ≈ 0.1 ms). Shorter dwell durations were excluded from the analysis because the detection of these events is frequently missed due to the effects of system filtering and the use of a half-height criterion. Idealized records were used to construct ensemble currents. Data are presented as means ± SEM. Statistical comparisons were performed in Origin v7.5, and significance was taken at P < 0.05.

Model Simulation and Parameter Estimation

Patch Model.

The nine-state Markov gating model was implemented in Matlab v7.5 (Mathworks) by solving the matrix equation:

where X(t) is a 9 × 1–state variable vector indicating the occupation of the states (i.e., R, CL, CL₂, O, BL₃, BL₄, BL₅, D_s, and D_f) at time t, X(0) = [1 0 0 0 0 0 0 0 0] initial state vector at time 0 assuming all channels in the resting R state, and Q(t) = the 9 × 9–state transition matrix of rate constants governing the transition rates between all connected states. The single open state is O, the singly and doubly liganded receptors are CL and CL₂, respectively, two desensitized states are D_s and D_f, and three blocked states of BL₃, BL₄, and BL₅ bind PB to one, two, and three inhibitory sites, respectively (see Fig. 6 A). The simulation period was divided into PB wash-in and wash-out, and changes in concentration at receptors occurred instantly. Parameter optimization used a least-squares technique (Matlab Optimization Toolbox 4.1; Mathworks) with a weighted error function and simultaneously fit a set of single-channel P(O)'s for 500 and 3,000 μM. P(O)'s were obtained by scaling mean macropatch currents, such that tail P(O)'s were equal to those of single channels. Early optimization resulted in parameter values that caused the model to poorly account for activation and early desensitization of the 3,000-μM response. As a result, errors arising from data points describing this portion of the response, up to ∼0.2 s, were weighted fivefold. This weighting strategy provided for a good fit to the entire target dataset and was used to determine the final set of optimal parameter values (Fig. 6).

PK Patch Model.

This model is the combination of the patch model and a three-compartment PK model (see Fig. 7 B). The associated three-state Markov model for the PK submodel was implemented by solving the matrix equation:

where C(t) is a 3 × 1–state variable vector reporting PB concentrations (i.e, C_P, C_EC, and C_L) at time t, and Q(t) = the 3 × 3–state transition matrix of rate constants governing the transition rates between all connected states in three PK compartments: perfusing solution (C_P), extracellular solution (C_EC), and the speculative lipophilic compartment (C_L). C(O) represents the initial condition of the state variables. C_EC contains GABARs so the concentration of this compartment provided the time-varying PB concentration used in the patch model. PB molecules in the perfusion solution were assumed to be inexhaustible, making C_P constant for any specific PB concentration.

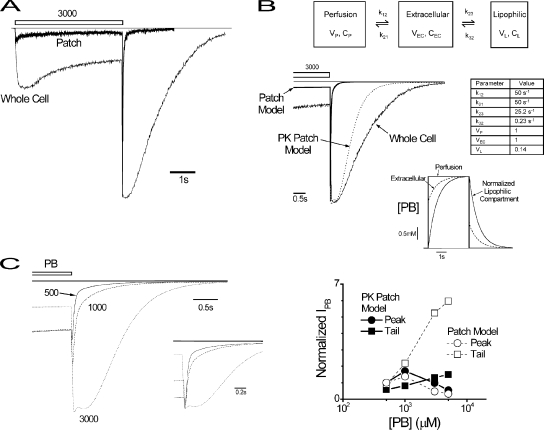
Figure 7.

Inclusion of three compartment PKs to patch model reproduces divergent features of rapidly perfused whole cells. (A) Plot of representative responses triggered by the application of 3,000 μM (open bar) obtained in whole cell and macropatch experiments as indicated. (B, top) PK model with three compartments representing perfusion solution (Perfusion), extracellular membrane solution (Extracellular), and a proposed third that is lipophilic (Lipophilic). The extracellular compartment contains GABARs and includes the unstirred layer (Maconochie and Knight, 1989). PB molecule movement between compartments is shown by single-headed arrows with the indicated rate constants. Model parameter values are given in the table, and values were obtained based solely on rapid whole cell wash-in kinetics, PB octanol-water partition coefficient, and whole cell onset kinetics (Fig. 2; see Results). (Bottom) 3,000-μM whole cell and patch model current responses from A and Fig. 6 B, respectively, on an expanded timescale to show current time courses before and after washout as indicated. The response of the PK patch model (combination of PK submodel and patch models) provides for reproduction (dashed line) of the whole cell response. (Inset) Simulated time course of compartmental PB concentrations of PK patch model for the displayed response. The concentration of the lipophilic compartment was normalized to that of the perfusion compartment for comparison of the nature of time course. (C, left) Family of simulated tail currents from PK patch model at the indicated concentrations. The straight line marks the baseline. (Right) Concentration–response relationships for patch and PK patch models for current peak, plateau, and tail amplitudes, and whole cell data in the form of Fig. 1 B (see Results).

RESULTS

Characterization of Currents in Rapidly Perfused Whole Cells

PB-triggered whole cell Cl⁻ currents (I_PB) were detected in single cells transfected with α₁, β₂, and γ_2S subunits. Fig. 1 A shows an I_PB family triggered by 10-s pulses over a range of PB concentrations. Increasing PB concentrations up to 500 μM enhanced peak current amplitudes and accelerated desensitization. Further increases continued to accelerate desensitization but also depressed peak current and triggered the enhancement of current upon PB washout, the tail current. Notably, tail current relaxation (deactivation) slowed with increasing PB concentration in which current persisted for seconds after washout (Fig. 1 C). These observations were confirmed in group data (Fig. 1 B). Current immediately before washout (plateau) was measured to determine the degree of current decay during the pulse. I_PB increased in amplitude with increasing PB concentrations, reached a maximum at 500 μM PB, and subsequently declined in peak and plateau with PB concentrations >500 μM, thereby yielding bell-shaped concentration–response relationships for both (Fig. 1 B), consistent with channel inhibition at higher concentrations. At concentrations of 500 μM and greater, PB washout also induced current “rebound” or tail current, suggesting relief of channel inhibition by the unbinding of PB from inhibitory sites. The slope of the peak current concentration–response relationship at low concentrations provides a lower limit on the number of agonist bindings sites that must be occupied to trigger channel opening (Katz and Thesleff, 1957; Colquhoun and Ogden, 1988). Peak current responses at low PB concentrations indicate that at least two binding sites are involved in channel activation (Fig. 1 B, right). Normalized tail current enhancement showed a sigmoidal dependence on PB concentration in which maximal amplitudes were similar to those for peak current during the pulse. These findings reproduce the coarse features of whole cell responses in previous reports (Akaike et al., 1987; Feng et al., 2004).

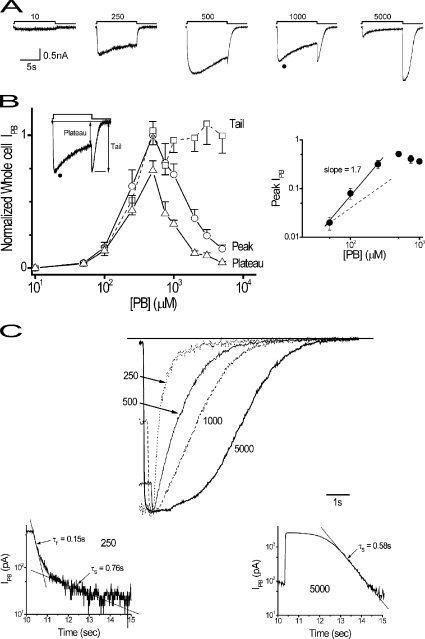
Figure 1.

PB induces a complex I_PB concentration–response relationship and tail current kinetics in whole cells. (A) Individual PB-triggered (−60-mV) Cl⁻ currents (I_PB) from a single cell expressing α₁β₂γ_2S receptors over a range of concentrations (top in μM), where downward deflection indicates increasing current. (B, left) Concentration–response amplitude relationships for peak, plateau, and tail I_PB normalized to peak current with 500 μM PB (means ± SEM; five to seven cells). (Inset) Replots 1,000-μM response (•) and identifies plateau and tail current magnitudes. (Right) Peak concentration–response relationship replotted on logarithmic axes showing linear relationship (solid straight line, slope = 1.7) at low concentrations. Linear relationship with slope = 1 (dashed straight line) shown for comparison. (C, top) Tail currents replotted from A, normalized for amplitude, and shifted temporally to align peaks at the indicated concentrations (μM). Straight line denotes baseline. (Bottom) Selected tail currents replotted on semilogarithmic axes to show exponential components (straight lines with fast [τ_F] and slow [τ_S] time constants as indicated) at designated concentrations to show exponential components of tail current deactivation time course. (Left) 250-μM response manifests biexponential relaxation with straight lines marking periods where each exponential component is dominant. (Right) 5,000-μM response shows a quasi-plateau period from tail current peak to point where the time course is accounted by a monoexponential function. Application period was >30 s.

Whole Cell Tail Currents Are Nonlinear and Time Varying

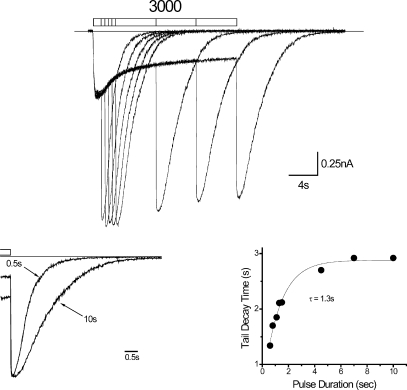
The primary focus of this study was to gain greater insight into the blocking process by analyzing tail currents that reflect channel unblock. Fig. 1 C (top) compares the current time courses upon PB washout over a range of concentrations and shows that increasing concentration slows deactivation as described previously (Rho et al., 1996; Wooltorton et al., 1997; Feng et al., 2004). In addition, the nature of the deactivation time course at 5,000 μM appears fundamentally different from those at lower concentrations in which a pseudo plateau lasting ∼1 s follows the rapid current upstroke. These features are also apparent in previous results in rapidly perfused whole cells (see Akaike et al., 1987, Fig. 6, and Akk et al., 2004, Fig. 5). The responses were replotted on semilogarithmic axes to investigate their kinetic nature. Deactivation at low concentration (250 μM) is biexponential, whereas at 5,000 μM, the time course remains nearly constant for ∼1 s before a monoexponential decline (Fig. 1 C, bottom). Similar observations were obtained in four other cells. The former is consistent with linear behavior, whereas the latter is not (see below).

Next, we examined the effects of the duration of PB application on tail currents at high PB concentrations. Fig. 2 (top) shows a family of currents triggered by PB application over a range of durations. Deactivation is slowed by longer duration pulse applications (Fig. 2, bottom left) where the onset of this effect depends on exposure duration in a monoexponential fashion (Fig. 2, bottom right), similar to previous reports for β₃ homomers expressed in HEK-293 cells (Wooltorton et al., 1997). These observations indicate that the effects of PB vary over time.

Figure 2.

Tail current deactivation is slowed by duration of PB application. (Top) Family of currents triggered by 3,000 μM PB delivered over a range of PB pulse durations represented by segmented bar above (0.5 to 10 s). (Bottom, left) Replots 0.5- and 10-s responses normalized for peak tail current from top to provide comparison of deactivation time courses. Open bar marks PB application. (Bottom, right) Plots tail current decay time (time from 90 to 10% of peak amplitude) for cell in panel versus PB pulse duration (see Results). Application period was >30 s.

Ligand-gated ion channels can be considered linear time-invariant systems under conditions of constant agonist concentration. Consequently, when the concentration is “jumped” to a new value, the state trajectory of a channel involving n states can be described by a system of n-l exponential functions (Chen, 1998). Both microscopic rates and initial state conditions determine coefficients, whereas time constants are determined exclusively by the former. The channel moves to a new state owing to the change in microscopic rates affected by the jump where the microscopic rates remain constant until another jump occurs. This presumes that the time course of the perturbing concentration jump is fast relative to rates of the fundamental exponential equations. Therefore, the time course of any variable after a jump is described by a sum of exponential functions with constant rates and coefficients. Time invariance adds the additional constraint that system rate constants remain unchanged over the period of interest. The current time course during washout at low concentrations (250 μM) can be described by a sum of exponentials based on semilogarthmic plotting (Fig. 1 C, left) and successful multi-exponential fitting (not depicted), consistent with a linear and time-invariant system. However, tail currents at high concentrations appear nonlinear and time variant because they fail in both of the above regards since they are modulated by the duration of PB application (Fig. 2).

Single-Channel Currents in Rapidly Perfused Outside-out Membrane Patches

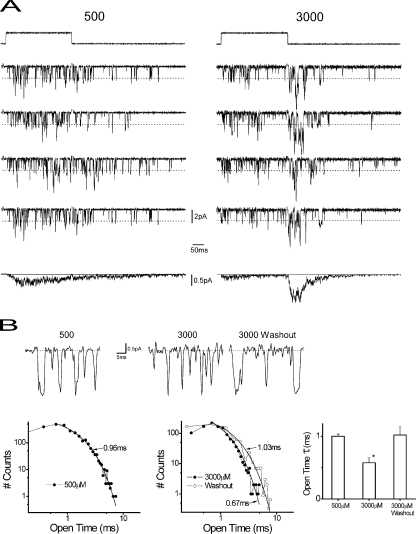
We next investigated the microscopic gating underlying macroscopic responses by studying rapidly perfused, outside-out single-channel cell-free membrane patches. Fig. 3 A shows representative single-channel sweeps from individual patches in response to 500 and 3,000 μM PB. Downward deflections from baseline represent single-channel openings to a primary conductance state of 27 pS (indicated by the dashed line), similar to previous reports in recombinant GABARs with the same subunit complement (Akk and Steinbach, 2000a; Krampfl et al., 2002). Ensemble current averages reproduce the qualitative features of responses from macropatches that include activation, desensitization, and tail currents. Openings triggered by PB at these concentrations are frequent and relatively brief. There is a surge of open-channel activity upon washout of 3,000 μM PB, which gives rise to the characteristic tail current observed in whole cells and macropatches. Channel openings were monoexponentially distributed, indicating a single, kinetically distinct open state. Increasing PB from 500 to 3,000 μM resulted in briefer openings during PB application (Fig. 3 B), consistent with open-channel block (Akk and Steinbach, 2000a). After PB washout, open durations were similar to those observed during continuous application of 500 μM PB, confirming in the same channels that PB reduces open durations. Precise channel counting (see Materials and methods) was performed at 3,000 μM upon washout, which appeared to trigger maximum single-channel open probability [P(O)] and stacking in multichannel patches. Peak P(O) was determined after washout of 3,000 μM (0.45 ± 0.08 SEM; n = 5), which underlies the maximum of the macroscopic tail current.

Figure 3.

Single-channel activity induced by PB. (A) Single-channel activity from two (left and right) rapidly perfused outside-out membrane patches from cells expressing α₁β₂γ_2S GABARs. (Top) Liquid junction potential response (see Materials and methods) representing the time course of PB pulses (upward deflection, 300 msec) indicated concentrations (μM) that were delivered every 15 s. 500-μM patch contains two active channels, whereas the 3,000-μM patch contains three active channels. (Middle) Four stacked representative single-channel records triggered by PB application. Downward current deflections mark openings of single α₁β₂γ_2S GABARs, with primary unitary current marked by dashed lines. The primary conductance of 27 pS was calculated using primary unitary current and an Ohmic relationship (chloride reversal potential = 0 mV; holding potential = −70 mV). (Bottom) Ensemble current average (irregular line) and solid line marks baseline. The vertical scale bars reflect single-channel amplitudes. (B, top) Selected periods of records from A to illustrate the difference in apparent open times under the indicated conditions. (Bottom, left) Open-time histograms from patches of A at the indicated concentrations. Solid line marks fitted monoexponential functions with the indicated time constants. Higher PB concentration reduces open time by approximately twofold, consistent with previous results and consistent with a blocking process acting on a single open state. (Right) Grouped data for time constants of open-time histograms for the indicated conditions (n = 3–4 patches). The asterisk indicates the difference with other groups (P < 0.05; unpaired t test; see Results).

Characterization of Macroscopic Currents from Rapidly Perfused Outside-out Membrane Patches

During our study of single-channel patches, we often encountered multichannel patches with sufficient channel number to render macroscopic gating. Unblocking kinetics are on the order of milliseconds as reported by current rebound in rapidly perfused cell-free macropatches (Krampfl et al., 2002; this study), whereas the solution exchange kinetics in whole cells are ∼20 ms (Gingrich et al., 1995). Therefore, we studied macropatch currents to be sure that the whole cell responses were not significantly distorted by the relatively slower solution exchange kinetics in whole cell experiments.

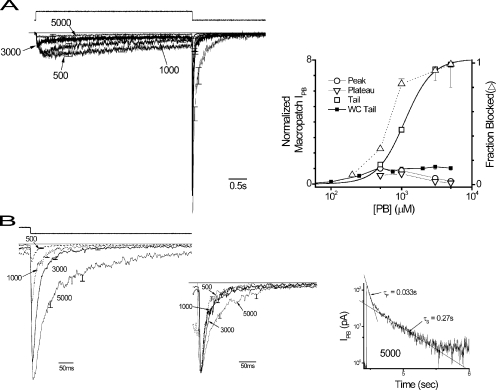
Fig. 4 A shows a family of macroscopic currents obtained from outside-out patches. Tail current rebound phases were well described by monoexponential functions (time constants, 2.24 ± 0.96 ms; n = 14), which were independent of concentration and expectedly more rapid (P < 0.00005) than in whole cells (12.5 ± 1.2 ms; n = 21; not depicted). The time course of I_PB during PB application and upon agonist withdrawal generally reproduced the qualitative features observed in whole cell experiments. Macropatch responses are roughly similar to those of whole cells (compare Fig. 1 A and Fig. 4 A, left) and with regard to concentration–response relationships (compare Fig. 1 B and Fig. 4 A, right). However, quantitative comparisons of peak, plateau, and tail current amplitudes demonstrate that macroscopic activity diverges clearly between whole cell and macropatch results. The amplitude and time course of macropatch tail currents were noticeably different from those obtained in whole cells (compare Fig. 4 A with Fig. 1 A), with tail peak amplitudes more than eight times greater (Fig. 4 A, right) and with a markedly faster deactivation time course (compare Fig. 4 B and Fig. 1 C).

Figure 4.

Gating kinetics manifest in rapidly perfused outside-out macropatches. (A, left) Mean I_PB responses from rapidly perfused outside-out cell-free macropatches triggered by PB applications (4 s) over a range of concentrations (μM) as indicated normalized to peak of a 500-μM response (means ± SEM; n = 3–5). Representative liquid junction potential response indicating the time of PB application (upward deflection). The application period was >30 s. (Right) Concentration–response relationships for macropatch I_PB peak, plateau, and tail amplitudes in the format used in Fig. 1 B. Smooth curve is the best fit of a logistic equation to tail current response (A = 8.1, x₀ = 1,100 μM, slope = 2.23; See Materials and methods). Whole cell tail current relationship (WC tail) reproduced from Fig. 1 B for comparison. Fraction of channels blocked at pulse end (fraction blocked) was calculated using I_PB, plateau, and tail amplitudes in the expression [(tail-plateau)/(tail)]. Fraction blocked approximates the conditional probability (P) of the block (B), given that it is either B or open (O) and is represented by the expression [ P{B | B or O} ] (see Results). The best fit of a logistic equation to fraction-blocked response (A = 0.97, x₀ = 620 μM, slope = 3.51) is not depicted. (B) Tail currents (means ± SEM) replotted from A on an expanded time scale at the indicated concentrations (μM). (Inset, left) Tail currents normalized by peak amplitude and time shifted to align current peaks to provide a comparison of deactivation time course. (Inset, right) 5,000-μM response replotted on semi-logarithmic axes showing that the time course is accounted for by a biexponential function that appears as linear phases (marked by straight lines), with associated fast and slow time constants (fast, τ_F; slow, τ_S).

We initially attributed these differences to slower solution exchange kinetics in whole cell rapid perfusion but later reasoned that they may arise from fundamental differences between these two preparations (see Whole Cell Currents are Nonlinear and Time Varying). We therefore focused on the kinetics of macropatch currents presuming that the responses reported genuine PB-triggered GABAR gating. We assumed that tail amplitude reflects the degree of channel blockade during the PB application (Serafini et al., 2000), and therefore the tail concentration–response relationships provide insight into the dependence of block on PB concentration. The relationship is well fit by a logistic equation with a slope factor of 2.23, suggesting the involvement of at least three binding sites in channel blockade. However, this relationship is also influenced by PB binding to sites involved in activation as well as other unrelated conformational changes. Therefore, we sought another endpoint that more selectively reflects inhibitory binding.

Open channels undergo direct blockade (Fig. 3), so an endpoint reporting the relative proportions of blocked and open channels would provide focused insight into PB binding underlying block. The tail current magnitude is the sum of the plateau, representing open unblocked channels before washout, plus the rapid current upstroke produced by washout and subsequent channel unblock. The upstroke magnitude reports the number of blocked channels and is the difference between tail and plateau current amplitudes. This endpoint may underestimate the number of blocked channels because channels may deactivate or desensitize before unblocking. However, these effects seem minor given that the rate of unblocking (∼500 s⁻¹) is more than an order of magnitude faster than that of the fastest component of deactivation (∼30 s⁻¹) and apparent desensitization (∼10 s⁻¹). Therefore, a good approximation of the fraction of blocked channels (fraction blocked) can be computed using the expression [(tail-plateau)/(tail)], which represents the conditional probability (P) of the channel being blocked (B) given that it is open (O) or B [(P{B | O or B}]. The fraction blocked versus PB concentration relationship (Fig. 4 A) is well fit by a logistic equation with a slope factor of 3.5, lending strong support for a minimum of three binding sites involved in blockade.

Fig. 4 B shows PB increased tail current amplitude in a concentration-dependent fashion. Tail current relaxation exhibited little dependence on PB concentration (see Fig. 4 B, inset, left) with similar 90–10% amplitude relaxation times for 500, 1,000, and 3,000 μM (64 ms ± 8.8 SEM). However, some slowing is apparent at the highest PB concentration tested (5,000 μM), but the deactivation time course was biexponential (Fig. 4 B, inset, right), consistent with linear behavior. Deactivation time course was independent of duration of PB application (not depicted).

We next analyzed macropatch I_PB time course during the application of PB to explore desensitization. This approach likely reports primary effects of desensitization, but contributions by channel block cannot be excluded. Fig. 5 A shows mean traces triggered over a range of PB concentrations. Increasing PB concentration decreased peak current in a fashion similar to whole cells. Current decayed after peak current, which appeared dependent on PB concentration where the degree of decay representing apparent desensitization was increased with concentration (Fig. 5 A, inset). I_PB activation and decay during the pulse were well described by the sum of multiple exponential components, which were dependent on concentration in a complex fashion (Fig. 5 B).

Analysis of the time course of a linear system provides insight into the minimum number of associated states. Generally, a time course with n resolvable exponential components provides a lower limit on the minimum number of states that is calculated from n+1. In reality, the actual number of states may greatly exceed n+1, owing to unobservable states or unresolvable exponential components. Applying this reasoning results in n number of states involved in a particular process assuming the existence of a state(s) independent of the process. Activation at 500 and 1,000 μM PB followed a biexponential time course, which became monoexponential at higher concentrations, consistent with at least two closed states preceding opening. Desensitization was described by two exponential components at most PB concentrations but was monoexponential at high and low concentrations. The results argue for at least two desensitized states.

Patch Model Reconciles Micro- and Macropatch Results

Channel activity in macropatches is linear, time invariant, and not likely to suffer from inadequate solution exchange kinetics. As a result, this preparation is expected to accurately report channel responses. Therefore, we used macropatch as well as single-channel data in model development. We wished to develop a parsimonious gating model that could account for our macropatch observations to understand how differing processes (binding, activation, desensitization, and blockade) may interact to account for channel activity. Such a model could then serve as a platform to investigate the possible mechanisms underlying divergent channel behavior between whole cells and macropatches. The empirical results argue that PB-triggered gating involves at least two agonist binding sites (Fig. 1 B), a single open state that undergoes open-channel block (Fig. 3 B), two desensitized states (Fig. 5 B), and at least three binding sites mediating channel blockade (Fig. 4 A). We started with the model that Akaike et al. (1987, Scheme 2) proposed to account for PB-triggered Cl⁻ currents in sensory neurons because many primary empirical observations accord with those here. However, in this study, fast and slow desensitization likely represent closing processes distinct from blockade because unblock is 50-fold faster. We therefore extended the Akaike model to distinguish between blocked and desensitized states, which provided a lower limit on the overall number of channel states.

Target empirical data used in parameter estimation used time-dependent single-channel open probabilities (see Materials and methods) at low and high concentrations (500 and 3,000 μM). We assumed that within each group of binding sites (two activation and three blockade), the sites were identical and independent. Fig. 6 A shows the structure of the final nine-state Markov model. We consider the connectivity not to be unique and the number of states to be a minimum. Parameter estimation involved k_on, k_off, β, k_on-b, k_off-b, d_on-s, d_off-s, d_on-f, and d_off-f. The fixed closing rate derived from monoexponentially distributed open-state dwell times after 3,000-μM washout (Fig. 3 B) was taken as the magnitude of α (1,000 s⁻¹) because in the absence of PB, the blocking rate constant is zero and rate constants of desensitization are orders of magnitude smaller (Fig. 5) so as to be negligible. After final parameter values were determined, model and empirical responses were compared (Fig. 6 B). The model reproduced the time course of activation, desensitization, and tail current responses for both 500- and 3,000-μM responses. Fig. 6 C (top) shows that model responses qualitatively account for empirical responses over a range of PB concentrations. We next evaluated the model's ability to reproduce concentration–response relationships. Derived peak, plateau, and tail current parameters are shown, which reproduce empirical macropatch data (compare Fig. 6 C, bottom, and Fig. 4 A, right). Overall, the final parsimonious gating scheme is a nine-state Markov model that quantitatively reproduces the response time courses at 500 and 3,000 μM; predicts the concentration–response relationships for peak, plateau, and tail amplitudes; and qualitatively accounts for empirical responses triggered over a range of concentrations.

It is generally held that inhibition occurs at much higher concentrations than those required for activation, and therefore few channels are blocked at therapeutic PB concentrations (∼100 μM). However, our macropatch data and subsequent modeling argue that the PB affinity of inhibitory sites (K_D = 1,400 μM) is nearly threefold greater than those for activation (K_D = 3,500 μM). Furthermore, actual block may occur at a roughly threefold lesser concentration still because PB binding to only one of the three inhibitory sites is necessary. Therefore, block occurs at approximately sixfold lesser concentrations than for activation. As a result, we became interested in using the patch model to determine the concentration dependence of blocked channels. In this model, only activated channels undergo blockade, and so we determined the fraction of activated channels that have become blocked (Fig. 6 C, right). This represents the conditional probability of blocked states given that the channel is in a state after activation (P{ BL₃, BL₄, or BL₅ | O, BL₃, BL₄, BL₅, D_s, or D_f }). The relationship indicates that nearly 20% of channels are blocked at therapeutic concentrations (100 μM), pointing to a possible contribution of blocked channels to activity at clinically relevant concentrations.

The Addition of Lipophilic PK Compartment to the Patch Model Accounts for Whole Cell Tail Currents

Divergent features of whole cell tail currents are nonlinearity, slowing of deactivation by increasing PB concentration and pulse duration, being time varying, and having an eightfold lesser amplitude relative to macropatches. We entertained three possible explanations for differences between macropatch and whole cell currents: acknowledged slower exchange kinetics in rapidly perfused whole cells; altered macropatch gating produced by membrane patch excision; and, given the high lipophilicity of PB (octanol/water partition coefficient = 108), a lipophilic PK compartment slowing the effective exchange of PB in the solution bathing the GABARs. Our line of reasoning excluded the first two possibilities (see Discussion), leaving the PK explanation for further consideration. This explanation is supported by transmonolayer diffusion experiments showing that similar barbiturates have low apparent transcellular permeation rates (∼0.4 μm/sec) (Behrens et al., 2001), which could introduce PKs on the order of seconds, consistent with the onset for PB application duration changes in whole cells (Fig. 2). We therefore extended the patch model to incorporate a PK submodel to create the PK patch model, and then tested its ability to account for the discordant whole cell results.

We considered the addition of a simple PK submodel with three compartments representing the perfusion solution, an extracellular compartment containing GABARs that includes the unstirred layer (Maconochie and Knight, 1989), and a speculative lipophilic compartment (Fig. 7 B). The concentration of the perfusion compartment (C_P) was considered fixed because the perfusion solution can be considered an inexhaustible source of PB molecules. Concentrations in the extracellular and lipid compartments were normalized by that of the perfusion compartment for simplicity, and its volume (V_P) was set arbitrarily to a value of 1. k₁₂ and k₂₁ were calculated to achieve an exchange time constant of 10 ms and equivalence of C_P and the concentration of the extracellular compartment (C_EC) at steady state in the absence of the lipid compartment. k₂₃, k₃₂, and the ratio of V_EC and V_L were determined using constraints of an octanol/water partition coefficient of PB (108) and an exchange time constant of 1.3 s between the extracellular and lipid compartment, which was derived from whole cell onset experiments (Fig. 2). In the latter, the time constant of time-dependent changes in tail deactivation (Fig. 2) was taken to reflect a slow component of PB wash-in in the extracellular compartment arising from the proposed PK mechanism. Overall, the synthesis of the PK submodel was completely specified by the identified constraints and therefore independent of the empirical data that it may account for once incorporated into the patch model. The PK submodel introduced a slow component to both PB wash-in and washout time courses in C_EC (Fig. 7 B, bottom, inset) and thereby transforms the patch model (PK patch model) behavior to reproduce the whole cell plateau value and tail current time course (Fig. 7 B). The PK patch model also predicts other divergent whole cell findings, including deactivation slowing by increasing PB concentration (Fig. 7 C, left) and application duration (not depicted), as well as reduced tail current amplitude concentration–response relationship (Fig. 7 C, right). These findings indicate that a PK mechanism can explain the divergence between whole cell and macropatch findings.

GABA Potentiates PB Blockade

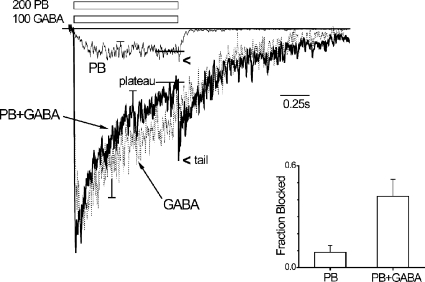
The results suggest that PB binding to sites mediating blockade occurs at lower concentrations than at those regulating activation (Fig. 6). GABA coapplication enhances PB blockade in hippocampal GABARs (Rho et al., 1996), which would suggest that during GABA-triggered activity the contribution of blocked channels to GABAR function would be even greater than suggested by our results so far with PB alone. We therefore investigated the effects of GABA on PB blockade in macropatches (Fig. 8). We were interested in the physiological significance of PB block, and so a 200-μM PB concentration was selected because it is as close to therapeutic concentrations (∼100 μM) but still triggered a measureable current with an observable tail. The current time course triggered by 200 μM PB alone (1 s) increased to reach a peak and plateau in ∼0.3 s, followed by a discernable tail at washout. 100-μM GABA application induced a current that reached a nearly eightfold greater peak within 50 ms, followed by desensitization and deactivation. PB coapplication caused a more rapid activation, enhanced desensitization, and introduced a marked tail current in the GABA-alone response. The tail current observed in PB alone was markedly enhanced by GABA coapplication. To gauge the effect on underlying PB binding, we calculated the fraction blocked (Fig. 8, inset), which shows that GABA enhanced binding by nearly fourfold with this endpoint. The results indicate that GABAR sensitivity to PB blockade is greater in the presence of GABA, and argue that PB-blocked states contribute to GABAR function with GABA-triggered activity.

Figure 8.

GABA potentiates channel blockade by PB. Plot of mean I_PB responses from rapidly perfused, outside-out cell-free macropatches. Current responses triggered by the application (1 s) of PB or GABA, or else their coapplication (PB + GABA), with application periods represented by open bars with the indicated concentrations (μM). Long solid bar marks the baseline. Short horizontal bars and arrowheads indicate the plateau and tail current amplitudes, respectively. The application period was >30 s. (Inset) Graph of calculated fraction blocked derived from the plateau and tail current amplitudes as in Fig. 4 A, with PB alone or coapplication of PB and GABA (means ± SEM; n = 4; see Results).

Patch Model Parameter Sensitivity

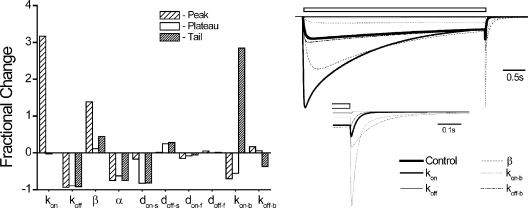
The role of states and gating transitions in model performance was investigated by examining the sensitivity to changes in model parameters (parameter sensitivity analysis). We examined changes in simulated patch model I_PB's to fivefold increases in parameter values (Fig. 9). k_on increased peak currents due to enhanced activation (Fig. 9, left). Peak and plateau currents were unaffected, owing to increased open-state probability. This enhanced slow desensitization in a nearly compensatory fashion, such that the end pulse current was nearly unchanged from control. Therefore, open probability is similar to control at pulse end, causing plateau and tail currents to be mostly unaffected (Fig. 9, right). k_off and α both weakened activation, leading to depression of all I_PB features. β enhanced activation and increased open probability, which promoted slow desensitization such that the plateau was little changed, similar to k_on. Tail current was increased and deactivation was slowed (Fig. 9, right) because greater open probability lead to a reduction of CL₂ probability and favored deeper blocked states. d_on-s directly enhanced slow desensitization, thereby reducing open probability. This depressed plateau and tail currents but failed to affect peak current because the activation rate remained markedly greater than that of slow desensitization. d_off-s had the expected converse effects. k_on-b increased tails due to enhanced blockade and thereby depressed peak and plateau current, whereas k_off-b had the expected converse effects. Currents appeared relatively insensitive to changes in d_on-f and d_off-f due to the combination of a low level of activation and blockade, which resulted in a small probability of BL₄ from which the channel directly transitions to D_f.

Figure 9.

Model parameter sensitivity analysis. (Left) Fractional change in features (peak, plateau, and tail current amplitudes) for a fivefold increase in the indicated patch model parameters in simulated patch model I_PB's triggered by 500 μM PB. (Right) Family of selected I_PB responses in control (thick solid lines) from the left panel with the indicated parameters. Open bar indicates PB application. (Insets) Responses replotted on an expanded timescale to illustrate the effects on the time course of tail currents (see Results).

DISCUSSION

Conclusions

This study is the first to compare PB-triggered transient gating in a homogeneous population of recombinant α₁β₂γ_2S GABARs obtained from three experimental techniques that include rapid perfusion of whole cells, as well as macroscopic and single-channel outside-out patches. The study provides new insights into the mechanism of PB blockade as well as PB-triggered gating in general. Whole cell tail currents showed slowing of the deactivation time course with increasing application time and PB concentration, deactivation occurred over seconds at high concentrations, and peak amplitudes were comparable to those of currents during PB application. These observations accord with previous reports in similar preparations but, remarkably, were absent in macropatch currents. Our initial reasoning (see Patch Model Reconciles Micro- and Macropatch Data in Results) presumed that slower solution exchange kinetics in rapidly perfused whole cells compared with membrane patches may underlie the divergence. As a result, our initial analysis focused on macro- and micropatch currents from rapidly perfused outside-out patches and, in combination with parsimonious mathematical modeling, led us to the following primary findings: the binding of at least five molecules of PB to the channel complex in which two sites govern activation and three sites mediate inhibition; a single dominant open state that undergoes direct blockade; and at least two desensitized states that are kinetically distinct from those of blockade. PB binding to any one of the inhibitory sites causes block of the open state, and subsequent binding to unoccupied inhibitory sites leads to deeper closed states. The associated gating (“patch”) model reproduces the empirical findings in macro- and micropatches.

The addition of a lipophilic PK compartment to the patch model (“PK patch”) provides reconciliation of all divergent features of whole cell tail currents. The results suggest that PB responses from rapidly perfused whole cell experiments may suffer marked kinetic distortions of current time course arising from effective exchange kinetics that are ∼100-fold slower than expected. These findings raise a significant question regarding the concentration time course of PB and other lipophilic drugs near membrane-bound receptors during rapid extracellular perfusion of whole cells, which may distort observed current time courses and thereby cast doubt on results obtained from this preparation.

Perhaps the most notable fundamental finding of the study is that blockade occurs at concentrations nearly sixfold less than for activation due to a threefold greater affinity of inhibitory over activation sites, and channel block arising from PB binding to only one of three sites. This finding is strongly supported by this first report of fractional millimolar PB concentrations causing block reported by tail currents in rapidly perfused macropatches, in conjunction with the results of parsimonious GABAR modeling. The findings suggest that the current thinking regarding the rank order of GABAR sensitivity to PB actions of potentiation > activation > blockade should be revised to potentiation > blockade > activation. Furthermore, greater sensitivity to blockade equates to a higher fraction of blocked channels at clinically relevant PB concentrations (<100 μM) and, when coupled with marked GABA potentiation of blockade, point to a role of blocked states in therapeutic PB modulation of GABA-triggered currents.

PB-induced Gating

Macroscopic currents triggered by the rapid application of PB to whole cells expressing α₁β₂γ_2S GABARs showed a bell-shaped peak current concentration–response relationship, enhancement of desensitization, and rebound or tail currents at higher concentrations (Fig. 1). These coarse features accord with similar previous whole cell studies with ex vivo and recombinant channels (Akaike et al., 1987; Rho et al., 1996; Thompson et al., 1996; Serafini et al., 2000; Feng et al., 2004). Such agreement points to general features of PB modulation of GABARs in whole cells and supports the generalizable findings from this study.

Tail Currents

The goal of this study was to gain greater understanding into the mechanism of PB inhibition. We focused on the investigation of tail currents as a reporter of channel blockade. Tail currents have been used previously to gain insight into PB blockade (Akaike et al., 1987; Serafini et al., 2000; Krampfl et al., 2002; Akk et al., 2004; Feng et al., 2004) and likely primarily reflect the unblocking process because tail current upstrokes are fast relative to deactivation (Akaike et al., 1987; Krampfl et al., 2002; and this study, Fig. 4). Previous investigations in rapidly perfused whole cells have reported that tail currents can be described by multi-exponential functions and show concentration-dependent slowing of deactivation (Rho et al., 1996; Serafini et al., 2000; Feng et al., 2004). Our results in whole cells accord with these findings at PB concentrations <2,000 μM. However, PB concentrations >2,000 μM produced tail currents with clear nonlinear features (see Whole Cell Tail Currents Are Nonlinear and Time Varying in Results). In contrast, the decay of macropatch tail currents showed little concentration dependence, except for some minor slowing of decay at the highest concentration tested where the time course remained linear (5,000 μM; see Fig. 4 B). We reasoned the divergence between whole cell and macropatch tail currents may arise from differences in the experimental preparations involving unrecognized slowing of extracellular PB washout. Such reasoning pointed us toward the analysis of macropatch currents in our investigation of PB blockade, especially because tail current upstroke proceeds with millisecond time constants (Krampfl et al., 2002; and this study) and because rapid perfusion techniques achieve wash-in rise times 10–90% of <20 ms in whole cell and <1 ms in cell-free membrane patches in our laboratory (Gingrich et al., 1995; Burkat et al., 2001). For these reasons, we relied on the analysis of currents obtained from rapidly perfused macropatches to initially investigate the mechanism of PB blockade.

Macropatch Currents

Macropatch results indicate that tail current amplitudes and fractional block both are steeply dependent on PB concentration (slope factors of 2.3 and 3.5, respectively), arguing strongly for the binding of at least three PB molecules in the mechanism of block (but see Krampfl et al., 2002). This refines earlier conclusions regarding the number of the underlying PB binding sites (Akaike et al., 1987; Akk and Steinbach, 2000a; Serafini et al., 2000; Akk et al., 2004). Activation was biexponential at lower concentrations and at high concentrations became monoexponential with time constants in the millisecond range. These results are roughly similar to those of Akaike et al., (1985) but differ quantitatively in that we show ∼10-fold faster activation. This may arise from differences in subunit composition or experimental techniques (whole cell vs. macropatch). Whole cell currents triggered by low concentrations indicate a supra-linear dependence of peak current on concentration (Fig. 1) and at least two activation sites, which accords with previous reports (Akaike et al., 1985; Rho et al., 1996; Akk and Steinbach, 2000a).

We considered current decay during PB application to primarily reflect channel desensitization. Our analysis shows that the magnitude of current decline increases with PB concentration and reaches a maximum of ∼70% relative to peak current (Fig. 5). The time course is well described by a biexponential function where both time constants decrease with concentration. These findings roughly accord with those in frog sensory neurons (Akaike et al., 1985). Furthermore, the magnitude of desensitization is comparable to previous reports in recombinant channels (Serafini et al., 2000; Feng et al., 2004) but is greater than in others (Rho et al., 1996; Dalziel et al., 1999; Krampfl et al., 2002). These differences may reflect differences in subunit complement because desensitization is dependent on subunit composition (Verdoorn et al., 1990; Gingrich et al., 1995; Feng et al., 2004). Overall, the results support at least two distinct desensitized states.

GABA coapplication markedly potentiated PB block, consistent with previous observations in hippocampal neurons (Rho et al., 1996). The degree of block was assayed by computing fractional block, which selectively reports the relative proportions of open and blocked channels. The results suggest that GABA coapplication markedly enhances PB binding to inhibitory sites by approximately fourfold. Therefore, in the presence of GABA, PB would be predicted to produce significant blockade at concentrations in the therapeutic range (∼100 μM). It is possible that GABA could have other effects on PB-induced gating not considered in this study. The implications of this single effect on the patch model are an increased probability of all blocked states directly and enhanced fast desensitization indirectly through an increased BL₄ probability.

Single-Channel Currents

PB-triggered α₁β₂γ_2S single-channel currents obtained with rapid perfusion of membrane patches in this study showed a primary conductance opening (27 pS) and a single kinetically distinct open state with a millisecond dwell time, in agreement with previous results of recombinant channels with similar subunit complement (Akk and Steinbach, 2000a; Krampfl et al., 2002). Krampfl et al. (2002) described a second kinetic state with a dwell time of 0.41 ms, which may be beyond the resolution of this study (see Materials and methods). The results of this study also accord with those in PB-activated currents in ex vivo GABARs (Rho et al., 1996). Akk and Steinbach (2000a) showed a single dominant open state with mean lifetime of ∼1.9 ms for α₁β₂γ_2L at 500 μm. However, similar studies in other expressed αβγ GABARs have reported three kinetically distinct open states (Akk et al., 2004; Feng et al., 2004), indicating the dependence of single-channel properties on subunit composition (Angelotti and Macdonald, 1993; Fisher and Macdonald, 1997).

The study of transient gating in rapidly perfused single-channel patches allowed for the construction of ensemble current averages that report the time dependence of single-channel open probability. This information is vital to understanding channel state probabilities on an absolute scale and where macroscopic currents are reproduced when ensemble currents are scaled up by the number of channels present (Hille, 2001). Importantly, ensemble current average time courses reproduced the coarse features of whole cells and provided direct quantification of open-channel probabilities (Fig. 3) and computation of time-dependent open-channel probabilities from macropatch currents.

Rapidly perfused single-channel patches also allowed for the direct examination of the effects of PB on open time in the same receptor by comparing dwell times in the presence of PB during the pulse and in its absence after washout. Fig. 3 B shows that dwell times increase upon washout of 3,000 μM PB to values similar to that observed with activation by low concentrations (500 μM), which presumably produced little discernible open-channel block. These results provide additional support for PB open-channel block, consistent with previous proposals based on steady-state single-channel studies (Akk and Steinbach, 2000a; Akk et al., 2004).

The mechanism of open-channel block may involve PB binding that leads either to pore occlusion or allosteric promotion of nonconducting channel conformations. Our results suggest that channel block may arise from the simultaneous binding of up to three PB molecules (Figs. 4 and 6). Steric hindrance makes it unlikely for three PB molecules to concurrently bind within the pore, as implied by simple pore occlusion. Therefore, we favor an allosteric mechanism involving three individual binding sites (see Possible Structure–Function of Binding Sites Mediating Block below) as described in the proposed patch model (Fig. 6). In this arrangement, the binding of the first PB molecule produces block by promoting a nonconducting conformation and where subsequent binding involves states already rendered nonconducting.

Patch Model

We were first interested in developing a parsimonious gating model to serve as a summary of proposed gating mechanisms that reconciles our empirical observations. If this were accomplished, the model would serve as a platform to explore prospective mechanisms underlying marked differences between macroscopic gating in patches and whole cells. Model development began with a prior gating scheme proposed to account for PB-gated Cl⁻ currents in frog sensory neurons (Scheme II in Akaike et al., 1987) as discussed previously (see Patch Model Reconciles Micro- and Macropatch Results in Results), culminating in the final patch model (Fig. 6 A). The model reconciles our findings in single channels and macropatches and thereby summarizes the function of transient gating of recombinant α₁β₂γ_2S GABARs in this study. These results coupled with model parsimony provide support for the proposed gating mechanisms describing activation, desensitization, and blockade. This is the first model to address PB activation, desensitization, and blockade of ex vivo or physiological recombinant GABARs. Previous modeling efforts have considered activation in combination with either blockade (Akaike et al., 1987; Akk and Steinbach, 2000a; Serafini et al., 2000; Krampfl et al., 2002) or desensitization (Feng et al., 2004). Wooltorton et al. (1997) proposed a model describing activation, desensitization, and blockade of β₃ GABARs, yet these channels are not present in vivo and manifest ligand-free spontaneous activation (Krishek et al., 1996).

Divergence in Whole Cell and Macropatch Tail Currents

We considered three possible explanations for the divergence between whole cell and macropatches: (1) kinetic distortion due to acknowledged slower exchange kinetics in rapid perfusion of whole cells versus macropatches; (2) altered gating produced by membrane patch excision; and (3) the presence of a lipophilic compartment slowing the exchange of extracellular PB. We first investigated whether slowing exchange kinetics to ∼20 ms could account for divergent whole cell features. We introduced a first-order kinetic component with a 20-ms time constant to the solution exchange section of the patch model, which depressed tail current amplitudes but failed to reproduce other features of whole cell tail current deactivation including nonlinearity, and slowing by concentration and application duration.

Alteration in channel gating associated with cell-free membrane patches may also explain the marked differences between whole cell and macropatch tail currents. Patch excision has been shown to reduce channel open times of embryonic nicotinic ACh receptors (Trautmann and Siegelbaum, 1983; Covarrubias and Steinbach, 1990; Akk and Steinbach, 2000b) by increasing a closing rate that is related to residues on the C terminus (Akk and Steinbach, 2000b). Similarly, gating of expressed Na⁺ channels is altered, which may be related to disruption of cytoskeletal attachments (Shcherbatko et al., 1999). We are unaware of similar reports in GABARs. Selective changes in a single microscopic rate seem unlikely to account for the marked differences between tail currents of whole cells and macropatches in this study. Furthermore, such changes cannot account for nonlinear behavior of whole cell tail currents observed at higher concentrations. Overall, this explanation appears less likely but cannot be excluded.

After discounting the above possibilities, we considered whether unrecognized cellular PK effects could be responsible by slowing extracellular PB exchange at membrane-bound GABARs. If exchange becomes similar to or slower than the kinetics of channel gating, the result is ineffective concentration clamp and subsequent obligatory nonlinear GABAR function. A PK mechanism influencing the availability of a lipophilic molecule has been proposed previously in nicotinic acetylcholine receptors (Forman, 1999). The introduction of a three-compartment PK submodel to the patch model (PK model) provides an accounting of all divergent features of whole cell tail currents (see The Addition of Lipophilic PK Compartment to Patch Model Accounts for Whole cell Tail Currents in Results).

What data support the involvement of a cellular PK mechanism? PB is highly lipophilic with an octanol-water partition coefficient of 10^2.06 (Martin-Biosca et al., 2000). Furthermore, the apparent permeability constant of methylphenobarbital, a barbiturate with physicochemical features similar to PB, is 0.4 μM/sec in transmonolayer diffusion experiments in intestinal Caco-2 cells (Behrens et al., 2001). Presuming that similar gross permeability constants apply to an ∼20-μM diameter HEK-293 cell, it becomes plausible that the movement of PB through the cell may occur on a timescale of seconds similar to the time course of changes in tail currents produced by increasing application time (Fig. 2). The cellular structures involved in this speculative PK compartment could involve lipophilic phospholipid bilayers composing the cell membrane, the envelopes of intracellular organelles, and lipid-containing vacuoles.

Possible Structure–Function of Binding Sites Mediating Block

The empirical and modeling findings point to the involvement of three PB molecules in channel blockade. Presuming two PB molecules bind to trigger activation, the GABAR complex must then bind a total of five PB molecules when all binding sites are occupied. This may occur by one PB molecule binding to GABAR subunits with a 1:1 stoichiometry, which is consistent with the current thinking regarding the GABAR molecular pharmacology of PB. GABARs composed of homomeric β₁ and β₃ receptors are largely insensitive to GABA but can be directly activated by propofol and pentobarbitone (Krishek et al., 1996), suggesting that fundamental structural determinants for intravenous anesthetic activation may be located within the β subunit.

Generation of chimeric GABA_A/GABA_C receptors and subsequent site-directed mutagenesis has led to the identification of a tryptophan at position 328 within the third transmembrane-spanning domain of the human ρ1 homo-oligomeric receptor, which imparts barbiturate insensitivity, wherein mutation of this residue produces sensitivity to PB (Amin, 1999). Mutation of Trp328 to methionine, in the GABA_A β₂ counterpart, confers barbiturate sensitivity. Conversely, substitution of Met286 with tryptophan within homo-oligomeric β₂ receptor abolishes pentobarbitone sensitivity. The loss of pentobarbitone function of the mutated β₂ subunit is reversed when coexpressed with α₁. Therefore, α subunits are implicated in barbiturate modulation of αβ GABARs (Thompson et al., 1996). When expressed with α and β subunits, the γ₂ subunit diminishes the GABA-modulatory effect of PB (Whiting et al., 1997). However, the influence of this subunit on PB activation remains unexplored. Recent insights derived from loose-packed models of GABAR extracellular and transmembrane domains resulting in a large amount of solvent-accessible space point to barbiturate-binding pockets on the M3 transmembrane-spanning domain of α and β subunits (Ernst et al., 2005) that may well extend to the γ subunit as well. The involvement of β M3-binding pockets with the intravenous anesthetic propofol is also supported by findings in cysteine protection experiments (Bali and Akabas, 2004). Overall, the evidence is consistent with two PB activation sites that likely reside on each of the β subunits, and three PB inhibitory sites where one each is present on the two α and one γ subunits.

Physiological Relevance

Significant PB blockade is apparent when current rebound is observed at millimolar concentrations. Therefore, one may conclude that this mechanism does not influence GABAR function at clinically relevant concentrations of ∼100 μM (Franks and Lieb, 1994), which produces primarily potentiation of GABA-triggered currents. However, our results suggest that block occurs at concentrations nearly an order of magnitude lower than previously thought, and that up to 20% of activated channels may be blocked by 100 μM PB (Fig. 6 C). Furthermore, PB blockade is potentiated by GABA (Rho et al., 1996; this study), consistent with enhancement of underlying PB binding. Therefore, GABA-triggered activity would be associated with even greater fractions of blocked channels at therapeutic PB concentrations. Barbiturates slow the decay of GABAergic inhibitory postsynaptic currents (Weiss et al., 1988; Otis and Mody, 1992; Zhang et al., 1993; Wan et al., 2003; Mathers et al., 2007), thereby enhancing phasic inhibitory neurotransmission at therapeutic concentrations. Emergence from nonconducting (desensitized) states slows the relaxation time course of GABAergic inhibitory postsynaptic currents (Jones and Westbrook, 1995). Therefore, it is interesting to speculate that barbiturate slowing of inhibitory postsynaptic currents may arise from the emergence of channels from nonconducting blocked states.