Simulation of DNA sequence evolution under models of recent directional selection

Abstract

Computer simulation is an essential tool in the analysis of DNA sequence variation for mapping events of recent adaptive evolution in the genome. Various simulation methods are employed to predict the signature of selection in sequence variation. The most informative and efficient method currently in use is coalescent simulation. However, this method is limited to simple models of directional selection. Whole-population forward-in-time simulations are the alternative to coalescent simulations for more complex models. The notorious problem of excessive computational cost in forward-in-time simulations can be overcome by various simplifying amendments. Overall, the success of simulations depends on the creative application of some population genetic theory to the simulation algorithm.

Significant advances in evolutionary/population genetic theory during the last two decades have been essential for the successful computational inference of functional genomic elements from DNA sequence variation. Identifying the genomic locations which underwent recent adaptive changes, a procedure known as ‘hitchhiking mapping’ [1–3] (Table 1), is one of the most important applications of a classical population genetic principle. If a certain allele produces an advantageous phenotype and spreads quickly through the population, the DNA sequence linked to the advantageous allele also increases to high frequency and experiences a loss of pre-existing polymorphism near the advantageous allele. This sudden local reduction of variation is called the ‘hitchhiking effect’ of the beneficial allele or a ‘selective sweep’ [4–6]. Screens of genome variability data revealed a large number of clear cases of selective sweeps (for reviews see [7–9]), and frequent positive selection is now considered a major determinant of the amount and pattern of DNA sequence polymorphism in natural populations [10, 11]. The detection of local selective sweeps is important not only in evolutionary biology but also in various other fields, for instance in medicine and agriculture. Prominent examples where hitchhiking mapping has successfully been applied in the past include the evolution of drug resistance at pfcrt and dhps in the malaria parasite Plasmodium falciparum [12, 13] and insecticide resistance at Cyp6g1 in Drosophila simulans [14]. In domesticated plant and animal species, selective sweeps are used to identify genes that were under recent artificial selection for agronomic traits (e.g. branching pattern, seed morphology in maize [3, 15, 16] or milk yield and composition in cattle [17]).

Table 1:

Glossary

Term	Explanation
Allele frequency spectrum	The distribution of polymorphisms which occur in given numbers of copies in the sample.
Ancestral recombination graph	A way to represent and model recombination events in a coalescent tree. A recombination event corresponds to a split of a lineage (when looking backward in time), where the ‘chromosome’ or the currently considered segment is split into a left and right subsegment. From this event onward (i.e. further backward in time) the two sub-segments have their own evolutionary history.
Balancing selection	A form of natural or artificial selection that favors the long-term maintenance of polymorphisms, of multiple alleles or haplotypes
Coalescent simulation	A method of simulating the genetic variability observable in a sample of genes or ‘chromosomes’. The coalescent is a binary tree where nodes represent the merger of ancestral lineages (i.e. edges, the length of which is proportional to time). Mutations occur according to a Poisson distribution ‘along the edges’. Any mutational event changes the ground state (wild-type allele) of some new site in all chromosomes which belong to the subtree under the current edge.
Demography	Generic term referring to any change of population size or population structure (panmictic or subpopulations with or without migration) in the evolutionary history of a population or species.
Directional selection	A form of natural or artificial selection that favors a single allele, haplotype or genotype.
Forward-in-time simulation	Type of computer simulation where the simulation runs from one (historical) generation to the next in natural direction of time
Generalized coalescent	Coalescent with nodes of degree k ≥ 3.
Heterozygosity	The probability that a pair of homologous alleles is nonidentical (neither by descent nor by state).
Hitchhiking mapping	Procedure by which the mutations which are causative for an adaptive phenotypic change are mapped to specific regions in the genome by examining features of the chromosomal profile of genetic diversity.
Linkage disequilibrium	The nonrandom association of alleles at two (or more) linked loci.
Random binary tree	A directed, acyclic graph with vertices of degree three. Randomness refers to the random merger of edges (or arbitrary labeling).
Recessive beneficial mutation	In diploid organisms: the mutation has a selective advantage only if it occurs in homozygous state
Selective sweep	The rapid fixation of an advantageous allele in a population and the concomitant reduction of genetic diversity.
Soft sweep	Selective sweep from standing variation; i.e. the advantageous allele is not introduced as a single copy at the onset of the sweep but present in multiple copies.
Tajima's D	A summary statistic based on the number of polymorphisms observable in a sample of (homologous) sequences and the average number of differences in pairwise comparisons from this sample. Under neutrality and constant population size this statistic is expected to be zero. Deviations from zero are expected under nonneutral evolution and/or demographic changes.
Time reversibility	Property of many quantities occurring in evolutionary studies. In particular, equilibria, for instance the mutation-drift equilibrium, in neutrally evolving populations can be obtained by considering the evolutionary process forward in time or backward in time.
Wright–Fisher model	Mathematical model to describe the change of allele frequencies from one generation to the next. Typical evolutionary forces which change allele frequencies include selection, mutation and genetic drift. While the change in allele frequency induced by the former two is modeled deterministically, the change due to drift is modeled by binomial (in case of two alleles) or multinomial (in case of multiple alleles) sampling.

Clear patterns of selective sweeps are observed if new beneficial mutations with large selective advantages occurred and became fixed in the population very recently. However, under various biological conditions, directional selection may occur with moderate strength or in a manner that generates a less obvious signature of genetic hitchhiking. For example, a less severe reduction of variation is expected if directional selection acts on a pre-existing variant, rather than on a new mutation, that was neutral or even slightly deleterious before a change in environmental conditions rendered the variant beneficial [18–20]. This scenario has been termed ‘soft sweep’ or ‘sweep from standing variation’ [19]. Examples for soft sweeps have recently been documented for instance for wheat [21] (a soft sweep near a gene affecting plant height) and P. falciparum [22] (a soft sweep near pfmdr1 associated with multi-drug resistance). However, if the signature of selection is weak, it is very difficult to distinguish it from the inherent background noise in local polymorphism patterns (Figure 2A). This noise can be substantial even under simple, yet realistic, demographic scenarios [23–25]. For instance, admixture of subpopulations, recent population bottlenecks or alternating phases of population size reduction and expansion can severely confound genetic and demographic signals in the polymorphism pattern. The mathematical theory for filtering the correct signature of selective sweeps from the noise is difficult to develop under general biological conditions (but see [26] for some recent progress on properties of sample statistics under general demographic models). Currently, the most important approach to model the pattern of selective sweeps is by computer simulation. In this article, we review different methods to simulate genetic data under various models of directional selection. These computer simulations are central for obtaining the distributions of the statistics, which are used for genome scans for positive selection and which are the basis for all statistical tests to identify candidate sites of selection. There can be many different computational strategies to achieve a goal. We will discuss how population genetic theory can help to design an efficient simulation strategy which is appropriate for the biological question under consideration.

Figure 2:

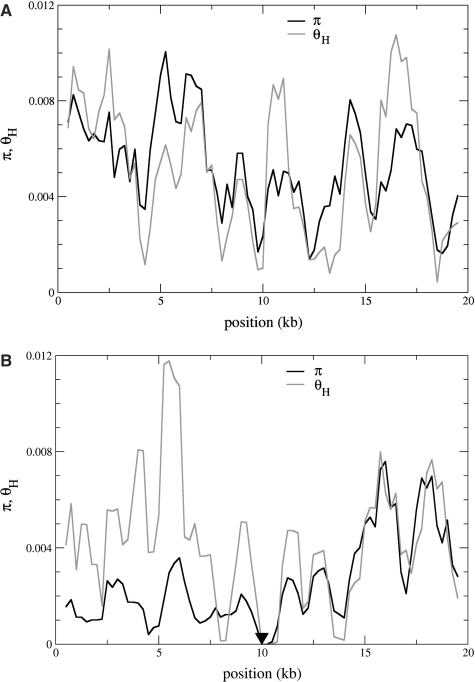
Variability profile along a sequence of 20 kb produced by coalescent simulation under the demographic model of [55] (a population with N = 10⁴ individuals undergoes a bottleneck with 3000 individuals that starts 600 generations ago and lasts for 200 generations. At the start of bottleneck, directional selection occurs on a beneficial mutation with s = 0.05 and the starting frequency of 0.001. Scaled recombination and mutation rates are 4Nr = 0.04 and 4Nμ = 0.005, respectively, per nucleotide). Variation is measured by π (solid curve) and θ_H (gray curve) and with a sliding window of 1 kb (A) without selection (B) with selection. The filled triangle at 10 kb indicates the position of the site where a beneficial mutation triggered a selective sweep. At first sight, both measures show a quite irregular pattern in both scenarios. However, they become distinguishable with the help of derived quantities, for instance the difference θ_H − π, which is much larger under selection than under neutrality. The distributions of such statistics can be obtained by coalescent simulations and then be used to define a significance level for rejecting the null hypothesis of neutral evolution.

COALESCENT SIMULATION

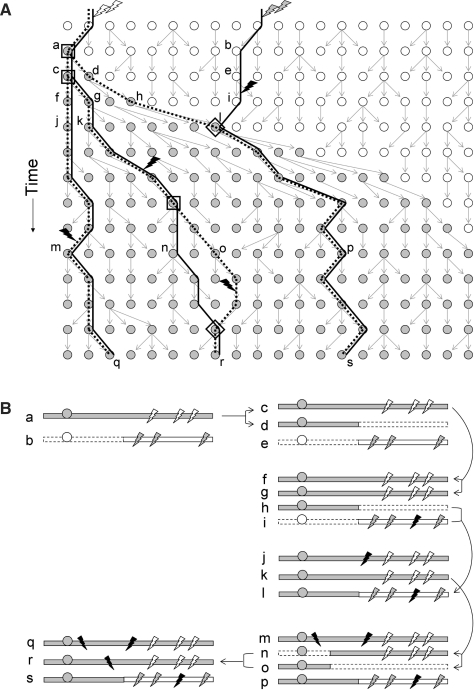
Coalescent simulation is the most widely used method for modeling patterns of selective sweeps. The coalescent (for a more detailed introduction to coalescent theory, see [27–29]) captures the evolutionary history of a sample of DNA sequences rather than of all sequences of a population. Since it is the genealogical history of the ancestors of the sampled sequences that matters for building summary statistics, one can often avoid reconstructing the evolutionary history of all individuals of a population. A coalescent simulation is conducted backward in time according to the probabilities of coalescence (two separate lineages find a common ancestor; Figure 1) or recombination (a lineage is split into two parental sequences) under a particular population genetic model. Once the genealogy of sampled sequences is constructed, mutations are placed (usually modeled as a Poisson process with rate μ representing the per generation mutation rate) along the lineages to generate polymorphic sites [29]. The coalescent process without recombination was first described by Kingman [30] as an approximation to the genealogical process in simple neutral models of reproduction, such as the Wright–Fisher model. The simulation of this process is extremely time efficient because it considers only the lineages which are ancestral to the sample and skips ‘un-interesting’ generations by a continuous-time approximation of the underlying discrete process (Table 2, row 1). The size of a sample is usually much smaller than that of the entire population. While Kingman's coalescent is represented as random binary tree, the coalescent with recombination is represented by the ancestral recombination graph of Griffiths and Marjoram [31]. Constructing an ancestral recombination graph is straightforward and, as long as a single locus or a small genomic region is simulated, the algorithm is fast enough to be practical for exploring an otherwise wide-parameter space. However, it becomes computationally demanding for large genomic regions since the number of edges to be tracked increases exponentially with increasing recombination rate. Modifications of the standard coalescent to efficiently simulate a large number of recombination events have been designed by McVean and Cardin [32] and Marjoram and Wall [33]. Essentially, their algorithms ignore a class of rare recombination events which would have no or little effect on the sample haplotypes. Keeping the memory demand limited is achieved by updating a previously generated genealogy, rather than constructing it de novo, when walking along the sequences. For large genomic regions and/or for very large sample sizes an additional problem may arise: the probability that multiple coalescent events happen at the same time may not be negligible and thus a fundamental assumption of the standard coalescent may be violated. To solve this problem one may resort to coalescent simulations with discrete generations (Table 2, rows 2, 3)—unfortunately only at the expense of computational efficiency. More advanced theory [34] considering generalized coalescents (for instance, so-called λ-coalescents) may come to help here.

Figure 1:

Gene genealogy under a model of strong directional selection and the corresponding pattern of sequence polymorphism, for a population of 20 haploid individuals (homologous sequences; shown as circles) which reproduce in discrete generations. (A) Each line in the graph represents one generation. Gray arrows indicate the inheritance of alleles at the locus under directional selection. Filled (empty) circles represent individuals carrying the beneficial (ancestral) allele at the selected locus. Due to strong directional selection, the beneficial allele quickly reaches fixation in the population, indicated by the presence of only filled circles in the lower third of the figure. Three sequences (q, r and s) were sampled in the current generation (bottom). The genealogy at the selected locus, traced backward-in-time from the sampled chromosomes, is shown by dotted lines. The genealogy at a neutral locus that is partially linked to the selected locus is shown by solid lines. Genealogies at the two loci are different due to recombination events (indicated by diamonds). Coalescent events are indicated by squares. The recombination event in the ancestral sequence (l) allows the neutral lineage of sequence s to escape the coalescence tree of the selected locus. Coalescent simulations create such genealogies by generating only the times of coalescence or recombination according to probabilistic models, without specifying the reproduction of the entire population at each generation. Genealogies at different loci merge to form an ancestral recombination graph. Therefore, squares and diamonds above correspond to nodes in the ancestral recombination graph. Lightning symbols along the lineages indicate mutation events that produce polymorphism in the sampled sequences. Empty and gray lightning represent mutation events which happened in earlier generations than the ones shown; however, they are still visible as polymorphisms in the sampled sequences q, r and s that are inherited along the indicated lineages. Black lightning represent mutation events which happened during the shown time interval. (B) Sketch of a possible course of evolutionary events leading to the observable polymorphisms in a present day sample (sequences q, r and s). The states of ancestral sequences at selected time points [sequences a to p indicated in (A)] are shown. Filled gray bars indicate the sequence on which the beneficial mutation first occurred (gray circle on sequence a) and its descendants. Empty bars represent DNA segments which recombined with the beneficial allele. A dashed outline of the empty bars indicates ancestral DNA segments, acquired by recombination, that do not leave descendants in the present-day sample.

Table 2:

Selected software resources

No.	±	Name	Purpose	Ref.
1	−	ms	Backward in time (coalescent) simulation of the segregating sites of a sample of haplotypes as in Figure 1B; allowing for recombination, gene conversion, migration among subpopulations and a variety of demographic histories. Although this program does not include any models of directional selection, simulations generated with ms are often used to produce a background distribution under neutral evolution of the statistics of interest.	[76]
2	−	GENOME	Coalescent-based approach to simulate whole-genome data. In addition to features of standard coalescent simulators, the program allows for recombination rates to vary along the genome and for flexible population histories. No simulation of models of selection.	[77]
3	−	SimCoal SimCoal2	Coalescent simulation with discrete generations; accommodates multiple loci in large genomic regions and complex population history. No simulation of models of selection.	[78]
4	−	SelSim	Simulation of DNA polymorphism data for a recombining region within which a single bi-allelic site has experienced natural selection. SelSim allows simulation from either a fully stochastic model of, or deterministic approximations to, natural selection within a coalescent framework.	[79]
5	−	ssw	Simulate selective sweeps following the model of refs [41] and [80]. Recombination of sequences via crossing-over and/or gene conversion is implemented. Versions simulating a stochastic trajectory of the focal allele and simple demographic changes are available.	[81]
6	−	mlcoalsim	Coalescent simulation to generate samples, similar to ms and ssw, with added features such as built-in statistical tests for output.	[82]
7	+	simuPOP	Forward-in-time population genetics simulation environment. simuPOP provides scripts that perform simulations of basic population genetic models and that can also generate datasets under more complex evolutionary scenarios, except models of selection.	[83, 84]
8	+	FPG	FPG (for forward population genetic simulation) simulates a population of constant size that is undergoing various evolutionary processes, including: mutation, recombination, natural selection and migration.	[85]
9	+	ForSim	Forward-in-time simulation program that allows users to define the number, lengths and location of genes and chromosomes, the genetic contributions and interactions, environmental effects and other conditions (number of populations, phenotype-based natural selection, gene flow and mate choice).	[86]
10	+	EasyPOP	An individual-based model that simulates neutral loci datasets under a very broad range of conditions.	[87]
11	+	FREGENE	Individual-based forward-in-time simulation that uses the rescaling method to reduce the computational burden. Directional and balancing selection are allowed at chosen loci. Various models of demography and recombination can be specified.	[88]

(±) indicates the type of simulation, backward-in-time (−) or forward-in-time (+).

For simulating a selective sweep (Table 2, rows 4, 5), one has to model coalescence and recombination events in a population which is subdivided into two genetic backgrounds: one class of lineages is linked to the beneficial allele and the other class is linked to the wild-type allele (Figure 1). Given the frequencies of the two alleles, beneficial and wild-type, the genealogical history is considered separately for each allelic class. At a linked neutral locus, lineages are allowed to move between the two classes by recombination. This idea of a genealogy conditional on a sequence belonging to either one of two allelic classes was first described by Hudson and Kaplan [35] and applied to modeling of selective sweeps by Kaplan et al. [5]. Braverman et al. [36] first simulated the genealogy under selective sweeps using the two-locus theory of coalescence and recombination [5]. Here, the first locus is under directional selection and the other locus carries only neutral alleles. This two-locus simulation, in which the neutral locus is represented as a nonrecombining sequence, is sufficient to generate the unique signature of selective sweeps in the form of a skewed allele frequency spectrum, i.e. an excess of mutant alleles in very low or high frequency in the sample [37]. Other important signatures of selective sweeps are a nonuniform distribution of polymorphic sites and an excess of linkage disequilibrium in the chromosomal region affected by the beneficial mutation [38, 39]. To detect these signatures, the genealogical correlation among multiple polymorphic sites, which critically depends on the recombination rate, should be correctly obtained. Later studies thus allowed recombination within the neutral locus under consideration (e.g. [40]). In particular, Kim and Stephan [41] implemented the algorithm of coalescent with recombination in which the selected site is located in the middle of a chromosome with arbitrarily many neutral loci around the selected site (Table 2, row 5). This allowed the assessment of the stochastic pattern of local reduction of variation and associated skew of frequency spectrum and linkage disequilibrium.

In these simulations of selective sweeps, the trajectory of a beneficial mutation, which divides the lineages in the population into two allelic classes in a time-dependent manner, was computed beforehand using the deterministic dynamics of an allele under directional selection. However, there is a drawback with this procedure: the deterministic trajectory of a beneficial mutation is quite different from the true stochastic trajectory that is subject to near-neutral genetic drift at the early stage when the frequency is low. Conditional on its eventual fixation, the stochastic trajectory of a beneficial allele relative to the deterministic one is shifted upward by ∼1/(2s) on average, where s is the selective advantage of the beneficial mutation [42, 43]. This difference significantly changes the outcome of the hitchhiking effect [4, 43, 44], as it shortens the initial phase of the selective sweep and therefore leaves less opportunity for recombination. Thus, with the stochastic trajectory the effect of hitchhiking is more drastic than with the deterministic trajectory. There have been three ways of modeling this property. First, the deterministic trajectory may be modified to mimic the stochastic effect. For example, one may assume that the frequency of the beneficial allele increases immediately from one to 1/(2s) copies and then grows deterministically. This ad hoc solution rectifies most of the error caused by using the complete deterministic trajectory in the initial phase [39]. Recently, Eriksson et al. [45] obtained a more accurate deterministic approximation to the stochastic trajectory. Second, one may specify the two allelic classes entirely by a stochastic (i.e. simulated) trajectory. One can use a forward-in-time simulation (Table 2, rows 8, 9) of directional selection to generate the trajectory of the beneficial allele and then use the recorded trajectory backward-in-time during the coalescent simulation. This procedure has been applied by Innan and Kim [18] and Teshima and Przeworski [46]. Alternatively, and because of time reversibility [47], the stochastic trajectory can be simulated backward-in-time and simultaneously with the construction of the ancestral recombination graph [48]. Finally, the genealogy under the hitchhiking effect can be approximated by a Yule process, a stochastic process quite different from the coalescent [49]. This method has the advantage that it is better tractable analytically and it does not require any explicit assumption or simulation of evolutionary dynamics at the focal locus.

One should also be aware of a further principle limitation for coalescent simulations of selective sweeps. The continuous time approximation of the discrete coalescent implicitly requires that an allele may leave at most two descendants or, equivalently, that a lineage may at most bifurcate per unit time. Not only for large genomic regions and large sample sizes mentioned above, but also for very strong selection this assumption may be violated. Therefore, the result of a simulation with large s (s close to one or larger) cannot be validated using the classical mathematical theory, which is a crucial step for error checking. While non-standard coalescent trees under strong selective sweeps are not implemented in currently available simulation software, theoretical framework to treat generalized coalescent trees [34, 50] (trees with ‘multiple collisions’) and trees with simultaneous multiple collisions [51] has been developed.

The use of simulated trajectories in the simulation of genetic hitchhiking is important not only for obtaining the accurate patterns of genetic variation but also for enabling the simulation of other complex models of directional selection, such as soft sweeps from a previously neutral allele [18, 20] and selection on recessive beneficial mutations [46]. In both cases, the frequency of the allele that divides the population into two genetic backgrounds (we may call it the ‘focal’ allele) experiences an extended period of neutral fluctuation before being lifted to fixation by positive selection. This approach of precomputing the trajectory of the focal allele and then building a sample genealogy conditional on two genetic backgrounds may also be used to simulate the genetic data under balancing or periodically oscillating selection. One should note, however, that applying this method to models of selection that do not assume codominance of selected alleles (e.g. recessive beneficial mutations or balancing selection due to over-dominance) introduces a subtle theoretical problem. For example, if the relative fitnesses of genotypes A₁A₁, A₁A₂ and A₂A₂ at the focal locus are 1+s, 1 and 1, respectively, and if all three genotypes are present in the population, A₁ lineages in homozygotes leave more descendants than A₁ lineages in the heterozygotes. It thus violates the assumption that lineages evolve neutrally within each allelic class. A similar problem arises with over-dominance. As the chromosomes carrying the same allele have unequal fitness, the effective number of chromosomes becomes smaller than the actual count, thus increasing the rate of coalescence within the allelic class. However, this increase will be only on the order of the selection coefficient s. Further studies are needed to evaluate the importance of this effect.

Furthermore, coalescent simulations for selective sweeps described above use the tacit assumption that the two genetic backgrounds at a given time originated from a single mutational event at the focal allele. Under reasonable biological scenarios this assumption might be violated. Namely, while the polymorphism at the focal locus, for example, with alleles A₁ and A₂, is maintained, some copies of A₁ may mutate to A₂, or vice versa. Then, a linked neutral lineage may switch genetic backgrounds (i.e. between A₁ and A₂) not only by recombination but also by mutation at the focal locus. Pennings and Hermisson [52, 53] showed that the possibility of the latter event cannot be ignored, even if strong selection produces a short trajectory of a beneficial mutation, as long as the mutation rate scaled by population size (4Nμ) is high. If such switching due to mutation (‘soft sweeps II’ [52]) happens, local variation is not completely wiped out. Therefore, it is recommended that, in all simulations of selective sweeps using the coalescent with recombination algorithm (i.e. simulations based on the model of Kaplan et al. [5]), extra terms be added to describe the transition of neutral lineages across genetic backgrounds due to mutational events at the focal locus.

Recent research focuses on identifying the pattern of selective sweeps under complex demography. A simple modification to introduce stepwise changes in population size before or after a selective sweep is possible by changing the rate of coalescence, while holding the rate of recombination constant [54]. The coalescent simulation of selective sweeps under a more complicated demography during plant domestication is described by Innan and Kim [55]. Developing an adequate coalescent model of selective sweeps under complex demographies, in particular if sweeps occur across subdivided populations, is very difficult because a given neutral lineage not only has to move between genetic backgrounds by recombination but also between sub-populations by migration. It is not clear whether these two events can be modeled to occur independently. The assumption of time reversibility of the evolutionary process, which underlies all coalescent models, may be violated in such cases. This is in contrast to the possibility of simulating diverse scenarios of complex demography under neutral evolution [56] (Table 2, rows 1–3, 6).

Figure 2 shows typical patterns of genetic variation with and without directional selection along a recombining chromosome simulated under the models of plant domestication in [55]. By chance the level of variability (y-axis in Figure 2A) may be reduced in certain regions (x-axis) even under neutral evolution. This poses the problem of distinguishing random genetic drift and directional selection as the possible causes for the reduction of variability. Close examination of the neutral versus selective patterns reveals important differences. One indicator is given by the frequency spectrum. At evolutionary equilibrium, the frequencies of derived (recently mutated) alleles at neutral loci are usually lower than those of ancestral (wild-type) alleles. In contrast, as a result of a selective sweep, frequencies of derived alleles increase transiently [37]. This change in the allele frequency distribution is called a skew in the frequency spectrum and quantified by the difference between the statistics θ_H (Fay and Wu's estimator of 4Nμ) and π (Tajima's estimator of 4Nμ). The former is a variability measure which is based on the derived allele frequencies, the latter is the expected heterozygosity and ignores whether an allele is derived or ancestral. Figure 2 shows that the difference θ_H − π is much larger in the area nearby the pocket of reduced variation caused by selection (Figure 2B) than without selection (Figure 2A). Note, that in the example shown in Figure 2B, the skew of variability is asymmetric, by chance, around the site which gave rise to the selective sweep. Therefore, observing such asymmetry in actual data would still be compatible with a single selective sweep and even with a constant recombination rate per site.

ALTERNATIVES TO THE COALESCENT: FORWARD-IN-TIME SIMULATION

Coalescent simulation has been widely used in many areas of evolutionary studies because of its computational efficiency and direct correspondence between simulation results and observations in sampled DNA sequences. However, coalescent simulations are not suited for all evolutionary processes involving selection. In practice, the simulation of selective sweeps is restricted to models of directional selection in which only one locus has segregating alleles under selection at any given time. More generally, if n loci are polymorphic with selected alleles, a linked neutral lineage may belong to any of potentially 2ⁿ genetic backgrounds. It is possible to ‘sample’ the joint trajectory of those beneficial alleles by forward simulation and use it to specify the change of multiple allelic classes during the coalescent simulation. However, if two or more loci under selection are partially linked, the transition of a neutral lineage, located between the selected loci, across genetic backgrounds by recombination may not be determined separately during the construction of the genealogy, because one cannot assume that recombination between the neutral locus and one of the selected loci does not affect the trajectory of beneficial alleles. Note that this is in contrast to one locus selective sweeps, where recombination between neutral and selected loci can occur without interfering with the process of directional selection. This problem becomes more serious when beneficial mutations at different loci interact nonadditively. A similar problem occurs when selective sweeps occur in a subdivided population. As mentioned above, the migration of neutral lineages and the spread of a beneficial mutation across subpopulations may not be independent in this case. There can be many other biological complexities that make coalescent simulations impossible or impractical.

Forward-in-time simulations (Table 2, rows 7–9) that reconstruct the evolutionary process of the entire population can overcome such limits imposed on the coalescent simulation. In principle, any complex model of reproduction can be simulated forward in time. However, there are also drawbacks of this procedure, biological as well as technical. As to the former, forward-in-time simulations have to be started with certain initial conditions. For instance, one has to make an assumption about the neutral equilibrium level of variation before a selective sweep occurs. Recent experimental results in Escherichia coli [57] cast doubt on the appropriateness of the concept of a neutral genetic background in which an adaptive mutation can arise. Lenski and coworkers have demonstrated that an adaptive Cit⁺ variant in an E. coli population could originate only in a certain genetic background, which they called ‘potentiating’, and which is historically contingent.

The technical drawback of forward-in-time simulations is the severely increased computational cost. Even with the power of current personal computers, simulations at the scale of a real natural population, i.e. simulating in silico the reproduction of all individuals, are still impractical. Not only memory but also processing speed is limiting. For example, it takes O(N) generations to observe an appreciable shift in allele frequency by neutral drift if there are N individuals in the population. Since the simulation time to complete the reproduction of one generation is proportional to N, the total simulation time for observing a desired pattern of variation increases proportional to N². However, there are ways to circumvent at least some of the problems incurred by whole-population forward-in-time simulations while still generating meaningful results. For example, [58] developed an algorithm for exact forward simulation that reduces memory usage and run time by generating short-term genealogical information, by which nonancestral chromosomes are identified and the manipulation of them is skipped. In other methods, population genetic theory plays an essential role for simplification. In the following, we will describe three such methods in more detail.

Simulation with scaled parameters

The time scale of evolutionary processes in population genetics depends on population size. As an important consequence, the magnitude of other parameters, such as mutation rate, selection coefficient, migration rate or recombination rate, scales with population size. The reason for this is that any evolutionary force that changes allele or haplotype frequencies exerts its effect relative to the scale of random genetic drift, which is O(1/N). For example, the effect of a single recent selective sweep on the reduction of neutral variation depends on the product Ns and the ratio of Nr and Ns, where s is the selection coefficient of the beneficial allele and r is the recombination rate, per generation, between the neutral and selected loci [39, 59]. Thus, one expects identical effects in a population with s = 10⁻³, r = 10⁻⁴ and N = 10⁶ or with s = 10⁻¹, r = 10⁻² and N = 10⁴. In addition, since the reduction of population size changes the time scale by the same factor, the effect will be achieved in less time. Therefore, a simulation would be much faster using the latter parameter values. This approach—dividing N by some constant λ (e.g. λ = 10), but maintaining the product of Nx, where x is another parameter—is widely used in forward-in-time simulations and implemented, for instance, in the FREGENE package [60] (Table 2, row 11) However, there are a number of potential problems. There might be unrecognized population genetic effects that depend on the absolute, not the scaled, value of parameters. The fixation probability of a beneficial mutation, which depends to first order on s but not on Ns, is one example. Furthermore, expressions involving higher order terms (e.g. the square of the recombination rate for double recombination events) are usually neglected for the sake of simplification of analytical treatments. It should also be noted that x in Nx cannot be increased indefinitely. For example, to simulate a sweep with Ns = 1000, and reducing N below 10 000 means s > 0.1. Most analytic solutions for directional selection are derived by assuming that s is much smaller than one. The diffusion approximation of the discrete Wright–Fisher model and, as mentioned above, the continuous time approximation of the discrete coalescent require that an allele leaves at most two descendants per unit time—an assumption which may be violated when selection is strong. Tachida [61] and Comeron and Kreitman [62] also pointed out that in forward simulations the sample size must be small compared to the population size. This is essential to obtain correct sample statistics that are sensitive to the size of the sample (such as Tajima's D) which is extracted from the whole population. Comeron and Kreitman [62] showed that forward simulations may generate a considerable degree of error when N becomes too small, while Ns is held constant.

Frequency-based simulation

If the biological process can be simplified into a two- or three-locus model of natural selection and the expected changes of genotype frequencies between generations can be correctly described by mathematical formulae, one may examine the distribution of (neutral) allele frequencies simply by simulating the numerical changes of allele frequencies forward-in-time. In many biological scenarios, it is straightforward to obtain equations for frequency changes in one generation under the action of selection, mutation, recombination and migration (e.g. [63]). The stochastic change of allele frequencies due to random sampling at each generation (for example, the Wright–Fisher model) is also easily simulated using binomial random number generators. This simulation method has been widely used since the 1960s [64, 65], stimulated by the elaborate treatment of the interplay of genetic drift with other evolutionary forces as a diffusion process [66, 67]. It still finds application in more recent studies (e.g. [68–70]). One of its advantages is that it is much faster than the individual-based forward-in-time simulation. By observing the allele frequency change in an equilibrium process over long periods or repeating short independent runs (thus sampling different allele trajectories) in a nonequilibrium process, both the long-term average and transient distribution of allele frequencies can be obtained [71]. One disadvantage of this simulation method is that the evolutionary dynamics of only a few (up to three say) loci can be treated reasonably well. Therefore, the aspects of genetic variation that depend on the occurrence of multiple polymorphic loci in a sample of finite-length sequences, such as the sample frequency spectrum, Tajima's D statistic or haplotype structures, may not be examined in this approach. Despite this disadvantage, it is a still underutilized, yet important, tool of investigation because it is simple and the general pattern of variation under models of selection or other evolutionary forces is easily obtained. In particular, this simulation approach will be very useful for analyzing the emerging large-scale data sets of polymorphisms which are spread across different whole chromosomes and therefore represent independent evolutionary outcomes. This situation directly corresponds to the collection of independent runs of a frequency-based simulation.

Whole-population forward simulation to examine temporal coalescence

In other complex models of evolutionary changes, per-generation changes in genotype/haplotype frequencies may not be expressed by analytic solutions, especially when the number of loci in the model is large. In these situations, individual-based whole-population simulation might be the only solution (Table 2, rows 7–11). However, if a researcher is interested in the effect of a recent evolutionary change, such as a recent selective sweep in a genomic region that had been in neutral equilibrium prior to the time of change (t_c), he or she may (i) assume the well-known neutral distribution [72] of allele frequencies at t_c, and (ii) conduct the forward simulation of the evolutionary change between time t_c and the present, and then combine (i) and (ii) to produce the pattern of genetic variation at present. This general principle leads to a simulation scheme, described below, that is very efficient when the goal of simulation is simply to examine the effect of evolutionary parameters on summary statistics of genetic variation, for instance on expected heterozygosity π.

Consider a population consisting of N chromosomes that reproduce in discrete generations following the Wright–Fisher model. At the beginning of the forward simulation, neutral alleles at each locus on different chromosomes are individually marked such that they can be distinguished from each other. For example, at each locus one may assign the ‘ancestral number’ i to represent the neutral allele on the i-th chromosome (i = 1,…, N). Suppose that p_ij(t) is the frequency of the ancestral number i in the population at generation t at the j-th locus. At generation 0 (beginning of the simulation), p_ij(0) = 1/N for all i and j. Then, p_ij(t) changes during the simulation of the evolutionary model of interest. For example, if the model assumes directional selection at many loci and the locus j is tightly linked to one of the selected alleles, p_ij(t) is likely to increase to a value much greater than 1/N if i marks the chromosome with relatively higher fitness (carrying more beneficial alleles), or reduce to zero otherwise. When the simulation is stopped after T generations, the level of genetic variation at the j-th locus can be measured by the identity by descent. Let ϕ_22j be the probability that two randomly chosen alleles at locus j at time T have distinct ancestors at time 0 (this is equivalent to p₂₂ in [5]). Then,

ϕ_22j corresponds to the probability that two randomly selected gene lineages do not coalesce between time T and 0 (when time runs backward). This quantity determines the expected heterozygosity at present: if new mutations at neutral loci can be ignored between time T and 0, two randomly selected alleles at locus j are different only if the two lineages do not coalesce between time T and 0 and if the two ancestral alleles at time 0 are different (with probability 4Nμ, where μ is the mutation rate). Therefore, the expected heterozygosity at locus j is given by 4Nμϕ_22j. Employing a similar logic, the expected level of linkage disequilibrium between two neutral loci can be obtained by tracking the two-locus genealogy between time T and 0 and then combining it with the equilibrium level of linkage disequilibrium (the necessary mathematical theory is given in [73]). This method of simulation is fast enough to be practical for exploring numerous parameter values, because any simulation run lasts only T generations and summary statistic can be obtained from the genealogical structure of the whole population. These are much less variable than the statistics based on the sample genealogy from backward-in-time coalescent simulations and therefore also require less simulation runs. This approach has also been used to examine the pattern of variation after fixation of two overlapping selective sweeps at closely linked sites [74] and of epistatically linked beneficial alleles (T. Wiehe and Y. Kim, manuscript in preparation).

CONCLUSION

In most population genetic studies that aim to infer the evolutionary history of natural selection using DNA sequence polymorphism, a coalescent simulation, if possible, is the most effective tool of investigation. Using the correct coalescent simulation, an accurate description of the stochastic patterns of variation in the sample can be obtained and thus the proper statistical method for the inference can be designed. Computational speed is also an important advantage of coalescent simulations, especially when considering the increasing use of simulations to analyze whole-genome variability data. Simulations are also an integral part of statistical inference, for example, in Approximate Bayesian Computation [75].

However, coalescent simulations are adequate only in the context of relatively simple evolutionary models, such as directional selection at one locus at any given time and in a not too complex demographical background. When considering more complex evolutionary scenarios one is left with whole-population forward-in-time simulation. This method is generally much slower and much more memory demanding than coalescent simulations. Still, by creatively using results of population genetic theory, forward simulations can be designed to capture the desired evolutionary properties and to generate patterns of variation at multiple loci with reasonable speed.

Key Points.

• Simulation of sequence evolution under directional selection is essential for discovering genetic changes of functional importance.

• Coalescent simulation is the most efficient method of generating the correct stochastic patterns of polymorphism in a sample of DNA sequences. However, its application is limited to simple models of directional selection.

• Whole-population forward-in-time simulation is the alternative to coalescent simulation for complex models. The notorious problem of computational inefficiency can be overcome by using modifications based on population genetic theory.

FUNDING

National Science Foundation (DEB-0449581 to Y.K.); German Science Foundation (DFG-SFB680 to T.W.).

Biographies

Yuseob Kim is an assistant professor at the School of Life Sciences at Arizona State University, Tempe, AZ, USA. His research interests are in theoretical and applied population genetics and in comparative genomics with special emphasis on nucleosome positioning. He held positions before at Ludwig Maximilian Universität München, Cornell University and University of Rochester.

Thomas Wiehe is an associate professor at the Institut für Genetik, Universität zu Köln, Köln, Germany. His research interests are in theoretical population genetics and sequence-based bioinformatics. He held positions before at FU Berlin, MPI for Chemical Ecology Jena and University of California at Berkeley.