Charge Carrier Field Emission Determines the Number of Charges on Native State Proteins in Electrospray Ionization

Abstract

Although multiple charging in electrospray ionization (ESI) is essential to protein mass spectrometry, the underlying mechanism of multiple charging has not been explicated. Here, we present a new theory to describe ESI of native-state proteins and predict the number of excess charges on proteins in ESI. The theory proposes that proteins are ionized as charged residues in ESI, as they retain residual excess charges after solvent evaporation and do not desorb from charged ESI droplets. However, their charge state is not determined by the Rayleigh limit of a droplet of similar size to the protein; rather, their final charge state is determined by the electric field-induced emission of small charged solute ions and clusters from protein-containing ESI droplets. This theory predicts that the number of charges on a protein in ESI should be directly proportional to the square of the gas-phase protein diameter and to E*, the critical electric field strength at which ion emission from droplets occurs. This critical field strength is determined by the properties of the excess charge carriers (i.e., the solute) in droplets. Charge-state measurements of native-state proteins with molecular masses in the 5–76 kDa range in ammonium acetate and triethyl ammonium bicarbonate are in excellent agreement with theoretical predictions and strongly support the mechanism of protein ESI proposed here.

Electrospray ionization (ESI) is unique among the ionization sources used for macromolecular mass spectrometry because it simultaneously aerosolizes and produces multiply charged macromolecules. Multiple charging allows remeasurement of high molecular weight macromolecules in mass spectrometers that have modest mass-to-charge (m/z) ranges; hence, the coupling of ESI to mass spectrometers has become ubiquitous. Despite the advantages of multiple charging in ESI, the origin of the excess charge on macromolecules in ESI (i.e., the precise reason that a macromolecular species has a specific number of charges after undergoing ESI) is unknown. The two theories for ESI of macromolecules, the charge residue mechanism (CRM) and the ion emission mechanism (IEM), do not fully provide an answer to this question.

In ESI, highly charged droplets are produced and undergo a series of evaporation and Coulombic-explosion (near the Rayleigh limit) events that reduce the droplet mass and charge, respectively¹. According to the CRM², nonvolatile analytes remain enclosed in ESI droplets throughout the evaporation-explosion process. Upon complete droplet evaporation, the residual charge remains with the nonvolatile species, giving rise to gas-phase ions. The charge per gas-phase ion is limited by the charge at the Rayleigh limit of the droplet that enclosed the ionized analytes just prior to complete evaporation; hence, the physical size of the analyte controls the charge state³.

Conversely, in the IEM, charged analytes emit directly from the surface of nanosized charged droplets, driven by the electric field present at the droplet surface⁴. Directly emitted ions exist first as ions in solution, and, therefore, the number of charges on a gas-phase ion produced by the IEM is a function of its chemical structure and composition^5,6.

The charging of macromolecules in ESI has been examined in several studies^3,4,7–11. In these studies, macromolecular charge distributions were interpreted in terms of the CRM and IEM. However, a complete, quantitative theory describing both the origin and number of charges on electrosprayed macromolecules, has not yet been established. In this communication, we develop a theory of ESI for native-state proteins that explains quantitatively the mechanism by which these proteins become multiply charged in ESI. This theory is strongly supported by mass spectrometric measurements of the charge distributions of a series of native-state proteins.

ESI will produce multiply charged nanometer-sized droplets, some of which contain a single protein macromolecule. The excess charge in each droplet is presumably carried by small ionic species and clusters as opposed to the protein in its native state. Solvent molecule evaporation increases the strength of the electric field at the droplet surface, driving emission of charge carriers from the droplet. Emission of charges reduces the electric field strength, preventing further charge emission as well as Coulombic explosions¹³, until a sufficiently large electric field is again generated by neutral solvent evaporation. If the effects of droplet curvature are neglected, then emission of an ion from the droplet will always occur when the electric field at the droplet surface is of a critical strength, E^*, and the number of charges, n on a droplet of diameter D can be calculated from the equation:

$$n=\left[\frac{\pi {\epsilon }_0{E}^{*}}{e}{D}^2\right]$$ (1)

where ε₀ is the permittivity of free space and e is the unit charge of an electron. As the excess charge on the droplet is carried by small ionic species and small solute and solvent clusters, the emitted charged species are ions and small clusters. The protein is not emitted from the droplet and resides within the droplet interior. After solvent evaporation, the remaining excess charges accumulate on the protein. Most native-state proteins have sufficient available surface sites to hold the remaining excess charges⁹, and the number of excess charges residing on a protein therefore depends on the protein’s gas-phase diameter. Gas-phase mobility (projected surface area based) diameter measurements¹⁴ recently made on a series of native-state proteins aerosolized by ESI^15–17 show that protein diameter is proportional to the 1/3^rd power of the protein molecular weight, and gas-phase proteins have a bulk density of approximately 0.57 g cm⁻³; hence, they are somewhat hydrated in the gas phase. As measurements have been verified using different techniques^16–17, measured diameters are presumably representative of the protein size at the moment solvent evaporation and ion emission cease. Therefore, it is reasonable to use gas-phase mobility measurements to determine protein diameter (D in equation 1). It should be noted, however, that the theory presented here is strongly supported by measurements regardless of the true gas-phase protein density, so long as the protein diameter is proportional to the 1/3^rd power of the protein mass and the bulk density less than ~1.4 g cm⁻³.

According to the proposed charging mechanism, proteins are charged residues, but their final charge state is also determined by emission of small ions from ESI droplets prior to complete solvent evaporation. E^*, the critical field strength at which ion emission occurs from a droplet, is a function of the solvation energy of charged species and clusters at the surface of the droplet. The excess charge in ESI droplets is presumably carried by multiple types of species, each with their own corresponding E^*. Charged species requiring the lowest E^* would emit first until the droplet is completely depleted of that species. At the point of depletion, a new charged species, requiring a higher E^*, would then begin to emit from the droplet (i.e., charged species emit from nanodroplets in order of those requiring the lowest E^* to the highest E^*). For a given ESI solution, the speciation of charge carriers in nanodroplets likely varies little between droplets. Therefore, the theory predicts that the protein mean charge state (taken as the centroid of the protein charge distribution) should have a square dependence on the protein diameter while a particular type of charged species is emitted from ESI droplets. Once the droplet is depleted of the emitted charged species, droplet evaporation proceeds until a new E^* is reached, the lowest E^* for all remaining charge carriers, and a different type of charge carrier emits from the droplet. Following the shift to higher E^*, the square dependence of protein charge on protein diameter should be maintained; however, a plot of the protein charge vs. the protein diameter should be shifted, corresponding to the shift in E^*. E^* and shifts in E^* are a determined only by the solvent and charge carriers; thus, once they are known for a given solute-solvent system¹³, they can be used to predict the number of charges on any protein in ESI with that solute-solvent system.

To test the proposed mechanism of ESI, proteins were electrosprayed under native-state conditions, and their charge states were measured by orthogonal ESI/time-of-flight mass spectrometry (Micromass Q-TOF micro). Two different solutes were used: 10 mM ammonium acetate (NH₄Ac), and 10 mM triethylammonium bicarbonate (TEAB), both of which are suitable for maintaining protein native-state confirmations^7,10. Proteins with molecular weights ranging from 5.8 kDa (insulin) to 76 kDa (holotransferrin) were used as tests. Protein mobility diameters were taken from gas-phase mobility measurements found in the literature or using a regression equation for protein mobility diameter as a function of protein molecular weight¹⁶ (see supporting information).

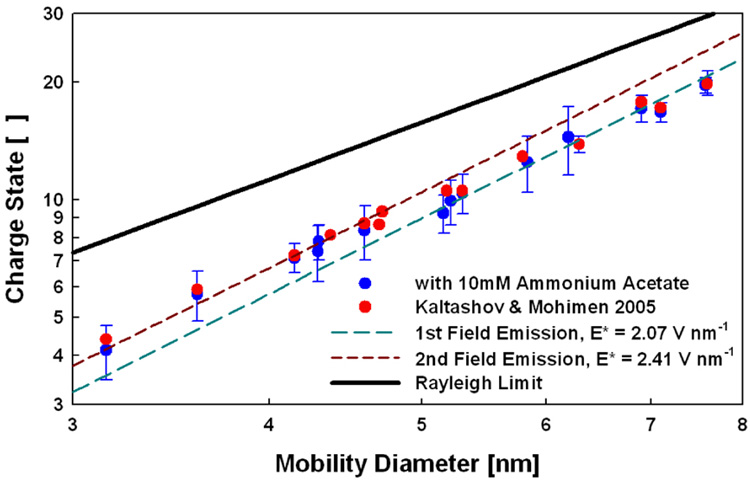
The mean charge state of each protein varies linearly with the square of the protein mobility diameter for ESI from aqueous 10 mM NH₄Ac (Figure 1). Error bars in y-direction represent the intrinsic standard deviation of each protein’s charge distribution. We also show the mean charge states of proteins measured by Kaltashov and Mohimen¹⁰ using an ESI solution of 10 mM NH₄Ac but a double focusing mass spectrometer for mass analysis. The data sets are in excellent agreement; thus, charge distributions appear to be independent of the mass spectral measurement method. The mean charge state of all proteins is below the Rayleigh limit, indicating that the charge state does not depend on this limit. Although square dependence of the protein charge state on the protein diameter is apparent, there is a detectable shift in the pre-exponential factor of the charge state-diameter relation (i.e., a shift in E^* from 2.07 to 2.41 V nm⁻¹ as seen by the second correlation line in Figure 1) in the 4.7–4.8 nm diameter range; this shift indicates a change in the type of charge carrier being emitted from droplets in that size range.

Figure 1.

Protein mean charge states as a function of protein mobility diameter in ESI from 10 mM ammonium acetate (log-log axes).

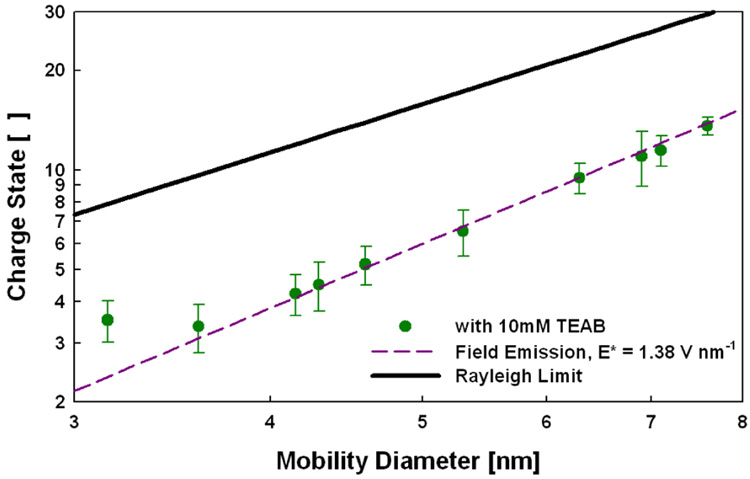
We again observed a square dependence of the mean protein charge state as a function of protein diameter when using 10 mM aqueous TEAB with a corresponding E^* of 1.38 V nm⁻¹ (Figure 2). No shift in E^* was apparent until a diameter of approximately 3.5 nm. The difference in E^* between NH₄Ac and TEAB as well as the difference in location of shifts in E^* is expected based on our proposed model of ESI. Overall, the charge-state measurements made here and in previous studies strongly support the described mechanism of ESI for native-state proteins.

Figure 2.

Protein mean charge states as a function of protein mobility diameter in ESI from 10 mM triethylammomium bicarbonate (log-log axes).

A better understanding of the ESI mechanism is of importance in mass spectrometry and its myriad applications in biology. The theory presented here has implications not only in macromolecular mass spectrometry but also in ESI-mass spectrometry of mixtures, as it proposes that charged species emit from droplets in order of their requisit E^*, from low to high. Further testing and refinement of this model will allow for prediction of m/z limits for various analytes, facilitating the design of mass spectrometers for macromolecular measurement. The theory can also open the door to new information obtainable from mass spectrometric measurements.

Supplementary Material

Table. Supporting Information Available.

Table of proteins measured, molecular weights, mobility diameters, measured and expected charge states based on proposed mechanism.