Noise Correlations Have Little Influence on the Coding of Selective Attention in Area V1

Abstract

Neurons in the visual primary cortex (area V1) do not only code simple features but also whether image elements are attended or not. These attentional signals are weaker than the feature-selective responses, and their reliability may therefore be limited by the noisiness of neuronal responses. Here we show that it is possible to decode the locus of attention on a single trial from the activity of a small population of neurons in area V1. Previous studies suggested that correlations between the activities of neurons that are part of a population limit the information gain, but here we report that the impact of these noise correlations depends on the relative position of the neurons' receptive fields. Correlations reduce the benefit of pooling neuronal responses evoked by the same object but actually enhance the advantage of pooling responses evoked by different objects. These opposing effects cancelled each other at the population level, so that the net effect of the noise correlations was negligible and attention could be decoded reliably. Our results suggest that noise correlations are caused by large-scale fluctuations in cortical excitability, which can be removed by a comparison of the response strengths evoked by different objects.

Introduction

Neurons in the visual cortex act as detectors: they code the properties of the stimulus in their receptive field. In early visual areas, the coding of basic features like orientations and colors is robust, and information about these stimulus properties is present as soon as the neurons are activated by the appropriate visual stimulus (Celebrini et al. 1993). This suggests that the neurons' selectivity is generated locally within the cortical column or inherited from the previous processing levels. In addition, the activity of neurons in early visual areas is modulated by the behavioral context. One type of task where these modulations are observed is perceptual grouping, where the subject's aim is to determine whether image elements belong to the same object or not. In such a task, the neurons that code the image elements that need to be grouped together enhance their response relative to neurons coding nongrouped features or background, as if the entire representation of the relevant object is “labeled” with an enhanced response (Lamme 1995; Roelfsema et al. 1998; reviewed by Roelfsema 2006). These response modulations have a correlate in psychology because object-based attention is directed to precisely those image elements that are labeled with the response enhancement (Houtkamp et al. 2003).

The perceptual grouping process starts to modulate neuronal responses after a delay relative to the initial response triggered by the appearance of a stimulus in the receptive field, which suggests that it requires a time-consuming integration of information within and between visual areas. We previously proposed that V1 neurons may actively participate in this process if they propagate the enhanced response through horizontal connections, which tend to link neurons tuned to contour elements in collinear configurations that are likely to belong to the same object (Roelfsema 2006). Area V1 provides a high-resolution representation of the visual scene, and this could be important for the correct grouping of nearby contour elements. In a curve-tracing task, where the subject has to determine which contour elements belong to the same elongated curve, V1 responses evoked by grouped contour elements are, indeed, enhanced relative to the responses evoked by nongrouped elements (Roelfsema et al. 1998). However, such a causal role of the primary visual cortex in the grouping process presupposes that the V1 neurons reliably code the set of contour elements that are grouped together. The modulation of neuronal responses during perceptual grouping is weaker than the feature-driven responses and might be difficult to detect in the presence of neuronal noise—the activity fluctuations that are observed from trial to trial if the stimulus is held constant (Tomko and Crapper 1974). Thus, it is not yet clear whether the response modulation in area V1 can reliably distinguish relevant, to-be-grouped image elements from irrelevant ones. In the present study, we therefore ask how well neurons in the primary visual cortex (area V1) differentiate between relevant and irrelevant image elements. Most previous studies on the neurophysiological correlates of visual attention investigated the average neuronal responses collected across a number of trials, but here we wish to decode the locus of attention on an individual trial. Specifically, we will try to combine the responses of different neurons recorded simultaneously on the same trial, instead of pooling across trials.

In general, multiple neurons should convey more information about the locus of attention than a single cell. The law of large numbers states that the variance of the average response of a population of neurons decreases linearly with neuron number if cells fire independently (Rice 1995). However, we know that the responses of neighboring cortical neurons are correlated, with correlation coefficients in the range of 0.1–0.2 (e.g., Gawne and Richmond 1993; Zohary et al. 1994; Gawne et al. 1996; Lee et al. 1998; Bair et al. 2001), and these so-called “noise correlations” influence the benefit of pooling. On the one hand, noise correlations reduce the reliability of the pooled responses if neurons are tuned to the same feature because the correlated variability also enters in their average response (Shadlen et al. 1996; Abbott and Dayan 1999). On the other hand, the correlations need not be detrimental when evaluating the responses of neurons tuned to different features. The differences between the magnitudes of responses of neurons tuned to dissimilar features are maintained in the presence of overall fluctuations in activity (Oram et al. 1998; Averbeck et al. 2006). Thus, the net effect of the noise correlations on the reliability of the attentional code remains to be determined.

In what follows, we will try to decode the locus of attention in a curve-tracing task in which monkeys had to group together contour segments of a target curve while ignoring a distracter curve. We will measure the reliability of the response enhancement at individual recording sites in area V1 and investigate how much information can be gained by pooling responses across recording sites. Here we will describe the modulation of neuronal responses by the curve-tracing task as a relative enhancement of responses evoked by the target curve. We note, however, that our study was not designed to determine whether the response modulation arises from an enhancement of responses to the target curve, a suppression of the responses evoked by the distracter curve or both. We will also determine the strengths of the noise correlations and evaluate whether they are helpful or harmful for the population code.

Materials and Methods

We analyzed data from a previous study on the strength of synchrony and noise correlations in area V1 (Roelfsema et al. 2004). This previous study did not estimate if and how the noise correlations influence the reliability of attentional effects in area V1.

Behavioral Task

Three monkeys participated in the study. They were seated at a distance of 0.75 m from a monitor (resolution 1024 × 768, frame rate 70 Hz) while they performed a curve-tracing task. A trial started as soon as the monkey's eye position was within a 1- × 1-degree window centered on the fixation point (0.2 degree). After an interval of 300 ms, 2 circles and 2 curves appeared on the screen (Fig. 1) while the monkey maintained fixation. The circles and the fixation point were red and the curves white (luminance 85 cd m⁻²) on a black background (luminance 1.5 cd m⁻²). After an additional 600 ms, the fixation point disappeared and the monkey had to make an eye movement to one of the circles. Eye movements to the circle that was connected to the fixation point by a curve that will be called target curve were rewarded with apple juice, whereas eye movements to the circle on the end of the other curve (distracter) were not. A small change close to the fixation point switched the target and distracter curve (compare the 2 stimuli in Fig. 1). We presented the 2 stimulus configurations in a randomly interleaved sequence so that the same curve could appear as target or distracter.

Figure 1.

The curve-tracing task. Every trial started with the presentation of a fixation point for 300 ms. Then 2 curves and 2 saccade targets (the 2 big dots at the end of the 2 curves) were presented. After 600 ms, the fixation point disappeared and the monkey had to make a saccade (gray arrow) to the saccade target at the end of the curve connected to the fixation point (target curve). During the fixation and stimulus period, the monkey maintained fixation within a 1-degree window centered on the fixation point.

Surgical Procedure

The animals underwent 2 surgeries under general anesthesia that was induced with ketamine (15 mg kg⁻¹ injected intramuscularly) and maintained after intubation by ventilation with a mixture of 70% N₂O and 30% O₂, supplemented with 0.8% isoflurane, fentanyl (0.005 mg kg⁻¹ intravenously), and midazolam (0.5 mg kg⁻¹ h⁻¹ intravenously). In the first operation, a head holder was implanted and a gold ring was inserted under the conjunctiva of one eye for the measurement of eye position (Bour et al. 1984). In the second operation, 40–50 Teflon-coated or polyimide-coated platinum–iridium wires (diameter 25 μm, impedance 0.1–0.8 MΩ at 100 Hz) were implanted chronically in area V1. The tips of the wires were positioned 1–2 mm below the cortical surface. The animals recovered for at least 21 days before training was resumed, and data collection was initiated. All procedures complied with the National Institutes of Health Guide for Care and Use of Laboratory Animals (National Institutes of Health, Bethesda, MD) and were approved by the institutional animal care and use committee of the Royal Netherlands Academy of Arts and Sciences.

Recordings

The eye position was measured with a double magnetic induction technique, sampled, and recorded at a rate between 500 and 1000 Hz (Bour et al. 1984). To record multiunit activity (MUA), the signals from the chronically implanted electrodes were amplified, band-pass filtered (750–5000 Hz), full-wave rectified, and then low-pass filtered at 500 Hz (Legatt et al. 1980; Supèr and Roelfsema 2005). MUA represents the pooled activity of a number of single units in the vicinity of the tip of the electrode. The population response obtained with this method is expected to be identical to the population response obtained by pooling across single units. We recently compared MUA with single-unit data in a curve-tracing and a figure-ground segregation task and found that MUA, indeed, provides a reliable estimate of the average single-unit response (Supèr and Roelfsema 2005). Moreover, the reliability of the attentional effect at MUA recording sites was in the same range as the reliability of single-unit responses (Supplementary Information). We measured the receptive field dimensions of every recording site by determining the onset and offset of the response to a slowly moving light bar for each of 8 movement directions (Kato et al. 1978). The median receptive field size was 0.54 degree² (range 0.11–9.4 degree²).

We quantified visual responsiveness by calculating the mean activity and the standard deviation (SD), s, across trials in 2 time windows relative to stimulus onset: w₁ = [−200, 0] ms (spontaneous activity) and w₂ = [0, 200] ms (initial response) and then computed . Only recording sites with a good visual response (r_Visual > 1) were included in the analyses. If we recorded the activity of a combination of recording sites more than once (e.g., on different days), then we included only one of these measurements in the analysis, namely the measurement with the maximal product of the r_Visual's. The mean number of trials per stimulus condition was 89 (range 36–199).

Data Analysis

To compute the population responses, we first normalized the responses before averaging across recording sites. We estimated the spontaneous activity (Sp) by taking the mean activity in the time window of w₁ = [−200, 0] ms relative to stimulus onset and the peak response (Pe) by taking the maximum of the average response over all conditions (smoothed with a moving window of 25 ms). We normalized neuronal responses by subtracting Sp and dividing the result by (Pe − Sp). To quantify the strength of the attentional effects, we computed the modulation index (MI), which we defined as the difference in response strength normalized to the average response: (T − D)/((T + D)/2). Here T and D are the responses to the target and distracter curve after subtraction of the spontaneous firing rate, in a time window of w₃ = [200, 600] ms relative to stimulus onset.

The strength of the noise correlation, that is, the degree of coupling of the response strengths at different recording sites across trials, was quantified with the correlation coefficient. If we compared distributions of correlation coefficients, then we first applied Fisher's z-transformation to obtain normal distributions. We showed 2 complementary stimuli, and we, therefore, obtained 2 correlation coefficients for every pair of recording sites. These correlation coefficients are expected to be comparable for pairs of recording sites with receptive fields (RF) on different curves (1-1 pairs) because for both stimuli one RF was on the target curve and the other one on the distracter curve. However, if the RFs fell on the same curve, they both fell either on the target curve or on the distracter curve (2-0 pairs). We compared the average strength of the noise correlations for 2-0 pairs evoked by the target and distracter curve and found them to be equivalent (Wilcoxon signed-rank test, P = 0.11). We will therefore report the average correlation coefficients for the 1-1 and 2-0 pairs. In the Supplementary Information, we describe how we have used the monopole mapping to estimate the cortical distance in millimeters between a pair of V1 electrodes from the locations of their RFs (Balasubramanian et al. 2002 and see Supplementary Information).

Neuronal Discrimination between Attentional Conditions

We estimated the linear function that optimally discriminates between attention conditions, by maximizing the difference between responses evoked by the 2 complementary stimuli relative to the variance of the responses (Fisher 1936). If we have the activity vector y of p neurons on N trials with stimulus A and M trials with stimulus B, then our aim is to find the p-dimensional weight vector a that best separates the scalar quantities $z_{A_i}={\mathbf{a}}^T{\mathbf{y}}_{A_i}$ (with mean and SD s_A) and $z_{B_j}={\mathbf{a}}^T{\mathbf{y}}_{B_j}$ (with mean and SD s_B) across trials, where A_i and B_j are single trials of the 2 stimulus conditions (T denotes the transpose). If the distributions of the responses in the 2 stimulus conditions are Gaussian with the same variance, the squared standardized difference between the z values, , is maximal for , where s_z is the pooled SD of s_A and s_B, S⁻¹ is the inverse of the covariance matrix, and _A and _B are mean activity vectors for the 2 stimuli (Rencher 2002). In order to compare weights, we can standardize them by multiplying every weight with the SD of the corresponding variable: a* = [s₁a₁, s₂a₂, …, s_pa_p] (Rencher 2002). The linear discriminant function with the standardized weights is then $L=a_1^{*}{R}_1+a_2^{*}{R}_2+\dots +a_p^{*}{R}_p$, where R is the response strength minus the mean response strength divided by the SD (z-score). The discriminability, d² (square of the d-prime value), can be defined as (Averbeck and Lee 2006). To study the impact of the correlations, we also quantified the discriminability under the assumption that the correlations are zero. Specifically, we computed , where ${\mathbf{S}}_d^{-1}$ is obtained by setting the off-diagonal elements of the covariance matrix to zero. The effect of the correlation on the discriminability is computed as $\Delta d^2=d^2-d_{\text{shuffled}}^2$ (Averbeck and Lee 2006). Thus, Δd² is larger than zero if the noise correlations improve discriminability and negative if they degrade discriminability. To measure how much information is present in the pattern of neuronal activity on a single trial, we also computed the classification rate, the percentage of trials where the stimulus is correctly decoded from the neuronal responses by applying the linear discriminant. We used a cross-validation procedure to prevent overfitting: we partitioned the trials into a training set (random selection of half of the data) and a validation set (other half of the data), estimated the optimal weights in the training set, and used these weights to measure classification in the validation set. We then repeated this procedure with taking the second half of the data as the training set and the first half as the validation set and averaged these 2 values.

Results

The curve-tracing task is illustrated in Figure 1. The monkey had to mentally trace a target curve while ignoring a distracter curve (see Materials and Methods). The performance of the monkeys was 99.1% correct, averaged across all recording sessions. During this task, we recorded MUA from chronically implanted electrodes in area V1 of 3 macaque monkeys. In monkey 1, recordings were obtained from the left and right hemisphere (N = 42), in monkey 2 from the left hemisphere (N = 35), and in monkey 3 from the right hemisphere (N = 21). Figure 2 shows the centers of the receptive fields of all recording sites.

Figure 2.

Location of the RF centers of the recording sites. Different symbols denote recording sites in the 3 monkeys.

At 55 of 98 recording sites, the target curve evoked a significantly stronger response than the distracter curve (Fig. 3A). This response modulation by selective attention does not occur during the initial transient response but develops after an additional delay. We will refer to the recording sites with significant attentional modulation as A-sites (attention sites; P < 0.05, U-test), whereas we refer to the sites that do not discriminate between target and distracter curve as N-sites (Fig. 3B, no effect of attention; P > 0.05, U-test). At 2 recording sites, the responses evoked by the distracter curve were stronger than those evoked by the target curve, and these sites were included with the N-sites (total N = 43). To investigate the possibility that N-sites are poor or noisy recordings, we compared the visual responsiveness (r_Visual, described in Materials and Methods) of N- and A-sites but found it to be similar (P > 0.1). We quantified the strength of the attentional modulation by computing the MI (MI = (target response − distracter response)/average). The distributions of the MIs across the population of N-sites (average MI = 0.05) and A-sites (average MI = 0.31) are shown in Figure 3C. These distributions indicate that the difference between the populations of A- and N-sites is not absolute but that they rather fall in different regions of a continuum.

Figure 3.

Attentional modulation of neuronal responses. (A, B) Population responses for the recording sites that were significantly modulated by attention (A-sites) (A) and sites not modulated by attention (N-sites) (B). Solid traces show responses evoked by the target curve and dotted traces responses evoked by the distracter curve. The gray areas around the traces show ±2 standard error of the mean. Data were smoothed with a moving window of 25 ms. (C) Distribution of the attentional MI of A-sites (white bars) and N-sites (black bars) in a window from 200 to 600 ms after stimulus presentation. (D) Distribution of the d-prime for A- and N-sites. Arrows show the means.

The MI is a measure for the difference between the average responses evoked by the target and distracter curve, but it does not indicate how much information the recording sites convey about the identity of the curve in the RF on a single trial. We therefore also computed the d-prime for all our recording sites (Fig. 3D). The mean d-prime was 1.09 for A-sites, whereas it was 0.16 for N-sites. From the figure, it is apparent that there are clear differences between the reliability of A-sites: the first quartile, the median, and third quartile of the d-prime distribution are 0.66, 0.89, and 1.52, respectively (corresponding to a classification rate of 61%, 67%, and 75%).

We carried out a number of control analyses to ensure that the observed response modulation was not caused by 1) a nonclassical RF surround effect of the contour element that connected the fixation point to one of the curves or (2) a systematic difference in eye position between conditions. These results have been described in Supplementary Information.

Pairs of Recording Sites

The responses at 2 recording sites are expected to convey more information about the identity of the target and distracter curve than the response of a single site. Previous theories showed that the information gain depends on the correlation between firing rates of recording sites across trials (Shadlen et al. 1996; Oram et al. 1998; Abbott and Dayan 1999; Averbeck et al. 2006). We therefore started our analysis of paired recordings with a quantification of the noise correlation. We computed the noise correlations in a window from 200 to 600 ms after stimulus presentation because the attentional response modulation was most pronounced in this epoch. First, we investigated how the noise correlation depends on the distance between recording sites. We compared the noise correlation between pairs of recording sites with nearby receptive fields (<1 degree, N = 122) and pairs of recording sites with receptive fields that were farther apart (>1 degree, N = 265). The noise correlation was slightly stronger for the neurons with nearby receptive fields (median correlation coefficient 0.24 vs. 0.19, U-test, P < 0.05), which may be due to common input from the lateral geniculate nucleus. In the rest of the Results, we will focus on the pairs of recording sites with distant receptive fields (>1 degree) as our aim is to compare the influence of noise correlations for combinations of neurons with receptive fields on the same and on different curves, and we did not attempt to stimulate neurons with overlapping receptive fields with different curves. Within the subgroup of pairs with nonoverlapping receptive fields, the noise correlation did not exhibit a strong dependence on the receptive field distance (r = 0.04, P > 0.5, see Fig. 4A). Also, the noise correlation within this subgroup did not depend on the estimated cortical distance between electrodes (r = 0.02, P > 0.5, Fig. 4B). To investigate if and how the noise correlation changed during a trial, we computed the noise correlations in 4 different time windows relative to stimulus onset, [−200, 0], [0, 200], [200, 400], and [400, 600] ms for all paired recordings. The noise correlation was similar across these time windows (repeated-measures analysis of variance, F_3,1158 = 0.18, P = 0.97) and is thus fairly constant over time. In Supplementary Information, we demonstrate that the noise correlations are not caused by variations in eye position across trials.

Figure 4.

Noise correlation statistics. (A) Relation between the distance between the centers of 2 receptive fields and the noise correlation. Black points on the gray background are pairs with RF distance smaller than 1 degree and the white line is their mean noise correlation and gray points on the white background are the pairs with RF distance larger than 1 degree and the black line is their mean. n Indicates number of pairs, r correlation coefficient, and P significance for the pairs with RF distance larger than 1 degree. (B) Relation between estimated cortical distance and the noise correlation. (C) Distributions of the noise correlation coefficients for pairs of recording sites with RFs on the same curve (white bars) and on different curves (black bars).

In some of our paired recordings, the 2 receptive fields fell on the same curve, that is, they either both fell on the target curve or both fell on the distracter curve, and we will refer to these pairs as “2-0 pairs.” The other paired recordings will be called “1-1 pairs”: one receptive field was on the target curve, whereas the other was on the distracter curve. The strength of the noise correlation differed between 2-0 and 1-1 pairs (see also Roelfsema et al. 2004). This effect is illustrated in Figure 4C, which shows the distribution of correlation coefficients of 2-0 and 1-1 pairs as white and black bars, respectively. Although there is a large overlap between the 2 distributions that are both shifted to positive values, the distribution for 2-0 pairs (median = 0.21) is shifted to larger values than the distribution for 1-1 pairs (median = 0.16; U-test, P < 0.05).

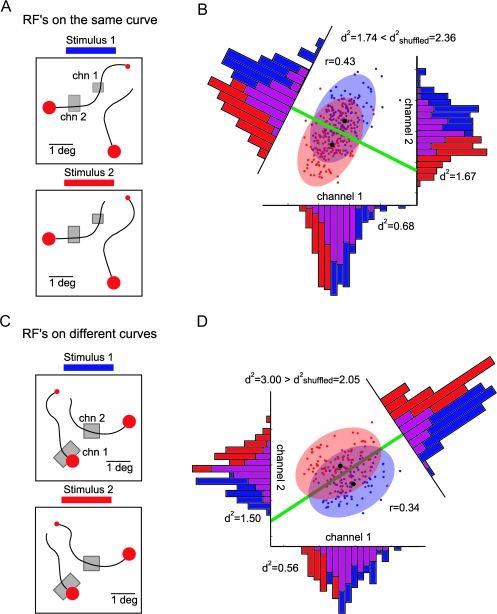
Because the single-trial responses of many A-sites carried incomplete information about the identity of the target and distracter curve, we investigated how the discrimination improves for pairs of recording sites and how this improvement depends on the noise correlation. Figure 5 illustrates the distributions of single-trial responses at 2 pairs of recording sites during the curve-tracing task. Figure 5A shows a 2-0 pair with receptive fields on the same curve. Every point of the scatterplot shows the (normalized) single-trial responses of the 2 recording sites in a window from 200 to 600 ms, evoked by the distracter curve (red points, see stimulus 2 in Fig. 5A) and the target curve (blue points, see stimulus 1 in Fig. 5A). The shaded ellipses show the 90% confidence intervals of these 2 distributions, where the elongation of the ellipses reflects the noise correlation, which was equal to 0.43. The discrimination of the individual recording sites corresponds to a projection of the data points onto the x and y axis (i.e., the marginal distributions shown on the coordinate axes of Fig. 5A), and the d² values (d² is the square of the d-prime value) of these recording sites were 0.68 and 1.67 (with classification rates of 66% and 75%). We next computed the linear combination of the 2 responses that best separates the 2 distributions (linear discriminant, see Materials and Methods). The tilted histogram in Figure 5A shows the optimal linear combination of the 2 responses, which gives rise to a d² of 1.74 and a classification rate of 75%. The projection that best separates the 2 linear distributions involves a weighted addition of the responses at the 2 recording sites, with L_2-0 = 0.29R₁ + 1.16R₂ (here the weights and the responses R₁ and R₂ are standardized as explained in Materials and Methods). To investigate the effect of the noise correlation on the discrimination, we also computed the $d_{\text{shuffled}}^2$, which is the square of the d-prime value that would be obtained in the absence of correlation. In general, $d_{\text{shuffled}}^2$ is the sum of the d² values of the individual recording sites. The $d_{\text{shuffled}}^2$ for the pair of Figure 5A was 2.36, which is higher than the observed d² of 1.74, indicating that the positive noise correlation reduced the information gain. This effect can be understood by inspecting Figure 5A: the positive noise correlation causes the confidence ellipses to be elongated along the line that connects the means of the 2 distributions, and it, therefore, causes these distributions to overlap more.

Figure 5.

Example combinations of 2 recording sites. (A) Stimuli used to evoke responses at 2 recording sites with RFs on the same curve (2-0 pair). The gray rectangles show the receptive fields. (B) Coding of attention by the 2-0 pair. Abscissa, the neuronal activity evoked at recording site 1. Ordinate, neuronal activity of site 2. The blue and red points in the scatterplot represent the activity of the neurons in individual trials with stimulus 1 and 2, respectively. Blue and red ellipses represent 90% confidence ellipses, and the black dots show the means of the 2 distributions. The marginal distributions of response strengths for the 2 sites are shown on the 2 axes. The tilted histogram shows the projection that optimally separates the joint distribution and the green line is the linear discriminant border. (C) Stimuli used to evoke responses at a pair of recording sites with RFs on different curves (1-1 pair). (D) Coding of attention by the 1-1 pair; conventions are as in (B).

Figure 5B illustrates a pair of recording sites with RFs on different curves (1-1 pair) with a noise correlation of 0.34. The d² values of the individual recording sites were 0.56 and 1.50 (with classification rates of 63% and 75%). Note that the linear discriminant now has a positive slope. This indicates that a weighted “difference” between the responses, L_1-1 = 1.30R₁ − 1.66R₂, best separates the 2 distributions. The d² of the optimal linear combination was 3.00 (with a classification rate of 83%), which is larger than the $d_{\text{shuffled}}^2$ of 2.05. Thus, the positive noise correlation is beneficial for the 1-1 pair: the joint distribution contains more information about the identity of the target and distracter curve than would have been expected in the case of no correlation. It can be seen in Figure 5B that the noise correlation causes the 2 distributions to contract along a line that connects the 2 means, giving rise to a reduced overlap. In other words, by subtracting the 2 responses from each other, it is possible to remove activity fluctuations that are common to the 2 recording sites.

In the examples of Figure 5, the positive noise correlations reduced the reliability of the attentional code of the 2-0 pair, whereas they improved the reliability for the 1-1 pair. A population analysis indicated that these observations were typical for the pairs of V1 recording sites. In this population analysis, we included pairs only if the distance between the RFs was larger than 1 degree and if the neurons at both recording sites were modulated by attention (2 A-sites). For the 2-0 pairs (N = 69), the average d² for the individual A-sites was 2.08 with a classification rate of 70%. The d² value increased to an average of 3.74 if the information from the 2 recording sites was combined and the classification rate increased to 76%. The positive noise correlations caused an average increase in d² for the pairs that was smaller than the $d_{\text{shuffled}}^2$ of 4.16, which would have been expected in case of no correlation, and the average $\Delta d^2=d^2-d_{\text{shuffled}}^2$ was significantly smaller than zero (mean −0.42, dotted gray curve in Fig. 6A; Wilcoxon signed-rank test, P < 10⁻⁷). Thus, the positive noise correlation caused the joint distributions of responses evoked by the target and distracter curve to overlap more, as was discussed in relation to Figure 5A.

Figure 6.

Distributions of Δd²; the difference between d² and $d_{\text{shuffled}}^2$. (A) Distribution of Δd² for pairs of recording sites with RFs on the same curve (2-0 pairs, gray dotted line) and pairs of recording sites with RFs on different curves (1-1 pairs, in black). (B) Distributions of Δd² for 3-0 triplets (gray dotted line) and 2-1 triplets (black). (C) Distribution of Δd² for 4-0 quadruplets (gray dotted line), 3-1 quadruplets (dashed line), and 2-2 quadruplets (black).

The average d² of individual A-sites in the sample of 1-1 pairs (N = 49) was 1.63 (with a classification rate of 70%), which is slightly, but not significantly (P > 0.5, U-test), lower than the d² of the A-sites contributing to the 2-0 pairs. The average d² for the combinations of 1-1 pairs was 3.84 (with a classification rate of 78%), which was larger than the average $d_{\text{shuffled}}^2$ of 3.26. Accordingly, the distribution Δd² was shifted to positive values (mean 0.59, solid black curve in Fig. 6A; Wilcoxon signed-rank test, P < 2.10⁻⁶). Thus, for 1-1 pairs, the positive noise correlations increased the separation between the joint distributions of firing rates evoked by the 2 stimuli (just as was observed in Fig. 5B).

More than 2 Recording Sites

Our analysis is easily extended to more than 2 recording sites. Figure 7 shows an example where we recorded simultaneously from 6 A-sites. Figure 7A shows the 2 stimuli that only differed at a location close to the fixation point, outside the neurons' receptive fields. Figure 7B illustrates the discrimination performance achieved by combining 1, 2, 3, 4, 5, and 6 sites. The d² reaches a value of 13.0 when all 6 recording sites are combined, and the classification rate was 96%. Note that in this example, noise correlations do not degrade the discrimination but rather enhance it (Δd² = 2.7).

Figure 7.

The combination of information from multiple recording sites. (A) Stimuli that were used to evoke responses at 6 recording sites. The gray rectangles show the receptive fields. (B) Distributions of the linear combinations of the responses across trials with the maximal separation. Blue bars, single-trial responses evoked by stimulus 1. Red bars, single-trial responses evoked by stimulus 2. The number of recording sites included in the analysis increases from 1 (left panel) to 6 (right panel). Note that the d² increases steadily with the number of recording sites, from 1.7 to 13.0.

We next evaluated at the population level how the discrimination improves for recording sessions with more than 2 A-sites. We obtained a sufficient number of combinations of 3 and 4 A-sites for a population analysis, whereas the number of cases where we recorded from more than 4 A-sites was too small. We recorded from a total of 164 combinations of 3 A-sites: 89 of these were 3-0 triplets and 75 were 2-1 triplets. For the 3-0 triplets, we obtained a mean d² of 4.50 (mean classification rate of 81%), whereas the mean d² for 2-1 triplets was 6.53 (classification rate of 87%). The positive correlations among the 3-0 triplets caused an information reduction about where attention was relative to what would have been expected in the case of no correlation. The mean Δd² was −1.23, which was significantly smaller than zero (Wilcoxon signed-rank test, P < 10⁻¹⁰; dotted gray curve in Fig. 6B). In contrast, the positive noise correlations were beneficial for the attentional code for 2-1 triplets. Here the mean Δd² was 1.14, which was significantly larger than zero (P < 10⁻⁵; solid black curve in Fig. 6B). Similar results were obtained for 85 quadruplets of A-sites. We recorded from 34 quadruplets with RFs on the same curve (4-0 quadruplets). The mean d² for these quadruplets was 4.40, with a classification rate of 83%, and the mean Δd² was −2.09, which was significantly smaller than zero (P < 10⁻⁶; dotted gray curve in Fig. 6C). The mean d² for the 3-1 quadruplets (N = 32) was 9.17 with a mean classification rate of 90% and a mean Δd² of 1.14 (P < 0.02; dashed curve in Fig. 6C), whereas the mean d² for the 2-2 quadruplets (N = 19) was 8.98 with a mean classification rate of 92% and a mean Δd² of 2.62, significantly larger than zero (P < 10⁻³; solid black curve in Fig. 6C). Thus, an equal number of recording sites with receptive fields on the 2 curves generally yielded an information gain beyond the expectation in the case of no correlation, whereas neuronal responses evoked by the same curve carried redundant information.

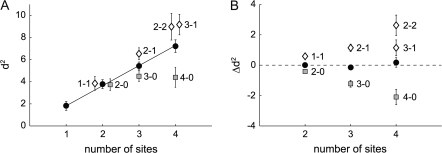
Figure 8 summarizes the results of the population analysis for pairs, triplets, and quadruplets of recording sites. The black line in Figure 8A gives an impression of the d² if neurons would fire independently (it is simply the average d² multiplied by the number of sites): discriminability should increase linearly with the number of recording sites. Combinations of recording sites with RFs on both curves tend to fall above this line, whereas combinations with all RFs on a single curve tend to fall below this line. If we average across all the RF configurations, however, these opposing effects largely cancel each other (black circles), and the overall d² is surprisingly close to the black line. This effect is also seen clearly in Figure 8B, which shows the Δd² as a function of the number of recording sites. Δd² is positive for combinations with RFs on both curves, negative for combinations with RFs on the same curve, and close to zero if we average across all combinations. These results, taken together, suggest that the noise correlations in area V1 hardly influence the reliability of the attentional code.

Figure 8.

d² and Δd² as a function of the number of recording sites. (A) Black filled circles are the mean d² for combinations of 2, 3, and 4 sites. The gray squares are the mean d² for the combinations with all RF's on the same curve and the white diamonds are combinations in which not all RF's lie on the same curve. The black line is the mean d² for single sites multiplied with the number of sites. Error bars show standard error of the mean. (B) Black filled circles show the mean Δd² across all combinations of 2, 3, and 4 sites. The gray squares and white diamonds are the average Δd² for the various combinations.

Discussion

The aim of our study was to investigate how much information neurons at individual recording sites in area V1 convey about where attention is on a single trial and how much information can be gained by combining the responses of neurons at different recording sites. We quantified the amount of information with the d² value (square of d-prime) and found that this measure increases approximately linearly with the number of recording sites, so that a d² value of approximately 7 (corresponding to a classification rate of ∼90%) is reached with an average of 4 A-sites. This result implies that we can infer the identity of the target and distracter curve reliably with a relatively small sample of the neuronal activity in area V1. In addition, we found that the effects of noise correlations on decoding depended on the location of the receptive fields. The noise correlations decreased the information gain for recording sites with RFs on the same curve, whereas they enhanced the information gain for recording sites with RFs on different curves.

Attentional Effects at Individual Recording Sites

V1 neurons are traditionally characterized as specialized for the coding of orientation or contrast (Hubel and Wiesel 1962; Albrecht and Hamilton 1982), whereas the demonstration of attentional effects in area V1 is of a more recent date (Motter 1994; Roelfsema et al. 1998; Vidyasagar 1998; Roberts et al. 2007). There is a temporal separation between the coding of basic tuning properties, which is apparent from the onset of the response, and the attentional effects that are weaker and occur after an additional delay (Lamme and Roelfsema 2000) in area V1 as well as in extrastriate areas (Chelazzi et al. 1993; Motter 1994; Reynolds et al. 1999; reviewed by Treue 2001). In the curve-tracing task, it takes about 130 ms before all the contour elements belonging to the target curve are labeled with an enhanced neuronal response (Roelfsema et al. 2003). When we studied a variant of this task in human subjects, we found that they direct their attention to all the contour elements that belong to a target curve. This suggests that labeling contour elements with an enhanced response (attention) is the way that the visual system can “bind” these contour elements into a coherent representation of an elongated curve (reviewed by Roelfsema 2006).

The reliability of the attention signal in area V1 is consistent with an active role in the grouping process. V1 provides a retinotopic map with a high spatial resolution so that perceptual objects can be segregated from each other, even if they are close together. We note, however, that not all V1 neurons carry information about attention. We distinguished between A-sites that are modulated by attention and N-sites that are not (Roelfsema et al. 2004). The N-sites (∼40% of recording sites) represent the contour elements irrespective of the context in which they occur, and they may thereby provide a “veridical” map of the visual scene that is independent of attention shifts. Here we have focused on the A-sites (∼60%) that may form another map of the visual field highlighting the objects relevant for behavior. The classification rate at some of these A-sites was only slightly better than chance, at others it was almost perfect, whereas the average classification rate was approximately 70%. In a recent study, Li et al. (2006) investigated the activity of single V1 neurons in another contour integration task where monkeys had to discriminate between a string of collinearly aligned contour elements and a random arrangement of contour elements. The discrimination performance of most of their neurons was striking: they were as sensitive to the collinear contour alignments as the monkeys were at a behavioral level. This contrasts with our finding that there is a substantial proportion of N-sites in the curve-tracing task, which represent clusters of nearby neurons not modulated by attention. This difference between results may be related to the task, as Li et al. manipulated the alignment of contour elements in the vicinity of the neurons' RFs, whereas the cue segment in the curve-tracing task that determines the identity of target and distracter curve is generally at a larger distance from the RFs. Another difference is that Li et al. mainly recorded from the superficial layers of cortex whereas most of our electrodes were in the deep layers. Previous studies on the neurophysiological correlates of attention shifts in striate and extrastriate cortex almost invariably found a mixture of “A-neurons” modulated by attention shifts and “N-neurons” that were not (Chelazzi et al. 1993; Motter 1994; Treue and Maunsell 1996; Reynolds and Desimone 1999). These previous studies did not quantify the single-trial classification rates, but the attentional effects were generally weak if compared with the visual responses, just as in the present study. It is therefore important to understand how the responses from multiple neurons can be combined to increase the reliability of coding of attention and how the noise correlations influence the combined reliability.

Noise Correlation

The distribution of noise correlation coefficients between activities at the V1 recording sites was shifted to positive values with an average value of 0.21. This value is consistent with a number of previous studies in V1 (0.22 in Gawne et al. 1996; 0.25 in Reich et al. 2001; 0.20 in Kohn and Smith 2005) and other areas, including inferior temporal cortex (0.23 in Gawne and Richmond 1993) supplementary motor area (0.13 in Averbeck and Lee 2006) and the middle temporal visual area (0.19 in Zohary et al. 1994). We did not observe a strong relationship between the strength of the noise correlations and the distance between the V1 recording sites and noticed that the strength of the noise correlations was similar before and after stimulus presentation. These results are consistent with a previous study by Chen et al. (2006) who used voltage-sensitive dyes to measure the activity of a V1 region in a target detection task. Chen et al. (2006) found that the presentation of the visual stimulus has little effect on the noise correlation, just as was found in the present study. Moreover, in the study of Chen et al. (2006), the average correlation decreased gradually with cortical distance within the imaged region of 4 mm, which is consistent with our finding that the correlation was stronger for the neurons with nearby receptive fields (<1 degree) than for neurons with more distant receptive fields. Our study adds to these results by showing that the noise correlation does not decrease further with larger distances within area V1 as it remained relatively constant for distances between 4 and 24 mm. These results, taken together, seem to suggest that a large fraction of the noise correlation represents relatively global variations in cortical excitability as could be caused, for example, by fluctuations in the activity of neuromodulatory systems that are related to variations in arousal. We note, however, that the pattern of the noise correlations is not entirely unstructured because the correlations are slightly but significantly stronger between neurons with RFs on the same curve than between neurons with RFs on different curves (see also Roelfsema et al. 2004).

Influence of Noise Correlation on the Reliability of the Attentional Code

Theoretical work suggested that the impact of noise correlations depends on the tuning of the neurons that are combined: positive correlations between neurons that have the same tuning are harmful, whereas positive correlations between neurons with different tuning allow for subtraction of common noise (Johnson 1980; Snippe and Koenderink 1992; Oram et al. 1998). Initial empirical work emphasized the adverse effects of noise correlations between neurons with similar tuning curves (Zohary et al. 1994). However, a recent study by Romo et al. (2003) showed that the effects of noise correlations on coding accuracy in primary and secondary somatosensory cortex of monkeys performing a vibrotactile discrimination task are mixed. Some cells in these areas prefer higher stimulus frequencies, whereas others prefer lower frequencies. Romo et al. (2003) observed a loss in accuracy caused by positive correlations (with an average correlation coefficient of 0.12) between neurons tuned to the same frequency, but this was partially offset by an improvement caused by positive correlation between neurons tuned to different frequencies. Thus, if the aim is to decode a sensory property in the presence of common noise, then it is beneficial to compare the response of neurons tuned to different features.

Our results are compatible with the findings of Romo et al. (2003), although we recorded the activity from neurons in another sensory modality and focused on the neurons’ attentional modulation rather than on their tuning. Noise correlation decreased the information gain for neuronal responses evoked by the same curve (with Δd² < 0) and increased the information gain for responses evoked by different curves (Δd² > 0). Overall, the decreases in accuracy for the 2-0 pairs were offset by a comparable increase in accuracy for the 1-1 pairs so that pooling across the neurons improved the accuracy of the code considerably. Thus, in the presence of widespread positive correlations, neurons coding for the same object provide partially redundant information, whereas neurons coding for different objects can be used to remove the influence of global activity fluctuations (common noise) unrelated to selective attention. The optimal discriminant, indeed, removed the common noise by computing the difference between the responses evoked by the target and distracter curve. These results generalized to triplets and quadruplets of recording sites as discrimination continued to improve when information from additional recording sites was added, in particular, if these recording sites had RFs on different curves. Remarkably, the adverse and beneficial effects of the noise correlations cancelled each other for combinations of 2, 3, and 4 recording sites so that the overall coding accuracy was close to that expected in the absence of noise correlations.

Mechanisms for Removal of Common Noise

The removal of global fluctuations in neuronal activity can be achieved in several ways. Here we only recorded from neurons with an RF on one of the curves and compared the strengths of neuronal responses evoked by the target and distracter curve. This comparison is presumably difficult to implement in neuronal hardware, especially if the shape of the curves changes from trial to trial, because the weights of the linear discriminant depend on the RFs that fall on the same and on different curves. We note, however, that the only requirement for the removal of common noise is an estimate of the overall V1 activity level, which can be obtained in several ways. First, it is possible to compare the activity of neurons at A- and N-sites with overlapping RFs. This activity difference gives a reliable measure of the locus of attention in the presence of global variations of neuronal activity. If a contour element is relevant for the task, then the A-neurons are more active than the N-neurons, whereas the 2 classes of neurons are equally active if the contour element in their RF is part of the distracter. Thus, a connection scheme where A-neurons are excited by neighboring A-neurons but inhibited by the N-neurons can propagate the response enhancement along the target curve. Second, measures of the overall V1 activity can be obtained in higher areas where neurons have large receptive fields. Bair et al. (2003) provided evidence that these higher areas provide inhibitory feedback to area V1, and we suggest that the neuronal response at an A-site can also be compared with the strength of such a feedback signal in order to determine whether a contour element is relevant or not.

Finally, we note that the linear discriminants used in the present study can be implemented in an anatomical projection from lower to higher areas. Downstream neurons involved in the selection of a behavioral response can extract the relative saliency of one of a number of objects if they receive excitation from the representation of this object and inhibition from the representation of the other ones. The response modulations observed in early visual areas that are associated with attention shifts are reflected by comparable response modulations in areas involved in response selection, like the frontal eye fields (Schall and Thompson 1999). Neurons in the frontal eye fields code the eye movement to a particular location in the visual field, and they receive excitatory visual input from the corresponding retinotopic location and inhibition from other retinotopic locations and engage in a competitive process where the eye movement plan receiving most activation eventually wins (Bruce et al. 1985; Seidemann et al. 2002). Thus, also at this level, differences between the activation of eye movement plans determine the outcome of the competition, so that global fluctuations in activity cancel out.

Here we have shown that the focus of attention can be decoded from a relatively small sample of the activity in area V1. We hypothesize that the processes that propagate the enhanced response along the target curve and that select the required eye movement take advantage of the proposed mechanisms for noise cancellation, so that all the information present in the neuronal responses can be brought to bear during such an attention-demanding task.

Funding

The European Union (EU IST Cognitive Systems, project 027198 “Decisions in Motion”); The Netherlands Organization for Scientific Research Vici grant awarded to P.R.R.

Supplementary Material

Supplementary Information can be found at: http://www.cercor.oxfordjournals.org/.