Predicting DNA recognition by Cys₂His₂ zinc finger proteins

Abstract

Motivation: Cys₂His₂ zinc finger (ZF) proteins represent the largest class of eukaryotic transcription factors. Their modular structure and well-conserved protein-DNA interface allow the development of computational approaches for predicting their DNA-binding preferences even when no binding sites are known for a particular protein. The ‘canonical model’ for ZF protein-DNA interaction consists of only four amino acid nucleotide contacts per zinc finger domain.

Results: We present an approach for predicting ZF binding based on support vector machines (SVMs). While most previous computational approaches have been based solely on examples of known ZF protein–DNA interactions, ours additionally incorporates information about protein–DNA pairs known to bind weakly or not at all. Moreover, SVMs with a linear kernel can naturally incorporate constraints about the relative binding affinities of protein-DNA pairs; this type of information has not been used previously in predicting ZF protein-DNA binding. Here, we build a high-quality literature-derived experimental database of ZF–DNA binding examples and utilize it to test both linear and polynomial kernels for predicting ZF protein–DNA binding on the basis of the canonical binding model. The polynomial SVM outperforms previously published prediction procedures as well as the linear SVM. This may indicate the presence of dependencies between contacts in the canonical binding model and suggests that modification of the underlying structural model may result in further improved performance in predicting ZF protein–DNA binding. Overall, this work demonstrates that methods incorporating information about non-binding and relative binding of protein–DNA pairs have great potential for effective prediction of protein–DNA interactions.

Availability: An online tool for predicting ZF DNA binding is available at http://compbio.cs.princeton.edu/zf/.

Contact: mona@cs.princeton.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The mapping of transcriptional networks is a key step in understanding the regulatory mechanisms of gene expression. While high-throughput experimental procedures have been applied for uncovering the genome-wide DNA binding of particular transcription factors (Harbison et al., 2004), cost-effective computational methods are still necessary to characterize the regulatory networks of the increasing number of fully sequenced genomes.

Most computational approaches for predicting the binding sites of a particular transcription factor use experimentally determined DNA binding sites to build a sequence representation, such as a consensus sequence or a position-specific scoring matrix, that can then be used to search for additional binding sites for this protein (Hannenhalli, 2008; Osada et al., 2004; Stormo, 2000). While broadly applicable and widely used in practice, such approaches can only be applied for proteins for which some binding sites are already known. However, by focusing on a particular structural class of transcription factors, and considering the contacts in its protein–DNA interfaces, it is possible to predict the DNA binding sites for a protein within this class even without any prior knowledge of any of its binding sites (Benos et al., 2001; Kaplan et al., 2005; Mandel-Gutfreund and Margalit, 1998; Suzuki et al., 1995).

Here, we focus on predicting the DNA binding sites of proteins within the Cys₂His₂ zinc finger (ZF)¹ structural class of transcription factors. These proteins comprise the largest family of eukaryotic transcription factors, with several hundred proteins known in the human genome (Venter et al., 2001). ZFs have been extensively studied, with crystal structures and experimental studies having elucidated their highly conserved modular structure (Pabo et al., 2001; Wolfe et al., 2000). Analysis of co-crystal structures of ZF proteins bound to DNA has led to the formulation of the so-called ‘canonical model’ which posits that ZF–DNA specificity is explained by four essential contacts per zinc finger (Elrod-Erickson et al., 1998), though other ZF–DNA configurations have also been observed (Wolfe et al., 2000).

The apparent simplicity of the ZF protein binding interface in the canonical case and the ample quantity of experimental binding data make these proteins attractive for developing theoretical models for protein–DNA binding prediction. Over a decade, several computational methods based on expert knowledge, statistical, structural and experimental binding data have been applied to this problem (Benos et al., 2002; Kaplan et al., 2005; Liu et al., 2005; Maeder et al., 2008; Mandel-Gutfreund and Margalit, 1998; Suzuki et al., 1995). Despite these attempts, an accurate prediction of ZF transcription factor binding sites remains a challenging task.

Here, we exploit support vector machines (SVMs) to predict protein-DNA interactions mediated by ZFs. The SVM is a state-of-the-art classification technique (Vapnik, 1995) that is known for obtaining excellent generalization performance for binary classification in high-dimensional spaces. The Cys₂His₂ zinc finger protein–DNA interaction interface is modeled by the pairwise amino acid–base interactions that make up the canonical structural interface. By utilizing a classification framework, we incorporate known examples of non-binding ZF–DNA pairs. Additionally, we are able to incorporate, for the first time, information about relative binding affinities of ZF–DNA pairs when utilizing a linear kernel; much data of this type has been generated in previous experimental work attempting to characterize ZF–DNA binding specificity (see Supplementary Table S1). Alternatively, a polynomial SVM captures dependencies among the canonical contacts and thus provides an indirect means for testing the canonical model for interaction. SVMs therefore provide us with a flexible means for incorporating a wide assortment of information about ZF–DNA binding. While it is possible to employ other kernels with SVMs, we have used these two for predicting ZF–DNA interactions due to their physical interpretability. In a wide-range of rigorous cross-validation testing, as well as on testing on the TRANSFAC database, we demonstrate that SVM-based methods are highly effective in practice. Specifically, the SVM with a degree two polynomial kernel outperforms previous methods. This suggests a role for pairwise correlations between contacts in the canonical model, consistent with the nucleotide-based analysis of Bulyk et al. (2002) and a very recent context-dependent neural network model (Liu and Stormo, 2008). This implies that either inclusion of additional contacts or a higher order binding model may lead to better results in predicting ZF–DNA binding.

2 METHODS

2.1 Structural model

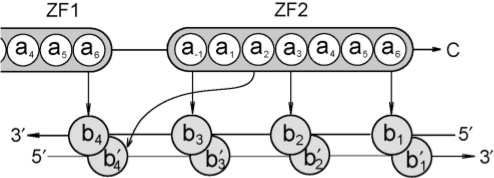
Structural studies (Elrod-Erickson et al., 1996; Pavletich and Pabo, 1991) have suggested that the ZF–DNA binding interface can be understood with respect to a ‘canonical binding model’ where each finger contacts DNA in an antiparallel manner. The α-helix in each finger fits into the major groove of the DNA, and each consecutive finger contacts four base pairs which overlap by one DNA position. For each zinc finger, the amino acid positions that contact DNA are called −1, 2, 3 and 6, and are specified as such because of their position relative to the start of the helix. Amino acids a₋₁, a₃ and a₆ are well positioned to make contacts with bases in the primary DNA strand, while amino acid a₂ can make a contact with the complementary DNA strand (Fig. 1).

Fig. 1.

Schematic representation of the canonical binding model. Amino acids are numbered according to their sequential number with amino acid 1 as the first residue in the ZF helical domain. Bases are numbered sequentially from 5 to 3 of the primary DNA chain, and are primed in the complementary DNA chain.

We use the canonical structural model to represent each potential protein–DNA complex by a feature vector x={x_abc}, where x_abc=1 for every amino acid a ∈ {Ala, Cys,…,Trp} interacting with base b ∈ {A, C, G, T} at contact position c. This representation scheme leads to a feature space containing 320 dimensions representing all possible abc combinations (20 amino acids × 4 bases × 4 contacts).

2.2 Prediction algorithms

2.2.1 Support vector machines

Our vector representation of a ZF–DNA binding interface has a natural physical interpretation corresponding to the potential contacts that would form for each pairing. Our goal is to deduce how good or bad each possible amino acid-nucleotide interaction is in each of the four canonical contacts. We apply the widely used support vector machinery to do this. Given a dataset of training examples x_i, SVMs search for a weight vector w that best separates binding and non-binding examples (Cristianini and Shawe-Taylor, 2000). That is, for a particular set of known binding interactions and non-interactions, the SVM finds w by optimizing:

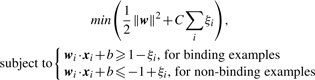(1)

where there are slack variables ξ_i ≥ 0 for ∀i and C is a regularization parameter (the tradeoff between finding a ‘least complicated’ w and fitting of the training data). The trained weight vector w can be used to make predictions for an unknown configuration by calculating the score w · x + b for the feature vector x corresponding to that configuration of protein and DNA. A more positive score predicts stronger binding.

In our framework, we have many cases of relative binding affinities where a particular protein–DNA pair is known to be a stronger binder when compared with another protein–DNA pair (see Section 2.3.2). Similar to the approach taken for predicting coiled-coil protein interactions (Fong et al., 2004), the general SVM model presented in model (1) can be modified so that experimental information on comparative binding affinities (i.e. when configuration x binds more strongly than configuration y) is used to additionally constrain the weight vector w by requiring that w · x > w · y. We modify the SVM by setting b=0 and adding z=y−x as a negative example, thereby capturing the desired relation. The modified inequalities (1) can be rewritten as:

(2)

We also experiment with the SVM framework utilizing polynomial kernels K(x, y)=(x · y+1)ⁿ which capture higher order relationships between canonical contacts in a finger. We have found that the quadratic polynomial kernel (n=2) performs well, while increasing the degree to cubic or higher decreases SVM performance. Therefore, we use the quadratic polynomial kernel function throughout this work. Polynomial kernels map each feature vector x into a new higher dimensional space using a mapping function φ(x); however, the kernel function allows avoiding explicit computation of φ(x), as it efficiently computes the necessary inner products for SVM optimization (the so-called kernel trick). It has to be noted, though, that the adaptation of comparative experimental data given above [Equation (2)] cannot be applied as it requires the explicit construction of the features in the higher dimensional space. That is, use of the polynomial kernel as above does not permit incorporating information about relative binding affinities.

2.2.2 Previous methods for predicting zinc finger protein–DNA binding

Several previous approaches have been developed for predicting zinc finger interactions based on a combination of sequence and structural knowledge. These include biophysical structure-based approaches (Endres and Wingreen, 2006; Morozov et al., 2005), as well as primarily sequence-based methods. Four sequence-based methods with published scoring tables are used here for comparison to our SVM testing. Of these, the first two methods are general methods for predicting protein–DNA interactions, while the last two methods have been developed specifically for the Cys₂His₂ ZF protein class. Each method is denoted here using the initials of the authors and the publication year.

‘SBGY95’ is a method based on expert knowledge of biochemical principles (Suzuki et al., 1995), and can be used to evaluate any type of protein–DNA interaction interface. Chemical rules of protein–DNA binding are based on the inherent chemical compatibility of amino acids and bases, and weights are given to amino acid-base pairings. The numerical amino acid–base compatibilities (Fig. 1a in the original publication) are used to compute binding scores according to the canonical model for ZF proteins.

‘MGM98’ is a computational method based on hydrogen bonding patterns extracted from co-crystal structures of various proteins in the PDB and NDB (Mandel-Gutfreund and Margalit, 1998). The log-odd scores (from Table 2 in original publication) used in this method represent more general trends found in protein–DNA interactions, and can be applied to general protein–DNA interfaces. Testing on ZF proteins uses the canonical binding model.

Table 2.

Results of Mann-Whitney significance test for Bulyk microarray data

Protein	SVM linear	SVM polyn.	SBGY95	MGM98	BLS02	KFM05
RSDH	+	+	+
LRHN		+	+	+
RGPD	+	+		+	+
REDV	+	+	+		+
KASN*

^*KASN protein shows no specificity in the microarrays for binding DNA.

For each protein and method, a ‘+’ indicates that the scores by the method for the DNA binding the protein and the DNA not binding the protein are significantly different, as judged by Mann-Whitney test at P=0.05. The SVM with a polynomial kernel outper-forms the other methods.

‘BLS02’ is a probabilistic computational model of Zif268 binding trained on SELEX and phage display experimental data gathered from the literature (Benos et al., 2002). The model was fit in order to maximize the specificity of the binding zinc finger. The position-specific energy matrix (Table 2 in original publication) is used for scoring.

‘KFM05’ is a probabilistic method trained on binding sites for properly spaced three and four finger ZF proteins in the TRANSFAC database (Kaplan et al., 2005). TRANSFAC does not provide exact sites, but provides a longer sequence in which the binding site resides. Thus, in order to use this database, expectation maximization was used to learn both the probabilities associated with the contacts in the canonical model as well as the locations of binding sites. Potential binding sites are scored using the canonical model position-specific counts of amino acid–nucleotide interactions listed in Supplementary Table S2 (Kaplan et al., 2005).

2.3 Data

2.3.1 Raw data

An extensive literature search was performed to gather examples of binding and non-binding configurations of Cys₂His₂ ZFs and DNA. We collected in vitro experimental data from 25 individual manuscripts published in 1990–2005 (see Supplementary Table S1). This data exists primarily of zinc finger protein mutants whose specificity has been probed by in vitro randomization experiments, such as SELEX and phage display (Benos et al., 2002), and whose nucleotide-amino acid contacts can be inferred. Data for Bulyk et al. (2002) were downloaded from the Supplementary Material web site; data for Benos et al. (2001, 2002) were taken from a public file, and all other data were entered manually. We also utilized all the 20 Cys₂His₂ ZF–DNA X-ray co-crystal structures found in the Protein Data Bank (Berman et al., 2000). The zinc finger regions in the proteins were identified from the original manuscripts or from the PDB structures, with the pattern CX₂₋₆CX₁₂HX₂₋₆H giving the correct positioning of the amino acids into the −1, 2, 3 and 6 positions.

2.3.2 Data processing

In order to apply machine learning techniques, the experimental database is further sorted into three categories: positive examples (protein binds the DNA), negative examples (protein does not bind to the DNA) and comparative examples (one protein–DNA pair represents a stronger binding than another protein–DNA pair, when several residues or nucleotides are substituted). ZF protein–DNA pairs determined to bind in the literature are positive examples. In addition, every example with experimentally determined K_d < 200 nM is considered a positive example. Together, there are 1312 positive examples in our database.

Each case reported in the literature where a protein does not bind to a DNA segment results in up to 10 negative examples in the database. This is because if a protein does not bind a particular DNA with a primary sequence given, then it does not bind to its complementary sequence either. Analogously, the protein is not likely to bind to a DNA sequence shifted by 1 or 2 nt towards the 3′ or the 5′ direction. Thus, for each experimental non-binding example, there are up to 10 DNA subsequences considered (one original, plus single and two-base shifts to the both ends, both in the primary and complementary strand). This results in 8081 negative examples.

Some experimental results, while not containing any quantitative information about binding affinity, provide an indication of the relative binding affinities between two configurations, as explicitly stated by authors. All the experimental data of this sort results in 914 comparative examples in our database. This number is significantly increased by adding comparative data created by comparing experimental K_d values of different examples within individual publications. In this case, a protein–DNA pair with disassociation constant K_d1 is considered a stronger binder than a protein-DNA pair with disassociation constant K_d2 if K_d2/K_d1 > 2. This procedure allows us to use experimental data that does not result in either positive or negative examples and finally gives a total of 65 414 comparative examples.

All duplicated data are filtered out from the dataset (i.e. examples of proteins with identical zinc fingers and identical corresponding DNA sequences). In rare cases where the same protein–DNA pair is reported as a positive and, alternatively, a negative binding example, the negative data are excluded from the database as having lower confidence.

Each example is converted to the vector representation. For the linear SVM, all examples are considered at the per-protein level (i.e. including contacts from all fingers). For the polynomial SVM, in order to limit the pairwise interactions to contacts within individual zinc fingers (i.e. so that they are physically realizable), individual examples are created separately for each finger in an interface for training the SVM (i.e. there are at most four non-zero entries in these vectors). For training, the vectors are normalized using the Euclidean norm. For all methods, testing is performed at the protein level by summing over the contributions of all fingers, with no normalization.

2.3.3 Software

SVM-light version 6.01 (Joachims, 1999) is used to train the SVMs. For all experiments, the regularization parameter C is automatically chosen by SVM-light. When training on the entire dataset, SVM-light uses C=0.84 with the linear kernel and learns 3170 support vectors, and uses C=0.33 with the polynomial kernel and learns 1865 support vectors.

2.4 Testing scenarios

To evaluate the binding model and to compare the SVMs with other prediction methods, we split our dataset into several types of training and testing subsets, each time ensuring that there is no overlap between testing and training data at the per-protein level (i.e. no protein sequence is used as an example in both testing and training sets). We use three types of cross-validation testing. We also test all methods using alternative data extracted from the TRANSFAC database.

2.4.1 New/old validation

We performed this cross-validation to mimic the situation of ‘old’ and ‘newly appearing’ data. In this test, we split the data into two sets, based on whether they were published in papers appearing before 2003 or in 2003 and afterwards. Any protein in the test set that occurs in the ‘old proteins’ dataset is removed from the testing set. The test set consists of 135 positive and 1357 negative examples (no comparative data are used for testing).

2.4.2 Holdout validation

In this test, we randomly select 100 positive and 1000 negative examples from the initial database (to conserve the 1 : 10 positive/negative ratio used in the previous test), and the remaining observations are retained as a training set. All examples involving proteins pulled for the test set are filtered out of the training dataset. To avoid any possible irregularities, this procedure is repeated 1000 times and an averaged ROC curve is created for method.

2.4.3 Testing on ANN, CNN, GNN and TNN subsets

To test whether removing data of the same type from the training set can alter the SVM's ability to predict protein–DNA interactions, we select four data subsets based on whether they bind TNN, GNN, ANN or CNN according to Barbas and colleagues (Blancafort et al., 2003; Dreier et al., 2000, 2001, 2005; Segal et al., 1999). We perform four cross-validation tests when all the examples of the same type (CNN, GNN, GNN or TNN) from these papers are pulled for testing and all duplicate proteins filtered out from the training set. These data make a major contribution in our high-confidence database: the ANN set includes 30 positive and 2500 negative examples; the CNN set has 84 positives and 1330 negatives; the GNN set has 83 positives and 3187 negatives; and TNN, the least studied, includes only 13 positive and 27 negative examples.

2.4.4 ROC curves

For the three testing scenarios just described, receiver operating characteristics (ROC) graphs computed as in Fawcett (2006) are used for comparing the methods. In the holdout and ANN/CNN/GNN/TNN validations, an individual ROC curve is computed at each iteration and these curves are averaged for every method tested by computing an average number of predicted true positives (TP) at every false positive (FP) rate.

2.4.5 Testing on Zif268 variants microarray data

The binding affinities of wild-type Zif268 and its four variants have been carefully studied on microarrays containing all possible 64 3-bp binding sites (Bulyk et al., 2001, 2002). Four proteins exhibit binding specificities, whereas one protein, KASN, shows no preference to any specific binding site. The provided binding affinity measurements represent a good experimental dataset to test the ability of theoretical techniques described here to predict short-specific DNA binding sites.

For each protein tested, according to the measured K_a values, all 64 DNA sequences were divided into two groups: ‘positives’ having high affinity to the target protein and ‘negatives’ with experimental fluorescence intensities at or below the background intensity of the respective microarray (Bulyk et al., 2001). We test whether each method can differentiate the positives from the negatives by testing whether the assigned scores can be attributed to two different distributions, at the P=0.05 level according to the non-parametric Mann–Whitney U-test.

2.4.6 Testing on the TRANSFAC database

In addition to cross-validation, the ability of SVMs to classify Cys₂His₂ protein–DNA binding examples is also tested on the TRANSFAC database. The TRANSFAC database operated by BIOBASE Corporation (Beverly, MA, USA) contains data on transcription factors, their experimentally proven binding sites, and regulated genes (Matys et al., 2003). The public release used here (ver 7.0, September 30, 2005) contains 244 Cys₂His₂ ZF proteins with corresponding DNA binding sequences, and with the number of zinc fingers varying from 1 to 29 (Supplementary Table S4). We use a stronger selection for the class, when exactly 12 residues must lie between the second Cys and the first His in zinc finger sequence. Only non-overlapping sequence patterns of the form CX₂₋₆CX₁₂HX₂₋₆H are considered further as zinc finger proteins. The TRANSFAC database gives relatively long DNA sequences (10−240 bp) without knowledge about a specific binding site. In order to score this DNA sequence, first the number of zinc fingers in each protein sequence is determined. This number allows estimation of the binding site length l (e.g. for three zinc fingers l=3^*3+1 = 10 bp long). For each method, the long DNA fragment is scanned for a specific binding site using l as sliding window. The score of the protein on this DNA fragment is taken as the highest scoring window. To evaluate the significance of this score, the highest score obtained for the target DNA is compared with the distribution of maximum scores obtained for 1000 randomized DNA sequences generated by random picking nucleotides with uniform probability. The P-value for a score by a particular method is calculated for every protein–DNA combination as P_i = n_i/1000, where n_i is the number of randomized DNA sequences scoring higher than the original target DNA. The methods are compared by fraction of correctly recovered protein–DNA pairs at different P-values. When scoring a protein in TRANSFAC, we ensure that protein and its binding sites are not in the training set for the SVM methods.

We limit our initial analysis to ZF proteins with three C₂H₂ zinc fingers. These triple C₂H₂ zinc fingers, as classified by Iuchi (2001), contain exactly three zinc fingers and provide an ideal initial test case for several reasons. First, while having less than three zinc fingers is thought not to provide enough binding specificity; structural studies have showed that the DNA binding model for proteins with four or more zinc fingers is significantly more complicated. When there are more than three fingers, it is common that the fingers bind non-sequential regions of the DNA or that some of the fingers are involved in protein–protein or other ligand interactions (Iuchi, 2001; Nolte et al., 1998; Pavletich and Pabo, 1993; Siggers and Honig, 2007). Second, when it comes to the number of protein–DNA combinations listed in TRANSFAC, the highest number of interacting DNAs comes from proteins with three zinc fingers (see Supplementary Table S2). Therefore, for our primary TRANSFAC testing, all methods are evaluated on the 305 three finger ZF protein–DNA combinations listed in TRANSFAC. Nevertheless, as a secondary test, we also consider Transfac proteins with four and five zinc fingers. In this case, we assume for all methods that all fingers bind DNA, and do so in consecutive overlapping 4-bp units.

3 RESULTS

3.1 New/old cross-validation testing

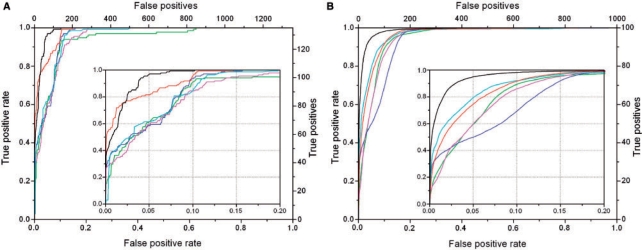
As described in Section 2, all data published in 2002 and earlier are used for training the SVM, while more recent data are used for testing all methods. Figure 2A compares the ROC curves for the linear and polynomial SVM classifiers with the four previously published methods to predict negative and positive data in the test set.

Fig. 2.

ROC curves for cross-validation analysis. (A) Testing on new data and (B) holdout cross-validation. Key: linear SVM (red), polynomial SVM (black), BLS02 (green), MGM98 (magenta), SBGY95 (cyan) and KFM05 (blue).

As is clearly seen, when classifying binding and non-binding examples obtained from high-quality experiments, SVMs outperform all previously published methods. The polynomial SVM exhibits exceptional performance. However, the linear SVM classifier outperforms the polynomial SVM in predicting the top 100 TP examples (initial jump with FP<20). The SVM curves cross at FP=20 and the polynomial SVM exhibits top performance afterwards, reaching the maximum TP=135 value at FP=70. Note that though we could have chosen another date with which to divide the data, we choose this one to compare to the BLS02 method, published in 2002, which is also based on similar experimental data obtained from the literature.

3.2 Holdout cross-validation testing

We also perform a holdout cross-validation where a validation test set is formed by 100 positive and 1000 negative examples pulled randomly from the original 1312 positives and 8081 negatives. Similar to the previous test, the polynomial SVM classifier outperforms all other methods in this holdout validation (Fig. 2B), despite the fact that some of the testing data were used for BLS02 training. The linear SVM shows good performance at FP rate>0.1, but is apparently outperformed by SBGY95 at lower FP rates (Fig. 2B). Interestingly, SBGY95, the oldest method based on general chemical rules, outperforms some of the more modern methods in this testing.

3.3 Cross-validation testing on ANN, CNN, GNN and TNN subsets

SVMs show excellent performance in the previous cross-validations where testing examples were selected independently of their protein or DNA sequences. Though those experiments are based on per-protein cross-validation, an even more difficult test is cross-validation where a subset of data describing the same DNA category is excluded from the training set. The group of Barbas III has performed an extensive search for artificial transcription factors recognizing the DNA sequences containing either adenine (ANN), cytosine (CNN), guanine (GNN) or thymine (TNN) in the DNA position interacting with the amino acid residue in position 6. Testing results are presented in Table 1 as an area under ROC curves (AUC) averaged over the four cross-validation tests (individual subset ROC curves are available as Supplementary Fig. S1).

Table 1.

AUC values for cross validation testing on ANN, CNN, GNN and TNN subsets

Subset	SVM linear	SVM polyn.	SBGY95	MGM98	BLS02	KFM05
ANN	0.9819	0.9875	0.962	0.9424	0.9841	0.9153
CNN	0.9787	0.9868	0.9496	0.9358	0.9362	0.9458
GNN	0.9799	0.9856	0.9766	0.9673	0.9788	0.9856
TNN	0.9858	0.9943	0.8661	0.9202	0.9801	0.8519

Highest AUC values are shown in bold.

Similar to the previous cross-validation tests, the polynomial SVM outperforms other methods (Table 1). Again, the linear SVM outperforms the polynomial kernel on the ‘initial jump’, at FP <0.02 when both SVM reach TP∼0.8. Detailed analysis discovers differences in method performances when tested on different data subsets (see Supplementary Fig. S1). In particular, the KFM05 method (based on TRANSFAC database) shows top performance on the GNN set, outperforming SVMs. This may be explained by a high number of guanine-rich DNA regions represented in the TRANSFAC database. On the other hand, removing the GNN data from the SVM training set may reduce the ability of the SVM for accurate prediction.

3.4 Zif268 variant microarray data

It is useful to evaluate the ability of different methods to classify 3-bp binding sites for the wild-type Zif268 and its four variants as this has been carefully studied on microarrays (Bulyk et al., 2001, 2002). Consistent with the experimentally determined poor binding specificity of KASN protein variant (Bulyk et al., 2001), none of the methods is able to differentiate the positives and negatives for this protein (Table 2). For all the other four proteins, the polynomial SVM shows the best performance in differentiating the positive and negative groups, and rejects the null hypothesis that these two populations come from the same distribution.

The linear SVM and the SGBY95 methods ascertained for three variants that the experimentally preferred DNA sequences are scored significantly higher than the negatives; this occurs twice for MGM98 and BLS02. Interestingly, KFM05 scores do not pass the significance threshold to attribute them to two different distributions, showing the inability of this method to predict DNA sequences recognized by Zif268 variants in vitro; this may be due to the training of this method on TRANSFAC data. Detailed data are available in Supplementary Table S3.

3.5 Testing on the TRANSFAC database

Successful testing on a high-quality experimental database suggests that the SVM methods may be useful in locating exact binding site in experiments when only a longer DNA region, and not the particular site, is known to be recognized by a particular transcription factor [e.g. as in data resulting from ChIP-chip experiments (O'Geen et al., 2007)]. We first test all methods on the 305 three-finger ZF protein–DNA combinations listed in the TRANSFAC database (Matys et al., 2003).

In order to test different prediction methods, the relative scores for the TRANSFAC protein–DNA combinations are compared to randomized DNA sequences as described in Section 2. Table 3 represents the percentage of the 305 protein-DNA pairs for which each method finds a binding site at different P-values. Of the methods, KFM05 most often finds significant binding sites (as judged at P-values of 0.005, 0.01 and 0.05). This is as expected, as the KFM05 method is trained on TRANSFAC. Excluding KFM05, the polynomial SVM most commonly identifies binding sites, outperforming other methods, but closely followed by BLS02 (Table 3, Supplementary Fig. S2-A). The linear SVM shows a limited performance in this test when compared with other methods. The advantage of the polynomial kernel over the linear SVM may suggest the limitation of the originally used representation where all protein–DNA interactions are constrained to the four canonical contacts, especially when the natural protein sequences may differ from the Zif268 canonical model. Since all methods assume the canonical Zif268 binding model, and much of the data that the SVM methods are trained on are based on Zif268, we also repeat this analysis on only the non-Zif268 three-finger ZF proteins in TRANSFAC; the relative performance of the methods stays the same (see Supplementary Fig. S2-B). Finally, we test the performance of all methods on three- and four-finger zinc finger proteins in TRANSFAC. All methods perform significantly worse, and identify a fewer fraction of proteins as containing binding sites at the P=0.05 level. For example, KFM05 identifies only 56% of these proteins as having a binding site at the P=0.05 level, even though this method uses four-finger ZF proteins in training; this number is 48% for the SVM with the polynomial kernel (see Supplementary Fig. S2-C). The lower performance of all methods is likely due to the more complex binding patterns of zinc finger proteins with more than three-fingers (Iuchi, 2001).

Table 3.

The percentage of correctly predicted binding sites in Transfac database by all methods at different P-values

P-value	SVM linear	SVM polyn.	SBGY95	MGM98	BLS02	KFM05
0.005	25.9	63.3	45.6	48.5	59.7	(66.9)
0.01	42.3	75.7	56.7	57.4	68.9	(78.7)
0.05	76.4	87.5	82.0	80.3	86.6	(91.8)

The highest percentages are shown in bold (excluding the Transfac-trained KFM05 method which is shown in brackets for comparison)

3.6 Learned SVM models

We release the linear and polynomial SVM models that result from training on the entire high-confidence database. These files are available at http://compbio.cs.princeton.edu/zf/. The explicit calculation of the weight vector w is possible from the linear SVM model. The linear SVM weight vector is further analyzed to find the dimensions determining the boundaries in the classification space. The weight vector coordinates with highest values are listed according to their magnitudes in Supplementary Table S4. While many of most important contacts originate from the well-known Zif268-DNA complex, the linear SVM is able to learn many alternative contacts positively contributing towards ZF protein-DNA binding.

4 DISCUSSION

The Cys₂His₂ ZF proteins represent one of the most studied transcription factor protein families. Their modular structure makes them amenable to statistical and computational approaches for predicting their DNA binding specificities given only their protein sequences. Here, we have presented an SVM-based approach for predicting ZF protein–DNA binding. Whereas most previous computational methods for predicting protein–DNA interactions have used only known binding examples, our approach additionally utilizes examples of proteins known not to bind particular DNA regions. In addition, with a linear SVM, we also use relative binding data in the form of comparative examples.

The canonical binding model for ZF protein–DNA binding (Fig. 1) attributes the protein–DNA interaction to only four canonical amino acid-base contacts. This simple model has served well for a number of experimental and theoretical studies and has been confirmed by the majority of co-crystal structures. However, zinc finger binding can be altered by variations in the protein sequence and can result in reorganization of the DNA-interacting interfaces (Wolfe et al., 2001). Consistent with this, we have found that the polynomial SVM outperforms previous methods, as well as the linear SVM, in a wide assortment of testing. SVMs with a polynomial kernel map feature vectors into a higher dimensional space, thereby making possible implicit inclusion of higher order interactions not listed in the original canonical model (Luscombe et al., 2001). It is highly possible that certain amino acid residues are able to interact with more than one base in the DNA sequence, thus complicating the sequence recognition pattern. Therefore, the success of the polynomial SVM may indicate the necessity to adjust the canonical structural model.

Linear SVMs show limited performance when tested on the TRANSFAC database. In general, most proteins from the high-confidence database used for SVM training were designed on the basis of Zif268. In contrast, the proteins listed in the TRANSFAC database and used for testing are natural ZF proteins and can have sequences significantly different from the Zif268 family. Therefore, the binding interface of these proteins could be different from that described by the canonical model. This fact may result in decreased linear SVM performance, compared with the polynomial model which implicitly considers alternative contacts. However, the good performance of the linear SVM in cross-validation testing appears very promising for further improving its performance. In particular, use of the polynomial kernel does not allow the incorporation of relative binding information through the use of comparative examples. By modifying the canonical model to explicitly consider higher order interactions, a linear SVM can be applied again with its advantage of using quantitative and comparative experimental data.

For the linear SVM, it is possible to examine the learned weights to ascertain which contacts are learned to be most important for predicting ZF protein–DNA interactions (see Supplementary Table S3). The contacts originating from the Zif268 protein–DNA complex have large weight vector coordinates, stressing the prominence of Zif268-derived examples in our training set and suggesting that a likely source of improvement for the linear SVM is inclusion of data from a more diverse set of ZF proteins. Such data would likely to improve the performance of all methods. Interestingly, the Pearson correlation coefficient observed between the linear SVM weight vector coordinates and the weights assigned to corresponding interactions by other methods is weak; this is also true when considering pairwise relationships between the other methods (data not shown). This suggests that combining different theoretical approaches may lead to better predictions where the methods complement each other.

Significant further challenges remain in developing a complete system for predicting ZF protein–DNA interactions. The relatively poor performance of all methods in predicting the binding of four-and five-finger ZF proteins suggests that for improved performance for proteins with many zinc fingers, it will be necessary to develop methods for predicting which fingers are binding DNA and whether the fingers are binding in tandem along the DNA, or in several separate regions. Furthermore, it is important to note that all the methods tested here evaluate whether a particular ZF protein can in principle bind a fragment of DNA; they do not evaluate whether this binding occurs in vivo. To better assess whether interactions occur in vivo, these predictions should be used in conjunction with other types of information, such as expression data or cell and tissue type.

In conclusion, we present a new approach for predicting ZF protein–DNA binding based on SVMs. Our approach allows utilizing a wide range of experimental data, from positive to negative to comparative binding examples. Overall, this methodology makes substantial progress on the problem of predicting a transcription factor's DNA binding sites, and should provide a basis for predicting binding sites at the genome level. While, we have described our methodology for predicting ZF–DNA binding, in principle the approach can be applied to any conserved structural interface. Furthermore as more high-throughput, experimental techniques are developed and applied for quantitatively determining DNA binding specificity (Bulyk et al., 2001, 2002; Mukherjee et al., 2004), approaches such as the one outlined here will become increasingly important.

Funding

National Institutes of Health (GM076275); NSF (IIS-0612231 and MCB-0093399); DARPA; NIH Center of Excellence (P50 GM071508).

Conflict of Interest: none declared.