Combining multiple positive training sets to generate confidence scores for protein–protein interactions

Abstract

Motivation: High-throughput experimental and computational methods are generating a wealth of protein–protein interaction data for a variety of organisms. However, data produced by current state-of-the-art methods include many false positives, which can hinder the analyses needed to derive biological insights. One way to address this problem is to assign confidence scores that reflect the reliability and biological significance of each interaction. Most previously described scoring methods use a set of likely true positives to train a model to score all interactions in a dataset. A single positive training set, however, may be biased and not representative of true interaction space.

Results: We demonstrate a method to score protein interactions by utilizing multiple independent sets of training positives to reduce the potential bias inherent in using a single training set. We used a set of benchmark yeast protein interactions to show that our approach outperforms other scoring methods. Our approach can also score interactions across data types, which makes it more widely applicable than many previously proposed methods. We applied the method to protein interaction data from both Drosophila melanogaster and Homo sapiens. Independent evaluations show that the resulting confidence scores accurately reflect the biological significance of the interactions.

Contact: rfinley@wayne.edu

Supplementary information: Supplementary data are available at Bioinformatics Online.

1 INTRODUCTION

Networks of interacting proteins mediate a wide range of biological processes. Maps of protein–protein interactions (PPI) provide clues about the functions of individual proteins and enable systems-level analyses of cellular processes (Ideker and Sharan, 2008; Uetz and Finley, 2005). To realize the potential of protein networks for systems analysis, a number of experimental and computational approaches have been implemented for large-scale mapping of PPI. These methods are producing a large amount of data that is contributing significantly to our understanding of biological systems. A major limitation to the value of this data, however, is the presence of false positive interactions that have no biological significance, with estimated false discovery rates as high as 91% in some datasets (Mrowka et al., 2001; von Mering et al., 2002). Thus, there is a critical need for methods to address the noise in PPI data.

A number of approaches have been proposed to assign confidence scores to represent the probability that an interaction is a biologically relevant true positive (Bader et al., 2004; Deane et al., 2002; Deng et al., 2003; Giot et al., 2003; Parrish et al., 2007; Qi et al., 2005; Scott and Barton, 2007; Sharan et al., 2005) [see, Suthram et al. (2006) for review]. These scoring systems generally try to classify interactions as true positives or false positives by correlating features of the data with sets of training data including known true positives and true negatives. A disadvantage of many scoring schemes is that they work within a single type of data, such as PPI detected in a yeast two-hybrid screen (e.g. Bader et al., 2004; Deng et al., 2003; Giot et al., 2003; Parrish et al., 2007), or by co-affinity purification and mass spectrometry (e.g. Ewing et al., 2007; Gavin et al., 2006; Krogan et al., 2006). The result is that scores derived for different datasets are not comparable to each other. This is a particular problem as individual datasets are incomplete and must be combined to maximize the coverage for an interactome.

A second disadvantage of many scoring systems is that they use training data that consist of interactions that are only assumed to be true positives. In addition to the uncertain accuracy of these training datasets, it is unclear how well any one of them represents true interaction space. Training positives have been derived, for example, by assuming that biological true PPI are enriched among interactions detected in multiple species, between proteins known to function in the same pathway, or in results from small-scale experiments (Giot et al., 2003; Parrish et al., 2007; Qi et al., 2005; Sprinzak et al., 2003; Titz et al., 2008; von Mering et al., 2005; Yamanishi et al., 2004). Because these and similar approaches are based on simple assumptions about true positives they may produce training sets that are biased toward particular types of PPI. Training sets may be biased, for example, toward highly conserved interactions or particularly well-studied pathways. Use of any single set of training data, therefore, could lead to bias in the resulting confidence scores and could further skew all downstream analyses of the interaction networks (Myers et al., 2006).

Here, we propose a method to score PPIs across data types. We developed a method to use multiple sets of positives to train independent models and to combine the results into a final confidence score for each interaction. We applied the method to both Drosophila melanogaster (fly) and Homo sapiens (human) interaction data. We show with multiple independent lines of evidence that the confidence scores accurately reflect the biological significance of the interactions. We also scored a set of yeast interactions and demonstrated that our method outperforms other scoring methods applied to the same data. The scoring system can be used to annotate a PPI network so that interactions become weighted or probabilistic links useful for a variety of downstream analyses. The scoring system is readily updateable as new information becomes available.

2 METHODS

Results from all published high-throughput screens and other archived physical protein interactions were collected from online interaction databases for Drosophila and human (Beuming et al., 2005; Chatr-aryamontri et al., 2007; Guldener et al., 2006; Kerrien et al., 2007; Mishra et al., 2006; Pacifico et al., 2006; Stark et al., 2006; Vastrik et al., 2007; Yu et al., 2008). In order to enlarge coverage of the interaction maps, we also collected physical interactions for Caenorhabditis elegans (worm) and Saccharomyces cerevisiae (yeast). Interologs for fly were then mapped from human, worm and yeast interactions and those for human were mapped from fly, worm and yeast interactions using Inparanoid (O'Brien et al., 2005) to identify orthologous proteins (see Supplementary Material).

We synthesized four different sets of training positives, based on interactions that (i) are associated with at least 10 Pubmed identifiers (PMIDs) in the interaction databases; (ii) are putative conserved interactions, which are those found in common between interaction sets for any two species (fly, human, worm and yeast; iii) are high-throughput interactions reported to have high confidence by the original publications; and (iv) have expression correlation higher than 0.6 (see Supplementary Material). For each positive set, a negative set of equal size was synthesized by drawing random samples from the list of all interactions, excluding those in that positive set.

The attributes used for each interaction are listed in Section 3 and were calculated as described in detail in Supplementary Methods. An attribute was not used in the training process if it was used in generating the specific positive set. For example, when training was done based on positive set 1, number of PMIDs was not used as an interaction attribute in the training process.

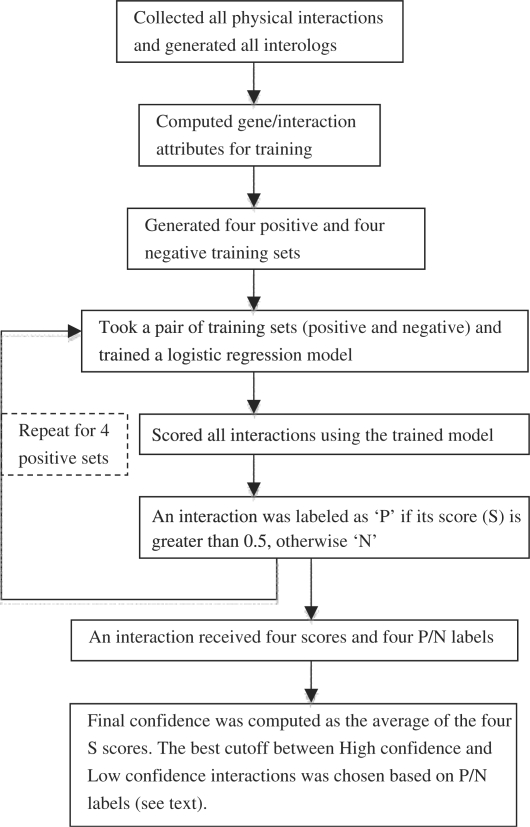
The scoring process proceeds in the following fashion (Fig. 1). A logistic regression model (using the glm function with binomial family in R, http://www.r-project.org) was trained on each positive set, combined with its corresponding negative set. The model was then used to score all interactions. We labeled an interaction ‘P’ if its score (S) is greater than 0.5, and otherwise ‘N’. Thus, the four positive training sets produced four scores and four P/N labels for each interaction. The final confidence of each interaction is the arithmetic average of the four scores produced by the four models learned from the four positive sets. The final confidence scores have values between 0 and 1, representing the possibility that an interaction is a biological true interaction. To pick the best cutoff to separate high confidence interactions from low confidence ones, we went through an iterative process as follows. As mentioned above, at the end of the training and scoring process, each interaction received four scores and four P/N labels. We labeled an interaction ‘T’ (for possible True interaction) if it has two or more ‘P’ labels; otherwise it was labeled as ‘F’ (for possible False interaction). We then picked a random cutoff (starting at 0.1) and computed its performance in calling ‘T’ and ‘F’ interactions; the cutoff was then incremented by 0.01 and the process repeated. The best cutoffs were chosen based on their performance in classifying interactions to the ‘T’ and ‘F’ classes (Supplementary Fig. 1). The optimal cutoffs were 0.41 for Drosophila, 0.40 for human and 0.44 for yeast. For subsequent analyses, therefore, we define interactions with confidence scores greater than the cutoff as the high confidence set (HCS), and those with confidence score less than or equal to the cutoff as the low confidence set (LCS).

Fig. 1.

Confidence scoring procedure.

We evaluated our scoring results using four independent types of data that were not used in the training and scoring process:, (i) sharing of Gene Ontology (GO) annotations (The Gene Ontology Consortium, 2000); (ii) overlap with genetic interactions (Crosby et al., 2007); (iii) overlap with Prolinks predictions (Bowers et al., 2004); and (iv) participants in the same KEGG (Kanehisa et al., 2008) pathways. Evaluation was performed using a uniform approach for all four data types, as follows. We first removed all positive training interactions and then computed a performance index X (described further below) for the remaining HCS. We then sampled 200 sets of low confidence interactions from the remaining LCS (each set has the same number of interactions as HCS) and computed X for each set. We also sampled 200 equal-sized sets of random gene pairs (RPS for random pair set) and computed X for each set. We, therefore, obtained a single data point for HCS, a histogram for LCS and another histogram for RPS. Differences among them are evident from the graphs (e.g. Figs 3 and 4). Based on GO, we computed three performance indices. The first is the fraction of gene pairs sharing at least one GO annotation; the second is the average of the deepest level of shared GO annotations for a gene pair; and the third is the average specificity of shared GO annotations for a gene pair. Additional details can be found in Supplementary Material.

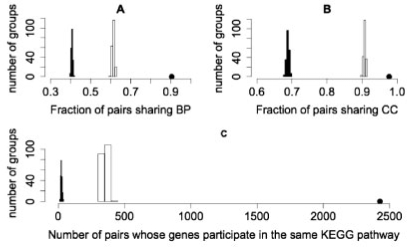
Fig. 3.

Evaluation of Drosophila confidence scores based on GO and KEGG. (A) Fraction of interactions where gene pairs share at least one GO biological process (BP) annotation, (B) fraction of interactions where gene pairs share at least one GO cellular component (CC) annotation, (C) number of interactions where gene pairs participate in the same KEGG pathway. The dot represents HCS and the histograms represent sets of LCS (white) and RPS (black) PPI. All training positives were removed from HCS and LCS for this evaluation.

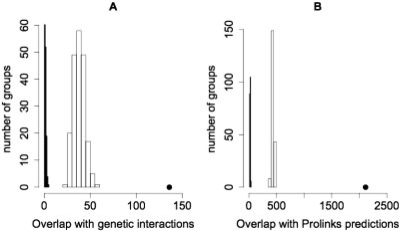
Fig. 4.

Evaluation of Drosophila PPI scores based on overlap with (A) genetic interactions, (B) Prolinks predictions. The dot represents HCS and the histograms represent sets of LCS (white) and RPS (black) PPI. All training positives were removed from HCS and LCS for this evaluation.

3 RESULTS

3.1 Interaction and training data

We set out to assign confidence scores for all physical PPI, regardless of how they were detected. First, we generated large interaction datasets for Drosophila and human by combining experimental data from a variety of sources and by predicting additional interactions based on results with orthologous proteins from other organisms (see Section 2). The Drosophila dataset, which is available in DroID, a comprehensive database for Drosophila gene and protein interactions (Yu et al., 2008) includes 131 659 PPI among 9511 proteins. The dataset for human has 211 151 PPI among 13 447 proteins.

To avoid possible bias associated with any single set of training positives we chose to train multiple independent scoring models, each based on a different set of training positives and corresponding negatives. We generated four independent sets of training positives for each organism by selecting subsets of PPI expected to be enriched for true positives based on different assumptions (see Section 2). The training positive sets consisted of interactions that are more likely to be reliable because they are reported in many different publications; potentially evolutionarily conserved PPI detected in more than one species; high-throughput PPI that were scored as high confidence by dataset-specific scoring systems; and interactions between proteins encoded by genes with similar expression patterns. For Drosophila, the four training positive sets had from 4022 to 7781 PPI, while for human they had from 3017 to 14 033 PPIs. In support of the notion that these training sets are derived from independent measures of biological significance, they only minimally overlap with each other (Supplementary Fig. 2).

3.2 Attribute contributions

The scoring system that we used is based on finding features or attributes of the PPI that correlate with presence in the positive or negative training data. Since we aimed to score interactions derived from many different methods we chose not to use attributes specific to certain detection methods. Instead, we computed gene or interaction attributes that are applicable to any type of PPI. In addition, we chose attributes that were previously shown to correlate with biological significance for at least some PPI networks. These included attributes describing the topological position of the interaction in the entire network, including the number of interactions (degree) for the two proteins, the extent of local clustering around the interaction (clustering coefficient), and the fraction of common neighbors for the two proteins (Bader et al., 2004; Giot et al., 2003; Parrish et al., 2007). Other attributes included the number of published papers that reported the PPI as recorded by the online interaction databases, the correlation of expression patterns for the two genes from genome-wide expression studies, and whether or not the two proteins have domains known to interact based on the 3DID database (Stein et al., 2005). The number of PMIDs and expression correlation were not used as attributes in conjunction with the training data based on these same features, respectively (see Section 2 and Supplementary Material).

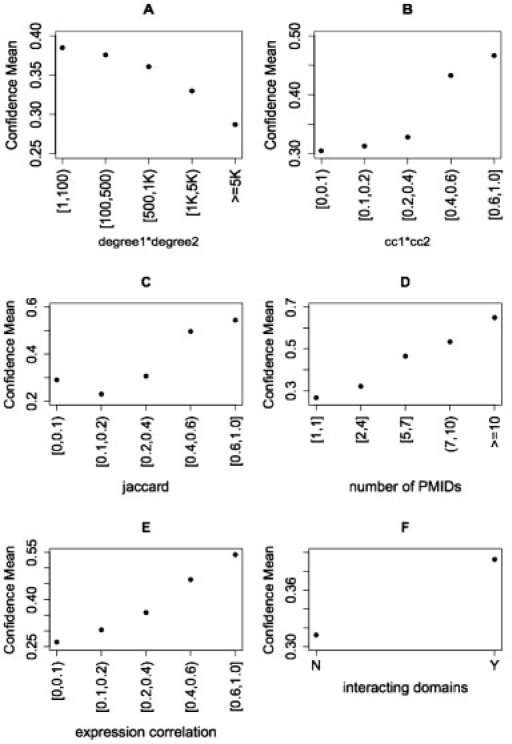
To evaluate how the different attributes correlate with the final scores, we computed Pearson correlation coefficients (PCC). The PCC is a measure of the linear association between an attribute vector and the final confidence scores. We found that the combined degree of the interacting proteins is a negative predictor of high scores, while clustering coefficient, fraction of common neighbors (jaccard), number of PMIDs, expression correlation and domain–domain interactions are all positive predictors (Table 1). Figure 2 shows in more detail the relationship between attribute values and the computed confidence scores. The attribute values show clear trends as the confidence scores increase. These results show that the attributes we chose each have at least modest predictive power. By combining the attributes, however, we can create an effective scoring system as demonstrated in the following sections.

Table 1.

PCC between feature values and confidence scores

Featurea	PCC between feature and confidence scores
degree	−0.051
cc	0.117
jaccard	0.442
numpmids	0.712
exprcorr	0.488
hasDDI	0.076

^aDegree, product of degrees (number of interactions) of the two proteins in an interaction; cc, product of clustering coefficients of the two proteins; jaccard, fraction of common interacting neighbors of the two proteins; numpmids, number of PMIDs associated with an interaction; exprcorr, expression correlation of two genes in an interaction; and hasDDI, whether the two proteins in an interaction have one or more pairs of domains known to interact with each other.

Fig. 2.

Mean confidence scores of interactions with different attribute values. Interactions were binned according to their attribute values and the average confidence score was then computed for each bin. (A) Product of degrees of the two proteins, (B) product of clustering coefficient of the two proteins, (C) jaccard, fraction of common interacting neighbors of the two proteins, (D) number of PMIDs annotated with an interaction, (E) gene expression correlation and (F) whether an interaction has a pair of interacting domains.

3.3 Scoring Drosophila and human PPI

We used the attributes and multiple training datasets to score PPI from Drosophila and human as described in Figure 1 (see Section 2). For Drosophila, we scored 124 275 PPI from DroID (Yu et al., 2008). We found that 24 850 (20%) of the interactions received scores greater than the cutoff for Drosophila (0.41, see Section 2), and we refer to these as the high confidence interactions (HCS). We also scored the 211 151 human PPI and found that 32 485 (15%) received a score greater than the cutoff for human (0.40) and refer to these as the human HCS (Supplementary Fig. 3).

The fractions of interactions assigned to the higher confidence sets was similar to those for other systems that scored individual datasets (Ewing et al., 2007; Formstecher et al., 2005; Giot et al., 2003; Stanyon et al., 2004; Stelzl et al., 2005). The reason that a smaller fraction of the human interactions were scored as high confidence compared with the Drosophila interactions is unclear. One factor may be the large number of low confidence human interactions contributed by predictions from the model organisms such as yeast. Another factor may be the currently lower coverage of human interactome compared with that of fly. Nevertheless, using data from other species to predict interactions is valuable, as is evident from the Drosophila network, which includes a large number of high confidence PPI predicted from both human and yeast (Supplementary Fig. 4).

3.4 Evaluation of confidence scores

To evaluate how well the confidence scores reflect biological significance, we removed all of the training positives and then compared the remaining HCS with random samples of the remaining lower confidence interactions (scores ≤0.41; LCS), and sets of random pairs of proteins (RPS). We compared HCS, LCS and RPS using information that did not directly contribute to the confidence scores. We found similar results for both Drosophila (below) and human (Supplementary Material). First, we used GO annotations and asked how many interactions in HCS, LCS and RPS involved pairs of proteins that share the same annotation, as might be expected for biologically relevant interactions. As shown in Figure 3A and B the Drosophila HCS contains a significantly larger fraction of interactions with shared GO annotations than LCS and RPS, indicating that HCS contains more functionally meaningful interactions. Moreover, LCS protein pairs share significantly more GO annotations than RPS, demonstrating that the interactions we collected as a whole are enriched with true positives even if some of them were assigned low confidence scores. We found a similar relationship between HCS, LCS and RPS when looking at how specific the shared GO annotations were as measured by their levels in the GO hierarchy (Supplementary Fig. 5).

We also examined whether protein pairs were annotated to the same pathway based on the KEGG database, a manually curated database of pathways (Kanehisa et al., 2008). We found that the number of interactions between pairs of proteins that participate in the same KEGG pathway was much larger in HCS than LCS, and that LCS had more interactions belonging to the same KEGG pathways than RPS (Fig. 3C)

Next, we compared the scored Drosophila PPI with two independent datasets that should be enriched for biologically relevant interactions (Fig. 4). First, we compared the extent that HCS, LCS and RPS overlap with a set of known genetic interactions derived from Flybase (Crosby et al., 2007). Genetic interactions represent functional relationships between genes. It has been shown that pairs of genes that genetically interact are more likely to encode interacting proteins than random pairs of genes (Kelley and Ideker, 2005; Tong et al., 2004; Wong et al., 2004). Consistent with this, we found that the Drosophila HCS has a much larger overlap with genetic interactions than LCS and RPS (Fig. 4A). LCS also has a larger overlap with genetic interactions than RPS. Next, we looked at overlap with computational predictions of PPI found in the Prolinks database (Bowers et al., 2004). These predictions are based on phylogenetic profiles, gene fusion events, genome proximity and operon structure. These features are independent from the attributes used in our scoring system. Figure 4B shows that HCS has a much larger overlap with Prolinks predictions than LCS and RPS, and that LCS overlaps with Prolinks predictions more than RPS. Combined, these results show that PPI with higher confidence scores are more likely to be biologically relevant than those with lower scores. Similar results were obtained with the scored human PPI (Supplementary Figs 6 and 7).

3.5 Correlation of confidence score and biological significance

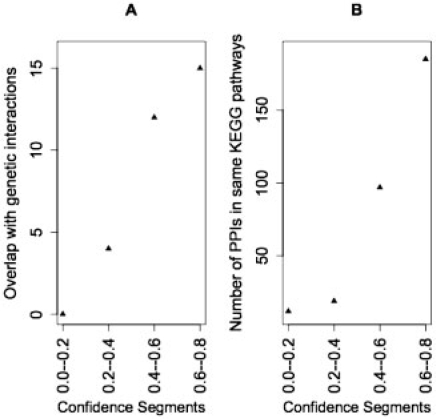
The analyses presented above showed that HCS interactions contain significantly more biological true positives than LCS interactions and random pairs. Next, we asked whether the scoring system has the potential to make finer distinctions among interactions that are more or less likely to be true positives. To do this, we divided the fly interactions into five bins according to their computed confidence scores. Bin 1 contained PPI with confidence scores between 0.0 and 0.2, bin 2 contained those with scores between 0.2 and 0.4 and so on to bin 4, which contained PPI with scores between 0.6 and 0.8. Bin 5, with scores between 0.8 and 1.0, did not have enough interactions to make a meaningful comparison. For each bin, we randomly sampled 600 interactions and computed their overlaps with genetic interactions and the fraction of interactions sharing KEGG pathways. As shown in Figure 5, we found that as the confidence scores increase, there is increasing likelihood of overlap with the test data. These results suggest that the scores reflect the likelihood that each interaction is biologically significant.

Fig. 5.

Confidence scores correlate with likelihood of biological significance. Interactions, excluding training positives, were binned according to their assigned confidence scores and indexes representing biological significance were computed. (A) Overlap with genetic interactions, (B) number of interactions whose proteins participate in the same KEGG pathways.

3.6 Comparison with other methods

The above results indicate that the scores we assigned to Drosophila and human interactions will be useful for ranking PPI based on their likelihood of being biologically significant. Next, we set out to compare our scoring approach with those reported by others. Surprisingly, we found such a comparison to be difficult using Drosophila or human interaction data because very few scoring methods have been applied to these organisms, and each method scored different subsets of the interactions that we scored (Chatr-aryamontri et al., 2007; Giot et al., 2003; Scott and Barton, 2007). Thus, for a more meaningful comparison of scoring methods we turned to a set of yeast interactions that were scored by a number of previously published scoring systems.

We applied our scoring method to the same set of yeast interactions that were used by Suthram et al. (2006) to compare several different confidence scoring methods. The methods that were compared, which are described in detail in Suthram et al. (2006) and in the original papers (Bader et al., 2004; Deane et al., 2002; Deng et al., 2003; Qi et al., 2005; Sharan et al., 2005), each used a single set of gold standard positives to assign probability scores to the yeast interactions or to classify them as high, medium or low confidence. To compare the different scoring methods, Suthram et al., calculated the Spearman rank coefficient between the confidence scores and the deepest GO terms shared between pairs of genes. We adopted the same method to compare scores by recalculating the Spearman rank coefficients based on updated GO annotations (see Supplementary Material for details). As shown in Table 2, the relative performance of the different methods that we calculated with the updated GO annotations is very similar to the relative performance calculated by Suthram et al. (2006), with the BADER_HIGH method ranking as the best followed closely by the DENG method. As pointed out previously, however, the BADER_HIGH method used GO annotations to derive confidence scores, and thus has an unfair advantage in this particular comparison. Discounting the BADER_HIGH method for this reason shows that the DENG approach (Deng et al., 2003) is the best in both analyses. Table 2 shows that our approach produced results very similar to that of DENG, and better than all other approaches.

Table 2.

Correlation of computed confidence scores with GO similarity

Scoring method	Spearman correlation	SC reported in
	coefficient(SC)	Suthram et al. (2006)
BADER_HIGH	0.462	0.501
(Bader et al., 2004)
BADER_LOW	0.387	0.424
(Bader et al., 2004)
DEANE	0.359	0.385
(Deane et al., 2002)
DENG	0.461	0.490
(Deng et al., 2003)
SHARAN	0.434	0.471
(Sharan et al., 2005)
QI	0.381	0.425
(Qi et al., 2005)
This work	0.459	NA

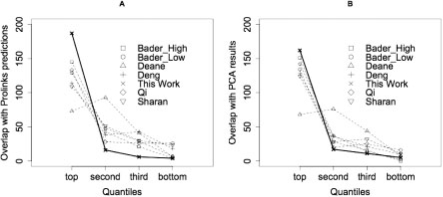
While our method and the DENG method (Deng et al., 2003), performed similarly based on the metric of shared GO annotation, other features of the scores suggest that our method has some advantages. The DENG method assigned only five different scores to all of the interactions, whereas our method resulted in a score distribution that enables a finer distinction between interactions with different probabilities (Supplementary Fig. 8). As shown above (Fig. 5), the magnitude of the scores that we generated correlates well with biological significance. We also compared the different scoring methods based on overlap with two independent sets of interactions that should be enriched for true positives: the Prolinks predictions and a recent set of binary interaction data derived from large-scale protein complementation assays (PCA) (Tarassov et al., 2008). We first sorted the interactions in each dataset by computed confidence scores, from highest to lowest, and then binned them into four quantiles, each containing 25% of the interactions. Finally, we calculated the overlap of each quantile with the Prolinks predictions (Fig. 6A) and the PCA interactions (Fig. 6B). The results showed that our scores were better at predicting interactions that could be detected by other computational (Prolinks) or experimental (PCA) methods. These results suggest that the scoring system described here provides a useful measure of the probability that any given interaction is biologically significant.

Fig. 6.

Overlap with independent datasets. (A) overlap with Prolinks predictions, (B) overlap with PCA interactions.

4 DISCUSSION

Experimental and computational approaches have begun to define the protein interaction networks for a number of organisms. While these PPI networks provide an invaluable framework for systems-level insights into biological processes, the high rates of false positives and false negatives limit their usefulness. The false negatives stem from the inability of any one approach or screen to detect all relevant PPI. This problem can be alleviated at least in part by integrating PPI data from multiple approaches to maximize coverage of an interactome. False positives, on the other hand, have proven more difficult to identify as no system has been devised to accurately distinguish true and false positives, particularly across several different datasets. Thus, the value of PPI networks could be increased by generating confidence scores that reflect the likelihood that each interaction is a biologically relevant true positive. In this way, an interaction network consisting of binary links becomes a map of weighted or probabilistic links, which enables more powerful network analyses, as has been shown for functional gene networks (e.g Asthana et al., 2004; Lee et al., 2004).

Here, we developed a PPI confidence scoring system that uses multiple independent sets of training positives and interaction attributes that are common to a variety of datasets. We trained independent logistic regression models based on each positive training set and took their average to be the final confidence score for each interaction. It is possible to envision two other ways to combine the positive training sets. One way would be to combine them into a single training set. A problem with this approach is that each positive training set represents a different and apparently biased subset of the true interactions, leading to poor learning performance. Another way would be to use the intersection of the positive training sets. This would be expected to increase the accuracy of the model since PPI supported by multiple forms of evidence are generally more likely to be true positives. This approach, however, would not be viable with the different training dataset presented here because they exhibit only minimal overlap. For example, the intersection of all positive training sets used here was only 14 for Drosophila and only three for human, too few to enable meaningful model learning (Supplementary Fig. 2). We postulate that using multiple positive sets in the way described here may also enhance the learning performance of models beyond those based on logistic regression.

Multiple lines of independent evidence confirmed that the confidence scores we generated correlated well with biological significance. Thus, the confidence scores generated here should be useful to biologists and researchers in the interactomics field. Nevertheless, as with other scoring systems this one could be further refined. While the scores correlated well with biological significance, a small fraction of high scoring PPI are expected to be false positives and a small fraction of low scoring PPI are expected to be true interactions. A key feature of the scoring system we describe is that the scores can be refined as new information becomes available. Addition of new PPI datasets to increase coverage, for example, could change the values of the topological attributes for many PPI enabling an update to all of the scores. Moreover, entirely new attributes could be incorporated to further refine the scores. Finally, new training datasets could be added to enhance the scoring accuracy and coverage. Even training data that has known or undefined bias would be expected to improve this scoring system by giving representation to another region of true interaction space.

Funding

National Institutes of Health (HG001536; RR18327).

Conflict of Interest: none declared.