Origins of heterogeneity in tissue perfusion and metabolism

Abstract

Aims

In the heart and other tissues, perfusion and metabolic activity are heterogeneous and spatially correlated. The goal of this work is to investigate the causes of this behaviour. Theoretical simulations are used to examine the effects on flow distribution and oxygen levels in terminal vascular beds of inherent irregularity in network structure, considering structural adaptation of vessel diameters to haemodynamic and metabolic stimuli, and adaptation of oxygen demand to local oxygen availability.

Methods and results

A mathematical model based on experimentally observed microvascular network structures (rat mesentery and m. sartorius) is used to simulate blood flow, oxygen transport, and adaptation of vessel diameters and tissue oxygen demand. Inherent geometric heterogeneities of vascular networks cause heterogeneity of blood flow and oxygen levels that cannot be eliminated by increasing metabolic sensitivity of diameter adaptation. Adaptation of oxygen demand to differences in oxygen availability causes increased oxygen extraction, implying improved functional capacity, and establishes a correlation between local oxygen demand and flow rate, as observed experimentally. Such a correlation is not predicted if the heterogeneity of oxygen demand is assumed to be an intrinsic tissue property.

Conclusion

A central mechanism generating heterogeneous perfusion is the inevitable structural heterogeneity of terminal vascular beds, which cannot be fully compensated by structural adaptation of vessel diameters. Heterogeneity of metabolism may result from adaptation of tissue function to the heterogeneous oxygen availability. These findings are of interest for the understanding of tissue function, including the heart, and of results obtained by corresponding imaging approaches.

1. Introduction

Since the introduction of microsphere and tracer deposition techniques for the study of local tissue perfusion, ample evidence has accumulated that perfusion is very heterogeneous, especially in the heart.^1–4 The observed coefficient of variation (CV) increases with decreasing sample size.^4–7 Typical values range from about 0.2 for sample sizes of ∼1 g to about 0.35 for sample sizes of ∼0.1 g.⁴ The pattern of flow distribution is stable over hours.¹ Parameters indicating local oxygen consumption and metabolic activity also exhibit significant heterogeneity⁸ and correlate with local flow.^8–12 While it is not currently feasible to measure functional parameters (e.g. contraction work in the heart) with the necessary spatial resolution, it seems likely that local differences in metabolism are paralleled by corresponding differences in function.⁹ Advanced imaging techniques have shown heterogeneity in flow and metabolism in patients and animal experiments.^13–15

These findings lead to the question of underlying cause and effect relations: does the heterogeneity in metabolism cause a corresponding heterogeneity in flow, or vice versa? In the heart, the observed fractal characteristics of flow heterogeneity led to the suggestion that the branching structure of the coronary network is responsible.^6,16,17 This would suggest that flow is the primary variable, possibly driving adjustments of local metabolism and function. Conversely, heterogeneity in the oxygen turnover capacity of local tissue regions has been considered to be the primary event, with flow distribution controlled according to variations in demand.⁹

This ‘chicken or egg’ question is not easily addressed by direct experimental investigation. However, a possible answer is suggested by considering the biological processes involved. There is no obvious reason that the function or oxygen consumption of tissue cells, such as cardiac myocytes, should be highly heterogeneous on small spatial scales. Variations on larger scales, e.g. between the free wall of the heart and papillary muscles or between subendocardial and subepicardial layers, reflect spatial dependence of the mechanical workload or other functional requirements. In contrast, two fundamental mechanisms tend to cause heterogeneity in local blood flow on small scales: the stochastic nature of the angiogenic process and the ‘dimensional problem’ as defined below.

In the generation of new vessels by sprouting angiogenesis,^18–20 local signals lead to the generation of sprouts which then grow without carrying blood flow until they contact a draining (or feeding) vessel. With the exception of the formation of the large conductance vessels, this process is not guided by a deterministic genetic ‘blueprint.’ A large number of vessels are generated, forming an immature vascular network, which is then refined through elimination of redundant vessels by ‘pruning’.²¹ In this stochastic process, spatial variation in vascular density and perfusion is inevitably generated.

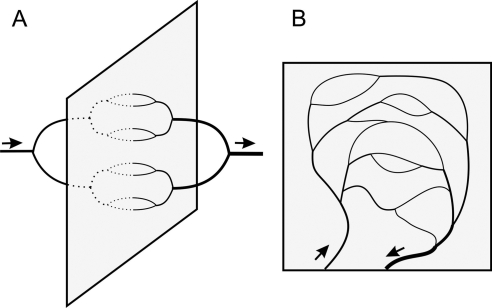
A second source for structural heterogeneity in terminal vascular beds is referred to here as the ‘dimensional problem.’ Vascular systems including feeding and draining trees are embedded in the tissue they supply and must share its dimensionality (whether two- or three-dimensional). If the vascular tree supplying and draining a thin sheet-like tissue (such as the mesentery) were to use the third dimension and approach the tissue from both sides, all flow pathways could in principle be of equal length (Figure 1A). However, the feeding arterial and draining venous trees are constrained to lie in the tissue plane, generating a substantial variation between short and long flow pathways (Figure 1B). The commonly observed pairing of the vessels feeding and draining a given region contributes further to this variation. Similar arguments hold for networks supplying three-dimensional tissue regions.

Figure 1.

The ‘dimensional problem’ of vascular supply, illustrated for a sheet-like tissue. (A) If feeding and draining vessels could occupy a third dimension perpendicular to the sheet, a network structure with equivalent path lengths and providing uniform perfusion and oxygenation would be possible. (B) In reality, the constraint that vessels must lie in the tissue plane leads to heterogeneity of path lengths.

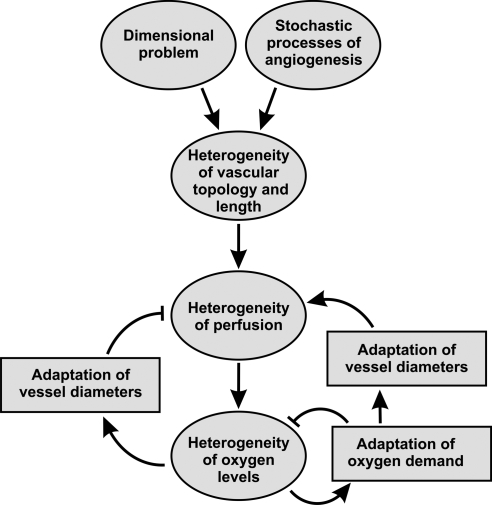
These constraints inevitably lead to vascular networks with shorter and longer flow paths as well as non-uniform vascular densities. However, vessels are known to adjust their inner diameters in response to metabolic and haemodynamic stimuli.^22–25 This adaptation tends to compensate for the impact of topological and path length heterogeneity on heterogeneity of perfusion and oxygen availability (Figure 2, lower left).

Figure 2.

Schematic representation of mechanisms leading to heterogeneity of flow and oxygen levels. Arrows with blunt ends represent negative effects. Vascular networks inevitably exhibit substantial heterogeneity in topology and segment length due to the stochastic processes involved in angiogenesis and the ‘dimensional problem’. The resulting heterogeneity in perfusion may be reduced by adaptation of vessel diameters to metabolic signals (bottom left) or modified by local adaptation of oxygen demand to oxygen availability (bottom right).

Two types of tissue response to the remaining heterogeneity of local oxygen supply can be envisaged. If oxygen demand were to remain constant throughout the tissue, at a level that avoids local hypoxia, then the overall oxygen extraction and thus overall organ function would be relatively low. On the other hand, the local metabolic activity and oxygen demand of tissue might adapt to local oxygen availability, tending to increase in well-oxygenated regions. Such adaptation has the potential to increase overall oxygen extraction. However, it would also create a positive feedback loop in which oxygen consumption increases in regions of relatively high perfusion, providing a metabolic stimulus for outward vascular remodelling and further increases in perfusion (Figure 2, lower right). This mechanism would tend to increase spatial heterogeneity of tissue oxygen levels and local metabolic rate.

In the present study, we use a theoretical approach to simulate the effects of structural adaptation of blood vessels and of local adaptation of tissue metabolism on blood flow and oxygen transport in microvascular networks, and to investigate the consequences of different adaptation characteristics for the observable heterogeneity in the distributions these variables. Two linked hypotheses are explored. (I) The stochastic nature of angiogenesis and geometrical constraints leads to heterogeneity in the topology and length distribution in terminal vascular beds. This causes heterogeneity of flow and oxygen distribution, which cannot be abolished completely by structural adaptation of vessel diameters in response to local oxygen levels. (II) Given the remaining heterogeneity of flow and oxygen distribution, overall oxygen extraction can be increased and tissue function can be enhanced by adaptation of local oxygen demand to local oxygen availability.

While the discussion on sources and consequences of spatial heterogeneity has been stimulated mainly by observations on the heart, the above hypotheses are of a fundamental nature and also apply to other tissues. Thus, they can in principle be tested in any microvascular structure. The theoretical approach used here requires a detailed description of microvascular network architecture, which is difficult to obtain for the heart. Therefore, rat mesenteric and skeletal muscle microvascular networks are used, for which exceptionally complete experimental data sets are available.

2. Methods

2.1. Networks

Animal experiments were performed according to pertinent rules and regulations, after obtaining approval by the University and State authorities for animal welfare. The investigation conforms to the Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health (NIH Publication No. 85-23, revised 1996). Vascular networks in the mesentery of two male Wistar rats prepared for intravital microscopy were observed and analysed as described before.²⁶ The small bowel was exteriorized, and fat-free portions of the mesentery selected. In these preparations, no spontaneous tone was observed. To avoid any development of vascular smooth muscle contraction during the experiment, Papaverine (10⁻⁴ M) was continuously applied to suppress active vessel tone.

Microvascular networks were scanned and video-recorded. From the video recordings, diameter and length were measured for all segments between branch points using a digital image analysis system,²⁷ determining the topological and spatial arrangement of segments. Haematocrit values and centre-line velocities for vessels entering and leaving the network were measured with a digital image analysis system.^28,29 Centre-line velocity (v_cl) was converted into mean blood velocity (v_b), with the empirical relationship v_b = v_cl/1.3.

Two mesenteric networks containing 546 and 913 vessel segments were reconstructed. In addition, a vascular network from the cat sartorius with 111 vessel segments from the literature³⁰ and an artificial network with 122 asymmetrically connected segments were used. Most calculations were performed for the mesenteric network with 546 vessel segments (Figure 3). The other networks were used to check that the results do not depend on specific assumed network properties, such as topology or distribution of segment lengths. The artificial network was similar to the mesenteric networks but was fed and drained by a single paired arteriole and venule.

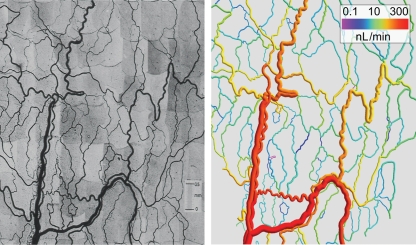
Figure 3.

Photomontage (left) and computer reconstruction (right) of a mesenteric microvascular network. The network was recorded in about 300 microscopic fields of view. The spatial arrangement of the network was obtained using custom-made digital image analysis software and is shown in a computer rendering with each segment colour-coded for blood flow rate. In this representation, vessel diameters are increased by a factor of 1.5 to allow a better judgement of the colour for small vessels.

2.2. Calculation of network haemodynamics and oxygen distribution

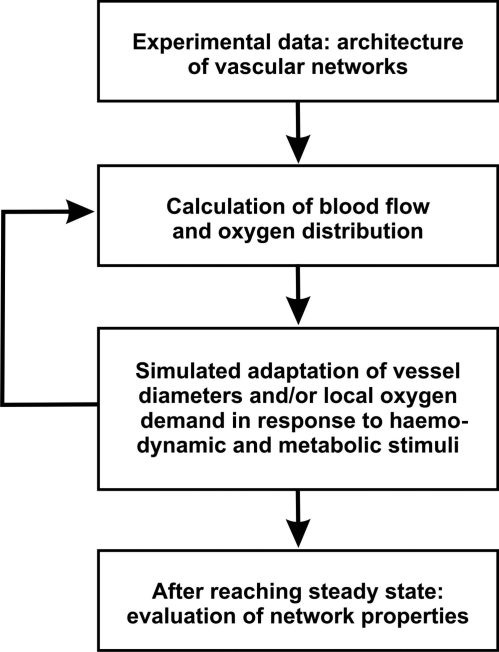
The simulation method is summarized in Figure 4. The mathematical procedures to calculate network haemodynamics and oxygen distribution have been described earlier.^24,31 Information on topology, length and diameter of the vessel segments, and boundary conditions were used as input to the haemodynamic model to estimate distributions of blood flow, shear stress, pressure, and oxygen partial pressure.^22,23 The boundary conditions comprise volume flow rates derived from velocity measurements, haematocrit for all segments feeding the network, and volume flow rates for the vessels feeding or draining the network, with the exception of the main venular draining vessel that was assigned a pressure of 13.8 mmHg to provide a fixed pressure reference.

Figure 4.

Schematic representation of the simulation approach. Input into the model includes data on the connections, length, and initial diameter of each segment. Distributions of haemodynamic parameters (flow, shear stress, pressure) and metabolic parameters (oxygen partial pressure, PO₂) for all vessel segments are calculated.²² Next, the adaptation of individual vessel segment diameters to locally available signals derived from these haemodynamic and metabolic parameters is simulated. For some simulations, adaptation of oxygen consumption is included. After each time step, the calculation of network haemodynamics and oxygen distribution is repeated with updated vessel diameters. This iteration is repeated until convergence is achieved. Finally, functional network parameters (oxygen deficit, coefficient of variation of the shear stress, pathway length, overall energy demand and consumption, heterogeneity of flow and PO₂) are calculated.

For given values of diameter, length, and apparent blood viscosity in each vessel segment, volume flow rates and nodal (junction of segments) pressures were calculated by iteratively solving a system of linear equations.³¹ The haematocrit distribution was updated using the resulting volume flow rates and a parametric description of red cell distribution at divergent bifurcations (phase separation effect) based on experimental findings in vivo.^24,32 The resulting haematocrit values together with vessel diameters were then used to estimate local effective blood viscosity values (Fahraeus–Lindqvist effect) according to a parametric description of blood rheology in microvessels.³³ Computations of flow distribution and local haematocrit and viscosity were iterated until convergence was achieved.

A simplified model was to simulate oxygen transport, in which oxygen is assumed to diffuse out of each vessel segment at a fixed rate per unit vessel length until the saturation in a given segment drops to zero. Typically, this occurs in small fraction of segments and mixed venous saturation from the network remains positive. Possible effects of spatial vascular arrangement and diffusive crosstalk between vessels are neglected. Each vascular cross-section is assumed to supply a tissue region with cross-section area 4000 µm². With a demand of 0.01 cm³O₂/(cm³ × min) typical for connective tissue, this corresponds to a demand per unit vessel length and time of 4 × 10⁻¹¹ cm³O₂/(μm × min). Oxygen consumption is assumed to equal oxygen demand in the tissue supplied by a given vessel as long as the saturation remains positive. For the simulation of inherently heterogeneous local oxygen demand, the oxygen demand in the tissue associated with a given vessel segment was multiplied by a random number with a mean of 1 and an adjustable SD.

The rate of convective oxygen influx to a vessel segment was calculated as Q × C₀ × H_D × S_O2ⁱⁿ, where Q is the blood flow rate, C₀ = 0.5 cm³O₂/cm³ is the oxygen binding capacity of red blood cells, H_D is the flow fraction of red cells (discharge haematocrit), and S_O2ⁱⁿ is the fractional oxygen saturation in the inflow to the segment. Average vascular oxygen saturation (S_O2^av) was calculated from S_O2ⁱⁿ and the oxygen consumption in the vascular segment and used to estimate average oxygen partial pressure (P_O2^av) for each vessel segment using Hill's equation P₅₀ × [S_O2^av/(1 − S_O2^av)]^1/Nox with P₅₀ = 38 mmHg, N_OX = 3 according to experimental data for rat blood. Saturation in the blood entering the networks was assumed to be 0.94. The total blood flow and convective oxygen supply to each network were held constant during variations of other parameters.

2.3. Adaptation of vascular diameters

The diameter (D) of each segment in the network was assumed to vary with time in proportion to haemodynamic and metabolic stimuli. This adaptation process includes long-term changes of vessel diameter due to structural remodelling or change of time-averaged vessel tone. It was simulated in the model by calculating the change in diameter at a sequence of discrete time steps and continuing this process until an equilibrium state is achieved (Figure 4). The change in diameter at each time step is assumed proportional to a stimulus (S_tot) derived from shear stress, transmural pressure, and oxygen partial pressure:²³

1

where S_t + k_pS_p represents responses to haemodynamic forces, k_m[S_m + k_cS_c] gives the metabolic component, and k_s represents a basal tendency of vessels to shrink in the absence of positive growth stimuli. S_t is calculated from wall shear stress, τ_w, as log τ_w and S_p from transmural pressure, P, as log τ_e(P) where τ_e(P) = 100 − 86 exp[−5000 (log(log P))^5.4] describes the shear stress set point as a function of P according to experimental data.³⁴ The vascular sensitivity to pressure is controlled by the parameter k_p.

The stimulus corresponding to the local metabolic conditions (S_m) was computed from the intravascular flux (J_m) of a metabolic signal substance relative to the blood flow rate (Q) as S_m = log[1 + J_m/(Q + Q_ref)] where Q_ref, the reference value for blood flow, is a small constant included to avoid singular behaviour at low blood flow value. The metabolic signal substance was assumed to be added to flowing blood in each vessel in proportion to L_s(1 − P_O2^av/P_O2,ref) where L_s is the vessel length and P_O2,ref a reference level for P_O2.³⁵

A signal (J_c) originating in each segment in proportion to the local value of the metabolic stimulus (S_m) is assumed to be conducted upstream along the vessel wall.³⁵ At branch points, the sum of the conducted stimuli from the draining segments is distributed evenly to the segments feeding into this branch point. The corresponding conducted stimulus (S_c) depends on the value of J_c with a saturable response, S_c = J_c/(J_c + J₀), where J₀ is the respective reference value. The vascular sensitivity to metabolic stimuli in general and to the conducted stimulus is determined by the parameters k_m and k_c, respectively.

2.4. Adaptation of local oxygen demand

To simulate adaptation of local metabolic activity to local oxygen availability, the oxygen demand of the tissue supplied by a given vessel segment was obtained by multiplying the standard demand by a factor (CF) related to P_O2^av, the average P_O2 of the segment:

2

where P_O2^net is the mean P_O2 over all segments of the network. DSS (demand supply sensitivity) gives the sensitivity of the oxygen demand in tissue surrounding a given segment to local oxygen availability. A DSS of zero corresponds to homogeneous oxygen demand throughout the tissue.

2.5. Variation of adaptation sensitivities

The theoretical model makes it possible to vary the strength of an individual mechanism in a graded fashion, while holding all other parameters fixed. Two parameters, k_m and DSS, were thus varied, to examine the effects of adaptation of vessel diameters to metabolic stimuli and adaptation of tissue oxygen demand to local oxygen levels. All other parameters were set to values determined previously for mesenteric microvascular networks³⁵ by minimizing the deviations between predicted and measured segment diameters and velocities.

2.6. Characteristic network parameters

Based on the results obtained for the individual vessel segments of a given network, a number of global parameters were calculated to describe functional network properties. The oxygen deficit (O_{2 def}) of the supplied tissue is defined as

3

where O_{2 demand} is the oxygen demand of the entire network and O_{2 extraction} is the difference in summed oxygen convection between all inflow and outflow segments of a given network. O_{2 demand} is indicated in nL/min. The path length is the flow-weighted mean of the lengths of all pathways for flow of blood through a network. The shear rate heterogeneity (τ_het) is the relative root mean square deviation of wall shear stress (τ_i) over all vessel segments of a given network (i = 1 to N, with N equal to the total number of segments) from its mean value (i.e. CV) weighted according to the flow rate (Q_i):

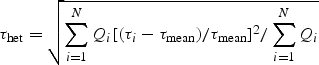4

It represents a measure of the departure of the network from the optimality condition defined by Murray.³⁶ The capillary flow heterogeneity (CV_flow) and the capillary PO₂ heterogeneity (CV_PO2) give the CV of blood flow rate and PO₂, respectively, for vessels connecting the arterial and the venous vessel trees of the investigated networks. The energy dissipation is the total value for the network due to the flow of blood, calculated from the flow-weighted pressure drop across all vessel segments (given in Joule per litre of flow, J/L).

3. Results

3.1. Adaptation of vascular diameter

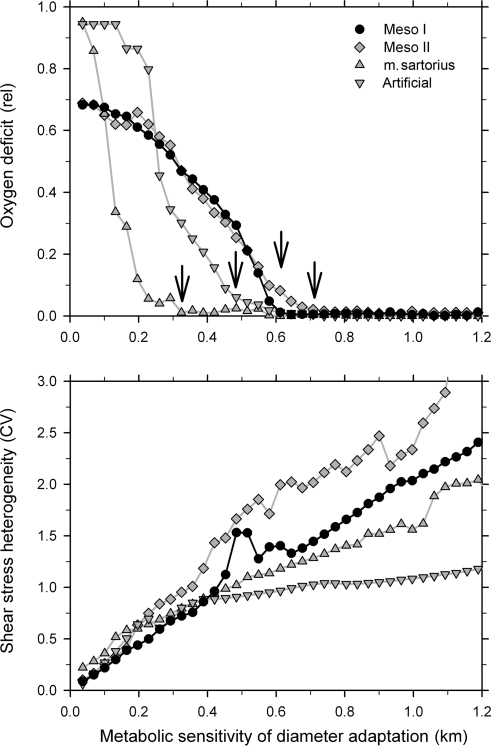
Figure 5 shows effects of changes in the sensitivity of vascular adaptation to metabolic signals (k_m) for four vascular networks. An increase in metabolic sensitivity above a certain threshold leads to a drop of the oxygen deficit to near zero values. With increasing metabolic sensitivity, the corresponding sensitivity to haemodynamic signals decreases, and consequently the heterogeneity of shear stress increases, approximately in proportion to the metabolic sensitivity. The results for the four networks exhibit quantitative differences, but qualitative trends are similar, showing that the predicted behaviour is independent of the exact network topology. Therefore, the following results are only presented for one of the mesenteric networks.

Figure 5.

Variation of two characteristic global network parameters, the oxygen deficit (O_{2 def}, top) and the coefficient of variation of the shear stress (τ_het, bottom) for different levels of the vascular sensitivity to metabolic stimuli (k_m). Results are shown for two mesenteric networks with 546 (Meso I) and 913 (Meso II) segments, for a network in the sartorius muscle (111 segments) and an area-filling artificial network (122 segments). For all four networks, the increase in metabolic sensitivity above certain threshold values (indicated by arrows) leads to a drop of the oxygen deficit to near zero values.

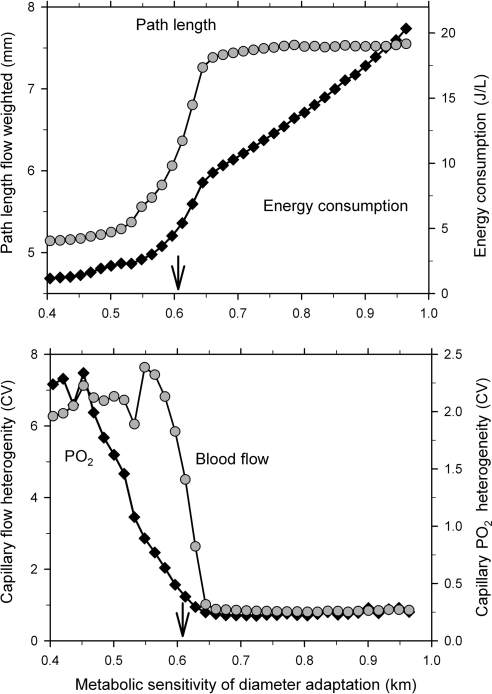
A major reason for the development of oxygen deficit, when the metabolic sensitivity drops below a threshold value, is the shunting of blood flow through a few short arterio-venous flow pathways. This is evident from the decrease in flow-weighted pathway length and a large increase in the heterogeneity of capillary perfusion and oxygen partial pressure (Figure 6). On the other hand, an increase in the metabolic sensitivity above the threshold for sufficient oxygen supply leads to a continuous increase in energy dissipation due to the increasing heterogeneity of shear stress distribution, which deviates from the conditions of Murray's minimal energy principle.³⁶ Figure 6 shows results for one mesenteric network with 546 vessel segments. For metabolic sensitivities above the threshold, CV_PO2 and CV_flow range between about 0.2–0.25 and 0.7–0.8, respectively, for the networks investigated.

Figure 6.

For one of the mesentery networks used for Figure 5 (Meso I), values of the flow-weighted mean pathway length, the overall energy consumption (top), and the heterogeneities of flow (CV_flow) and PO₂ (CV_PO2) on the capillary level (bottom) are shown for varying k_m. The threshold value for vascular sensitivity to metabolic stimuli below which oxygen deficit starts to develop is indicated by arrows.

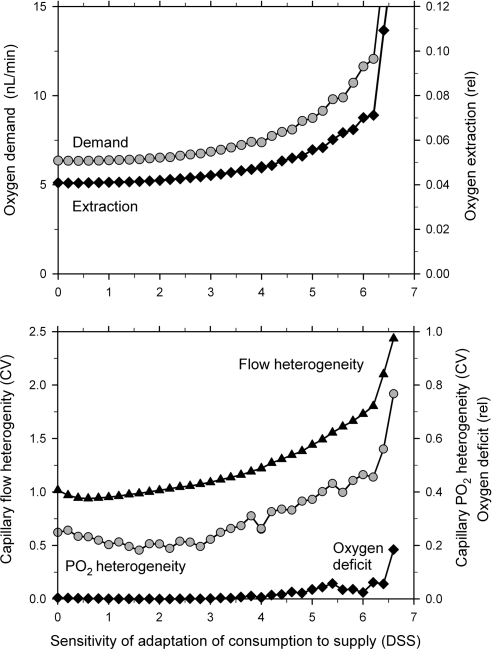
3.2. Adaptation of local oxygen demand

The effect of adaptation of local oxygen demand to local oxygen availability on functional network parameters is shown in Figure 7. Oxygen demand and oxygen extraction increase with increasing values of the sensitivity parameter (DSS). The heterogeneities of capillary blood flow and PO₂ exhibit a small decline before they increase with increasing DSS. Over most of the range, no significant oxygen deficit develops. For values of DSS above about 6, the system becomes unstable. This behaviour can be understood in terms of a positive feedback loop which is created by the combined effect of diameter adaptation and adaptation of oxygen consumption rate. Increased flow in a given vessel leads to a local higher oxygen level, triggering increased consumption and further flow increase. This positive feedback also accounts for the increase in PO₂ heterogeneity as DSS is increased above 3, and the eventual increase in oxygen deficit.

Figure 7.

Response of functional network parameters to changes in the sensitivity of the local adaptation of oxygen demand to changes on the local P_O2 (DSS). Data are shown for the same network as used in Figure 6.

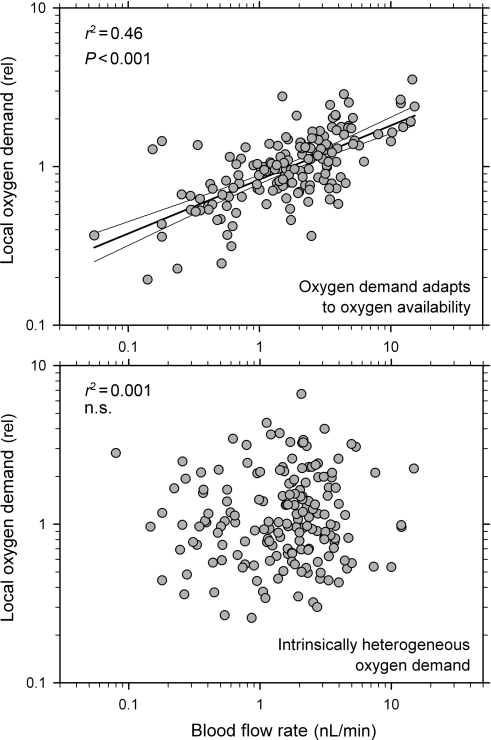
For the highest DSS values showing low oxygen deficits (5–6), the values of CV_PO2 and CV_flow are ∼0.42 and ∼1.6, respectively. For a DSS value of 4.5, Figure 8 shows the correlation of local oxygen demand to blood flow rate on the capillary level. For comparison, corresponding results are shown for the case in which heterogeneous oxygen demand is assumed independent of variations in oxygen level.

Figure 8.

Relationship between local oxygen demand and local blood flow rate for individual capillaries (n = 172) from the network used in Figures 5 and 6. (Upper panel) Oxygen demand adapts to oxygen availability, DSS = 4.5. Results of corresponding linear regression analyses are included. (Lower panel) Heterogeneous oxygen demand, independent of variations in oxygen level.

4. Discussion

The results of these simulations support Hypothesis I. For experimental and artificial networks, the heterogeneity in the distributions of blood flow and local oxygen partial pressure (CV_flow and CV_PO2) cannot be abolished by increasing the metabolic sensitivity of diameter adaptation (Figure 6). Above the threshold value needed to bring the oxygen deficit to near zero, CV_PO2 and CV_flow remain at levels of 0.2–0.25 and 0.7–0.8, showing that vascular adaptation to metabolic signals during vascular development and remodelling cannot completely suppress perfusion heterogeneity. While this level of heterogeneity does not lead to oxygen deficits at the assumed oxygen consumption rate (Figure 5), it would lead to reduction of maximal overall oxygen extraction and work rate in a muscular organ.

As indicated by Figures 5 and 6, the heterogeneity of wall shear stress³⁷ and the energy required to maintain flow increase continuously if the metabolic sensitivity of diameter adaptation is increased above the threshold value. Thus, a sensitivity value closely above the threshold seems to be an optimal setting. Indeed, previous studies for mesenteric networks^23,38 have shown that the discrepancy between segmental velocity values as predicted by simulation and direct experimental measurements was minimal at a sensitivity of vascular adaptation to metabolic signals in this range (value about 0.65). This supports the assumption that values in this range best describe the actual in vivo situation.

The results also support Hypothesis II. A substantial increase in oxygen extraction (by >63%) can be achieved if adaptation of local oxygen demand in response to local oxygen availability is assumed (Figure 7). The level of oxygen deficit stays low over a wide range of adaptation sensitivities. However, such behaviour establishes a positive feedback as mentioned above, which eventually leads to instability if the feedback gain (i.e. the sensitivity of demand to supply adaptation, DSS) is too high. At low levels of DSS, increasing DSS causes a decrease in CV_PO2 as expected (Figure 2). However, further increases in DSS cause CV_PO2 and CV_flow to increase from about 0.23 and 0.75 to about 0.42 and 1.6.

For the heart, experimental values of flow heterogeneity have been reported.^{2–4,7,9,15,39,40} The respective CV values range up to about 0.35 for sample sizes of 0.1 g⁴ and are thus much smaller than the values reported here for CV_flow. However, the present values pertain to single capillaries, supplying an average tissue mass of ∼0.3 µg, more than 4 orders of magnitude less than the smallest samples reported in the literature. It is observed that the degree of heterogeneity increases with decreasing sample size.⁷

In Figure 8, local oxygen demand is plotted against corresponding values for local blood flow assuming either that adaptation of oxygen demand to local oxygen availability occurs in parallel to vessel adaptation or that an intrinsically heterogeneous oxygen demand drives vessel adaptation. If intrinsically heterogeneous oxygen demand is assumed, these two variables exhibit no correlation, in contrast to experimental data from the heart showing a significant positive correlation between local perfusion and local metabolic activity.^10,11 In contrast, such a correlation is generated when adaptation of local oxygen demand in response to the local oxygen availability is assumed (Figure 8, upper panel). The r² value of 0.44 calculated for the present data is similar to values reported by Schwanke et al. (0.38–0.59) between local perfusion and local metabolic activity. In principle, this finding is independent of the tissue or specific angioarchitecture considered and suggests that intrinsic heterogeneity in tissue oxygen demand has only a limited effect on the observed heterogeneity in flow and in local tissue metabolism.

The present study predominantly uses experimental data on rat mesenteric and skeletal muscle microvascular networks. These are the only available data sets that contain complete morphological (vessel diameter, vessel length) and topological (vessel connection pattern) for self-contained microvascular networks including volume flow rates for the boundary vessels feeding or draining the network.^22,31 In addition, for one of these networks (Meso I, 546 segments), the flow velocity has been measured in all vessel segments. Velocity distributions within a network are very sensitive to even small changes in vessel diameters. Therefore, a comparison between these velocity values and those predicted by a simulation of vascular adaptation can be used to test the assumptions made with respect to the response characteristics of the structural vascular adaptation.^23,38 With the exception of the parameters varied here (metabolic sensitivity of diameter adaptation, sensitivity of local oxygen demand to local oxygen supply), all adaptation parameters used were derived by minimization of mean squared velocity error for this network.

Comparable data sets for essentially three-dimensional tissues, including the heart, are not available due to the technical difficulties involved, and so the approach used here cannot be directly applied to such tissues. As a consequence, an extrapolation of detailed quantitative results obtained in the present study to other tissues is not justified. However, the biological mechanisms described in the hypotheses are applicable to all tissues irrespective of variations in parameters such as oxygen demand per tissue volume, capillary density, or microvascular architecture. The absence of significant tone in the tissue used (see Section 2) avoids an additional confounding parameter in the control of inner vessel diameter and thus distribution of perfusion, but also renders the results less relevant for other tissues with high levels of resting tone. However, it has been shown that the perfusion pattern in the primate heart and its heterogeneity seem to be relatively stable for different levels of exercise.¹ This indicates that the underlying mechanisms are to some degree independent of the regulation of vascular tone.

The main conclusion of the present investigation is that inevitable structural and topological properties of vascular networks underlie the observed heterogeneity in flow and oxygen consumption. Vascular diameter adaptation in response to local oxygen partial pressure reduces but not abolishes this heterogeneity. Adaptation of local oxygen consumption to supply increases the heterogeneity but also the overall oxygen extraction and tissue performance. Organs must be capable of accommodating the resulting functional heterogeneity, for instance local variations in the amount and dynamics of tension development in the myocardium. The phenomena discussed here are also relevant for the interpretation of high-resolution functional images of the heart¹⁵ and other organs, and for the investigation of pathological mechanisms related to the perfusion pattern, for example, during ischaemia/reperfusion.⁴¹

Funding

This work was supported by National Institutes of Health (NIH) grant HL034555.