Size matters: just how big is BIG?

Abstract

Background Despite earlier doubts, a string of recent successes indicates that if sample sizes are large enough, it is possible—both in theory and in practice—to identify and replicate genetic associations with common complex diseases. But human genome epidemiology is expensive and, from a strategic perspective, it is still unclear what ‘large enough’ really means. This question has critical implications for governments, funding agencies, bioscientists and the tax-paying public. Difficult strategic decisions with imposing price tags and important opportunity costs must be taken.

Methods Conventional power calculations for case–control studies disregard many basic elements of analytic complexity—e.g. errors in clinical assessment, and the impact of unmeasured aetiological determinants—and can seriously underestimate true sample size requirements. This article describes, and applies, a rigorous simulation-based approach to power calculation that deals more comprehensively with analytic complexity and has been implemented on the web as ESPRESSO: (www.p3gobservatory.org/powercalculator.htm).

Results Using this approach, the article explores the realistic power profile of stand-alone and nested case–control studies in a variety of settings and provides a robust quantitative foundation for determining the required sample size both of individual biobanks and of large disease-based consortia. Despite universal acknowledgment of the importance of large sample sizes, our results suggest that contemporary initiatives are still, at best, at the lower end of the range of desirable sample size. Insufficient power remains particularly problematic for studies exploring gene–gene or gene–environment interactions.

Discussion Sample size calculation must be both accurate and realistic, and we must continue to strengthen national and international cooperation in the design, conduct, harmonization and integration of studies in human genome epidemiology.

Introduction

By 2020, common chronic diseases will account for almost three-quarters of deaths worldwide.¹ The quest to find genetic variants underlying these disorders is in a ‘fast-moving, exciting and highly productive phase’.² If the common disease common variant hypothesis^3–8 is true for at least some genetic determinants of chronic diseases, their aetiological effects will typically be weak^{9,10 and they will be identified more readily by association rather than linkage studies.11} In consequence, although alternative strategies could have been adopted,¹² the majority of contemporary gene discovery studies are based on association studies in unrelated individuals.

A series of recent publications has convincingly identified or replicated genetic associations for a range of chronic diseases including: type 1 diabetes;^{13,14 type 2 diabetes;14–18} coronary artery disease;^{14,19–21 breast cancer;22,23 colorectal cancer;24–26} prostate cancer;^{27,28 age-related macular degeneration29–31} and Crohns disease.^{14,32 But, prior to these recent contributions, genetic association studies were strikingly inconsistent.7–9,33–42 Although numerous scientific and technical issues were blamed,10,33,35,37,40,43–47 perhaps the most fundamental problem was a serious lack of statistical power.10,33,35,37,40,43–47 This raises important questions: how large must stand-alone and nested case–control studies really be if they are to power contemporary gene discovery? And specifically, will the current generation of ‘large’ initiatives,14,48,49http://www.genome.gov/17516722, http://www.p3gobservatory.org, generate enough power to study the joint effects of genes and environment?50}

These questions are crucial. Governments and funding agencies worldwide are deciding whether, and how much, to invest in population genomics. Difficult strategic decisions, with imposing price tags and substantial opportunity costs have to be taken. In Europe, for example, national governments must decide whether to adopt the European Union's regional road map for research infrastructures in ‘big science’. This proposes development of a harmonized pan-European network of biobanks. But, are pre-existing projects, like UK Biobank,⁴⁸ the Wellcome Trust case control consortium (WTCCC),¹⁴ EPIC (European prospective investigation into cancer and nutrition)⁵¹ and BioHealth Norway⁵² already large enough to service all foreseeable needs, or is further investment required to facilitate larger pooled analyses and more powerful replication studies?

Rigorous power calculations are needed, but conventional approaches disregard key elements of analytic complexity, including the bioclinical complexity of causal pathways leading to disease and the inferential complexity that arises from key aspects of study design, conduct and analysis. For example, errors in assessing disease status and aetiological determinants are known to dramatically reduce statistical power if the primary outcome is a quantitative disease-related phenotype.⁵³ But, although their importance has been emphasized,⁵⁴ they are typically ignored by conventional power calculations for case–control studies.

This article describes and applies a simulation-based approach to power calculation for case–control studies in population genomics, generating a realistic power profile across a range of meaningful bioclinical scenarios. It also explores the incidence of common chronic diseases in a typical population-based cohort study recruiting middle-aged adults. Taken together, these data provide a logical basis for deciding the appropriate size of major new initiatives in population genomics, including the construction of disease-based and population-based biobanks and the pulling together of consortia based on case series, population controls, case–control projects and/or cohort studies.

Materials and methods

All simulations were carried out in the statistical programming environment ‘R’.⁵⁵

The required size of case–control analyses

Simulation-based power calculation involves two steps—simulation and analysis. Here, both steps were based on logistic regression. All analyses in the main paper utilize an unmatched case–control design enrolling unrelated individuals with four controls per case (alternative case: control ratios are considered in Supplementary materials, and Supplementary Figure S1). Unless otherwise stated, genetic and environmental determinants are all dichotomous (as explained in Supplementary Box S1). Supplementary methods include: (i) full specification of the mathematical models used (equations A–K); (ii) an annotated version of the R code for the primary simulation programme and (iii) discussion of the key assumptions invoked in the analysis and the effect of modifying them. Formal estimates of type 1 error were all nominal (Supplementary Table S1).

Genetic variants were modelled as having two levels: ‘at risk’ and ‘not at risk’. This would apply, for example, under a dominant genetic model (Supplementary box S1): one detrimental allele puts you ‘at risk’, but that risk is increased no further by a second copy. Under such a model, 9.75% of the general population would be ‘at risk’ if the minor allele frequency (MAF) was 5%, and at-risk prevalences of 19, 51 and 75% would correspond to MAFs of 10, 30 and 50%, respectively. A dichotomous genetic variant represents the setting of least power that is commonly encountered and it was for this reason that it was used as the default in the main paper. When it is mathematically valid, more power and a smaller sample size requirement, may be obtained if an additive genetic model (in contrast to a dichotomous model) is used. This model, which is used widely—e.g.¹⁴—is considered further in the discussion.

Interaction terms reflect departures from a multiplicative model—i.e. from additivity on the scale of log odds—[Supplementary methods, equations (A–C)]. In simulation studies, where a gene–environment interaction is of primary interest, the main effect ORs (odds ratios) associated with the genetic and environmental determinant is fixed at 1.5 while the magnitude of the interaction term is varied: results are insensitive to changing this fixed magnitude (Supplementary Table S2).

Step 1 (simulation)

The parameters characterizing each scenario (a series of simulations all using the same bioclinical parameters) were set, and varied, under the following assumptions: (i) Prevalence of the ‘at risk’ genotypic and environmental determinants [0.0975 (MAF = 5%) or 0.51 (MAF = 30%), and 0.1 or 0.50, respectively]; (ii) ORs associated with genotypic and environmental main effects (1.10–3.0), and gene–environment interactions (1.20–10.00); (iii) Sensitivity and specificity of disease assessment appropriate to the particular disease under consideration (e.g.⁵⁶, Supplementary box S2); Supplementary materials and Supplementary Figure S2 explore the impact of changing sensitivity and specificity; (iv) Controls assessed clinically in the same way as cases (except in the real WTCCC data); (v) Errors in classifying genotypes modelled as if arising primarily from incomplete linkage disequilibrium (LD) between an observed marker and a causative variant [R² = 1.00 (no error), 0.80⁵⁷ or 0.50]; (vi) Lifestyle/environmental exposure status determined by dichotomization of an underlying quantitative variable measured with error equivalent to a test–retest reliability of (a) 100%, (b) 90%, (c) 70%, (d) 50% or (e) 30%; (vii) Heterogeneity of underlying disease risk modelled using a random effect⁵⁸ with a variance reflecting a 10-fold ratio in baseline risk between individuals on ‘high’ (95%) and ‘low’ (5%) population centiles; Supplementary materials and Supplementary Figure S3 investigate changing the heterogeneity of risk; (viii) Disease prevalence appropriate to the particular disease under consideration⁵⁶; Supplementary materials and Supplementary Figure S4 explore changing disease prevalence; (ix) Statistical significance defined at 10⁻⁷ for a genome wide association (GWA) study and 10⁻⁴ for a candidate gene study or for gene–environment interactions (Supplementary methods) and (x) No correction was made for substructure in population ancestry.¹⁴

Having set the required parameters, a dataset (D₁) was simulated (Supplementary methods, equations A–F), containing cases and controls each associated with a set of aetiological determinants (e.g. a gene and an environmental determinant) distributed as would be expected for a case–control study given the particular bioclinical parameters specified.

Step 2 (analysis)

Dataset D₁ was analysed using unconditional logistic regression (Supplementary methods, equations G–J), as if it were a real case–control study. This generated estimates (and associated standard errors and P-values) for the regression coefficients reflecting the genetic and environmental main effects and, where incorporated, a gene–environment interaction. On the basis of the pre-specified type 1 error, D₁ was categorized as either ‘significant’ or ‘non-significant’ for each of the genetic, environmental and interaction effects.

Under each scenario, steps 1 and 2 were repeated many times (≥1000), generating and analysing datasets D₂, D₃, …, etc. The empirical statistical power of the test for each effect was then estimated as the proportion of the simulated datasets for which step 2 generated a ‘statistically significant’ result. Given the estimated power of a study based on whatever number of cases and controls had actually been specified under the particular scenario being considered, the sample size for an equivalent study (including the same ratio of controls to cases) that would generate a power of 80% was estimated as described in Supplementary methods (equation K). In exploring the power profile across a range of ORs, the required sample size for each OR was calculated, tabulated and plotted (Figures 1 and 2).

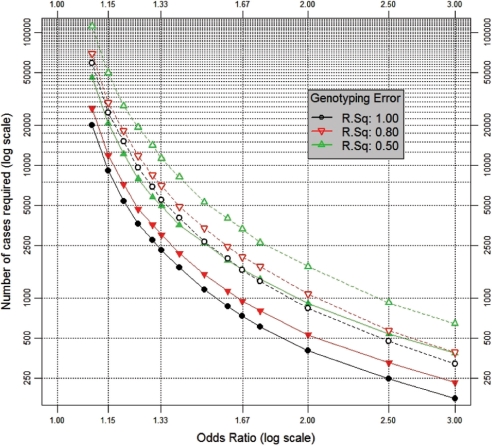
Figure 1.

A genetic main effect, in a candidate gene study. The number of cases required to detect ORs from 1.1 to 3.0 for a genetic main effect with a power of 80% (at P < 0.0001—assuming a vague candidate gene) in a study with four controls per case. Assumptions (see Materials and methods section for details): (i) population genotypic prevalence = 9.75% [dashed lines] or 51% [solid lines], corresponding to dominant SNP effects with MAFs (minor allele frequencies) of 5 and 30%, respectively; (ii) genotypic ‘error’ corresponding to: R² = 1.0, 0.8 or 0.5; (iii) case-status determined with sensitivity 89.1% and specificity 97.4%: as for a study of diabetes diagnosed by a composite test (GP diagnosis or HbA1C ≥2 SD above the population mean⁵⁶); (iv) controls phenotypically assessed in the same way as cases; (v) incorporation of heterogeneity in the baseline risk of disease arising from unmeasured determinants, corresponding in magnitude to a 10-fold risk ratio between individuals on the high (95%) and low (5%) centiles of population risk

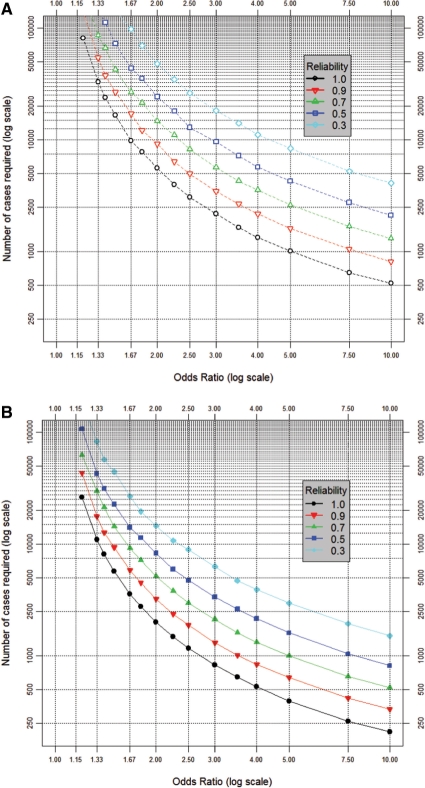
Figure 2.

(A) An uncommon interaction. The number of cases required to detect ORs from 1.2 to 10.0 for a gene–environment interaction with a power of 80% (at P < 10⁻⁴) in a study with four controls per case. Assumptions (see Materials and methods section for details): (i) population genotypic prevalence = 9.75%, corresponding to a dominant SNP effect with a MAF of 5%; (ii) population prevalence of binary environmental determinant = 20%; (iii) genotypic ‘error’ corresponding to r² = 0.8; (iv) environmental error corresponding to dichotomization of an underlying normally distributed latent quantitative variable measured with a reliability of 100, 90, 70, 50 or 30%; (v) case–control status determined with sensitivity 89.1% and specificity 97.4%: as for a study of diabetes diagnosed by a composite test (GP diagnosis or HbA1C ≥2 SD above the population mean⁵⁶); (vi) controls phenotypically assessed in the same way as cases; (vii) incorporation of heterogeneity in the baseline risk of disease arising from unmeasured determinants, corresponding in magnitude to a 10-fold risk ratio between individuals on the high (95%) and low (5%) centiles of population risk. The prevalences of the ‘at risk’ genotype and the ‘at risk’ environmental determinant imply a prevalence of ∼2% for the doubly ‘at risk’ interaction. (B) A common interaction. As (A), but assuming: population genotypic prevalence = 51% (corresponding to MAF = 30%) and prevalence of the environmental determinant = 50%, implying prevalence of the doubly ‘at risk’ interaction ∼25%

This approach is very flexible and can easily be extended by adding additional terms (Supplementary methods).

The expected incidence of chronic disease in population-based cohorts

The number of incident cases of selected chronic diseases of public health relevance expected to accumulate over time was estimated in a simulated cohort of 500 000 individuals, recruited over 5 years, with equal numbers enrolled in all 5 year age bands between 40 and 69 years at entry (Figure 3). This simulated cohort corresponds closely to the design of UK Biobank⁴⁸ and provides important parallels to other cohorts worldwide (www.p3gobservatory.org). Each recruit was simulated in ‘R’ and his/her subsequent life-course was simulated taking appropriate account of the chance occurrence of disease, migrations, loss to follow-up and deaths (sources for the vital statistics are detailed in Supplementary Table S3). Adjustment was also made for the ‘healthy cohort effect’, whereby subjects recruited to cohort studies typically experience lower rates of morbidity than the general population.

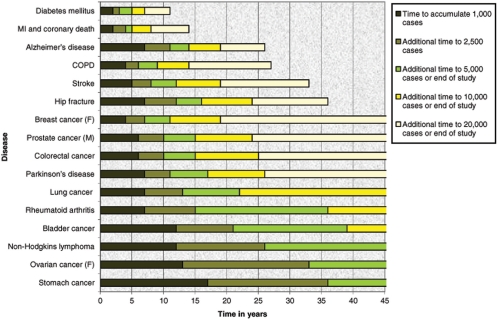
Figure 3.

Time to achieve required numbers of cases. The expected rate of generation of incident cases of 16 common complex diseases (MI = myocardial infarction; COPD = chronic obstructive pulmonary disease) in a cohort of 500 000 men and women recruited over 5 years, aged 40–69 years at baseline, assuming rates of mortality and morbidity as in the UK and that drop-out mirrors that of the British 1958 birth cohort and with adjustment for the ‘healthy cohort’ effect (for full details see⁶⁸)

Results

Figure 1 presents the sample size needed for 80% power to detect (at P < 0.0001) the main effect of a dichotomous (binary) genetic variant in a vague candidate gene, using an unmatched case–control design enrolling four controls per case. As detailed in the Materials and methods section, and summarized in the figure legend, these calculations all incorporate cardinal elements of realistic analytic complexity. Table 1 details the multiplicative factor by which the sample sizes in the figure should be scaled if a P-value other than P < 0.0001 is to be used or if one requires a power of 50 or 90% rather than 80%.

Table 1.

The multiplicative change in required sample size, for a statistical power of 50, 80 or 90% using different levels of statistical significance, relative to the sample size indicated by Figures 1 and 2 (i.e. when P < 0.0001 and power = 80%)

P-value defining ‘statistical significance’	Sample size multiplier for specified power
	Power = 50%	Power = 80%	Power = 90%
Significance thresholds conventionally used in medical statistics
P < 0.05	0.172	0.350	0.469
P < 0.01	0.296	0.522	0.664
Significance thresholds widely used in candidate gene studies
P < 0.005	0.352	0.594	0.746
P < 0.001	0.484	0.762	0.933
P < 0.0005	0.541	0.834	1.013
P < 0.0001	0.676	as in figures	1.195
Significance thresholds widely used in GWA studies
P < 5×10−7	1.128	1.538	1.777
P < 10−7	1.267	1.699	1.950
P < 5×10−8	1.327	1.768	2.024
P < 10−8	1.467	1.929	2.196

Sample size multipliers more than 1 indicate that the required sample size is larger than implied by the figures, values less than 1 that it is smaller.

Figures 2A and B present sample size requirements for studies of gene–environment interaction (see Materials and Methods section, with details in Supplementary methods). Phenotypic and genotypic characteristics are detailed in the figure legend. Figure 2A considers an uncommon interaction where ‘doubly-at-risk’ individuals (i.e. subjects exposed to the at-risk level of both the genetic and the lifestyle determinant) represent ∼2% of the general population. Figure 2B addresses a common interaction with ∼25% of individuals being doubly-at-risk. Each figure details the sample size profile for a range of errors in assessing the environmental factor (see Materials and methods section). As a benchmark, Table 2 presents bioclinical exemplars that are typically measured with a corresponding reliability. Significance testing is at P < 0.0001: i.e. it is assumed that research involving the joint effects of genes and environment will focus on specific interactions with at least some vague basis for candidature. If a more rigorous threshold is required, the sample size multipliers in Table 1 may be used.

Table 2.

Formal estimates of test–retest reliability for a number of exemplar lifestyle/environmental determinants that are widely studied

Reliability of measurement	Lifestyle/environmental factor
≥0.95	Body mass index (BMI) calculated from measured height and weight in various studies76
∼0.9	Measured hip or waist circumference76,77
∼0.7	Blood pressure measurement in the Intersalt Study78
∼0.5	Many nutritional components in a dietary recall study, mean of four 24 h assessments79
∼0.3	Many nutritional components in a dietary recall study, a single 24 h assessment79

In light of the daunting sample size requirements implied by Figures 1 and 2, Figure 3 demonstrates that a cohort of 500 000 middle-aged recruits may be expected to generate 10 000 incident cases of very common conditions (e.g. diabetes and coronary artery disease) within 7–8 years, and 20 000 cases within 15 years. But even for the commonest cancers it will take ∼20 years or more to generate 10 000 cases and >40 years to generate 20 000 cases. Such targets will never be attained for rarer conditions. However, population-based cohort studies also recruit prevalent cases of chronic disease (Supplementary Table S4) and, if it is appropriate, these can be used to supplement statistical power.

Discussion

‘Big’ bioscience is critically poised. It is now known that genetic associations with complex diseases can reliably be detected and replicated if sample sizes are large enough. This will fuel international investment in biobanking. But, how far should that investment go?

It is essential to close the ‘reality-gap’ that currently exists between the sample sizes really required to detect determinants of scientific interest that have plausible bioclinical effects, and the sample sizes that are typically used when studies are being designed. Extensive theoretical work has been undertaken to explore statistical power and sample size in human genomics. This includes studies of the effect of genotype misclassification on power,^59–62 and of strategies for power optimization for genetic main effects^63–64 and for gene–gene⁶⁵ and gene–environment interactions.⁶⁶ Furthermore, the effect of measurement error in both outcomes and exposures on statistical power of gene–environment interaction studies has been explored thoroughly for quantitative traits.⁵³ But, previous work on the power of case–control analyses (i.e. binary traits) has not addressed the impact of realistic assessment errors in both exposures and outcomes and the impact of unmeasured aetiological determinants. The important original contributions of the current article are 3-fold, therefore: (i) to extend the classes of analytic complexity addressed in a straightforward simulation-based power calculation engine; (ii) to use this calculator to undertake realistic sample size calculations for a class of analyses (case–control analyses with unavoidable assessment errors in both exposures and outcomes) that will be utilized widely over the next few decades—analyses in this class are the least powerful that are likely to be applied commonly, and the resultant calculations, therefore, provide a valuable guide to study design in the many large-scale biobanks that are currently being conceived and launched; (iii) to alert readers, particularly those setting up new biobanks, to a web-based implementation—ESPRESSO (Estimating Sample-size and Power in R by Exploring Simulated Study Outcomes)—of the power calculator used in this article and to provide detailed information (in Supplementary methods) about the mathematical models on which it is based.

Studies enrolling several hundred subjects are commonplace in human genome epidemiology. But, even conventional power calculations⁶⁷ indicate that 400 cases and 400 controls provide <1% power to detect (at P < 0.0001) an OR of 1.4 for a binary ‘at risk’ genetic variant with a general population frequency of 0.0975 (e.g. a dominant risk-determining allele with MAF = 0.05). There can be no doubt that a study involving several hundred cases and controls demands hard work and is large by historical comparison; nevertheless, the reality is that to generate a power of 80%, such a study would actually require 4000 cases and 4000 controls.

But even these figures substantially understate the challenge that really faces us. Conventional power calculations ignore many aspects of analytic complexity. Using ESPRESSO, the R-based⁵⁵ simulation-based power calculator⁶⁸ jointly developed by P³G, PHOEBE and UK Biobank (www.p3gobservatory.org/powercalculator.htm), such complexities can be taken into proper account. Using this approach to mimic the conventional power calculation (above)—i.e. assuming disease and genotype to be assessed without error and no heterogeneity in disease risk—confirms a requirement for approximately 4000 cases and 4000 controls. But the sensitivity and specificity of the diagnostic test ought to be taken into proper account: e.g. 0.891 and 0.974, respectively, for a published screening test for type 2 diabetes based on glycosylated haemoglobin⁵⁶ (see Supplementary box 2). Genotyping error must also be considered. It may, for example, be reasonable to assume that this corresponds to incomplete LD with an R² of 0.8.⁵⁷ Finally, heterogeneity in disease risk might be reflected in an assumed 10-fold ratio in the risk between subjects on high (95%) and low (5%) centiles of population risk. Having built in these assumptions, the required sample size more than doubles to 8500 cases and 8500 controls.

It might be argued that substantial power could be gained if a multiplicative model based on additive allelic effects [Supplementary methods, equations (H and I)], as in WTCCC,¹⁴ were used instead of a binary genetic model (Supplementary box S1). Statistical power will be increased if there is a systematic gradation in the strength of association across the three genotypes defined by two alleles. This may reflect biological reality, or it may arise as an artefact of the decay of incomplete LD when working with a linked marker rather than a causative variant. But (Supplementary Figure S5), the reduction in required sample size (typically, 5–50%) is only substantial for SNPs with a common minor allele. This is because when the minor allele is rare, subjects homozygous for the minor allele will be very rare and the genetic determinant will effectively act as if it were a binary exposure. But, power limitation is less of a problem for SNPs with a common minor allele and so the impact of moving to a valid multiplicative genetic model is less dramatic than might otherwise be assumed.

One of the landmark genomic studies of 2007 was the WTCCC that reported robust ‘hits’ in seven of eight complex diseases in its main experiment.¹⁴ But the basic design—involving 2000 cases and 3000 controls for each disease—seems, at first sight, to be at the lower limit of required sample size as implied by our calculations (Figure 1). Therefore, it is tempting to conclude either that the WTCCC was lucky or that our calculations are overly conservative. But, the main experiment of WTCCC had a number of design features that contrast with the assumptions of the primary power calculations reported in our article.¹⁴ The most relevant of these are: (i) use of a model invoking an additive genetic effect rather than a binary ‘at-risk’ genotype; (ii) cases rigorously phenotyped so that few, if any, non-diseased subjects will have appeared as cases; (iii) a P-value threshold of 5 × 10⁻⁷; (iv) a case : control ratio of 2 : 3; (v) no phenotyping of controls so diseased subjects will have contaminated the controls to an extent determined solely by general population prevalence. On the basis of simulations that invoke all of these assumptions, Supplementary Figure S6 presents the precise equivalent to Figure 1, but uses the design parameters of the WTCCC. On the basis of their own simulation-based power calculations (incorporating errors consequent upon incomplete LD),¹⁴ the design team of the WTCCC estimated that its power would be ‘43% for alleles with a relative risk of 1.3, increasing to 80% for a relative risk of 1.5’.¹⁴ These power calculations were based on averaging across all MAFs > 0.05,¹⁴ and the design should, therefore, be underpowered for SNPs with an uncommon minor allele and to have more power than required for common SNPs.¹⁴ Our methods ([Supplementary Figure S6]) concur that for SNPs with a MAF in the range 0.2–0.5, the WTCCC design was well powered to detect heterozygote ORs¹⁴ of 1.3 or greater and that even ORs as low as 1.2 should have been detected with a non-negligible probability (power ∼9%). On the other hand, the power to detect rarer SNPs (MAF = 0.05–0.1) with ORs <1.5 should have been low. Without knowing which SNPs are truly associated with which complex disease, or how strong those associations might be, it is impossible to use the empirical evidence to precisely quantify how accurately our approach predicts the power of the WTCCC. But, the predicted power profile is certainly consistent with the results reported in Table 3 of the WTCCC paper.¹⁴ Three of the 19 SNPs they identified as having a ‘significant heterozygous OR’, had a MAF between 0.05 and 0.1 and these all had OR > 1.5. In contrast, 13 had a MAF between 0.2 and 0.5 and of these, four exhibited an OR < 1.3 (1.19–1.29), five an OR between 1.3 and 1.5 and four an OR > 1.5. SNPs with a rarer minor allele are typically most common,⁵⁷ and if power was not a substantial issue, one would have expected more ‘hits’ to arise in rare SNPs. It is true that the observed ORs would have been subject to the ‘winner's curse’,⁶⁹ but this does not detract from the consistency of the overall pattern that was found. As a second test of its validity, the ESPRESSO model was then used to estimate the power of the WTCCC to reconfirm the effect of 12 (non-HLA) loci that had been ‘previously robustly replicated’.¹⁴ On the basis of the published bioclinical characteristics of these 12 variants (Supplementary Table S5), our simulations predicted a 24% probability that all 12 would replicate and probabilities of 44, 26 and 6%, respectively, that 11, 10 or ≤9 would replicate. These predictions are closely consistent with the published WTCCC analysis in which 10 of the 12 actually replicated.¹⁴ Of course, these analyses provide no more than a rudimentary check of the calibration of our approach, nevertheless, it is encouraging that the predictions appear sensible and it would, therefore, seem reasonable to apply the methods to new problems, including those involving environmental as well as genetic determinants.

The fact that our power estimates appear consistent with those of the WTCCC team itself suggests that any additional elements of analytic complexity that were addressed by our methods had a limited impact on required sample size in this particular setting. Therefore, we explored the relative contribution to increased sample size requirement that was consequent upon those specific elements of our model that are not included in a conventional power calculation. Across an arbitrary, but not atypical, set of models incorporating a gene–environment interaction (see Supplementary materials, and Supplementary Table S6), it was found that it is a realistic level of error in assessing the environmental determinant that was most influential in inflating the required sample size. But, the WTCCC analysis focused solely on genetic main effects and so this was irrelevant. Furthermore, all cases in WTCCC were carefully phenotyped. Specificity was, therefore, close to 100% and very few, if any, healthy subjects would have appeared as cases (Supplementary materials and Supplementary Figures S2a and S2b). Finally, the sophisticated power calculations undertaken by WTCCC took appropriate account of error arising from incomplete LD, and so the only additional factor that did come into play in the WTCCC was heterogeneity in underlying disease risk—but, on its own, this has little impact (Supplementary Table S6).

Can biobanks ever be large enough? Although our methods are in accord with the power calculations undertaken by the WTCCC and suggest that it was appropriately powered to detect the effects that it set out to study, larger—sometimes much larger—sample sizes will be required (Figures 1 and 2) to reliably detect: (i) ORs at the lower end of the plausible range; (ii) SNP effects associated with rarer minor alleles; (iii) genotypic effects that are binary rather than multiplicative in nature; (iv) gene–environment (or, gene–gene) interactions or (v) aetiological effects in case series subject to less exhaustive phenotyping. If bioscience aims to rigorously investigate such effects, it will be necessary to design studies enrolling not thousands, but tens of thousands of cases. But, studies of such a size should not be contemplated unless relative risks ≤1.5 are really worth investigating. A central aim of modern bioscience is to understand the causal mechanisms underlying complex disease^{49,70 and each quantum of new knowledge has the potential to provide an important insight that may have a dramatic impact on disease prevention or management. This implies that scientific interest may logically focus on any causal association that can convincingly be identified and replicated—it need not be ‘strong’ by any statistical or epidemiological criterion. The fundamental need, therefore, is for research platforms to support analyses powered to detect plausible aetiological effects. But, what does this mean? The majority of genetic effects on chronic diseases that have so far been identified and replicated are characterized8,9,13–32 by allelic or genotypic relative risks of 1.5 or less—many in the range 1.1–1.3. Effect sizes may be greater for causal variants than for markers in LD, but it would be unwise to assume that the gain will necessarily be substantial. Although the search for ‘low hanging fruit’ must continue, therefore, we agree with Easton et al.22} that much of the future harvest will be rather higher up the tree. But, even if they are of scientific interest, can ORs ≤1.5 reliably be detected by any observational study? In 1995, Taubes argued that: ‘[observational epidemiological studies]… are so plagued with biases, uncertainties, and methodological weaknesses that they may be inherently incapable of accurately discerning … weak associations’.⁷¹ Fortunately, several of the central arguments underlying this bleak assessment do not hold in human genome epidemiology. Randomization at gamete formation renders simple phenotype–genotype associations robust to life style confounding and to uncertainty in the direction of causality—in other words, enhanced inferential rigour is a direct, but wholly fortuitous, consequence of what is often called Mendelian randomization.^70,72–74 At the same time, the increasing accuracy and precision of measurements in genome epidemiology^14,53,54 mean that—in the absence of intractable confounding and reverse causality—sufficient statistical power can realistically be accrued to draw meaningful inferences for small effect sizes. Despite important caveats,^70,73,75 therefore, small effects reflecting the direct impact of genetic determinants (main effects and gene–gene interactions) or the differential impact of genetic variants in diverse environmental backgrounds (gene–environment interactions) are more robust than their counterparts in traditional environmental epidemiology.

Finally, we note that the primary simulations that underpin our conclusions are all based on a case: control ratio of 1 : 4, while a 1 : 1 ratio was adopted in considering the ‘conventional’ power calculations (see above). Furthermore, most of the case–control studies that we reference (including the WTCCC) are based on ratios that are much closer to unity.^13–32 But this presentation was deliberate. Given access to a fixed number of cases and an unrestricted number of well-characterized controls, substantial additional power can be obtained using a design based on four or more controls per case (Supplementary Figure S1). In the future, the existence of massive population-based biobanks such as UK Biobank⁴⁸ and extensive sets of nationally representative controls (e.g. as in WTCCC¹⁴) will mean that designs based on multiple controls will be highly cost effective and will be widely used. It would, therefore, have been inappropriate to present power calculations based primarily on the 1 : 1 design as this would have increased the estimated sample size requirement, thereby strengthening our main message in a manner that could have been seen as misleading. On the other hand, in exploring the implications of conventional power calculations (see above), most contemporary work is based on designs with approximately equal number of cases and controls and it was, therefore, felt to be more intuitive for readers to focus on designs of this nature. For the sake of completeness, Supplementary Figures S7, S8a and S8b replicate Figures 1, 2A and B but use equal numbers of cases and controls.

To finish, we note that the basic conclusions we have reached are stark and may appear disheartening. But, pessimism is unwarranted. Disentangling the causal architecture of chronic diseases will be neither cheap nor easy and it would be unwise to assume otherwise. But it has the potential to return investment many-fold with future improvements in promoting health and combating disease. Therefore, it is encouraging that several international case–control consortia have already managed to amass sample sizes of the magnitude that is realistically required.^{16,19,22,26 Furthermore, the largest contemporary cohort-based initiatives48,49,51,52 will generate enough cases to study the commonest diseases in their own right (Figure 3). To take things further, three complementary strategies will markedly enhance the capacity to study plausible relative risks right across the spectrum of complex diseases: (i) improve the accuracy and precision of measurements and assessments;14,53,54 (ii) increase the size of individual studies and biobanks8} and (iii) harmonize protocols for information collection, processing and sharing^{10,46–49,70} (http://www.p3g.org). Taken together, these actions will provide for a powerful global research platform to drive forward our understanding of the causal architecture of the common chronic diseases. But, such a platform will be of little value unless power calculations are both accurate and realistic. It is our hope that this article and access to ESPRESSO will be viewed as providing valuable guidance to those setting up individual biobanks and designing the case–control analyses to be based upon them.

Supplementary data

Supplementary data are available on the P3G Observatory http://www.p3gobservatory.org.