The Malthusian parameter of ascents: What prevents the exponential increase of one’s ancestors?

Abstract

The reason that the indefinite exponential increase in the number of one’s ancestors does not take place is found in the law of sibling interference, which can be expressed by the following simple equation:

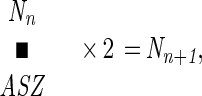where N_n is the number of ancestors in the nth generation, ASZ is the average sibling size of these ancestors, and N_n+1 is the number of ancestors in the next older generation (n + 1). Accordingly, the exponential increase in the number of one’s ancestors is an initial anomaly that occurs while ASZ remains at 1. Once ASZ begins to exceed 1, the rate of increase in the number of ancestors is progressively curtailed, falling further and further behind the exponential increase rate. Eventually, ASZ reaches 2, and at that point, the number of ancestors stops increasing for two generations. These two generations, named AN SA and AN SA + 1, are the most critical in the ancestry, for one’s ancestors at that point come to represent all the progeny-produced adults of the entire ancestral population. Thereafter, the fate of one’s ancestors becomes the fate of the entire population. If the population to which one belongs is a successful, slowly expanding one, the number of ancestors would slowly decline as you move toward the remote past. This is because ABZ would exceed 2. Only when ABZ is less than 2 would the number of ancestors increase beyond the AN SA and AN SA + 1 generations. Since the above is an indication of a failing population on the way to extinction, there had to be the previous AN SA involving a far greater number of individuals for such a population. Simulations indicated that for a member of a continuously successful population, the AN SA ancestors might have numbered as many as 5.2 million, the AN SA generation being the 28th generation in the past. However, because of the law of increasingly irrelevant remote ancestors, only a very small fraction of the AN SA ancestors would have left genetic traces in the genome of each descendant of today.

Because of the exponential nature of the increase in cell numbers after successive cell divisions, a microscopic fertilized egg in mammals grows into a fully formed newborn within a matter of weeks and months; 30 cell divisions yield about 1 billion (1,073,421,824) cells, and 40 cell divisions yield about 1 trillion (1,100,183,947,776) cells. It is a curious fact that in spite of the early concern about potential and actual population explosions, which was expressed by R. A. Fisher as the Malthusian parameter of population genetics (1), little attention has been paid to the potential for the equally exponential increase in the number of one’s ancestors. Inasmuch as it takes two to make one, this potential is present in all sexually reproducing organisms. Fig. 1 shows that as one looks into the past, the number of ancestors should increase exponentially with ascending generations in the exact same manner as the increase in cell numbers after successive cell divisions. With the length of a generation in our own species being 20 years, the number of our ancestors should have passed the 1 billion mark at the end of 14th century, which is 30 generations in the past. Although the worldwide combined human population of today passed the 6 billion mark in 1996, there is a little doubt that at 6 billion strong, human beings are very, very close to the upper limit of the earth’s carrying capacity. Yet, if we look back to 800 years ago, only 40 generations away, Fig. 1 shows that our ancestors should have numbered more than 1 trillion. Clearly something is amiss in Fig. 1.

Figure 1.

The unbridled exponential increase in one’s ancestors is illustrated from the 1st generation to the 50th generation from the present. Years from the present of pertinent generations are also indicated for our own species. Inserted at the bottom is the genealogical tree back to four generations of a product of the first-cousin mating. Ancestral siblings are shown as two thick vertical solid bars, whereas ancestors lost as a consequence are indicated by dotted lines.

On the other hand, we also know that each modern species had its predecessor and that predecessor had its own predecessor. Accordingly, the ancestry should transcend a successive speciation process. Thus, we are faced with a seemingly insurmountable dilemma. In the long term of millions of years, the number of our ancestors should be enormous, yet in the short term of hundreds of years, there should be far fewer ancestors than the exponential expectation indicates.

The Law of Sibling Interference

The only reason that the actual number of ancestors starts to fall behind the exponential expectation is the eventual inclusion of siblings (brothers and sisters) among one’s ancestors. Needless to say, in practice, half siblings sharing only one parent but not the others should also be considered. The same individual appearing in different positions (e.g., in the maternal and paternal halves) in the genealogical tree should also be treated as siblings. This principle is illustrated by the simplest example at the bottom of Fig. 1. In this example, one is a product of the first-cousin mating. Accordingly, two of the four grandparents are siblings of each other. As a consequence, the number of great-grandparents is reduced from the exponential expectation of eight to six. It was found that this principle of sibling interference can be expressed in the following simple equation:

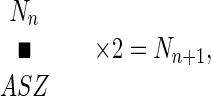where N_n is the number of ancestors in the nth generation in the past, ASZ is the average sibling size of these ancestors, and N_n+1 is the number of ancestors in the next older generation (n + 1). In the case of the first-cousin mating, the average sibling size among the four grand parents is 4/3, which is 1.3333. It follows that the number of great-grandparents should be 4/1.3333 × 2, which is 6.

It is apparent that how recently in one’s genealogy the sibling interference begins is entirely dependent upon the degree of the inbreeding in the past. At the very extreme of continuous brother–sister matings, the sibling interference begins in the parents and the number of ancestors remains at 2 for the duration in which consecutive brother–sister matings have been practiced. This is because 2/2 × 2 is still 2. Such an extreme of the inbreeding need not be a laboratory oddity, for it has been shown that cheetahs of South Africa are as inbred as any inbred strain of the laboratory mouse (2).

The AN SA Generation and the Effective Population Number

Once the sibling interference begins, it is expected that the average sibling size among the ancestors would steadily increase as we delve further back into ancestral generations of the more remote past. This is because, as the absolute numbers of ancestors increase, more and more siblings and half siblings would be included among the rank of ancestors. Instances of the same individual appearing in different branches of the ever-expanding genealogical tree should also increase. Inevitably, there would eventually be a generation at which the average sibling size reaches 2. The hallmark of this generation is that the number of ancestors of this generation and that of the generation immediately before it should remain exactly the same, for the simple reason that N_n/2 × 2, which is N_n+1, is still the same as N_n. The earlier of the two generations is defined as the AN SA generation and the older one as the AN SA + 1 generation. In this nomenclature, AN stands for ancestry, and SA stands for saturated. The above noted temporary halt in the number of ancestors is due to the inclusion of all the progeny-produced adults of the ancestral population as the ancestors. It follows that the number of the AN SA ancestors becomes an apparent equivalent of the effective population number in population genetics known as N_e (3). This equivalence, however, is more apparent than real. At the extreme of the inbreeding is a product of continuous brother–sister matings. For this type of individual, the number of ancestors at the AN SA generation is 2 for the duration of inbreeding as already noted. Yet, there are still several hundred progeny-producing cheetahs in the South Africa. Accordingly, N_e for the cheetah of the South Africa would be not 2 but several hundreds. Looking at this extreme, one realizes that there can be more than one AN SA generation for a species if not for a population. It has been stated that the cheetahs of South Africa went through two successive bottlenecks, and only the first one, occurring in the late Pleistocene some 10,000 years ago, affected the cheetah as a whole (2). It follows that the pre-Pleistocene cheetah must have had another AN SA generation, the AN SA ancestors of that time numbering far greater then 2.

Numbers of Ancestors in Generations Older than the AN SA + 1 Generation

As all the progeny-produced adults of the entire population came to be included in one’s ancestry at the AN SA generation, numbers of ancestors of all generations older than the AN SA + 1 too became all the progeny-produced adults of the entire population of each generation. Consequently, the steady increase in the numbers of ancestors in generations older than the AN SA also became a clear revelation of a failing population in which the average sibling size among the progeny-produced adults had fallen below 2. Such a population had been shrinking for sometime. It follows that the present AN SA was the secondary AN SA under this particular circumstance; therefore, there must have been a previous AN SA involving a far larger number of ancestors when that population enjoyed a greater success. This point was already made in connection with a product of successive brother–sister matings.

From the above, it becomes quite clear that if it was the primary AN SA of a reasonably successful population, the number of ancestors at the AN SA had to be very large, since even with a very moderate average progeny size of 2.033, the number of ancestors in the 12th generation before the AN SA would have fallen to 83% of the AN SA number. Shown in Fig. 2 is the one simulation depicting initial rise in the number of ancestors until the arrival of the AN SA and subsequent decline, under the following conditions. (i) The average sibling size among the ancestors became 1.01 at the 10th generation from the present when the ancestors numbered 1,024. (ii) Thereafter, there was an incremental increase of 0.01 per generation for 10 generations in the average sibling size. (iii) After reaching the average sibling size of 1.10 at the 19th generation into the past, the incremental increase became 0.1 per generation for the next 10 generations, thus, reaching the AN SA generation at the 28th generation from the present; for human beings, this generation falls in the middle of 15th century. (iv) After reaching the AN SA, the average sibling size for the ancestors of generations older than the AN SA stabilized at 2.033. As shown in Fig. 2, it would be noted that the AN SA ancestors at the 28th generation away from the present numbered roughly 5.2 million. This number is only 1% of the exponential expectation; nevertheless, it is large enough to indicate that this is the primary AN SA of a rather successful population that had steadily been expanding at a moderate rate of 1.0165 per generation until the AN SA.

Figure 2.

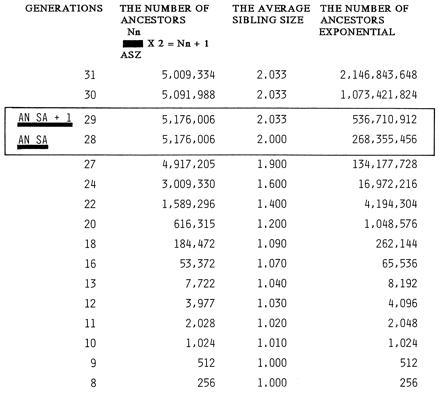
A particular simulation (under the specific conditions described in the text) of the rise and subsequent fall in the number of ancestors around the AN SA generation. This simulation is based upon the law of sibling interference and is compared with the simple, exponential increase in the number of ancestors. The AN SA and AN SA + 1 generations are boxed.

The Validity of One Universal Genealogical Myth

All the long-settled families in the Alsace region of France invariably include heroic Charlemagne of eighth century in their genealogical trees. Charlemagne, who was king of the Franks, later became emperor of all the Romans. Similarly, all the Japanese families of the Genji lineage include emperor Seiwa of ninth century as the most illustrious ancestor in their genealogies, whereas another emperor, Kanmu of eighth century, plays the same role in the genealogical trees of those belonging to the Heike lineage. Such a genealogical claim has traditionally been dismissed outright as an absurd fantasy borne of a wishful delusion. Quite to the contrary, this study reveals that unlike the N_e of population genetics, the number of ancestors at the AN SA generation was very large, probably numbering in the millions, and the ancestors of the AN SA and all generations previous to the AN SA included all the progeny-produced adults of the entire ancestral population. It follows that among them had to be all the local kings of the times. Not to be forgotten, however, are other ancestors of the times, for also included in the ancestry were murderers, thieves, embezzlers, prostitutes, and all other social misfits of the times.

The Law of Increasingly Irrelevant Remote Ancestors

The expression of “diluted blood” is frequently used to lament the ineptness of a descendant in comparison with his or her illustrious, but remote, ancestor. Indeed, as one’s ancestors fade into the remote past, there is an ever-increasing chance that they have become totally irrelevant in the genetic sense in that they left no trace in the genome of one of their descendants of today.

Individual genes of all eukaryotes can be placed as beads on a finite number of strings; this finite number is 23 in the case of our own species. Each chromosome (string), however, is not a heritable unit, since each becomes a mixture of segments derived from paternal and maternal grandparents due to crossovers after the chiasma formation during first meiosis of germ cells in both parents. Accordingly, the true unit of inheritance is a chromosomal segment of variable lengths produced by meiotic crossovers. In the case of humans as well as the mouse, the data suggest that a mean chiasma count at diakinesis is about 50 (4). Although crossovers might be a little more frequent in female germ cells than in male germ cells, such a small difference can be ignored for the present. It follows that, on average, each human individual inherits roughly 100 chromosomal segments from each of the two parents, a total of 200 segments. Assuming that each crossover occurs at random along the entire length of each chromosomal pair, the total number of chromosomal segments to be inherited from one’s grandparents is 400. It follows that at the maximum, only 4,000 ancestors of the 20th generation in the past left one tiny chromosomal segment each in a given individual genome of today. The simulation shown in Fig. 2 suggests that the actual number of ancestors 20 generations ago likely numbered 616,315. It follows that 4,000 ancestors amounted to only 0.65% of the total ancestors of 20 generations ago. Consequently, at least 98.7% of those ancestors became forever irrelevant, as they left no genetic trace in each of us today. However, relevance and irrelevance being more or less random affairs, of two overtly unrelated individuals of the same population today, the relevant 4,000 ancestors as a set of one is bound to be very different from those of the other. This might explain why overtly unrelated individuals of a fairly homogeneous population still display divergent phenotypes.