Characterization of the nucleation barriers for protein aggregation and amyloid formation

Abstract

Despite the complexity and the specificity of the amino acid code, a variety of peptides and proteins unrelated in sequence and function exhibit a common behavior and assemble into highly organized amyloid fibrils. The formation of such aggregates is often described by a nucleation and growth mechanism, in which the proteins involved also form intermediate oligomeric aggregates before they reorganize and grow into ordered fibrils with a characteristic cross-β structure. It is extremely difficult to experimentally obtain an accurate description of the early stages of this phenomenon due to the transient nature and structural heterogeneity of the oligomeric precursors. We investigate here the phenomenon of ordered aggregation by using the recently introduced tube model of polypeptide chains in conjunction with the generic hypothesis of amyloid formation. Under conditions where oligomer formation is a rare event—the most common conditions for forming amyloid fibrils by experiment—we calculate directly the nucleation barriers associated with oligomer formation and conversion into cross-β structure in order to reveal the nature of these species, determine the critical nuclei, and characterize their dependence on the hydrophobicity of the peptides and the thermodynamic parameters associated with aggregation and amyloid formation.

The assembly of proteins into highly ordered aggregates, known as amyloid fibrils, is a much-studied phenomenon because of its implications for human health (Chiti and Dobson, 2006; Lansbury and Lashuel, 2006; Teplow et al., 2006). A wide range of experimental strategies is currently being developed in order to improve our fundamental understanding of the molecular mechanisms leading to the formation of these aggregates (Rochet and Lansbury, 2000; Krishnan and Lindquist, 2005; Jahn and Radford, 2005; Chiti and Dobson, 2006). It is becoming possible to experimentally probe—with increasing molecular detail—the process of self-assembly, for example, by monitoring the formation of inter-residue contacts by fluorescence methods (Ban et al., 2004; Krishnan and Lindquist, 2005) or photoinduced cross linking (Lomakin and Teplow, 2006), and of β-sheet aggregates by isotope-edited infrared spectroscopy (Petty and Decatur, 2005) or by atomic force microscopy (Mastrangelo et al., 2006). Advances in kinetic techniques, including quasi-elastic light scattering spectroscopy (Lomakin and Teplow, 2006) and fluorescence methods (Bieschke et al., 2005), are also providing information about the mechanisms of fibril formation (Chiti et al., 2002), and about crucial parameters that characterize the dynamics of aggregation, such as the lag phase and the aggregation rate (Jarrett and Lansbury, 1993; Rochet and Lansbury, 2000; Serio et al., 2000; Lomakin and Teplow, 2006), which are difficult to measure experimentally because of the stochastic nature of the various processes involved, and the frequent heterogeneity of the products (Chiti and Dobson, 2006; Teplow et al., 2006).

In this paper, we approach such questions from a theoretical perspective (Thirumalai et al., 2003; Nguyen and Hall, 2004; Ma and Nussinov, 2006) and simulate the aggregation of polypeptide chains from their solvated state into fibrillar aggregates. Our choice of the model is guided by the “generic hypothesis” of amyloid formation (Dobson and Karplus, 1999), according to which the ability to assemble into ordered cross-β structures is not an unusual feature exhibited by a small group of peptides and proteins with special sequence or structural properties, but it is an inherent characteristic of polypeptide chains. Indeed, although amyloid fibril cores exhibit a characteristic cross-β structure, peptides and proteins in all major classes of native protein folds have been shown to be able to form amyloid assemblies (Fandrich et al., 2001; Fandrich and Dobson, 2002; Dobson, 2003; Ferguson et al., 2006). By adopting the view that the generic nature of the phenomenon of amyloid formation originates in the fundamental properties of polypeptide chains, in particular the ability of backbone groups to form hydrogen bonds and the mutual attraction of side-chain groups through hydrophobic and van der Waals interactions, we consider here a recently proposed tube-like representation of proteins (Hoang et al., 2004). The distinctive feature of this model (see “Materials and Methods”) is that the protein backbone is assigned a finite thickness to account for the volume occupied by the backbone atoms; the interactions between the different amino acids include pair-wise additive interaction and hydrogen bonding terms (Hoang et al., 2004).

In order to obtain insight into the process of amyloid formation, one strategy is to carry out all-atom molecular dynamics simulations in explicit water. Indeed, this approach has already been shown to provide a detailed understanding of the molecular events that lead to the aggregation of peptides and proteins (Hwang et al., 2004; Buchete et al., 2005; Cruz et al., 2005; Wu et al., 2005; Ma and Nussinov, 2006; Teplow et al., 2006; Nguyen et al., 2007). Powerful intermediate-resolution models have also provided the opportunity to study larger systems and longer timescales (Nguyen and Hall, 2004; Borreguero et al., 2005; Nguyen and Hall, 2006; Pellarin and Caflisch, 2006; Tozzini et al., 2006). However, since our goal is to identify the fundamental properties of polypeptide chains that are responsible for the process of amyloid formation, we study a model that specifically includes the factors that we have identified as the essential ones and ignore those shown not to be essential, such as a varying amino acid sequence (Fandrich and Dobson, 2002). Of course, simple models are unable to describe in detail the complex phenomenology associated with the different behavior of specific polypeptide chains, such as, for example the different propensities of mutant forms of peptides and proteins to form amyloid fibrils or oligomeric intermediates (Chiti et al., 2002), or their different toxicities in neurological disorders, such as Alzheimer’s, Parkinson’s, and Creutzfeldt–Jakob diseases (Conway et al., 2000). However, they should be able to play a crucial role in obtaining fundamental insights into the origin of the experimental observations of those aspects of the phenomenon of protein aggregation that are common to most of the peptides and proteins that have been analyzed. Examples include the existence of lag phases (Jarrett and Lansbury, 1993) and of a series of disordered oligomeric assemblies that appear prior to the formation of amyloid fibrils (Rochet and Lansbury, 2000; Serio et al., 2000).

It has also been suggested that other forces, in addition to those that we considered here, are important in the process of amyloid formation. In particular, according to the “steric-zipper hypothesis” (Nelson et al., 2005; Sawaya et al., 2007), the generic nature of amyloid formation is caused by the specific interdigitation of the side-chains of specific regions of the sequences of peptides and proteins. Since the length of these regions is quite short, ranging from four to seven residues, many polypeptide chains are likely to exhibit them; and hence be able to form amyloid structures. In principle, therefore, it should be possible to carry out calculations of simple models in which the generic nature of polypeptide chains is accounted for explicitly but in which more specific interactions are ignored.

In this paper, we report that the assumptions made to construct the tube model—which has been already shown to describe the variety of structures observed for native states of proteins (Hoang et al., 2004)—are able to reproduce the experimental result that sequences of identical residues can self-assemble into the cross-β structure and can also generate results consistent with the common observations of the presence of lag phases (Jarrett and Lansbury, 1993) and disordered oligomeric assemblies (Rochet and Lansbury, 2000; Serio et al., 2000) in protein aggregation. The simplicity of the tube model provides us with the opportunity to investigate through computer simulations the universal features of the phenomenon of amyloid formation under conditions where it is a rare event, which is the most common case in experiments. We directly calculate the nucleation barriers involved in the aggregation of peptides and proteins into the characteristic cross-β structure of amyloid fibrils, and show how these barriers can be used to rationalize the appearance of recurrent behaviors during the assembly process.

RESULTS

A two-step condensation-ordering mechanism

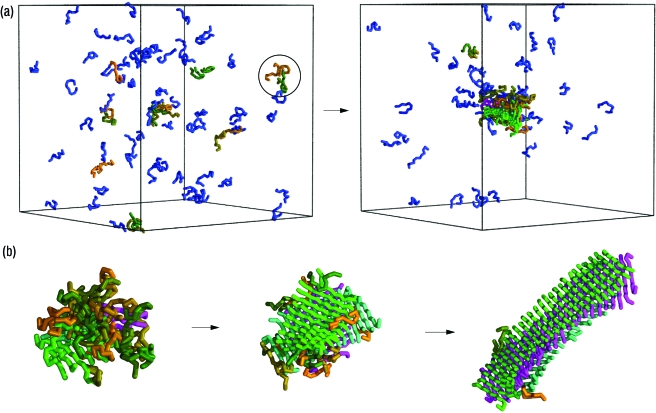
We first performed numerical simulations to investigate the self-assembly of a system consisting of 80 12-residue peptide molecules with an α-helical native state, which we use as a prototype to understand the nucleation events associated with protein aggregation and that enables us to investigate the competition between folding and aggregation. This type of system is known to form spontaneously amyloid fibrils both experimentally (Blondelle et al., 1997; Fandrich and Dobson, 2002; Kammerer et al., 2004; Giri et al., 2007), and computationally (Ma and Nussinov, 2002; Nguyen and Hall, 2006). Our results are consistent with a two-step condensation-ordering mechanism in which the polypeptide chains first come together (the “condensation step”) from their solvated phase into a disordered oligomer [Fig. 1(a), Supplementary animations], and subsequently transform (the “ordering step”) into a cross-β structure characteristic of amyloid fibrils [Fig. 1b]. The existence of such a two-step mechanism, which has also been referred to as “nucleated conformational conversion” (Serio et al., 2000), has been suggested from experimental (Serio et al., 2000; Chiti and Dobson, 2006) and theoretical studies (Nguyen and Hall, 2004; Pellarin and Caflisch, 2006; Ma and Nussinov, 2006). Here we show that the properties of excluded volume, hydrogen bonding, and hydrophobicity are sufficient as driving forces to produce this behavior. We then investigated the dependence of the two-step condensation-ordering transition on temperature, concentration, and the hydrophobicity of the peptides. Lowering the temperatures leads to a more rapid condensation of the initial monomeric polypeptide chains into oligomers, and their structure is initially formed by rather native-like monomers. At even lower temperatures, the peptides remain trapped in oligomeric configurations that do not transform into β-sheet rich structures on the timescale of the simulations [Supplementary Fig. 6(a)]. By contrast, we find that high temperatures disfavor the formation of oligomers, and the individual polypeptide chains remain fully solvated [Supplementary Fig. 6(b)]. Our simulations at different peptide concentrations reveal the existence of a critical concentration above which oligomers form without nucleation (Supplementary Fig. 7), as for the case shown in Fig. 1. Furthermore, lowering the hydrophobicity of the peptides disfavors the formation of oligomers, so that they do not form spontaneously. However, once a β-sheet seed is introduced into the system, it grows without the formation of oligomers (Supplementary Fig. 8). Taken together, these results indicate the existence of substantial nucleation barriers for both the formation of oligomers and their subsequent ordering into cross-β structures.

Figure 1. Illustration of the condensation-ordering mechanism of amyloid formation.

The calculations are carried out at concentration c=12.5 mM and temperature T^*=0.66 using the method described in the text. The ratio of the energies to form one hydrogen bond and one hydrophobic contact is e_HB∕e_HP=20. (a) Initially, at t⩽3,000, the peptides are in a solvated state (left). As the simulation progresses, at t=6,000, a small disordered oligomer appears (right). Here the progress variable t is the number of Monte Carlo moves performed in the simulation, and one unit of t is a block of 10⁵ Monte Carlo moves. The color code is such that peptides that do not form interchain hydrogen bonds are shown in blue, those with interchain hydrogen bonds are assigned a random color, as for example the peptides indicated by the circle in the left figure. Peptides within the same β-sheet are assigned the same color. (b) Conversion of a disordered oligomer into an amyloidlike structure during the simulation: t=6,000 (left), t=9,000 (middle), t=15,000 (right).

Nucleation barriers

In order to calculate the nucleation barriers associated with this two-step mechanism, we adopt two progress variables. To describe the formation of oligomers we use n, the number of polypeptide chains that comprise them, and to describe the formation of β-sheets we use m, the total number of intermolecular hydrogen bonds. As the timescale for the observation of a nucleation event is usually much longer than the timescale of the microscopic dynamics of the system, we used an enhanced Monte Carlo sampling method that enables us to directly calculate the barriers associated with the formation of the critical nuclei (ten Wolde et al., 1995; Auer and Frenkel, 2001) (see “Materials and Methods”).

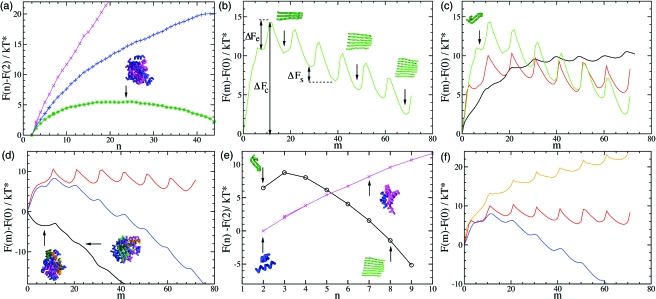
We first calculated the nucleation barrier F(n) for the formation of disordered oligomers. In order to avoid the correlations between the nucleation barrier for oligomer formation and the nucleation barrier for β-sheet formation, we performed the calculations at a temperature below the midpoint of folding so that the peptides do not transform spontaneously into β-sheet structures [see also Supplementary Fig. 6(a)]. The shape of the resulting barrier [Fig. 2a] is typical for the formation of a spherical nucleus in a supersaturated system (Kelton, 1961). Its existence can be explained by the competition between the free energy loss in forming an interface between the oligomeric aggregates and the solution containing monomeric polypeptide chains, and the free energy gain when a polypeptide chain is transferred from its solvated state into the oligomer. At small oligomer sizes, n<n_c, where n_c is the number of molecules in the oligomer corresponding to the highest free energy, the surface term dominates (as a result of their small volume-to-surface ratios) and the free energy increases; by contrast for larger oligomer sizes, n>n_c, (corresponding to large volume-to-surface ratios) the bulk term dominates, and the free energy decreases. An oligomer of critical size, n_c, is shown in Fig. 2a. As shown in the figure, an increase in concentration lowers the nucleation barrier, and at the concentration where we investigated the self-assembly of the peptides (Fig. 1), it is vanishingly small.

Figure 2. Direct calculation of the free energy barriers associated with amyloid formation.

(a) Free energy barriers for the formation of an oligomer as a function of n (the number of peptides). The calculations are carried out at a temperature T^*=0.51 and at concentrations c=1.2 mM (magenta), c=4.9 mM (blue), c=6.7 mM (green). The ratio of the energies to form one hydrogen bond and one hydrophobic contact is e_HB∕e_HP=20. (b) Free energy barrier for the formation of a β-sheet as a function of m (the number of interchain hydrogen bonds) calculated at c=4.9 mM, T^*=0.45, and e_HB∕e_HP=50. The configurations shown in the figure illustrate the relationship between the free energy barrier and the size of the β-strands. (c) Temperature dependence of the free energy barrier shown panel (b); results are shown for T^*=0.6 (black), T^*=0.51 (red), and T^*=0.45 (green). (d) Free energy barriers at three different polypeptide concentrations c=1.2 mM (red), c=4.9 mM (blue), c>6.7 mM (black) at T^*=0.51, and e_HB∕e_HP=20 (e) Comparison of the free energy barriers obtained for the formations of oligomers (magenta) and β-sheets (black) at T^*=0.51, c=1.2 mM, and e_HB∕e_HP=20. (f) Free energy as a function of hydrophobicity: e_HB∕e_HP=−20 (yellow), e_HB∕e_HP=50 (red), and e_HB∕e_HP=20 (blue) at T^*=0.51, and c=4.9 mM.

To calculate the nucleation barrier F(m) for β-sheet formation we considered conditions, such as low concentration or weak hydrophobicity, under which disordered oligomers do not form spontaneously. We found that the nucleation barrier for aggregation in these cases consists of a series of local maxima and minima [Fig. 2b]. In its helical native state, each polypeptide chain forms nine intramolecular local hydrogen bonds; instead, a dimer in an extended β-structure can at most form ten intermolecular hydrogen bonds. The maxima in F(n) appear every ten intermolecular hydrogen bonds, each corresponding to the attachment of a single polypeptide to the growing β-sheet structure. Once the first of the ten intermolecular hydrogen bonds is formed, the free energy of the aggregate decreases until the new polypeptide chain forms an optimal set of eight intermolecular hydrogen bonds with the existing aggregate; polypeptide chains form eight rather than ten intermolecular hydrogen bonds because entropy favors flexible β-sheets. Since the formation of a β-sheet involves the growth of an essentially linear structure, and hence the surface-to-volume ratio is essentially constánt, the existence of a nucleation barrier for β-sheet formation cannot be explained by the competition between a surface and a bulk free energy term, as in the case of the nucleation barrier for the formation of oligomers. By contrast, in this case, the existence of the nucleation barrier is caused by the free energy changes associated with the configurational transitions that polypeptide chains undergo when they attach to the cross-β aggregate.

In this particular case, the highest free energy point is at m_c=11, indicating that the critical nucleus consists of three polypeptide chains (n_c=3) and its free energy of formation is ΔF_c. In the growth regime, where the number of polypeptide chains in the β-sheet is larger than the critical size (n>n_c) the attachment of each new polypeptide chain always requires the same amount of free energy; the system first needs to overcome the barrier for elongation ΔF_e, before it can gain the free energy ΔF_s, as the β-sheet grows from size n to size n+1. The relatively small value of ΔF_s is consistent with the observation that growth is reversible (Carulla et al., 2005) and that fibrils are prone to fragmentation (Tanaka et al., 2006), as the overall downhill slope of the free energy of elongation is small.

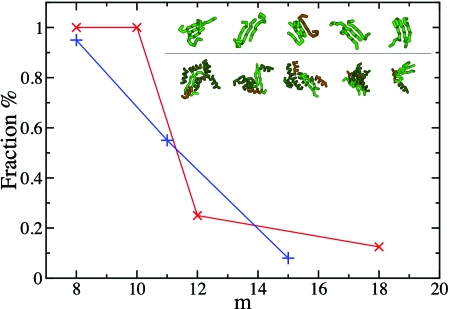
To verify these estimates of n_c and m_c, we determined the probability of growth of putative critical conformations. Conformations for which this probability is about 50% are identified as the critical nuclei (Fig. 3). These structures show how critical nuclei are formed by relatively heterogeneous conformations of trimers (top row in the inset in Fig. 3) or multimers (bottom row in the inset in Fig. 3), characterized by m_c=10 or 11. Critical nuclei of size n_c ranging from two to four have been observed experimentally (Wright et al., 2005; Nelson et al., 2005), and the identification of the structures of such species is a central result of this work.

Figure 3. Determination of the critical nuclei for β-sheet formation.

At different values of m, which is the number of interchain hydrogen bonds, we created an ensemble of up to 20 independent putative configurations for the nuclei and performed unbiased Monte Carlo simulations in order to measure the fraction of configurations that grow or shrink. Results are shown for c=4.9 mM, T^*=0.45, and e_HB∕e_HP=50 (blue symbols), and for c=6.7 mM, T^*=0.51, e_HB∕e_HP=20 (red symbols), which correspond to the nucleation barriers shown in Fig. 2c (green) and Fig. 2d (black) respectively; in the latter case, the polypeptide chains collapse into a disordered oligomer. (Inset) Gallery of nuclei comprising a number m of interchain hydrogen bonds close to the critical value for β-sheet formation; (top row) e_HB∕e_HP=50, m=10, and (bottom row) e_HB∕e_HP=20, m=11.

In Fig. 2c, we illustrate the effect of temperature on the stability of β-sheet aggregates. We note that a temperature decrease stabilizes larger oligomers relative to smaller ones, as ΔF_s decreases. Lowering the temperature also increases the free energy of formation of a critical nucleus, ΔF_c, as well as the barrier for elongation ΔF_e. We also found that in simulations in which small β-sheets were introduced as seeds, β-sheets can grow under conditions where they do not form spontaneously, and that the growth of the β-sheet is slowed down at lower temperatures (Supplementary Fig. 8), as we expect from our calculations of the free energy barrier. This competition between the increase in the stability of the β-sheet and the increase in ΔF_c and ΔF_e is an important factor in finding an ideal temperature for fibril formation.

The concentration dependence of the nucleation barriers for the formation of disordered oligomers is illustrated in Fig. 2d. At low concentrations, we observe the formation of cross-β structures without the previous condensation of disordered oligomers; in this case, the free energy barrier for the formation of disordered oligomers is very high. By contrast, at high concentrations there is no nucleation barrier to form a disordered oligomer, while the nucleation barrier for β-sheet formation remains. The transformation of the disordered oligomer into a fibrillar structure takes place through the formation of a critical nucleus within the oligomer, in this case a dimer, which subsequently grows into a β-sheet by a reorganization process involving a step-by-step elongation. This behavior suggests that under these conditions the direct pathway of formation of cross-β structures is in competition with the pathway in which disordered oligomers are formed first, and that the formation of the oligomer almost eliminates the barrier for fibril elongation.

In Fig. 2e, we compare the nucleation barriers for the formation of a β-sheet and a disordered oligomer at low concentration. Even though the formation of a β-sheet initially requires more free energy than the formation of a disordered oligomer, for sizes n>4 its free energy becomes lower and a β-sheet can grow; whereas the disordered oligomer cannot. We also investigated the effect on the nucleation barrier for β-sheet formation of changes in the hydrophobicity. Our results, summarized in Fig. 2f, indicate that for the range of hydrophobicities we investigated, the free energy barriers ΔF_c, ΔF_e, and ΔF_s decrease with increasing hydrophobicity.

A unified framework for protein aggregation and amyloid formation

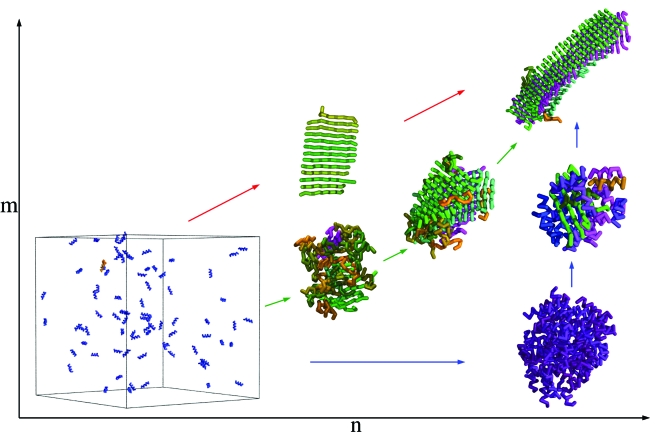
Taken together, our results indicate that the nucleation barrier for oligomer formation can be explained by the balance between the surface and the bulk free energies, whereas the nucleation barrier for β-sheet formation is essentially caused by the conformational changes of individual polypeptide chains associated with their attachment to the growing cross-β structure. The two-step condensation-ordering mechanism underlying this particular combination of free energy barriers provides a conceptual framework (Fig. 4) that encompasses various mechanisms of protein aggregation and amyloid formation put forward on the basis of experimental data for specific systems (Serio et al., 2000; Chiti and Dobson, 2006). From our simulations we observe that at low concentrations or weak hydrophobicity, the formation of fibrillar structures does not proceed via the formation of disordered oligomeric precursors, but rather the polypeptide chains convert directly into β-sheet structures, as also observed experimentally (Nelson et al., 2005; Gosal et al., 2005; Tanaka et al., 2006) and computationally (Nguyen and Hall, 2004; Pellarin and Caflisch, 2006). With increasing concentrations, the formation of disordered oligomers becomes increasingly favorable, but their structural properties are strongly temperature dependent. Below their unfolding temperature, individual polypeptide chains within the oligomers remain substantially folded. By contrast, with increasing temperatures, the fraction of unfolded polypeptide chains increases, and the oligomers become more disordered. These results are consistent with the experimental observation that aggregation of soluble proteins involves either the initial population of partially unfolded states prior to oligomer formation (Serio et al., 2000; Lomakin and Teplow, 2006; Bader et al., 2006), or, perhaps less frequently, via the formation of nativelike oligomeric intermediates (Plakoutsi et al., 2005).

Figure 4. Schematic illustration of the condensation-ordering mechanism for polypeptide aggregation and amyloid formation.

The use of the progress variables n and m enables visualization of the competition between the initial condensation of polypeptide chains and their subsequent ordering into hydrogen-bonded cross-β structures. Different trajectories in the (n,m) space can be realized by variations of temperature, concentration, or the hydrophobicity of the polypeptide chains. Weakly hydrophobic polypeptide chains and even more hydrophobic ones at low concentrations aggregate directly into β-sheet structures (red arrows); this one-step process is a limiting case of the condensation-ordering mechanism. By contrast, hydrophobic polypeptide chains at higher concentrations form first oligomers (blue and green arrows), whose structure depends strongly on the temperature. At temperatures below their folding temperature, polypeptide chains are highly nativelike in the oligomer (blue arrows). An increase in the temperature leads to more disordered oligomers (green arrows). The colors are chosen as described in Fig. 1.

Kinetic implications

We have investigated the effects of the free energy barriers that we calculated on the kinetics of fibril formation. We use classical nucleation theory (CNT) (Kelton, 1991) to express the steady-state nucleation rate I_S and the lag time θ in terms of a nucleation barrier and a growth rate. As we have noted that the formation of β-rich aggregates is a two-step process, we write the steady-state nucleation rate as (Frenkel and Schilling, 2002)

$$I_S=\kappa \exp [-\beta \mathrm{\Delta }{F}_c]\{1-\exp \left(\beta \mathrm{\Delta }{F}_s\right)\},$$ (1)

where κ is a kinetic prefactor. Note that κ is proportional to the elongation rate, $\kappa \sim k_e^{+}$, which itself is proportional to the barrier for elongation (Frenkel and Schilling, 2002), $k_e^{+}\sim \exp [-\beta \Delta F_e]$. Furthermore, CNT also provides an expression for the time dependence of the total number of nuclei formed in the system, N(t) and, for simplicity, we employed the expression in the limit of long times (Kashchiev, 1969), i.e.,

$$N\left(t\right)=I_S(t-\theta ),t⪢\theta ,$$ (2)

where

$$\theta \sim 1∕k_c^{+}$$ (3)

is the transient time (lag phase). This transient time is inversely proportional to the rate of attachment of polypeptide chains to the critical nucleus, which itself depends exponentially on the barrier for elongation: $k_c^{+}\sim \exp (-\beta \Delta F_e)$. The latter results can be rationalized through the structures that we have determined to represent the critical nuclei [Fig. 2c], since they reveal that polypeptide chains can attach to a nucleus or to an elongating filament only by adopting a β-strand conformation. The important result of this analysis is that it reveals that the existence of a barrier for fibril elongation, ΔF_e, modulates exponentially the amplitude of the steady-state nucleation rate, I_S, and the length of the lag phase, θ.

Quantitative experimental estimates of θ and I_S have been obtained by time-resolved optical experiments that measure the fluorescence signal arising from the binding of dye molecules, notably congo red or thioflavin T, that bind to protein aggregates (Ban et al., 2004; Krishnan and Lindquist, 2005; Bieschke et al., 2005). In Fig. 5, we show a schematic plot of this type of measurement and discuss its relationship to the total number of nuclei, N(t), that form in solution. The inset of this figure illustrates how even small variations in ΔF_e can dramatically affect the time dependence of N(t). Furthemore, by using Eqs. 1, 2, 3, we can relate the results of our simulations for the nucleation barrier as a function of temperature and concentration to N(t). The barrier for amyloid fibril elongation has been measured experimentally for Aβ(1-40) at 300 K by using quasi-elastic light scattering resulting in an estimate of 7 kcal∕mol (Kusumoto et al., 1998), a number close to those that we report in Fig. 2. More recently, equilibrium measurements have provided an estimate of the change upon mutation in the free energy difference between two successive states during elongation (Williams et al., 2006). Furthermore, a quartz crystal oscillator was used to measure the nucleation barrier for fibril elongation as a function of protein and denaturant concentration, and temperature (Knowles et al., 2007). Our results provide a theoretical framework to obtain further insight into the results of these experiments.

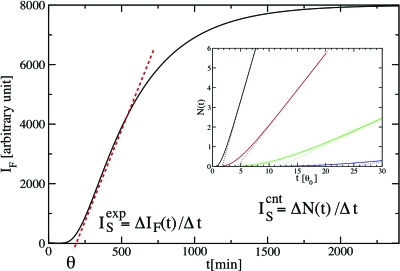
Figure 5. Schematic plot of a fluorescence signal.

Initially, for times t smaller than a transient time θ, called the lag time, no fibrils are observed. After θ, the fluorescence signal I_F increases with time and flattens out at later times because of the decrease of the concentration of proteins in the solution. The aggregation rate is usually taken to be the slope of I_F in the linear regime: $I_S^{\exp }=\Delta I_F\left(t\right)∕\Delta t$ (indicated by the red dashed line), and the lag time θ is determined by the extrapolation to zero of the red dashed line. In the inset, we illustrate the effect of a change in the barrier for elongation on the total number of oligomers, N(t), formed in the solution. The solid lines are based on the analytical expression of Kashchiev (1969) and the dashed lines describe their long-time behavior based on Eq. 2. The values for the barriers for elongation are: ΔF_e∕kT^*=0 (black), 1 (red), 2 (green), and 3 (blue), while all other parameters are unchanged. The unit time is set to be the lag time θ₀ for ΔF_e=0. In CNT, the steady-state nucleation rate is defined by: $I_S^{CNT}=\Delta N\left(t\right)∕\Delta t$, and $I_S^{CNT}$ and θ are determined, as in the experimental case, by the slope of the red dashed line and its extrapolation to zero, respectively. Hence, $I_S^{\exp }$ and $I_S^{CNT}$ can be compared qualitatively.

CONCLUSIONS

We have used computer simulations to investigate the origin of the common behavior observed experimentally in the aggregation of peptides and proteins, which include the recurrent appearance of lag phases and disordered oligomeric intermediates. By adopting the hypothesis that these widespread observations arise from fundamental properties of peptide and proteins, we have carried out calculations in which polypeptide chains are represented as self-avoiding tubes capable of forming highly directional hydrogen bonds and nonspecific hydrophobic interactions. Our calculations show that the interplay between these two forces results in a commonly observed two-step condensation-ordering mechanism in which disordered oligomeric aggregates are formed first and then reorganize into well organized amyloid fibrils. The specific shape that we calculate for the free energy barriers associated with this two-step mechanism provides a rationalization of the universal features that characterize the aggregation of proteins in terms of the fundamental interactions that they experience, thus revealing a better insight into the origin of the generic hypothesis of amyloid formation.

MATERIALS AND METHODS

Description of the model

In the model that we used, a polypeptide chain is represented by a tube (Hoang et al., 2004) in which the position of each residue is specified by the coordinates of its C_α atom. Neighboring atoms are connected in a chain (the protein backbone) with a fixed distance of 3.8 Å. In the original description of the model (Hoang et al., 2004), the finite thickness of the chain was imposed by requiring the radius of the circle drawn through any three C_α atoms to be larger than 2.5 Å. Here, we take the computationally efficient approach of considering the lines joining the C_α atoms to be the axes of hard spherocylinders (cylinders capped by hemispheres) of diameter 4 Å. Spherocylinders that do not share a C_α atom are not allowed to interpenetrate. Bond angles are restricted to the range of 82°–148°, and bending stiffness is introduced by an energetic penalty of e_S>0 for angles less than 107.15°; these are the same criteria used by Hoang et al. (2004). Hydrophobicity enters through a pairwise-additive interaction energy of e_HP (positive or negative) between any pair of residues i and j>i+2 that approach closer than 7.5 Å.

The cylindrical symmetry of the tube is broken by hydrogen bonds. A hydrogen bond has energy e_HB<0 and is considered to be present between two residues when the two normal vectors defined by each C_α atom and its two neighbors are mutually aligned to within 37°, and at the same time each of these vectors lies within 20° of the vector joining the C_α atoms. These geometrical requirements were deduced (Hoang et al., 2004) from a study of native protein structures. There is also a distance criterion, which is different for local hydrogen bonds (between residues i and j=i+3), and nonlocal (j>i+4) hydrogen bonds. No more than two hydrogen bonds per residue are permitted, and the first and last C_α atom cannot form interchain hydrogen bonds. Hydrogen bonds may form cooperatively (Tsemekhman et al., 2007) between residues (i,j) and (i+1,j+1), thereby gaining an additional energy of 0.3e_HB. For details of the distance and angle criteria, the reader is referred to Table 1 of Hoang et al. (2004).

To set the energy scale of the model, the energy of a hydrogen bond is fixed in all simulations at e_HB=−3kT_o, where kT_o is a reference thermal energy and k is Boltzmann’s constant. This value is chosen to reproduce the experimental value of the hydrogen bond interactions in proteins, which is of about 1.5 kcal∕mol at room temperature (Fersht et al., 1985). Values of the hydrophobicity and stiffness parameters e_HP and e_S are given in units of kT_o and the reduced temperature is T^*=T∕T_o. In all our simulations, we set e_S=0.9, whereas the hydrophobicity can be either e_HP=−0.06 or e_HP=−0.15. (To investigate the effect of hydrophobicity, we also simulated a hydrophilic system e_HP=0.15.) We investigated the effect of the ratio of a hydrogen bonding energy to hydrophobic energy e_HB∕e_HP on the two-step condensation-ordering transition and the nucleation barriers. Values in the region of e_HB∕e_HP=20, which we used here, are commonly used to simulate protein (Nguyen and Hall, 2004). As the number of hydrophobic contacts within an oligomer is usually about one order of magnitude larger than the number of hydrogen bonds, these interactions contribute equally to the potential energy of the system.

Simulation techniques

In the simulations that we carried out to characterize the two-step condensation-ordering transition for the formation of cross-β structures (Fig. 1), we performed Monte Carlo simulations using crankshaft, pivot, reptation, displacement, and rotation moves (Frenkel and Smit, 1996). Furthermore, we used a cubic box and applied periodic boundary conditions.

To calculate the probabilities P(n) and P(m), we performed Monte Carlo simulations with the sets of moves mentioned above. The corresponding nucleation barriers for oligomer formation and β-sheet formation are given by F(n)=F₀−kT^*ln[P(n)] and F(m)=F₀−kT^*ln[P(m)], respectively. Here F₀ is an arbitrary reference free energy, k is Boltzmann’s constant, and T^* is the reduced temperature. To enhance the sampling for larger values of n and m, we used the umbrella sampling technique (Frenkel and Smit, 1996) where we included an additional parabolic biasing potential, W=α(n−n₀)² for n, and W=α(m−m₀)² for m, in the energy function. Here α=0.25 is a constant, and n₀ and m₀ determine the ranges of n and m values, respectively, which are sampled in the simulation. The calculations of P(n) and P(m) were split into a number of smaller calculations, where each simulation was restricted to sample only a small range of different n and m values. We used the sequence n₀=5,10,15,20,25,30,… (m₀=3,5,8,10,13,15,…), and we performed at least 8×10⁸ Monte Carlo moves in each simulation. All free energy calculations were finally combined into one free energy landscape by the multihistogram technique (Frenkel and Smit, 1996). In our calculations of P(m) we used 48 polypeptide chains, and in the calculations of P(n) we used 512 polypeptide chains. In order to make the latter case computationally possible we did not perform crankshaft and pivot moves in these simulations and, as a consequence, all polypeptide chains remained in their helical native state. This choice is justified as the temperature we use in the calculation is below the folding temperature such that they remain folded in their native helical state during the simulation. The method of calculation of the nucleation barriers is similar to that used in calculations of crystal nucleation in colloidal suspensions (Auer and Frenkel, 2001).