The subtle benefits of being promiscuous: adaptive evolution potentiated by enzyme promiscuity

Abstract

In this commentary we discuss recent progress in our understanding of adaptive protein evolution. We begin with a general introduction to proteins and their evolution, quickly focusing on the question of how natural selection produces proteins with novel functions. We then summarize the theory of latent protein adaptation advanced by the joint articles by Amitai et al. (2007), HFSP J. 1, 67–78 and Wroe et al. (2007) HFSP J. 1, 79–87, published in the first issue edition of the HFSP Journal. This theory provides a biophysical framework linking the effects of individual mutations on promiscuous protein function, neutral genetic drift, and gene duplication to the process of adaptive protein evolution.

Proteins are, from one prospective, extremely simple molecules; each protein is a linear heteropolymer of amino acids, which share a common molecular backbone but differ in their variant side-chain configurations (Creighton, 1993). Despite their simplicity, however, proteins are among the most versatile and flexible molecules around. It appears that proteins composed of right combination and ordering amino acids can catalyze just about any chemical reaction, assemble to make any conceivable molecular machine, or comprise substances with any desirable property (Branden and Tooze, 1999).

Moreover, the exact amino acid sequence of a protein is determined by instructions encoded at the protein’s gene sequence (Creighton, 1993). This gene sequence, written in the DNA alphabet of As, Gs, Cs, and Ts, is transcribed and translated by a complex set of machines—themselves mostly proteins—into a linear chain of amino acids. This chain then folds into a compact molecule with a highly specific three-dimensional structure. The position of each atom in this structure, plus their collective motions, determines the properties of the protein.

Just as with all life on Earth, the currently extant proteins are evolutionarily related to one another. Though the details remain unclear, at some point in the past there were only a handful of “simple” peptides that over billions of years diversified into the millions of contemporary, distinct protein sequences (Ranea et al., 2006; Woese, 1998; Woese, 1987). So not only can one accomplish anything as a protein, any arbitrary protein can evolve into any other protein through a series of functional intermediates. Protein evolution is analogous to being able to, given enough time and the right encouragement, transform your toaster into a watch, a laptop, or a Formula-1 racecar.

The evolutionary relationships among proteins across all organisms are themselves highly structured. By comparing their amino acid sequences, proteins can be grouped into closely related families, where members exhibit highly similar structures and functions despite their different sequences (Branden and Tooze, 1999). The PFam database of protein families contains nearly 9000 families that collectively cover nearly three-quarters of all known protein sequences (Bateman et al., 2004). Such databases have provided us with very detailed knowledge of the medium- and long-term patterns of protein evolution. Among the most celebrated and controversial observations is that sequences within a protein family accumulate mutations at an approximately constant rate over time (Kimura, 1983; Zuckerkandl and Pauling, 1965). Indeed, this clock-like rate of protein evolution argues forcefully and convincingly for a neutral theory of molecular evolution, which holds that the fixation of random, neutral mutations accounts for the vast majority of the sequence differences among proteins (Kimura, 1983).

Our current understanding of protein evolution does not address, in this author’s opinion, the really exciting properties of proteins. On one hand, we know quite a lot about the process of divergence within functional conserved protein families. But in large part, proteins are fascinating because they are functionally diverse. And due to their common heritage, this functional diversity implies that evolution readily derives novel functions from existing proteins. Moreover, the process of adaptation—the movement of a population of organisms toward a phenotype that best fits its present environment (Fisher, 1930; Orr, 2005)—is often associated with functional changes in its proteins, such as resistance evolution in human pathogens (Mellinghoff and Sawyers, 2002; Richman, 2001; Walsh, 2003), catabolism of environmental pollutants in bacteria (Wackett, 2004), and even laboratory evolution of viruses and bacteria to novel environmental conditions, hosts, or carbon sources (Elena and Lenski, 2003).

We know surprisingly little about the molecular details of the processes that drive adaptive protein evolution, especially when considered relative to our quite advanced understanding of the process of neutral evolution (Orr, 2005). This situation is due in part to the experimental challenge of studying rare adaptive substitutions (Bull and Otto, 2005; Gillespie, 1991; Kimura and Ota, 1974), though a traditional bias against studying adaptive substitutions in evolutionary genetics also plays a role (Orr, 2005). Fortunately, several parallel lines of research have begun to tackle the problems of adaptation in general and adaptive protein evolution in particular using techniques from population genetics to protein chemistry. A series of pioneering theoretical and experimental studies on the process of adaptation itself provided some of the first expectations on the number and magnitude of steps during adaptive walks (Orr, 1998; Orr, 2003; Rokyta et al., 2005). Directed enzyme evolution has yielded significant insights into the constraints, or lack thereof, on protein functions (Arnold et al., 2001). Genetic engineering has enabled researchers to selectively add and remove mutations separating gene sequences to study the properties of mutational intermediates, in essence reconstructing the transiently occupied alleles on adaptive walks (DePristo et al., 2007; Lunzer et al., 2005; Weinreich et al., 2006; Zhu et al., 2005). Studies of simple protein models and RNA structures have shown that sequence space is itself a highly organized and richly interconnected network of neutral and functional sequences (Bastolla et al., 1999; Deeds and Shakhnovich, 2007; Fontana and Schuster, 1998; Li et al., 1996; Stadler et al., 2001).

One major outstanding question about adaptive protein evolution follows from the observation that since each protein already carries out some function, how can a protein suddenly gain a novel function without sacrificing the old one? For enzymes, this problem is particularly clear; if some protein is optimized to catalyze reaction a, then surely mutations that improve the catalysis of reaction b reduce performance with respect to a. Isopropylmalate dehydrogenase provides an excellent example of such a functional trade-off. Only six mutations are needed to switch coenzymes specificity between nicotinamide adenine dinucleotide and nicotinamide adenine dinucleotide phosphate, but none of the 512 examined sequence combinations perform well with both coenzymes (Lunzer et al., 2005; Miller et al., 2006).

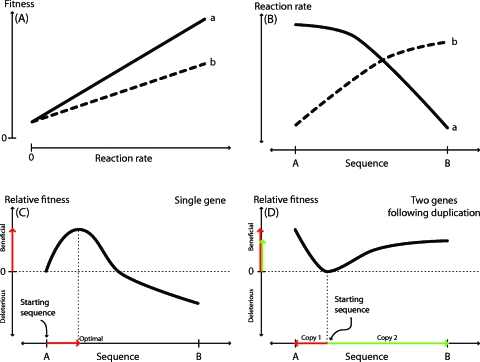
As such constraints can seriously limit the generation of novel functions, gene duplication is thought to be an essential precursor to adaptive protein evolution (Kimura and Ota, 1974; Lynch and Katju, 2004; Ohno, 1970; Ohta, 2000). In this model (Fig. 1), suppose the current organism carries an enzyme A catalyzing reaction a, but catalyzing both reactions a and the similar reaction b confers a fitness advantage. The similarity of these two reactions allows enzyme A to evolve to effectively catalyze reaction b. However, the mutations that improve b reduce a, thereby constraining evolution to the suboptimal allele A. Following duplication of A to produce A^′, evolution can now maintain in one copy, A, the capacity to catalyze reaction a, but now natural selection is free to drive the fixation of mutations in the A^′ copy to improve b. In general, gene duplication can unleash an adaptive burst because it uncouples trade-offs between functions and thereby allows functional innovation in one gene copy.

Figure 1. The example relationships between reaction rate, enzyme sequence, and organismal fitness.

(A) shows the relationship between reaction rate and fitness for two reactions a and b, where a is a larger determinant of fitness than b. (B) shows how reaction rates for a and b vary as the enzyme sequence moves between the sequences A and B. The reaction-rate–fitness and sequence–reaction-rate functions in the top two panels produce the single enzyme fitness landscape (C) for enzyme sequences between A and B. First, the optimal enzyme sequence is intermediate between specialists A and B, reflecting the trade-off between A and B. Consequently, an initial sequence of A will be pushed by natural selection toward this intermediate sequence with the accompanying gain in fitness (red arrows). Finally, panel (D) reflects the consequences of duplicating this enzyme and thus freeing evolution from the trade-off between reactions a and b and inducing an adaptive burst in both duplicates. One copy is free to specialize in reaction a (red arrows) while the second copy can specialize in b (green arrows). The total fitness is the sum of the two independent gains, indicating that duplication and specialization enables natural selection to produce an organism with overall higher fitness than is possible with a single enzyme sequence alone.

A novel function, however, may not be mutationally adjacent to an ancestral function, so that some exploration may be necessary around the original gene sequence before uncovering beneficial mutations leading to a novel function. During this period, the duplicated gene may fix mutations that render it non-functional (Lynch et al., 2001). Genome-wide studies of gene duplication suggest that loss, not adaptation, is the standard fate of most duplicates, as the mutation rate to null alleles is dangerously high (Lynch et al., 2001). Clearly then, mutational proximity to a novel function determines in part the evolutionary outcome of a duplicated gene (Lynch et al., 2001; Walsh, 1995).

One potential mechanism to reduce mutational distance to novel functions comes from the observation that many enzymes are promiscuous, meaning that they can catalyze a spectrum of reactions with varying efficiencies (Khersonsky et al., 2006). Such enzymes exhibit both highly efficient native activities and less efficient but still biologically significant activities against a wide variety of alternative nonnative substrates (Khersonsky et al., 2006; Schmidt et al., 2003; Yang and Metcalf, 2004). Only a few mutations are necessary to increase manyfold the catalytic performance of a promiscuous enzyme toward its nonnative substrates (Khersonsky et al., 2006; Schmidt et al., 2003). However, such changes usually come at a cost, reducing the native activity by a small but potentially evolutionarily significant amount (Aharoni et al., 2005). Additionally, higher nonnative activity can confer a substantial fitness advantage (Schmidt et al., 2003). These features of promiscuous enzymes indicate that under the right conditions natural selection could readily drive the fixation of mutations that improve promiscuous activities.

VIVA LA DIFFÉRENCE

Framed against this backdrop of protein evolution we can now appreciate the contributions in the joint experimental and computational papers by Amitai et al. (2007) and Wroe et al. (2007) in the first issue of the HFSP Journal. In the first paper, Amitai et al. (2007) map the neutral sequence space surrounding the wild-type sequence of serum paraoxonase (PON1) by random mutagenesis and selection to isolate 311 “apparently neutral” PON1 alleles exhibiting near wild-type levels of protein abundance and activity against the native substrate. Around 10% of these apparently neutral alleles exhibited substantial changes in activity and selectivity toward at least one of five nonnative substrates. The subset of alleles with altered phenotypes possessed several mutations in and around the active site, though none of these mutations were at residues directly involved in catalysis. Amitai et al. (2007) discuss in detail an allele that differs from wild-type PON1 at six sites, retains 50% of the expression level and 30% of wild-type PON1, but also has tenfold greater specific activity toward a nonnative aryl ester substrate, despite being generated without explicit selection for aryl ester activity. As further proof that these apparently neutral alleles represent a sample of the true neutral sequence space surrounding PON1, the authors show that the sequence variation among their set of mutagenized alleles mirrors the variation found among members of the mammalian serum paraoxonase–arylesterase gene family. The key advance of Amitai et al. (2007) is beautifully depicted in Fig. 6, which shows the neutral sequence network surrounding wild-type PON1, partitioned into regions with improved nonnative activities [link to Fig. 6 in Amitai, et al. (2007). “Latent evolutionary potentials under the neutral mutational drift of an enzyme.” HFSP J. 1, 67–78].

In the companion paper, Wroe et al. (2007) propose a simple biophysical model for promiscuous enzyme activity. Since proteins do not adopt a single static structure but rather fluctuate among similar but nonidentical conformations (Frauenfelder et al., 1991), Wroe et al. (2007) hypothesize that functional promiscuity results from different conformations in the ensemble catalyzing different reactions, with the native activity catalyzed by the most stable (ground-state) conformation. In this model, a mutation that increases the stability of a nonnative conformation increases its occupancy in the ensemble and therefore the activity corresponding to this conformation. Moreover, the stability of this nonnative conformation can be increased substantially without a necessarily concomitant reduction in the occupancy of the native conformation, providing a biophysical rationale for the puzzling experimental observation that nonnative activities can be increased greatly without an equivalent sacrifice in native activity.

Wroe et al. (2007) then ask how, within the above framework, natural selection will drive the increase in nonnative activity using a lattice protein model for which they can calculate exact thermodynamic parameters. They begin by identifying the most thermodynamically stable sequence (S^X). They then initiate evolutionary simulations from S^X in which a population of sequences mutate and reproduce based on their fitness, defined for a sequence S_i by the occupancy of a target structure X_j in the thermodynamic ensemble of structures for S_i. This corresponds, in their model, to exerting a selection pressure for a nonnative activity, as the nonnative target structure X_j does not correspond to the native (i.e., most stable) structure S^X.

They draw several interesting conclusions from the evolutionary dynamics observed in their simulations. First and perhaps obviously, evolution can drive a population of sequences toward ones with higher occupancies of X_j in the thermodynamic ensemble. This process, however, occurs mostly through enriching X_j in “excited” (not most stable) states of the thermodynamic ensemble, even passing through a ground-state structure dissimilar to both the initial S^X and the target X_j structures. Moreover, adaptation for X_j is significantly faster when including the fitness contributions of excited-state conformations, compared to simulations where only sequences with X_j ground-state structures are awarded a fitness advantage. Altogether, Wroe et al. (2007) provide a biophysical model relating functional promiscuity to thermodynamic stability and evidence that, within this model, nonnative states may play an important role in adaptation.

Together, these joint experimental and computational papers by Amitai et al. (2007) and Wroe et al. (2007) draw a detailed picture of how functional promiscuity, neutral sequence evolution, and natural selection can operate to potentiate a gene for the rapid generation of novel functions following duplication. Their argument, in essence, is that natural selection can drive the fixation of mutations that increase the nonnative activity of an enzyme without sacrificing too much native activity. This pressure produces a gene sequence balanced between the native and promiscuous activities (Fig. 1). Following gene duplication, this gene is better situated to acquire the adaptive mutations that transform its previously promiscuous activity into a full-stature, native activity. In other words, this gene undergoes latent adaptation before duplication. This process improves the potential for adaptive evolution by reducing a gene’s mutational distance to a novel, beneficial function and thereby accelerates the rate of adaptation following duplication. Ultimately, this increases the likelihood that duplication events will produce a gene with a novel, adaptive function.

FUTURE DIRECTIONS, OUTSTANDING QUESTIONS, AND CONCLUSIONS

These two papers demonstrate that functional promiscuity may potentiate adaptive evolution. Like other biochemical studies of protein evolution, their results suffer from one major concern: though clearly possible in the laboratory, does this process actually play a role in natural evolution? Many factors may limit the role of this process in adaptation. For example, it may be that mutations increasing nonnative activity are too costly, as natural selection is sensitive to even minute changes in fitness. Generally, natural selection operates effectively on mutations for which N_e×s>1, where N_e is the effective population size and s is the selection coefficient (Ohta and Kimura, 1972). Since N_e ranges from 10⁸ for prokaryotes to 10⁴–10⁵ for vertebrates (Lynch and Conery, 2003), this implies that mutations with effects as small as s>10⁻⁵ (>10⁻⁸ for prokaryotes) are significant in the eyes of natural selection. So substitutions that reduce an enzyme’s performance by even a few percent may be far too large to be tolerated by natural selection. What is clearly needed is a “smoking gun” example of natural adaptive evolution proceeding first through intermediates optimizing a nonnative activity while maintaining the native activity [for an non-enzymatic example, see (Bridgham et al., 2006)]. One could in principle conduct experiments analogous to Amitai et al. (2007) on protein sequences from adaptive trajectories collected in laboratory evolution experiments or from observing adaptation in the wild (Elena and Lenski, 2003; Grenfell et al., 2004; Mellinghoff and Sawyers, 2002; Richman, 2001; Wackett, 2004).

Nevertheless, the results of Amitai et al. (2007) and Wroe et al. (2007), along with other recent advances in understanding gene duplication, functional promiscuity, the structure of protein sequence space, and adaptation in general, provide a very compelling new view of adaptive protein evolution. This view provides a biophysical framework linking the effects of individual mutations on nonnative protein activities, neutral genetic drift, and gene duplication to the generation of novel functions in proteins. Moreover, the increasingly sophisticated techniques for laboratory evolution experiments and finer monitoring of the ubiquitous process of natural evolution, place us in an ideal position to challenge, refine, and expand our blossoming understanding of the mechanistic basis of adaptive protein evolution.