Abstract
In this Commentary, we discuss the paper Quantitative Determination of Size and Shape of Surface-Bound DNA Using an Acoustic Wave Sensor [Tsortos et al., Biophys. J. 94(7), 2706–2715 (2008)]. The paper under discussion presents a novel theory that uses the response of a Shear-Horizontal Surface Acoustic Wave device to characterize surface-attached double- and triple-strand DNA. The authors relate the length and curvature of the DNA strands to the interfacial viscosity using classical polymer theory. In this Commentary, we discuss their results in the broader context of acoustic wave detection of biochemical interactions and some of the factors involved when probing “soft” surfaces. Specifically, we present a review of interfacial coupling and slip, and discuss how these phenomena can affect biosensors employing acoustic wave detection techniques.
There has been significant attention paid in recent years to biosensor technologies for the detection and measurement of signaling biochemical interactions. Areas of investigation range from the fundamental study of biological macromolecules on surfaces, to applications for clinical assays and drug discovery. Conventional approaches are often based on the use of labeling agents such as radiochemical or fluorescent tags. However, the use of direct, label-free sensing offers a number of distinct advantages and, accordingly, there has been a large body of published work with this in mind. Two techniques that have received considerable attention are surface plasmon resonance technology and devices based on the instigation of acoustic waves in a substrate. Acoustic wave sensing is based on electric or electromagnetic field excitation of high frequency acoustic waves in a piezoelectric material such as quartz. A number of structures have been employed in bio-detection, such as thickness shear wave devices, surface acoustic wave sensors, and shear-horizontal surface acoustic wave (SH-SAW) or Love-wave detectors. Operation of these types of devices is the subject of this Commentary.
PAPER UNDER COMMENTARY
In Quantitative Determination of Size and Shape of Surface-Bound DNA Using an Acoustic Wave Sensor, the authors attached various length DNA strands to an SH-SAW∕Love-wave biosensor, and inferred the bending of double- and triple-strand nucleic acid, based on the sensor response (Tsortos et al., 2008). The authors claim to be able to obtain very high resolution of bending-angle detection for angles determined from surface viscosities, which were predicted by classical polymer solution theory. The sensor responses used were the amplitude shift, ΔA, and the phase shift, ΔPh, of the acoustic envelope. The former parameter is a measure of a change in dissipation near the surface-liquid interface, in response to a surface perturbation, while ΔPh corresponds to a change in energy storage at the surface. Dissipation at the sensor-liquid interface is usually caused by viscous interactions within the surface-bound species or acoustic losses into the contacting liquid. Energy storage is normally linked to material deposition on the sensor surface, but it can also be affected by changes in the viscoelasticity of the interface and coupling of the acoustic wave into the liquid.
The authors apply classical polymer solution theory to determine the flow properties at the interface. Modification of the interfacial viscosity is attributed to the presence of the surface-attached DNA strands as polymeric elements that affect the fluid flow at the surface. This approach is very novel in that it makes use of known physical properties of DNA that can be measured or computationally modeled and correlated to the interfacial behavior of the acoustic device, and is accomplished without resort to phenomenological fitting parameters. In their analysis, the authors make the assumption that the change in amplitude depends entirely on the viscosity at the surface-liquid interface, which is explicitly influenced by the surface concentration of the DNA molecules, . Another assumption is that the phase change depends only on the surface concentration, which leads to the ratio
| (1) |
This approximation is likely valid for ds- and tsDNA, as the helix structures of these biomolecules ensure that they are sufficiently rigid, so there will be very little phase changes due to changes in stiffness of the DNA strands. However, this may not be the case for highly viscoelastic biomolecules such as certain proteins. In these cases, the phase shift will be a function of the surface concentration and the viscoelasticity of the protein layer and Eq. 1 will not apply. In this paper, however, we will not consider these cases, which have been covered in detail elsewhere (Martin et al., 1991; Martin, 1991; McHale et al., 2000).
Another approximation implicit in Eq. 1 is that the affinity of the surface for the liquid remains constant for both neutravidin and the DNA surface. In other words, the acoustic energy coupled into the liquid by the surface remains constant between State 1: the neutravidin-coated surface, and State 2: the DNA-modified surface. Changes in acoustic coupling at the sensor-liquid interface, which could be a manifestation of interfacial slip, may have large effects on the device signal, and may pose significant problems in the analysis of those signals. The question of whether slip occurs has been the subject of great debate, both in the acoustic sensor field and in the broader fluid dynamics area as a whole (Barrat and Bocquet, 1999; Bonaccurso et al., 2003; Cottin-Bizonne et al., 2003; Ponomarev and Meyerovich, 2003; Neto et al., 2005). These reviews on the subject of solid–liquid slip are comprehensive, so the general topic will not be considered here. Instead, we focus on instances of slip in the acoustic sensor field to date, and consider the implications of interfacial phenomena and their applicability to biosensing. We center our discussion on models for transverse-shear mode (TSM) devices, the so-called quartz crystal microbalance, although the arguments can be easily adapted to other shear wave sensing techniques, such as shear-horizontal surface acoustic wave (SH-SAW) and acoustic plate mode sensors, and Rayleigh wave devices (SAW).
It is important to note that the points we illustrate in this Commentary are not directly applicable to the paper under discussion by Tsortos et al. The authors did not observe any anomalous signals that may be attributable to slip, and hence our discussion on interfacial coupling does not explicitly refer to their system. Their results do not indicate a manifestation of slip.
However, the authors’ theory, which is only strictly valid for rigid biomolecules like dsDNA, may not be applicable to a wide range of biochemical surface moieties, such as many proteins. As such, we present a description that we believe can affect a very wide range of “soft” surfaces. The controversial area of slip and interfacial coupling is important in acoustic wave biosensing, due to the heterogeneity of the biochemical surfaces under study, and that it needs to be brought to the attention of the broader biosensing community.
EFFECT OF CHANGES IN INTERFACIAL COUPLING ON THE SIGNAL
When an acoustic wave sensor is operated in a liquid, the sensor surface induces motion in the adjacent liquid particles, transmitting the shear acoustic energy wave into the liquid. In the liquid, it decays as the wave progresses away from the surface. The response of the device when immersed in a liquid is very well characterized, and involves changes in the energy stored and dissipated by the device (Bruckenstein and Shay, 1985; Kanazawa and Gordon, 1985; Martin et al., 1991). Both of these energy shifts are proportional to the square root of the product of the density and viscosity of the contacting liquid. Traditionally, it is assumed that the lateral velocity of the sensor surface is equal to that of the contacting liquid, which is the no-slip condition. Any discontinuity in velocities at the interface represents a manifestation of slip, and will have an effect on the propagation of the acoustic wave and the storage and dissipation of energy into the liquid. This, in turn, has an effect on the sensor response. The nature of these changes, and the factors that lead to them, is the question that is addressed by the study of slip. However, before considering the effect of slip on the propagation of an acoustic wave, we concisely review the important equations that govern fluid dynamics and discuss a simple yet widely used model for interfacial slip.
Hydrodynamics
A discussion of fluid dynamics begins with the Navier-Stokes equation for constant-viscosity, incompressible fluid flow, such that ∂ρ∕∂t=0,
| (2) |
where v is the velocity vector field, ρ is the mass density of the fluid, D∕Dt=∂∕∂t+v⋅∇ is the material derivative, ∇p is the gradient of the pressure, η is the shear viscosity, and F is the external force acting on the fluid volume. The right-hand side of Eq. 2 is a momentum balance between the internal pressure and viscous stress, and the external forces on the fluid body. Any excess momentum contributes to the material acceleration of the fluid volume on the left-hand side.
When considering a solid–liquid interface, the simplest case involves steady shear flow parallel to the surface, with Dv∕Dt=0 and v=vxx. Equation 2 reduces to Newtonian viscous flow
| (3) |
where σx is the shear stress in the x plane and the shear rate is the slope of the velocity gradient normal to the wall. At the wall, the tangential shear stress becomes
| (4) |
where the wall boundary is at z=0.
Definitions of slip and friction
Frictional Stokes flow can be used to describe the shear stress on a planar surface caused by a slipping fluid flowing across it,
| (5) |
where vs is the slip velocity and k is the friction coefficient, in units of viscosity per unit length. Friction is also known as the interfacial viscosity, which is written as η2, as it represents interfacial, two-dimensional drag. Equation 5 describes the friction or drag stress on a solid object in a flow field. Equating Eqs. 5, 4 yields
| (6) |
Slip is included in the model with the slip length, due originally to Navier (Navier, 1827). In this approach, if slip occurs, the slip velocity vs is proportional to the velocity gradient at the wall ∂vx∕∂z,
| (7) |
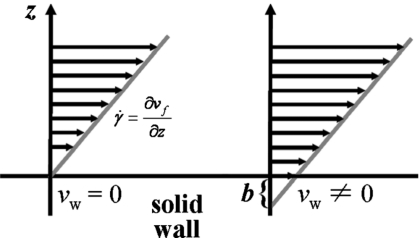
where the proportionality constant is the slip length b, an imaginary extrapolation length into the solid wall required to recover the no-slip condition, as shown in Fig. 1. This concept has been explored extensively by de Gennes and co-workers (Brochard and de Gennes, 1992; de Gennes, 1997). Combining Eqs. 6, 7, the relationship for the slip length as the ratio of the bulk and interfacial viscosities becomes
| (8) |
This ratio implies that slip will increase as the bulk viscosity increases relative to the interfacial viscosity, or as the liquid self-cohesiveness increases and liquid-surface affinity decreases. This concept, although simple, has been used extensively to model flows of polymer melts (Leger et al., 1997; Horn et al., 2000) and Newtonian liquids (Pit et al., 2000; Zhu and Granick, 2001; Bonaccurso et al., 2003; Cottin-Bizonne et al., 2002; Cottin-Bizonne et al., 2003; Spikes and Granick, 2003). The description of slip depicted in Eqs. 7, 8 is an empirical, two-parameter fit to data and only provides a way of describing slip phenomena. It does not offer any physical interpretation of the effect or its causes.
Figure 1. No-slip condition and slip condition with slip length, for one-dimensional shear flow.
The slip length b is the extrapolation distance into the solid, to obtain the no-slip point. The slope of the linear velocity profile near the wall is the shear rate .
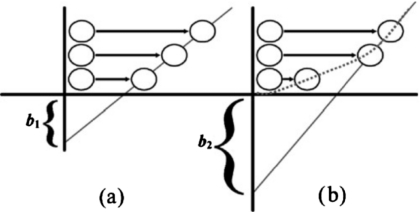
It is important to differentiate between true molecular slip and macroscopic partial slip. True molecular slip indicates an actual velocity discontinuity between the solid surface molecules and the contacting liquid molecules [Fig. 2a]. True slip is difficult to observe and often must be inferred from hydrodynamic measurements at the nanometric length scale. Partial slip is characterized by a very steep velocity gradient near the wall, which appears as a large apparent slip length [Fig. 2b].
Figure 2. True (a) and apparent (b) slip.
In (a), there is a discernible slip velocity at the wall, giving a measurable but small slip length. In (b), the slip velocity at the wall is negligible, but the slope of velocity profile near the wall is very steep. Because the flow quickly becomes fully developed, it takes the appearance of a large slip length.
Due to the high shear rates and small length scales involved in acoustic biosensor operation, it is highly likely that slip is possible at the surface liquid interface. Especially in the case of sensors coated with heterogeneous biochemical moieties, coupling changes at the interface are very likely. Slip can be due to a wide range of causes, including changes in surface affinity, roughness, and heterogeneity in either of these factors. In fact, slip may even be possible on mildly hydrophobic metal surfaces, which could occur in many studies where proteins such as avidin are immobilized on the surface.
MODELS OF SLIP FOR ACOUSTIC SENSORS
TSM response without slip
While this topic has been covered extensively in the literature, we mention it briefly here to provide context for the discussion on slip. The device response can be approximated from the acoustic load impedance at the device surface ZL, which is the ratio of the surface shear stress to the horizontal velocity. The sensor response can be estimated in terms of changes in the load impedance from the small-load approximation,
| (9) |
where f0 is the resonant frequency of the unloaded device and Zq is the acoustic impedance of quartz (Tessier et al., 1994). For a 9 MHz device, Zq≅8.8×106 kg m−2 s−1. Δf is the change in resonant frequency and ΔΓ is the change in bandwidth, a measure of dissipation. It is used here instead of Rm or Q because the two expressions have the same prefactor, although conversion to the other parameters is easily performed. Both the purely gravimetric (Sauerbrey, 1959) and purely viscous (Kanazawa and Gordon, 1985) responses can be derived from Eq. 9. In the case of a thin, rigid coating on the sensor surface in contact with a nonslipping liquid, the gravimetric and viscous liquid responses can be observed separately:
| (10) |
Equation 10 is the Thin-Film Approximation, and is only strictly valid for a rigid film with very little dissipation and the no-slip condition at the interface. In other cases, the load impedance is also sensitive to the viscoelastic nature of any film adsorbed on the surface (Martin et al., 1991; McHale et al., 2000) and interfacial coupling between the device surface and the contacting liquid, which will be discussed in the next section.
Models of slip for the TSM
We now turn the discussion to examples of slip on acoustic sensors and how they have been described. Krim and co-workers studied adsorption of thin gas films on the sensor surface, and found that molecular-level slip occurred in many cases (Krim and Widom, 1988;Watts et al., 1990; Sokoloff et al., 1993; Mak and Krim, 1998). From a quantum derivation they introduced a slip-time τslip. The slip time can be understood in terms of a thin film adsorbed at the sensor surface, moving with velocity va. If the substrate stops suddenly, the velocity of the adsorbed layer will decay exponentially, and the slip time is the time constant of the exponential decay. The slip time can be approximated as τslip≈bhaρliq∕ηliq where b is the slip length, ha is the thickness of the adsorbate film, and ρliq and ηliq are the density and viscosity of the bulk liquid. Cieplak et al. derived an expression for the slip time in terms of anharmonic coupling between phonon modes and substrate-induced deformations in the adsorbed monolayer (Cieplak et al., 1994).
Around the same time, Thompson and co-workers found that the signals for the adsorption of biological molecules on sensor surfaces could not be explained by gravimetric effects, nor was the amount of dissipation consistent with viscosity or viscoelasticity (Thompson et al., 1987; Duncan-Hewitt and Thompson, 1992; Yang and Thompson, 1993; Yang et al., 1993). They attributed these discrepancies to slip at the sensor-liquid interface resulting from changes in the strength of the surface-liquid interaction because of the biological surface modification. They developed a number of models to explain these phenomena; however, application of these effects presented difficulties because predicting the nature of the surface-liquid interaction remained a significant challenge. Ferrante et al. modeled the ratio of the solid and liquid displacements at the interface with a complex slip parameter α (Ferrante et al., 1994). By allowing the slip parameter to be complex, the ratio of the displacements or velocities at the interface could have both magnitude and phase. Hayward and Thompson extended this treatment to include slip at any interface (Hayward and Thompson, 1998) and Ellis et al. showed that in the limit of a rigid solid and purely viscous liquid, the complex slip could be modeled as the real valued slip length b (Ellis and Hayward, 2003; Ellis et al., 2003). This equivalency, however, is only valid if the velocity profile is linear near the wall, and may not be applicable to viscoelastic surfaces or liquids, including biological films. For these films, a complex slip parameter may be required (Willmott and Tallon, 2007).
The models described above apply a slip boundary condition through an explicit discontinuity in the displacement or velocity boundary conditions. Other models apply a friction term to the force balance equation, equivalent to Eq. 6. Rodahl and Kasemo equated the shear stresses in the liquid to the frictional stress due to the liquid on the surface (Rodahl and Kasemo, 1996). In the absence of slip, the stresses balance, as do the velocities. However, if the velocities at the boundary are not equal, then the stress balance can be modeled with a friction coefficient, such that the friction force depends on the difference in velocities between the surface and the liquid. Their model had the form
| (11) |
where χ is the friction coefficient in units of s−2 and ρa is the surface density in units of kg cm−2. The velocity difference vq−vliq is the slip velocity vs of Eq. 7, so the factor χρa is equivalent to the Stokes friction k in Eq. 6. Daikhin et al. modeled slip at the adsorbate-liquid interface, where the adsorbate is rigidly coupled to the surface, by including an extra viscous dissipation term in the wave equation of the device and a similar boundary condition as Eq. 11, but using the slip length b=η∕k (Daikhin et al., 2000). They found that the inclusion of slip resulted in extra frequency and bandwidth effects of the form
| (12) |
where a=b∕δ is a dimensionless parameter. The shifts shown in Eq. 12 are those due to slip effects alone, so the total frequency and bandwidth shifts for an adsorbed layer in a liquid with slip, assuming the thin-film approximation [Eq. 10], would be Δftot=Δfa+Δfliq+Δfslip and ΔΓtot=ΔΓliq+ΔΓslip. Mass adsorption on the device surface has no effect on the bandwidth. What is important to note in Eq. 12 is that the effect of slip at the surface-liquid interface is that frequency increases and bandwidth decreases. As well, it is not a pure viscous decoupling, so the change in frequency and bandwidth are not equal and opposite, as would be the case for a change in the density or viscosity of the liquid.
McHale et al. used a similar description of slip, but modeled it at different layers using a slip parameter for layer i, si=1∕k (McHale et al., 2000). For slip at the surface-liquid interface, their model yields the same result as Eq. 12. The acoustic load impedance for an adsorbed layer with slip at the adsorbate interface is
| (13) |
where s is the slip parameter at the adsorbate-liquid interface, Za, ρa, and Ga are the acoustic impedance, density, and shear modulus of the adsorbate, Zliq is the acoustic impedance of the liquid, and ZL is the load impedance for the no-slip case. If the adsorbate is a thin rigid film, such that Ga is large, Eq. 13 reduces to
| (14) |
which gives the result in Eq. 12 for sliq=aδ∕η. Equation 13 can be used to estimate material and interfacial properties of biological adsorbate layers and biosensing from experimental data. Du et al. derived a model for heterogeneous slip by including a secondary flow field that depends on the Fourier components of the slip heterogeneity (Du et al., 2004). They included liquid-surface slip in the model as
| (15) |
where the effect due to slip is described with the parameter B. Through a lengthy derivation, they found thatB=2(brms)2∕δ 2, where brms is the rms value for the slip length heterogeneity on the surface. While this model is still simply a parameter fit to the experimental data, it does provide a method for estimating the device response if the slip heterogeneity is known. In previous papers, we have related the slip length b, and thus the complex slip parameter α, to other slip parameters, such as s and a above (Ellis et al., 2003; McHale and Newton, 2004).
None of these models inherently describes biological systems or biosensors. In fact, they are all phenomenological fitting parameters that could be used to describe any situation, but only provide information regarding the flow characteristics at or near the surface. Two models have been proposed recently to describe slip in terms of molecular forces between the sensor surface, an attached molecule, and the surrounding fluid. The first describes the interface as a viscoelastic material and modeled it with a complex interfacial shear modulus, using the boundary condition
| (16) |
where G*=G′+jωG″ is the viscoelastic modulus of the interfacial layer, d is the intermolecular spacing between the particles at the surface, γ is the strain, and the ub are the shear displacements of the quartz and liquid, respectively, at the boundary (Lu et al., 2003; Lu et al., 2004a; Lu et al., 2004b; Lu et al., 2005). The authors related this slip model to the slip parameter α as
| (17) |
where rliq is the liquid particle radius, ρliq is the liquid density at the boundary, and Zliq is the liquid characteristic impedance , where Gliq is the generalized shear modulus of a viscoelastic liquid. Equation 17 is useful for developing mesoscopic models of the solid liquid interface, although it has not been applied extensively to model experimental results, apart from some preliminary studies (Lu et al., 2005).
The advantage of this model is that it treats the surface and the interface as a combined molecular mechanical system, rather than as a phenomenological discontinuity. The discontinuity is instead displayed on a molecular level as an interfacial coupling problem, rather than as slip problem. This approach has the advantage of avoiding experimental fitting parameters with purely phenomenological meaning, and at the same time introducing biologically relevant information, such as interaction forces and molecular size factors. While biosensor data have not yet been applied to this model, we feel that it, along with similar descriptions that will emerge in the future, will provide a real link between coupling phenomena and biochemical systems analysis.
The description proposed by Tsortos et al. also uses a bio-molecular approach to estimate the interfacial parameters and calculate these parameters to predict the sensor response (Tsortos et al., 2008). It has also been tested with real biological data and models, and the sensor response can be used to predict the oligonucleotide shape, which is in essence the “Holy Grail” of the acoustic biosensor. In this it is quite successful and presents an appropriate starting point for studying the effect of biochemical coatings on interfacial fluid properties for surfaces undergoing mechanical oscillations. However, the model requires many assumptions, both implicit and explicit, and therefore might not be generally applicable to the wide range of situations that can arise from biochemical surface modification. As well, it does not discuss in detail the heterogeneity of surface properties resulting from different modifications, some of which could lead to interfacial coupling. Our impression is that models that are more complex are required for more complex, “soft” coatings.
SUMMARY
Despite the increasing body of evidence indicating that the pure mass-response model cannot explain complex surfaces, many studies that employ acoustic wave detection are interpreted based on this notion. Many researchers continue to adhere to this interpretation to the extent that other contributions to signals may be ignored. The reason for this likely lies in a desire for simplicity in terms of “counting” molecules deposited or lost at surfaces. In reality, the acoustic physics of biochemical interfaces provides tremendous potential for the measurement of structural information not presently offered by other techniques. Unfortunately, the great importance of interfacial coupling with respect to its role in biosensing has been largely overlooked by many researchers. The heterogeneity of biochemically modified surfaces, as well as the heterogeneity of their material properties, makes this issue especially crucial when detecting reactions involving proteins and nucleic acids. While modeling of coupling interactions on these types of surfaces still presents some challenges, it can provide a large amount of information that would otherwise be unavailable.
The study by Tsortos et al. presents a refreshingly novel and intelligent take on analysis of surface shape on an acoustic biosensor surface (Tsortos et al., 2008). As discussed above, it is limited in its scope because it can only be applied to systems that are structurally rigid, such as dsDNA. However, the authors of the paper under commentary, as well as others, are working on extending their theoretical approach to other cases of interest to the biology community (E. Gizeli, personal communication, 2008) and as such, we eagerly await more general models applicable to a wider range of biomolecules.
ACKNOWLEDGMENTS
The authors are grateful to the Natural Sciences and Engineering Research Council of Canada for support of their own work on the acoustic physics of biochemical species and on bio-detection science.
References
- Barrat, J L, and Bocquet, L (1999). “Large slip effect at a nonwetting fluid-solid interface.” Phys. Rev. Lett. 10.1103/PhysRevLett.82.4671 82(23), 4671–4674. [DOI] [Google Scholar]
- Bonaccurso, E, Kappl, M, and Butt, H J (2002). “Hydrodynamic force measurements: boundary slip of water on hydrophilic surfaces and electrokinetic effects.” Phys. Rev. Lett. 10.1103/PhysRevLett.88.076103 88(7), 076103. [DOI] [PubMed] [Google Scholar]
- Brochard, F, and de Gennes, P G (1992). “Shear-dependent slippage at a polymer solid interface.” Langmuir 10.1021/la00048a030 8(12), 3033–3037. [DOI] [Google Scholar]
- Bruckenstein, S, and Shay, M (1985). “Experimental aspects of use of the quartz crystal microbalance in solution.” Electrochim. Acta 10.1016/0013-4686(85)85005-2 30(10), 1295–1300. [DOI] [Google Scholar]
- Cieplak, M, Smith, E D, and Robbins, M O (1994). “Molecular-origins of friction—the force on adsorbed layers.” Science 10.1126/science.265.5176.1209 265(5176), 1209–1212. [DOI] [PubMed] [Google Scholar]
- Cottin-Bizonne, C, Barrat, J L, Bocquet, L, and Charlaix, E (2003). “Low-friction flows of liquid at nanopatterned interfaces.” Nat. Mater. 10.1038/nmat857 2(4), 237–240. [DOI] [PubMed] [Google Scholar]
- Cottin-Bizonne, C, Jurine, S, Baudry, J, Crassous, J, Restagno, F, and Charlaix, E (2002). “Nanorheology: an investigation of the boundary condition at hydrophobic and hydrophilic interfaces.” Eur. Phys. J. E 9(1), 47–53. [DOI] [PubMed] [Google Scholar]
- Daikhin, L, Gileadi, E, Tsionsky, V, Urbakh, M, and Zilberman, G (2000). “Slippage at adsorbate-electrolyte interface. Response of electrochemical quartz crystal microbalance to adsorption.” Electrochim. Acta 10.1016/S0013-4686(00)00444-8 45(22, 23), 3615–3621. [DOI] [Google Scholar]
- de Gennes, P-G (1997). Soft Interfaces: the 1994 Dirac Memorial Lectures, Cambridge University Press, Cambridge. [Google Scholar]
- Du, B, Goubaidoulline, I, and Johannsmann, D (2004). “Effects of laterally heterogeneous slip on the resonance properties of quartz crystals immersed in liquids.” Langmuir 10.1021/la0483515 20(24), 10617–10624. [DOI] [PubMed] [Google Scholar]
- Duncan-Hewitt, W C, and Thompson, M (1992). “4-layer theory for the acoustic shear-wave sensor in liquids incorporating interfacial slip and liquid structure.” Anal. Chem. 10.1021/ac00025a017 64(1), 94–105. [DOI] [Google Scholar]
- Ellis, J S, and Hayward, G L (2003). “Interfacial slip on a transverse-shear mode acoustic wave device.” J. Appl. Phys. 10.1063/1.1627949 94(12), 7856–7867. [DOI] [Google Scholar]
- Ellis, J S, McHale, G, Hayward, G L, and Thompson, M (2003). “Contact angle-based predictive model for slip at the solid-liquid interface of a transverse-shear mode acoustic wave device.” J. Appl. Phys. 10.1063/1.1619195. 94(9), 6201–6207. [DOI] [Google Scholar]
- Ferrante, F, Kipling, A L, and Thompson, M (1994). “Molecular slip at the solid-liquid interface of an acoustic-wave sensor.” J. Appl. Phys. 10.1063/1.357475 76(6), 3448–3462. [DOI] [Google Scholar]
- Hayward, G L, and Thompson, M (1998). “A transverse shear model of a piezoelectric chemical sensor.” J. Appl. Phys. 10.1063/1.366956 83(4), 2194–2201. [DOI] [Google Scholar]
- Horn, R G, Vinogradova, O I, Mackay, M E, and Phan-Thien, N (2000). “Hydrodynamic slippage inferred from thin film drainage measurements in a solution of nonadsorbing polymer.” J. Chem. Phys. 10.1063/1.481274 112(14), 6424–6433. [DOI] [Google Scholar]
- Kanazawa, K K, and Gordon, J G (1985). “Frequency of a quartz microbalance in contact with liquid.” Anal. Chem. 10.1021/ac00285a062 57(8), 1770–1771. [DOI] [Google Scholar]
- Krim, J, and Widom, A (1988). “Damping of a crystal-oscillator by an adsorbed monolayer and its relation to interfacial viscosity.” Phys. Rev. B 10.1103/PhysRevB.38.12184 38(17), 12184–12189. [DOI] [PubMed] [Google Scholar]
- Leger, L, Hervet, H, Massey, G, and Durliat, E (1997). “Wall slip in polymer melts.” J. Phys.: Condens. Matter 10.1088/0953-8984/9/37/006 9(37), 7719–7740. [DOI] [Google Scholar]
- Lu, F, Lee, H P, and Lim, S P (2003). “Mechanical description of interfacial slips for quartz crystal microbalances with viscoelastic liquid loading.” Smart Mater. Struct. 10.1088/0964-1726/12/6/004 12, 881–888. [DOI] [Google Scholar]
- Lu, F, Lee, H P, and Lim, S P (2004a). “Detecting solid-liquid interface properties with mechanical slip modelling for quartz crystal microbalance operating in liquid.” J. Phys. D 10.1088/0022-3727/37/6/014 37(6), 898–906. [DOI] [Google Scholar]
- Lu, F, Lee, H P, and Lim, S P (2004b). “Quartz crystal microbalance with rigid mass partially attached on electrode surfaces.” Sens. Actuators, A 112(2-3), 203–210. [Google Scholar]
- Lu, F, Lee, H P, Lu, P, Su, X D, and Lim, S P (2005). “Experimentally fitting the attraction strength of an interface by the response of the thickness shear-mode acoustic wave sensor.” J. Phys. D 10.1088/0022-3727/38/10/015 38(10), 1599–1607. [DOI] [Google Scholar]
- Lucklum, R, and Hauptmann, P (1997). “Determination of polymer shear modulus with quartz crystal resonators.” Faraday Discuss. 10.1039/a703127k 107, 123–140. [DOI] [Google Scholar]
- Mak, C, and Krim, J (1998). “Quartz-crystal microbalance studies of the velocity dependence of interfacial friction.” Phys. Rev. B 10.1103/PhysRevB.58.5157 58(9), 5157–5159. [DOI] [Google Scholar]
- Martin, S J, Granstaff, V E, and Frye, G C (1991). “Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading.” Anal. Chem. 10.1021/ac00020a015 63(20), 2272–2281. [DOI] [Google Scholar]
- McHale, G, Lucklum, R, Newton, M I, and Cowen, J A (2000). “Influence of viscoelasticity and interfacial slip on acoustic wave sensors.” J. Appl. Phys. 10.1063/1.1326855 88(12), 7304–7312. [DOI] [Google Scholar]
- McHale, G, and Newton, M I (2004). “Surface roughness and interfacial slip boundary condition for quartz crystal microbalances.” J. Appl. Phys. 10.1063/1.1630373 95(1), 373–380. [DOI] [Google Scholar]
- Navier, C LM (1827). “Sur les lois du mouvement des fluids.” Mem. Acad. Sci. Inst. Fr. 6, 389–440. [Google Scholar]
- Neto, C, Evans, D R, Bonaccurso, E, Butt,H.-Jr., and Craig, V SJ (2005). “Boundary slip in Newtonian liquids: a review of experimental studies.” Rep. Prog. Phys. 10.1088/0034-4885/68/12/R05 68(12), 2859. [DOI] [Google Scholar]
- Pit, R, Hervet, H, and Leger, L (2000). “Direct experimental evidence of slip in hexadecane: solid interfaces.” Phys. Rev. Lett. 10.1103/PhysRevLett.85.980 85(5), 980–983. [DOI] [PubMed] [Google Scholar]
- Ponomarev, IV, and Meyerovich, A E (2003). “Surface roughness and effective stick-slip motion.” Phys. Rev. E 10.1103/PhysRevE.67.026302 67(2), 026302. [DOI] [PubMed] [Google Scholar]
- Rodahl, M, and Kasemo, B (1996). “On the measurement of thin liquid overlayers with the quartz-crystal microbalance.” Sens. Actuators, A 10.1016/S0924-4247(97)80002-7 54(1-3), 448–456. [DOI] [Google Scholar]
- Sauerbrey, G (1959). “Verwendung von Schwingquarzen zur Wagung dunner Schichten und zur Mikrowagung.” Z. Phys. 10.1007/BF01337937 155(2), 206–222. [DOI] [Google Scholar]
- Sokoloff, J B, Krim, J, and Widom, A (1993). “Determination of an atomic-scale frictional force law through quartz-crystal microbalance measurements.” Phys. Rev. B 10.1103/PhysRevB.48.9134 48(12), 9134–9137. [DOI] [PubMed] [Google Scholar]
- Spikes, H, and Granick, S (2003). “Equation for slip of simple liquids at smooth solid surfaces.” Langmuir 10.1021/la034123j 19(12), 5065–5071. [DOI] [Google Scholar]
- Tessier, L, Patat, F, Schmitt, N, Lethiecq, M, Frangin, Y, and Guilloteau, D (1994). “Significance of mass and viscous loads discrimination for an AT-quartz blood-group immunosensor.” Sens. Actuators B 19(1-3), 698–703. [Google Scholar]
- Thompson, M, Dhaliwal, G K, Arthur, C L, and Calabrese, G S (1987). “The potential of the bulk acoustic-wave device as a liquid-phase immunosensor.” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 34(2), 127–135. [DOI] [PubMed] [Google Scholar]
- Tsortos, A, Papadakis, G, Mitsakakis, K, Melzak, K A, and Gizeli, E (2008). “Quantitative determination of size and shape of surface-bound DNA using an acoustic wave sensor.” Biophys. J. 94(7), 2706–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts, E T, Krim, J, and Widom, A (1990). “Experimental-observation of interfacial slippage at the boundary of molecularly thin-films with gold substrates.” Phys. Rev. B 10.1103/PhysRevB.41.3466 41(6), 3466–3472. [DOI] [PubMed] [Google Scholar]
- Willmott, G R, and Tallon, J L (2007). “Measurement of Newtonian fluid slip using a torsional ultrasonic oscillator.” Phys. Rev. E 10.1103/PhysRevE.76.066306 76(6), 066306. [DOI] [PubMed] [Google Scholar]
- Yang, M, and Thompson, M (1993). “Surface-morphology and the response of the thickness-shear mode acoustic-wave sensor in liquids.” Langmuir 10.1021/la00032a016 9(8), 1990–1994. [DOI] [Google Scholar]
- Yang, M S, Thompson, M, and Duncan-Hewitt, W C (1993). “Interfacial properties and the response of the thickness-shear- mode acoustic-wave sensor in liquids.” Langmuir 10.1021/la00027a033 9(3), 802–811. [DOI] [Google Scholar]
- Zhu, Y X, and Granick, S (2001). “Rate-dependent slip of Newtonian liquid at smooth surfaces.” Phys. Rev. Lett. 10.1103/PhysRevLett.87.096105 8709(9), 096105. [DOI] [PubMed] [Google Scholar]