Collective behavior in animal groups: theoretical models and empirical studies

Abstract

Collective phenomena in animal groups have attracted much attention in the last years, becoming one of the hottest topics in ethology. There are various reasons for this. On the one hand, animal grouping provides a paradigmatic example of self-organization, where collective behavior emerges in absence of centralized control. The mechanism of group formation, where local rules for the individuals lead to a coherent global state, is very general and transcends the detailed nature of its components. In this respect, collective animal behavior is a subject of great interdisciplinary interest. On the other hand, there are several important issues related to the biological function of grouping and its evolutionary success. Research in this field boasts a number of theoretical models, but much less empirical results to compare with. For this reason, even if the general mechanisms through which self-organization is achieved are qualitatively well understood, a quantitative test of the models assumptions is still lacking. New analysis on large groups, which require sophisticated technological procedures, can provide the necessary empirical data.

Collective behavior in animal groups is a widespread phenomenon in biological systems, at very different scales and levels of complexity. Bird flocks gathering over the roost at dusk (Emlen, 1952), fish schools milling under water (Radakov, 1973; Pitcher, 1983), swarms of insects (Kennedy, 1951), trails of foraging ants (Wilson, 1971), herds of mammals (Sinclair, 1977), are only a few examples of collective behavior, which are familiar to many of us. Collective behavior is not only observed in social insects, like ants or honey bees, which are genetically related and cooperate within the colony, but also in aggregations of unrelated “selfish” individuals, like fish or birds. In many cases cohesive groups are formed, which act as a whole with remarkable coordination and adaptability, and are sustained spontaneously by the mutual attraction of members.

In all previous examples collective behavior emerges in absence of centralized control: individual members act on the basis of some limited local information—coming from interaction with neighbors or chemicals deposition—and this information flows through the system producing collective patterns. The example of flocking birds is paradigmatic: each individual bird flies in the same direction as its neighbors, and this local tendency gives rise to a coherent moving flock. This mechanism, which produces global patterns from local rules, is known as self-organization (Nicolis and Prigogine, 1977; Camazine et al., 2001; Sumpter, 2006; Garnier et al., 2007).

From a more general perspective, collective behavior and self-organization are key concepts in many different areas of science, including physics (Haken, 1983), economics and finance (Cont and Bouchaud, 2000), social sciences (Helbing et al., 2000; Helbing, 2001), control theory (Jadbabaie et al., 2003), and mobile robotics (Cao et al., 1997). In physics, for example, ordering phenomena and phase transitions have dominated theoretical and experimental research in the last 50 years. In this context, the origin and emergence of collective behavior have been understood in great detail, and this is why physics is often regarded as an inspiration source for interpreting and modeling collective phenomena in other fields. There are at least two main facts, which occur in physical systems and may be relevant to other disciplines: (i) A system of individual units (particles, magnetic moments, etc.) that interact locally in space can generate, under appropriate conditions, an ordered state with collective global properties. (ii) The mechanisms leading to collective behavior are very general; for example, the large-scale features of many order-disorder transitions do not depend on the details of the local interaction but only on some general characteristics of the system (such as the dimensionality of the space or the nature of the variable describing order)—what is known as universality (Cardy 1996). These two properties, locality of the interactions and universality, have been thoroughly proven in physics. Still, they provide a broader paradigm also in other fields. It is nowadays a well-accepted idea in biology that aggregations of individuals subject only to local behavioral rules can self-organize into complex coherent groups, as in physical systems. The issue of generality is subtler. Whether self-organization represents an exhaustive principle also in biological systems is an open question (Sumpter, 2006). The individual units are in this case much more complex than particles, endowed with cognitive abilities and diversified from species to species. It is reasonable that the individual complexity is redundant and only a few characteristics are necessary to explain group formation (Camazine et al., 2001). Still, at some point, the specificities of the individual may become crucial. There is no a priori criterion to decide what is relevant and what is not; this often depends on the precise question to be addressed and on the scale at which the collective phenomenon is observed. The problem of the “relevant detail” is a nontrivial one (Levin, 1991) and the analogy with physics is clearly limited in this respect.

Investigating collective behavior in biological systems is therefore a complicated task. What may appear a satisfactory and general explanation at a qualitative level is not always consistent with a quantitative analysis of empirical data, when differences among species become evident. A continuous feedback between empirical observations and modeling is thus indispensable to understand the origin of collective phenomena and appropriately characterize them.

Many successful analyses of self-organized systems have been performed to date. Still, comparison between models and experiments needs to be improved. For three-dimensional (3D) animal groups, like birds or fish, empirical data have been scarce and limited to small systems until recently. This has restrained the possibility of a reliable statistical analysis of empirical data and a comparison with the predictions of the models.

In this review I will describe some of the models developed to address collective behavior in animal groups, and several empirical studies performed on gregarious and social animals, both in the laboratory and in the field. Given the limited space, my aim is not to give an exhaustive overview of existing research on animal groups (for this, the reader is referred to Parrish and Hammer, 1997; Camazine et al., 2001; Krause and Ruxton, 2002; Couzin and Krause, 2003). Rather, I will focus on a few examples, especially in animal groups in 3D, and outline some methodological and conceptual issues particularly relevant for future perspectives in this field. In particular, I will:

• Summarize how models and empirical findings have improved our understanding of animal collective behavior so far.

• Underline the importance of gathering large sets of empirical data to test and further improve theoretical models.

• Illustrate the benefits of an interdisciplinary approach to collective behavior, and how concepts and techniques developed for physical systems can be useful to address biological groups.

• Go beyond the physics paradigm and discuss the biological aspects of collective behavior.

THEORETICAL MODELS

Models of self-organized collective behavior can be of different types, according to (i) the scale, in space and time, at which the collective phenomenon is analyzed; (ii) the kind of local information individuals use to aggregate (direct response to other individuals or indirect cues); (iii) the mathematical complexity.

Agent-based flocking models

Agent-based models of animal grouping assume behavioral rules at the level of the individual. An evolution equation is specified for each agent in the system, and its microscopic dynamics described in terms of the social forces acting upon it. They are generally used to investigate systems like schools, flocks, and swarms, where the force experienced by an individual is due to neighbors directly interacting with it (see, however, Camazine et al., 2001, for other kinds of models based on probabilities and the cellular automaton).

Agent-based models were originally developed for fish schools (Aoki, 1982; Okubo, 1986; Huth and Wissel, 1992) and bird flocks (Reynolds, 1987; Heppner and Grenander, 1990), and were eventually applied to mammal herds (Gueron et al., 1996) and other vertebrate groups (Couzin and Krause, 2003). In these systems cohesive and polarized groups are formed, which exhibit remarkable coordination and adaptability. Collective behavior results from three simple and general behavioral rules followed by individuals: move in the same direction as your neighbors; remain close to them; avoid collisions. These rules are modeled using three distinct contributions to the inter-individual interactions: (i) alignment of velocities, which makes neighboring birds fly in the same direction; (ii) attraction, which ensures no bird remains isolated; (iii) short-range repulsion, which prevents dangerous proximity. At group level, these three components should grant the directional polarity (alignment) and cohesion of the aggregation (attraction), preserving individual integrity (short-range repulsion).

The precise ways the rules are implemented differ from model to model, depending on the target biological system and on the modeler’s opinion as to which are the most reasonable behavioral assumptions. In general, the model specifies an equation for the update of the individual velocities. If ${\vec{d}}_i$ is the direction of motion of agent i then its update equation typically looks like:

$${\vec{d}}_i(t+1)=\frac{1}{n_{in}}\underset{\mathrm{alignment}}{\sum _{j=1}^{n_{in}}{w}_j{\vec{d}}_j\left(t\right)}+\frac{1}{n_{in}}\underset{\mathrm{attraction}∕\mathrm{repulsion}}{\sum _{j=1}^{n_{in}}{f}_{ij}\frac{{\vec{r}}_{ij}\left(t\right)}{\mid {\vec{r}}_{ij}\left(t\right)\mid }}+\underset{\mathrm{noise}}{{\vec{\eta }}_i\left(t\right)},$$

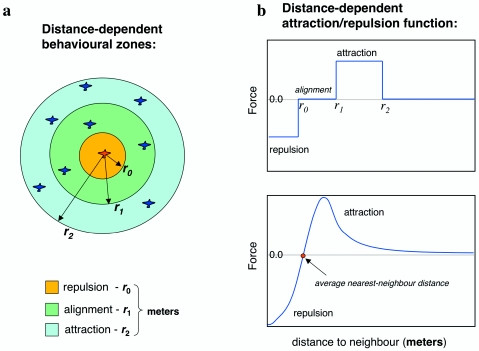
where ${\vec{r}}_{ij}$ indicates the distance vector from agent i to agent j, and ${\vec{\eta }}_i$ is a stochastic noise modeling the uncertainty of the decision-making process. The first term on the right hand side of this equation, alignment, is usually the average over the directions of motion of the n_in interacting neighbors (simple or, more generally, with weights w_j). The second term represents the positional response to neighbors, the “forces” f_ij specifying how agent i is attracted∕repelled by agent j. At short distances it gives a negative increment in heading away from too close neighbors; at larger scales, instead, the increment is positive and towards the average position of neighbors. Most models assume that the interacting neighbors are those within a given region in space around the focal individual. Some models specify behavioral zones of different spatial extent where alignment, attraction, and repulsion occur (Aoki, 1982; Reynolds, 1987; Huth and Wissel, 1992; Couzin et al., 2002)—see Fig. 1. Some others assume a functional dependence of the forces f_ij due to neighbors on distance (Warburton and Lazarus, 1991; Vicsek et al., 1995; Gregoire et al., 2003; Mogilner et al., 2003), the decay scale of this function defining the average region where inter-individual interactions take place (Fig. 1). In all these cases the models have an intrinsic metric nature, since what matters is the distance between an individual and other members of the group.

Figure 1. Behavioral rules in numerical models.

(a) Many models assume discrete behavioral zones in space where the three contributions, alignment, repulsion and attraction, take place. (b) Attraction∕repulsion force (f_ij in the text) as a function of the mutual distance between individuals. Upper panel: in models that assume behavioral zones the force is negative for distances smaller than the repulsion range r₀, it is zero in the region where alignment takes place (r₀<r<r₁), and it is positive within the attraction zone. Lower panel: a schematic representation of a typical force function, repulsive at short range and attractive at larger distances. The equilibrium value where the force is zero (marked with a red dot) determines the average nearest-neighbor distance between individuals and therefore it fixes the density of the aggregation. The force decays to zero at large distances: the decay range plays the same role as the size of the attraction zone.

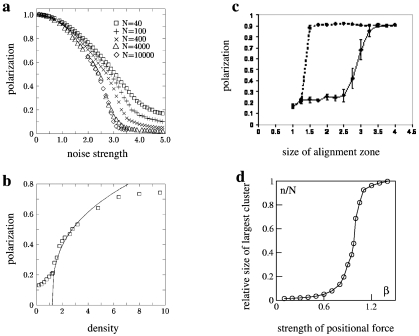
Agent-based models cannot be solved exactly, since the number of individuals is large and the resulting set of coupled dynamical equations formally untreatable. Rather, they are easily implemented using numerical simulations. The main result that these models provide us with is a general one: local rules can indeed produce collective behavior, with an appropriate choice of parameters. This is an explicit demonstration of self-organization, which may seems obvious nowadays, but was less so in the past. More detailed predictions concern both global features, like the shape and dynamics of the group, its average velocity and polarization (degree of alignment between the individual velocities); and structural properties, such as, for example, the distribution of nearest-neighbor distances and mutual orientations, or density variations through the group. Predictions may differ at a qualitative or quantitative level when different rules are used. Modellers explored several kinds of behavioral assumptions, by varying the parameters entering the model, or the variables determining the interaction strength (Parrish, Viscido, and Grunbaum, 2002; Couzin and Krause, 2003). For example, the interaction between two individuals can depend on their distance or also on their mutual orientation, to take into account the blind volume often present in the field of perception. Many authors investigated how neighbor preferences (in angle or distance) can influence collective behavior (see, e.g., Huth and Wissel, 1992). In Couzin et al. (2002) the relative extension of the behavioral zones was tuned to obtain in 3D qualitatively different groups in terms of shape, packing, and degree of alignment [see Fig. 2c]: from swarm-like aggregations (cohesion and low polarization), to toroidal milling groups (high polarization and global angular momentum), and coherent dynamic groups (cohesion, high polarization and low momentum). The effect of the relative strength of the interaction terms was analyzed in Viscido, Parrish, and Grunbaum (2004) and in several cohesion models (see, for example, the morphological and stability analysis of Warburton and Lazarus, 1991; Mogilner et al., 2003; D’Orsogna et al., 2006). Heterogeneities in the behavioral rules were investigated in several papers, by assuming for each individual different speeds, noise, turning rate (Romey, 1996; Couzin et al., 2002), zones extensions (Couzin et al., 2002) and body size (Hemelrijk and Kunz, 2005). These analyses showed that differences among individuals influence the positions occupied within a group (self-sorting) and determine group stratification, shape, and trajectory.

Figure 2. Transition from disorganized to organized collective motion as a function of the model parameters.

The quantity used to pinpoint the transition is the polarization, or global alignment, defined as the modulus of the average normalized velocity of the group $1∕N\mid {\sum }_{i=1}^N{\vec{v}}_i\mid$. In the Vicsek model only alignment is considered and the only two relevant parameters are the noise strength and density, defined as the number of individuals N divided by the whole volume of the simulation box. (a) Polarization as a function of the noise strength: for low noise a coherent moving group (large polarization) is present. (b) Polarization as a function of density: increasing density triggers the transition to collective motion. Reprinted figures from Vicsek T et al., Phys. Rev. Lett.75, 1226 (1995). Copyright 1995 by the American Physical Society. Reprinted with permission of the American Physical Society. (c) Change in polarization as the size of the zone of alignment is increased (bold line) or decreased (dotted line). Reprinted from Couzin ID et al., “Collective memory and spatial sorting in animal groups,” Journal of Theoretical Biology218, pp. 1–11. Copyright 2002, with permission from Elsevier. In this model the authors consider three distinct behavioral zones for repulsion, attraction, and alignment, plus a blind volume behind the focal individual. Only for large enough values of the alignment zone can the collective state be achieved. The degree of alignment depends on the increase∕decrease protocol used (hysteresis), which is typical of first order transitions. (d) Transition from a dispersed gas-like aggregation to a cohesive group in the model of Gregoire et al. (2003), where attraction/repulsion forces are used together with alignment of velocities. The figure shows the relative size of the largest cohesive cluster (number of individuals belonging to the cluster divided by total number of individuals) as a function of the strength of the attraction∕repulsion force. Reprinted from Gregoire G et al., “Moving and staying together without a leader,” Physica D181, pp. 157–170. Copyright 2003, with permission from Elsevier.

The final aim of all these attempts is to find the appropriate model to describe specific animal groups and, at the same time, unveil the microscopic origin of their aggregation. In this respect, comparison with empirical data has a prominent role, as I will discuss.

The perspective of agent-based models is that behavior at the global scale can be understood in terms of the statistical aggregate behavior of individual units. From this point of view, the approach is the same as statistical mechanics for physical systems, the theory that derives the macroscopic behavior of materials from the microscopic behavior of their components. This analogy has stimulated physicists to develop their own models of self-organized motion (Vicsek et al., 1995; Czirok et al., 1996; Gregoire et al., 2003;Gregoire and Chate, 2004). These models are simpler than those developed by biologists, and the very questions they wish to address are more conceptual and less related to real biological instances. Their aim is to build the “minimal” setup necessary to produce a cohesive moving group. Only the ingredients that are thought to be indispensable to achieve grouping are considered, and in the simplest possible form. In this way the number of parameters is kept to a minimum and their whole space can be exhaustively investigated. For example, in their model of Self-Propelled Particles (SPP), Vicsek et al. considered only alignment without attraction in the microscopic rules and assumed velocities to be constant in modulus. They showed with numerical simulations in two dimensions (2D) that, in a confined space, this is sufficient to produce polarized flocks. They also investigated the transition from disordered aggregations to ordered groups, as the noise strength or the number of individuals is varied [Figs. 2a, 2b]. Jadbabaie et al. (2003) provided us with a theoretical explanation for this behavior, demonstrating that flocking is achieved as long as the network of agent interactions remains connected in time (Tanner et al., 2007). In the Vicsek model this condition is realized when the density of particles/agents is sufficiently large, so that each individual remains within the interaction range of its neighbors. However, when the available space becomes large enough, dynamical fluctuations can drive individual agents too far and cohesion is lost: attraction between individuals must be introduced to ensure cohesion in open space (Gregoire et al., 2003). The presence of positional forces (attraction and repulsion) complementing the orientational component (alignment of velocities), gives rise to a nontrivial phase diagram in terms of the structure of the aggregation, where the group can be more or less ordered in space according to the relative strength of the two contributions [Fig. 2d].

Models of self-organized motion have been extensively studied in 2D. Many animal groups live, however, in three dimensions, so that it became progressively more important to extend and generalize numerical simulations also in 3D. This has been done recently (Couzin et al., 2002; Chaté et al., 2008; Gönci et al., 2008; Hemelrijk and Hildenbrandt, 2008) showing that many of the qualitative results obtained in 2D also hold in 3D. Achieving cohesion and synchronization becomes more difficult, though, as the space dimension is larger.

Finally, we note that in existing models birds interact in pairs, trying to mutually align. When looking at the force experienced by one single bird, this comes from all the interacting pairs to which it belongs (i.e., the pairs with its interacting neighbors j=1,…n_in—see equation above). Whether multiple simultaneous interactions are relevant is an open question for future research.

From micro to macro: Eulerian models

Eulerian models represent a complementary approach to agent-based models. They work at a coarse-grained level: instead of describing the dynamical evolution of each individual, space is represented as a lattice and the number of individuals inside each cell is followed in time. The relevant variables become in this case the number of individuals $n(\vec{x},t)$ in a cell located at position $\vec{x}$ of the lattice at time t (or, alternatively, the density $n(\vec{x},t)∕V_{\mathrm{cell}}$), and the average velocity $\vec{v}(\vec{x},t)$ possessed by individuals in that cell. When the continuum limit is considered (in space and time) this approach leads to convection-diffusion equations for the population density (Okubo, 1980), much in the same way hydrodynamic equations can be derived for fluids. From a conceptual point of view, how to perform this limit is a delicate task, if one wants to keep track of the peculiar way individuals take their decisions by exploiting local cues, for example by averaging over their neighborhood (Grünbaum, 1994; Durrett and Levin, 1994). Alternatively, partial differential equations for the population density can be written heuristically, by including all the relevant diffusion, convection, and interaction terms.

Whether adopting agent-based (sometimes called Lagrangean) or Eulerian models depends on the system studied, on the question addressed, and on the scale of interest (Flierl et al., 1999). Dealing with coarse-grained variables (the cell population and average velocity), Eulerian models implicitly assume that a group is already formed, with a large enough number of members to make the coarse graining meaningful. Besides, they cannot address those features that occur on scales smaller than the cell size, and on times shorter than the time needed for information to propagate outside the cell. In this respect, agent-based models are more appropriate to investigate the mechanisms of decision making and group formation, and how behavioral attitudes translate into global features. Eulerian models are prominently used to describe the population evolution on long time scales and to study patterns that develop at large spatial scales (as compared to the interaction range) like the formation of patches and the propagation of density waves through the aggregation (Flierl et al., 1999). For example, the existence of traveling band solutions is analyzed in Mogilner and Edelstein-Keshet, 1999, using continuum advection-diffusion equations for swarming behavior. Propagating density waves are also found in Toner and Tu, 1998, where a continuum model for self-propelled particles is introduced. Here, the authors formulate hydrodynamic equations for the coarse-grained density and velocity of birds, very close in spirit to the Navier–Stokes equations for fluids. The model is then analyzed with techniques developed for nonequilibrium dynamical systems in condensed matter physics (e.g., scaling, the renormalization group), and quantitative predictions computed for the long-distance, long-time behavior of density and velocity correlation functions. Similar hydrodynamic equations can be derived from Viscek-like individual rules starting from the Boltzmann equation (Bertin et al., 2006).

Phenomenological models

Eulerian models deal with populations; still they retain much of the complexity of agent-based models, fully accounting for correlations between individuals at several length scales. These correlations derive from the local interactions between individuals and represent one of the most striking features of animal groups like flocks, swarms, and schools. As a counterpart, even if a large literature exists both in biology and physics, the analysis of these models is far from trivial.

Sometimes the collective behavior to be explained and the questions to be answered can be addressed within a simpler mathematical formulation. A paradigmatic case is when individuals interact indirectly via chemical cues: the number of individuals performing a certain task depends on the amount of perceived chemical, which in turn depends on the number of individuals depositing it. The most renowned example is the one of ant trails (Wilson, 1971). When a scout ant discovers a food source, after feeding, it deposits pheromone on its way back to the nest. Other ants that meet the trail use it to find the food and on the return journey they reinforce it in turn, by laying other pheromone. In this example, the mechanism producing the collective pattern is local mass recruitment and the consequent positive feedback due to pheromone reinforcement. Given a set of possible paths, a set of nonlinear equations can be written, describing the evolution in time of the flows of foragers along the paths (Goss et al., 1989; Beckers et al., 1992; Edelstein-Keshet, 1994). The models specify mathematically how local recruitment occurs, i.e., proportionally to the pheromone concentration on the trail. Similar phenomenological models have been used for several instances of collective behavior. They have the great advantage of being mathematically simple providing with quantitative predictions in terms of a small number of parameters. From this point of view, they represent a powerful mean to test the underlying mechanisms (mass recruitment, positive feedback, amplification of local fluctuations) in those systems where the parameters entering the model can be empirically measured and∕or tuned.

EMPIRICAL STUDIES

Several experiments and empirical observations on animal groups have been performed in the last 50 years to test theoretical hypothesis on self-organization and empirically characterize grouping behavior.

Some of the most studied systems are aggregations of social insects, like ants, which can be kept under laboratory control even in large numbers, due to the small size of the individuals. For example, the mechanism of pheromone-led recruitment in ant trails has been deeply investigated. Experiments were performed where foragers could choose between two distinct paths leading from the nest to the food source (Goss et al., 1989; Beckers et al., 1992). If the paths had the same length only one of them was selected, each with the same probability: the recruitment mechanism indeed enhances initial fluctuations by positive feedback polarizing the flux on a single trail. On the contrary, when one path is shorter than the other, the very same mechanism allowed foragers to spontaneously select the optimal one since pheromone accumulation along the shorter path occurs faster, catalyzing recruitment and breaking the symmetry. In all these cases the models’ predictions for the distribution of ants along the trails were consistent with the empirical results. More recently this approach was modified to investigate traffic along ant trails under crowded conditions: the same setup with two possible branches from nest to food source was studied, with a variable number of individuals and branch widths (Dussutour et al., 2004). A transition from asymmetrical traffic at low densities (one trail established) to symmetrical traffic at high crowding (both branches used by foragers) was observed and successfully described with a nonlinear model for traffic flows. Another experiment (Beekman et al., 2001) showed how the size of the colony (and in particular the number of foragers) could induce a discontinuous transition from disorganized (no pheromone trail established, only random search) to organized (trail-based) foraging, due to pheromone volatility. Also in this case, a simple mean-field nonlinear model can be used to predict the occurrence of the transition (see also Rauch et al., 1995; Bonabeau et al., 1998). Other interesting examples of experiments on self-organized behavior can be found in Seeley et al., 1996 (recruitment dance in honeybees); Amé et al., 2006 (shelter selection in cockroaches), Theraulaz et al., 2002 (formation of cemeteries in ants).

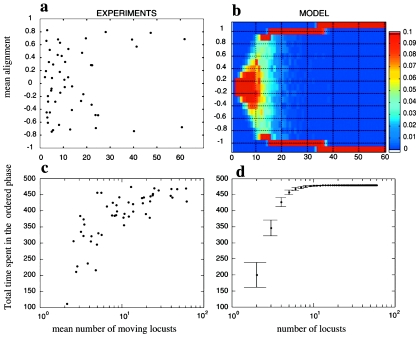
The occurrence of a transition from disordered to ordered behavior tuned by density was also recently observed in marching locusts (Buhl et al., 2006). Hoppers of desert locusts were placed in a circular arena and their dynamics observed with several values of the density of individuals. The analysis of the collective alignment (average polarization) showed a transition from a disorganized state of locusts moving independently to coordinated marching bands at larger densities [Figs. 3a, 3c]. A one-dimensional version of the Vicsek model was used to describe the transition [Figs. 3b, 3d]. Similar results were also obtained in fish schools (Becco et al., 2006) and cells (Szabó et al., 2006), indicating that such simple models of self-organized motion well depict the onset of collective behavior.

Figure 3. Transition from disorganized to collective motion in locust nymphs.

Locusts were placed in a ring-shaped arena and the alignment calculated as the average instantaneous orientation (relative to the center of the arena) for all moving individuals. Results of the experiment were compared with numerical simulations performed on a variant of the one-dimensional Vicsek model. (a) Mean alignment (averaged in time) as a function of the number of moving locusts; each point represents an experimental trial. (b) Distribution of the mean alignment in numerical simulations (1000 samples). The behavior of the instantaneous alignment is intermittent for intermediate values of the number of locusts, passing from aligned to unaligned states over time. (c) and (d) Total time spent in the aligned phase in experiments and simulations. From Buhl J et al. (2006), Science312, pp. 1402–1406. Reprinted with permission from AAAS.

All previous examples concern collective patterns that occur in one- or two-dimensional spaces. Some of the most striking examples of animal grouping, such as bird flocks, fish schools, and insect swarms, occur, however, in three dimensions. The study of animal groups in 3D is much more demanding (Parrish and Hammer, 1997), especially for what concerns experiments. This difficulty is related to the fact that individuals often have larger sizes and naturally move in a much larger environment. Laboratory control can be problematic, while techniques for field observations may prove extremely complicated.

The first landmark contribution to the field of empirical 3D studies was performed by Cullen and co-workers (Cullen et al., 1965; Pitcher and Partridge, 1979; Partridge et al., 1980; Partridge, 1980) who analyzed groups of up to 50 fishes in laboratory tanks. Schooling behavior was investigated in aggregations of several sizes, and different species (from weakly facultative to obligate schoolers). A characterization of the 3D structure and shape of the groups was performed, by looking at occupation volumes and nearest-neighbor distributions in distance and angles. Even if, as I will discuss, the statistical analysis suffered of some methodological problems, this was the first attempt to establish a quantitative basis for 3D observational data. Many more recent studies also focused on fish (Van Long et al., 1985; Parrish and Turchin, 1997; Viscido et al., 2004; Tien et al., 2004), since experiments can be performed in laboratory tanks, under variable conditions. Moreover, fishes are often studied in shallow water, where they form pseudo-2D schools, making the experimental analysis much easier.

Obtaining data for birds is more difficult, since this must be done in the field. After some early pioneering works (Miller and Stephen, 1966; Van Tets, 1966), Major and Dill reconstructed birds’ positions in groups of up to 70 individuals (Major and Dill, 1978). These flocks, however, were moving from the feeding site to the roost, and they were not very cohesive. Pomeroy and Heppner obtained for the first time the individual trajectories in groups of up to 16 birds (Pomeroy and Heppner, 1992). More recently, Budgey studied flocks of up to 30 birds (Budgey, 1998).

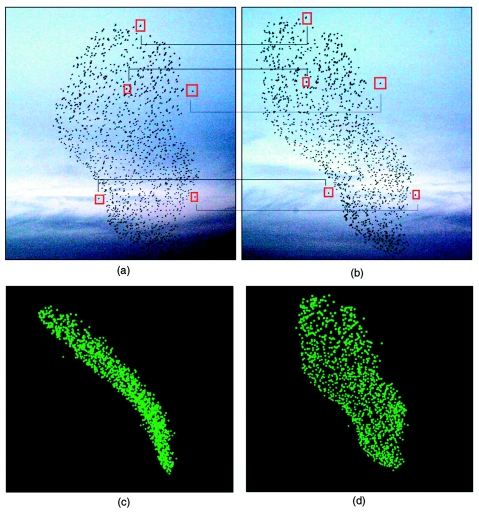
In all these cases, however, the number of individuals in the group was rather small (few tens), and the group arrangements were often loose. The reason is essentially a technical one. To reconstruct the 3D position of an object, optical techniques (stereometry, orthogonal method, shadow method) require putting in correspondence (matching) different images of it (Osborn, 1997; Hartley and Zisserman, 2003). For example, when using stereoscopic photography with animal groups, two images of the same group are shot simultaneously from different observation points. Then, every individual on one photograph must be matched with the corresponding individual in the second photograph [see Figs. 4a, 4b]. Only at this point, stereometric formulas can be applied to recover from each pair of matched individuals in the photo the physical 3D coordinates of the individual in space. The matching problem can become extremely severe when groups are large and compact: photographic images of flying flocks are typically very dense sets of almost featureless points (Cavagna et al., 2008c).

Figure 4. A typical flock analyzed in the empirical study of Ballerini et al. (2008a).

This group consists of 1246 starlings, flying at approximately 70 m from the stereoscopic apparatus at about 11 ms⁻¹. (a) and (b) Left and right photographs of the stereo pair, taken at the same instant of time, but 25 m apart. To perform the 3D reconstruction, each bird’s image on the left photo must be matched to its corresponding image on the right photo. Five matched pairs of birds are visualized by the red squares. Once the matching is performed, the 3D coordinates of each individual bird can be retrieved using stereometric formulas. (c) and (d) 3D reconstruction of the flock under two different points of view. Panel (d) shows the reconstructed flock under the same perspective as the right photograph (b). Reprinted from Ballerini M et al. (2008a), Proc. Natl. Acad. Sci. USA105, pp. 1232–1237. Copyright 2008, National Academy of Sciences of the USA.

Due to these limitations, only small groups were analyzed until recently, preventing for a long time an exhaustive comparison between theories of self-organized grouping and empirical results. Collective behavior in natural groups very often involve aggregations of an enormous number of individuals (from hundreds to tens of thousands) and one may wonder whether the mechanism for group formation is the same when small systems are considered. Besides, the analysis of small systems is very strongly biased by border effects, since a large percentage of individuals are located on the boundary of the aggregation. Often this bias has not been taken into account in the statistical analysis of empirical data: the risk is that of looking at “surface properties,” which depend on the shape of the group and are therefore highly fluctuating, rather than “bulk” properties, that are much more stable and only depend on the inter-individual interactions (Cavagna et al., 2008b).

Analysis of small systems, both with numerical simulations and experiments, can be useful to understand how individual behavior changes when socialization occurs, and to what extent coordination can be achieved, even with few individuals, and eventually controlled. This problem may have important technological applications in artificial systems of controlled units and has attracted much interest at a theoretical level (Paley et al., 2007). When the focus is on the emergence of collective behavior on large scales, however, analysis of large enough groups is mandatory.

Recently, in Ballerini et al. (2008a, 2008b) an observational study of flocking behavior in starlings has been performed, where groups of up to 3000 birds were reconstructed (Fig. 4) and empirical 3D data statistically analyzed. This work improved previous benchmarks in various respects. From a technical point of view, using statistical mechanics, optimization theory, and computer vision techniques, the matching problem was solved allowing for the 3D reconstructions of large groups (Cavagna et al., 2008c), see Fig. 4. Besides, analysis of the data was performed taking into account border effects, and with techniques from statistical mechanics and physics of liquids. In this way, for the first time, morphological, dynamical, and structural features of flocking events were quantitatively characterized for large groups of individuals. Flocks were found to be relatively thin and to slide parallel to the ground, a feature that is completely missed by any two-dimensional reduction of the group, as the one performed by simple photographs or far away observers. The groups were very variable in size, density, volume, and velocity, allowing for a systematic analysis of mutual correlations between macroscopic properties. For example, density and nearest neighbor distance were found to be independent on the number of individuals belonging to the group, contrary to previous observations on small groups. The shape of the flocks exhibited constant proportions, despite their volumes spanned a large range of values, suggesting the presence of an underlying self-organizing mechanism. Having large groups also allowed an accurate determination of how individuals are distributed through the flock. The angular distribution of neighbors around a focal individual revealed a strong anisotropy, where nearest neighbors are more likely to be found on the sides rather than in the direction of motion, as also suggested by observations in small groups of fishes (Partridge et al., 1980). The distribution of nearest neighbor distances was quantitatively characterized showing that flocks are relatively sparse systems of interacting units. The fluctuations in density through the aggregation could be analyzed, revealing that the groups are denser at the border than in the center. The dynamics of the group as a whole was analyzed, indicating that flocks perform peculiar turning maneuvers where the shape remains approximately unaltered and velocity rotates with respect to the flock’s main axes. All these findings could be obtained because the sample statistics were appropriate (natural aggregations in the field) and groups were large.

DISCUSSION

Empirical data, particularly on large groups, can provide a reliable characterization of the mechanistic laws of animal grouping. Models, on their part, can elucidate how specific local rules lead to certain collective patterns. This information altogether can help to better understand the phenomenon of grouping. In this respect, there are several issues to be addressed: (i) theoretical predictions must be compared to empirical results, to select successful models and explain the mechanisms of group formation; (ii) appropriate conceptual and methodological tools must be developed to deal with data analysis and interpretation; (iii) the function of grouping must be investigated under a more general biological perspective.

Testing model assumptions with empirical data

An empirical quantitative description of grouping is the starting point to retrospectively test the behavioral assumptions of theoretical models. Sometimes these assumptions may only need fine tuning, sometimes, as reasonable as they may appear, they could require deep revision. The analysis performed on starlings offers an explicit example of this strategy. Individual birds were found to have a region around them where neighbors did not penetrate (Ballerini et al., 2008b), consistently with the repulsion zone assumed by models. The extension of this region is of the order of the wingspan and provides with a quantitative value to “feed” models for better predictions. At larger scales, however, interactions between individuals were found to depend on the “topological” distance (whether two birds are first, second, third . . . neighbors) rather than on metric distance (how far apart they are). It was shown that each bird interacts with a fixed number of neighbors (six-seven), irrespective of their distance, rather than with all the neighbors within a well-defined region in space—as assumed by the vast majority of agent-based models (see Fig. 5). The authors argued that this topological feature is indispensable to maintain cohesion of the groups in spite of large density fluctuations, which are frequent in flocking due to predator attacks. In fact, under a perturbation the mutual distances between some individuals may increase beyond any presumed interaction range or zone, causing fragmentation in smaller groups and stragglers in the case of distance dependent interactions (very rarely observed in starling aerial display). Numerical simulations in simple 2D models confirmed this hypothesis, suggesting that topological interactions, which are well known to occur in social networks, may play an important role also in biological systems. This result suggests a new kind of microscopic rule to be implemented. A few models already incorporate numerical preferences (Inada and Kawachi, 2002) or topological constraints (Gregoire et al., 2003) together with distance dependent interactions. A purely topological response, however, has never been tested (with the exception of the simulations in Ballerini et al., 2008a). A step in this direction is in Hemelrijk and Hildenbrandt (2008), where metric interactions were assumed, but with a range that rescales with the local density, making the interaction de facto topological. Whether topological interactions are limited to starlings (or birds) or represent a more general paradigm is an interesting open question. Empirical studies on different species are necessary to investigate this issue.

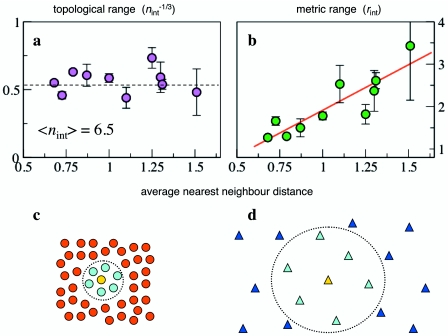
Figure 5. To investigate the nature of the inter-individual interactions in starling flocks, Ballerini et al. (2008a) considered the interaction range measured in meters (metric range) and in number of intermediate neighbors (topological range), for several flocks with different average nearest-neighbor distance (NND) and, therefore, density.

(a) Topological interaction range n (to power −1∕3) as a function of the NND. (b) Metric interaction range as a function of NND. The topological range fluctuates around an average value (⟨n⟩=6.5), while the metric range is strongly correlated with NND. This shows that every bird interacts on average with 6–7 neighbors, irrespective of density. Figures reprinted from Ballerini M et al. (2008a), Proc. Natl. Acad. Sci. USA105, pp. 1232–1237. Copyright 2008, National Academy of Sciences of the USA. (c) and (d) Schematic illustration of a topological interaction: in two groups of different density the number of interacting neighbors is the same, but the metric interaction range is different.

The finding that each bird interacts with its first seven neighbors has other interesting consequences. A possible explanation for this number is related to the prenumeric abilities of individual birds. Empirical studies performed on several species (Nieder, 2005; Emmerton and Delius, 1993) have shown that seven is the maximum numerosity a bird can discriminate. It is then plausible than when flying in a group each individual keeps track of at most seven neighbors. This shows that the cognitive abilities of individuals may determine in a non-trivial way their behavioral rules.

The analogy with physical systems: conceptual and methodological tools

The problem of group formation is, within certain respects, independent of the nature of its components, and results in animal collective behavior have indeed triggered interdisciplinary interest and applications. Physics has provided an important conceptual paradigm, which has been extensively used in developing numerical and mathematical models. Individuals in a group are treated as simple interacting units, and global features derived from the local microscopic interactions, much in the same spirit as macroscopic observables are computed for physical systems of particles, molecules, or spins. The analogy with physics proved extremely useful, but nevertheless has several limits. In physical systems the individual units can be fully characterized and the nature of the interactions between them is known ab initio. On the contrary, in biological systems the individual features specified in the models always depend on some preconceptual simplification of a much more complex behavior, and interactions between individuals do not come from physical laws but rather derive from complicated biological processes. This may lead to crucial differences. A vivid example is the result found in starlings, where individuals exhibit topological interactions: in physics all the interactions depend on distance and systems of particles could never display the behavior observed in starling flocks. In this case, the cognitive abilities of the individuals make the difference, determining the nontrivial nature of the interactions. More generally, animals are not passive units, but adaptive individuals. They can modify their behavior substantially according to environmental, social, or biological cues and they can learn, from past experience or from other individuals. As a consequence, the strength or even the nature of inter-individual interactions can vary in time. In this way, the signal to noise ratio can be endogenously tuned leading to different collective patterns. This is another difference with physical systems, where interactions are given once for all, and the global state (e.g., ordered or disordered) can be changed only tuning external parameters (e.g., temperature, pressure, magnetic field) (see Detrain and Deneubourg, 2006, for a thorough discussion of these issues).

Apart from the mechanistic analogy, physics provides sophisticated methodological tools of analysis, which can also be applied to biological groups. In particular, it suggests appropriate observables to quantify collective behavior in large systems. For example, a system of physical particles subject to attractive mutual interactions and short-range repulsion may be found in several states (gas, liquid, solid) and display several dynamical behaviors. Liquid theory tells us what to compute to quantify the internal structure of the system, susceptibility to perturbations, dynamical features, and diffusion properties (Allen and Tildesley, 1989; Torquato, 2002; Binder and Kob, 2005). The same quantities can also be computed in animal groups (see Ballerini et al., 2008b; Cavagna et al., 2008b and 2008a for examples in starling flocks).

Most of the data analysis performed in empirical observations, experiments, and numerical simulations on animal groups have focused on average aggregate quantities and one-point functions. Examples are the average velocity of the group, the polarization, or the local density of individuals. A higher level of quantitative investigation, very much used in physical systems, is provided by two-point correlation functions. These functions describe how the behavior of individuals in a certain region of the group and at a certain time is related to the behavior of individuals in another group location and∕or at another time.

Spatial correlation functions can help to characterize the structure of the group and how individuals are positioned one with respect to the other. Density-density correlations, for example, exhibit different (and identifiable) patterns in correspondence of disordered or crystalline arrangements of individuals. An empirical analysis of these correlations in starling flocks (Cavagna et al., 2008a) showed that, even if flocks exhibit some spatial structure (somewhat intermediate between a liquid and a gas), a crystalline arrangement must be excluded.

More generally, correlation functions describe how information and perturbations propagate through the group measuring the mutual sensitivity in positional and speed changes of members. Efficiency in information transfer is a key feature of animal grouping, which may explain its evolutionary success: a quantitative analysis of this efficiency is therefore of primary theoretical interest. Despite some empirical analysis on small systems (see, e.g., Aoki, 1980; Parrish and Turchin, 1997) a systematic analysis of two-point correlations has not been performed yet. Accurate measurements of these functions over their full range require large statistics and, therefore, data sets relative to large groups. The same is true when dealing with diffusion properties, which describe how individuals move through the group and how they exchange their mutual positions. Theoretical predictions on diffusion typically concern large-scale behavior (see, e.g., Toner and Tu, 1998) and one may need large enough groups (and long enough sampling) to empirically test them.

Gathering data on large groups thus appears as a crucial prerequisite for a more detailed statistical analysis. This may be technically demanding, as the difficulties encountered to get 3D stereoscopic reconstructions show. A similar problem is given by the dynamical tracking needed to retrieve the trajectories of individuals through the group. These trajectories are the starting point to compute diffusion properties and multi-time correlation functions, and are an important objective for future empirical research.

Biological function of grouping

From a biological perspective a crucial issue is to understand what is the function of grouping and how selective pressure acts on individuals to promote functional properties at group level (Parrish and Edelstein-Keshet, 1999).

Living in groups can be advantageous within many respects. One of the traditional motivations, especially invoked for bird flocks and fish schools, is associated with the anti-predatory response (Pitcher and Parrish, 1993; Vine, 1971; Parrish, 1992). Belonging to a group of similar individuals guarantees anonymity and decreases the probability of being caught (dilution effect). Moving together also confuses the ability of predators to focus on an individual and capture it (confusion effect). Being in a group of many, the probability of detecting predator attacks increases (many eyes hypothesis – see Krause and Ruxton, 2002). Besides, the strong correlations present between members of the group allow information on incoming attacks to propagate: the response of few individuals, directly aware of predators, can trigger collective escape maneuvers thanks to the imitative nature of the individual dynamics. This same mechanism, where a local signal is reinforced and transferred by imitation, can be used to convey different kinds of information such as the presence of obstacles (Goss et al., 1989), or the distribution and location of resources (Seeley et al., 1991; Pitcher and Magurran, 1983), more informed individuals dragging the whole group to the preferred destination (Couzin et al., 2005). Similarly, social interactions can improve exploitation of environmental gradients (taxis), allowing for a better detection of even mild signals (Grünbaum, 1997). All these features represent adaptive benefits, which can be invoked to explain the evolutionary success of animal grouping. In this respect, empirical analyses that quantify the efficiency of information transfer are particularly useful and two-point correlation functions are, as I have discussed, a possible tool. Besides, it would be desirable to obtain data on response events (e.g. when a predator attack occurs). Unfortunately, escape strategies typically involve fast changes in shape, density, and direction of the group, difficult to retrieve with actual technologies. From a theoretical point of view, models can elucidate how information transfer and response to external stimuli can be optimized within a given class of behavioral rules. In general terms, group members average the “signals” (orientational and positional coordinates) coming from their neighbors. In so doing, if the relevant information is shared, to some extent, by all neighbors then the average suppresses noise, enhancing propagation of the signal. If only a few neighbors have the relevant information, however, it can be damped by the average and inefficiently propagate. These two effects have been investigated, with particular attention to the number of interacting neighbors, in the context of social klinotaxis (Grünbaum, 1997) and anti-predatory response (Inada and Kawachi, 2002).

Another issue concerns the “robustness” of collective behavior. We expect groups to sustain efficiently external perturbations and environmental changes. This means, for example, that under predator attacks, not only must information be propagated fast, but also cohesion should be retained. This is what actually occurs in many natural groups: for example, bird flocks, in spite of extraordinary maneuvers and density changes, rarely disaggregate. One may wonder what is the appropriate mechanism to ensure such a robust cohesion. Topological interactions, as the ones observed in starlings, provide a possible explanation: if each individual interacts with a fixed number of neighbors irrespective of their distances, density changes (and therefore variations in mutual distances) do not affect the strength of social relationships and the degree of cohesion remains the same. Simulations on simple 2D models indicate that topological interactions are more efficient than metric ones to maintain cohesion under perturbations (Ballerini et al., 2008a). Still, further analysis is necessary to investigate this hypothesis in 3D models, and to empirically assess under what circumstances and in which species topological interactions are prevalent.

Cohesion needs to be robust also with respect to endogenous stresses. Not all positions in a group are equivalent in terms of individual fitness, and those that are advantageous in certain circumstances (defense, foraging, migration, etc.) may not be in others (Krause, 1994). Individuals must experience a reasonable trade-off between costs and benefits to explain persistence of aggregation (Hammer and Parrish, 1997). Thus, the same mechanisms leading to group formation must also account for an appropriate redistribution of risks within the group members. For example, the finding that starling flocks are denser on the border than in the center may be related to risk avoidance strategies. Further empirical analysis of how individuals are positioned within group and dynamically rearrange, complemented by appropriate modeling exercise, can help to elucidate this point.

CONCLUSIONS

Theoretical models and empirical studies progressively improved our understanding of animal collective behavior. Several mechanisms driving group formation are now well understood at a theoretical level, and experimentally verified. These mechanisms appear to be rather general: global coordination from local rules; positive feedback based on neighbors’ imitation; local recruitment; density-driven transitions from disorganized to collective motion. Within such a general framework, models then perform detailed assumptions to describe exactly how these mechanisms occur in a specific biological system. In some cases, simple models fully account for the empirical evidence (as in ant trail experiments, or for the transition of locust nymphs from disorganized groups into ordered marching bands). More generally, however, models have been tested only on small groups and their predictive power is still to be ascertained. Recently, field observations provided with large data sets for flocking birds in 3D. These data revealed unexpected features of the inter-individual interactions, showing how crucial an empirical feedback can be in testing models’ assumptions. The importance of obtaining empirical data for large systems cannot be overstressed and represents one of the major challenges for future research. This will also allow a more detailed analysis of how information transfer and response to perturbations occur in large groups, leading to a better understanding of the biological function of grouping.

Observations and experiments in three dimensions nowadays require sophisticated techniques of computer vision and optimization theory. Large data sets offer the possibility of new types of analysis and the expertise matured in other fields, of longer quantitative tradition, may become precious. Therefore, a multi-disciplinary approach seems indispensable to tackle the many aspects of theoretical modeling and empirical investigation of animal groups.