Abstract
Contemporary fetal growth standards are created by using theoretical properties (percentiles) of birth weight (for gestational age) distributions. The authors used a clinically relevant, outcome-based methodology to determine if separate fetal growth standards are required for singletons and twins. All singleton and twin livebirths between 36 and 42 weeks’ gestation in the United States (1995–2002) were included, after exclusions for missing information and other factors (n = 17,811,922). A birth weight range was identified, at each gestational age, over which serious neonatal morbidity and neonatal mortality rates were lowest. Among singleton males at 40 weeks, serious neonatal morbidity/mortality rates were lowest between 3,012 g (95% confidence interval (CI): 3,008, 3,018) and 3,978 g (95% CI: 3,976, 3,980). The low end of this optimal birth weight range for females was 37 g (95% CI: 21, 53) less. The low optimal birth weight was 152 g (95% CI: 121, 183) less for twins compared with singletons. No differences were observed in low optimal birth weight by period (1999–2002 vs. 1995–1998), but small differences were observed for maternal education, race, parity, age, and smoking status. Patterns of birth weight-specific serious neonatal morbidity/neonatal mortality support the need for plurality-specific fetal growth standards.
Keywords: birth weight, fetal development, gestational age, infant mortality, morbidity
Traditional fetal growth standards, also called neonatal anthropometric charts, are based on the birth weight distribution of livebirths at each gestational age (1, 2). Ultrasonographic fetal growth standards, on the other hand, are based on estimates of fetal weight obtained through a longitudinal follow-up of healthy fetuses (3, 4). Both methods have well-recognized disadvantages; traditional fetal growth standards use cross-sectional information from liveborn infants to model longitudinal growth in utero (5), while ultrasonographic measurements suffer from an inability to accurately estimate fetal weight (6).
Perhaps the most important deficiency common to both methods arises because cutoffs for abnormal fetal growth are determined by using statistical features of the weight distribution (e.g., the 3rd or 10th percentile). This reliance on theoretical aspects of weight distributions (without sufficient empirical support) is responsible for various problems including a lack of consensus in the current literature with regard to normative values of birth weight for gestational age in several situations. For example, some fetal growth standards are customized for maternal race (2, 7–10), parity (4, 7, 8, 10–13), plurality (14, 15), height (4, 13), weight (4, 13), and other characteristics, while others are not (16, 17). In fact, some fetal growth standards simultaneously customize their cutoffs on the basis of a multitude of criteria (8, 18). Although proponents of such standards, created by using percentile-based methods, provide post hoc evidence for customization (by demonstrating appropriate perinatal mortality differences (19–21)), this justification has been disputed (22, 23).
Contemporary fetal growth standards are also responsible for other unexpected inconsistencies. Neonatal mortality rate differentials (mortality odds ratios) between small for gestational age infants (at the 3rd or 10th percentile) and appropriate for gestational age infants (e.g., between the 45th and 55th percentiles) vary substantially by gestational age (24, 25). In addition, fetal and neonatal mortality rates are higher among some “appropriate” birth weight for gestational age subsets of births (e.g., those between the 10th and 25th percentiles) as compared with some “abnormal” birth weight for gestational age subsets of births (e.g., those above the 90th percentile) (26).
Because the utility of fetal growth standards is dependent on their ability to identify subpopulations at higher risk for perinatal mortality and serious neonatal morbidity, we proposed that patterns of serious neonatal morbidity and neonatal mortality should directly guide the creation of fetal growth standards. In this paper, we used this alternative, clinically relevant, outcome-based method for creating fetal growth standards to answer a specific question: Do singletons and twins require separate fetal growth standards?
MATERIALS AND METHODS
Data were obtained from the perinatal mortality data files of the National Center for Health Statistics for the years 1995–2002. All singleton and twin livebirths with a clinical estimate of gestation between 36 and 42 weeks born to white or black mothers resident in the United States were included in the study. The exclusion criteria included livebirths with the following attributes: 1) with unknown sex, birth weight, or gestational age; 2) with improbable combinations of birth weight for gestational age (16); 3) with congenital anomalies or those from a state that did not report congenital anomalies; 4) with an ending in neonatal death due to homicide or accident; and 5) with missing information on serious neonatal morbidity. The data set included 32,428,118 livebirths and, after exclusions, 17,811,922 livebirths were available for analysis (a substantial fraction of the data was excluded because California did not report the clinical estimate of gestational age). The same exclusion criteria were applied for both singletons and twins. Because it was not possible to identify twin pairs in the data files, only twin infants affected by the above criteria were excluded.
As per traditions in perinatology (27, 28), the primary outcome of interest was deemed to be serious neonatal morbidity or neonatal death (<28 days after birth). Serious neonatal morbidity included any of the following: 5-minute Apgar score of <4, assisted ventilation for 30 minutes or more, and neonatal seizures. Such perinatal events are very strongly associated with death and serious disability in long-term follow-up studies (29, 30). Gestational age was based on the clinical estimate of gestation because it typically avoids misclassification errors and is more relevant to clinical practice (31–33).
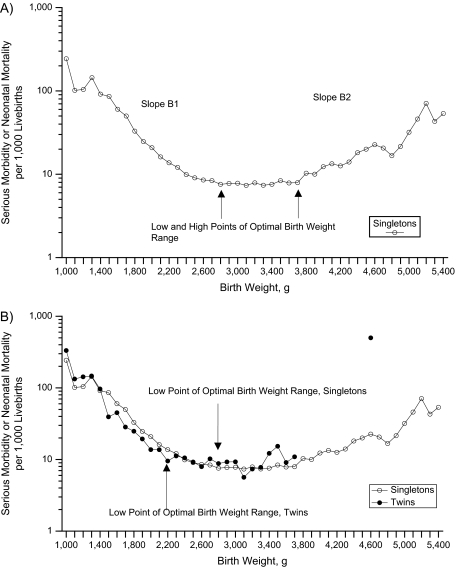
On the basis of empirical observation, we proposed that birth weight-specific patterns of serious neonatal morbidity or neonatal death at each gestational age would follow a specific pattern, that is, that neonatal morbidity/mortality rates decrease exponentially with increasing birth weight in the low birth weight range (Figure 1, part A). This declining pattern then changes to a flat, stable rate at “optimal” birth weight before serious neonatal morbidity/neonatal mortality rates increase with increasing birth weight at very high birth weights. We, therefore, categorized the birth weight range at each gestational age by estimating 3 cutpoints, namely, 1) the birth weight at which the probability of serious neonatal morbidity/neonatal mortality changed from 1 (i.e., no survival) to less than 1 (viability weight); 2) the birth weight at which the inverse relation between birth weight and serious neonatal morbidity/neonatal mortality changed to a flat relation (i.e., the lower bound of optimal birth weight (labeled low optimal weight)); 3) the birth weight at which the flat relation between birth weight and serious neonatal morbidity/neonatal mortality changed to a positive relation (i.e., the upper bound of optimal birth weight (labeled high optimal weight)). We also estimated 2 slopes, namely, 1) the inverse relation between birth weight and serious neonatal morbidity/neonatal mortality over a restricted birth weight range (slope B1); and 2) the positive relation between birth weight and serious neonatal morbidity/neonatal mortality over a restricted birth weight range (slope B2).
Figure 1.
Birth weight-specific rates of serious neonatal morbidity and neonatal mortality at 37 weeks’ gestational age among singletons (part A) and among singletons and twins (part B), United States, 1995–2002.
The estimation of cutpoints and slope parameters was carried out by maximum likelihood methods, by using nonlinear minimization of the appropriate binomial −2 log likelihood. This procedure involved estimation of the above-mentioned 5 parameters that define the piecewise linear model for the log probability of serious neonatal morbidity or neonatal death at a particular gestational age. We incorporated additional parameters in order to allow the model parameters to vary by week of gestation. We also incorporated simple constraints to ensure that the viability weight was nonnegative, the viability weight at any gestation was lower than the low optimal weight at that gestation, the slope B1 was negative, and the slope B2 was positive; 95% confidence intervals based on the asymptotic distribution were estimated around these birth weights.
The primary determinant included in the model was plurality (twins vs. singletons), and the parameters of primary interest were the lower bound of the optimal birth weight range for singletons and twins at each gestational period. These cutpoints disregard the absolute values of serious neonatal morbidity/neonatal mortality among singletons and twins and focus on the birth weight at which morbidity/mortality reaches its nadir. Other determinants added to the model included terms for infant's sex (females vs. males), period (1995–1998 vs. 1999–2002), maternal educational status (<12 years of schooling vs. ≥12 years), race (black vs. white), age (≥35 vs. <35 years), parity (nulliparous vs. parity ≥1), and smoking (yes vs. no). The a priori expectation was that the low optimal birth weight would be different across infants’ sex categories but not across period.
We carried out supplementary analyses to assess the effects of potential inaccuracies in the perinatal mortality files with regard to diagnoses of serious neonatal morbidity by repeating the regression using neonatal mortality as the outcome. In a second supplementary analysis, we used the menstrual-based estimate of gestational age instead of the clinical estimate.
Analysis was carried out by using the SAS nonlinear programming procedure PROC NLP, version 9.1 (SAS Institute, Inc., Cary, North Carolina). The data were randomly divided into quarters for computational ease, and parameters were obtained by combining the 4 sets of results by using weights based inversely on the variance of the estimates. The study was approved by the Research Ethics Board of the IWK Health Centre.
RESULTS
Of the 17,811,922 livebirths included in the study, 17,554,934 were singletons and 256,988 (1.4%) were twins. The overall frequency of neonatal death was 0.57 per 1,000 livebirths, while the frequency of serious neonatal morbidity was 5.4 per 1,000 livebirths (Apgar score of <4 at 5 minutes, 1.1 per 1,000; assisted ventilation for ≥30 minutes, 3.6 per 1,000; and neonatal seizures, 0.6 per 1,000 livebirths). The neonatal death rate was 0.56 per 1,000 livebirths among singletons and 0.95 per 1,000 livebirths among twins; the rate of serious neonatal morbidity was 5.3 and 11.3 per 1,000 livebirths among singletons and twins, respectively.
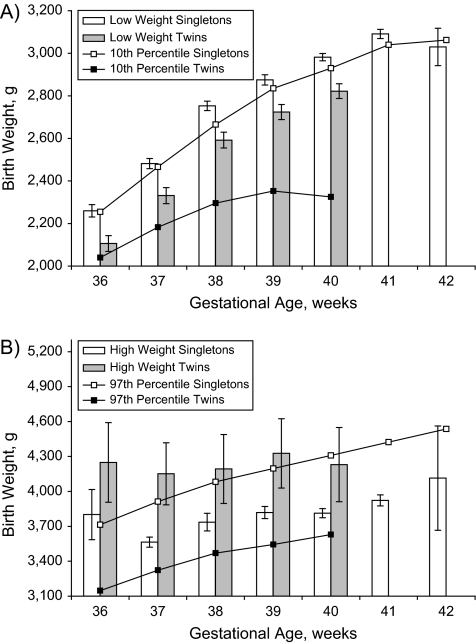
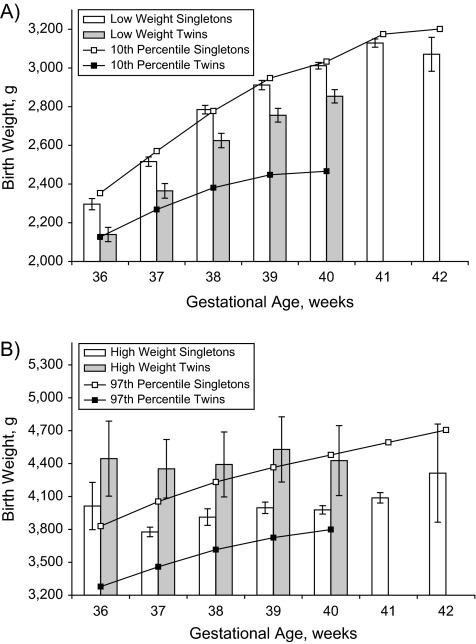
Figure 1, part B, shows the patterns of serious neonatal morbidity/mortality among singletons versus twins at 37 weeks’ gestation, with rates calculated within arbitrary 100-g categories of birth weight (1,000–1,099 g, 1,100–1,199 g, etc.). Although the absolute rates of serious neonatal morbidity/mortality were similar at most birth weights, there were few outcome events at higher birth weights among twins, and visual inspection suggested that singletons and twins had different low optimal birth weight cutoffs. Table 1 provides the point estimates for the low and high optimal birth weights for female and male singleton livebirths from the regression model. The low optimal birth weight at 40 weeks’ gestation was 2,982 g (95% confidence interval (CI): 2,965, 2,999) for females and 3,012 g (95% CI: 3,008, 3,018) for males. Similarly, the birth weight cutoff at the high end of the optimal birth weight range was 3,813 g (95% CI: 3,774, 3,852) for females and 3,978 g (95% CI: 3,976, 3,980) for males. The average low optimal birth weight cutoff for females was 37 g (95% CI: 21, 53) less than the same value for males, while the average high optimal birth weight cutoff for females was 206 g (95% CI: 168, 244) less. The low optimal birth weight cutoffs were generally close to the 10th percentile, and the high optimal birth weight cutoffs were generally close to the 90th percentile of birth weight for gestational age. However, the 10th percentile values were lower than the low optimal birth weight and outside the 95% confidence interval for several of the gestational weeks among females (Figure 2). Among the males, on the other hand, the 10th percentile values were higher than the low optimal birth weight and outside the 95% confidence interval for several of the gestational weeks (Figure 3). The low optimal birth weight cutoff estimates were reasonably precise, except at 36 and 42 weeks’ gestation, while the high optimal birth weight estimates were much less precise.
Table 1.
Estimates of the Low and High Optimal Birth Weight and Percentiles of the Birth Weight Distribution at 36–42 Weeks’ Gestational Age Among Female and Male Singleton Livebirths, United States, 1995–2002
| Gestational Age, weeks | Low Optimal Birth Weight, g |
High Optimal Birth Weight, g |
Birth Weight, g, by Percentile |
|||||
| Estimate | 95% Confidence Interval | Estimate | 95% Confidence Interval | 3 | 10 | 90 | 97 | |
| Females | ||||||||
| 36 | 2,260 | 2,231, 2,289 | 3,801 | 3,585, 4,017 | 1,985 | 2,255 | 3,345 | 3,714 |
| 37 | 2,482 | 2,458, 2,506 | 3,564 | 3,502, 3,608 | 2,211 | 2,466 | 3,572 | 3,912 |
| 38 | 2,753 | 2,731, 2,775 | 3,736 | 3,661, 3,811 | 2,438 | 2,665 | 3,771 | 4,082 |
| 39 | 2,875 | 2,851, 2,899 | 3,819 | 3,767, 3,871 | 2,595 | 2,835 | 3,912 | 4,196 |
| 40 | 2,982 | 2,965, 2,999 | 3,813 | 3,774, 3,852 | 2,693 | 2,930 | 4,025 | 4,309 |
| 41 | 3,091 | 3,069, 3,113 | 3,923 | 3,876, 3,970 | 2,807 | 3,040 | 4,139 | 4,423 |
| 42 | 3,030 | 2,942, 3,118 | 4,114 | 3,667, 4,561 | 2,807 | 3,062 | 4,224 | 4,536 |
| Males | ||||||||
| 36 | 2,296 | 2,268, 2,324 | 4,013 | 3,794, 4,232 | 2,070 | 2,353 | 3,463 | 3,830 |
| 37 | 2,516 | 2,495, 2,537 | 3,777 | 3,710, 3,844 | 2,296 | 2,570 | 3,714 | 4,054 |
| 38 | 2,785 | 2,763, 2,807 | 3,912 | 3,833, 3,991 | 2,523 | 2,778 | 3,912 | 4,232 |
| 39 | 2,912 | 2,888, 2,936 | 3,997 | 3,944, 4,050 | 2,693 | 2,948 | 4,054 | 4,366 |
| 40 | 3,012 | 3,008, 3,018 | 3,978 | 3,976, 3,980 | 2,778 | 3,033 | 4,167 | 4,479 |
| 41 | 3,129 | 3,106, 3,152 | 4,088 | 4,016, 4,160 | 2,898 | 3,175 | 4,309 | 4,593 |
| 42 | 3,071 | 2,983, 3,159 | 4,313 | 3,860, 4,766 | 2,920 | 3,202 | 4,394 | 4,706 |
Figure 2.
Estimates and 95% confidence intervals for the low optimal birth weight and the 10th percentile of birth weight for gestational age (part A) and the high optimal birth weight and the 97th percentile of birth weight for gestational age (part B) among female singletons and female twins, United States, 1995–2002.
Figure 3.
Estimates and 95% confidence intervals for the low optimal birth weight and the 10th percentile of birth weight for gestational age (part A) and the high optimal birth weight and the 97th percentile of birth weight for gestational age (part B) among male singletons and male twins, United States, 1995–2002.
Table 2 shows the same low and high optimal birth weight estimates for twin livebirths. On average, the low optimal birth weight estimate was 152 g (95% CI: 121, 183) less for twins compared with singletons, and the high optimal weight was 402 g (95% CI: 94, 710) more for twins compared with singletons. The low optimal birth weights for twins were substantially higher than the 10th percentile birth weight for gestational age estimates among both male and female twins, and the high optimal birth weight estimates were substantially higher than the 97th percentile, although these latter estimates had wide confidence limits.
Table 2.
Point Estimates of the Low and High Optimal Birth Weight and Percentiles of the Birth Weight Distribution at 36–40 Weeks’ Gestational Age Among Female and Male Twin Livebirths, United States, 1995–2002
| Gestational Age, weeks | Low Optimal Weight, g |
High Optimal Weight, g |
Birth Weight, g, by Percentile |
|||||
| Estimate | 95% Confidence Interval | Estimate | 95% Confidence Interval | 3 | 10 | 90 | 97 | |
| Females | ||||||||
| 36 | 2,106 | 2,069, 2,143 | 4,248 | 3,906, 4,590 | 1,814 | 2,040 | 2,920 | 3,147 |
| 37 | 2,331 | 2,293, 2,369 | 4,151 | 3,884, 4,418 | 1,956 | 2,183 | 3,085 | 3,323 |
| 38 | 2,592 | 2,555, 2,629 | 4,193 | 3,897, 4,489 | 2,070 | 2,296 | 3,232 | 3,470 |
| 39 | 2,724 | 2,689, 2,759 | 4,327 | 4,029, 4,625 | 2,126 | 2,353 | 3,290 | 3,544 |
| 40 | 2,822 | 2,788, 2,856 | 4,230 | 3,911, 4,549 | 2,126 | 2,325 | 3,345 | 3,629 |
| Males | ||||||||
| 36 | 2,139 | 2,101, 2,177 | 4,445 | 4,098, 4,792 | 1,899 | 2,126 | 3,033 | 3,278 |
| 37 | 2,365 | 2,327, 2,403 | 4,353 | 4,093, 4,613 | 2,041 | 2,268 | 3,204 | 3,459 |
| 38 | 2,625 | 2,587, 2,663 | 4,392 | 4,102, 4,682 | 2,135 | 2,381 | 3,350 | 3,615 |
| 39 | 2,756 | 2,718, 2,794 | 4,529 | 4,237, 4,821 | 2,183 | 2,448 | 3,459 | 3,725 |
| 40 | 2,854 | 2,820, 2,888 | 4,427 | 4,119, 4,735 | 2,211 | 2,466 | 3,487 | 3,799 |
Table 3 shows the results of the regression model for low and high optimal birth weight. The low and high optimal birth weights were 3,012 g and 3,978 g for the referent group (singletons at 40 weeks’ gestation). The period (1999–2002 vs. 1995–1998) did not change the low optimal birth weight. Education for <12 years and smoking reduced the low optimal birth weight significantly, while nulliparity, African-American race, and advanced maternal age increased the low optimal birth weight estimate. The magnitude of these effects was small, being approximately the same or lesser than the effect of gender.
Table 3.
Results of Regression Modeling of Birth Weight-specific Serious Neonatal Morbidity and Neonatal Mortality Rates Showing Estimates of Low and High Optimal Birth Weight by Infant and Maternal Characteristics, United States, 1995–2002
| Determinant | Low Optimal Weight, g |
P Value | High Optimal Weight, g |
P Value | ||
| Estimate | 95% Confidence Interval | Estimate | 95% Confidence Interval | |||
| 40 weeks (referenta) | 3,012 | 3,007, 3,017 | 3,978 | 3,976, 3,980 | ||
| 36 weeks | −724 | −752, −696 | <0.001 | 7 | −212, 226 | 0.95 |
| 37 weeks | −491 | −513, −469 | <0.001 | −148 | −216, −80 | <0.001 |
| 38 weeks | −247 | −271, −223 | <0.001 | −53 | −132, 26 | 0.19 |
| 39 weeks | −107 | −131, −83 | <0.001 | 35 | −18, 88 | 0.20 |
| 41 weeks | 99 | 76, 122 | <0.001 | 140 | 68, 212 | <0.001 |
| 42 weeks | 42 | −45, 129 | 0.35 | 335 | −118, 788 | 0.15 |
| Female sex | −37 | −53, −21 | <0.001 | −206 | −244, −168 | <0.001 |
| Twins | −152 | −183, −121 | <0.001 | 402 | 94, 710 | 0.01 |
| Period, 1995–1998 | 1 | −12, 14 | 0.86 | 47 | −3, 97 | 0.07 |
| Education <12 years | −42 | −58, −26 | <0.001 | −106 | −170, −42 | 0.001 |
| Nulliparous | 31 | 18, 44 | <0.001 | 328 | 255, 402 | <0.001 |
| African American | 23 | 8, 38 | 0.003 | −347 | −384, −310 | <0.001 |
| Smoker | −42 | −58, −26 | <0.001 | −310 | −407, −213 | <0.001 |
| Age ≥35 years | 26 | 6, 46 | 0.009 | −54 | −135, 27 | 0.19 |
Referent estimates apply to infants at 40 weeks who are male, singletons, born between 1999 and 2002, with maternal education ≥12 years, parity ≥1, white race, nonsmoking status, and <35 years of age.
Supplementary analyses showed that serious neonatal morbidity was strongly associated with neonatal and postneonatal mortality (neonatal mortality rates were 32.9 and 0.41 per 1,000 livebirths, respectively, and postneonatal mortality rates were 8.0 and 1.4 per 1,000 neonatal survivors, respectively, among those with and those without serious neonatal morbidity). Analyses with neonatal mortality as the outcome showed a −345 g difference in low optimal birth weight between singletons and twins (Table 4). However, the difference in low optimal birth weight for singletons between the 2 models (3,012 vs. 3,244 g among males at 40 weeks) meant that the low optimal birth weight for twins was similar between the 2 models (2,860 vs. 2,899 g among males at 40 weeks). Differences in low optimal birth weight were observed for other gestational weeks, parity, education, and race. The precision of some estimates could not be determined because of problems estimating the covariance matrix. Similar results were obtained with regard to the high end of optimal birth weight and from the model by using gestational age based on menstrual dates (low optimal birth weight for singletons = 3,051 g) (difference between singletons and twins = 391 g, 95% CI: 428, 354).
Table 4.
Results of Supplementary Analyses Showing Estimates of Low Optimal Weight From a Model Based on Neonatal Mortality, United States, 1995–2002
| Determinant | Low Optimal Birth Weight, g |
P Value | |
| Estimate | 95% Confidence Interval | ||
| 40 weeks (referenta) | 3,244 | —b | |
| 36 weeks | −464 | — | — |
| 37 weeks | −284 | −324, −244 | <0.001 |
| 38 weeks | −172 | −220, −124 | <0.001 |
| 39 weeks | −4 | −49, 41 | 0.86 |
| 41 weeks | 140 | 85, 195 | <0.001 |
| 42 weeks | 246 | 77, 415 | 0.004 |
| Female sex | −121 | — | — |
| Twins | −345 | −406, −284 | <0.001 |
| Period, 1995–1998 | 17 | — | — |
| Education <12 years | −60 | −93, −27 | <0.001 |
| Nulliparous | 127 | 92, 162 | <0.001 |
| African American | −185 | −227, −143 | <0.001 |
| Smoker | −244 | −298, −190 | <0.001 |
| Age ≥35 years | 20 | −25, 65 | 0.12 |
Referent estimates apply to infants at 40 weeks who are male, singletons, born between 1999 and 2002, with maternal education ≥12 years, parity ≥1, white race, nonsmoking status, and <35 years of age.
—, could not be determined because of problems in estimation of the covariance matrix.
DISCUSSION
Our study showed that patterns of birth weight-specific serious neonatal morbidity and neonatal mortality identify a low end of the optimal birth weight for gestational age range that differs among singletons and twins between 36 and 42 weeks’ gestation. This difference was substantial, being 152 g (95% CI: 121, 183), in comparison with a smaller difference of 37 g (95% CI: 21, 53) between male and female livebirths. The finding that the low optimal birth weight cutoff was lower for twins than for singletons has important clinical implications, especially from the standpoint of obstetric intervention. Although the estimated fetal weight for gestational age is but one of several different inputs into the decision regarding obstetric intervention, this empirical justification for separate cutoffs for singletons and twins provides an additional rationale for more careful fetal monitoring in multifetal pregnancy.
Standards of birth weight for gestational age are typically used for 3 purposes: 1) obstetric identification of abnormal fetal growth (with medically indicated early delivery an option, given seriously compromised growth); 2) neonatal identification of growth-restricted newborns (for growth monitoring and nutritional supplementation); and 3) identification of populations with high rates of fetal growth restriction for public health surveillance and as a focus for intervention. Creating a standard for this third purpose probably represents the least challenging task, as identifying regional variations, temporal trends, or high-risk subpopulations can be accomplished with an arbitrary but constant standard. Creating standards for the first 2 clinical uses, however, requires an outcome-based, clinically relevant criterion that statistical percentiles of birth weight for gestational age fail to provide. Our alternative methodology attempted to directly address the neonatal need for identifying growth-restricted newborns, since serious neonatal morbidity/mortality rates are higher outside the birth weight range identified by the low and high optimal birth weight cutoffs. In an indirect sense, these cutoffs also provide birth weight for gestational age information for the obstetric identification of growth-restricted fetuses, since neonatal morbidity/mortality patterns are a reflection of fetal health and well-being. However, the absolute values of optimal birth weight for gestational age are of little obstetric use, because estimation of fetal weight is currently inaccurate and obstetricians increasingly rely on other measures of compromised fetal growth, such as umbilical artery systolic/diastolic ratios (34). From an obstetric perspective, therefore, the primary finding of our study relates to the qualitative difference noted in optimal birth weight for gestational age between singletons and twins. This implies a lower birth weight for gestational age threshold for medically indicated intervention among twins relative to singletons. The low optimal birth weight for twins identified in our study was between the 10th percentile of birth weight for gestation for singletons and the 10th percentile of birth weight for gestational age for twins (Figures 2 and 3).
The small difference in the low and high optimal birth weight cutoffs for males and females seen in our study was in line with a priori expectations. The lack of an effect with regard to calendar period was also expected; the pattern of birth weight-specific neonatal morbidity/mortality (at a given gestation) is not likely to be affected by secular increases in birth weight for gestational age (35, 36). The differences noted in the optimal birth weight range with regard to African Americans were unexpected. Previous studies have shown that available customized fetal growth standards for whites and African Americans (10) are not consistent with observed patterns of perinatal mortality seen under the fetuses at risk formulation (37, 38). In addition, the racial differences in low optimal birth weight found in this study were small at 23 g (95% CI: 8, 38). Because such small differences may not be clinically relevant and possibly also confounded by uncontrolled factors, we do not believe that this study supports separate fetal growth standards by race, educational status, parity, smoking, and maternal age.
The approximate concordance between the low optimal birth weight and the 10th percentile of birth weight for gestational age among singletons merits further comment. Pediatric weight-for-age standards, created on the basis of the weights of normal children (39), have used the third percentile (or the equivalent mean minus 2 standard deviations) for identifying growth faltering (analogous to the use of a P value cutoff of 5% for statistical significance under the null hypothesis). Fetal growth standards, on the other hand, have tended to use the 10th percentile of birth weight for gestational age as a cutoff for identifying growth-restricted fetuses/infants. The higher percentile cutoff for fetal growth standards (typically created by using vital statistics data) was intended to account for the mixed normal and abnormal population (i.e., fetuses from complicated and uncomplicated pregnancies) used in standard creation. The approximate concordance between our low optimal birth weight cutoffs and the 10th percentile among singletons is a testament to the general validity of this logic.
The strengths of our study include a methodology that is outcome based and clinically relevant. Moreover, the cutoffs identified were based on the clinical estimate of gestation; this estimate is free from the errors typically present in menstrual-based estimates (31–33) and increases the clinical utility of our findings. The general congruence between the model with neonatal morbidity/mortality versus the model with neonatal mortality also lends support to our inference; gestational age-specific patterns of serious neonatal morbidity are approximately similar to neonatal mortality (40). The large numbers of subjects in the study, despite the exclusion of livebirths likely to negatively affect study results (including those with imputed birth weight, congenital anomalies, etc.), also represent a strength.
The limitations of the study include the data quality weaknesses inherent in large perinatal databases. We excluded stillbirths because their estimates of birth weight and gestational age (at death) are known to be inaccurate (41, 42). A gestational age restriction (36–42 weeks) was required because the number of livebirths aged <36 weeks was relatively small. Our findings are probably generalizable to gestations below 36 weeks, although further work is required to determine optimal birth weights at early gestation. The truncation of the lifecourse in our model (which used livebirths rather than fetuses at risk) may have causal implications (24, 43), even if our comparisons were within determinant categories; for example, the optimal low birth weight for twins was based on patterns of morbidity/mortality among twins. Livebirths in our study represent fetuses who did not deliver before 36 weeks’ gestation. Because the rates of spontaneous and iatrogenic delivery prior to 36 weeks are higher among twins than among singletons, singleton fetuses surviving to 36 weeks are likely different from twins surviving to 36 weeks (especially at both extremes of birth weight). Thus, birth weight for gestational age is probably better viewed as a noncausal predictor of serious neonatal morbidity/mortality (along with other prognostic indicators). The relatively wide confidence intervals and some inconsistent estimates of the high optimal birth weight among twins show that this analytical method is sensitive to a paucity of outcome events. Gestational age misclassification (identification of 40-week infants as 36-week infants) is another plausible explanation for inconsistent patterns, and the higher likelihood of cesarean delivery for larger twins may, in part, explain the infrequent adverse outcomes at high birth weight. Other limitations included potential inaccuracies in the reporting of serious neonatal morbidity (although such errors would not affect our results unless they were differential by gestational age or birth weight) and our inability to treat twins pairs as nonindependent observations (although analyses with Nova Scotia data suggest that this limitation would have had a relatively modest effect on the precision of the estimates in this study). Our analyses also did not incorporate various risk factors, such as birth weight discordance, and we did not use smoothing procedures.
In conclusion, we have proposed a clinically relevant, outcome-based method for developing fetal growth standards that identifies optimal birth weight for gestational age based on patterns of serious neonatal morbidity and neonatal mortality. Substantial differences were noted at the low and high ends of the optimal birth weight range for singletons and twins. Specifically, the low optimal birth weight cutoffs at each gestation (between 36 and 40 weeks), at which the rates of serious neonatal morbidity and neonatal mortality increase, are lower for twins than for singletons. This finding has clinical implications and identifies the need for different thresholds for both obstetric intervention among singleton and twin fetuses and for growth monitoring and nutritional supplementation among singleton and twin infants.
Acknowledgments
Author affiliations: Perinatal Epidemiology Research Unit, Departments of Obstetrics and Gynaecology and of Pediatrics, Dalhousie University and the IWK Health Centre, Halifax, Nova Scotia, Canada (K. S. Joseph, John Fahey, Alexander C. Allen); Departments of Pediatrics and of Epidemiology and Biostatistics, McGill University, Montreal, Quebec, Canada (Robert W. Platt, Michael S. Kramer); Department of Obstetrics and Gynaecology, University of British Columbia, Vancouver, British Columbia, Canada (Robert M. Liston); Department of Pediatrics, University of Alberta, Edmonton, Alberta, Canada (Shoo K. Lee); Departments of Pediatrics and of Community Health Sciences, University of Calgary, Calgary, Alberta, Canada (Reg Sauve); and Maternal and Infant Health Section, Public Health Agency of Canada, Ottawa, Ontario, Canada (Shiliang Liu).
This study was funded by the Canadian Institutes of Health Research (grant MOP-67125) and carried out under the auspices of the Fetal and Infant Health Study Group of the Canadian Perinatal Surveillance System. Dr. Joseph is supported by a Peter Lougheed New Investigator Award from the Canadian Institutes of Health Research. Dr. Kramer is a Senior Scientist of the Canadian Institutes of Health Research.
Although the study proposal and results were discussed in detail at meetings of the Fetal and Infant Health Study Group of the Canadian Perinatal Surveillance System, the funding agency played no role in the design and conduct of the study.
Conflict of interest: none declared.
Glossary
Abbreviation
- CI
confidence interval
References
- 1.Lubchenco L, Hansman C, Dressler M, et al. Intrauterine growth as estimated from liveborn birth weight data at 24 to 42 weeks of gestation. Pediatrics. 1963;32(11):793–800. [PubMed] [Google Scholar]
- 2.Williams R, Creasy R, Cunningham G, et al. Fetal growth and perinatal viability in California. Obstet Gynecol. 1982;59(5):624–632. [PubMed] [Google Scholar]
- 3.Di Battista E, Bertino E, Benso L, et al. Longitudinal distance standards of fetal growth. Intrauterine and Infant Longitudinal Growth Study: IILGS. Acta Obstet Gynecol Scand. 2000;79(3):165–173. [PubMed] [Google Scholar]
- 4.Pang MW, Leung TN, Sahota DS, et al. Customizing fetal biometric charts. Ultrasound Obstet Gynecol. 2003;22(3):271–276. doi: 10.1002/uog.196. [DOI] [PubMed] [Google Scholar]
- 5.Bertino E, Milani S, Fabris C, et al. Neonatal anthropometric charts: what they are, what they are not. Arch Dis Child Fetal Neonatal Ed. 2007;92(1):F7–F10. doi: 10.1136/adc.2006.096214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dudley NJ. A systematic review of the ultrasound estimation of fetal weight. Ultrasound Obstet Gynecol. 2005;25(1):80–89. doi: 10.1002/uog.1751. [DOI] [PubMed] [Google Scholar]
- 7.Brenner WE, Edelman DA, Hendricks CH. A standard of fetal growth for the United States of America. Am J Obstet Gynecol. 1976;126(5):555–564. doi: 10.1016/0002-9378(76)90748-1. [DOI] [PubMed] [Google Scholar]
- 8.Gardosi J, Chang A, Kalyan B, et al. Customized antenatal growth charts. Lancet. 1992;339(8788):283–287. doi: 10.1016/0140-6736(92)91342-6. [DOI] [PubMed] [Google Scholar]
- 9.Amini S, Catalano P, Hirsch V, et al. An analysis of birth weight by gestational age using a computerized perinatal data base, 1975–1992. Obstet Gynecol. 1994;83(3):342–352. [PubMed] [Google Scholar]
- 10.Zhang J, Bowes W., Jr Birth-weight-for-gestational-age patterns by race, sex, and parity in the United States population. Obstet Gynecol. 1995;86(2):200–208. doi: 10.1016/0029-7844(95)00142-e. [DOI] [PubMed] [Google Scholar]
- 11.Källén B. A birth weight for gestational age standard based on data in the Swedish Medical Birth Registry, 1985–1989. Eur J Epidemiol. 1995;11(5):601–606. doi: 10.1007/BF01719316. [DOI] [PubMed] [Google Scholar]
- 12.Thomson AM, Billewicz WZ, Hytten FE. The assessment of fetal growth. J Obstet Gynaecol Br Commonw. 1968;75(9):903–916. doi: 10.1111/j.1471-0528.1968.tb01615.x. [DOI] [PubMed] [Google Scholar]
- 13.Johnsen SL, Rasmussen S, Wilsgaard T, et al. Longitudinal reference ranges for estimated fetal weight. Acta Obstet Gynecol Scand. 2006;85(3):286–297. doi: 10.1080/00016340600569133. [DOI] [PubMed] [Google Scholar]
- 14.Arbuckle T, Wilkins R, Sherman G. Birth weight percentiles by gestational age in Canada. Obstet Gynecol. 1993;81(1):39–48. [PubMed] [Google Scholar]
- 15.Physical status: the use and interpretation of anthropometry. Report of a WHO Expert Committee. World Health Organ Tech Rep Ser. 1995;854:1–452. [PubMed] [Google Scholar]
- 16.Alexander G, Himes J, Kaufman R, et al. A United States national reference for fetal growth. Obstet Gynecol. 1996;87(2):163–168. doi: 10.1016/0029-7844(95)00386-X. [DOI] [PubMed] [Google Scholar]
- 17.Kramer MS, Platt RW, Wen SW, et al. A new and improved population-based Canadian reference for birth weight for gestational age [electronic article] Pediatrics. 2001;108(2):E35. doi: 10.1542/peds.108.2.e35. [DOI] [PubMed] [Google Scholar]
- 18.Mongelli M, Figueras F, Francis A, et al. A customized birthweight centile calculator developed for an Australian population. Aust N Z J Obstet Gynaecol. 2007;47(2):128–131. doi: 10.1111/j.1479-828X.2007.00698.x. [DOI] [PubMed] [Google Scholar]
- 19.Clausson B, Gardosi J, Francis A, et al. Perinatal outcome in SGA births defined by customised versus population-based birthweight standards. BJOG. 2001;108(8):830–834. doi: 10.1111/j.1471-0528.2001.00205.x. [DOI] [PubMed] [Google Scholar]
- 20.McCowan L, Harding J, Steward A. Customised birthweight centiles predict SGA pregnancies with perinatal mortality. BJOG. 2005;112(8):1026–1033. doi: 10.1111/j.1471-0528.2005.00656.x. [DOI] [PubMed] [Google Scholar]
- 21.Ego A, Subtil D, Grange G, et al. Customized versus population-based birth weight standards for identifying growth restricted infants: a French multicenter study. Am J Obstet Gynecol. 2006;194(4):1042–1049. doi: 10.1016/j.ajog.2005.10.816. [DOI] [PubMed] [Google Scholar]
- 22.Zhang X, Platt RW, Cnattingius S, et al. The use of customised versus population-based birthweight standards in predicting perinatal mortality. BJOG. 2007;114(4):474–477. doi: 10.1111/j.1471-0528.2007.01273.x. [DOI] [PubMed] [Google Scholar]
- 23.Gardosi J, Clausson B, Francis A. The use of customised versus population-based birthweight standards in predicting perinatal mortality. BJOG. 2007;114(10):1301–1302. doi: 10.1111/j.1471-0528.2007.01432.x. author reply 1303. [DOI] [PubMed] [Google Scholar]
- 24.Boulet SL, Alexander GR, Salihu HM, et al. Fetal growth risk curves: defining levels of fetal growth restriction by neonatal death risk. Am J Obstet Gynecol. 2006;195(6):1571–1577. doi: 10.1016/j.ajog.2006.03.069. [DOI] [PubMed] [Google Scholar]
- 25.Hutcheon JA, Platt RW. The missing data problem in birth weight percentiles and thresholds for “small-for-gestational-age.”. Am J Epidemiol. 2008;167(7):786–792. doi: 10.1093/aje/kwm327. [DOI] [PubMed] [Google Scholar]
- 26.Seeds JW, Peng TC. Does augmented growth impose an increased risk of fetal death? Am J Obstet Gynecol. 2000;183(2):316–322. doi: 10.1067/mob.2000.107656. [DOI] [PubMed] [Google Scholar]
- 27.Hannah ME, Hannah WJ, Hewson SA, et al. Planned caesarean section versus planned vaginal birth for breech presentation at term: a randomized multicentre trial. Term Breech Trial Collaborative Group. Lancet. 2000;356(9239):1375–1383. doi: 10.1016/s0140-6736(00)02840-3. [DOI] [PubMed] [Google Scholar]
- 28.Wapner RJ, Sorokin Y, Thom EA, et al. Single versus weekly courses of antenatal corticosteroids: evaluation of safety and efficacy. Am J Obstet Gynecol. 2006;195(3):633–642. doi: 10.1016/j.ajog.2006.03.087. [DOI] [PubMed] [Google Scholar]
- 29.Mellits ED, Holden KR, Freeman JM. Neonatal seizures. II. A multivariate analysis of factors associated with outcome. Pediatrics. 1982;70(2):177–185. [PubMed] [Google Scholar]
- 30.Ellenberg JH, Nelson KB. Cluster of perinatal events identifying infants at high risk for death or disability. J Pediatr. 1988;113(3):546–552. doi: 10.1016/s0022-3476(88)80649-8. [DOI] [PubMed] [Google Scholar]
- 31.Joseph KS, Huang L, Liu S, et al. Reconciling the high rates of preterm and postterm birth in the United States. Obstet Gynecol. 2007;109(4):813–822. doi: 10.1097/01.AOG.0000255661.13792.c1. [DOI] [PubMed] [Google Scholar]
- 32.Mustafa G, David RJ. Comparative accuracy of clinical estimate versus menstrual gestational age in computerized birth certificates. Public Health Rep. 2001;116(1):15–21. doi: 10.1093/phr/116.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ananth CV. Menstrual versus clinical estimate of gestational age dating in the United States: temporal trends and variability in indices of perinatal outcomes. Paediatr Perinat Epidemiol. 2007;21(suppl 2):22–30. doi: 10.1111/j.1365-3016.2007.00858.x. [DOI] [PubMed] [Google Scholar]
- 34.Cunningham FG, Leveno KJ, Bloom SL, et al. Williams Obstetrics. 22nd ed. Toronto, Canada: McGraw Hill Co; 2005. [Google Scholar]
- 35.Kramer MS, Morin I, Yang H, et al. Why are babies getting bigger? Temporal trends in fetal growth and its determinants. J Pediatr. 2002;141(4):538–542. doi: 10.1067/mpd.2002.128029. [DOI] [PubMed] [Google Scholar]
- 36.Ananth CV, Wen SW. Trends in fetal growth among singleton gestations in the United States and Canada, 1985 through 1998. Semin Perinatol. 2002;26(4):260–267. doi: 10.1053/sper.2002.34772. [DOI] [PubMed] [Google Scholar]
- 37.Joseph KS, Wilkins R, Dodds L, et al. Customized birth weight for gestational age standards: perinatal mortality patterns are consistent with separate standards for males and females but not for blacks and whites [electronic article] BMC Pregnancy Childbirth. 2005;5(1):3. doi: 10.1186/1471-2393-5-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kramer MS, Ananth CV, Platt RW, et al. US black vs white disparities in foetal growth: physiological or pathological? Int J Epidemiol. 2006;35(5):1187–1195. doi: 10.1093/ije/dyl125. [DOI] [PubMed] [Google Scholar]
- 39.WHO Multicentre Growth Reference Study Group. Enrolment and baseline characteristics in the WHO Multicentre Growth Reference Study. Acta Paediatr Suppl. 2006;450:7–15. doi: 10.1111/j.1651-2227.2006.tb02371.x. [DOI] [PubMed] [Google Scholar]
- 40.Zhang X, Kramer MS. Variations in mortality and morbidity by gestational age among infants born at term. J Pediatr. doi: 10.1016/j.jpeds.2008.09.013. (doi:10.1016/j.jpeds.2008.09.013) [DOI] [PubMed] [Google Scholar]
- 41.Yudkin PL, Wood L, Redman CWG. Risk of unexplained stillbirth at different gestational ages. Lancet. 1987;1(8543):1192–1194. doi: 10.1016/s0140-6736(87)92154-4. [DOI] [PubMed] [Google Scholar]
- 42.Hovatta O, Lipasti A, Rapola J, et al. Causes of stillbirth: a clinicopathological study of 243 patients. Br J Obstet Gynaecol. 1983;90(8):691–696. doi: 10.1111/j.1471-0528.1983.tb09296.x. [DOI] [PubMed] [Google Scholar]
- 43.Joseph KS. Incidence-based measures of birth, growth restriction and death can free perinatal epidemiology from erroneous concepts of risk. J Clin Epidemiol. 2004;57(9):889–897. doi: 10.1016/j.jclinepi.2003.11.018. [DOI] [PubMed] [Google Scholar]