Hardy-Weinberg Equilibrium Testing of Biological Ascertainment for Mendelian Randomization Studies

Abstract

Mendelian randomization (MR) permits causal inference between exposures and a disease. It can be compared with randomized controlled trials. Whereas in a randomized controlled trial the randomization occurs at entry into the trial, in MR the randomization occurs during gamete formation and conception. Several factors, including time since conception and sampling variation, are relevant to the interpretation of an MR test. Particularly important is consideration of the “missingness” of genotypes that can be originated by chance, genotyping errors, or clinical ascertainment. Testing for Hardy-Weinberg equilibrium (HWE) is a genetic approach that permits evaluation of missingness. In this paper, the authors demonstrate evidence of nonconformity with HWE in real data. They also perform simulations to characterize the sensitivity of HWE tests to missingness. Unresolved missingness could lead to a false rejection of causality in an MR investigation of trait-disease association. These results indicate that large-scale studies, very high quality genotyping data, and detailed knowledge of the life-course genetics of the alleles/genotypes studied will largely mitigate this risk. The authors also present a Web program (http://www.oege.org/software/hwe-mr-calc.shtml) for estimating possible missingness and an approach to evaluating missingness under different genetic models.

Epidemiologic association studies are susceptible to unresolved confounding, reverse causation, and selection bias (1). Mendelian randomization (MR) is an epidemiologic method that, through the use of informative genotypes, permits the testing of causal relations between exposures and diseases. MR is based on the assumption that the association between a disease and a genetic polymorphism of known function (that mimics the biologic link between a proposed exposure and disease) is not generally susceptible to reverse causation or confounding (1). Thus, for example, if it is known that there is an association between a plasma protein and a disease, the direction of that association can be tested if genotypes of the gene encoding the protein are associated with the level of the protein. Because the quantity of the protein cannot cause the genotype but the genotype can influence the quantity of the protein, if the genotype is also associated with the disease it may be inferred that the level of the plasma protein is causally influencing the disease.

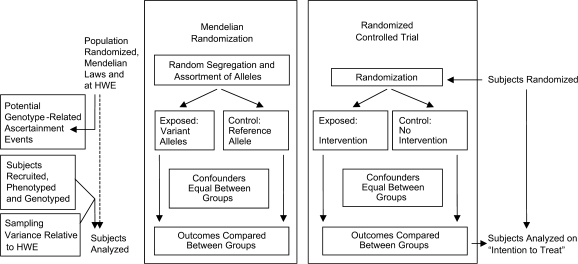
The MR approach is conceptually analogous to a randomized controlled trial (see Figure 1). Randomization in randomized controlled trials is undertaken at entry into the trial, and since many trials concern major diseases arising in later life, many studies are of older persons. The same applies to many cohort studies upon which MR will be based. Randomization in MR (random assignment to genotype) occurs during gamete formation and conception (1). This means that the principle of MR has the potential to strengthen inference from an observational study (such as a cohort study) toward the inferential robustness of a randomized controlled trial. In randomized controlled trials, one analyzes the data on the basis of “intention to treat” in most cases—this ensures that all possible differences between drug and placebo groups are taken into account in the final analysis. For MR to match this, there is a need to analyze the data on “intention to MR.” It follows that the randomly breeding population as a whole suits an MR test. However, when a random sample is taken from a population, especially at a time point likely to be far from the original fertilization (i.e., randomization) events, the nature of the sample needs to be carefully considered with respect to “intention to MR.”

Figure 1.

Mendelian randomization and randomized controlled trials. Adapted from the paper by Hingorani and Humphries (12). HWE, Hardy-Weinberg equilibrium.

A particular genetic feature of randomly breeding populations is that of Hardy-Weinberg equilibrium (HWE) (2, 3). Since alleles of diploid loci are randomly reassorted at each new conception, it follows that for allele frequencies p and q (where p + q = 1) for biallelic loci, the frequencies of genotypes are expressed by the expansion (p + q)².

In genetics, the test of whether the proportions of genotypes observed in a population sample are consistent with the prediction (p², 2pq, and q²) offers a fundamental test of biologic ascertainment for the genotypes. A sample from a homogeneous randomly mating population should only deviate from perfect HWE by small chance amounts, conforming to parametric sampling statistics. Large, statistically significant deviations are often caused by quality issues with laboratory typing data. However, given high-quality genotyping data, the HWE feature offers the opportunity to look for possible biologic ascertainment biases for the population sample relative to the genotype of interest.

In this paper, we consider the relations between sample HWE testing, genotyping error, chance deviations from exact HWE in the sample, and the use of genotype as an instrumental variable for MR analyses. We also present a Web tool for estimating possible missingness and a scheme for examining missingness under different genetic models (additive, threshold, heterosis). This approach more securely equates the principle of “intention to MR” with the “intention to treat” analysis principle of randomized controlled trials.

MATERIALS AND METHODS

We consider studies in which either there is an additive effect per allele in subjects or 1 homozygous group would be considered the phenotypically different group for trait and disease. For a locus with 2 alleles P and Q and overall population frequencies p and q, and taking a sample of size N, the genotypes in the possible resultant sample can be parameterized. When considering the sampling of P homozygotes, in a sample of N subjects, the variance of the observed number μ relative to the expected number Np² will be that of a binomial distribution—that is, Np²(1 − p²). These values were used to determine the standard deviation σ of the observed number in the sample relative to that expected from the population if chance variation did not occur. In turn, this permitted modeling for chosen 0 < p < 1 and a chosen boundary unlikelihood of sample characteristics (e.g., the 95% confidence interval (computed as μ ± 1.96σ) for samples that would usually be observed), to examine missingness which could be due to chance but could also be due to biologic ascertainment bias. Additionally, the “selective” effects of genotyping problems (e.g., failure to genotype heterozygotes because their 2 allelic signals may be weaker than the double-strength signal in homozygotes) were modeled by changing 1 genotype group by a proportion multiplier k, arbitrarily varied from a 20% loss to a 20% gain (from ×0.8 to ×1.2).

We started the simulations with allelic frequencies p_true and q_true and computed the expected true values for the 2 homozygote groups and for the heterozygotes assuming HWE. We then computed the number of persons in the no-call group who were lost/gained. These numbers were $2(1-k)N{p}_{\text{true}}{q}_{\text{true}}$ for heterozygotes and $(1-k)N{p}_{\text{true}}^2$ for homozygotes. For the computation of heterozygote losses/gains, we computed p_false and q_false—that is, the erroneous values of p and q that are obtained according to the loss or gain (chance or genotype assay-related or genotype-dependent ascertainment-related) of a genotype group dependent on k. Calculations were performed using programs written in Python (http://www.python.org).

and q_false = 1 − p_false.

Using both values, we computed the expected numbers of both homozygote groups and the heterozygotes. The observed number of heterozygotes was computed by subtracting/adding the number of the no-call group to the expected true values for the heterozygotes. We then computed the HWE Pearson χ² value for expected genotype counts versus observed genotype counts.

For the computation of homozygote losses or gains, we followed an analogous procedure, but with

and

To approach the typical study size generally anticipated for MR, we considered a range of N's from 1,000 (expected to be sufficient for major genotype effects) to 100,000 (believed to be reasonably powered for modest complex trait effects (4)).

We considered a range of cases with perfect HWE, for given combinations of allele frequencies (1 > p > 0) and sample sizes (100,000 > N > 5,000). We computed the 95% confidence limits of allele frequency from the formula (5)

We estimated expected genotypic counts from these estimates and computed the HWE χ² value. Analogous analyses were carried out for gain/loss of homozygotes and heterozygotes.

We evaluated the HWE χ² distributions for the single nucleotide polymorphisms (SNPs) analyzed in 2 genome-wide association studies, the study by the Wellcome Trust Case Control Consortium (WTCCC) (6) and the Framingham Study (7). For the WTCCC study, we computed the HWE χ² values for more than 400,000 SNPs from the observed genotype counts for each SNP in more than 2,000 controls. For the Framingham Study, we computed the HWE χ² values from the P values available for nearly 100,000 SNPs analyzed for association with prostate cancer in more than 600 unselected men. We also analyzed the HWE χ² value from publications in the literature that reported the HWE χ², the P value for the HWE χ² test, or the genotypic counts for the apolipoprotein E (APOE) polymorphism. We considered the first 30 studies (see Web Table 1, which is posted on the Journal’s Web site (http://aje.oxfordjournals.org/)) observed with the scientific research tool “scirus” (http://www.scirus.com/) using the search terms “APOE” and “Hardy-Weinberg” on April 11, 2008.

We created Q-Q plots in SPSS, version 15.0 (SPSS, Inc., Chicago, Illinois), in order to compare the observed and expected χ² values (with 1 df) for WTCCC controls and for cases with the 7 diseases analyzed in the WTCCC study. We also analyzed the Q-Q plots for the Framingham prostate cancer cases and for the 30 studies of APOE.

Since

and 2Npq, Np², and Nq² represent the 3 genotype counts in a sample in perfect HWE (χ² = 0), it is possible to use 2 groups’ observed values to estimate the expected value for the third group, and hence for each group to assess possible missingness (or excess). We developed a Web program (http://www.oege.org/software/hwe-mr-calc.shtml) both to conduct a standard HWE test (Pearson χ²) based on the 3 groups and to calculate counts (changing any 1 group) to create perfect HWE.

We applied the effect of missingness and deviations from HWE to an MR example consisting of a sample of 10,000 persons with genotypic, intermediate trait, and outcome information. We added persons who were missing based on HWE and computed the significance of the new MR studies. MR analyses were carried out in Stata/IC 10.0 for Windows (Stata Corporation, College Station, Texas) using the command “ivregress.”

RESULTS

In Web Table 2 (http://aje.oxfordjournals.org/), for representative values of p (0 < p < 1) and N (1,000 ≤ N ≤ 100,000), we present σ/μ and 95% confidence intervals for expected numbers of p homozygotes. Estimated σ/μ ranged from 0.10% to 3.16% and was inversely related to both p and N. Table 1 shows a subset of these results.

Table 1.

Measures of Dispersion for Sample Sizes of 5,000, 20,000, and 50,000 and for Allele Frequencies (p and q) Ranging From 0.05 to 0.95

Sample Size	p	q	σa	95% Confidence Interval		μ	σ/μb
				Lower Bound	Upper Bound
5,000	0.05	0.95	3.53	−6.92	6.92	250	0.0141
5,000	0.20	0.80	13.86	−27.16	27.16	1,000	0.0139
5,000	0.50	0.50	30.62	−60.01	60.01	2,500	0.0122
5,000	0.80	0.20	33.94	−66.52	66.52	4,000	0.0085
5,000	0.95	0.05	20.98	−41.11	41.11	4,750	0.0044
20,000	0.05	0.95	7.06	−13.84	13.84	1,000	0.0071
20,000	0.20	0.80	27.71	−54.32	54.32	4,000	0.0069
20,000	0.50	0.50	61.24	−120.02	120.02	10,000	0.0061
20,000	0.80	0.20	67.88	−133.05	133.05	16,000	0.0042
20,000	0.95	0.05	41.95	−82.22	82.22	19,000	0.0022
50,000	0.05	0.95	11.17	−21.89	21.89	2,500	0.0045
50,000	0.20	0.80	43.82	−85.88	85.88	10,000	0.0044
50,000	0.50	0.50	96.82	−189.78	189.78	25,000	0.0039
50,000	0.80	0.20	107.33	−210.37	210.37	40,000	0.0027
50,000	0.95	0.05	66.33	−130.01	130.01	47,500	0.0014

^aStandard deviation of the observed number of subjects in the sample.

^bMean of the observed number of subjects in the sample.

Table 2 gives values of N and p with 1 homozygote group adjusted to the lower 95% confidence limit. Table 3 applies the same approach to heterozygotes. Results for a larger range of conditions can be seen in Web Tables 3 and 4 (http://aje.oxfordjournals.org/). In each instance, these demonstrate a loss of persons in 1 genotype group, which could frequently occur by chance, through genotyping failure, or through biologic/clinical ascertainment bias. The tables show that in most instances, the χ² values would generate a firm conclusion: “no significant deviation from HWE.” The HWE test is insensitive to heterozygote loss (for detection of the 95% confidence interval of group count), whatever the value of p, and is only sensitive to homozygote loss where p has a low value. As an example, for N = 5,000 and p = 0.2, 200 rare homozygotes would be expected, but within the 95% confidence interval, this value could range from 173 to 227. In this example, the HWE test χ² value was 2.48, well below the 5% limit (χ² ≥3.84) typically used for samples in which all 3 genotype groups would be free to vary by chance. There is, nonetheless, deviation from perfect HWE (χ² = 0) and (assuming perfect genotyping) uncertainty as to whether this is due to chance or clinical ascertainment bias.

Table 2.

Deviation From Hardy-Weinberg Equilibrium for Sample Sizes of 5,000, 20,000, and 50,000 and for Allele Frequencies Ranging From 0.05 to 0.95, After Subtracting From the Homozygote 1 Group a Number Equivalent to 1.96 Standard Deviations

Sample Size	ptruea	Hz1 Truea	Het Truea	Hz2 Truea	pfalseb	Hz1 Expc	Het Expc	Hz2 Expc	Hz1 Obsd	No Calld	χ2e
5,000	0.05	13	475	4,513	0.0487	12	462	4,519	6	7	3.65
5,000	0.20	200	1,600	3,200	0.1956	190	1,565	3,217	173	27	2.48
5,000	0.50	1,250	2,500	1,250	0.4939	1,205	2,470	1,265	1,190	60	0.75
5,000	0.80	3,200	1,600	200	0.7973	3,136	1,595	203	3,133	67	0.06
5,000	0.95	4,513	475	13	0.9496	4,471	475	13	4,471	41	0.00
20,000	0.05	50	1,900	18,050	0.0493	49	1,875	18,063	36	14	3.55
20,000	0.20	800	6,400	12,800	0.1978	781	6,330	12,835	746	54	2.42
20,000	0.50	5,000	10,000	5,000	0.4970	4,910	9,940	5,030	4,880	120	0.73
20,000	0.80	12,800	6,400	800	0.7987	12,672	6,389	805	12,667	133	0.06
20,000	0.95	18,050	1,900	50	0.9498	17,968	1,900	50	17,968	82	0.00
50,000	0.05	125	4,750	45,125	0.0496	123	4,710	45,145	103	22	3.52
50,000	0.20	2,000	16,000	32,000	0.1986	1,969	15,890	32,055	1,914	86	2.40
50,000	0.50	12,500	25,000	12,500	0.4981	12,358	24,905	12,548	12,310	190	0.73
50,000	0.80	32,000	16,000	2,000	0.7992	31,798	15,983	2,008	31,790	210	0.06
50,000	0.95	45,125	4,750	125	0.9499	44,995	4,749	125	44,995	130	0.00

Abbreviations: Exp, expected; Het, heterozygote; Hz, homozygote; Obs, observed.

^ap_true are the allele frequencies used to start the simulations. They were also used to estimate the true frequencies of homozygotes (Hz1 True and Hz2 True) and heterozygotes (Het True) assuming Hardy-Weinberg equilibrium.

^bp_false are the allele frequencies observed after subtracting 1.96 standard deviations from the homozygote 1 group.

^cHz1 Exp, Het Exp, and Hz2 Exp are the expected values of the 3 genotype groups computed from p_false and q_false (1 − p_false).

^dHz1 Obs are the observed values for each genotype group after subtracting 1.96 standard deviations from the homozygote 1 group (which equates to the number presented in the “No Call” column). The observed values of the other 2 genotype groups used to compute the deviations from Hardy-Weinberg equilibrium (Het Obs and Hz2 Obs) are equal to Het True and Hz2 True, respectively.

^eHardy-Weinberg equilibrium χ² value.

Table 3.

Deviation From Hardy-Weinberg Equilibrium for Sample Sizes of 5,000, 20,000, and 50,000 and for Allele Frequencies Ranging From 0.05 to 0.95, After Subtracting From the Heterozygote Group a Number Equivalent to 1.96 Standard Deviations

Sample Size	ptruea	Hz1 Truea	Het Truea	Hz2 Truea	pfalseb	Hz1 Expc	Het Expc	Hz2 Expc	Het Obsd	No Calld	χ2e
5,000	0.05	13	475	4,513	0.0463	11	438	4,511	434	41	0.36
5,000	0.20	200	1,600	3,200	0.1961	190	1,556	3,190	1,535	65	0.86
5,000	0.50	1,250	2,500	1,250	0.5000	1,233	2,465	1,233	2,431	69	0.97
5,000	0.80	3,200	1,600	200	0.8039	3,190	1,556	190	1,535	65	0.86
5,000	0.95	4,513	475	13	0.9537	4,511	438	11	434	41	0.36
20,000	0.05	50	1,900	18,050	0.0482	46	1,826	18,046	1,819	81	0.34
20,000	0.20	800	6,400	12,800	0.1980	779	6,312	12,779	6,271	129	0.85
20,000	0.50	5,000	10,000	5,000	0.5000	4,965	9,931	4,965	9,861	139	0.97
20,000	0.80	12,800	6,400	800	0.8020	12,779	6,312	779	6,271	129	0.85
20,000	0.95	18,050	1,900	50	0.9518	18,046	1,826	46	1,819	81	0.34
50,000	0.05	125	4,750	45,125	0.0488	119	4,634	45,119	4,621	129	0.34
50,000	0.20	2,000	16,000	32,000	0.1988	1,967	15,861	31,967	15,796	204	0.84
50,000	0.50	12,500	25,000	12,500	0.5000	12,445	24,890	12,445	24,781	219	0.96
50,000	0.80	32,000	16,000	2,000	0.8012	31,967	15,861	1,967	15,796	204	0.84
50,000	0.95	45,125	4,750	125	0.9512	45,119	4,634	119	4,621	129	0.34

Abbreviations: Exp, expected; Het, heterozygote; Hz, homozygote; Obs, observed.

^ap_true are the allele frequencies used to start the simulations. They were also used to estimate the true frequencies of homozygotes (Hz1 True and Hz2 True) and heterozygotes (Het True) assuming Hardy-Weinberg equilibrium.

^bp_false are the allele frequencies observed after subtracting 1.96 standard deviations from the heterozygote group.

^cHz1 Exp, Het Exp, and Hz2 Exp are the expected values of the 3 genotype groups computed from p_false and q_false (1 − p_false).

^dHet Obs are the observed values for each genotype group after subtracting 1.96 standard deviations from the heterozygote group (which equates to the number presented in the “No Call” column). The observed values of the other 2 genotype groups used to compute the deviations from Hardy-Weinberg equilibrium (Hz1 Obs and Hz2 Obs) are equal to Hz1 True and Hz2 True, respectively.

^eHardy-Weinberg equilibrium χ² value.

Tables 4 and 5 present combinations of allele frequency p, sample size N, and proportional multiplier k (0.8 ≤ k ≤ 1.2), modifying the observed number of 1 genotype group such that HWE testing would suggest no significant deviation from HWE. Although a significant deviation from HWE is more likely with large values of N and k (Web Tables 5 and 6 (http://aje.oxfordjournals.org/)), there is a wide range of observed population samples in which potential ascertainment bias would not be recognized under a usual statistical test. These (for HWE χ² < 3.84) are shown in Web Figure 1 (http://aje.oxfordjournals.org/) as 3-dimensional plots with axes for N, p, and |1 − k|. Web Figure 1 shows that a greater variation of the parameter |1 − k| in homozygotes results in more nonsignificant deviations from HWE for homozygotes than for heterozygotes.

Table 4.

Hardy-Weinberg χ² Values (in Parentheses) for Particular Combinations of Allele Frequency, Gain/Loss of Homozygotes, and Sample Size

Allele Frequency	Gain/Loss, %	Sample Size
0.05	±5	5,000 (0.03), 100,000 (0.57)
0.05 (0.03), 0.50 (0.81)	±5	5,000
0.05	±5 (0.03), ±20 (0.46)	5,000

Table 5.

Hardy-Weinberg χ² Values (in Parentheses) for Particular Combinations of Allele Frequency, Gain/Loss of Heterozygotes, and Sample Size

Allele Frequency	Gain/Loss, %	Sample Size
0.05	±5	5,000 (0.12), 100,000 (2.36)
0.05 (0.12), 0.50 (3.14)	±5	5,000
0.05	±5 (0.12), ±20 (2.23)	5,000

Web Table 7 (http://aje.oxfordjournals.org/) shows the boundaries of allele frequencies and the associated χ² values observed for a combination of allele frequencies and sample sizes in situations of perfect HWE from observed allele frequencies. The maximum values of HWE χ² computed from the 95% confidence interval allele frequencies range from 3.56 to 4.18.

For gain/loss of heterozygotes (Web Table 8 (http://aje.oxfordjournals.org/)), the maximum difference between χ² computed from the 95% confidence interval of allele frequencies and χ² computed from the observed allele frequencies is 1,132 (corresponding to |1 − k| = 0.20, p = 0.65, and N = 100,000). The minimum difference is 0.4 (|1 − k| = 0.09, p = 0.05, N = 5,000), and the median difference is 38.6. The results for variations of homozygotes (Web Table 9 (http://aje.oxfordjournals.org/)) were comparable: a maximum of 3,686, a minimum of 0.19, and a median of 23.87.

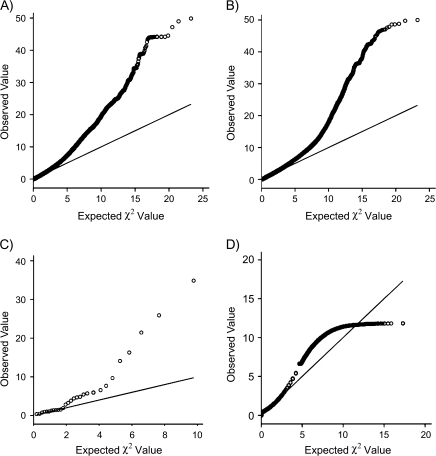
The observed Q-Q plots in WTCCC controls are not dissimilar to those observed for the 7 WTCCC case collections (Web Figure 2 (http://aje.oxfordjournals.org/)). Figure 2 shows results for WTCCC controls and cases with bipolar disorder. In all instances, there are considerably more high χ² values than expected, a situation that is more extreme in the 7 WTCCC case collections. A similar result is observed for the 30 studies of APOE (Figure 2). For Framingham Study prostate cancer cases, the Q-Q plot is different, with an inflection around χ² values of 11.5 (Figure 2).

Figure 2.

Q-Q plots comparing the expected and observed χ² values for controls from the Wellcome Trust Case Control Consortium (WTCCC) (6) and one of the 7 case collections (cases of bipolar disorder). The Q-Q plots (which are similar) for all of the other 6 case collections can be seen in Web Figure 2 (http://aje.oxfordjournals.org/). Also shown is a Q-Q plot comparing the expected and observed χ² values for 30 studies of the apolipoprotein E (APOE) polymorphism taken from the literature and a Q-Q plot comparing the expected and observed χ² values for Framingham Study (7) prostate cancer cases. A) Q-Q plot for WTCCC controls; B) Q-Q plot for WTCCC bipolar disorder cases; C) Q-Q plot for the 30 APOE studies; D) Q-Q plot for the Framingham prostate cancer cases.

Table 6 shows a nonsignificant MR association observed in the original study. This association becomes significant after the addition of missing persons (to give perfect HWE) with intermediate phenotypes following 3 different criteria. Note that deviations from HWE are not significant in the original study.

Table 6.

Effect on Mendelian Randomization of Both Deviations From Hardy-Weinberg Equilibrium and Additions of Missing Persons to Conform to Perfect Hardy-Weinberg Equilibrium^a

Original Study		Addition of Missing Personsb		Addition of Missing Personsc		Addition of Missing Personsd
MR Probability	HWE χ2	MR Probability	HWE χ2	MR Probability	HWE χ2	MR Probability	HWE χ2
0.0697	3.32	0.0477	0	2.91−16	0	7.54−30	0

Abbreviations: HWE, Hardy-Weinberg equilibrium; MR, Mendelian randomization.

^aAnalyses were carried out in a study of 10,000 persons with information on a genetic marker, an intermediate trait, and a disease outcome.

^bAddition of 507 homozygote 1 subjects with a diseased status and a mean body mass index (weight (kg)/height (m)²) equal to that of subjects in the original study.

^cAddition of 507 homozygote 1 subjects with a diseased status and a body mass index greater than or equal to the highest 75th percentile of body mass index for subjects in the original study.

^dAddition of 507 homozygote 1 subjects with a diseased status and a body mass index greater than or equal to the highest 95th percentile of body mass index for subjects in the original study.

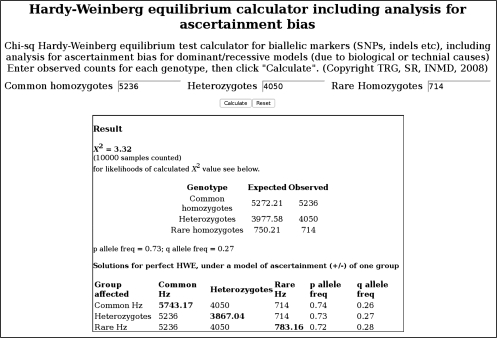
In Figure 3 we show, with an explanatory legend, the Web tool written both to perform a Pearson χ² HWE test and, using 2 genotype groups, to estimate what the third genotype would be under perfect HWE (χ² = 0).

Figure 3.

Illustration of output from the Web tool (see Materials and Methods section and http://www.oege.org/software/hwe-mr-calc.shtml) developed for Hardy-Weinberg equilibrium (HWE) analysis with estimations of possible ascertainment bias. In this example, the user input was genotype group counts of 5,236 (commoner homozygotes), 4,050 (heterozygotes), and 714 (rarer homozygotes). The output χ² value of 3.32 approaches but does not reach statistical significance (at P < 0.05). The table of solutions for perfect HWE (χ² = 0) shows, in red, the count that would be necessary if one of the 3 groups were accordingly adjusted. The differences from observed counts identify the possible missingnesses or excesses, which can then be considered in a subsequent genotype-phenotype or Mendelian randomization analysis. Hz, homozygotes; SNPs, single nucleotide polymorphisms. (TRG, SR, and INMD represent the authors’ initials.)

DISCUSSION

Missingness of subjects of a particular genotype group from a population sample may be due to chance, genotyping assay errors, or clinical ascertainment bias related to that genotype. We have examined chance variation of the observed count for a particular genotype group (common or rare homozygotes (1 > p > 0) and heterozygotes (1 > p > 0.5)) in relation to HWE testing and missingness of subjects from a population sample. We have illustrated the differences between perfect HWE and “no statistically significant deviation from HWE” in terms of possible subject missingness. While such missingness could be attributed to chance, it could equally well represent a clinical ascertainment bias related to the genotype in question.

We demonstrate, in both genome-wide and specific published data, despite high-quality data from the use of modern methods, a clear excess of inflated (though not necessarily statistically significant) χ² values, pointing either to residual erroneous typing or to sample ascertainment biases. We also present an approach and a Web tool for estimating possible missingness by genotype within HWE analyses and a flow chart showing how, for different genetic models, to estimate the bounds of effect of possible genotype-dependent missingness in MR analyses.

The results from the analyses of the Q-Q plots in WTCCC controls and cases, in Framingham prostate cancer cases, and in APOE studies published in the literature suggest that there might be missingness in all of these studies, since the observed distribution of χ² values does not fit well the expected distribution for 1 degree of freedom. Other possible reasons for the deviations from HWE (particularly in controls but also in cases) may include residual technical issues with SNP assays and SNP calling, ascertainment bias, sample subdivision (stratification or admixture), and other unknown or unrecognized sequence variation confounding SNP assays. Overall, these points put into perspective the difference between the often-used results statement “in HWE” and the reality “not statistically significantly deviant from HWE.” They also draw attention to the general excess of statistically significant deviations from HWE still evident in both focused and genome-wide studies, and to the general considerations necessary to be able to deploy HWE testing to be maximally informative regarding sample collection.

These points are relevant to MR studies. In a very large (outbred) population, there should be exact HWE at the point of conception. That is the moment at which the intention to randomize takes place, making MR directly comparable with a model randomized controlled trial. However, taking a population sample in later life and entering the successfully genotyped set into an MR analysis has the potential to violate the principle of “intention to analyze.”

It is outside the scope of this discussion to consider in detail the issue of biases in genotyping, except to note that even minor biases ranging from technical issues to covert null alleles (8), if unrecognized, may defeat the value of HWE assessment of the sample. A large sample size, which is necessary anyway in genetic epidemiologic studies of markers of small effect, is also important in increasing the power of the HWE test of the sample. In addition to being a test of genotype-dependent clinical ascertainment bias, the HWE test, in population genetics terms, assumes the absence of migration, mutation, natural selection, and assortative mating. Under these conditions, genotype frequencies at any locus are a function of the allele frequencies (p², 2pq, and q²), forming the basis of the standard HWE test (2, 3). Where genome-wide data are available, ancestral outliers may be inferred (and excluded) based on their constellation of SNP alleles (6). Where single markers are studied, reliance remains on good clinical data about ancestry.

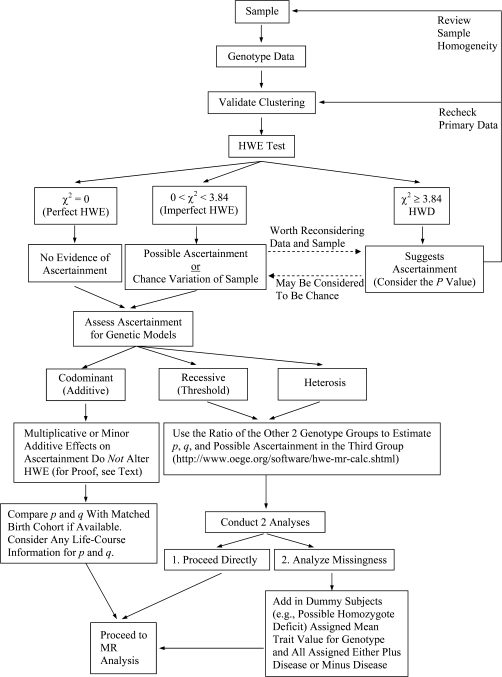
We have created (Figure 3) a new Web program (http://www.oege.org/software/hwe-mr-calc.shtml) which undertakes a standard Pearson χ² test following Hardy (2) and Weinberg (3)—that is, a parsimonious test based on observed allele counts. In addition, noting that (2Npq)² = 4(Np²)(Nq²), it is possible to use the ratio of 2 genotype counts, assumed unbiased, to estimate what should be the third genotype count under perfect HWE (χ² = 0). The program calculates this for the 3 possible combinations. For any genotype group (suspected in advance or not), missingness (or excess) relative to the observed count can thus be considered. The genetic model (recessive/threshold, codominant/additive, heterotic, X-linked, etc.) must first be specified in order to conduct genotype-phenotype or MR analyses and to consider genotype-dependent missingness (scheme in Figure 4).

1. For the threshold model, it may be possible to specify which homozygote group should be checked for missingness. If A were observed whereas the other 2 genotype groups gave the prediction that B was expected, then B minus A dummy subjects can be introduced into an MR analysis, assigned a distribution of the intermediate trait values that is characteristic of their genotype group, and all assigned either disease-positive or disease-negative. This allows reasonable bounds of inference to be characterized in relation to possible genotype-related missingness. If it is unknown in advance which homozygous group might be in deficit, then both models should be examined.

2. For heterosis, the heterozygous excess or deficiency can be considered along the same lines as in point 1 above.

3. For the additive model, HWE testing may not be sensitive to ascertainment biases. For the codominant (additive) model, consider that each allele q is subject to an ascertainment bias k (0 < k < 1, but typically k will be quite near 1 for complex traits). Thus, the ascertained heterozygote frequency will be 2kpq and the homozygote frequency will be k²q². However, since k²q² is (kq)², this will retain perfect HWE with new apparent q′ = kq and p′ = 1 − q′. Where k is near 1, the loss of subjects could be stated as loss m, where k = 1 − m and k² is approximately 1 − 2m (the m² term being negligible); so then, even under an additive model of loss (twice as much—that is, 2m loss of a homozygote group vs. the m loss of heterozygotes), relative genotype counts will remain very near HWE. This means that, under the additive model, the sample may show little or no deviation from HWE. However, life-course information on allele frequencies will be useful to confirm that effect sizes in genotype-trait-disease have not been underestimated, and this emphasizes the value of having data on allele frequencies in a large-scale early-life cohort that is matched to the general population.

Figure 4.

Steps needed to utilize Hardy-Weinberg equilibrium (HWE) testing for possible biologic ascertainment in genotype-phenotype or Mendelian randomization (MR) studies. HWD, Hardy-Weinberg disequilibrium.

It is impossible to prove that possible missing subjects were not unusually extreme for either an intermediate trait or disease status (e.g., numerous genotypes predispose to more than 1 disease), although sometimes reductio ad absurdum may suffice—for example, in a study of 100,000 persons and a possible ascertainment-driven missingness of 10 homozygotes, the missingness might be incapable of having any bearing on genotype-intermediate trait-clinical outcome associations even if those 10 subjects had an “absurd” value for an intermediate trait or clinical outcome. Even if this is not possible, it may be considered unlikely (though not proven) that a genotype could have driven missingness. For a gene believed only to be expressing a highly specific function in later life, this may be reasonable, but for genes with pleiotropy and particularly with expression in early fetal development, there might be more concern. Multifunctionality of the many forms recognized from detailed molecular studies of specific regions of the genome as in the ENCODE (Encyclopedia of DNA Elements) Project (9), microRNAs (10) with other regulatory functions, etc., arising from many genes, and other genes in the same linkage disequilibrium block (11) should be considered in drawing a reasonable conclusion.

The effects of missingness (chance vs. genotype-dependent clinical ascertainment) are no different in an MR study than in any other genotype-phenotype (genetic association) study. However, the consequences of misinference would be different. In principle, a false-negative result may be obtained by chance in any genotype-phenotype study, although one hopes that genotype-dependent clinical ascertainment bias might be evident with high-quality genotyping data combined with attention to HWE testing. Indeed, this is why case-control studies use HWE of controls (not cases) as a primary exploration of genotyping quality. However, MR studies are undertaken because there is already a focus based on knowledge of a potentially important association (albeit of unknown direction) between an intermediate trait (e.g., dietary factor, blood measure) and an outcome (e.g., disease event). In this case, if the genotype-outcome association draws a false-negative inference (e.g., because persons with the genotype-dependent outcome had failed to enter the study), the finding of important causality will have been falsely excluded. In this paper, we have illustrated the effects of “Hardy-Weinberg uncertainty” for “intention to MR”; have identified general strategies for gaining maximal information from the HWE test; and have developed a Web tool and scheme which will allow possible genotype-dependent missingness to be factored into MR analyses.

The main limitation of our study is that the phenotypes of any subjects missing or potentially missing in a real MR study are unknown. Potentially missing subjects may have had atypical intermediate trait values or disease status (or other diseases related to the same genotype). While the analytical scheme presented here takes account of missingness based on “reasonable” trait values, one cannot predict extremes; this would require tracking of a complete cohort from conception throughout the life course.

Glossary

Abbreviations

APOE

apolipoprotein E

HWE

Hardy-Weinberg equilibrium

MR

Mendelian randomization

SNP

single nucleotide polymorphism

WTCCC

Wellcome Trust Case Control Consortium