Thermodynamic Analysis Reveals a Temperature-dependent Change in the Catalytic Mechanism of Bacillus stearothermophilus Tyrosyl-tRNA Synthetase^,

Abstract

Catalysis of tRNA^Tyr aminoacylation by tyrosyl-tRNA synthetase can be divided into two steps. In the first step, tyrosine is activated by ATP to form the tyrosyl-adenylate intermediate. In the second step, the tyrosyl moiety is transferred to the 3′ end of tRNA. To investigate the roles that enthalpic and entropic contributions play in catalysis by Bacillus stearothermophilus tyrosyl-tRNA synthetase (TyrRS), the temperature dependence for the activation of tyrosine and subsequent transfer to tRNA^Tyr has been determined using single turnover kinetic methods. A van't Hoff plot for binding of ATP to the TyrRS·Tyr complex reveals three distinct regions. Particularly striking is the change occurring at 25 °C, where the values of ΔH⁰ and ΔS⁰ go from –144 kJ/mol and –438 J/mol K below 25 °C to +137.9 kJ/mol and +507 J/mol K above 25 °C. Nonlinear Eyring and van't Hoff plots are also observed for formation of the TyrRS·[Tyr-ATP]^‡ and TyrRS·Tyr-AMP complexes. Comparing the van't Hoff plots for the binding of ATP to tyrosyl-tRNA synthetase in the absence and presence of saturating tyrosine concentrations indicates that the temperature-dependent changes in ΔH⁰ and ΔS⁰ for the binding of ATP only occur when tyrosine is bound to the enzyme. Previous investigations revealed a similar synergistic interaction between the tyrosine and ATP substrates when the “KMSKS” signature sequence is deleted or replaced by a nonfunctional sequence. We propose that the temperature-dependent changes in ΔH⁰ and ΔS⁰ are because of the KMSKS signature sequence being conformationally constrained and unable to disrupt this synergistic interaction below 25 °C.

Aminoacyl-tRNA synthetases catalyze the transfer of amino acids to the 3′ end of tRNA in a two-step reaction shown as Reactions 1 and 2,

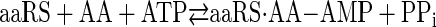REACTION 1

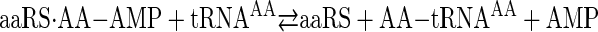REACTION 2

where aaRS,2 AA, and tRNA^AA represent the aminoacyl-tRNA synthetase, its amino acid substrate, and the cognate tRNA, respectively, and “·” and “–” represent noncovalent and covalent interactions, respectively. In general, the first step of the reaction (the activation of the amino acid) does not require the binding of tRNA to the enzyme (1–5). This allows the two steps in the tRNA aminoacylation reaction to be run independently of each other.

The aminoacyl-tRNA synthetases can be separated into two classes that are structurally distinct (6–10). Class I aminoacyl-tRNA synthetases are characterized by an amino-terminal Rossmann fold domain containing the active site and two signature sequences, “HIGH” and “KMSKS” (6, 7, 10–15). These sequences stabilize the transition state for the amino acid activation step of the reaction (16–24). In class II aminoacyl-tRNA synthetases, the active site domain consists of a seven-stranded β-sheet surrounded by three α-helices (25–33). With the exception of the tyrosyl- and tryptophanyl-tRNA synthetases, which are functional homodimers, all of the class I aminoacyl-tRNA synthetases are functional monomers (34). In contrast, all of the class II aminoacyl-tRNA synthetases are functional dimers (34).

The class I aminoacyl-tRNA synthetases contain an insertion domain, known as the CP1 domain, between the two halves of the Rossmann fold (10, 11, 35). In tyrosyl-tRNA synthetase (and the structurally related tryptophanyl-tRNA synthetase), the CP1 domains of the two monomers form the dimer interface. Although tyrosyl-tRNA synthetase (TyrRS) is composed of two identical monomers, in solution it displays an extreme form of negative cooperativity, known as “half-of-the-sites” reactivity, with respect to tyrosine binding and tyrosyl-adenylate formation (36, 37).

Kinetic analysis of the tyrosine activation reaction supports a random order mechanism for the binding of tyrosine and ATP to tyrosyl-tRNA synthetase (38–40). In contrast, initial analysis of the Bacillus stearothermophilus tyrosyl-tRNA synthetase crystal structure suggested that the tyrosine binding pocket is blocked when ATP is bound to the enzyme (6, 7). This apparent contradiction between the kinetic and structural results was initially resolved by invoking a virtual equilibrium for the binding of tyrosine to the TyrRS·ATP complex (41). More recently, analysis of the structurally related tryptophanyl-tRNA synthetase and molecular dynamics simulations of tyrosyl-tRNA synthetase suggest that the enzyme·ATP complex exists in an open conformation that allows access to the amino acid binding pocket (42, 43). This model is consistent with a random order mechanism for substrate binding to tyrosyl-tRNA synthetase.

In general, interactions between tyrosyl-tRNA synthetase and the tyrosine substrate form on the initial binding of tyrosine and do not change in strength throughout the course of the reaction (41). In contrast, the initial binding of ATP is relatively weak (K′ ^ATP_d = 4.7 mm for B. stearothermophilus tyrosyl-tRNA synthetase; where K′ ^ATP_d indicates the dissociation of ATP from the TyrRS·Tyr·ATP complex), with most of the interactions between the enzyme and ATP being formed in the transition state of the reaction (41). In other words, tyrosyl-tRNA synthetase uses tyrosine binding energy to increase the specificity of the active site and ATP binding energy to catalyze the activation of tyrosine. In addition, tyrosyl-tRNA synthetase variants, in which the KMSKS signature sequence has been deleted or made nonfunctional through mutagenesis, display a 20-fold increase in ATP binding affinity relative to that of the wild-type enzyme (19, 22). This increased affinity for ATP is dependent on the binding of tyrosine to the enzyme (22). These observations indicate that there is a synergistic interaction between the tyrosine and ATP substrates that occurs in the TyrRS·Tyr·ATP complex when the KMSKS sequence is absent or nonfunctional. One of the functions of the KMSKS sequence is to disrupt this synergistic interaction during the initial binding of ATP, allowing it to instead be used to stabilize the transition state of the amino acid activation step of the reaction (22).

In this study, we investigate the role that enthalpy and entropy play in catalysis of tRNA^Tyr aminoacylation by B. stearothermophilus tyrosyl-tRNA synthetase using single turnover conditions. Although the standard free energy for this reaction is not significantly affected by increasing temperatures, there is a dramatic shift in both the van't Hoff and Eyring plots at ∼25 °C for the tyrosine activation reaction. The hypothesis that a synergistic interaction between tyrosine and ATP is responsible for this temperature-dependent change is tested.

EXPERIMENTAL PROCEDURES

Materials—Reagents were purchased from the following sources: DE52 anion-exchange resin, Whatman; β-mercaptoethanol, disodium pyrophosphate, and inorganic pyrophosphatase, Sigma; nitrocellulose filters, Schleicher & Schuell; Source 15Q-Sepharose and NAP-25 columns, Amersham Biosciences. All other reagents were purchased from VWR International.

Purification of Recombinant B. stearothermophilus Tyrosyl-tRNA Synthetase—Purification of the wild-type tyrosyl-tRNA synthetase was performed as described previously (19, 44). Briefly, the wild-type enzyme was expressed in Escherichia coli TG2 cells, and the cells were lysed by sonication and incubated at 55 °C for 40 min to denature the E. coli proteins. Denatured proteins were removed by centrifugation, and the cleared lysate was dialyzed against Buffer 1 (20 mm Tris, pH 7.78, 1 mm EDTA, and 5 mm β-mercaptoethanol) containing 0.1 mm tetrasodium pyrophosphate to remove any bound tyrosyl-adenylate from the wild-type enzyme, followed by three changes of Buffer 2 (20 mm BisTris, pH 6.0, 1 mm EDTA, and 5 mm β-mercaptoethanol). The lysate was then loaded onto a Source 15Q-Sepharose anion-exchange column and eluted using a gradient from 20 mm BisTris, pH 6.0, to 20 mm BisTris, pH 6.0, 1.0 m NaCl. A peak eluting at 180 mm NaCl was collected and dialyzed against Buffer 1. This protein solution was repurified on the Source 15Q column using a gradient from 20 mm Tris, pH 7.78, to 20 mm Tris, pH 7.78, 1 m NaCl. A peak eluting at 220 mm NaCl was collected and dialyzed overnight against Buffer 1 plus 10% glycerol (v/v). The purified protein was stored at –70 °C. SDS-PAGE analysis indicated that the purified B. stearotheromophilus tyrosyl-tRNA synthetase was greater than 95% pure. The enzyme concentration was determined by the following: 1) a filter-based active-site titration assay, in which the incorporation of [¹⁴C]tyrosine into the enzyme-bound tyrosyl-adenylate intermediate is monitored, and 2) A₂₈₀ measurements in the presence of 6 m guanidine hydrochloride. These results indicated that >95% of the purified protein is active tyrosyl-tRNA synthetase.

Purification of tRNA^Tyr—The tRNA^Tyr substrate was obtained by in vitro transcription from a FokI-linearized pGFX-WT plasmid as described by Xin et al. (44). In vitro transcribed tRNA^Tyr was purified by a modification of the procedure described by Uter et al. (45). The in vitro reaction was loaded onto a 5-ml DE52 anion-exchange column, and eluted with elution buffer (100 mm HEPES-KOH, pH 7.5, 12 mm MgCl₂, 600 mm NaCl). Fractions containing tRNA^Tyr were pooled and desalted on a NAP-25 column. Fractions from the NAP-25 column that contained tRNA^Tyr were pooled and precipitated by adding double the volume of 100% ethanol and incubating it at –20 °C overnight. After centrifugation, the tRNA pellet was dried and resuspended in 100 μl of 10 mm MgCl₂. Annealing of tRNA^Tyr was achieved by incubation at 80 °C for 10 min, followed by slow cooling overnight. A nitrocellulose filter assay, in which the incorporation of [¹⁴C]tyrosine into the Tyr-tRNA^Tyr product was monitored, was used to determine the concentration of tRNA^Tyr (46).

Kinetic Procedures—All kinetic analyses were performed in 144 mm Tris buffer, pH 7.78, 10 mm β-mercaptoethanol, and 10 mm MgCl₂ (Buffer 3) over a temperature range of 5–35 °C. The pH of this buffer was adjusted using HCl or NaOH at 5 °C intervals to minimize temperature-dependent effects on the pH. ATP was added as the Mg²⁺ salt to maintain the free concentration of Mg²⁺ at 10 mm.

Tyrosine Activation—The kinetics for the activation of tyrosine were analyzed according to Fig. 1. Formation of the enzyme-bound tyrosyl-adenylate intermediate is associated with a decrease in the intrinsic fluorescence of tyrosyl-tRNA synthetase (47). Comparison of the forward rate constant (k₃, where k₃ is the forward rate constant for the activation of tyrosine) calculated from stopped-flow fluorescence and quenched-flow measurements indicates that this change in intrinsic fluorescence corresponds to the chemical step of the tyrosine activation reaction (47, 48). Although the binding of ATP to tyrosyl-tRNA synthetase does not induce a change in the intrinsic fluorescence of the enzyme, the equilibrium constants for the dissociation of ATP from the TyrRS·Tyr·ATP and TyrRS·ATP complexes can be determined kinetically. This is done by monitoring formation of the TyrRS·Tyr-AMP intermediate under conditions where the enzyme is initially present as either the TyrRS·Tyr complex (i.e. [Tyr] ≥ 10 × K_d^Tyr, where K_d^Tyr = 12 μm; K_d^Tyr is the equilibrium constant for the dissociation of tyrosine from the TyrRS·Tyr complex) or the free enzyme (i.e. [Tyr] ≤ 0.1 × K_d^Tyr) (18, 49). Specifically, both the equilibrium constant for the dissociation of ATP from the TyrRS·Tyr·ATP complex, K′ ^ATP_d, and the forward rate constant for the activation of tyrosine, k₃, are calculated from the variation of k_obs with ATP concentration in the presence of 200 μm tyrosine. Similarly, the equilibrium constant for the dissociation of ATP from the TyrRS·ATP complex (K ^ATP_d) is calculated from the variation of k_obs with respect to the ATP concentration in the presence of either 0.1 or 1.0 μm tyrosine (similar values for K ^ATP_d were obtained for both concentrations of tyrosine). Under these conditions, at least 90% of the tyrosyl-tRNA synthetase is present as the free enzyme (49). In general, the experimental setup for determining rate and dissociation constants is as follows: syringe 1 contains 0.5 μm tyrosyl-tRNA synthetase, 1 unit/ml inorganic pyrophosphatase, and either 1 or 200 μm tyrosine in Buffer 3; syringe 2 contains 0.6–20 mm MgATP, 1 unit/ml inorganic pyrophosphatase, and either 1 μm or 200 μm tyrosine in Buffer 3. The addition of inorganic pyrophosphatase to each syringe prevents pyrophosphate from rebinding to the TyrRS·Tyr-AMP intermediate and re-forming the TyrRS·Tyr·ATP complex. Equal volumes from each syringe are mixed, and the decrease in the intrinsic fluorescence of tyrosyl-tRNA synthetase is monitored using an Applied Photophysics SX 18.MV stopped-flow spectrophotometer (λ_ex = 295 nm, λ_em > 320 nm). A minimum of six fluorescence traces are collected and averaged. The resulting average trace is then fit to a single exponential equation with a floating end point.

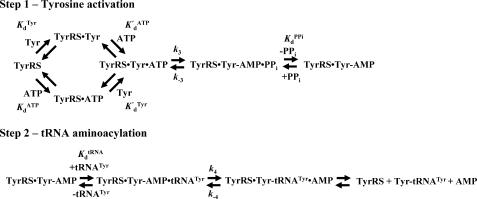
FIGURE 1.

Reaction diagram for catalysis of the tRNA^Tyr aminoacylation reaction by tyrosyl-tRNA synthetase. The activation of tyrosine and subsequent transfer of the activated amino acid to the 3′ end of tRNA^Tyr are shown. Dissociation and rate constants are shown above or below the step with which they are associated. Noncovalent and covalent bonds are represented by · and –, respectively.

The equilibrium constant for the dissociation of tyrosine from the free enzyme (K_d^Tyr) is calculated from the decrease in the intrinsic fluorescence of tyrosyl-tRNA synthetase on binding tyrosine (47). This change in intrinsic fluorescence is specific for the binding of tyrosine to the free enzyme and is in addition to the decrease in intrinsic fluorescence associated with formation of the enzyme-bound tyrosyl-adenylate intermediate. The experimental setup is similar to that described above, except that syringe 1 contains only tyrosyl-tRNA synthetase in Buffer 3 and syringe 2 contains only tyrosine in Buffer 3. The binding of tyrosine to tyrosyl-tRNA synthetase obeys the following rate law (47) shown in Equation 1,

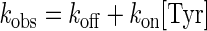(Eq. 1)

where k_obs is the observed rate constant, k_on is the rate constant for the binding of tyrosine to the unliganded enzyme, and k_off is the rate constant for the dissociation of tyrosine from the TyrRS·Tyr complex. The equilibrium constant for the dissociation of tyrosine from the TyrRS·Tyr complex was calculated from the Haldane relationship (50) shown in Equation 2,

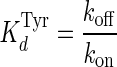(Eq. 2)

Pyrophosphorolysis—The kinetics for pyrophosphorolysis of the ATP moiety were determined by monitoring the reverse reaction for tyrosine activation. Conversion of TyrRS·Tyr-AMP + PP_i to TyrRS + Tyr + ATP is accompanied by an increase in the intrinsic fluorescence of tyrosyl-tRNA synthetase that is associated with formation of the transition state for the reverse reaction (47). The enzyme-bound tyrosyl-adenylate complex was prepared by incubating the tyrosyl-tRNA synthetase with 10 mm MgATP, 200 μm tyrosine, and 1 unit/ml inorganic pyrophosphatase in Buffer 3 for 30 min at 25 °C. The TyrRS·Tyr-AMP complex was separated from free tyrosine and MgATP by gel filtration on NAP-25 columns (18). The experimental setup for monitoring the reverse reaction is similar to that described above for the activation of tyrosine, except that syringe 1 contains the TyrRS·Tyr-AMP complex (0.3 μm) in Buffer 3 and syringe 2 contains 0.1–0.9 mm disodium pyrophosphate in Buffer 3.

Transfer of Tyrosine to tRNA^Tyr—Formation of the TyrRS·[Tyr-tRNA^Tyr·AMP]^‡ complex is accompanied by an increase in the intrinsic fluorescence of the protein (46). An Applied Photophysics SX 18.MV stopped-flow spectrophotometer was used to monitor changes in the intrinsic fluorescence of the TyrRS·Tyr-AMP intermediate on the addition of tRNA^Tyr as described by Xin et al. (44). Briefly, the TyrRS·Tyr-AMP intermediate, prepared as described above, is mixed with various concentrations of in vitro transcribed B. stearothermophilus tRNA^Tyr in the stopped-flow spectrophotometer, and the changes in the intrinsic fluorescence of the protein are monitored over time using an excitation wavelength of 295 nm and an emission filter with cutoff above 320 nm.

Analysis of Kinetics—All of the kinetic data were fit to a single exponential equation with a floating end point using the Applied Photophysics stopped-flow software package to determine observed rate constants (k_obs). The KaleidaGraph software was used to plot k_obs versus the substrate concentration and to fit these plots to the hyperbolic function as in Equation 3,

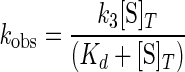(Eq. 3)

where k₃ is the forward rate constant for the formation of the TyrRS·Tyr-AMP complex; [S]_T is the total substrate concentration, and K_d is the dissociation constant for the substrate of interest. The equilibrium constant for binding of the substrate to the enzyme complex, K_a, is determined by taking the reciprocal of the K_d value. The reverse rate constant for the tyrosine activation reaction, k_–3, and the equilibrium constant for the dissociation of pyrophosphate from the TyrRS·Tyr-AMP·PP_i complex, K ^PPi_d, were calculated using a hyperbolic equation analogous to Equation 3. Similarly, the forward rate constant for the transfer of the tyrosyl moiety to the tRNA^Tyr, k₄, and the equilibrium constant for the dissociation of tRNA^Tyr from the TyrRS·Tyr-AMP·tRNA^Tyr complex, K ^tRNA_d, are calculated using a hyperbolic equation analogous to Equation 3.

Calculation of Standard Enthalpy (ΔH⁰), Entropy (ΔS⁰), and Gibbs Free Energy (ΔG⁰)—Two different models were used to fit the temperature dependence of the equilibrium and rate constants for each step in the tRNA^Tyr aminoacylation reaction. In the first model, the enthalpy is assumed to be constant over the temperature interval of the experiment (i.e. ΔC_p = 0). This results in linear van't Hoff and Eyring equations. van't Hoff plots were fit to Equation 4 (51),

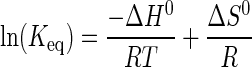(Eq. 4)

where K_eq is either the association or dissociation constant (K_a and K_d, respectively), depending on whether the step involves substrate binding (K_a) or product dissociation (K_d); R is the universal gas constant; T is the temperature in K, ΔH⁰ is the standard enthalpy, and ΔS⁰ is the standard entropy. Similarly, Eyring plots were fit to Equation 5 (52)

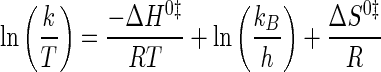(Eq. 5)

where k represents the forward or reverse rate constant for the tyrosine activation and tRNA aminoacylation reactions (k₃, k_–3, and k₄); R is the universal gas constant; k_B is the Boltzmann constant; h is Planck's constant, and ΔH^0‡ and ΔS^0‡ are the standard enthalpy and standard entropy for the transition state, respectively.

In the second model, the enthalpy is not assumed to be temperature-independent (i.e. ΔC_p ≠ 0). The resulting nonlinear van't Hoff plots were fit to Equation 6 (53),

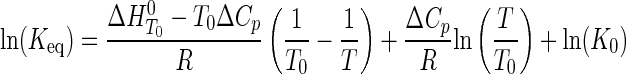(Eq. 6)

where K_eq is the equilibrium constant for either substrate binding (K_a) or product dissociation (K_d); K₀ is the equilibrium constant at the reference temperature (typically 298 K); ΔH⁰ is the standard enthalpy; ΔC_p is the change in heat capacity at constant pressure; and R is the universal gas constant. Nonlinear Eyring plots were fit to Equation 7 (54),

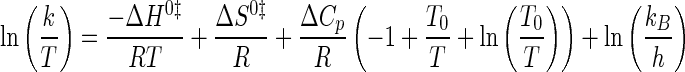(Eq. 7)

where k represents the forward or reverse rate constant for the tyrosine activation and tRNA aminoacylation reactions (k₃, k_–3, and k₄); R is the universal gas constant; k_B is the Boltzmann constant; h is Planck's constant; ΔH⁰, ΔS⁰, and ΔC_p are the standard enthalpy, standard entropy, and change in heat capacity for the transition state, and T and T₀ are the temperature and reference temperature (298 K), respectively.

Standard free energy (ΔG⁰) values are calculated by one of two methods. If the van't Hoff and Eyring curves contain the 298 K data point, ΔG⁰ is calculated using Equations 8 and 9, respectively (55),

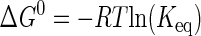(Eq. 8)

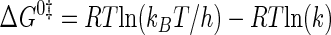(Eq. 9)

where K_eq is the equilibrium constant for substrate binding (K_a) or product dissociation (K_d); R is the universal gas constant; k_B is the Boltzmann constant; h is Planck's constant, and k is the rate constant for the reaction (i.e. k₃, k_–3, or k₄). If the regions of the van't Hoff and Eyring curves being fit do not contain the 298 K data point, ΔG⁰ is calculated using Equation 10 (51),

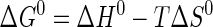(Eq. 10)

where the temperature T is 298 K. Data are fit to the van't Hoff and Eyring equations using least square analysis. For plots in which there is an inflection point, the data before and after the inflection point are fit independently.

To compare the thermodynamic values obtained using single turnover kinetics with previously published thermodynamic values obtained using steady state (multiple turnover) kinetic methods, a plot shown in Equation 11

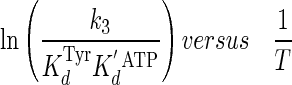(Eq. 11)

was fit to the following Arrhenius Equation 12 (49),

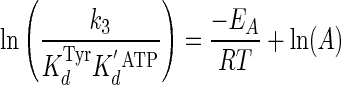(Eq. 12)

where E_A is the activation energy for the tyrosine activation reaction, and ln(A) is a pre-exponential factor. ΔH^0‡ and ΔS^0‡ values were calculated from Equations 13 and 14 (55),

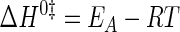(Eq. 13)

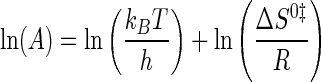(Eq. 14)

where k_B is the Boltzmann constant; h is Planck's constant; R is the universal gas constant, and T is the standard temperature (298 K). ΔG^0‡_{TyrRS·[Tyr-ATP]}^‡ was calculated from ΔH^0‡ and T ΔS^0‡ using Equation 10.

Calculation of the Enthalpy-Entropy Compensation and Isokinetic Effects—To determine whether enthalpy-entropy compensation exists for the tRNA^Tyr aminoacylation reaction, a plot of ΔH⁰ versus ΔS⁰ values determined from the van't Hoff and Eyring plots was fit to a linear equation using least squares analysis. To determine whether there is an isokinetic effect, the free energy for each complex was plotted as a function of temperature. The free energies for this plot are calculated from the rate and dissociation constants for the activation of tyrosine determined at each temperature using Equations 15, 16, 17, 18, 19, 20, 21 (assuming standard states of 1 m for ATP, tyrosine, and pyrophosphate) (39, 46),

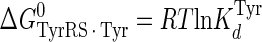(Eq. 15)

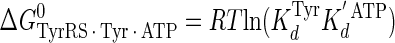(Eq. 16)

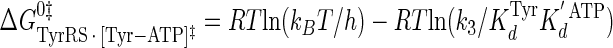(Eq. 17)

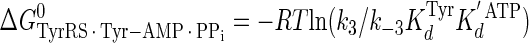(Eq. 18)

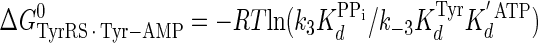(Eq. 19)

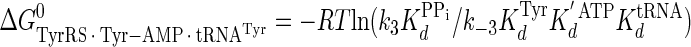(Eq. 20)

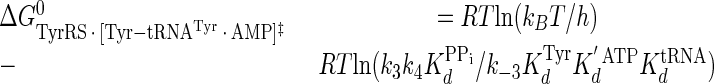(Eq. 21)

where ΔG⁰ is the Gibbs standard free energy change; R is the universal gas constant; T is the absolute temperature; k_B is the Boltzmann constant; h is the Planck's constant; · and – represent noncovalent and covalent bonds, respectively; ^‡ denotes the transition state, and PP_i is inorganic pyrophosphate (39). Standard free energies for each complex in Equations 15, 16, 17, 18, 19, 20, 21 are calculated relative to the standard free energy of the unliganded enzyme. The Gibbs activation energy for the formation of the TyrRS·[Tyr-ATP]^‡ transition state (ΔG^0‡_step1) was calculated by taking the difference in free energies between the TyrRS·[Tyr-ATP]^‡ transition state complex (Equation 17) and the TyrRS·Tyr·ATP complex immediately preceding the transition state (Equation 16) as shown in Equation 22 (39),

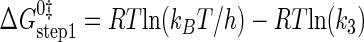(Eq. 22)

where ΔG^0‡, R, T, k_B, h, and k₃ are as defined above. Similarly, the Gibbs activation energy for the formation of the TyrRS·[Tyr-tRNA^Tyr·AMP]^‡ transition state complex (ΔG^0‡_step2) was calculated by taking the difference in free energies between the TyrRS·[Tyr-tRNA^Tyr·AMP]^‡ transition state complex (Equation 21) and the TyrRS·Tyr-AMP·tRNA^Tyr complex immediately preceding the transition state (Equation 20) as shown in Equation 23 (39),

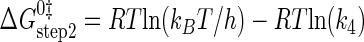(Eq. 23)

RESULTS

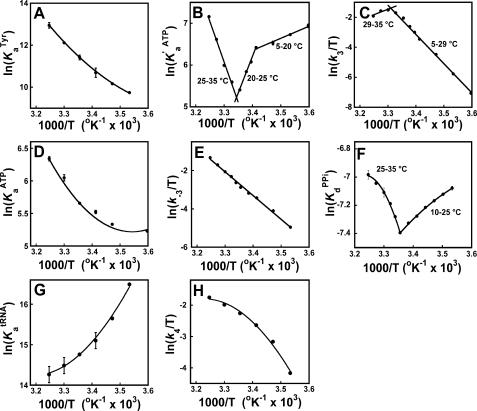
Single turnover kinetic methods were used to monitor the temperature dependence for each step in the tRNA^Tyr aminoacylation reaction (Fig. 1). The data were fit to two different models. In the first model, the enthalpy is assumed to be constant over the temperature interval of the experiment (ΔC_p = 0). This results in linear van't Hoff and Eyring equations (Equations 4 and 5). In the second model, the enthalpy is not assumed to be temperature-independent (i.e. ΔC_p ≠ 0). This results in nonlinear van't Hoff and Eyring equations (Equations 6 and 7). In all cases, the data were fit to both models to determine the appropriate model for each step (Fig. 2, Table 1, and supplemental material). Curvature in van't Hoff and Eyring plots may arise from a variety of sources, including the presence of multiple conformations of the enzyme (model 1) and temperature-dependent changes in enthalpy (model 2) (56). As a result, one cannot exclude the possibility that the ΔC_p values reported in Table 1 are artifacts resulting from fitting the data to an incorrect model.

FIGURE 2.

van't Hoff and Eyring plots for the tRNA^Tyr aminoacylation reaction. van't Hoff and Eyring plots are shown for the binding of tyrosine to unliganded tyrosyl-tRNA synthetase (panel A), the binding of ATP to the TyrRS·Tyr complex (panel B), formation of the TyrRS·[Tyr-ATP]^‡ complex (panel C), binding of ATP to unliganded tyrosyl-tRNA synthetase (panel D), formation of the TyrRS·Tyr-AMP·PP_i complex (panel E), dissociation of pyrophosphate from the TyrRS·Tyr-AMP·PP_i complex (panel F), binding of tRNA^Tyr to the TyrRS·Tyr-AMP intermediate (panel G), and formation of the TyrRS·[Tyr-tRNA^Tyr·AMP]^‡ complex (panel H). Least squares analysis was used to fit the data to either a linear equation (model 1), using Equations 4 and 6, or a nonlinear equation (model 2), using Equations 5 and 7. Error bars indicate standard deviations for the experimental measurements. In most cases, the error bars are smaller than the symbols used to represent the data points and are obscured.

TABLE 1.

Standard enthalpy, entropy, and free energy values for the tRNA^Tyr aminoacylation reaction

—, No value is expected for ΔC_p.

Enzyme complex	ΔHo	ΔSo	ΔGo	ΔCp
	kJ/mol	J/mol K	kJ/mol	kJ/mol
TyrRS + Tyr ⇄ TyrRS·Tyr
5-35 °C	103 (±2)	437 (±4)	-27.2a	3.0 (±0.3)
TyrRS + ATP ⇄ TyrRS·ATP
5-35 °C	39 (±3)	180 (±10)	-14.0a	2.5 (±0.4)
TyrRS·Tyr + ATP ⇄ TyrRS·Tyr·ATP
5-20 °C	-24 (±2)	-29 (±3)	-15.4 (±0.1)	—
20-25 °C	-144 (±6)	-438 (±6)	-13.3a	—
25-35 °C	137.9 (±0.2)	507 (±1)	-13.3a	—
TyrRS·Tyr·ATP ⇄ TyrRS·[Tyr-ATP]‡
5-29 °C	167.6 (±0.5)	347 (±2)	64.7 (±0.2)	—
29-35 °C	-65 (±1)	-425 (±4)	61.5 (±0.2)	—
TyrRS·[Tyr-ATP]‡ ⇄ TyrRS·Tyr-AMP·PPi
10-35 °C	103.2 (±0.9)	125 (±3)	-65.7 (±0.5)	—
TyrRS·Tyr-AMP·PPi ⇄ TyrRS·Tyr-AMP + PPi
10-25 °C	-18.7 (±0.4)	-124 (±2)	18.3a	-0.57 (±0.06)
25-35 °C	55.8 (±0.2)	126 (±1)	18.3a	-5.0 (±0.6)
TyrRS·Tyr-AMP + tRNATyr ⇄ TyrRS·Tyr-AMP·tRNATyr
10-35 °C	-52 (±3)	-50 (±10)	-36.6b	3.5 (±0.4)
TyrRS·Tyr-AMP·tRNATyr ⇄ TyrRS·[Tyr-tRNATyr·AMP]‡
10-35 °C	53 (±4)	-40 (±10)	65.1b	4.7 (±0.9)

^aValues calculated from data in (18).

^bValues calculated from data in (46).

Binding of Tyrosine to the Unliganded Tyrosyl-tRNA Synthetase—Stopped-flow fluorescence spectroscopy was used to monitor the binding of tyrosine to unliganded tyrosyl-tRNA synthetase from 5 to 35 °C. These experiments were performed in the absence of ATP for all temperatures. When tyrosine is mixed with tyrosyl-tRNA synthetase, a rapid single exponential decrease is observed in the relative fluorescence above 320 nm. This decrease in fluorescence results from a blue shift in the intrinsic fluorescence of tyrosyl-tRNA synthetase and is correlated to the binding of tyrosine to the enzyme. The dissociation constant, K_d^Tyr, was calculated for each temperature using Equations 1 and 2. As the resulting van't Hoff plot is slightly concave in shape, the results were fit to Equation 6 (Fig. 2, panel A). The ΔH⁰ and ΔS⁰ values for the binding of tyrosine to the unliganded enzyme are shown in Table 1.

Binding of ATP and Subsequent Formation of the Transition State Complex Reveals a Temperature-dependent Change in the Catalytic Mechanism of Tyrosyl-tRNA Synthetase—Like the binding of tyrosine to tyrosyl-tRNA synthetase, formation of the TyrRS·Tyr-AMP complex is accompanied by a blue shift in the intrinsic fluorescence of the enzyme (16, 46). As this blue shift correlates with formation of the TyrRS·[Tyr-ATP]^‡ transition state complex, stopped-flow fluorescence can be used to monitor the single turnover kinetics for the first step of the tRNA^Tyr aminoacylation reaction (i.e. the activation of tyrosine to form the TyrRS·Tyr-AMP intermediate). Determination of K′ ^ATP_d is achieved by fitting a plot of k_obs versus [ATP] in the presence of saturating concentrations of tyrosine (200 μm) to Equation 3.

To determine ΔH⁰ and ΔS⁰ for the binding of ATP to the TyrRS·Tyr complex, the association constant, K′ ^ATP_a, was calculated for a range of temperatures from 5 to 35 °C, and the data were fit to Equation 4. The plot revealed three distinct regions as follows: 5–20 °C, 20–25 °C, and 25–35 °C (Fig. 2, panel B). Particularly striking is the transition that occurs at 25 °C where the slope of the line changes sign. Although the 25–35 °C region showed some curvature, fitting this region to model 2 (Equation 6) resulted in an unusually large ΔC_p value (ΔC_p = 18 kJ/mol). As ΔC_p values for ligand binding are generally between –7 and +2 kJ/mol (57), Equation 4 (model 1) was used to fit the temperature dependence of K′ ^ATP_d. The ΔH⁰ and ΔS⁰ values for the three regions are shown in Table 1. The results are consistent with a temperature-dependent shift in the catalytic mechanism of the enzyme, with the binding of ATP to the TyrRS·Tyr complex being enthalpically driven below 25 °C and entropically driven above 25 °C.

The forward rate constant, k₃, was determined from analysis of the ATP dependence for the activation of tyrosine at saturating tyrosine concentration (200 μm). As is the case for K′ ^ATP_d, fitting the temperature dependence of k₃ to model 2 (Equation 7) results in an unusually large ΔC_p value (ΔC_p = –26 kJ/mol). As a result, model 1 was used to fit the data. Fitting the k₃ data to Equation 5 reveals two regions: 5–29 and 29–35 °C (Fig. 2, panel C). Above 29 °C, the slope of the line changes sign, suggesting that there is a temperature-dependent change in the transition state of the reaction. The ΔH^0‡ and ΔS^0‡ values for the TyrRS·[Tyr-ATP]^‡ complex are shown in Table 1. The results indicate that below 29 °C, formation of the TyrRS·[Tyr-ATP]^‡ transition state complex is enthalpically unfavorable but entropically favorable, whereas above 29 °C, it is enthalpically favorable but entropically unfavorable.

Enzyme-bound Tyrosine Is Responsible for the Dramatic Changes in ΔH⁰ and ΔS⁰ Observed at 25 °C—It has previously been shown that in the absence of a functional KMSKS sequence, there is a synergistic interaction between tyrosine and ATP that stabilizes the TyrRS·Tyr·ATP complex (22). To determine whether the temperature-dependent change in the catalytic mechanism of the enzyme is dependent on the presence of tyrosine, the temperature dependence of the equilibrium constant for the dissociation of ATP from the TyrRS·ATP complex, K ^ATP_a, was determined (Fig. 2, panel D). K ^ATP_a was calculated using the method described for K′ ^ATP_a, except that the concentration of tyrosine was at least 10-fold below the dissociation constant for tyrosine. Under these conditions, the enzyme is present in the unliganded state prior to binding ATP. The overall slope from the van't Hoff plot is positive and reveals two distinct regions of linearity (5–20 and 20–35 °C). In contrast to the binding of ATP to the TyrRS·Tyr complex, in which binding of ATP is enthalpically driven below 25 °C, the binding of ATP to the unliganded enzyme is entropically driven at all temperatures. These data indicate that the increased affinity of tyrosyl-tRNA synthetase for ATP below 25 °C is dependent on the presence of enzyme-bound tyrosine. The ΔH⁰ and ΔS⁰ values for the TyrRS·ATP complex are shown in Table 1.

Pyrophosphorolysis and Pyrophosphate Dissociation—The reverse rate constant, k_–3, was determined from analysis of the reverse tyrosine activation reaction, and the results were fit to the Eyring equation, assuming ΔC_p = 0 (model 1, Equation 5). A single linear region is observed (Fig. 2, panel E). The ΔH⁰ and ΔS⁰ values for formation of the TyrRS·Tyr-AMP·PP_i complex are shown in Table 1.

To determine ΔH⁰ and ΔS⁰ for the dissociation of pyrophosphate from the TyrRS·Tyr-AMP·PP_i complex, the dissociation constant for pyrophosphate, K ^PPi_d, was determined from 10 to 35 °C, and the data were fit to the van't Hoff equation, assuming ΔC_p≠0 (model 2, Equation 6). The plot revealed two distinct regions from 10 to 25 and 25 to 35 °C (Fig. 2, panel F). The dissociation of pyrophosphate from the TyrRS·Tyr-AMP·PP_i complex is enthalpically driven below 25 °C and entropically driven above 25 °C. The ΔH⁰, ΔS⁰, and ΔC_p values for formation of the TyrRS·Tyr-AMP·PP_i complex are shown in Table 1.

Transfer of the Tyrosyl Moiety to tRNA^Tyr—Transfer of the tyrosyl moiety to the 3′ end of tRNA^Tyr is accompanied by a red shift in the intrinsic fluorescence of the TyrRS·Tyr-AMP·tRNA^Tyr complex (46). As this red shift correlates with formation of the transition state for the second step of the aminoacylation reaction (i.e. transfer of the tyrosyl moiety to tRNA^Tyr), stopped-flow fluorescence can be used to monitor the single turnover kinetics for the second step (46). This is achieved by pre-forming the TyrRS·Tyr-AMP intermediate, mixing it with tRNA^Tyr in the stopped-flow fluorometer and monitoring the increase in fluorescence above 320 nm. The equilibrium constant for the binding of tRNA^Tyr to the TyrRS·Tyr-AMP complex and the forward rate constant for transfer of the tyrosyl moiety to the 3′ end of tRNA^Tyr, K ^tRNA_d, and k₄, respectively, are determined by fitting a plot of k_obs versus [tRNA^Tyr] to Equation 3.

To determine ΔH⁰ and ΔS⁰ for the binding of tRNA^Tyr to the TyrRS·Tyr-AMP intermediate, K ^tRNA_a was calculated for a range of temperatures from 10 to 35 °C (Fig. 2, panel G). As the resulting van't Hoff plot is concave, the data were fit to Equation 6 (model 2, ΔC_p ≠ 0). The ΔH⁰, ΔS⁰, and ΔC_p values are shown in Table 1. The results indicate that the initial binding of tRNA^Tyr to the TyrRS·Tyr-AMP intermediate is enthalpically driven.

To determine ΔH⁰ and ΔS⁰ for transfer of the tyrosyl moiety from the enzyme-bound tyrosyl-adenylate to tRNA^Tyr, k₄ was calculated for a range of temperatures from 10 to 35 °C (Fig. 2, panel H). As the resulting Eyring plot is convex, the data were fit to Equation 7 (model 2, ΔC_p ≠ 0). The ΔH⁰, ΔS⁰, and ΔC_p values are shown in Table 1. The results indicate that formation of the TyrRS·[Tyr-tRNA·AMP]^‡ complex is both enthalpically and entropically unfavorable.

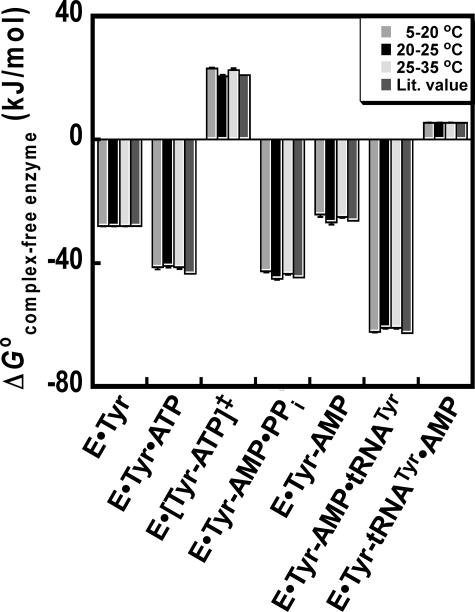
Determination of the Free Energy for Each Step along the Reaction Pathway—Gibb's free energy values have previously been determined for each enzyme-bound complex in the tRNA^Tyr aminoacylation reaction (relative to the unliganded enzyme) using Equations 15, 16, 17, 18, 19, 20, 21 (18, 46). To compare the results presented in this study with previously published results, ΔG⁰ values for each enzyme-bound complex were calculated from ΔH⁰ and TΔS⁰ as follows: 1) ΔH⁰ and ΔS⁰ values were estimated from all van't Hoff plots by fitting the data to Equation 4 (model 1, ΔC_p = 0); 2) ΔG⁰ values corresponding to each step along the reaction pathway were calculated from ΔH⁰ and ΔS⁰ for each step; and 3) the sum of the ΔG⁰ values for each step leading up to the enzyme-bound complex was calculated (e.g. ΔG_{TyrRS·Tyr·ATP} = ΔG⁰ _{(TyrRS+Tyr⇄TyrRS·Tyr)} + ΔG⁰ _{(TyrRS·Tyr+ATP⇄TyrRS·Tyr·ATP)}). In all cases, there is good agreement between the ΔG⁰ values calculated from ΔH⁰ and TΔS⁰, and previously published ΔG⁰ values (Fig. 3).

FIGURE 3.

Comparison of standard free energies of the tRNA^Tyr aminoacylation reaction. The standard free energy for each tyrosyl-tRNA synthetase complex (relative to the free enzyme) was calculated. ΔG⁰ values for the 10–20, 20–25, and 25–35 °C temperature ranges were calculated from the ΔH⁰ and TΔS⁰ values presented in Table 1 using Equation 6. These temperature ranges were chosen based on the three discontinuous regions in Fig. 2, panel B. For cases where the natural logarithm of the rate or equilibrium constant is linear with respect to 1/T for two or more temperature ranges (e.g. ln(K_d^Tyr)), the same values for ΔH⁰ and TΔS⁰ were used for each temperature range. For the TyrRS·[Tyr-ATP]^‡ complex, the 20–25 and 25–35 °C temperature ranges are replaced by 20–29 and 29–35 °C. ΔG⁰ values labeled “Lit. Value” are calculated from literature values for the equilibrium and rate constants determined at 25 °C using Equations 15, 16, 17, 18, 19, 20, 21 (18).

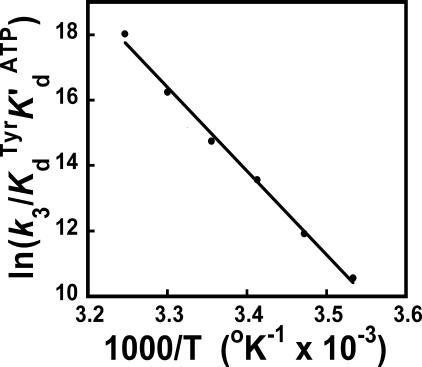
Comparison of Enthalpy and Entropy Values Calculated from Single and Multiple Turnover Kinetic Experiments—Wells et al. (49) previously used a steady state (multiple turnover) pyrophosphate exchange assay to analyze the enthalpic and entropic contributions to the stability of the TyrRS·[Tyr-ATP]^‡ complex. An analogous Arrhenius plot, using the single turnover kinetic data presented in this study, is shown in Fig. 4. Despite the nonlinearity of the van't Hoff and Eyring plots shown in Fig. 2, panels B and C, the Arrhenius plot is surprisingly linear. This is qualitatively similar to the results obtained by Wells et al. (49) using the steady state assay, except for a small deviation from linearity at 18 and 45 °C. Fitting the data to Equations 10 and 14 indicates that ΔH^0‡, ΔS^0‡, and ΔG^0‡ are 210.4 kJ/mol, 623 J/mol K, and 24.8 kJ/mol, respectively. For the equivalent Arrhenius plot determined by Wells et al. (49) using multiple turnover conditions, the values of ΔH^0‡, ΔS^0‡, and ΔG^0‡ are 57.9 kJ/mol, 159.4 J/mol K, and 10.5 kJ/mol, respectively.

FIGURE 4.

Arrhenius plot for the activation of tyrosine. In the Arrhenius plot shown, ln((k₃)/(K ^Tyr_dK′ ^ATP_d)) corresponds to the standard free energy of the TyrRS·[Tyr-ATP]^‡ transition state relative to that of the free enzyme (Equation 17). Values for ΔH^0‡, ΔS^0‡, and ΔG^0‡ were calculated from the slope and y-intercept based on Equations 4, 5, 6, 7.

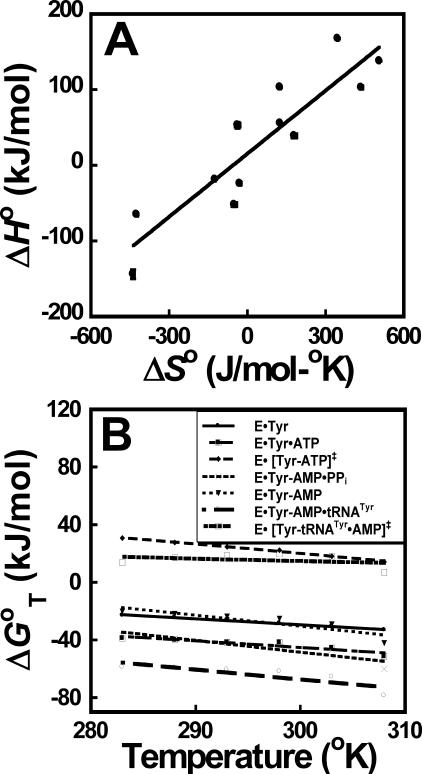
The tRNA^Tyr Aminoacylation Reaction Displays Enthalpy-Entropy Compensation—Enthalpy-entropy compensation is defined as a linear relationship between ΔH and ΔS for a series of reactions (i.e. ΔH_i = α + βΔS_i) (58). As can be seen in Fig. 5, panel A, plotting ΔH⁰ versus ΔS⁰ for each state in the tRNA^Tyr aminoacylation reaction results in a linear relationship. This relationship is observed despite significant temperature-dependent changes in the values calculated for ΔH⁰ and ΔS⁰.

FIGURE 5.

Enthalpy-entropy compensation and isokinetic plots for the aminoacylation of tRNA^Tyr. Enthalpy-entropy compensation (panel A) and isokinetic plots (panel B) are shown for each step in the tRNA^Tyr aminoacylation reaction. Standard enthalpy (ΔH⁰) and entropy (ΔS⁰) values are calculated from the slopes and y-intercepts of the plots shown in Fig. 2. For plots where there is more than one linear region (e.g. Fig. 2, panel B), ΔH⁰ and ΔS⁰ values are calculated for each of the linear regions. The data are fit to a linear equation using least squares analysis. Standard deviations in ΔH⁰ and ΔS⁰ are indicated by error bars unless they are obscured by the symbols used to represent the data points.

In some cases, there is a unique temperature at which all members of a series of reactions will display the same rate or equilibrium constant. This is known as the isokinetic effect (58). The temperature at which the reactions display the same rate or equilibrium constant can be determined from the point at which the lines intersect in a plot of ΔG versus temperature. As can be seen in Fig. 5, panel B, no isokinetic effect is observed for the tRNA^Tyr aminoacylation reaction.

DISCUSSION

In this study, we have used single turnover kinetic methods to analyze the thermodynamics of the tyrosyl-tRNA synthetase-catalyzed aminoacylation of tRNA^Tyr. In contrast to steady state kinetic methods, single turnover kinetics gives the rate and dissociation constants for each individual step in the reaction. This approach has allowed the entire tRNA^Tyr aminoacylation reaction to be analyzed. The results of this analysis, and interpretation of their meaning, are summarized below.

What Is the Physical Basis for the Temperature-dependent Inflection in the van't Hoff and Eyring Plots?—The dramatic temperature-dependent changes in the slopes of the van't Hoff and Eyring plots (Fig. 2) suggest that tyrosyl-tRNA synthetase undergoes significant temperature-dependent conformational changes during the course of the reaction. This is most apparent at three steps in the reaction pathway as follows: the initial binding of ATP to the TyrRS·Tyr complex, formation of the TyrRS·[Tyr-ATP]^‡ transition state of the reaction, and the release of pyrophosphate from the TyrRS·Tyr-AMP·PP_i complex. Interestingly, in each of these complexes, the signs of ΔH⁰ and ΔS⁰ change at ∼25 °C. This suggests that the temperature-dependent changes in ΔH⁰ and ΔS⁰ for each of these steps may arise from conformational changes involving the same groups or regions in tyrosyl-tRNA synthetase. In this model, these groups are conformationally constrained and unable to contribute to catalysis below 25 °C, whereas above 25 °C, they are able to adopt conformations that facilitate catalysis.

Conformational changes have previously been proposed to play a role in the catalytic mechanism of tyrosyl-tRNA synthetase. The observations that 1) mutation of lysines 230 and 233 to alanine destabilizes the transition state of the tyrosine activation reaction, and 2) lysines 230 and 233 are at least 8 Å away from the active site in the unliganded B. stearothermophilus tyrosyl-tRNA synthetase structure suggest that these residues move into the active site during catalysis (41). Lysines 230 and 233 are part of the KMSKS signature sequence and are located in a loop that connects the Rossmann fold domain (containing the active site of the enzyme) to the anticodon binding domain. Analysis of 1,5-({2-[(iodoacetyl)amino]ethyl}amino)-naphthalene-1-sulfonic acid (1,5-IAEDANS)-labeled bovine tyrosyl-tRNA synthetase using fluorescence resonance energy transfer is consistent with the hypothesis that tyrosyl-tRNA synthetase undergoes a conformational change during the tyrosine activation reaction (59). More recently, crystal structures of several tyrosyl-tRNA synthetase complexes have revealed three different conformations adopted by the KMSKS loop as follows: an open form, in which the KMSKS loop is positioned away from the active site; a closed form, in which the side chains of the two lysines in the KMSKS sequence are appropriately positioned to form hydrogen bonds with the α- and γ-phosphate groups of ATP, respectively; and a semi-open form in which the KMSKS loop forms a 3₁₀ helix, resulting in a more open active site than is found for the closed form (6, 7, 60–63).

The observation that the binding of ATP to unliganded tyrosyl-tRNA synthetase is entropically driven at all temperatures (Fig. 2, panel D; Table 1) suggests that the sharp transition that occurs at 25 °C for the binding of ATP to the TyrRS·Tyr complex (Fig. 2, panel B) results from the interaction between tyrosine and ATP. Previous observations indicate that one of the functions of the KMSKS sequence is to disrupt a synergistic interaction between the tyrosine and ATP substrates in the TyrRS·Tyr·ATP complex, thereby preventing the TyrRS·Tyr·AMP complex from falling into a thermodynamic “pit” prior to formation of the transition state (19), allowing the energy from this interaction to instead be used to stabilize the TyrRS·[Tyr-ATP]^‡ transition state (22). Based on these observations, and the van't Hoff and Eyring plots shown in Fig. 2, we postulate that below 25 °C, the KMSKS sequence is conformationally constrained and unable to move into the active site, whereas above 25 °C, the KMSKS loop is unconstrained and is able to move into the active site, where it participates in catalysis. The observation that the transition at 25 °C is relatively sharp (Fig. 2, panels B, C, and F) suggests that the conformational change responsible for this transition is highly cooperative.

What Is the Driving Force at Each Step in the tRNA^Tyr Aminoacylation Reaction?—The changes in standard enthalpies for each step in the tRNA^Tyr aminoacylation reaction may arise from a number of sources, including changes in protein-solvent and protein-ligand hydrogen bonds, van der Waals interactions, formation or dissociation of salt bridges, and solvent reorganization at the surface of the protein (64). Similarly, changes in the standard enthalpies for each step in the reaction may also arise from a variety of sources, including hydration effects, changes in configurational degrees of freedom in the protein and ligand, and changes in the number of molecules that are present in solution (64). In the following discussion, a physical model based on the thermodynamic results is presented for each step along the reaction pathway. Although other interpretations are possible, the following models appear to provide reasonable explanations for the thermodynamic results presented in this study.

1) Formation of the TyrRS·Tyr Complex—Kinetic analysis of tyrosyl-tRNA synthetase variants indicates that nearly all of the interactions between the enzyme and tyrosine substrate are formed on the initial binding of tyrosine and do not change throughout the course of the reaction (41, 65). In other words, tyrosyl-tRNA synthetase uses binding energy to specifically recognize the tyrosine substrate. Whereas tyrosine recognition appears to involve formation of specific bonds between the enzyme and tyrosine substrate, thermodynamic analysis indicates that the driving force for the binding of tyrosine is entropic (Fig. 2, panel A; Table 1). This is consistent with the binding of tyrosine being driven by the release of water molecules from the binding site, as has previously been proposed for ligand binding in other systems (reviewed in Ref. 64).

2) Formation of the TyrRS·Tyr·ATP Complex—In contrast to the binding of tyrosine, kinetic analysis of tyrosyl-tRNA synthetase variants indicates that most of the interactions between the enzyme and ATP do not occur on the initial binding of ATP, but instead occur on formation of the TyrRS·[Tyr-ATP]^‡ transition state complex (41). In other words, the ATP binding energy is used to stabilize the transition state complex, rather than the TyrRS·Tyr·ATP complex. Analysis of the thermodynamics for the binding of ATP to the TyrRS·Tyr complex indicate that below 25 °C, the binding of ATP is enthalpically driven, whereas above 25 °C, it is entropically driven (Fig. 2, panel B; Table 1). This is consistent with the hypothesis that the KMSKS sequence is conformationally constrained below 25 °C and is unable to disrupt the synergistic interaction between the tyrosine and ATP substrates. This additional interaction leads to an increase in the binding enthalpy for ATP, resulting in the reaction being enthalpically driven. In contrast, above 25 °C, the KMSKS sequence is able to disrupt the synergistic interaction between the substrates, decreasing the binding enthalpy and allowing entropic effects to dominate formation of the TyrRS·Tyr·ATP complex.

3) Formation of the TyrRS·[Tyr-ATP]^‡ Transition State—Stabilization of the TyrRS·[Tyr-ATP]^‡ transition state is primarily because of the formation of interactions between the enzyme and the pyrophosphate moiety of ATP (18, 21, 66). In particular, the KMSKS signature sequence plays a central role in stabilizing the pyrophosphate moiety in the transition state complex. If the hypothesis is correct that the conformation of the KMSKS loop is constrained below 25 °C, then one would predict that enthalpic effects should play a larger role in stabilizing the transition state above 25 °C than they do below this temperature. Except for the observation that the transition in the Eyring plot occurs slightly above 25 °C for formation of the TyrRS·[Tyr-ATP]^‡ transition state complex (Fig. 2, panel C), this is exactly what is observed.

4) Cleavage of the Scissile Bond between the α- and β-Phosphates of ATP—Analysis of the interactions in the TyrRS·Tyr-AMP·PP_i complex is complicated by the inability to kinetically separate the reverse rate constant (k_–3) from the dissociation constant for pyrophosphate (K ^PPi_d) in tyrosyl-tRNA synthetase variants that affect the stability of this complex. It appears likely, however, that those amino acids that interact with the pyrophosphate moiety in the TyrRS·[Tyr-ATP]^‡ transition state (i.e. Thr-40, His-45, Lys-82, Arg-86, Lys-230, Lys-233, and Thr-234) also stabilize the pyrophosphate moiety in the TyrRS·Tyr-AMP·PP_i complex (18, 21, 66). The observation that cleavage of the scissile bond between the α- and β-phosphates of ATP is entropically favorable (Fig. 2, panel E; Table 1) suggests that the driving force for this process may be due to an increase in conformational entropy resulting from bond cleavage.

5) Release of the Pyrophosphate Product from the TyrRS·Tyr-AMP·PP_i Complex—The observation that above 25 °C, the release of the pyrophosphate is enthalpically unfavorable (Fig. 2, panel F; Table 1) suggests that the interactions between the enzyme and pyrophosphate in the TyrRS·Tyr-AMP·PP_i complex are stronger above 25 °C than they are below it. This is consistent with the hypothesis that below 25 °C, the KMSKS loop is conformationally constrained and is unable to interact with the pyrophosphate product, whereas above 25 °C, the KMSKS loop is able to interact with the pyrophosphate product. As a result, above 25 °C, there are more interactions between the enzyme and the pyrophosphate product that must be broken before pyrophosphate is released.

6) Binding of tRNA^Tyr to the TyrRS·Tyr-AMP Intermediate—Although crystal structures of tyrosyl-tRNA synthetase complexed with tRNA^Tyr show two tRNA^Tyr molecules bound per dimer, in solution the tyrosyl-tRNA synthetase dimer binds a single tRNA^Tyr molecule (18, 60, 62, 67). tRNA^Tyr interacts with the enzyme through its 3′ end acceptor stem, variable loop, and anticodon stem and loop (62). Binding of tRNA^Tyr to tyrosyl-tRNA synthetase is enthalpically favorable and entropically unfavorable (Fig. 2, panel G; Table 1). The observation that binding of tRNA^Tyr to tyrosyl-tRNA synthetase is enthalpically driven is consistent with several previous investigations of protein-RNA interactions (68–71). In particular, both the binding of tRNA^Ile to isoleucyl-tRNA synthetase, and the binding of the group I intron P4-P6 domains to Neurospora crassa mitochondrial tyrosyl-tRNA synthetase (CYT-18) are enthalpically driven (69, 70). Caprara et al. (72) have previously shown that the P4-P6 domains of the group I intron mimic the D stem and anticodon stem of tRNA^Tyr in their interactions with tyrosyl-tRNA synthetase. It is notable that the binding of tRNA^Tyr to B. stearothermophilus tyrosyl-tRNA synthetase and the binding of the P4-P6 domains to CYT-18 overcome unfavorable binding entropy through favorable enthalpic effects. Record et al. (73) have previously observed that electrostatic interactions between the nucleic acid phosphodiester backbone and protein leads to the release of bound cations, resulting in a favorable binding entropy for the protein:nucleic acid association (73). Caprara et al. (72) argue that, in the case of CYT-18, the favorable entropy resulting from the release of bound cations is offset by entropically unfavorable conformational changes that restrict the RNA and/or protein motion or flexibility. A similar explanation appears plausible for the unfavorable entropy observed for the association of tRNA^Tyr with B. stearothermophilus tyrosyl-tRNA synthetase.

7) Formation of the TyrRS·[Tyr-tRNA·AMP]^‡ Transition State—Formation of the TyrRS·[Tyr-tRNA·AMP]^‡ transition state is stabilized by the following: 1) interactions between the 3′ end of tRNA^Tyr (i.e. adenosine 76) and Thr-40, Lys-82, and Arg-86 of tyrosyl-tRNA synthetase; and 2) strengthening of the hydrogen bond between the amine group of the tyrosyl moiety in the tyrosyl-adenylate intermediate and Gln-173 in tyrosyl-tRNA synthetase (65). Interactions between tyrosyl-tRNA synthetase and the 3′ end of tRNA^Tyr position adenosine 76 for nucleophilic attack on the carboxyl group of the tyrosyl-adenylate intermediate. Strengthening of the hydrogen bond between the tyrosyl amine group and Gln-173 in tyrosyl-tRNA synthetase is postulated to weaken the scissile bond between the tyrosyl and AMP moieties in the tyrosyl-adenylate intermediate (65).

Formation of the TyrRS·[Tyr-tRNA·AMP]^‡ transition state is enthalpically unfavorable, indicating that there is a net decrease in bonding strength on formation of the transition state. That formation of the TyrRS·[Tyr-tRNA·AMP]^‡ transition state is enthalpically unfavorable may seem paradoxical, particularly because formation of the transition state leads to bond formation between the tyrosine substrate and tRNA^Tyr, as well as new hydrogen bonds forming between the 3′ end of tRNA^Tyr and Thr-40, Lys-82, and Arg-86 in tyrosyl-tRNA synthetase, and an increase in the strength of the hydrogen bond between Gln-173 and the tyrosine substrate. In addition to these changes, however, the scissile bond between the tyrosyl and AMP moieties is being broken during formation of the transition state. This may lead to a decrease in bonding between the enzyme and AMP that more than offsets the enthalpic contributions of Thr-40, Lys-82, Arg-86, and Gln-173. If this scenario is correct, it suggests that transfer of the tyrosyl moiety to tRNA^Tyr occurs through a dissociative transition state. This would be consistent with the hypothesis that strengthening of the hydrogen bond between Gln-173 and the tyrosine substrate weakens the scissile bond between the tyrosyl and AMP moieties of the tyrosyl-adenylate intermediate (65).

The unfavorable entropy observed for formation of the transition state suggests that there is a decrease in the conformational entropy of tRNA^Tyr and/or tyrosyl-tRNA synthetase that accompanies formation of the TyrRS·[Tyr-tRNA·AMP]^‡ complex. This is consistent with the hypothesis that the interaction between tyrosyl-tRNA synthetase and tRNA^Tyr constrains the conformation and orientation of the 3′ end of tRNA^Tyr.

What Is the Source of the Observed Enthalpy-Entropy Compensation?—Enthalpy-entropy compensation is commonly observed in biological systems (64). A number of explanations have been proposed for this phenomenon, including the following: 1) the stronger intermolecular interactions that increase ΔH⁰ are accompanied by a reduction in configurational freedom of the protein and ligand; 2) solvent effects dominating the ΔH⁰ and ΔS⁰ components of ΔG⁰; and 3) constraints in ΔG⁰ forcing a correlation between ΔH⁰ and ΔS⁰ when |ΔG⁰| < |ΔH⁰| (reviewed in Refs. 58, 74). This last explanation predicts a linear correlation between ΔH⁰ and ΔS⁰ with a slope approximately equal to 298 °C (i.e. ΔH⁰ = ΔG⁰ + T ΔS⁰). The observation that the slope of the enthalpy-entropy plot shown in Fig. 5 is 280 (±40) °C is consistent with this explanation.

Interpretation of Heat Capacities—Nonlinear van't Hoff and Arrhenius plots may result from temperature-dependent changes in intra- and inter-molecular interactions (i.e. changes in ΔC_p), protein conformational changes, or, in the case of the Arrhenius plots, changes in the reaction mechanism or rate-limiting step (56). To distinguish between the above cases, the data presented in this study were fit to two models. In the first model, changes in the conformation of the protein are assumed to be responsible for the nonlinearity observed in the van't Hoff and Arrhenius plots (i.e. ΔC_p = 0). In the second model, this nonlinearity is assumed to be due to temperature-dependent changes in intra- and inter-molecular interactions (i.e. ΔC_p ≠ 0). In several cases (e.g. the binding of ATP to the TyrRS·Tyr complex), it is apparent that model 2 does not fit the data well, supporting the hypothesis that the nonlinearity results from conformational changes in tyrosyl-tRNA synthetase. In other cases (e.g. the binding of tyrosine to tyrosyl-tRNA synthetase), it is less obvious which model is more appropriate. In these cases, calorimetric methods will be needed to distinguish between the two models. It is intriguing, however, that the sign of the ΔC_p values for tyrosine and tRNA^Tyr binding, as well as for the dissociation of pyrophosphate, are atypical when compared with previously reported values of ΔC_p for ligand binding. In particular, in most receptor-ligand interactions ΔC_p ≤ 0 (57), whereas the ΔC_p values presented in this study are nearly all positive. Positive values for ΔC_p may arise from either solvation of hydrophobic groups or a cooperative to disordered transition involving many weak interactions (74–76). The former interpretation is not supported by the ΔH⁰ and ΔS⁰ values reported in this paper. Furthermore, structural analyses of tyrosyl-tRNA synthetase suggest that ligand binding is not accompanied by a cooperative to disordered transition (60). These observations suggest that the nonlinear van't Hoff and Arrhenius plots observed for tyrosine and tRNA^Tyr binding, as well as the dissociation of pyrophosphate, may be due to conformational changes in the protein, rather than temperature-dependent changes in intra- and inter-molecular interactions in the protein and ligand.

Comparing Single and Multiple Turnover Kinetic Analyses—Wells et al. (49) have previously used steady state kinetics to determine thermodynamic values for the transition state of the tyrosine activation reaction. To directly compare the ΔH^0‡, ΔS^0‡, and ΔG^0‡ values obtained from single turnover kinetics with those that Wells et al. (49) obtained using steady state (multiple turnover) kinetics, ΔH^0‡ and ΔS^0‡ for the transition state were calculated from the Arrhenius plot shown in Fig. 4. Surprisingly, despite the nonlinearity observed in the van't Hoff and Eyring plots, the Arrhenius plot is linear for the single turnover kinetic data. This observation indicates that the nonlinearity observed for the binding of ATP (Fig. 2, panel B) is entirely offset by the nonlinearity observed in k₃, the forward rate constant (Fig. 2, panel C). This suggests that the nonlinearity observed for formation of the TyrRS·Tyr·ATP and TyrRS·[Tyr-ATP]^‡ complexes has the same physical basis and is consistent with the hypothesis that the KMSKS sequence reduces the synergistic interaction between tyrosine and ATP on the initial binding of ATP, allowing it to instead be used to stabilize the TyrRS·[Tyr-ATP]^‡ transition state.

Conclusion—Single turnover kinetic methods have been used to analyze the thermodynamics for catalysis of the aminoacylation of tRNA^Tyr by B. stearothermophilus tyrosyl-tRNA synthetase. These analyses revealed a temperature-dependent change in the slopes of the van't Hoff and Eyring plots at several of the steps involved in catalyzing the tyrosine activation step of the reaction. To explain these observations, we propose a model in which the KMSKS signature sequence is conformationally constrained and unable to participate in catalysis below 25 °C. The results presented in this study lay the groundwork for future investigations into the thermodynamics governing the tRNA^Tyr aminoacylation reaction.