Measuring variability

Abstract

Gene expression is a noisy stochastic process, since it involves at its core interactions between single molecules: a polymerase and a binding site. However, many biological processes directly dependent upon gene expression are reliable. Prominent among them is morphogenesis: how are body parts so consistently generated and proportioned? In the early embryo, gradients of certain proteins called morphogens affect the pattern of cell differentiation and embryonic development. The variability in morphogen patterns and its effect in the proportions of the embryo has been intriguing biologists for a long time, but the limitations, variability and limited reproducibility of immunostaining of fixed embryos does not allow dynamic measurements. New tools now allow precise measurement of the variability of morphogen patterning in living Drosophila embryos, making it possible to probe the underlying mechanisms of development.

Scientists from the “quantitative” disciplines have always been attracted to biology; and all along, they have been fascinated by the inherent variability of living beings. Many times a careful analysis of such variability has significantly advanced our understanding of a given field. Examples that come to mind include the analysis of bacterial mutation rates by Luria and Delbrück, showing that a constant probability of acquiring a mutation results in large fluctuations in the size of revertant colonies (Luria and Delbrück, 1943); and Robert May’s influential paper on simple mathematical models of ecological dynamics with complex dynamical behavior, such as predator-prey systems, which strongly bolstered the development of the study of chaotic dynamical systems and their biological applications (May, 1976). Other times, the variability permits a measurement of an underlying process, such as the BOLD response that permits functional MRI measurements or intrinsic optical signal imaging of brain activity (Jezzard et al., 2003); or Chuck Stevens’ fluctuation analysis of ion channel chatter (Neher and Stevens, 1977). This classic work has shown that, whenever a quantitative analysis of variability and fluctuations can be carried out, it may be enormously rewarding in terms of biological understanding.

As a new generation of would-be quantitative scientists enters the life sciences, they try to push new areas of biology to more quantitative measurements. But analyzing variability requires accurate measurements, at least more accurate than the variability to be measured; and accurate measurements of biological phenomena can be difficult to perform. In particular, that an instrument may yield a figure does not necessarily mean that that figure is a fair representation of biological reality, and the technical reliability of the figure does not necessarily imply that it is a fair representation of the reliability (or lack thereof) of the underlying biological process. The fluorescent intensity of spots in DNA microarrays can be reliably measured; but this intensity is linked to the variable we really wish to measure—a level of gene expression—by protocols having a fairly low level of repeatability, high batch-to-batch variability, various nonlinearities and other issues. It took years from the initial development of microarray technology to develop robust hybridization and measurement protocols and data normalization techniques, until technical variability became smaller than biological variability; and this technology keeps on developing because more accurate measurements allow experiments in which the signal to be detected is more subtle.

Two recent back-to-back papers in Cell by Thomas Gregor and collaborators at Princeton University exemplify the introduction of a clean quantitative technique that will enable precise questions to be asked and answered (Gregor et al., 2007a, Gregor et al., 2007b).

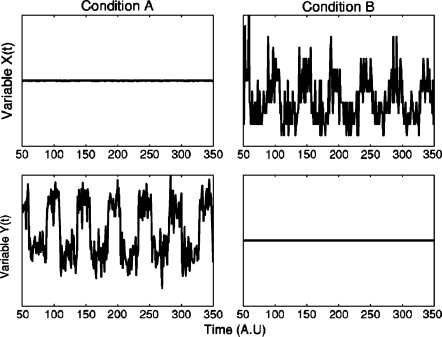
Before discussing these two papers, I would first like to mention a caveat illustrated by Dante Chialvo (currently at Northwestern University) in a lecture about 1∕f fluctuations in heart rate given in 1992 at the New York Academy of Medicine. Chialvo told the audience that he had measured time series for two variables of a system: a control variable and a controlled variable, in two conditions: a healthy one, and an unhealthy∕abnormal state. He then showed a figure in which these variables and conditions were shown: in the first column∕condition, the top variable was irregular while the bottom one was constant, and vice-versa in the second condition (see Fig. 1). Chialvo then facetiously asked the audience: which one is which? Which is the healthy state, which is the control variable?

Figure 1. Fluctuations and stability can change from healthy to disease states.

The top and bottom row show time series for two different variables, one a “controlling” and the other a “controlled” variable; the columns are two different conditions, one “healthy” and one “diseased.” Which one is which? See the text to find out. Courtesy of D. R. Chialvo.

The audience, obviously, was unable to answer the question, as the graph clearly was invariant under swapping of columns and rows. After letting the audience ponder for a few seconds on how do we ever get to know these things, Chialvo revealed the story. The system was his home’s refrigerator; the top row showed a time series of the power consumption of the fridge’s motor, while the bottom variable was the temperature inside the fridge. The left column was the “normal” state: in this state, the temperature within was fairly constant, but power consumption fluctuated as the motor tried to keep up with his kids opening the fridge at random intervals, the kitchen’s temperature changing through the day, and other daily fluctuations. On the right column, he had left the fridge’s door open, clearly an unhealthy state: the temperature fluctuated unhindered through the day, while the motor ran at constant top speed unable to control it. (Chialvo was unable to retrieve his original data from now-obsolete floppies for the purpose of this article, so he kindly reconstructed a simulation, see Fig. 1).

The moral here is that fluctuations in biological phenomena cannot be expected to be any simpler than in Chialvo’s fridge, and that fluctuations in changed, “diseased” or otherwise altered states may differ, not just in magnitude, but in quality or kind, from those in the healthy state. We do not usually have any means of measuring that are not invasive; most of the time, in order to perform measurements, we have to cause a “disease” or an unhealthy state, so the mere act of measurement may alter the fluctuations. This does not mean that we should give up, because, as argued above, fluctuation analysis usually is well worth the effort; but rather that vigilance must be constant.

The two Cell papers we’re concerned with are about morphogenesis, more specifically about anteroposterior patterning in Drosophila. The classical issue in morphogenesis is the “French Flag problem,” originally posed by Lewis Wolpert. In Wolpert’s own words:

“I, however, was primarily concerned with the ability of the sea-urchin embryo to develop a spatially normal pattern over an eight-fold size range. […] In order to formulate the problem more formally, I invented the French Flag Problem: how a line of similar cells could form a pattern such that one third was blue, one third white and one third red. I was collaborating with two theoreticians, Mary Williams and Michael Apter. Apter was keen on the obvious solution: number the cells from each end, and the cells can compute which third they are in! For some time I resisted this solution as being too complex but suddenly realized that, in more general terms, if cells knew their position, then a larger number of pattern problems could be accounted for. I was particularly encouraged that it could account for Curt Stern’s experiments on genetic mosaics in Drosophila.” (Wolpert, 1986).

Wolpert’s insight, that cells may use gradients of concentration of proteins (called morphogens) to specify and read a coordinate system, has been key to understanding many problems in embryogenesis. One of the most classic morphogenetic gradient problems in the “French flag” family is that of the distribution of Bicoid in the developing Drosophila embryo. As this system (anterio-posterior axis patterning) has been aptly discussed in detail in many other places (see, e.g., http:∕∕en.wikipedia.org∕wiki∕Morphogenesis) I shall only summarize the most relevant features. Bicoid is one of the maternal effect genes: genes whose mRNA is laid out in the unfertilized egg, and is translated into protein after fertilization, creating concentration gradients spanning the embryo. The maternally synthesized bicoid mRNAs are attached to the cytoskeleton and concentrate on one side of the egg which will develop, after fertilization, into the anterior pole of the embryo. As the Drosophila egg divides it stays, at first, a syncytium: the cytoplasm is not compartmented into separate cells after each nuclear division, so Bicoid protein can freely diffuse on the shared cytoplasm. As the nuclei form, they take up Bicoid protein which is translocated from the cytoplasm to the nuclei, and as the nuclear envelopes are dissociated at the next nuclear division, the nuclear Bicoid gets released again to the cytoplasm. The concentration gradient of Bicoid is quite well described by an exponential decay away from a source at the anterior pole; this has been interpreted as Bicoid’s dynamics being consistent with a source, diffusion away from the source and degradation under first order kinetics. Another gene, hunchback (hb), displays a more sigmoidal, almost threshold-like concentration pattern, highly activated at the maternal pole and dropping off abruptly, with a minor second peak at the posterior pole. This pattern had been interpreted as being formed through a “readout” of Bicoid: Hb would be induced by Bicoid, so that where Bicoid concentration is below a given threshold, the expression of Hb drops drastically. A study by Houchmandzadeh and colleagues (then at Princeton University) called this interpretation into question (Houchmandzadeh et al., 2002), by showing that the embryo-to-embryo variability of the location of any given threshold in Bicoid concentration was around 30%, far wider than the variability of position of the Hb edge, which was only 2%. In addition to this data the authors presented data on temperature compensation and size compensation in the patterns. The authors argued that further factors had to act to reduce this variability; in effect, that there must be an error correction mechanism to convert the highly unreliable positional information from Bicoid into the much more precise partitioning by Hb.

However, further studies showed that Bicoid’s pattern was far less variable than this previous study. Crauk and Dostatni, for example, constructed reporters for Bicoid, i.e., genes encoding a visible reporter that was induced by Bicoid in the same way that Hb is thought to be induced; they then showed that the position of the border of these Bicoid reporter patterns was as repeatable from embryo to embryo as the position of the Hb border, and in fact that the sharpness of the concentration pattern at the borders was similar; and suggested (see Fig. 7 in Crauk and Dostatni, 2005) that the previous study could be explained by the experimental variability of the immunodetection protocol.

Both of these papers had analyzed the protein expression patterns by looking at immunostained fixed embryos. This means that quantitation to this point had been performed by killing the embryos, fixing them in media, and then immunostaining them—in other words, a “diseased state,” the product of a fickle and nonlinear process having many potential entry points for variability, and particularly difficult to normalize consistently. Furthermore, this methodology does not allow the dynamics of the patterns to be probed at the single-embryo level, and hence one may not know whether the variability observed is frozen in time for each embryo, or changes.

The two Cell papers by Gregor and collaborators have addressed this problem by visualizing the Bicoid protein directly in vivo. Embryos were imaged while alive and developing using two-photon microscopy, which is better for quantification of time-lapse movies than confocal microscopy; a confocal microscope does not image out-of-focal-plane fluorophores, but it does excite them, while a two-photon microscope does not excite out-of-plane fluorophores (it does image them, though). Therefore the confocal microscope constantly bleaches a much larger proportion of fluorophores, which causes the normalization of a time-lapse movie to change with time. Absolute concentration data were obtained simply by immersing the embryo in fluid containing a known concentration of eGFP, and calibrating two-photon fluorescence with respect to the fluid.

Gregor and collaborators have developed a line of Drosophila in which the wild-type bicoid gene has been deleted and replaced with a bicoid-eGFP construct, carefully preserving both cis- and trans-acting elements required for its biological action. There are numerous things that could, and in fact usually do, go wrong with this kind of scheme, for it is, after all, a deeply diseased state; but Gregor and colleagues present sufficient calibration data to persuade even the skeptics. First, it would be quite normal to expect that the Bicoid-eGFP construct would not behave qualitatively like wild-type Bicoid because the tethered proteins interfere with each other; or, alternatively, that the eGFP portion fails to properly fold and oxydize, hence failing to fluoresce. Second, even if both Bicoid and eGFP are qualitatively functional, the construct could fail to quantitatively behave like wild-type Bicoid, either because it is synthesized at a wrong rate, has the wrong diffusivity, or is degraded anomalously: any of the three processes that quantitatively shape the Bicoid concentration pattern could be affected by the fluorescent hitchhiker. Third, even though the two pieces of the construct are synthesized at a 1:1 stoichiometric relation does not mean that their ratio remains stable: either the Bicoid or the eGFP could be differentially degraded, Bicoid could be separated from other proteins to which it is tethered, leaving us with either functional Bicoid tethered to partially digested nonfluorescent eGFP remains, or loose eGFPs that, outliving their Bicoid partners, accumulate and increase the background. These are phenomenal hurdles to try to jump through.

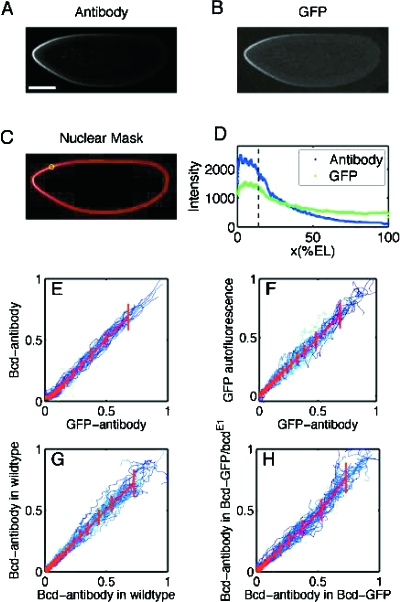
Remarkably, Fig. 2 of the first study (Gregor et al., 2007a) which is reproduced here, shows controls for all these potential artifacts. The engineered flies develop normally, and their embryos glow, settling the first issue. When embryos of the engineered flies are fixed and stained using standard anti-Bicoid antibodies and anti-GFP antibodies, they show patterns quantitatively similar to the wild type, controlling for the second issue. Finally, a series of panels displays linear relationships between anti-Bicoid and anti-eGFP stains, anti-Bicoid and eGFP fluorescence, and other combinations.

Figure 2 is so thorough and embodies so much work that it feels as though the rest of the paper almost follows. Perhaps because the subject has a rich history, once the new tool was developed, there were many things that it was imperative should be done. But in addition to these, some new ways of looking at the subject are developed, so there’s plenty of further material. The first paper continues to examine the dynamics of the Bicoid pattern, in a way that could not be done before. For example, the length scale of the pattern is thought to derive from a competition between the diffusivity of the molecules and their degradation rate; the diffusivity can now be directly measured through photobleaching techniques. Interestingly, the diffusion constant obtained from photobleaching is a relatively small value, small enough that it opens the question of how long it takes for the pattern to form.

Figure 2. Comparison of Bicoid profiles in Drosophila embryos expressing Bicoid-GFP.

(Embryos were formaldehyde fixed during nuclear cycle 14 and imaged at the midsagittal plane via confocal microscopy.) (A) Embryo stained with GFP antibodies. (Scale bar is 100 mm.) (B) GFP autofluorescence for the same embryo as in (A). (C) Nuclear layer obtained via image analysis software used to extract gradients from (A) and (B) by sliding a circular averaging area (yellow circle) along the edge of the embryo images. (D) Extracted raw gradients from (A) and (B) projected on embryo AP axis. Dashed line corresponds to location of yellow circle in (C) from cut sections of (A; mean and SD across embryos). (E-H) Scatter plots of fluorescence intensities extracted from Bcd profiles for different embryos. All profiles were normalized by a background subtraction and a scale factor (see Experimental Procedures in Gregor et al., 2007a). Both dorsal and ventral profiles are shown in each panel. Colors represent individual embryos, red lines correspond to the average profile scatter, and error bars are for equal amounts of data points. Deviations of the compared profiles from the diagonal indicate a difference in the shape of the profile. For more information see Supplemental Data of Gregor et al. (2007a). Reproduced from Gregor et al. (2007a) with permission from Elsevier.

The second paper focuses on the variability of the Bicoid pattern, how well it encodes positional information, how well it could be “read” and “interpreted,” and whether it is sufficient to explain the precision of the Hb boundary. The in vivo measurement shows a much smaller (10–15%) variability in Bicoid concentration from embryo to embryo. An interesting piece of data [Figs. 5(c) and 5(d)] shows that if two Bicoid genes are inserted, the concentration pattern exactly doubles—no dosage compensation or change in degradation rate is observed experimentally. Gregor and colleagues make here a subtle yet important distinction between the reproducibility of the patterns from embryo to embryo, and the reliability of the functional relation between Bicoid and Hb at the single embryo level, looking at how one protein concentration depends on the other, using the gradient as an implicit parameter. This second notion, to express the concentration of a gene in a coordinate system constructed from concentrations of other genes, has been used for mRNA expression values in microarray analysis, but it is a novel notion in the context of development and protein concentrations. This viewpoint leads them to arguments a la Purcell about the limiting physical factors to such reliability.

While the Bicoid variability is substantially smaller than reported in Houchmandzadeh et al. (2002), some quantitative challenges remain. In particular, the difference between the variability of Bicoid and Hb still remains somewhat controversial. Gregor et al. state the matter to have been resolved, but Reinitz (2007) and also Houchmandzadeh feel there is still a discrepancy remaining, albeit much smaller than originally thought. “I had originally concluded there should be some negative correlation between the overall maternal amount of bicoid and the pattern decay length,” says Houchmandzadeh, “but Gregor’s Fig. 5(d) contradicts this [hypothesis]. So the correcting mechanism has to be more complicated than that, possibly along the lines of the Jülicher or Barkai models” (personal communication).

As with the original motivation of Lewis Wolpert, the sea urchin, the Hb pattern compensates for changes in embryo size. Gregor and collaborators report that there is some degree of size compensation in the Bicoid pattern, in that the fluctuations in threshold position are smaller, when measured in relative rather than absolute spatial scales. The “standard” diffusion and degradation model of the exponential decay of Bicoid generates a length scale which is set by diffusivity and degradation rate alone, and is independent of size. Gregor et al. propose a different mechanism based on absorption and release by the nuclei, and argue that the different structure of the dynamics (dependent only on boundary condition) may show scale compensation, but do not show detailed simulations to prove so.

It is evident that this new tool is an impressive technical development. Is it worth the effort to construct a tool precise enough to measure fluctuations? Certainly. If you doubt so, just take a look at the movie in their Supplementary Materials.