How molecular motors shape the flagellar beat

Abstract

Cilia and eukaryotic flagella are slender cellular appendages whose regular beating propels cells and microorganisms through aqueous media. The beat is an oscillating pattern of propagating bends generated by dynein motor proteins. A key open question is how the activity of the motors is coordinated in space and time. To elucidate the nature of this coordination we inferred the mechanical properties of the motors by analyzing the shape of beating sperm: Steadily beating bull sperm were imaged and their shapes were measured with high precision using a Fourier averaging technique. Comparing our experimental data with wave forms calculated for different scenarios of motor coordination we found that only the scenario of interdoublet sliding regulating motor activity gives rise to satisfactory fits. We propose that the microscopic origin of such “sliding control” is the load dependent detachment rate of motors. Agreement between observed and calculated wave forms was obtained only if significant sliding between microtubules occurred at the base. This suggests a novel mechanism by which changes in basal compliance could reverse the direction of beat propagation. We conclude that the flagellar beat patterns are determined by an interplay of the basal properties of the axoneme and the mechanical feedback of dynein motors.

Cilia and flagella are slender cellular appendages of eukaryotic cells. They are motile structures that exhibit regular beat patterns and that play important roles in many different circumstances where motion on a cellular level is required (Bray, 2001). Their central core is an evolutionarily conserved organelle, the axoneme (Gibbons, 1981), that comprises a cylindrical arrangement of nine doublet microtubules surrounding a pair of singlet microtubules (Afzelius et al., 1995; Nicastro et al., 2006). Dynein motors located between adjacent doublet microtubules generate shear forces that cause sliding between the doublet microtubules (Brokaw, 1989; Gibbons and Rowe, 1965; Porter and Sale, 2000; Satir, 1965; Summers and Gibbons, 1971; Vernon and Woolley, 2002). Passive components such as nexin links and radial spokes provide constraints that maintain the axoneme’s structural integrity (Nicastro et al., 2006). These constraints convert sliding between adjacent microtubules into overall bending deformations.

Although, as described above, the mechanical conditions underlying axonemal bending are known, it is not understood what molecular mechanisms underlie the coordination of the motors that is necessary for the generation of regular, oscillatory beat patterns. The coordination manifests itself in two ways. First, if motors on opposite sides of the axoneme were equally active there would be no net bending. The observed bending therefore implies that the motor activity periodically varies from being higher on one side of the axoneme to being higher on the other side. And second, for the generation of a wave-like propagation of bends the activity of motors must be coordinated along the length of the axoneme. From a theoretical point of view, there are several possibilities for how axonemal oscillations could be generated. The activity of the motors along the axoneme could be regulated directly via a spatio-temporal traveling wave in the form of a biochemical or electrical signal. However, one observation strongly argues against this possibility: demembranated axonemes can still generate regular beat patterns (Gibbons and Gibbons, 1972). Alternatively, the motor activity could be regulated by the rotating central pair microtubules acting as a distributor (Nakano et al., 2003; Omoto et al., 1999; Smith, 2002). However, this can be ruled out as a general mechanism because there are examples of flagella that exhibit regular beat patterns despite lacking the central pair (Huang et al., 1982; Okada et al., 2005; Wakabayashi et al., 1997) and recent experiments suggest that the central pair rotation follows rather than directs the beat (Mitchell and Nakatsugawa, 2004).

The only currently discussed alternative hypotheses propose that the beat patterns are generated in a self-organized fashion (Brokaw, 1975; Jülicher and Prost, 1997) due to coordination of the activity of the motors by the geometry of the axoneme. Such coordination has been hypothesized to arise from regulation of motor activity by local axonemal curvature (Brokaw, 2002; Brokaw and Luck, 1985; Brokaw, 1971; Brokaw and Rintala, 1975; Hines and Blum, 1979; Machin, 1958), by transverse deformations perpendicular to the axonemal axis (Lindemann, 1994a,b, 2002), or by shear displacements parallel to the axonemal axis (Brokaw, 2005; 1975; Camalet and Jülicher, 2000; Camalet et al., 1999; Jülicher and Prost, 1997; Murase et al., 1989).

In this paper we address the question: which of the above motor coordination schemes can account for the observed flagellar beat patterns¿ To answer this question we have taken advantage of the fact, first pointed out by K. E. Machin, that the spatio-temporal pattern of internal force generation can be deduced from knowledge of the flagellar wave form (Machin, 1958). We have therefore used high speed microscopy, and temporal Fourier analysis to quantify the shape of beating bull sperm with high precision. By incorporating different coupling mechanisms between force generation and axonemal geometry into the dynamic equations that describe an actively bending filament we compared the experimentally determined shapes with calculated ones.

This direct comparison between experiment and theory has led to two important insights. First, we conclude that there is considerable sliding between microtubule doublets at the flagellar base (Vernon and Woolley, 2002, 2004), and show that the mechanical properties of the basal connection play an important role in determining the flagellar wave forms. And second, regulation of motors by shear displacements leads to an alternation of the activity of the motors between opposite sides of the axoneme and to wave forms reproducing the experimental data very well. This is in contrast to regulation by curvature control or by transverse deformations which do not lead to a satisfactory agreement between calculated beat patterns and the observed wave forms. Our results suggest that the flagellar beat is indeed self-organized, and that the underlying mechanism for the formation of regular oscillatory axonemal beat patterns is the collective motor behavior due to the load-dependent detachment of the motors (Brokaw, 1975; Camalet and Jülicher, 2000; Camalet et al., 1999; Jülicher and Prost, 1997). We term this regulatory mechanism sliding-controlled motor coordination.

THEORY

Flagellar shape and internal shear

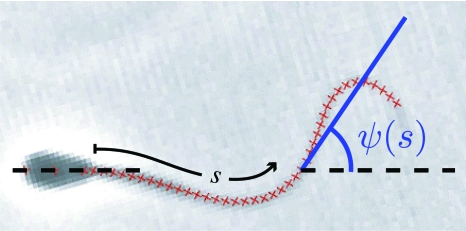
The shape of the wave form of a beating sperm at any given time can be described by the position vector r(s) of points along the center line, where s is the arc length along the center line. For a flagellum of length L, r(0) and r(L) correspond to the basal and distal ends, respectively. For a planar shape, such as the flagellar wave forms discussed herein, the two-dimensional curve r(s)=(x(s),y(s)) can be parametrized by the tangent angle ψ(s), see Fig. 1, such that

$$\mathbf{r}\left(s\right)=\mathbf{r}\left(0\right)+{\int }_0^s(\cos \psi \left(u\right),\sin \psi \left(u\right))\mathrm{d}u.$$ (1)

Figure 1. Snapshot of a beating bull sperm.

Superimposed on the image are red crosses tracing the contour of the flagellum as determined by the automated image analysis algorithm (see Materials and Methods section). The tangent angle ψ(s) is measured at each position defined by the arc length s. The centers of the red crosses are separated by 1.4 μm.

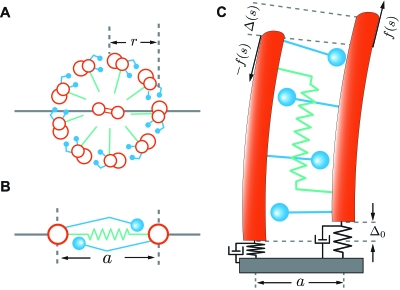
In the following we introduce a two-dimensional projection of the three-dimensional (3D) axoneme [Figs. 2A, 2B]. This is motivated by the fact that under our experimental conditions the flagellar beat patterns of bull sperm are almost planar with only small out-of-plane displacements. Constraint of flagellar motion to two dimensions could for instance be an effect of structural asymmetries within the flagellum (Afzelius, 1959; Lindemann et al., 1992; Olson and Linck, 1977; Si and Okuno, 1995), an issue we will not discuss here. In the three-dimensional axoneme, the motors between one pair of doublets cause sliding and axonemal bending in one direction, whereas the motors between the pair of doublets at the opposite side of the axoneme cause bending in the opposite direction. In other words, motors on opposite sides of the axoneme operate antagonistically. In the two-dimensional projection, the action of motors at opposite sides of the axoneme are therefore superimposed in an antagonistic manner. In this representation the effects of motors and passive cross-linkers between microtubule doublets in the axoneme are represented by a shear force per unit length f (s) directed parallel to the local axonemal axis. This force density acts in opposite directions on both filaments and causes a relative sliding displacement Δ(s) between the filaments, see Fig. 2C. The sliding displacement is related to the tangent angle ψ by

$$\Delta \left(s\right)={\Delta }_0+a(\psi \left(s\right)-\psi \left(0\right)),$$ (2)

where Δ₀ is the sliding displacement at the base and a is the axonemal diameter. Note that the two-dimensional representation of the axoneme shown in Fig. 2C is an abstraction. The equations of motion for planar flagellar beats can also be derived rigorously from the dynamics of a three-dimensional axoneme constrained to two dimensions (Hilfinger, 2006). In order to interpret the numerical values of the force density f (s) and the sliding displacement Δ(s) in the planar description, we will subsequently relate them to the force and displacement between the nine microtubule doublets in the real three-dimensional axoneme, see Appendix A.

Figure 2. Schematic diagram of the axonemal architecture and its two-dimensional representation.

(A) Cross section of an axoneme with radius r as seen from the basal end. The microtubule doublets and the central pair are shown in red, the dynein motors in blue, and the radial spokes in green. The horizontal gray line indicates the plane of the beat. With this beat plane, the largest sliding displacement occurs between adjacent microtubule doublets at the top and bottom. (B) Cross section of the two-dimensional representation of the axoneme in which two flexible filaments slide relative to each other in the beat plane. The shear forces are generated by active elements which operate antagonistically between the filaments. Passive elastic elements are represented in green. The separation of the two filaments is a=2r. (C) View on the beat plane of this “two-dimensional axoneme.” Indicated are the local sliding displacement Δ(s) and the internal shear force density f(s) due to the active elements (blue) and the passive cross-linkers (green). The basal connection has a finite stiffness and friction indicated by black springs and dashpots.

Flagellar dynamics

The action of internal force generators drives changes of the axonemal shape. In the overdamped limit of small Reynolds number and small amplitudes, the tangent angle satisfies the following dynamic equation (Camalet and Jülicher, 2000; Machin, 1958)

$${\xi }_{\perp }{\partial }_t\psi (s,t)=-\kappa {\partial }_s^4\psi (s,t)+a{\partial }_s^{2}f(s,t),$$ (3)

where ξ_⊥ is the hydrodynamic drag for motion perpendicular to the axoneme per unit length, κ is the bending rigidity of the axoneme, and f (s,t) represents the internal shear-force density due to active (e.g., motor proteins) as well as passive (e.g., nexin links) structures within the axoneme. For simplicity we have ignored hydrodynamic interactions between segments of the flagellum. Such interactions are unimportant if the flagellum is close to a surface. Far from a surface, inclusion of hydrodynamic effects would mainly lead to a friction coefficient that depends weakly on the wavelength of the beat (Brennen and Winet, 1977). The passive version of Eq. 3 with f (s,t)=0 describes the elastohydrodynamics of a rod in a viscous environment (Wiggins et al., 1998).

In order to discuss oscillatory patterns of shape changes with angular frequency ω we represent the wave form as a Fourier series in time

$$\psi (s,t)=\sum _{n=-\infty }^{\infty }{\tilde{\psi }}^{\left(n\right)}\left(s\right)e^{in\omega t},$$ (4)

where, because ψ (s,t) is a real quantity, ${\tilde{\psi }}^{\left(n\right)}\left(s\right)$ and${\tilde{\psi }}^{(-n)}\left(s\right)$ are complex conjugate functions. The amplitude and phase of the nth mode, ${\tilde{\psi }}^{\left(n\right)}$, represent the amplitude and phase of the nth harmonic of the oscillation. The Fourier modes ${\tilde{\Delta }}^{\left(n\right)}\left(s\right)$ and ${\tilde{f}}^{\left(n\right)}\left(s\right)$ of the sliding displacement and force density are defined similarly. As shown in the experimental section, the axonemal dynamics is dominated by the fundamental mode ${\tilde{\psi }}^{\left(1\right)}\left(s\right)$ [Fig. 3B]. In the following, we therefore focus on the first mode $\tilde{\psi }\left(s\right)\equiv {\tilde{\psi }}^{\left(1\right)}\left(s\right)$ and drop the superscript for n=1 such that $\tilde{\psi }\left(s\right),\hspace{0.17em}\tilde{f}\left(s\right),\hspace{0.17em}\tilde{\Delta }\left(s\right)$ refer to the fundamental modes of ψ (s,t), f (s,t) and Δ(s,t), respectively.

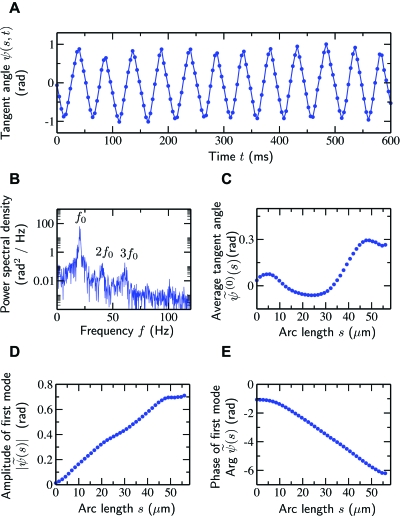
Figure 3. Time series analysis and Fourier modes of beat patterns.

(A) Typical measured time series of the tangent angle ψ (s,t) for a given point (s=28 μm) along a flagellum whose head was clamped. (B) The corresponding power spectrum of the oscillations reveals a clear peak at a frequency f₀=ω∕2π of 20 Hz containing more than 95% of the total power. (C) The time average of the tangent angle ${\tilde{\psi }}^{\left(0\right)}\left(s\right)$ at each point along the flagellum. Note that variations of ${\tilde{\psi }}^{\left(0\right)}\left(s\right)$ as a function of s lead to curved trajectories of freely swimming sperm cells. (D,E) Amplitude and phase, respectively, of the fundamental mode $\tilde{\psi }\left(s\right)$.

Motor mechanics

In a coarse-grained description, the mechanical properties of the active and passive cross-linkers within the axoneme can be characterized by a complex compliance α(ω), which describes the sliding displacement in response to a small oscillatory force $\tilde{\Delta }\left(s\right)\approx \alpha \left(\omega \right)\tilde{f}\left(s\right)$ (Jülicher and Prost, 1997). Correspondingly, the inverse response coefficient χ(ω)=α⁻¹(ω) characterizes the force response to a periodic sliding motion

$$\tilde{f}\left(s\right)\approx \chi \tilde{\Delta }\left(s\right).$$ (5)

Here we assume that χ is constant along the axoneme. Later we also discuss the possible effects of a position-dependent χ. The response coefficient χ is a complex quantity whose real and imaginary parts define a stiffness per unit length K(ω) and a friction coefficient per unit length λ(ω), with χ=K+iωλ. We therefore call χ the dynamic stiffness. For a collection of molecular motors coupled together such as the dynein motors in the axoneme, the values of K and λ can become negative (Camalet and Jülicher, 2000; Camalet et al., 1999; Grill et al., 2005; Jülicher and Prost, 1997; Pecreaux et al., 2006). This collective behavior can arise naturally when the detachment of motors is load dependent: this leads to coupling of motor activity to the sliding velocity, and thereby to the rate of change of the axonemal bend angle as detailed in Appendix B. We refer to Eq. 5 as sliding-controlled motor coordination. This relation between the Fourier modes of the dynamic forces and displacements is a generalization of the well known force-velocity relation for molecular motors to oscillatory motion. If the system operates at constant frequency, one can use either the absolute displacement or the shear rate as dynamic variables because the Fourier modes of both quantities differ only by a factor iω. We prefer to use the absolute shear displacement as it is this quantity that enters the shape equations. If K and λ are negative, the forces $\tilde{f}\left(s\right)$ perform on average work and the system can become unstable and undergo oscillations (Camalet and Jülicher, 2000; Camalet et al., 1999; Grill et al., 2005; Jülicher and Prost, 1997; Pecreaux et al., 2006).

The sperm equation

Equations 2, 3, 4, 5 lead to the following ordinary differential equation for the fundamental Fourier mode $\tilde{\psi }\left(\overline{s}\right)$ of the tangent angle

$$i\overline{\omega }\tilde{\psi }+{\tilde{\psi }}^{⁗}-\overline{\chi }{\tilde{\psi }}^{″}=0,$$ (6)

where we have introduced the dimensionless parameters$\overline{\omega }=\omega {\xi }_{\perp }{L}^4∕\kappa ,\overline{\chi }=\chi a^2{L}^2∕\kappa$ and the primes indicate derivatives with respect to the normalized arc length $\overline{s}=s∕L$. In the following we will refer to Eq. 6 as the sperm equation.

Our theoretical description includes the possibility of sliding between filaments even at the base. Balancing the internal shear forces at the base leads to the following equation of motion for the sliding displacement at the base:

$${\gamma }_{\mathrm{s}}\frac{\mathrm{d}}{\mathrm{d}t}{\Delta }_0\left(t\right)=-k_{\mathrm{s}}{\Delta }_0\left(t\right)-{\int }_0^{L}f(s,t)\mathrm{d}s,$$ (7)

where the integral term is the total force along the axoneme, γ_s is a basal friction coefficient, and k_s a basal stiffness. Equations 3, 7 determine the dynamics of sliding displacements and bending deformations for any given time-dependent distribution of internal force densities f(s,t). Making use of Eqs. 2, 5 allows us to determine the normalized amplitude of the basal sliding ${\overline{\Delta }}_0\equiv (1∕a){\tilde{\Delta }}_0$ by

$${\overline{\Delta }}_0=\frac{\overline{\chi }}{i\overline{\omega }{\overline{\gamma }}_{\mathrm{s}}+{\overline{k}}_{\mathrm{s}}+\overline{\chi }}(\tilde{\psi }\left(0\right)-{\int }_0^1\tilde{\psi }\left(\overline{s}\right)\mathrm{d}\overline{s}),$$ (8)

where ${\overline{k}}_{\mathrm{s}}=k_{\mathrm{s}}{a}^{2}L∕\kappa ,{\overline{\gamma }}_{\mathrm{s}}={\gamma }_{\mathrm{s}}{a}^2∕\left(L^3{\xi }_{\perp }\right)$. The normalized basal sliding amplitude ${\overline{\Delta }}_0$ plays an important role in the dynamics of the tangent angle because it enters the boundary conditions determining the allowed solutions of $\tilde{\psi }\left(s\right)$ as detailed below.

Boundary conditions

The solutions to the sperm equation 6 and Eq. 8 depend on the boundary conditions that describe the balance of torques and forces at the ends of the axoneme. Because the distal end $(\overline{s}=1)$ is free, no external torques and forces are acting there, which implies ${\tilde{\psi }}^{\prime }=0$ and $\kappa {\tilde{\psi }}^{″}=a{L}^2\tilde{f}$ at $\overline{s}=1$ (Camalet and Jülicher, 2000). Whereas the distal end is free to move, the basal end of the axoneme is anchored within the sperm head; this leads to external forces and torques acting at the base $(\overline{s}=0)$.

In order to discuss the head dynamics, we distinguish three experimental conditions as summarized in Table 1. First, the case in which the sperm head is attached to the cover slip in a way that it can neither move nor tilt, implying that $\tilde{\psi }=0$ at $\overline{s}=0$ (clamped head). Second, the case in which the head is attached to the cover slip such that its position is fixed but its orientation can change (pivoting head). And third, sperm swimming close to and parallel to the surface of the cover slip (planar swimming).

Table 1.

The different experimental conditions discussed in this paper and the boundary conditions used to determine the fundamental mode $\tilde{\psi }\left(\overline{s}\right)$. The basal end corresponds to $\overline{s}=0$ and the distal end to $\overline{s}=1$. The boundary conditions have been expressed using the dimensionless parameters ${\overline{k}}_{\mathrm{p}}=k_{\mathrm{p}}L∕\kappa ,{\overline{\gamma }}_{\mathrm{p}}={\gamma }_{\mathrm{p}}∕\left(L^3{\xi }_{\perp }\right),\overline{d}=d∕L$, and $\overline{\zeta }=\zeta ∕\left(L{\xi }_{\perp }\right)$.

Experimental conditions
Clamped head	$\overline{\zeta },{\overline{k}}_{\mathrm{p}},{\overline{\gamma }}_{\mathrm{p}}\to \infty$
Pivoting head	$\overline{\zeta }\to \infty$
Planar swimming	${\overline{k}}_{\mathrm{p}}\to 0$
Boundary conditions
${\tilde{\psi }}^{\prime }\left(0\right)+\overline{\chi }({\overline{\Delta }}_0-\tilde{\psi }(0\left)\right)+\overline{\chi }{\int }_0^1\tilde{\psi }\left(\overline{s}\right)\mathrm{d}\overline{s}-({\overline{k}}_{\mathrm{p}}+i\overline{\omega }{\overline{\gamma }}_{\mathrm{p}})\tilde{\psi }\left(0\right)=0$
${\tilde{\psi }}^{″}\left(0\right)-\overline{\chi }{\overline{\Delta }}_0-\overline{\zeta }\left({\tilde{\psi }}^{‴}\right(0)-\overline{\chi }{\tilde{\psi }}^{\prime }(0)+i\overline{\omega }\overline{d}\tilde{\psi }(0\left)\right)=0$
${\tilde{\psi }}^{\prime }\left(1\right)=0$
${\tilde{\psi }}^{″}\left(1\right)-\overline{\chi }({\overline{\Delta }}_0+\tilde{\psi }(1)-\tilde{\psi }(0\left)\right)=0$

In the case for which the position of the head is fixed (clamped and pivoting) we characterize the connection between the head and the cover slip by an angular stiffnessk_p and angular friction coefficient γ_p. Balancing internaland external torques at the head implies (Camalet and Jülicher, 2000) $\kappa {\tilde{\psi }}^{\prime }+a{L}^2{\int }_0^1\tilde{f}\left(\overline{s}\right)\mathrm{d}\overline{s}=L(k_{\mathrm{p}}+i\omega {\gamma }_{\mathrm{p}})\tilde{\psi }$ at $\overline{s}=0$. The balance of forces at the head involves for the case of a free head the friction force ζv_⊥, where ζ is a friction coefficient of the head and $v_{\perp }\simeq (\kappa {\tilde{\psi }}^{‴}-a{L}^2{\tilde{f}}^{\prime }+(i\omega d{\xi }_{\perp }{L}^3\left)\tilde{\psi }\right)∕L^3{\xi }_{\perp }$is the velocity perpendicular to the axonemal axis. The force balance at the head then reads $\kappa {\tilde{\psi }}^{″}-a{L}^2\tilde{f}=\zeta \left(\right(\kappa {\tilde{\psi }}^{‴}-a{L}^2{\tilde{f}}^{\prime })∕(L{\xi }_{\perp })+i\omega d{L}^2\tilde{\psi })$, where the distance between the pivot point of the head and the base of the flagellum is denoted by d. In our experiments we estimated d≈5.5 μm. In the case of a clamped or pivoting head, the force balance condition at the head is replaced by v_⊥=0. Making use of Eq. 5, the boundary conditions for the fundamental mode of the tangent angle can be expressed in a general form such that the different experimental conditions correspond to limiting cases, see Table 1.

The sperm equation is an ordinary homogeneous differential equation of fourth order. Because the overall amplitude and phase of solutions to such a linear system are undetermined, three complex boundary conditions are sufficient to find a unique solution. In our fitting procedure described below, the value of ${\overline{\Delta }}_0$ is inferred by using all four boundary conditions. The main role of nonlinearities is to set the amplitude of the beat. Nonlinearities are not expected to have a large effect on the shape of the beat (Hilfinger, 2006; Yu et al., 2006).

EXPERIMENTAL RESULTS

Flagellar wave forms of beating bull sperm (Gray, 1958) were quantified using high-speed video microscopy and automated image analysis. Images of flagellar wave forms were taken every 4 ms for a total duration of ∼4 s, see Fig. 1. Depending on the surface conditions of the cover slip (see Materials and Methods section) the observed sperm fell into one of three categories: clamped head, pivoting head, and planar swimming, as defined in the theory section. Using an automated image analysis algorithm we determined the tangent angle ψ(s,t) at 41 equally spaced points along the flagellum in the consecutive images. In this way, we determined a time series of angles at each point along the flagellum [Fig. 3A]. Because the oscillations were very stable over time, we computed the power spectrum at each point [Fig. 3B]. We found that all analyzed time series (n=18) were well approximated by their zeroth and first temporal Fourier modes, i.e.

$$\psi (s,t)\approx {\tilde{\psi }}^{\left(0\right)}\left(s\right)+\tilde{\psi }\left(s\right)e^{i\omega t}+{\tilde{\psi }}^{*}\left(s\right)e^{-i\omega t},$$ (9)

where the star denotes the complex conjugate. The second and third modes can be observed [see Fig. 3B], but they are small compared to the fundamental mode and account for less than 5% of the total beat power. In other words, the motion of each tailpoint was well approximated by a sinusoidal oscillation of amplitude $2\mid \tilde{\psi }\mid$ and angular frequency ω about an average tangent angle ${\tilde{\psi }}^{\left(0\right)}$. The time averaged tangent angle ${\tilde{\psi }}^{\left(0\right)}\left(s\right)$ and the amplitude and phase of the fundamental Fourier mode $\tilde{\psi }\left(s\right)$ are displayed in Figs. 3C, 3D, 3E as a function of arc length.

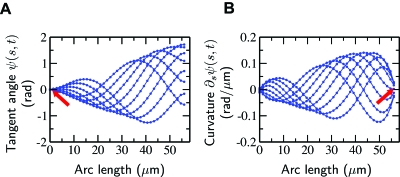
Another way to illustrate the flagellar beat graphically is to display the first mode of the tangent angle $\psi (s,t)=\tilde{\psi }\left(s\right)e^{i\omega t}+{\tilde{\psi }}^{*}\left(s\right)e^{-i\omega t}$ at several sequential times. An example is shown in Fig. 4, where the sperm attached so strongly to the cover slip with its head that the boundary condition $\tilde{\psi }\left(0\right)=0$ was satisfied (red arrow). We classified these as clamped-head beat patterns. All sperm analyzed in this study satisfied, within the error bars, the boundary condition ${\tilde{\psi }}^{\prime }\left(1\right)=0$ corresponding to zero curvature at the end (Fig. 4B, red arrow). This is expected because there is no external torque acting at the distal end.

Figure 4. The measured fundamental Fourier mode of the tangent angle and its derivative, the curvature, illustrate that two boundary conditions are satisfied.

(A) Snapshots of the measured fundamental Fourier mode of the tangent angle $\psi (s,t)=\tilde{\psi }\left(s\right)e^{i\omega t}+{\tilde{\psi }}^{*}\left(s\right)e^{-i\omega t}$at successive times with interval Δt=4 ms for a beat pattern satisfying the clamped head condition. (B) Same representation of the curvature, ∂_sψ (s,t). The arrows point to the base (A) and tip (B) of the axoneme and indicate the expected boundary conditions (zero tangent at the base and zero curvature at the tip). The estimated error of the tangent angle is less than 10⁻² rad. The estimated error of the curvature is 10⁻² rad∕μm, or approximately 5% of the maximum value. Note that the last experimental data point is approximately 2 μm before the actual end of the flagellum.

The fundamental modes are of high precision. The estimated error in $\tilde{\psi }\left(s\right)$ is approximately 0.4° or less than 10⁻² rad, see Materials and Methods section. This unprecedented high precision, which resulted from the Fourier averaging, allowed us to test several theoretical predictions regarding flagellar beat patterns, as described in the next section.

COMPARISON OF THEORY AND EXPERIMENT

Testing the sliding-controlled motor hypothesis

We compared the observed fundamental beating modes $\tilde{\psi }\left(\overline{s}\right)$ to solutions of the sperm equation 6 taking into account boundary conditions corresponding to the experimental conditions. This was done by fitting calculated wave forms to the experimental ones using the dimensionless dynamic stiffness $\overline{\chi }$ as a fit parameter, see Materials and Methods. Note that in this procedure, ${\tilde{\Delta }}_0$, the normalized basal sliding amplitude does not play the role of a free parameter. Rather, its value follows from imposing all four boundary conditions.

We first analyzed beating sperm whose heads were clamped to the coverslip as this condition is the most constrained one and involves the fewest free parameters. Given values of $\overline{\omega }$ and $\overline{\chi }$, the sperm equation 6 together with the boundary conditions determine a unique solution for $\tilde{\psi }\left(\overline{s}\right)$ and also provide a value of ${\overline{\Delta }}_0$. Because the dimensionless parameter $\overline{\omega }$ is determined by the beat frequency ω, the axonemal length L, the bending rigidity κ and the friction coefficient ξ_⊥, which are either known or can all be estimated as described in Appendix C (see legend to Table 2 for numerical values), the only free parameter is the unknown dynamic stiffness $\overline{\chi }$. Using the real and imaginary parts of $\overline{\chi }$ as fit parameters, the calculated wave forms were fit to the experimental data by minimizing the sum of squared distances between experimentally and theoretically determined modes $\tilde{\psi }\left(\overline{s}\right)$. The fits agreed well with the experimental data as illustrated in Fig. 5A (red theory, blue data). Figure 6 shows snapshots of the corresponding flagellar wave form r(s,t), reconstituted from the fundamental mode of the tangent angle ψ (s,t) using Eq. 1, directly comparing a theoretically determined wave form with experimentally observed beat patterns. The unknown basal stiffness ${\overline{k}}_{\mathrm{s}}$ and basal friction ${\overline{\gamma }}_{\mathrm{s}}$ can be determined from ${\tilde{\Delta }}_0$ using Eq. 8. The fit parameters obtained from the analysis of six different sperm are given in Table 2.

Table 2.

Mean and standard deviations of parameter values. For given oscillation frequencies ω∕2π, which were determined from the power spectrum [Fig. 3B] the stiffness per unit length K and the friction per unit length λ were used as fit parameters. The amplitude of basal sliding $\mid {\tilde{\Delta }}_0\mid$ and therefore the values of the basal stiffness and friction k_s and γ_s were inferred from the best fits. The normalized mean squared distance between experimental and theoretical curves, as defined in the Materials and Methods section, is denoted by Q. The number n of sperm for each condition is indicated. The values obtained by averaging over all experimental conditions are summarized in the bottom two rows. The fit parameters presented here were obtained from the dimensionless fit parameters using estimated values for the diameter of the axoneme, a=185 nm, its bending rigidity κ=1.7×10⁻²¹ N m², friction coefficient per unit length ξ_⊥, and flagellar length L=58.3 μm. Using a distance of 4 μm between the flagellum and the cover slip, we estimated ξ_⊥=3.4×10⁻³ N s∕m² for the experiments with clamped and pivoting head (observed at 22 °C) and ξ_⊥=2.5×10⁻³ N s∕m² for the swimming sperm (observed at 36 °C). The length L does not include the length d=5.5 μm between the head center and the beginning of the flagellum. The estimation of parameters is discussed in Appendix C.

	K$\left(\frac{\mathrm{kN}}{{\mathrm{m}}^2}\right)$	λ$\left(\frac{\mathrm{N}\bullet \mathrm{s}}{{\mathrm{m}}^2}\right)$	ks$\left(\frac{\mathrm{mN}}{\mathrm{m}}\right)$	γs$\left(\frac{\mathrm{mN}\bullet \mathrm{s}}{\mathrm{m}}\right)$	$\mid {\tilde{\Delta }}_0\mid$ (nm)	ω∕2π (Hz)	Q
Clamped head (n=6)
Mean	−1.62	−7.6	94.8	0.274	170	20.6	0.977
s.d.	0.04	0.1	2.6	0.006	18	1.2	0.005
Pivoting head (n=5)
Mean	−1.48	−7.9	88.6	0.299	145	20.0	0.958
s.d.	0.13	0.7	9.8	0.041	34	4.2	0.033
Planar swimming (n=7)
Mean	−1.63	−5.3	96.2	0.201	162	31.3	0.953
s.d.	0.06	0.1	3.3	0.008	17	1.9	0.019
All (n=18)
Mean	−1.58	−6.8	93.6	0.253	160	24.6	0.962
s.d.	0.10	1.3	6.3	0.048	24	6.0	0.023

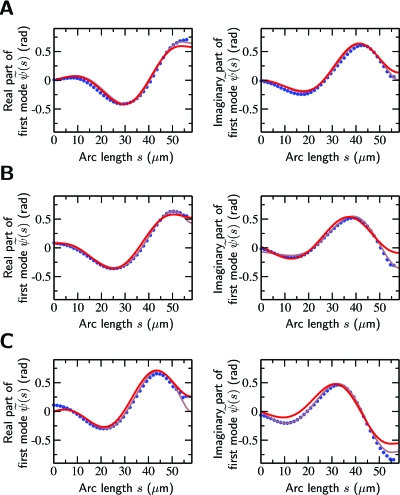
Figure 5. Comparison of experimental and theoretical beat patterns for sliding-controlled motors.

Fit solutions to the sperm equation for the fundamental mode of the tangent angle $\tilde{\psi }\left(s\right)$ (red line) compared to the experimental data (blue dots). (A) clamped head, (B) pivoting head, and (C) planar swimming. The frequencies of the beat patterns shown were 20, 16, and 33 Hz, respectively. The amplitude and phase of the modes were chosen to match the experimental data. The gray lines indicate improved fits obtained by allowing the dynamic stiffness $\overline{\chi }$ to take a different but constant value within the distal 5% of the flagellum.

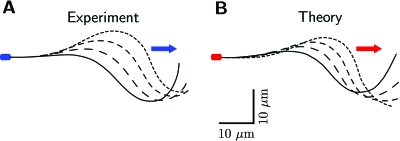
Figure 6. Shapes of flagellar beats.

Four snapshots of flagellar shapes r(s,t) of clamped-head beat patterns which correspond to the fundamental modes of the tangent angle presented in Fig. 5A. Shown is the first quarter of the beat cycle at equally spaced time points, as well as an arrow depicting the direction of the traveling wave. (A) experiment; (B) theory.

We then analyzed sperm beating in two additional experimental conditions, namely sperm whose heads were bound to the coverslip but pivoting and sperm that were swimming parallel to the coverslip. In these conditions, two additional parameters enter the boundary conditions describing the beat patterns, see Table 1. In the case of a pivoting head, these are the pivotal stiffness ${\overline{k}}_{\mathrm{p}}$ and pivotal friction coefficient ${\overline{\gamma }}_{\mathrm{p}}$. In the case of planar swimming, the two additional parameters are the angular friction ${\overline{\gamma }}_{\mathrm{p}}$ and the friction coefficient $\overline{\zeta }$ associated with the pivotal and translational movements of the head. The values of ${\overline{k}}_{\mathrm{p}}$, ${\overline{\gamma }}_{\mathrm{p}}$, ${\overline{\gamma }}_{\mathrm{p}}$, and $\overline{\zeta }$ were constrained to be positive, see Appendix C. These parameters, together with the real and imaginary parts of $\overline{\chi }$, constitute four fit parameters. Again, the fits agreed well with the experimental data, see Figs. 5B, 5C (red theory, blue data). The fit parameters obtained from the analysis of five different pivoting sperm and seven swimming sperm are summarized in Table 2.

The closeness of the fits was quantified by the positive parameter Q which is normalized such that Q=1 corresponds to a perfect fit, see Materials and Methods. Values of Q ranged from 0.95 to 0.98 for the three experimental conditions, see Table 2. The largest deviations between theory and experiments occurred near the distal end. Possible sources of these deviations include inhomogeneities along the length of the flagellum (see below) and effects of nonlinearities. Despite these deviations, we regard these fits to be satisfactory. Note that when we assumed that basal sliding does not occur $({\tilde{\Delta }}_0=0)$, no satisfactory fits could be obtained that obeyed the boundary conditions.

The fitting procedure provided estimates for the dynamic stiffness and basal sliding in terms of a two-dimensional representation of the axoneme. In order to relate these quantities to properties of the three-dimensional axoneme, we introduce corresponding quantities describing the dynamic stiffness and basal sliding between adjacent microtubule doublets, see Appendix A. The sliding displacement between a pair of adjacent microtubule doublets that lies approximately in the plane of beating is given by Δ_MT≈(π∕9)Δ. From the values given in Table 2, we estimated the maximum amplitude of sliding between adjacent microtubule doublets at the base, as

$$2\mid {\tilde{\Delta }}_{\mathrm{MT}}\left(0\right)\mid \approx 110\mathrm{nm.}$$ (10)

The relative error of this quantity is about 10% and arises from cell-to-cell variations and uncertainty in the value of the axonemal diameter a, see Appendix C.

We also estimated the stiffness K_MT and friction coefficient λ_MT per structural repeat of l=96 nm. These parameters characterize the response of the force between microtubule doublets per structural repeat ${\tilde{f}}_{\mathrm{MT}}$ to sliding displacements. The interdoublet force per structural repeat is related to the force density f in the two-dimensional representation by f_MT≈2fl∕π. It is related to interdoublet sliding according to ${\tilde{f}}_{\mathrm{MT}}={\chi }_{\mathrm{MT}}{\tilde{\Delta }}_{\mathrm{MT}}$, where χ_MT=K_MT+iωλ_MT. The following values were obtained using our fitting procedure:

$$K_{\mathrm{MT}}\approx -0.28\times {10}^{-3}\mathrm{N}∕\mathrm{m}$$

$${\lambda }_{\mathrm{MT}}\approx -1.2\times {10}^{-6}\mathrm{N}\bullet \mathrm{s}∕\text{m.}$$ (11)

The relative error of these quantities is dominated by uncertainty in the value of the viscous friction coefficient ξ_⊥, which depends on the distance between the flagellum and the cover slip, which was estimated to be 4 μm. We estimate, with 95% confidence, that the true values of this coefficient deviate by less than a factor of 2 from the stated values, see Appendix C. The relative error of the ratio of K_MT and λ_MT is much less, about 10%, because it does not depend on ξ_⊥, see Appendix C.

We now relate the values of the stiffness and friction coefficient per structural repeat to the properties of active and passive elements which connect microtubule doublets within the axoneme. The stiffness of the passive linkers which oppose sliding, thought to be nexin links, is positive and the experimental estimates (0.02 mN∕m per structural repeat, (Yagi and Kamiya, 1995); 0.02–0.1 mN∕m per structural repeat (Lindemann et al., 2005), are small compared to the absolute value of the estimate given in Eq. 11. The passive friction coefficient between sliding microtubules within the axoneme is positive. Estimating its magnitude based on viscous friction with the viscosity of water, it is of the order of 10⁻⁹ Ns∕m for one structural repeat. This is small compared to the absolute value of λ_MT given in Eq. 11. Because the passive stiffness and friction coefficient are small in magnitude and have opposite signs as compared to the values given in Eq. 11, they can probably be neglected and it is likely that the motors dominate the shear forces within the axoneme.

The coefficients K_MT and λ_MT can be related to molecular properties of dynein motor proteins. In Appendix B, we discuss the dynamic stiffness χ of many motors that operate collectively and generate a total force as the sum of many individual motors. We assume that the force generated by each motor domain is related to the velocity of motion by a linear force-velocity relationship with stall force $\overline{f}$ and slope f^′. Motor domains stochastically bind to and detach from microtubules; this is characterized by a relaxation time τ. The key property of motors that leads to active oscillations is that their detachment rate increases with increasing load force. This force dependence is described by a characteristic force f_c which is small if load dependence is strong. If the motors dominate the dynamic stiffness as argued in the previous paragraph, both K_MT and λ_MT become negative, as observed [Eq. 11], provided that the dependence of the detachment rate on load force is sufficiently strong $(f_c<\overline{f})$. We find that a value of $f_c=\overline{f}∕2$ is consistent with the measured values of K_MT and λ_MT. If $\overline{f}=2-4\mathrm{pN}$ per motor domain (corresponding to the measured values for inner arm dynein (Sakakibara et al., 1999), and for cytoplasmic dynein (Toba et al., 2006), respectively), then f_c=1−2 pN, which is about a quarter to a half of the value of 4 pN measured for kinesin (Schnitzer et al., 2000). The ratio of K_MT and λ_MT together with the angular frequency ω determine the relaxation time τ=4 ms. Using the estimate of 14 dynein motor domains per doublet microtubule per structural repeat (Burgess et al., 1991; Nicastro et al., 2006) the value of K_MT given in Eq. 11 implies $f^{\prime }\overline{p}=0.03\mathrm{\mu }\mathrm{N}\mathrm{s}∕\mathrm{m}$, where $\overline{p}$ is the fraction of motor domains that are bound to the microtubule. Even though the value of f^′ is not well constrained by experiments, a value of 1−10 mN s∕m is expected [a value of 10 mN s∕m has been measured for cytoplasmic dynein (Toba et al., 2006), axonemal dynein, however, is faster (Howard, 2001)]. This suggests a value for the fraction of bound motors of$\overline{p}\simeq 0.003-0.03$, consistent with axonemal dyneins being low duty ratio motors (Howard, 2001). In summary, the signs and magnitudes of K_MT and λ_MT as given by Eq. 11 are consistent with single-molecule properties of dynein motor proteins.

Tests of more general and alternative models

The results of the previous section showed that the observed wave forms are consistent with sliding-controlled motor activity. In this section, we compare the observed clamped-head beat patterns with patterns obtained from other models.

Role of structural inhomogeneities: Bull sperm are structurally inhomogeneous: the thickness of the flagellum decreases monotonically from the head towards the distal end. This tapering is due to changes in extra-axonemal structures such as the outer dense fibers, but not due to changes in the axoneme itself, which maintains a constant diameter along its length (and thus a constant relationship between sliding displacement and tangent angle). However, it has been suggested that the decrease in flagellar thickness leads to a decrease in flexural rigidity from base to tip (Lindemann, 1996; Rikmenspoel, 1965). In addition, there could also be systematic variations of the properties of force generators or passive cross-linkers along the flagellum. We investigated the effects of such inhomogeneities by considering a positional variation of the bending rigidity κ(s)=κ₀+κ₁s and of the dynamic stiffness χ(s)=χ₀+χ₁s. In the case of weak inhomogeneities (i.e., κ₁≪κ₀∕L, χ₁≪χ₀∕L), the fundamental modes $\tilde{\psi }\left(\overline{s}\right)$ satisfy

$$i\overline{\omega }\tilde{\psi }+{\tilde{\psi }}^{⁗}+3{\overline{\kappa }}_1{\tilde{\psi }}^{‴}-\overline{\chi }{\tilde{\psi }}^{″}-2{\overline{\chi }}_1{\tilde{\psi }}^{\prime }\approx 0,$$ (12)

where $\overline{\omega }\approx \omega {\xi }_{\perp }{L}^4∕{\kappa }_0,\hspace{0.17em}\overline{\chi }\approx {\chi }_0{a}^2{L}^2∕{\kappa }_0$, ${\overline{\kappa }}_1\approx L{\kappa }_1∕{\kappa }_0$, and${\overline{\chi }}_1\approx \overline{\chi }L{\chi }_1∕{\chi }_0$. We fit solutions of Eq. 12 to the experimental data, taking into account the appropriate boundary conditions. In this procedure, the real parameter ${\overline{\kappa }}_1$ and the real and imaginary parts of ${\overline{\chi }}_1$ serve as additional fit parameters. The parameter values of $\overline{\chi }$ and ${\overline{\Delta }}_0$ were still reliably determined and were similar to the previous estimates (within ±15%). However, the closeness of fit Q did not increase significantly and the additional fit parameters varied strongly between sperm. We thus conclude that gradually varying structural properties play a minor role in shaping the beat. Also note that in the absence of basal sliding we were not able to find satisfactory fits, even if we incorporated structural inhomogeneities. This is consistent with basal sliding playing an essential role in shaping the beat.

Histological sections of mammalian sperm flagella show that the most distal 2–3 μm of the axoneme lacks structural elements (Fawcett et al., 1994). This suggests that the properties at the distal end differ from those of the main part of the flagellum. In order to determine how such distal properties might affect the wave form, we fit the experimental data to beat patterns calculated with the assumption that $\overline{\chi }$ is constant in the first 95% of the flagellum and has a different constant value, ${\overline{\chi }}_{\mathrm{end}}$, in the remaining 5%. The corresponding fits improved the agreement between experiment (blue dots) and theory (gray lines) close to the distal end (Q=0.986±0.010, mean ± s.d., n=6), see Fig. 5. The best-fit values of $\overline{\chi }$ and ${\overline{\Delta }}_0$ were within 15% of the previous estimates. The values of ${\overline{\chi }}_{\mathrm{end}}$ varied strongly between sperm. These results show that changes of axonemal structure at the distal end can have significant effects on the wave forms near the distal end and may account for most of the deviation of the experimental data from solutions of the sperm equation with constant dynamic stiffness χ.

Motor control by transverse axonemal deformations: It has been suggested that the activity of motors is regulated by changes of the interdoublet spacing during axonemal deformations. Such an effect has been termed a geometric clutch (Lindemann, 1994a,b, 2002). According to this hypothesis, the sliding between microtubule doublets tenses elastic linkers such as nexin and this tension tends to reduce the interdoublet spacing. If the reduced spacing leads to an increased attachment rate, this amounts to a positive feedback and leads to a dynamic stiffness of the same form as Eq. 5, see Appendix D. However, in the case of motor control via interdoublet spacing, the dynamic stiffness χ=K+iωλ has a positive value of λ (in contrast to the sliding-controlled motor response), while K is negative. When we fit calculated beat patterns to the experimental data imposing the constraint of positive λ, we did not obtain close fits, see Fig. 7A. The closeness of the fit wasQ=0.564±0.069 (mean ± s.d., n=6) corresponding to the best-fit value for the stiffness per unit lengthK=−3.368±0.026 kN∕m². The best-fit value of the friction per unit length λ friction was zero (within numerical errors) in all cases. The basal friction coefficient inferred from these best-fit values was negative, which would correspond to an active element at the base, which is believed to be purely passive. The lack of a good fit is not surprising since it has been shown that the generation of self-sustained oscillatory beat patterns requires negative values of both K and λ (Camalet and Jülicher, 2000). In conclusion, control of motors by transverse deformations does not accord with the measured beat.

Figure 7. Comparison of experimental and theoretical beat patterns for geometric clutch and curvature control mechanisms.

The fundamental mode $\tilde{\psi }\left(s\right)$ measured from a clamped-head sperm (blue dots) is shown together with calculated beat patterns as a function of the arc length s. (A) Geometric clutch (B) curvature control. Note that the fits are worse than those for the sliding-controlled case presented in Fig. 5A.

Motor control via local curvature: It has been suggested that the activity of motors in the axoneme is controlled by the local axonemal curvature (Brokaw, 2002; Brokaw and Luck, 1985; Brokaw, 1971; Brokaw and Rintala, 1975; Hines and Blum, 1979; Machin, 1958). This implies that the force density $\tilde{f}\left(s\right)$ depends on the curvature $\mathrm{d}\tilde{\psi }∕\mathrm{d}s$. The force density $\tilde{f}\left(s\right)$ also depends on $\tilde{\Delta }$ via the dynamic stiffness χ=K+iωλ, reflecting the force-velocity relationship of the active force generators as well as the stiffness and friction associated with passive linkers. To linear order these effects can be expressed as

$$\tilde{f}\left(s\right)=\chi \tilde{\Delta }\left(s\right)+\beta \frac{\mathrm{d}\tilde{\psi }\left(s\right)}{\mathrm{d}s},$$ (13)

where β is a complex coefficient with units of force which describes the coupling of curvature to motor activity, see Appendix Eq. D2. This relation, together with Eq. 3, leads to the following equation for the fundamental mode:

$$i\overline{\omega }\tilde{\psi }+{\tilde{\psi }}^{⁗}-\overline{\beta }{\tilde{\psi }}^{‴}-\overline{\chi }{\tilde{\psi }}^{″}=0,$$ (14)

where $\overline{\beta }=\beta aL∕\kappa$.

To investigate whether curvature control can account for the observed beat patterns, we fit solutions of Eq. 14 to the experimental data, taking into account the appropriate boundary conditions and assuming that both K and λ are non-negative (which corresponds to an absence of sliding control). Using the real and imaginary parts of $\overline{\beta }$ and $\overline{\chi }$ as fit parameters, the best-fit value for the curvature control parameter was Re(β)=0.645±0.009 nN and Im(β)=−2.208±0.037 nN (mean ± s.d., n=6). The best-fit value of the constrained stiffness K and friction λ per unit length were approximately zero (within numerical errors). The best fits differed appreciably from the observed beat patterns in the basal region [see Fig. 7B] and were significantly worse (Q=0.870±0.021, mean ± s.d., n=6) compared to those for the sliding-control mechanism [see Fig. 5B]. Furthermore, the values of the inferred amplitude of basal sliding diverged to nonsensical values of the order of meters for the found best-fit values of $\overline{\chi }$. Upon removing the constraints on K and λ, the fits improved significantly and we obtained negative values of both K and λ which were similar to the ones given in Table 2. The best-fit values of $\overline{\beta }$ were in this case small, and their real and imaginary parts were both positive. These results imply that curvature control as the sole underlying mechanism of beat-pattern generation can lead to propagating bending waves that look similar to the observed beat patterns. However, direct comparison to our high-precision data shows that sliding control gives significantly better fits to the experimental data.

CONCLUSIONS AND DISCUSSION

We quantified the flagellar beats of bull sperm with high spatio-temporal resolution and determined the time average of the shape as well as the first temporal Fourier mode of the beat patterns for different experimental conditions. The observed beat patterns were dominated by their fundamental mode which contained more than 95% of the total power. We compared the observed fundamental modes to wave forms calculated within a theoretical framework in which the motors and passive linkers in the axoneme are described by a dynamic stiffness χ=K+iωλ. Theoretical wave forms and experimental data agreed well (see Fig. 5), which allowed us to estimate the value of the dynamic stiffness, for which we found that both K and λ were negative.

This inferred phase of the dynamic stiffness supports the hypothesis that the beat patterns are generated by collectively operating motors whose activity is coordinated by sliding between adjacent microtubule doublets. Negative values of K and λ can result from load dependent detachment of motors. Load dependent detachment leads to a positive feedback that can give rise to spontaneous oscillations: motors on the “winning” side, because they carry a smaller load per motor, spend more and more time attached, whereas those on the “losing” side, because they have a higher load per motor, spend more and more time detached. The switching of activity, and therefore the reversal of the sliding and bending, occurs because the flexural rigidity of the microtubules in the axoneme provides a restoring force that tends to keep the axoneme straight. The full wave propagation of the beat then arises from the interplay of many such oscillating segments along the length of the axoneme. Therefore the beat shape is nonlocally determined and depends on the axonemal length and on boundary conditions.

The microscopic origin of oscillations in the form of a strong load dependence of motor detachment should be accessible to direct experimental verification by measuring the load dependence of the detachment rate of purified axonemal dyneins in an in vitro assay. Such a load dependence of the detachment of molecular motors may underlie oscillations of motors in other biophysical systems such as spindle oscillations and asynchronous insect flight muscles (Grill et al., 2005; Pecreaux et al., 2006; Pringle, 1977).

Although a curvature control mechanism can generate propagating wave forms that resemble the flagellar beat, we found that the calculated wave forms in this case deviated appreciably from the measured beat patterns. Furthermore, the amplitudes of basal sliding corresponding to the fits for curvature control were unreasonably large, unlike those for sliding control. Thus the experimental results provide evidence against a motor coordination by curvature control and favor sliding-controlled motor activity. There is an additional argument in favor of a mechanism based on sliding control rather than curvature control: There is a plausible molecular basis for sliding control, namely the load-dependent detachment of the dyneins that has been established for other motor proteins (Schnitzer et al., 2000). In contrast, it is difficult to construct scenarios in which the dynein motors, which have dimensions on the order of 10 nm, can detect axonemal curvatures, whose radii are generally greater than 1 μm, a hundred times larger than molecular dimension. These arguments together suggest that curvature control is not the primary mechanism for generating axonemal beat patterns, though we do not rule out the possibility that it could play a supplementary role in shaping the beat. Likewise our results suggest that mechanisms based on transverse axonemal deformations, known as a geometric clutch, as well as structural inhomogeneities, are not central in shaping the flagellar beat, although they may play secondary roles.

Though a sliding control theory was first proposed several years ago (Camalet and Jülicher, 2000), it showed that for a clamped head and in the absence of basal sliding, the beat would propagate in the direction opposite to that observed in bull sperm and most flagella. Here, we find that basal sliding is required to obtain theoretical beat patterns which match the observed ones. In the absence of basal sliding we were not able to find theoretical beat patterns that agreed with our experimental observations. This necessity for basal sliding strongly supports the notion that there is compliance between microtubule doublets at the base of the flagellum as suggested in Vernon and Woolley (2002). We estimated the maximum amplitude of basal sliding between neighboring microtubules to be of the order of up to 100 nm, which is significantly larger, but of the same order of magnitude as estimates reported from chinchilla sperm (Vernon and Woolley, 2004). This previous report of basal sliding in mammalian sperm was based on electron micrographs of the connecting piece within the neck region of the sperm. It potentially underestimates the sliding amplitude of microtubules at the base of the axoneme. The basal sliding amplitudes deduced from our work should be accessible to direct experimental verification by measuring oscillation amplitudes of gold beads attached to microtubule doublets of beating bull sperm, following a method reported previously (Brokaw, 1989, 1991). Note that this previous study did not find evidence for basal sliding of large amplitudes in the nonmammalian sperm of the tunicate Ciona and the sea urchin Lytechinus. Differences in the structures by which the basal end of the axoneme is anchored in the head of the sperm could lead to differences of basal microtubule sliding in different species. In nonmammalian sperm the axoneme is anchored via the basal body (Gibbons, 1981), whereas in the mammalian case the axoneme is connected more indirectly via the connecting piece (Zamboni and Stefanini, 1971).

Our results suggest that basal sliding can shape flagellar beat patterns globally, because basal sliding is communicated to the motors throughout the axoneme [see Eqs. 2, 5]. This effect is illustrated by the earlier finding that sliding-controlled patterns obtained for clamped-head boundary conditions and no basal sliding travel from the distal end towards the head (Camalet and Jülicher, 2000). Thus regulation of basal compliance offers an elegant mechanism for reversing the direction of beat propagation that has been observed in cilia and flagella (Eckert, 1972; Phillips and Kalay, 1984; Ringo, 1967; Sugrue et al., 1988). In general, cellular regulation of the basal compliance alone, for example, by changes in calcium concentration or phosphorylation, could modulate the beat patterns without the need to regulate the motor proteins directly. In other words, the basal compliance could act as a spatially localized regulatory site that selects among possible beating modes generated by a fixed ensemble of motors that are distributed all along the axoneme. This regulation could operate on physiological time scales, selecting beating modes in a given axoneme or it could occur on evolutionary time scales, giving rise to a variety of beat patterns in different species.

MATERIALS AND METHODS

Sperm cells, microscopy, and imaging

Frozen bull sperm pellets of 100 μl volume provided by a cattle-breading institute (IFN Schönow, Germany) were stored under liquid nitrogen and prepared fresh each day according to the following procedure: One pellet was added to 0.9 ml pre-heated PBSMCG-buffer (2.7 mM KCl, 1.5 mM KH₂PO₄, 8.1 mM Na₂HPO₄, 58.6 mM NaCl; 1 mM MgSO₄, 2 mM CaCl₂, 5 mM glucose, pH=7.5) and incubated for 10 min at 36 °C, followed by three washing steps at room temperature (10 min centrifuging at 800 g, discarding supernatant and re-suspending with PBSMCG-buffer) and finally stored on ice. After thawing, usually about 10%–20% of the sperm cells were motile in PBSMCG buffer at 36 °C.

Sperm cells were studied under an inverted microscope (Axiovert 200M, Zeiss) at 22 or 36 °C in a copper observation chamber (12 mm diameter, 1 mm depth) whose internal surfaces had been coated with conventional nail polish to prevent metal ions leaking into the solution. Two type K thermocouple-sensors (Conrad) were attached to the chamber with tape and heat paste (Conrad) to monitor the temperature with an analog thermometer (Voltcraft 304∕K204, Conrad). The chamber was mounted on a microscope heating stage (Zeiss, Tempcontrol 37-2 digital, Universal Mounting Frame M-H) with tape and heat paste. The metal and the small sample volume facilitated a quick heat equilibration under the microscope.

Cover glasses (No. $1\frac{1}{2}18\times 18\mathrm{mm}$, Corning) served as both the top and the bottom of the chamber. The cover glasses were attached to the chamber with vacuum grease. The cover glasses were cleaned by sonication in a soap solution and afterwards rinsed with ACS-grade ethanol followed by double-distilled water. These cover glasses were either used without further treatment or were further incubated with 1% F-127 (Sigma) in PBS (as PBSMCG but without MgSO₄, CaCl₂, and Glucose) for 5 min. Without F-127 treatment the heads of the sperm cells usually stuck to the surface while their tails beat along their length close to the surface. The heads were either clamped or pivoted about a fixed point. When the surface was treated with F-127, the sperm did not stick but instead swam close to the surface, usually in circles of radii on the order of 40 μm. The circular motion was fortuitous because the sperm cells did not leave the field of view, allowing for a long observation time of freely swimming sperm.

Under the above conditions, single sperm cells beat for up to 10 min with constant frequency. Single sperm cells were imaged by phase-contrast microscopy at 10× magnification with illumination from a 100 W tungsten lamp onto a high speed camera (Fastcam, Photron). A pixel in the final image corresponds to 0.7 μm. The standard movie consisted of 1024 frames acquired at 250 frames∕s.

Wave form determination and Fourier analysis

All movies were automatically analyzed in MATLAB (The Math Works, Inc.). The customized algorithm determined in each frame the Cartesian coordinates of the tip and center of the head as well as of N=44 equally spaced (Δs=1.4 μm) points first along the center line of the head and then along the center line of the flagellum. From higher resolution still images we determined that the start of the flagellum corresponded to the fourth data point. The distance d from the center of the head to the starting point of the flagellum was measured to be 5.5 μm. The last data point along the flagellum that could still be reliably determined did not correspond exactly to the end of the flagellum. The flagellum could be tracked automatically up to an arc length of s=56 μm. Measurements from higher resolution still images of immotile sperm led to an estimate of L=58.3±0.6 μm (mean ± s.d.) for the length of the bull sperm flagellum. This has been taken into account in the comparison of calculated curves and experimental data, as illustrated by the fact that in Figs. 57 the last experimental data point corresponds to s=56 μm while the theoretical curves extend to the end of the flagellum ats=58.3 μm.

The orientation of the head and the tangent angles ψ (s,t) at each tailpoint relative to the head orientation were computed. An automated error-detection routine based on a maximum curvature criterion was used to reject frames contaminated by extraneous particles or fluctuations in light intensity. The frame failure rate was ≪1%. The precision of the automated tracking of the flagellum was on the order of 0.1 pixel, corresponding to 70 nm. Such a subpixel resolution was achieved by fitting Gaussians to the cross section of the tail, and furthermore fitting a local Chebyshev polynomial of degree 9 and span 5 through the x and y coordinates of the tail positions [see (Press, 2002) for further details]. Together with the added uncertainty in determining the arc length from frame to frame, this corresponds to an error of approximately 0.07 rad in the derived tangent angle ψ (s,t) (Riedel, 2005). A Fourier analysis in time for ψ (s_i,t)at each tail-point s_i as well as for the head orientation was carried out. A phase-preserving fast Fourier transform algorithm was used in combination with a Hanning window as implemented in MATLAB. The amplitude of the first eigenmode ${\tilde{\psi }}_1\left(s\right)$ was calculated by determining the power spectrum at each point s, fitting a Gaussian to estimate the full width at half maximum w of the main peak in each power spectrum and then determining the total power in this peak by summing over three standard deviations of that Gaussian. We found w∕f≤0.1, leading to a quality factor of f∕w≥10, which is a lower estimate due to potential undetected drift in the frequency over the observation time. Each Fourier mode was determined from a time series lasting approximately 100 beat cycles, leading to a further tenfold improvement of the precision, such that the estimated error in the amplitude of the fundamental Fourier mode ${\tilde{\psi }}_1\left(s\right)$ was about ≈0.5° or less than 10⁻² rad (Riedel, 2005).

Fitting routine

We fit calculated solutions ${\tilde{\psi }}_{\mathrm{th}}\left(s\right)$ to the experimental modes ${\tilde{\psi }}_{\mathrm{ex}}\left(s\right)$ by minimizing the sum of squared differences. This was done by determining analytical solutions to Eq. 6 and maximizing the closeness of fit parameter

$$Q=1-\frac{{\sum }_{i=1}^N{\mid {\tilde{\psi }}_{\mathrm{ex}}\left(s_i\right)-{\tilde{\psi }}_{\mathrm{th}}\left(s_i\right)\mid }^2}{{\sum }_{i=1}^N{\mid {\tilde{\psi }}_{\mathrm{ex}}\left(s_i\right)\mid }^2},$$

with Mathematica (Wolfram Research, Inc.), making use of the routines NMaximize and FindMaximum. The quantity Q is defined such that for any fit Q>0, and for a perfect fit Q=1. A closeness of fit parameter of Q≈0.90 corresponds roughly to the threshold of fits we still considered in acceptable agreement with the experimental data. Note that given a set of fit parameters the shape ${\tilde{\psi }}_{\mathrm{th}}\left(s\right)$ of the beat pattern is fully determined. The amplitude of the wave forms, however, cannot be determined within our linear theory. Hence we compared the beat patterns, by determining the amplitude of ${\tilde{\psi }}_{\mathrm{th}}\left(s\right)$ such that it corresponded with the amplitude of the experimentally observed wave form. The same holds for the arbitrary initial phase of the oscillations.

SUPPORTING INFORMATION

Movie S1. A typical raw video (phase contrast) of a bull sperm beating with 20 Hz under pivoting head condition. Scale: Length of head is approximately 10 μm. Frames were recorded every 4 ms; frame replay rate is 5 frames per second.

Movie S2. Measured tangent angle ψ (s,t) (blue dots) shown together with the fundamental Fourier mode $\tilde{\psi }\left(s\right)$ (gray line) animated as a function of time. Vertical axis in rad, frames separated by 4 ms are replayed 10 frames per second.

Movie S3. Fundamental mode $\tilde{\psi }\left(s\right)$ of the experimentally observed beating pattern (blue dots) shown together with the calculated best-fit solution to the theory for sliding-controlled motors (red line) animated as a function of time. Vertical axis in rad, time-scale as in S2.

Movie S4. Fundamental mode $\tilde{\psi }\left(s\right)$ of the experimentally observed beating pattern (blue dots) shown together with the calculated best-fit solution to the theory for curvature-controlled motors (red line), animated as a function of time. Vertical axis in rad, time-scale as in S2.

APPENDIX A: PLANAR PROJECTIONS AND AXONEMAL STRUCTURE

The three-dimensional axonemal surface can be parametrized by the arc length along the center line, s, and the azimuthal angle, ϕ. On this surface one can define a sliding displacement density Δ^3D(s,ϕ) and a force density f^3D(s,ϕ), corresponding to a continuous limit (Hilfinger, 2006). In the case of planar beat patterns, we define the coordinate system such that ϕ=±π∕2 corresponds to the plane of beat, which leads to the following relations between the 3D quantities and the two-dimensional projections Δ(s) and f (s) used throughout this article

$${\Delta }^{3\mathrm{D}}(s,\varphi )=\frac{\Delta \left(s\right)}{2}\cos \varphi$$$$f^{3\mathrm{D}}(s,\varphi )=\frac{2}{\pi }f\left(s\right)\cos \varphi .$$ (A1)

The surface densities Δ^3D(s,ϕ) and f^3D(s,ϕ) can be related to the sliding displacement and corresponding forces between microtubule doublets. Numbering the microtubule doublets i=1,…,9 we have for the sliding displacement between doublets i and i+1

$${\Delta }_{\mathrm{MT},i}\left(s\right)={\int }_{{\varphi }_i}^{{\varphi }_{i+1}}{\Delta }^{3\mathrm{D}}(s,\varphi )\mathrm{d}\varphi ,$$ (A2)

where ϕ_i=(i−1)2π∕9−π∕2. And for the force per structural repeat ℓ=96 nm between doublets i and i+1 we have

$$f_{\mathrm{MT},i}\left(s\right)=f^{3\mathrm{D}}(s,{\varphi }_i)\ell .$$ (A3)

Looking at the microtubule doublets which satisfy cos ϕ_i≈1 and therefore contribute most to the bending of the axoneme, this then leads to the geometric scalings as presented in the main text.

APPENDIX B: COLLECTIVE MOTOR DYNAMICS WITH LOAD DEPENDENCE

A simple positive feedback mechanism that can lead to oscillations of collections of motors is based on the idea that the motors detach more rapidly from their filament as the load increases (Jülicher and Prost, 1997). Such load-dependent unbinding is well known for protein-protein interactions (Bell, 1978; Evans, 2001) and has been observed for the motor protein kinesin (Schnitzer et al., 2000) and discussed in the context of the force generating elements involved in spindle oscillations (Grill et al., 2005; Pecreaux et al., 2006). This simple effect of load-dependent detachment gives rise to positive feedback because when the sliding speed increases, the load per motor decreases (because of the reciprocal relation between motor force and sliding speed) and so the detachment rate decreases, which in turn implies that there are more attached motors and therefore that the net force of the motors increases (if the load dependence is strong enough). Thus an increasing velocity can give rise to an increasing total force of a collection of molecular motors in contrast to the force-velocity response of a single motor in which an increasing velocity is associated with a decreasing load force (Jülicher and Prost, 1997). This “negative damping” gives rise to positive feedback and can create instabilities (Camalet and Jülicher, 2000; Grill et al., 2005; Jülicher and Prost, 1997; Pecreaux et al., 2006). Note that the motion eventually slows down because the flexural rigidity of the microtubules and other elastic elements oppose bending and therefore microtubule sliding.

In the following we provide a simplified quantitative description for this sliding-controlled motor coordination scenario in which collections of motor proteins act antagonistically and oppose one another. This applies to the axoneme, where dynein motors between doublets on opposite sides of the axoneme generate sliding forces that create bends in opposite directions. Suppose that the motors on one side of an axoneme (the “plus” side) have an attached probability, p₊, and each motor generates a force, f₊, when attached. The force per unit length exerted by the motors on the doublet is

$$F_{+}=-\rho p_{+}{f}_{+},$$ (B1)

where ρ is the motor density (the number of motor domains per unit length). The single-motor force is assumed to depend linearly on the sliding velocity according to

$$f_{+}\approx \overline{f}-f^{\prime }\dot{\Delta },$$ (B2)

where $\dot{\Delta }\equiv \mathrm{d}\Delta ∕\mathrm{d}t$ is the sliding speed, $\overline{f}$ is the stall force (the force at which the sliding speed equals zero) and f^′ is the slope of the force-velocity curve. The sign convention is chosen such that a positive f₊ corresponds to a load that slows the motor down. The attached probability satisfies

$${\dot{p}}_{+}\left(t\right)=-k_{\mathrm{off}}{p}_{+}+k_{\mathrm{on}}(1-p_{+}),$$ (B3)

where k_on and k_off are the on and off rates associated with the attachment and detachment of motors to and from the microtubule. The off rate is assumed to increase exponentially with load as observed experimentally for kinesin (Schnitzer et al., 2000)

$$k_{\mathrm{off}}\left(f_{+}\right)=k_0\exp (f_{+}∕f_{\mathrm{c}})\approx {\overline{k}}_{\mathrm{off}}(1-f^{\prime }\dot{\Delta }∕f_{\mathrm{c}}),$$ (B4)

where we have substituted the force-velocity relation B2 and assumed that the sliding speed is low (i.e., $f^{\prime }\dot{\Delta }∕f_{\mathrm{c}}\ll 1$). Here ${\overline{k}}_{\mathrm{off}}\equiv k_{\mathrm{off}}\left(\overline{f}\right)$ is the off rate at stall and f_c is the characteristic force; an increase in load force by f_c increases the detachment rate e fold. Assuming that the modulation δp of the attached probability about its mean value $\overline{p}=k_{\mathrm{on}}∕(k_{\mathrm{on}}+{\overline{k}}_{\mathrm{off}})$ is small, to linear order the attached probability satisfies ${\dot{p}}_{+}\left(t\right)=\overline{p}+\delta p\left(t\right)$ with

$$\delta p\approx \frac{f^{\prime }}{f_{\mathrm{c}}}\overline{p}(1-\overline{p})(\dot{\Delta }-\overline{\tau }\ddot{\Delta }+{\overline{\tau }}^2\stackrel{⃛}{\Delta }-\dots ),$$ (B5)

where $\overline{\tau }=(k_{\mathrm{on}}+{\overline{k}}_{\mathrm{off}}{)}^{-1}$, is the correlation time of motor attachments and detachments and $\ddot{\Delta }$ etc. are the sliding acceleration and higher time derivatives of Δ. Relation B5 can be verified by substitution back into B3. In the Fourier domain we can write

$$\widetilde{\delta p}\approx \frac{f^{\prime }}{f_{\mathrm{c}}}\overline{p}(1-\overline{p})\frac{i\omega \tilde{\Delta }}{1+i\omega \overline{\tau }}.$$ (B6)

The motors on the opposite side of the axoneme generate a force F₋=−ρp₋f₋. Because of the antagonistic arrangements of motors, the corresponding force and probability satisfy the following symmetry equations:

$$f_{-}\left(\dot{\Delta }\right)=-f_{+}(-\dot{\Delta })\mathrm{and}{p}_{-}(\dot{\Delta },\ddot{\Delta })=p_{+}(-\dot{\Delta },-\ddot{\Delta }).$$ (B7)

The total motor force density is given by

$$F_{+}+F_{-}\approx -2\rho \overline{f}\delta p+2\rho \overline{p}{f}^{\prime }\dot{\Delta }.$$ (B8)

This is accurate up to second order in Δ because the second order terms which are proportional to ${\dot{\Delta }}^2,\dot{\Delta }\ddot{\Delta },{\ddot{\Delta }}^2$ cancel by symmetry. The above relation implies that the Fourier transform of the motor force density is of the form ${\tilde{F}}_{+}+{\tilde{F}}_{-}\approx \chi \tilde{\Delta }$, where the dynamic stiffness is given by

$$\chi \left(\omega \right)=k+i\omega \gamma -2\rho \overline{f}\frac{f^{\prime }}{f_{\mathrm{c}}}\overline{p}(1-\overline{p})\frac{i\omega +{\omega }^2\overline{\tau }}{1+{\left(\omega \overline{\tau }\right)}^2}+2\rho \overline{p}{f}^{\prime }i\omega ,$$ (B9)

where we have included the forces arising from passive elements that resist sliding (for example, the nexin links), corresponding to a stiffness per unit length k and a friction coefficient per unit length γ (both positive). Note that due to the sign of the third term, both the real and imaginary parts of χ can be negative. Hence we conclude that collectively operating, load-dependent motors, can lead to a negative internal stiffness and negative internal friction as derived from our experimental beat patterns.

Because all the motor parameters ($\rho ,\overline{f},f_{\mathrm{c}},f^{\prime }$ and $\overline{\tau }$) can be estimated, the linear response coefficient χ derived from the shape of the axoneme can be compared with that expected for molecular motors and passive cross-linkers as done in the results section. Equation B9 is equivalent to a previously derived expression (Camalet and Jülicher, 2000)

$$\chi \left(\omega \right)=k+i\omega \gamma -\rho \kappa \Omega \frac{i\omega \overline{\tau }+{\left(\omega \overline{\tau }\right)}^2}{1+{\left(\omega \overline{\tau }\right)}^2},$$ (B10)

where κ is the stiffness of a motor domain and Ω; is a dimensionless “control parameter” that depends on the rate constants and their strain dependence (Jülicher and Prost, 1997).

APPENDIX C: PARAMETER VALUES

Viscous friction coefficient

The perpendicular friction coefficient per unit length of a slender rod of radius r near a surface (at height h from surface to rod center) is given by (Howard, 2001)

$${\xi }_{\perp }=\frac{4\pi }{{\cosh }^{-1}(h∕r)}\eta \approx \frac{4\pi }{\ln (2h∕r)}\eta .$$ (C1)

Estimating h≈4 μm for the bull sperm flagellum, and using the fact that r varies between 500 to 100 nm from head to tail, we chose a value of ξ_⊥∕η;=3.5. At 36 °C the viscosity of water is η;≈0.71×10⁻³ N s m⁻², which leads to a friction coefficient of ξ_⊥≈2.5×10⁻³ N s m⁻². At 22 °C the viscosity of water is η;≈0.96×10⁻³ N s m⁻², which leads to a friction coefficient of ξ_⊥≈3.4×10⁻³ N s m⁻². These values were used as estimates for the viscous friction coefficient. Due to uncertainties in h, we estimate that with 95% confidence the value of the viscous friction coefficient has lower and upper bounds equal to one half and two times the value used.

Flagellar bending rigidity

The bending rigidity of sea urchin sperm flagella [in a relaxed state with adenosine diphosphate (ADP) and vanadate] at 20 °C is κ≈0.9×10⁻²¹ N m² (Howard, 2001). The bending rigidity of a pure axoneme can also be estimated from the bending rigidity of individual microtubules. A single microtubule consists of 13 protofilaments, whereas a microtubule doublet consists of 24 protofilaments. A microtubule doublet is therefore expected to be (24∕13⁾²≈3.4 times as rigid as a singlet microtubule, and the 9+2 axoneme is therefore expected to be approximately 33 times stiffer than a single microtubule (assuming free sliding between microtubules), for which (in the presence of the microtubule stabilizing protein tau) κ≈23×10⁻²⁴ N m² was measured at 25 °C (Gittes et al., 1993). This leads to an estimated bending rigidity of an axoneme of κ≈0.8×10⁻²¹ N m², similar to that measured for sea urchin sperm (see above). Bull sperm flagella contain additional structural elements such as outer dense fibers that are not found in axonemes of sea urchin flagella. We therefore expect the bull sperm flagellum to be stiffer than the above. In order to estimate the bending rigidity of bull sperm flagella, we performed fits in the clamped-head case allowing the ratio of R=κ∕ξ_⊥ to be an additional fit parameter. We found that R needs to be within R=0.8±0.2×10⁻¹⁸ m³ s⁻¹ for acceptable fits (data not shown). Given the above perpendicular friction coefficient this corresponds to κ≈1.7×10⁻²¹ N m², about a factor of 2 larger than that of a relaxed sea urchin sperm, consistent with experimental estimates (Lindemann et al., 1973). This is the value that was assumed throughout the paper.

Basal compliance

The best-fit values of k_s and γ_s correspond to the mechanical properties of the basal connection. In the case of mammalian sperm the 9+2 axonemal structure is anchored within the sperm head by a complex arrangement called the connecting piece, in which the outer microtubule doublets are connected to the proximal centriole via the outer dense fibers and the striated column (Zamboni and Stefanini, 1971). For the sake of interpreting the best-fit values of k_s and γ_s to microscopic properties we oversimplify this picture and interpret the basal compliance as the result of a single visco-elastic cross bridge between the outer microtubule doublets, such that the cross-bridge elasticity per microtubule doublet is k_s,MT≈(9∕2)k_s. Assuming a rod-like cross bridge, we can estimate the bending rigidity κ_cb of such a connecting structure corresponding to the stiffness k_s,MT as deduced from our best fits by κ_cb=k_s,MT(Δℓ)³∕3, where Δℓ is the length of the cross bridge corresponding to the interdoublet spacing (Howard, 2001). For Δℓ=30 nm andk_s,MT≈0.4 N∕m, this leads to an estimation of the cross bridge bending rigidity of κ_cb≈4×10⁻²⁴ Nm², roughly a tenth of that of a single microtubule (Howard, 2001). Hence the fit result for k_s is in agreement of what is expected from a rough estimate of the basal connection based on an oversimplified representation of the connecting piece, which is held together by the microtubules of the proximal centriole. The expected friction associated with basal sliding is difficult to estimate, as hardly anything is known about the mechanical properties of the components surrounding the microtubules in the basal region.

Head dynamics

In the pivoting head and planar swimming cases, there are two additional fit parameters in the theoretical description that characterize the motion of the head. In the fit procedure they were not allowed to vary freely, but were restricted to positive values only. In all cases the best-fit values for these head parameters could not be determined with high confidence, because the calculated curves did not depend strongly on the values of (k_p,γ_p) and (ζ,γ_p), respectively. We found in the pivoting head case k_p=40±22×10⁻²¹ Nm and γ_p=0.03±0.06×10⁻²¹ Nm s (mean ± s.d., n=5). Note that in four out of five cases the best-fit value of γ_p was approximately zero, suggesting that the friction of the head angle motion is negligible in the pivoting head case. The best-fit value found for the torsional elasticity k_p is of the order of magnitude expected from the elasticity of permanent protein links between the head and the cover slip. In the planar swimming case the best-fit values found were γ_p=4710±60×10⁻²¹ Nm s and ζ=5.9±0.5×10⁻³ N s∕m (mean±s.d.,n=7). However, as noted above, the width of the local maximum in parameter space with respect to the head parameters is very large. In particular changing the value of ζ and γ_p over several orders of magnitude did not significantly change the calculated curves, implying that the best-fit values cannot be used reliably to infer the dynamic properties of the interaction between the head and the cover slip.

Systematic and statistical errors

The standard deviation of the dimensionless fit parameters lead to a relative standard error of the mean (n=18) of 2% for the real part of $\overline{\chi }$ and 4% for the imaginary part of $\overline{\chi }$ and for ${\overline{\Delta }}_0$. As discussed above, the ratio of bending rigidity κ to viscous friction coefficient was estimated with a precision of 25%. The axonemal radius a and the axonemal length L are known with an estimated uncertainty of less than 5%. Given the rescaling relation ${\Delta }_0=a{\overline{\Delta }}_0$, this leads to an estimated relative error of less than 10% for the maximum amplitude of basal sliding $\mid {\tilde{\Delta }}_{\mathrm{MT}}\left(0\right)\mid$. In order to estimate the uncertainty of the stiffness K_MT and damping coefficient λ_MT per structural repeat we look at the rescaling relation $\chi =\overline{\chi }\kappa ∕\left(a^2{L}^2\right)$. Taking into account that errors are dominated by the systematic uncertainty of the friction coefficient ξ_⊥ and the statistical uncertainty of the ratio R=κ∕ξ_⊥, we conclude that with 95% confidence K_MT and λ_MT are within a factor of 2 of the best-fit values presented in the main text.

APPENDIX D: OTHER MOTOR-CONTROL HYPOTHESES

Two alternative hypotheses concerning the mechanism of axonemal beat generation can also be formulated within our linear response framework.

Geometric clutch hypothesis

It has been suggested that the activity of motors could be regulated through changes in interdoublet during axonemal bending (Lindemann, 1994a,b, 2002). During the bending of the axoneme, nexin links that connect the filaments stretch. The tension in these links creates a force that tends to decrease the distance between the doublets. The hypothesis is that the shorter the distance, the easier it is for dynein to bind. As a result, it is thought that the dynein on-rate, k_on, increases as the doubling spacing decreases. This hypothesis is conceptually appealing, as it results in a positive feedback such that if the force at a particular place is increasing then the distance between the doublets is decreasing, which means that as dynein motors become more active, the number of attached dyneins increases which in turn leads to an increase in force. The simplest way to formalize this is to write

$$k_{\mathrm{on}}\left(\Delta \right)={\overline{k}}_{\mathrm{on}}(1+\frac{\Delta }{\delta }),$$ (D1)

where δ is a characteristic sliding distance over which the on rate increases e fold. We might expect that δ is on the order of the total sliding displacement between adjacent microtubule doublets, ∼100 nm. Note that the larger the sliding displacement, the larger the lateral force pulling microtubule doublets together, and the higher the attachment rate. This corresponds to the “t-force mechanism”—as we understand it—suggested by Lindemann (Lindemann, 1994a, 2002). Following the same line of argument as in Appendix B we find that the modulation δp of the attached probability about its mean value satisfies

$$\widetilde{\delta p}\approx \frac{1}{\delta }\overline{p}(1-\overline{p})\frac{\tilde{\Delta }}{1+i\omega \overline{\tau }}.$$ (D2)

Because of the antagonistic arrangements of motors [Eqs. B7, B8] the linear response has the form ${\tilde{F}}_{+}+{\tilde{F}}_{-}\approx \chi \tilde{\Delta }$, with

$$\chi \left(\omega \right)=k+i\omega \gamma -2\rho \overline{f}\frac{1}{\delta }\overline{p}(1-\overline{p})\frac{1-i\omega \overline{\tau }}{1+{\left(\omega \overline{\tau }\right)}^2}+2\rho \overline{p}{f}^{\prime }i\omega .$$ (D3)

where $\overline{f}$ is the mean motor force and k and γ represent the elasticity and friction of the passive crosslinkers (all positive). From Eq. D3 we see that the imaginary part of the linear response coefficient χ resulting from a geometric clutch feedback mechanism is positive.

Curvature control

The curvature control hypothesis postulates that the activity of motors is subjected to a feedback via the local curvature. In the simplest case such a relation between local motor activity and local curvature takes the following mathematical form (Brokaw, 1971; Brokaw and Rintala, 1975)

$$f_{\mathrm{a}}(s,t)=AC(s,t-\tau )$$ (D4)

where C(s,t) is the local curvature, f_a(s,t) is the force density along the axoneme due to the active elements, τ is a time delay, and A is a constant. Taking into account the passive crosslinkers and the force-velocity curve of a single motor, this leads to the following relation in Fourier space

$$\tilde{f}=\chi \tilde{\Delta }+\beta \frac{\mathrm{d}\tilde{\psi }}{\mathrm{d}s},$$ (D5)

where to linear order β≈A(1−iωτ). Note that considering simple traveling wave-solutions of the form $\psi \sim e^{i(\overline{\omega }\overline{t}-\overline{k}\overline{s})}$ with a dimensionless real wave-vector $\overline{k}$, Eq. 14 leads to the following characteristic equation

$$i\overline{\omega }+{\overline{k}}^4-i\overline{\beta }{\overline{k}}^3+\overline{\chi }{\overline{k}}^2=0,$$ (D6)

which illustrates that the terms $\overline{\beta }{\psi }^{\prime }$ and $\overline{\chi }{\psi }^{″}$ in Eq. 14 differ with respect to the symmetry of possible wavectors k. Namely, in the case for $\overline{\beta }=0$, the equation is invariant with respect to the transformation $\overline{k}\to -\overline{k}$, whereas in the case for $\overline{\chi }=0$, the equation is not invariant under such inversion of the wave direction. Hence in the absence of any sliding control $(\overline{\chi }=0)$ the phase of the complex parameter $\overline{\beta }$ determines the direction of the traveling wave, by

$$\overline{\beta }=\frac{\overline{\omega }}{{\overline{k}}^3}-i\overline{k},$$ (D7)

whereas in the absence of curvature control $(\overline{\beta }=0)$ the phase of the complex parameter $\overline{\chi }$ does not determine a unique sign of $\overline{k}$ and therefore a direction of wave propagation, as can be seen from

$$\overline{\chi }=-i\frac{\overline{\omega }}{{\overline{k}}^2}-{\overline{k}}^2.$$ (D8)

This indicates that within a curvature control scenario there is an inherent direction in wave propagation, and that propagating solutions in opposite directions are not found unless the coupling between motors and local curvature is changed along the entire length of the flagellum.