Quantitative analysis of fluorescence lifetime imaging made easy

Abstract

Fluorescence lifetime imaging is a valuable and versatile tool for the investigation of the molecular environment of fluorophores in living cells. It is ideally suited—and is therefore increasingly used—for the quantification of the occurrence of Förster Resonance Energy Transfer, a powerful microscopy method for the detection of subnanometer conformational changes, protein-protein interactions, and protein biochemical status. However, careful quantitative analysis is required for the correct and meaningful interpretation of fluorescence lifetime data. This can be a daunting task to the nonexpert user, and is the source for many avoidable errors and unsound interpretations. Digman and colleagues (Digman et al., 2007, Biophys. J. 94, L14–6) present an analysis technique that avoids data fitting in favor of a simple graphical polar data representation. In this “phasor” space, the physics of lifetime imaging becomes more intuitive and accessible also to the inexperienced user. The cumulated information from image pixels, even over different cells, describes patterns and trajectories that can be visually interpreted in physically meaningful ways. Its usefulness is demonstrated in the study of the dimerization of the uPAR receptor (Caiolfa et al., 2007, J. Cell Biol. 179, 1067–1082).

The major challenge of modern cell biology is to understand the functional interplay and dynamic organization of cellular protein machinery as it reacts to stimuli. In contrast to the “hard-wired” diagrams that we have come to know from schematic representations of signaling pathways, most interactions between proteins are not static, and are often conditional on, or coincident with the biochemical modification of one or more interaction partners, e.g., conformational changes, nucleotide binding status, membrane binding, (de)-phosphorylation, and proteolytical cleavage. However, biochemical analysis alone does not provide the vantage point from which the function of complex protein machines can be derived as the localization and even compartmentalization in different organelles or multi-protein clusters can change.

With the advent of autofluorescent proteins and other genetically coded tags, a tool has become available that allows the study of individual proteins in their natural environment of the living cell, with high sensitivity and speed. Furthermore, detailed biophysical information can be obtained on the molecular environment of the labeled components by the use of a variety of advanced fluorescence imaging techniques. As a consequence, fluorescence microscopy is increasingly used as an analytical tool for the quantification of cellular events. Fluorescence images are in actual fact rich multidimensional quantitative data sets, carrying information on morphological changes, protein location and dynamics, and protein molecular environment.

One of the most useful fluorescence metrics is the fluorescence lifetime, i.e., the average duration of the excited state of a fluorescent molecule. As the fluorescence lifetime depends on both radiative decay—giving rise to fluorescence photons, and nonradiative energy losses of the excited state—quenching the effective fluorescence yield, it is a measure for the specific brightness of a fluorophore. Interactions of the fluorophore with its biochemical environment can be read out from differences in fluorescence lifetime (Wouters et al., 2001). Most importantly, at typical physiological concentrations the fluorescence lifetime of a fluorophore does not depend on its concentration and is therefore ideally suited for use in cells where differences in concentration, path length, and compartmentalization would complicate the quantification of brightness changes. In addition to “trivial” interactions governed by, e.g., solvent polarity, viscosity and the presence of quenching compounds (e.g., halide ions), such an interaction can also be specifically engineered; when a second suitably spectrally matched fluorophore is brought within nanometer distance of the first fluorophore that is in its excited state, they couple to transfer the excited state energy from the “donor” to the “acceptor” fluorophore in a process called Förster resonance energy transfer (FRET). By supplying an additional (nonradiative) decay path for the donor excited state energy, its fluorescence emission yield and lifetime are reduced in proportion to the efficiency of the FRET process. The reduction in donor emission yield and the concomitant emergence of acceptor fluorescence from the energy arriving in its excited state through FRET—called sensitized emission—forms the basis of many FRET-based assays for protein states. Intensity-based FRET measurements can be fast and do not require specialized instrumentation; however, these methods are more sensitive to spectral cross-talk contaminations and do not provide for quantification of heterogeneous systems.

The fluorescence decay of fluorophores participating in FRET, on the other hand, can provide information on stoichiometry and the fractional contribution of molecular species. This measurement is robust, sensitive and intrinsically quantitative. However, fluorescence lifetime imaging (FLIM) is a technique that has only recently become widely available to the nonspecialist user. The most important criterion for its proper use is the correct interpretation of the lifetime results. Different analysis techniques have been developed to extract biologically meaningful information from lifetime images. The phasor approach presented by Digman and colleagues (Clayton et al., 2004; Digman et al., 2007) offers an intuitive representation of lifetime data that can serve as a powerful visual data mining tool, allowing the immediate extraction of quantitative information like lifetime mixture composition, FRET efficiency and relative fraction without the need for complicated fitting routines or other elaborate postacquisition data processing.

Imaging fluorescence lifetimes

Fluorescence lifetimes of biologically relevant fluorophores are between 1 and 10 ns and thus require specialized detection equipment. In recent years, these have become commercially available for scanning and wide-field microscopes. Furthermore, advances in high-frequency modulated light sources and camera techniques have made these systems increasingly affordable (Colyer et al., 2007; Esposito et al., 2006). As a consequence of its greater diffusion, the number of publications using FLIM for the quantification of FRET is rising and it is well on its way to becoming a routine laboratory technique.

Different practical implementations of FLIM exist today, both in scanning and wide-field microscopes, that operate in either the time or frequency domain (Esposito et al., 2007). In short, both methods measure the dynamic changes in the fluorescence response to a time-encoded excitation pattern, caused by the presence of a lifetime delay between excitation and emission. In the time domain, the impulse response is probed, i.e., the excited state is (practically) instantaneously populated by a very short excitation pulse, and the ensuing stochastic emission decay is followed over many cycles and fitted to an exponential function where the exponential factor(s) represent the lifetime decay(s) in the sample. In the frequency domain, the harmonic response is probed, i.e., the phase shift and demodulation of fluorescence emission upon excitation with a high-frequency periodically modulated illumination pattern (sine, rectangular, pulse) is measured, mostly by cross-correlation techniques. Both methods are fundamentally functionally equivalent and data from both types of FLIM equipment can be equally evaluated using the existing quantitative analysis methods and the phasor approach.

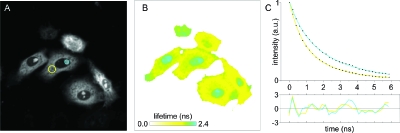
Figure 1 shows an example lifetime image acquired in the time domain on a time-correlated single photon counting system (TCSPC). Shown are HeLa cells co-expressing a tandem fusion of cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP) that exhibits FRET and localizes to the cytoplasm, and nucleolarly targeted CFP. At these two locations, the fluorescence lifetimes are equal to 1.75±0.13 ns (mean ± standard deviation) and 2.28±0.05 ns, respectively, i.e., the CFP-YFP fusion construct exhibits ∼23% FRET efficiency.

Figure 1. Fluorescence lifetime detection: CFP intensity (A) and lifetime (B) image of HeLa cells co-expressing nucleolar CFP and a cytoplasmic CFP-YFP fusion construct.

Panel C shows the fluorescence decays from the regions marked in panel A. The lower graph shows the standardized residuals.

Phasor analysis

Ironically, the attribute that makes FLIM the most suitable measurement for FRET is also its weakest point; the reliance on a fluorescence metric other than the well-known and intuitive color and intensity complicates the biological interpretation of its results. Particularly, the user should realize that fluorescence detection from each pixel represents a compound measurement over multiple molecules and fluorescence cycles. The average decay time may thus be not immediately informative. In an ideal FRET experiment between nondiffusing donor and acceptor molecules, there are two discrete donor lifetimes; that of the fluorophores that do not engage in FRET, and that of those that do and exhibit an altered fluorescence decay. Furthermore, not all fluorophores are intrinsically single-lifetime emitters and cells exhibit autofluorescence, introducing additional lifetime components; there is likely some degree of variability in the precise docking arrangement between two interacting proteins, introducing further heterogeneity in the measured lifetime distributions; and variation in the expression levels of donor- and acceptor-labeled proteins will lead to varying degrees of donor participation in FRET. The FRET efficiency in the molecular donor-acceptor complex itself is not necessarily very meaningful as it depends on distance and orientation differences that are difficult to control or know. How can one differentiate between a small fraction of donor-labeled proteins undergoing efficient FRET and a large fraction participating in energy transfer with less efficiency? The translation to biochemical entities like specific activity and concentrations of bound molecules is given by the local relative contribution of the FRET-engaged donor molecule to the lifetime mixture.

The extraction of fractions of interacting (FRET-engaged) species implies the fitting of the data to a chosen model; if two discrete and spatially invariant lifetimes are assumed, then the presence of lifetime heterogeneity may lead to errors because the variation is forcibly incorporated into the discrete lifetimes eventually causing the model to fail. Alternatively, one can consider a continuous distribution of lifetimes (Esposito et al., 2005; Redford and Clegg, 2005), for instance representing different interaction docking constellations, or conformational intermediates in or between proteins, and use our estimator to quantitatively describe heterogeneity, but these scenarios become more and more difficult to relate to biological interpretations.

The phasor method for lifetime analysis takes a different approach (Clayton et al., 2004; Digman et al., 2007; Forde and Hanley, 2006; Hanley and Clayton, 2005; Jameson et al., 1984; Redford and Clegg, 2005). Sine (S) and cosine (G) transforms of the lifetime data generate a new coordinate system (G, S). In this new space, lifetime information behaves in an intuitive manner; single lifetime emitters describe a half-circle called the “universal circle” (Jameson et al., 1984) which can only be escaped by the occurrence of photochemical reactions in the excited state (Lakowicz and Balter, 1982). Heterogeneous systems will occupy positions within the universal circle, with points moving further inward as the heterogeneity of fluorescence emission increases. This representation of lifetimes was introduced to study frequency-domain data where lifetimes are estimated from the relative phase delay (φ) and demodulation (M) of the fluorescence emission. In the (G,S) space, ϕ and M are the polar coordinates of the phasors; scatter plots of the G and S coordinates for all pixels as shown in Fig. 2 are therefore also called polar plots (Redford and Clegg, 2005) and provide a graphical tool to quantify lifetime heterogeneity (Clayton et al., 2004; Esposito et al., 2005). Digman et al. now generalize the phasor analysis to include time-domain data and introduced the helpful concept of trajectories in the phasor space.

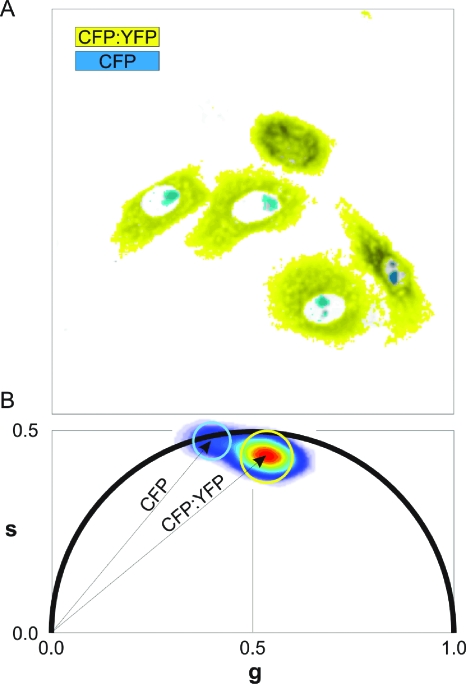
Figure 2. Segmentation (A) and polar plot representation (B) of the TCSPC data shown in Fig.1.

Cells were segmented according to the selections in the phasor space. Nucleolar regions and cytoplasm are shown in cyan and yellow, respectively, and overlaid with the intensity image. Note the precise selection of the nucleoli, and the exclusion of the remaining nuclear material containing mixtures of the lifetimes of both constructs that lie on the line connecting both pixel clouds.

Mixtures of lifetimes lie on straight lines, and these lines can only be left by nonlinear events like FRET. With FRET a curved trajectory is followed, where the position along the trajectory gives the FRET efficiency and the starting point provides the unquenched donor lifetime and its background contribution. Phasors do not require data fitting, therefore permitting the user to assess the data content without requiring prior assumptions on the decay model and its initial parameter guesses that may introduce biases in the final estimations. Rather, they provide an immediate visual representation of the data that avoids computationally expensive iterative methods. Phasors permit the visualization of trajectories and pixel clustering with which rapid and quantitative image segmentation can be performed. For instance, in a first biological application of the approach in collaboration with the same authors (Caliolfa et al., 2007), the transmembrane signaling mechanism of the urokinase-type plasminogen activator (uPAR) receptor was investigated. This glycosylphosphatidylinositol (GPI)-anchored receptor binds to a variety of proteins and the extracellular matrix protein vitronectin to play a role in a variety of cellular responses, including cellular migration, adhesion, chemotaxis and proliferation. The phasor approach was used to investigate the dimerization status of the uPAR receptor in apical and basal membranes as a function of adhesion on different substrates and during different stages of receptor endocytosis recycling. It was found that the lifetime characteristics of GFP-labeled uPAR, co-expressed with monomeric red fluorescent protein (mRFP)-uPAR to form a FRET pair, could be completely segmented between both membrane localizations by a relatively small phasor selection. When selecting phasors of co-expressing cells on the line connecting the GFP-uPAR only and nontransfected background fluorescence locations, most pixels of the apical membrane were selected and virtually none of the basal membrane. When, however, phasors away from this line (corresponding to 8–24% FRET) were selected, almost all pixels in the basal membrane were mapped, and only very little of the apical membrane. This result was obtained for cells grown on serum- and vitronectin-coated coverslips, but not for cells grown on fibronectin, which is not a substrate for uPAR. This result shows that the feedback between phasor and image data intuitively allows the confident and complete differentiation between monomeric uPAR in the apical membrane, where it does not see its preferred substrate, and the basal membrane in the presence of the wrong substrate, and dimeric uPAR in the basal membrane on the proper substrate. Exposure of cells to extracellular uPA-PAI1 (plasminogen activator inhibitor 1), known to induce uPAR endocytosis, dissociated the dimers. After washing of the cells and allowing the internalized receptors to recycle to the plasma membrane, FRET in the basal membrane was again restored.

The phasor-based segmentation of the lifetime images shown in Fig. 1 is illustrated in Fig. 2. The analysis and representation for the segmentation of cytoplasmic and nucleolar locations required only a few seconds to perform and did not involve assumptions. Instead, it takes minutes to execute a pixel-by-pixel data fitting of the image to a dual-exponential model, followed by thresholding of the obtained distributions to reach the same final result.

Quality assessment and quantitative estimations

A fundamental problem in quantitative imaging is the limited number of photons that can be collected from a biological sample due to fluorophore photobleaching and phototoxicity. For instance, at least 10% of statistical variation is to be expected in the lifetime determination at the pixel level if only 100 photons are collected (Esposito et al., 2007). More complex models (multi-exponential decays or stretched exponentials) are necessary to fit lifetime heterogeneity, but these demand very high signal levels that typically necessitate data binning or extremely long exposure times. Furthermore, careful analysis of the χ² values and residuals of the fit results is required to decide on the most appropriate model. The polar plots aid in the quality assessment of the data. The spread of the pixel clusters is related to the noise content of the lifetime image, and cluster shape is related to the lifetime composition. Phasor-assisted image segmentation permits the facile computation of average lifetimes over biologically relevant regions of interest. This corresponds to an estimation of the center of mass (G₀, S₀) of a pixel cluster, which can typically be determined with high confidence. G₀ and S₀ are analytically related to the lifetime and lifetime heterogeneity of the sample (Esposito et al., 2005), but do not requiring data fitting. Alternatively, complex models can be fitted to the ensemble of photons collected in the segmented regions, which is beneficial for the speed and precision that can be achieved with these models.

Global analysis (Pelet et al., 2004; Verveer and Bastiaens, 2003) is equivalent to the data fitting of the pixel ensemble with assumptions on global parameters such as the presence of two constant lifetimes. This approach can significantly increase the signal-to-noise ratio and the computational speed in lifetime images. It was shown (Clayton et al., 2004) that global analysis can be performed very efficiently in the phasor space. Hanley and colleagues refer to phasor space as “AB-plots” and extended the analysis to spectrally resolved lifetime imaging (Hanley and Clayton, 2005; Forde and Hanley, 2006). This is possible because the sum of two exponential decays is represented in the phasor space by a line, and simple linear regression therefore suffices for a global fit.

The concept of trajectories in the phasor space can be generalized in order to quantitatively and efficiently investigate single or multiple images. For instance, Digman et al. showed how trajectories for energy transfer behave in the phasor space.

Concluding remarks

The complicated analysis of FLIM datasets can be a bottleneck for its widespread application in the life sciences, where this imaging technique can catalyze the quantitative investigation of cellular processes using sophisticated FRET assays. Such a tool will be central to systems’ biological approaches that aim at understanding the workings of the molecular machines generating complex response pathways and constituting the inner workings of the living cell. The recent development in biolabeling techniques and FLIM instrumentation aid this goal. What is needed is a user-friendly and generalized data analysis “standard” to help the user interpret experimental results quantitatively. The phasor representation of FLIM data provides an intuitive yet very powerful analytical tool that allows the visual inspection and standardized data analysis of different photophysical scenarios with the help of data clustering and trajectories. The immediate feedback between selections in phasor space and the intensity image allow the segmentation of—even complex—photophysically different behaviors, without the need for assumptions or other prior knowledge. It is this aspect that makes the method most useful for the life scientist as he∕she can now build a phasor picture with which to segment a fluorescently labeled population exhibiting biologically relevant behavior. The phasor picture can be globally refined by including many representative cells of a given condition or treatment to achieve increasingly precise segmentations and species defined at increasing specificity. Phasors thus provide biology-guided contrast generation on a firm quantitative and physical basis. It brings specialist tools to the nonexpert user and is bound to become the universal standard for the representation and interpretation of lifetime data, permitting FLIM to become a cornerstone microscopy technique in the life sciences.