Abstract
This study provides direct functional evidence that differential adhesion, measurable as quantitative differences in tissue surface tension, influences spatial positioning between zebrafish germ layer tissues. We show that embryonic ectodermal and mesendodermal tissues generated by mRNA-overexpression behave on long-time scales like immiscible fluids. When mixed in hanging drop culture, their cells segregate into discrete phases with ectoderm adopting an internal position relative to the mesendoderm. The position adopted directly correlates with differences in tissue surface tension. We also show that germ layer tissues from untreated embryos, when extirpated and placed in culture, adopt a configuration similar to those of their mRNA-overexpressing counterparts. Down-regulating E-cadherin expression in the ectoderm leads to reduced surface tension and results in phase reversal with E-cadherin-depleted ectoderm cells now adopting an external position relative to the mesendoderm. These results show that in vitro cell sorting of zebrafish mesendoderm and ectoderm tissues is specified by tissue interfacial tensions. We perform a mathematical analysis indicating that tissue interfacial tension between actively motile cells contributes to the spatial organization and dynamics of these zebrafish germ layers in vivo.
This study addresses a fundamental and recurring theme in developmental biology: the establishment of compartments and boundaries between different tissues and the physical forces underlying this process. Gastrulation is the central process through which blastoderm cells rearrange to form the three primary germ layers: ectoderm, mesoderm, and endoderm (Solnica-Krezel, 2005; Stern, 2004). In zebrafish, gastrulation starts at around 50% epiboly, a point at which the blastoderm has spread and covered half of the large yolk cell, and with the internalization of hypoblast cells near the blastoderm margin at the dorsal side of the gastrula. These earliest internalizing cells form anterior axial mesendodermal (prechordal plate) tissue, expressing the homeobox gene goosecoid (gsc), while cells later internalizing at the dorsal blastoderm margin become chordamesoderm (notochord precursors), expressing the homeobox gene floating head (flh) (Dougan et al., 2003; Gritsman et al., 2000; Montero et al., 2005; Warga and Kimmel, 1990; Warga and Nusslein-Volhard, 1999). Progressive single cell ingression and convergence movements, causing cell compaction at the dorsal blastoderm margin, lead to the formation of the embryonic organizer (shield), the analog of the amphibian Spemann organizer (Dougan et al., 2003; Feldman et al., 1998; Gritsman et al., 2000; Montero et al., 2005; Schier and Talbot, 1998; Solnica-Krezel, 2006). Once internalized, prechordal plate progenitors migrate as a cohesive group of cells away from the blastoderm margin and towards the animal pole of the gastrula. Recent studies indicate that they use the underside of the adjacent noninternalizing ectodermal progenitor cell layer (epiblast) as a substratum for their movement (Montero et al., 2005; Ulrich et al., 2003; Ulrich et al., 2005). Initial findings have indicated that differential adhesion of the two tissues, involving E-cadherin, might play an important role (Montero et al., 2005; Ulrich et al., 2005) [reviewed in Solnica-Krezel (2006)].
Holtfreter used the term “tissue affinities” (Holtfreter, 1939) to denote that certain tissues of amphibian embryos preferentially associate with certain others, leading to the embryo’s progressive self-organization. These preferential tissue configurations can emerge not only from the appositions of intact tissue masses but also by a sorting-out process after the random intermixing of their dissociated cells (Steinberg, 1962; Steinberg, 1970; Townes and Holtfreter, 1955). The differential adhesion hypothesis (DAH) explains this approach to a common configuration via opposite pathways as an approach to a configuration of force equilibrium by heterogeneous cell populations rendered liquid-like by their possession of two properties fundamental to liquids: the constituent cells (1) cohere while (2) remaining mutually mobile. Coherent mobile cells spontaneously rearrange to maximize their mutual bonding, and the interfacial tensions between cell populations specify the most stable configuration of the “phases” (Steinberg, 1962). Tissue surface tensions have now been traced experimentally to intercellular adhesive interactions (Foty and Steinberg, 2005). Other factors, such as cell mechanics, have been suggested to also play a role, but have not yet been explored rigorously (Armstrong, 1989). Surface and interfacial tensions, immiscibility, and the order of mutual spreading are all principles well known in fluid mechanics. The application of these principles to living tissues requires that such tissues exhibit liquid behavior.
The question we set out to answer in this study is to what extent differential adhesion between the forming germ layers contributes to germ layer positioning during zebrafish gastrulation. We addressed this question by (1) determining whether embryonic tissues behave as viscoelastic materials with a biologically understandable finite relaxation time (by culturing these primary germ layer tissues in vitro, we were able to rigorously quantify their mechanical properties, a task which would be impossible to accomplish in vivo); (2) measuring quantitative differences in the cohesivity, expressible as surface tensions, of zebrafish ectoderm and mesendoderm tissues and correlating these values with the tissue’s behavior in vitro; (3) introducing an image analysis method that allows a quantitative description of the various cell sorting configurations; (4) comparing these in vitro results to in vivo cell movements; and (5) altering the cohesive relationship between these germ layers and observing effects on spatial organization.
RESULTS
Viscoelastic properties of zebrafish embryonic tissues
Irregular fragments of zebrafish embryonic mesendodermal and ectodermal tissues, when placed in tissue culture, round up and∕or fuse, in the absence of external forces (Supplemental Material, Movies 1 and 2) to form spheres. Spheroid formation and fusion of tissue aggregates in culture are classic examples of surface minimization processes which, in ordinary liquids, are driven by surface tension (Frenkel, 1945; Geguzin, 1977; Gordon et al., 1972). To characterize the mechanical properties of zebrafish embryonic mesendodermal and ectodermal tissues, we compressed spherical aggregates between parallel plates in a tissue surface tensiometer [TST, Fig. 1A]. When such aggregates are compressed, they display a characteristic time-dependent behavior. On short time scales (seconds), they behave like elastic solids, immediately reassuming a spherical shape when the compressive force is released. If, on the other hand, aggregates are compressed for one hour or more, they remain flattened when the compressive force is released and slowly approach their original shape over several hours [Fig. 1B (iv) and Supplemental Material, Movies 3 and 4]. This can only take place if cells in the aggregates’ interior rearrange to dissipate the imposed stress, a characteristic typical of liquids. Collectively, these data demonstrate that zebrafish embryonic mesendodermal and ectodermal tissues are viscoelastic: they behave as elastic solids on short time scales and as viscous liquids on long time scales.
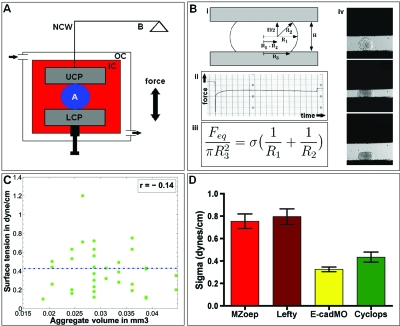
Figure 1. Surface tension measurements of zebrafish tissues.
(A) and (B) The tissue surface tensiometer (TST) and calculation of surface tension. An aggregate (A), placed between two parallel plates, is deformed by moving the plates closer together at time zero (B) (i). The upper (UCP) and lower compression plate (LCP) are not to scale and are magnified for better illustration (panel A). The UCP is connected to an electrobalance (B) through a nickel-chromium wire (NCW). The balance ensures that the UCP’s position is kept constant, i.e., the deformation initiated on the aggregate by moving the LCP up (at t=0) is kept constant over time, and the change in force is recorded (B) (ii). For a detailed description of the working principle, see Materials and Methods. From the geometry of the aggregate (B) (i) and the force at equilibrium, i.e., the force plateau in panel (B) (ii), the surface tension can be calculated by application of the Young–Laplace equation (B) (iii). R1 and R2 are the two primary radii of curvature, at the aggregate’s equator and in a plane through its axis of symmetry, respectively. R3 is the radius of the contact circle with either compression plate. H is the distance between upper and lower compression plates (from Foty et al., 1994). (B) (iv) shows a zebrafish aggregate before compression (top), under compression (middle), and 1 sec after release from a 1.5 h-compression (bottom). The aggregate remains flattened right after release and only rounds up again slowly after force removal. (C) Surface tension is independent of aggregate size. (C) shows that surface tension values are independent of the size of the aggregate (volume) for the mesendodermal tissue. Data points are in green, and the mean surface tension is drawn as a dashed blue line. r denotes the correlation coefficient, whose low negative value shows that there exists a negligible negative correlation between aggregate volume and surface tension. This confirms that the calculated aggregate surface tension is a material property. (D) Surface tension values of the different zebrafish tissues. Error bars represent standard error of the mean σ values. Sample numbers for MZoep, Lefty, E-cadMO, and Cyclops represent the number of compressions performed for each data set and are 35, 38, 39, and 35, respectively. Statistical analysis was by ANOVA and Newman-Keul’s multiple comparisons test. Statistical difference (p<0.001) in σ-values was found between MZoep and MZoep+E-cadMO, MZoep and Cyclops, Lefty and MZoep+E-cadMO, and Lefty and Cyclops, respectively.
Surface tension measurements of zebrafish embryonic tissues
The liquid character of zebrafish embryonic ectoderm and mesendoderm tissues on long time scales allowed us to directly measure their tissue surface tensions (Foty et al., 1994; Foty et al., 1996) by TST [Fig. 1A], and investigate whether these tissues differ in this physical property. Surface tensions were calculated from the aggregate geometry [Fig. 1B (i)] and measured force at equilibrium [Fig. 1B (ii)] by application of the Young-Laplace equation [Fig. 1B (iii)]. The results from the surface tension measurements are presented in Fig. 1D and Table 1. Aggregates of maternal zygotic one-eyed-pinhead (MZoep) and lefty mRNA-over-expressing wild-type fish, both lacking endoderm and most mesoderm, thus effectively representing ectodermal tissue (Supplemental Material Fig. S1 and Chen and Schier, 2002; Gritsman et al., 1999; Thisse and Thisse, 1999), were found to have the highest surface tension (mean±sem) with σ of 0.75±0.06 dynes∕cm (N=35) and 0.80±0.07 dynes∕cm (N=38) (1 dyne=10 μN), respectively. Cyclops (cyc) mRNA overexpressing cells, representing axial mesoderm and endodermal tissue, “axial mesendoderm” (Chen and Schier, 2002; Montero et al., 2005; Schier and Shen, 2000; Thisse and Thisse, 1999), generated aggregates with an average surface tension of 0.43±0.04 dynes∕cm (N=35), a value significantly lower than that of the ectodermal tissue. Down-regulation of E-cadherin expression levels in the ectoderm by injecting MZoep embryos at the single cell stage with a specific translation-blocking E-cadherin morpholino oligonucleotide (E-cadMO) resulted in aggregates with a mean surface tension of 0.33±0.02 dynes∕cm (N=39), a value significantly lower than that of both ectodermal and mesendodermal tissue. A one-way ANOVA and Newman–Keuls multiple comparison test confirmed that a statistically significant difference exists between the mean σs of tissues of ectodermal (±E-cadherin MO) and mesendodermal origin (p<0.001) as well as between the ectodermal tissues (MZoep, Lefty) and the E-cadMO-injected ectoderm. We confirmed aggregate liquidity by demonstrating that aggregate surface tension (σ) was independent of aggregate size [Fig. 1C] and remained constant in response to different degrees of compression. Table 1 shows that for aggregates of all four tissues, the mean surface tension values measured after compression 1 (σ1) and after a stronger compression 2 (σ2) were statistically identical when compared by an unpaired t-test. The ratio σ2∕σ1 approaches a value of 1 and the ratio of compressive forces F2∕F1 was significantly greater than σ2∕σ1, as expected for a liquid system.
Table 1.
Surface tension measurements and confirmation of aggregate liquidity of zebrafish ectoderm and mesendoderm-derived tissues. σ1 and σ2 are aggregate surface tensions at two different levels of compression, the second greater than the first. Means and standard errors are for aggregates on which two successive compressions were performed. σ1,2 represent composite surface tension measurements of aggregates on which both double and single compressions were performed. The ratios of σ2∕σ1 and F2∕F1 were calculated using only aggregates on which double compressions were performed.
| σ1 | σ2 | p σ1 vs σ2 | σ1,2 | σ2∕σ1 | F2∕F1 | p σ2∕σ1 and F2∕F1 | |
|---|---|---|---|---|---|---|---|
| MZoep (Ecto) | 0.80±0.11 | 0.67±0.07 | 0.33 | 0.75±0.06 | 0.83±0.05 | 1.93±0.17 | <0.0001 |
| Lefty (Ecto) | 0.80±0.11 | 0.75±0.11 | 0.72 | 0.80±0.07 | 0.92±0.05 | 1.52±0.11 | <0.0001 |
| E-cadMO (Ecto) | 0.36±0.03 | 0.33±0.03 | 0.46 | 0.33±0.02 | 0.93±0.05 | 1.53±0.08 | <0.0001 |
| Cyclops (Meso) | 0.40±0.05 | 0.47±0.08 | 0.51 | 0.43±0.04 | 1.13±0.09 | 1.93±0.10 | <0.001 |
In vitro sorting and envelopment behavior of zebrafish tissues correlates with aggregate surface tension
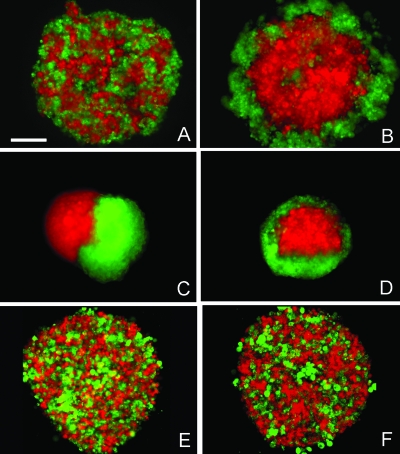
The DAH predicts that for immiscible, mutually adhesive tissues whose cells are not strongly polarized, the one of lower surface tension will always adopt a position external to the one of higher surface tension (Foty et al., 1994; Foty et al., 1996). (Morphogenetic effects of polarization are discussed below.) Accordingly, sorting and envelopment experiments were performed to determine whether aggregate surface tension predicts the relative positions adopted by mixed ectodermal (σ=0.75±0.06 dynes∕cm) and mesendodermal (σ=0.43±0.04 dynes∕cm) cells. Figure 2 shows coaggregated MZoep ectoderm cells labeled with rhodamine-dextran (red) and cyc mRNA-injected (mesendodermal) cells labeled with fluorescein-dextran (green) at the initiation of sorting, 2.5 h [Fig. 2A] in culture. After 16 h of incubation, the two cell populations had sorted out with ectoderm cells adopting an internal position relative to the mesendoderm cells [Fig. 2B]. Also, separate aggregates of ectoderm and mesendoderm tissue were combined in hanging drop culture. Figure 2C shows the adjacent tissue aggregates after they made contact, at 2.5 h in culture. Thirteen hours later, the ectoderm aggregate had become completely enveloped by the mesendodermal tissue [Fig. 2D]. Control experiments were performed by mixing cells of only one type, i.e., mesendoderm-mesendoderm or ectoderm-ectoderm, one partner labeled with fluorescein-dextran and the other with rhodamine-dextran. In both controls, cells failed to sort out and remained intermixed as illustrated in Fig. 2E (2.5 h) and Fig. 2F (16 h) for the mesendoderm-mesendoderm case. In total, more than 30 experiments on different days, each consisting of 20–30 hanging drops, were performed.
Figure 2. In vitro re-arrangement of zebrafish ectoderm and mesendoderm tissue.
Time-dependent sorting (A,B) and envelopment (C,D) assays of MZoep (ectoderm, red) and Cyclops (mesendoderm, green) cells after 2.5 h (A,C) and 16 h (B,D) in hanging drop culture. Irrespective of whether tissues were initially mixed as single cells or as fused aggregates, the system reached a stable state with the ectoderm occupying the internal position relative to the mesendoderm. Intermixed Cyclops (red) and Cyclops (green) mesendoderm cells after 2.5 h (E) and 16 h (F) in culture. Here, no sorting occurs. Scale bar=150 μm.
Studies in Xenopus have shown that fibronectin is required for the migration of involuting mesodermal progenitors during early gastrulation (Winklbauer and Keller, 1996). Cultured gastrulating zebrafish mesendodermal cells also bind to fibronectin (Puech et al., 2005), although it is not yet clear whether such binding plays a significant role in their gastrulation movements. As both mesendodermal and ectodermal tissues are in contact with the yolk cell during embryonic development, we tested whether the presence of a fibronectin-coated substrate would alter the relative positioning of these tissues. For this, single cells of both types were co-plated on fibronectin-coated plastic, and their clustering and sorting behavior was observed. Over time, cells aggregated into small clusters and sorted out in the same manner as they did in the hanging drop cultures, with mesendoderm surrounding ectoderm (Supplemental Material, Fig. S2 A,B). This indicates that the presence of the additional substrate does not significantly alter ectoderm-mesendoderm positioning. Solely, the geometry of the system as a whole was affected, i.e., the final configuration achieved was not a sphere-within-a-sphere, but a flattened-out cluster of seemingly arbitrary shape (see Supplemental Material, Fig. S2 A,B).
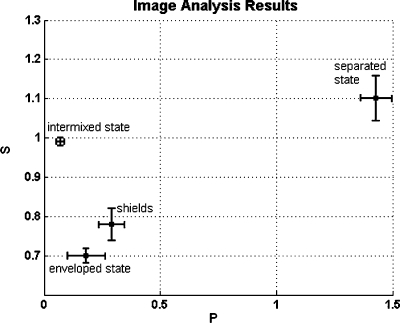
We tested whether the observed cell sorting behavior was influenced by injection into only one cell type or by differences in genetic background of wild-type and mutant fish lines. Accordingly, we over-expressed lefty mRNA in the same wild-type fish line used for cyclops mRNA over-expression. Lefty mRNA injection at the one-cell stage led to a phenotype strongly similar to MZoep, as shown previously (Thisse and Thisse, 1999; Chen and Schier, 2002) and confirmed by in situ hybridization (Supplemental Material, Fig. S1). Mixing of lefty and cyclops-injected cells led to the same sorting behavior as described earlier, with the ectodermal cells adopting an internal position in a sphere-within-a-sphere configuration (Fig. S2D). This configuration was predicted from the surface tension measurements carried out earlier, showing that lefty aggregates have a significantly higher surface tension (0.80±0.07 dynes∕cm) than cyclops aggregates (0.43±0.04 dynes∕cm). The two types of ectoderm, lefty and MZoep, were expected to stay intermixed according to their identity and their indistinguishable surface tension values (0.80±0.07 dynes∕cm and 0.75±0.06 dynes∕cm, respectively). This was indeed the case since mixed ectodermal cells remained as a single phase and did not separate into two distinct domains (Fig. S2C). Taken together, these results rule out the possibility that perturbation by injection or differences in genetic background caused the observed cell sorting behavior. The cell sorting images in Fig. 2 can clearly be evaluated by eye due to the large number of cells and the equal cell-cell ratios. There are experimental situations, however, where the number of cells is limited and∕or the cell-cell-ratio is unequal (see shield assay below). In order to interpret cell sorting configurations under these conditions, we developed an image analysis method (Appendix), which allows us to define two parameters (P,S) that differ quantitatively depending on whether the sorting images were of enveloped, intermixed, or separated states. Calculation of P and S depends solely on the distribution and brightness of pixels in a given image. The configurations observed in Fig. 2 serve as standards to clearly define the three “classes” each with specific parameters (P,S). Figure 5 in the Appendix demonstrates that each state possesses clearly different values of P and S. Having clearly defined P and S for each of the three states, we then calculated this parameter set for situations in which the cell sorting is less distinct, making it possible to interpret the numerical values within the framework of the three standards.
Figure 5. P-S diagram of the results presented in Table 2.
The image analysis parameters P and S allow us to quantitatively distinguish various cell sorting configurations without any assumptions of cell-cell interaction. The horizontal axis denotes the normalized mathematical analog to a dipole moment, P, and the vertical axis denotes the normalized ratio of scattering amplitudes of red and green cells, S. Indicated are (mean±sem) of N=15 individual experiments for intermixed, enveloped, and separate states, and N=10 for the shield experiment. For the intermixed state image analysis was performed for MZoep ectoderm and Cyclops mesendoderm cells before sorting started or on mixtures of the same cell types. For the separated state a combination of ectoderm and mesendoderm aggregates prior to tissue engulfment was analyzed. The images analyzed for the enveloped state were ectoderm surrounded by mesendoderm. The shields analyzed were extracted from gsc-GFP embryos, which had been injected with rhodamine. The shield tissues assumed a final configuration similar to that of the enveloped state.
Reducing ectoderm aggregate surface tension results in phase reversal
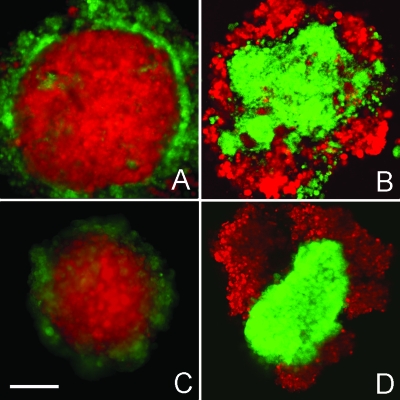
The observation that mixed ectoderm and mesendoderm tissues achieve a completely enveloped sphere-within-a sphere configuration suggests that they have different adhesive properties, and that these differences are determined by the level and∕or type of adhesion molecule expressed (Duguay et al., 2003). The best candidate to investigate in this context was E-cadherin (cdh1), since it has been shown to play a role in early zebrafish development and to be expressed in both tissues (Babb et al., 2001; Babb and Marrs, 2004; Montero et al., 2005; Solnica-Krezel, 2006; Ulrich et al., 2005). We down-regulated E-cadherin expression in both tissues, using a cdh1-specific morpholino oligonucleotide (MO) (Babb and Marrs, 2004). Cells from MO-injected cyclops-mRNA embryos were loosely associated and did not form spheroids, indicating that their surface tension was too low to drive surface minimization. When these cells were mixed with untreated ectoderm in hanging drops, a sphere-within-a-sphere configuration was achieved, with ectodermal tissue inside and mesendoderm+E-cadMO outside (data not shown). When we injected the E-cadherin morpholino into the MZoep ectoderm, tissue fragments could still round up into spheroids, but their surface tension values decreased by 50% to 0.33±0.02 dynes∕cm (N=39), below the surface tension of cyclops mesendoderm (0.43±0.04 dynes∕cm; N=35) [see Fig. 1D, Table 1]. This, according to the DAH, should result in a reversal of phase distribution with (E-cadMO-injected) MZoep ectoderm now occupying an external position relative to the mesendoderm. Figures 3A, 3C represent sorting and envelopment control experiments in which uninjected MZoep ectoderm was mixed with cyclops mesendoderm. In both cases, ectoderm adopted an internal position relative to mesendoderm. Figures 3B, 3D represent sorting and envelopment assays of mixtures of E-cadMO-injected MZoep ectoderm and cyclops mesendoderm. As predicted by the DAH, ectoderm+E-cadMO cells adopted an external position relative to the mesendoderm. A time course of both cell mixtures, i.e., MZoep ectoderm and cyclops mesendoderm, and E-cadMO-injected MZoep ectoderm and cyclops mesendoderm, is provided in Supplemental Material, Fig. S3. Here, 15 different experiments, consisting of 20–30 drops each, were performed. Phase reversal was observed in more than 90% of these drops.
Figure 3. E-cadherin-dependent phase-reversal of zebrafish ectoderm and mesendoderm tissue.
Sorting (A,B) and envelopment (C,D) assays of control MZoep ectoderm (red) and Cyclops mesendoderm (green) (A,C) and E-cadherin MO-injected MZoep (red) and Cyclops mesendoderm (green) (B,D) after 16 h. In A and C, ectoderm is enveloped by mesendoderm, whereas in B and D, mesendoderm is enveloped by ectoderm+E-cadherin morpholino. The scale bar=150 μm.
Tissue rearrangement in the embryonic shield
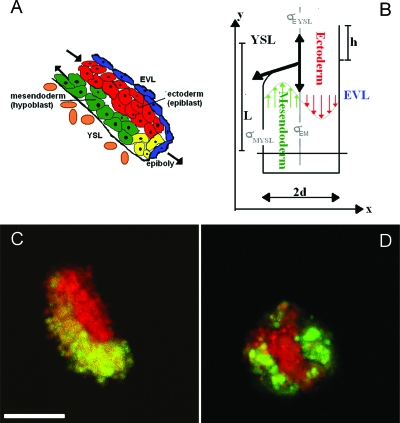
As pointed out in the introduction, in the zebrafish embryonic organizer (shield) there are two additional layers present in proximity to the ectoderm and mesendoderm tissues: the outermost enveloping layer (EVL) and the yolk syncytial layer [YSL; see Fig. 4A]. Mesendoderm (hypoblast) cells are positioned between the YSL and the ectoderm (epiblast). The epiblast cells themselves adopt a position subjacent to the highly polarized EVL, which becomes a transient extraembryonic layer. From outside the embryo towards the yolk cell, the position of tissues is therefore given by: EVL–ectoderm–mesendoderm–YSL. Consequently, instead of an external spreading of mesendoderm cells over the ectoderm, as occurs in vitro, a spreading of the mesendodermal tissue between the YSL and the ectoderm is observed in vivo. There are two possible explanations for this difference in spatial organization: First, the in vitro tissues might not behave like their endogenous counterparts because they have been altered by mRNA over-expression or, second, the observed relative positions of ectoderm and mesendoderm in the embryonic shield may be due to constraints posed by the presence of the YSL and∕or the EVL. To distinguish between these two possibilities, we isolated the shield region of a zebrafish transgenic goosecoid (gsc)-green fluorescent protein (GFP) fish line. Goosecoid is an axial mesendoderm marker; consequently, only these cells fluoresce green and can be distinguished from the neighboring ectoderm. We carried out hanging drop experiments with the excised shields and observed their behavior in culture over several hours.
Figure 4. Endogenous zebrafish shield tissue.
(A) Sketch of the zebrafish shield region with different cell types: yolk syncytial layer (YSL), axial hypoblast (axial mesendodermal progenitors), epiblast (ectodermal progenitors), and epithelial enveloping layer (EVL). (B) The shield as a 2D-rectangular object. The axes are denoted x,y. We assume symmetry in z-direction and can thus treat the 3D problem in two dimensions. The arrows indicate the parabolic velocity profile in the x-direction. (C, D) Hanging drop experiments of endogenous zebrafish shield tissue. Just after excision, anterior axial mesendoderm progenitor (green) and ectoderm progenitor (red) tissues lie adjacent to one another (C). After several hours in hanging drop culture, the axial mesendoderm tended to adopt an external position relative to the ectoderm (D). Scale bar=100 μm.
When shields were first excised, the mesendoderm and ectoderm tissues were adjacent to one another with a clear interface between them [Fig. 4C]. Over time, however, mesendoderm progressively spread over the ectoderm, ultimately generating a sphere-within-a-sphere configuration [Fig. 4D] similar to that adopted by the mRNA-injected ectoderm and mesendoderm tissues. We quantified the final configurations of ten shields with the introduced parameters P and S (see Appendix), and found that they also quantitatively resembled the sphere-within-a-sphere configuration (see Fig. 5 and Table 2 in the Appendix). These data show that the endogenous ectoderm and mesendoderm tissues behave like the mRNA-overexpressing tissues, suggesting that constraints imposed by neighboring tissues within the embryo lead to their final spatial organization in the shield during gastrulation.
Table 2.
Quantitative analysis of sorting patterns. The normalized parameters P and S for various sorting-configurations in hanging drop experiments. Means and standard errors are for N=15 images of the intermixed, enveloped and separated states and N=10 for the shield experiment. The results are illustrated in Fig. 5 in a P-S-diagram.
| Intermixed state | Enveloped state | Separated state | Shields | |
|---|---|---|---|---|
| P | 0.07±0.01 | 0.18±0.05 | 1.43±0.06 | 0.29±0.03 |
| S | 0.99±0.01 | 0.70±0.02 | 1.10±0.04 | 0.78±0.04 |
DISCUSSION
Tissue surface tensions correlate with in vitro sorting and envelopment behavior
We have shown that zebrafish ectodermal and mesendodermal tissue behave like viscoelastic materials. We quantified the effective surface tensions of mesendodermal and ectodermal tissues by tissue surface tensiometry (Foty et al., 1994; Foty et al., 1996) and confirmed that internal stress caused by compressive forces was relaxed via cell slippage, and that the measured surface tensions were independent of the force applied (Table 1). Furthermore, we found that ectodermal tissue, derived from either the MZoep mutant fish line or from lefty-mRNA injected WT zebrafish, showed a surface tension two-fold greater than that of mesendoderm tissue derived from cyc-mRNA injected WT fish. The surface tensions of the two types of ectodermal tissue were indistinguishable, indicating that surface tension is independent of the genetic background from which the tissues were isolated and is not influenced by injecting the embryos. To our knowledge, this study is the first to quantify the viscoelastic properties of zebrafish germ layer tissue.
Surface tension measurements of zebrafish embryonic tissues correlated with their adoption of an internal or external position when mixed as dispersed cell suspensions or combined as separate spheres. Thus, irrespective of the original topology of the mixture, over time, both approached the same “equilibrium” configuration, for which surface tension measurements predicted perfectly the spatial position adopted. It has been previously shown that tissue surface tensions accurately predict whether chick embryonic tissues assume an internal or external position when combined (Foty et al., 1996). However, the combinations of chick embryonic tissues used in those studies included tissues, which would not naturally encounter one another in vivo. The tissues investigated here are in direct contact during zebrafish gastrulation. Moreover, since they were prepared by non-enzymatic means and utilized as quickly as possible after dissection, their mechanical properties are as close as possible to those of native tissues. Accordingly, it is possible to more directly compare the behavior of zebrafish mesendoderm and ectoderm in vivo by investigating their interaction in vitro. Only one paper currently exists (utilizing frog tissues) that explores how differential adhesion can specify sorting and envelopment of germ layer tissues (Davis et al., 1997). In that study, observations very similar to those presented here were reported. When fragments of deep endoderm, involuted lateral mesoderm and deep blastocoel roof ectoderm were combined as pairs in vitro, endoderm spread over mesoderm which in turn spread over ectoderm (Holtfreter, 1939; Phillips and Davis, 1978; Townes and Holtfreter, 1955).
A major finding of our study is that in vitro sorting and envelopment behavior in these zebrafish germ layer tissues is specified by tissue surface tensions, which have previously been traced to intercellular adhesive interactions (Foty and Steinberg, 2005). Changes in adhesion molecule expression during differentiation could, in principle, alter the physical properties of germ layer tissues during the sorting process and influence the relative spatial positioning of tissues, even in a hanging drop system. Indeed, previous studies have demonstrated that cells can change their behavior over time, resulting in phase reversal in a sorted aggregate (Armstrong and Niederman, 1972; Wiseman et al., 1972). Evidence presented in this manuscript, however, argues against differentiation during culture being a major player in specifying cell sorting and tissue engulfment of our zebrafish tissues. First, cell sorting and tissue engulfment started almost immediately upon mixing, since the tissues were dissociated mechanically and not enzymatically. We show movies of cell sorting (5 and 6) as Supplemental Material demonstrating this. Second, small aggregates (103–104 cells) of mixed ectoderm and mesendoderm cells sorted out in as little as four hours. In situ experiments on fresh tissue aggregates and six to seven hours in culture (Supplemental Fig. S1) suggest that no terminal differentiation has taken place during that time. Third, the achievement of shape equilibrium is dependent on the size of the aggregate: the larger the aggregate, the longer the time required for sorting or engulfment. However, we found no qualitative or quantitative difference in the final sorting configuration of small vs large aggregates. Supplemental Fig. S4 shows that even a large aggregate is already partially sorted after six hours. Finally, the surface tensions measured were stable over several hours, confirming that the adhesive properties of the tissues did not change over the measurement time. Taken together, the data point to tissue surface tension and not to differentiation as the main driving force for cell sorting of zebrafish germ layer tissues.
Downregulation of E-cadherin-based cohesivity in the ectoderm leads to phase reversal
The analysis of surface tension and sorting∕envelopment behavior of germ layer progenitor cells in amphibians (Davis et al., 1997) and teleosts (this study) suggests that differential adhesion is involved in guiding germ layer morphogenesis during gastrulation. To determine whether differences in tissue surface tension directly influence sorting behavior, we altered the adhesive relationship of one of the germ layer progenitors and explored effects on surface tension and on sorting∕envelopment behavior. We showed that injecting MZoep fish at the one cell stage with an E-cadherin morpholino (E-cadMO) resulted in a significant reduction in surface tension to levels below those measured for mesendoderm [Table 1, Fig. 1D]. Consistent with the observed changes in surface tension, this resulted in a reversal of position, ectoderm+E-cadMO now adopting an external position relative to the mesendoderm. This result is in agreement with previous studies utilizing genetically engineered cell lines with well-controlled cell surface adhesion molecule expression. These studies showed that merely changing the expression level of a single adhesion system can result in markedly altered sorting behavior (Duguay et al., 2003; Foty and Steinberg, 2005). In zebrafish E-cadherin mutant and morphant embryos, mesendodermal germ layer morphogenesis is initially largely unaffected (Babb and Marrs, 2004; Kane et al., 2005; Montero et al., 2005; Shimizu et al., 2005), indicating that E-cadherin activity is not critical for mesendodermal progenitor cell ingression and early migration. The key difference between our in vitro experiments and the situation in E-cadherin mutant and morphant embryos is that we specifically down-regulated E-cadherin expression in one of the two germ layer tissues, whereas in the mutant and morphant embryos E-cadherin expression of both germ layers was equally affected. Most likely, when E-cadherin activity is ubiquitously absent in E-cadherin mutant∕morphant embryos, other adhesion molecules might still be expressed at sufficient levels to maintain differential adhesion between the forming germ layers. In contrast, in our in vitro sorting and envelopment studies, we selectively reduced E-cadherin activity in ectodermal cells, which was sufficient to trigger phase reversal. Future studies in vivo will require selective E-cadherin inactivation in ectodermal progenitors in order to determine the effects of phase reversal in the endogenous situation. However, in vivo experiments selectively disrupting cadherin activity in ectoderm progenitors are not possible with current experimental techniques.
Surface tensions and normal germ layer arrangement
As shown here, mesendoderm tissue spreads on ectoderm tissue upon contact, in the manner of one immiscible liquid wetting another. In the hanging drop experiments, these two tissues do not contact other tissues or substrates, leading to a sphere-within-a-sphere configuration in which ectoderm is enveloped by mesendoderm. This final configuration was adopted by both mRNA-overexpressing tissues and shields placed in hanging drops. This apparent difference in spatial organization between our in vitro experiments and the in vivo situation can be explained by considering the potential adhesive relationships among the tissues involved. The EVL, like other epithelia, is polarized, with basolateral surfaces adherent to their neighbors and an apical surface that is nonadherent to other cells. Thus the apical surface is forced to face a cell-free space, in this case the extraembryonic medium. The YSL and the EVL are tightly connected at the germ ring. It is within these boundaries that ectoderm and mesendoderm segregate (Montero, 2005), their relative positions adjacent to EVL or YSL possibly reflecting preferential adhesions to one or the other of these layers. In the absence of either the YSL and∕or EVL the relative positions adopted by ectoderm and mesendoderm may markedly differ. A related situation, discussed in Davis et al. (1997), exists in the amphibian embryo (Holtfreter, 1944). As in the present experiments with zebrafish tissues, frog (deep) mesoderm or endoderm enveloped (deep) ectoderm in vitro. The key to understanding the reverse of this sequence in the intact embryo was provided by Holtfreter (1943), who showed that the apical surfaces of the cells of the amphibian blastula are nonadhesive to other cells. He called this apical region the “surface coat” and showed that cells bearing it are forced to lie at free surfaces like those facing the outside or the archenteron. Thus, “unlike the immediately subjacent region of the same germ layer, a “coated” cell layer cannot be enveloped by any other tissue” (Davis et al., 1997). Indeed, substitution of “coated” for uncoated frog ectoderm in combinations with deep mesoderm and deep endoderm caused these three tissues to arrange themselves in the “normal” inside–outside sequence instead of the inverted sequence (Phillips and Davis, 1978) observed in vitro, i.e., ectoderm enveloped by mesoderm enveloped by endoderm (Phillips and Davis, 1978). The measured surface tensions of spheroids from these tissues fell in the precise sequence required to explain not only these spreading preferences but, also, together with the phase-reversing properties of the polarized surface ectoderm, tissue layering in normal gastrulation. The external surface of the teleost EVL, like that of the amphibian ectoderm, appears to be nonadhesive to other cells (Betchaku and Trinkaus, 1978). We do not know whether EVL cells are retained when shields are extirpated, but it is likely that the final configuration adopted by ectoderm and mesendoderm cells is influenced by the presence or absence of EVL, as is the case for amphibian tissue.
Remarkably, not only do the relative values of the amphibian and teleost germ layer surface tensions fall in the same sequence but even their absolute values are essentially the same. Frog deep endoderm and lateral mesoderm σs were reported to be 0.36 and 0.56 dyne∕cm, respectively, compared with 0.43 dyne∕cm for zebrafish mesendoderm, while frog deep ectoderm’s was reported to be 0.80 dyne∕cm, compared with 0.75–0.80 dyne∕cm for zebrafish ectoderm. A salient advantage of the current study over those previously reported for chick and frog tissues is that we demonstrate that down-regulating E-cadherin expression and surface tension in ectoderm results in phase reversal. This functionally connects changes in cohesion with altered sorting or envelopment behavior and is the first demonstration for a role of differential adhesion in teleost germ layer positioning.
Is the interfacial tension between ectoderm and mesendoderm sufficient to account for the observed mesendoderm spreading speed in the shield in vivo?
Our experiments show that the surface and interfacial tensions of ectoderm and mesendoderm are sufficient to favor their sorting and mutual spreading behavior in vitro. A separate question is whether interfacial tension alone is sufficient to drive tissue spreading at the observed speeds in vivo or whether additional forces, such as intrinsic cellular motor activity, accelerate spreading in the developing embryo. The role of active cellular motor activity in interfacial tension-guided cell sorting and tissue spreading has been addressed previously in studies of chick embryonic cell sorting and tissue spreading in vitro, using cytochalasin B (CB) to inhibit cellular intrinsic motile activity (Carter, 1967). It was found in two tissue combinations (heart ventricle plus either liver or pigmented retina) that cell sorting was reversibly blocked by a concentration of CB sufficient to prevent both cell locomotion and ruffling in vitro (Armstrong and Parenti, 1972; Steinberg and Wiseman, 1972). This was interpreted to indicate that, in these cell mixtures, adhesive differentials sufficient to favor and guide cell sorting were not sufficient to actually drive it, requiring active cell motility to do so, as provided for in the DAH (Steinberg, 1962). In a third tissue combination, however, (pigmented retina plus neural retina) cell sorting proceeded under the same circumstances (Armstrong and Parenti, 1972). In that tissue combination it appeared that adhesive differentials alone were sufficient to drive cell sorting even in the absence of active cell motility. Subsequent measurements of these tissues’ surface tensions (Foty et al., 1996) revealed that those of pigmented vs neural retina differ very greatly (ratio of 7.9:1) whereas those of heart ventricle vs pigmented retina or liver differ by much less (1.5:1 and 1.8:1). Thus, it appears that in vitro cell sorting and tissue spreading of these chick embryonic tissues, while guided by interfacial forces, are actually driven by a combination of those forces and active cell motility. The ratio of surface tensions of zebrafish ectoderm and mesendoderm tissues is also small: 1.7:1, suggesting that interfacial tension alone may not be sufficient to drive cell sorting. Furthermore, the time required for complete sorting or envelopment of our zebrafish tissues depended on the number of cells (system size) but typically took several hours. The spreading of the hypoblast in vivo, however, from the onset of ingression until the first hypoblast cells reach the animal pole of the embryo, takes only about 2.5 h. This suggests that additional driving forces in vivo support the interfacial tension guided cell sorting during gastrulation. The interfacial tension between the zebrafish ectoderm and mesendoderm tissues can be calculated with the Young equation (Isenberg, 1992) from the surface tension values of the individual tissues together with the contact angle of their interaction at shape equilibrium. In the case of zebrafish embryonic tissues, the contact angle Φ was 0° in all cases (complete wetting); thus we can only determine an upper boundary for the mesendoderm-ectoderm interfacial tension at the onset of complete wetting (Beysens et al., 2000; Isenberg, 1992) to be σm,e⩽0.32 dyne∕cm or 32×10−5 N∕m. A more detailed description of how interfacial tension is calculated, together with a discussion of the relationship between surface and interfacial tensions and cell sorting∕tissue engulfment, is provided as Supplemental Material. To investigate the contribution of the interfacial tensions to the endogenous cell movements, we set out to roughly estimate the cell speed that would be generated by the tensions alone and compare this value to the speeds observed in vivo. For this, we carried out the following analysis: Let us assume that there are no forces driving mesendoderm progenitor movement in vivo other than the interfacial tension between mesendoderm, ectoderm, and YSL. Based on the experimental data and a simple geometrical picture of the shield as being symmetric along the z-axis (anterior-posterior axis), we can model the tissue movements as a fluid flow in a two-dimensional x-y-rectangle [Fig. 4B]. In this simple scenario, we neglect the critical region of tissue transformation at the tip and, since the mesendoderm progenitor tissue is not in contact with the EVL, we can also neglect the presence of the EVL. For time scales sufficiently larger than the relaxation time of the tissues, both mesendoderm and ectoderm progenitors can be regarded as Newtonian fluids, moving in opposite directions. The tissue flow is characterized by high friction and no inertia (zero Reynolds number) and assumed to be in steady state (dv∕dt=0) over the length L. The width of the rectangle is 2d, with d the thickness of the germ layers (from side-views of the shield, we estimate d=50 μm) and the length,L, is given approximately by the path of the mesendoderm progenitor cells, L⩾4d. We assume that conservation of mass is valid (no growth, and all liquid exiting one side entering on the other side) and get vepi=vhypo=v (co-moving frame vepiboly=0) and, assuming incompressibility, ∇v=0. Furthermore, we assume no-slip boundary conditions, i.e., the liquid layer at the boundary has the velocity of the boundary (here zero). The velocity has only a component in the y-direction,
This reduces the Stokes equation to: ∂p∕∂y=η(∂2vy∕∂x2), where p=p(x,y) the pressure driving the fluid flow in the channel over the length L, ∂p∕∂y=Δp∕L, and η the tissue viscosity. The tissue viscosities η for both tissues were calculated to be of the order 104 Pas from the tissue fusion movies. Double integration of the governing equation with respect to the boundary conditions leads us to the expression for the velocity v(x)=(1∕η)(Δp∕L)((d2∕2)−x2). Its maximal value is given by vmax=v(x=d∕2)=(d2∕4L)(Δp∕η). According to our simplified model, interfacial tensions between the two germ layer tissues as well as between the mesendoderm and the underlying yolk cell are the only driving force. Spreading will proceed as long as there exists a force imbalance among the three interfacial tensions acting along the phase boundaries [drawn in thick black arrows in Fig. 4B]. Analogous to the earlier described scenario in vitro, in order for mesendoderm to exhibit complete wetting as observed in vivo, the interfacial tension between the ectoderm and the YSL, σE,YSL, must be greater than the sum of the interfacial tensions between ectoderm-mesendoderm, σEM, and mesendoderm-yolk, σM,YSL: σE,YSL⩾σEM+σM,YSL. The YSL has been found previously to express E-cadherin (Babb and Marrs, 2004), suggesting that the interfacial tension between the germ layer tissues and the YSL is smaller than the tissue surface tension against culture medium. Thus, we can use σE as an upper boundary for the estimation of σE,YSL and substitute the pressure gradient appearing in the expression for the maximum velocity.
When we replace Δp with σE,YSL∕d, we obtain vmax=(d∕4L)(σE,YSL∕η)(1). Furthermore, by inserting the values for d, L, η, and σE,YSL⩽75×10−5 N∕m into the equation for the maximum cell speed in the y-direction, generated by interfacial tensions alone, we obtain: vmax⩽0.3 μm∕min <vobserved∕2 (Ulrich et al., 2003; Ulrich et al., 2005; and unpublished results). This result shows that interfacial tension as a driving force gives the right order of magnitude for the observed in vivoy-velocities of hypoblast movement. However, since we estimated σE,YSL with its maximum upper boundary, σE, the result also implies that the interfacial tension between the germ layers, while making a significant contribution to the force propelling their relative movement and determining relative tissue positioning, requires amplification to produce the velocity of movement that is observed. Furthermore, one can also see from expression (1) that the maximum velocity depends on the spreading length, L. For L≈70 μm, vmax=vobserved≈0.8 μm∕min. With increasing L, the purely interfacial tension driven velocity, vmax decreases. Such a decrease in mesendoderm spreading velocity was not observed in our cell tracking experiments (unpublished data), again implying the presence of additional driving mechanisms. The presence of intrinsic cellular motile activity, involving the active extension and subsequent active contraction of cellular protrusions offers a reasonable mechanism by which cell rearrangements promoted by differential adhesion might be enhanced. Random extension of filopodia by cells in a heterogeneous population would increase the number of neighbors contacted by a given cell while the subsequent active contraction of these filopodia would test the relative strengths of these contacts, the stronger ones surviving at the expense of the weaker ones. This process, reiterated, would selectively accelerate cell rearrangements favored by tissue interfacial tensions.
Vertebrate gastrulation is a complex process the details of which differ among different vertebrates. Its components at the tissue level include epiboly, delamination, convergence movements, and extension movements. The individual cells participating in these tissue-level processes may locomote, change shape, divide, and∕or intercalate, in the course of which they may be guided by chemotaxis, by tensions originating in the cytoskeleton, by localized endocytosis of cell surfaces, by the polarized extension and retraction of protrusions, and∕or by differential cell-cell adhesion, which has been the focus of the present work. Dorsal convergence in lateral regions of the zebrafish gastrula has previously been attributed to the generation of a dorsoventral gradient of calcium-dependent cell-cell adhesiveness induced by Bmp signaling of ventral origin (von der Hardt et al., 2007). Here we show that tissue cohesivity, generated at least in part by E-cadherin and measurable as tissue surface tension, influences delamination and the arrangement of the germ layers.
MATERIALS AND METHODS
Fish stocks: Wild-type embryos were obtained from WIK, TL, and AB zebrafish lines. Maternal-zygotic one-eyed-pinhead (Mzoep) mutant fish were used to obtain embryos consisting almost exclusively of ectodermal cells (Gritsman et al., 1999). Embryos were grown at 32 °C in E3 medium and staged according to Kimmel et al. (1995).
Injections: For mRNA over-expression, 100 pg of lefty mRNA, 50 pg (TST, sorting assays), and 100 pg of cyc mRNA, with or without additional fluorophore (0.5% fluorescein- or 0.5% rhodamine-dextran), was injected into wild-type one-cell-stage embryos. Cyclops encodes a nodal-related transforming growth factor-β (TGFβ) signal required for mesendoderm formation and patterning in zebrafish (Dougan et al., 2003; Sampath et al., 1998; Schier and Shen, 2000). Thus, overexpression of cyclops mRNA in one-cell-stage wild-type embryos induces exogenous axial mesendoderm in all blastomeres [Supplemental Material Fig. S3 and Dougan et al. (2003); Sampath et al. (1998); Schier and Shen (2000)]. Maternal zygotic one-eyed-pinhead (MZoep) mutants, consisting nearly exclusively of ectodermal tissue [Supplemental Material Fig. S1 and Gritsman et al. (1999)] were either left uninjected or injected at the one cell stage with 0.5% fluorescein- or 0.5% rhodamine-dextran. For E-cadherin MO injections, 4–6 ng (TST, sorting assays) or 8–9 ng (sorting assays) of an E-cadherin specific MO was injected into one-cell-stage embryos as previously described (Babb and Marrs, 2004). While injection of 4–6 ng of E-cadMO resulted in a significant reduction in surface tension to levels below those measured for mesendoderm, in the hanging drop experiments this amount led to partial sorting out and not to complete phase reversal. For complete phase reversal to occur, it was necessary to inject 8–9 ng of E-cadMO. Such aggregates, however, were not sufficiently cohesive to form spherical aggregates and could not be used for TST measurements. Lefty mRNA overexpression induces ectodermal cell fate and has been shown previously to display a phenotype strongly similar to MZoep mutant embryos (Supplemental Material, Fig. S3 and Thisse and Thisse, 1999). For the shield excision experiments, the transgenic goosecoid-GFP fish line Tg(−1.8 gsc:gfp)ml1 (Doitsidou et al., 2002) was used and transgenic embryos were injected with 0.5% rhodamine-dextran. We confirmed tissue identity by performing in situ hybridization experiments utilizing specific markers of ectoderm and mesendoderm (see Supplemental Material, Fig. S1).
Aggregate formation: For all experiments except the shield isolation, embryos were first dechorionated using pronase (2 mg∕ml, Roche, Germany) at high to oblong stage [3–4 h post fertilization (pf)] and washed four times in E3 buffer before dissection. Embryos were dissected by manually separating cells from the yolk sac under a stereo-microscope using watchmaker’s forceps. Tissue fragments were transferred into 2%-agarose-coated dishes containing degassed CO2-independent medium (Gibco-BRL, NY) supplemented with 10% FCS and antibiotics. Spherical aggregates ranging in diameter between 0.35–0.5 mm and containing 104 to 105 cells formed within 1 hour and were maintained at room temperature until used.
Tissue surface tensiometry: Aggregate cohesivity was measured by tissue surface tensiometry (TST) as previously described (Foty et al., 1994; Foty et al., 1996). Briefly, spherical aggregates were positioned on the lower compression plate (LCP) of the tissue surface tensiometer [Fig. 1A]. The compression cell is composed of two chambers. The outer chamber (OC) is connected to a 28 °C circulating water pump, and serves to regulate the temperature of the inner chamber (IC). The chambers are constructed of milled Delrin and contain quartz windows for visualization of the aggregate. The inner chamber contained pre-warmed, degassed CO2-independent medium (Gibco-BRL, NY) supplemented with 10% FCS and antibiotics. The upper compression plate (UCP), attached to a nickel-chromium wire (NCW), was then positioned above the aggregate and connected to a Cahn∕Ventron model 2000 recording electrobalance (B). The weight of the UCP was zeroed to establish a pre-compression UCP weight baseline. In order to minimize adhesion of cell aggregates to the compression plates, both the lower and upper plates were pre-coated with poly-2-hydroxyethylmethacrylate (poly-HEMA, Sigma, MO), a polymeric material to which cells do not adhere (Folkman and Moscona, 1978). Compression was initiated by raising the LCP until the aggregate became compressed against the UCP. Adjusting the height of the LCP controlled the degree of compression. The force with which the aggregate resisted compression was monitored by the Cahn recording electrobalance. Aggregate geometry was monitored through a 25×Nikon dissecting microscope equipped with a CCD video camera and connected to a Macintosh Power PC computer. Images of aggregates were captured, digitized and their geometries were analyzed using NIH Image (Bethesda, MD). Each aggregate was subjected to two compressions between parallel plates, the second greater than the first. Measurements of aggregate geometry [Fig. 1B (i)] and the force of resistance to the compressive force [Fig. 1B (ii)] were then utilized in the Young–Laplace equation [Fig. 1B (iii)] (Davies and Rideal, 1963),
producing numerical values of apparent tissue surface tension (σ). Here, Feq is the resistance force at shape equilibrium, is the area of the surface of the aggregate upon which the compressive force F is exerted, and R1 and R2 are, respectively, the radius of the equator of the compressed aggregate and the radius of an arc defining its surface profile normal to the compressing plates and extending between them [Fig. 1B (i)]. Of the three radii, R3 is the most difficult to measure because of limited resolution. We, therefore, estimated R3 from measured values of R1, R2 and the distance between the compression plates (H) as
This estimate corresponds to a finite contact angle between aggregate and compression plate. If the contact angle is small, we would estimate R3 as
The estimate is about 10% smaller than R3 for our experiments. We use the simpler estimate of R3 to calculate tissue surface tensions. TST-measurements of the surface tension of the shields could not be performed due to their extremely small size (102–103 cells).
Data analysis: For TST measurements, a mean and standard error were calculated for each tissue type. Mean and standard error were calculated for σ values and for the ratio F2∕F1. A one-factor analysis of variance (ANOVA) and Neuman–Keul’s multiple comparison test were performed to resolve statistically significant differences when comparing σs between groups (Motulsky, 2003). Statistical analysis was performed using Graphpad Prism 4 software.
Sorting and envelopment assays: For sorting assays, fluorescent ectodermal (rhodamine-dextran, ± E-cadMO) and mesendodermal (fluorescein-dextran) aggregates were generated as described above and mixed 1:1 or 2:1 (50–60 aggregates per 500 μl) and mechanically disrupted by gentle trituration in sterile E3 medium. Single cells were resuspended in CO2-independent medium (Gibco) at a concentration of 1–6×106 cells∕ml and placed in 13 μl hanging drops. Drops were deposited on the underside of the lid of a 10 cm polystyrene tissue culture dish and the lid was inverted over 10 ml of PBS for hydration. Hanging drops were imaged at 20× magnification either by conventional epifluorescence microscopy using a Nikon Eclipse microscope equipped with a Photometrics Coolsnap ES cooled CCD camera (Tucson, AZ), or by confocal microscopy using either a Zeiss LSM 150 (Thornwood, NY), or a Biorad MRC600 (Hercules, CA) scanning laser confocal microscope. For envelopment assays, ectodermal and mesendodermal aggregates of stained tissues were cut into smaller aggregates using a pair of fine scalpels. These tissue fragments were allowed to round up again and similar sized aggregates of the two tissue kinds were placed together in 15 μl hanging drops. The time scale of both assays depended on the number of cells in culture as well as the size of the hanging drops. For small aggregates (103–104 cells), sorting∕envelopment was completed after 4–6 h, whereas larger aggregates (105–106 cells) required up to 16 h for complete sorting∕envelopment. For all cases, hanging drops were imaged immediately and then again after 2.5, 5, and 8 h, and then in 4 h-intervals over a 24-hour period. For the experiments on fibronectin-coated plastic, single cell solutions were prepared as described above and cultured in CO2-independent medium on plastic petri dishes coated with 10 μg∕ml fibronectin. For time-lapse movies of cell sorting (Supplemental Material, Movies 5 and 6), hanging drops were plated on glass and sealed to prevent evaporation.
Calculation of interfacial tension: In the example of two immiscible tissues in cell culture medium, there will be three surface tension forces present at the contact line between them. In our experiments, mesendoderm tissue spreads upon ectodermal tissue; thus, we chose the notation: tissue 1: E, tissue 2: M, and surrounding cell culture medium: CM. We can now denote the three tensions to be σ(EM), σ(MCM), and σ(ECM). In the equilibrium configuration, all forces are balanced, and we obtain the following relationship for the three tensions:
This is the Young equation for calculating the interfacial tension σ(EM) from knowledge of the contact angle between the tissues, Φ, and the surface tensions between tissue and cell culture medium, σ(MCM) and σ(ECM). At the onset of complete wetting, lim Φ→0, one obtains
Shield assay: Transgenic goosecoid-GFP embryos were injected with 0.5% rhodamine-dextran at the one-cell stage and allowed to develop at 32 °C in E3 medium until 50% epiboly. The dye did not influence normal development of these embryos in any detectable way. Goosecoid protein is only expressed in axial mesendoderm cells; consequently, only these cells fluoresce green. Due to rhodamine injection, however, all cells of the embryo fluoresce red. Embryos were dechorionated using pronase (2 mg∕ml; Roche, Germany) and washed four times in E3 medium. At the shield stage, embryos showing a GFP-signal were collected and placed into an embryo mounting dish. Shields were isolated under a Zeiss dissecting microscope using a customized oil-based syringe-system with a thin glass pipette, similar to the method described in detail in (Saude et al., 2000). Isolated shields were transferred into an agarose-coated cell culture dish containing CO2-independent medium, then placed in 13 μl hanging drops. Shields were imaged by confocal microscopy after 1 hour and then again in 2 h intervals over a 12-hour period. Shield assays were repeated 5 times, each experiment containing about 5-10 shields. In all of these shield cases there was more ectoderm than mesendoderm and thus the envelopment configuration was never complete. This situation made it important to characterize the observed configuration quantitatively and to compare the obtained parameters with the results of the cell sorting∕tissue spreading configurations of the mRNA overexpressing tissues for better interpretation. To do so, we developed an image analysis protocol that allowed us to classify the three cell sorting configurations of the mRNA overexpressing tissues (intermixed, separated and enveloped) by the introduction of two independent parameters, which have corresponding analogs in physics: the vector of the dipole moment P and the tensor of inertia I. We then calculated the values of these two parameters for the observed shield configurations and compared the results to the values obtained for the three classified sorting configurations. By using this quantitative approach, we determined that the shield configuration obtained after several hours was very similar to the enveloped state, confirming the visual impression. An extensive description of the quantitative image analysis method is presented in the Appendix.
ACKNOWLEDGMENTS
The authors thank J Goodhouse and J Peychl for technical assistance with the microscopes; E Wieschaus for the use of his confocal microscope; DongXuan Jia for her help with the TST-experiments; F Ulrich and S Schneider for help in various issues regarding zebrafish handling; and M Gonzalez-Gaitan, A Oates, SF Nørrelykke,K Echeverri, and W Bialek for reading and comments on the manuscript at various stages. The work was supported by a Ph.D. grant from the Studienstiftung des dt. Volkes to EMS, a travel fellowship from the Company of Biologists to support EMS to perform experiments at UMDNJ, and Princeton University, by grants from the Deutsche Forschungsgemeinschaft and the Max-Planck-Society to CPH, and from the Department of Defense (Grant No. W81XWH-04-1-0265) to RAF.
APPENDIX: QUANTITATIVE IMAGE ANALYSIS
The basic idea of the image analysis method is to define two parameters which allow a quantitative distinction between the intermixed, enveloped, and separated states, which can then serve as a framework for classifying less clear experimental data in a quantitative manner. These parameters do not have a biological interpretation; they serve solely as a means for the quantitative distinction between different images. The parameters we chose for this image analysis have physical analogs in the electrical dipole moment P and the (mass) moment of inertia I. However, in the context of the present study, they do not have a physical meaning; the analogy is solely based on a mathematical description. For the calculation of these two parameters P and S, RGB images were split into their red and green channels using ImageJ 1.36b (NIH, USA) and analyzed in Matlab 7.0.1 (The MathWorks, Inc.). Images were converted to matrices and the pixel brightness at each pixel position (i,j) was used for the calculation of P and I. We determine P as the discrete sum of pixel brightness ρe(i,j) at matrix positions (i,j): P=∑i,jρe(i,j)⋅(i,j), with the normalized density ∑i,j∣ρe(i,j)∣=1. Here, for one of the channels, the pixel brightness was designated negative, whereas for the other the pixel brightness was designated positive–in analogy to negative or positive charges. It is important to note that this method does not require any information about the underlying image; it simply captures and quantifies the pattern of the image according to pixel position weighted by pixel intensity (brightness). P was calculated for each channel individually and normalized by the radius R of the system, to allow comparison of different aggregate sizes, where and A the total area of the aggregate. A was calculated as A=4⋅sqrt(det(J)) with
the diagonalized second moment of the RGB image. The overall P value (P=∣P∣) of the RGB image is the sum of the results for the individual channels. P allows us to distinguish the separated state, where the normalized P value is larger than 1, from the intermixed and enveloped states, which have a negligible P value. It does not allow a distinction between the cases of intermixed cells and enveloped configuration, since for an external observer both configurations have zero P values, as positive and negative counted pixel values cancel each other out in these cases. In order to additionally distinguish these two scenarios a second parameters is needed. This second parameter, I, allows investigation of the cell scattering around the center of mass of red and green cells, expressed as the ratio of scattering amplitudes S, where S=Sred∕Sgreen and Sred∕green are the scattering amplitudes of the red and green channel, respectively (Fig. 5). The calculation of the scattering amplitudes has been slightly modified from its application of analyzing Brownian motion of DNA-tethered beads (Tolic-Norrelykke et al., 2006). For a two-dimensional image, the tensor of inertia I is given by the following matrix
with
where ∑i,jρm(i,j)=1, ρm(i,j) is again the pixel brightness (in analogy to a the mass density) at position (i,j), and (X,Y) the center of mass of the RGB image. I can be diagonalized, and the entries of the diagonalized tensor are called the principal moments of inertia. We denote them with Imin and Imax according to their difference in magnitude. They are given by
With the help of these principal moments of inertia, one can now calculate the scattering amplitudes (standard deviation around the center of mass) for the individual channels as well as the ratio S=Sred∕Sgreen. The latter is <1 if the red cells are less scattered around the center of mass than the green cells. S=1if cells are scattered equally, as in the intermixed state, and S>1 if the red cells are scattered more than the green cells, as occurring in the separated state where cluster sizes and shapes of red and green aggregates often differ. We analyzed 15 images of each configuration, from 15 different experiments. Table 2 shows the numerical values for the norm of P (P=∣P∣) and the ratio of scattering amplitudes S, which are illustrated in Fig. 5. Since both parameters are normalized by the aggregate radius and aggregate area, respectively, they only assume small values. P is close to 1 in the case of adjacent aggregates (separated state), where red and green cells are clearly separated from each other, but close tozero for the intermixed and the enveloped states. (In an ideal case of exactly matching cell numbers, P would vanish completely.) The calculated values for P (mean±sem) obtained were 0.07±0.01 for the intermixed state, 0.18±0.05 for the enveloped state, and 1.43±0.06 for the separated state. The ratio of scattering amplitudes, S, for the intermixed and the separated states is similar (Sintermixed=0.99±0.01 and Sseparated=1.10±0.04) as expected, since in both cases red and green cells are equally scattered far from the common center of mass. These values are clearly different from the ratio of scattering amplitudes of the enveloped state (Senveloped=0.70±0.02) with red ectoderm cells located in the aggregate center surrounded by green mesendoderm cells. Thus, each of the three configurations, intermixed, enveloped, and separated, possesses a unique combination of P and S values, which quantitatively determine its class. We used this classification system in the present study in order to more clearly interpret the shield images, where cell numbers were small and the cell–cell ratio was unequal. Under such conditions the resulting sorting configuration was better interpreted by quantification.
References
- Armstrong, P B (1989). “Cell sorting out: the self-assembly of tissues in vitro.” Crit. Rev. Biochem. Mol. Biol. 24, 119–149. [DOI] [PubMed] [Google Scholar]
- Armstrong, P B, and Niederman, R (1972). “Reversal of tissue position after cell sorting.” Dev. Biol. 28, 518–527. [DOI] [PubMed] [Google Scholar]
- Armstrong, P B, and Parenti, D (1972). “Cell sorting in the presence of cytochalasin B.” J. Cell Biol. 10.1083/jcb.55.3.542 55, 542–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babb, S G, Barnett, J, Doedens, A L, Cobb, N, Liu, Q, Sorkin, B C, Yelick, P C, Raymond, P A, and Marrs, J A (2001). “Zebrafish E-cadherin: expression during early embryogenesis and regulation during brain development.” Dev. Dyn. 221, 231–237. [DOI] [PubMed] [Google Scholar]
- Babb, S G, and Marrs, J A (2004). “E-cadherin regulates cell movements and tissue formation in early zebrafish embryos.” Dev. Dyn. 230, 263–277. [DOI] [PubMed] [Google Scholar]
- Betchaku, T, and Trinkaus, J P (1978). “Contact relations, surface activity, and cortical microfilaments of marginal cells of the enveloping layer and of the yolk syncytial and yolk cytoplasmic layers of fundulus before and during epiboly.” J. Exp. Zool. 206, 381–426. [DOI] [PubMed] [Google Scholar]
- Beysens, D A, Forgacs, G, and Glazier, J A (2000). “Cell sorting is analogous to phase ordering in fluids.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.97.17.9467 97, 9467–9471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter, S B (1967). “Effects of cytochalasins on mammalian cells.” Nature 213, 261–264. [DOI] [PubMed] [Google Scholar]
- Chen, Y, and Schier, A F (2002). “Lefty proteins are long-range inhibitors of Squint-mediated Nodal signaling.” Curr. Biol. 72, 2124–2128. [DOI] [PubMed] [Google Scholar]
- Davies, J T, and Rideal, E K (1963). Interfacial Phenomena, Academic, New York. [Google Scholar]
- Davis, G S, Phillips, H M, and Steinberg, M S (1997). “Germ-layer surface tensions and “tissue affinities” in Rana pipiens gastrulae: quantitative measurements.” Dev. Biol. 192, 630–644. [DOI] [PubMed] [Google Scholar]
- Doitsidou, M, Reichman-Fried, M, Stebler, J, Koprunner, M, Dorries, J, Meyer, D, Esguerra, C V, Leung, T, and Raz, E (2002). “Guidance of primordial germ cell migration by the chemokine SDF-1.” Cell 111, 647–659. [DOI] [PubMed] [Google Scholar]
- Dougan, S T, Warga, R M, Kane, D A, Schier, A F, and Talbot, W S (2003). “The role of the zebrafish nodal-related genes squint and cyclops in patterning of mesendoderm.” Development 130, 1837–1851. [DOI] [PubMed] [Google Scholar]
- Duguay, D, Foty, R A, and Steinberg, M S (2003). “Cadherin-mediated cell adhesion and tissue segregation: qualitative and quantitative determinants.” Dev. Biol. 10.1016/S0012-1606(02)00016-7 253, 309–323. [DOI] [PubMed] [Google Scholar]
- See EPAPS Document No. E-HJFOA5-2-005801 for Supplemental material. This document can be reached via a direct link in the online article’s HTML reference section or via the EPAPS homepage (http://www.aip.org/pubservs/epaps.html).
- Feldman, B, Gates, M A, Egan, E S, Dougan, S T, Rennebeck, G, Sirotkin, H I, Schier, A F, and Talbot, W S (1998). “Zebrafish organizer development and germ-layer formation require nodal-related signals.” Nature 395, 181–185. [DOI] [PubMed] [Google Scholar]
- Folkman, J, and Moscona, A (1978). “Role of cell shape in growth control.” Nature 10.1038/273345a0 273, 345–349. [DOI] [PubMed] [Google Scholar]
- Foty, R A, Forgacs, G, Pfleger, C M, and Steinberg, M S (1994). “Liquid properties of embryonic tissues: measurement of interfacial tensions.” Phys. Rev. Lett. 10.1103/PhysRevLett.72.2298 72, 2298–2301. [DOI] [PubMed] [Google Scholar]
- Foty, R A, Pfleger, C M, Forgacs, G, and Steinberg, M S (1996). “Surface tensions of embryonic tissues predict their mutual envelopment behavior.” Development 122, 1611–1620. [DOI] [PubMed] [Google Scholar]
- Foty, R A, and Steinberg, M S (2005). “The differential adhesion hypothesis: a direct evaluation.” Dev. Biol. 10.1016/j.ydbio.2004.11.012 278, 255–263. [DOI] [PubMed] [Google Scholar]
- Frenkel, J (1945). “Viscous flow of crystalline bodies under the action of surface tension.” J. Phys. 9, 385. [Google Scholar]
- Geguzin, J (1977). Kaplja (the drop), Academy of Science, Moscow, USSR. [Google Scholar]
- Gordon, R, Goel, N S, Steinberg, M S, and Wiseman, L L (1972). “A rheological mechanism sufficient to explain the kinetics of cell sorting.” J. Theor. Biol. 10.1016/0022-5193(72)90114-2 37, 43–73. [DOI] [PubMed] [Google Scholar]
- Gritsman, K, Talbot, W S, and Schier, A F (2000). “Nodal signaling patterns the organizer.” Development 127, 921–932. [DOI] [PubMed] [Google Scholar]
- Gritsman, K, Zhang, J, Cheng, S, Heckscher, E, Talbot, W S, and Schier,A F (1999). “The EGF-CFC protein one-eyed pinhead is essential for nodal signaling.” Cell 97, 121–132. [DOI] [PubMed] [Google Scholar]
- Holtfreter, J (1939). “Gewebeaffinität, ein Mittel der embryonal Formbildung.” Arch. Exptl. Zellforsch. Gewebezucht 23, 169–209. [Google Scholar]
- Holtfreter, J (1943). “Properties and functions of the surface coat in amphibian embryos.” J. Exp. Zool. 93, 251–323. [Google Scholar]
- Holtfreter, J (1944). “A study of the mechanics of gastrulation.” J. Exp. Zool. 95, 171–212. [Google Scholar]
- Isenberg, C (1992). The Science of Soap Bubbles, Dover Inc., New York. [Google Scholar]
- Kane, D A, McFarland, K N, and Warga, R M (2005). “Mutations in half baked∕E-cadherin block cell behaviors that are necessary for teleost epiboly.” Development 132, 1105–1116. [DOI] [PubMed] [Google Scholar]
- Kimmel, C B, Ballard, W W, Kimmel, S R, Ullmann, B, and Schilling, T F (1995). “Stages of embryonic development of the zebrafish.” Dev. Dyn. 203, 253–310. [DOI] [PubMed] [Google Scholar]
- Montero, J A, Carvalho, L, Wilsch-Brauninger, M, Kilian, B, Mustafa, C, and Heisenberg, C P (2005). “Shield formation at the onset of zebrafish gastrulation.” Development 132, 1187–1198. [DOI] [PubMed] [Google Scholar]
- Motulsky, H (2003). Statistical Analyses for Laboratory and Clinical Researchers, 4th Edition, GraphPad Software, San Diego. [Google Scholar]
- Phillips, H M, and Davis, G S (1978). “Liquid-tissue mechanics in amphibian gastrulation: germ layer assembly in Rana pipiens.” Am. Zool. 18, 81–93. [Google Scholar]
- Puech, P H, Taubenberger, A, Ulrich, F, Krieg, M, Muller, D J, and Heisenberg, C P (2005). “Measuring cell adhesion forces of primary gastrulating cells from zebrafish using atomic force microscopy.” J. Cell. Sci. 10.1242/jcs.02547 118, 4199–4206. [DOI] [PubMed] [Google Scholar]
- Sampath, K, Rubinstein, A L, Cheng, A M, Liang, J O, Fekany, K, Solnica-Krezel, L, Korzh, V, Halpern, M E, and Wright, C V (1998). “Induction of the zebrafish ventral brain and floorplate requires cyclops∕nodal signalling.” Nature 395, 185–189. [DOI] [PubMed] [Google Scholar]
- Saude, L, Woolley, K, Martin, P, Driever, W, and Stemple, D L (2000). “Axis-inducing activities and cell fates of the zebrafish organizer.” Development 127, 3407–3417. [DOI] [PubMed] [Google Scholar]
- Schier, A F, and Shen, M M (2000). “Nodal signalling in vertebrate development.” Nature 403, 385–389. [DOI] [PubMed] [Google Scholar]
- Schier, A F, and Talbot, W S (1998). “The zebrafish organizer.” Curr. Opin. Genet. Dev. 8, 464–471. [DOI] [PubMed] [Google Scholar]
- Shimizu, T, Yabe, T, Muraoka, O, Yonemura, S, Aramaki, S, Hatta, K, Bae, Y K, Nojima, H, and Hibi, M (2005). “E-cadherin is required for gastrulation cell movements in zebrafish.” Mech. Dev. 122, 747–763. [DOI] [PubMed] [Google Scholar]
- Solnica-Krezel, L (2005). “Conserved patterns of cell movements during vertebrate gastrulation.” Curr. Biol. 15, R213–R228. [DOI] [PubMed] [Google Scholar]
- Solnica-Krezel, L (2006). “Gastrulation in zebrafish—all just about adhesion?” Curr. Opin. Genet. Dev. 16, 433–441. [DOI] [PubMed] [Google Scholar]
- Steinberg, M S (1962). “On the mechanism of tissue reconstruction by dissociated cells, III. Free energy relations and the reorganization of fused, heteronomic tissue fragments.” Proc. Natl. Acad. Sci. U.S.A. 48, 1769–1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinberg, M S (1970). “Does differential adhesion govern self-assembly processes in histogenesis? Equilibrium configurations and the emergence of a hierarchy among populations of embryonic cells.” J. Exp. Zool. 173, 395–433. [DOI] [PubMed] [Google Scholar]
- Steinberg, M S, and Wiseman, L L (1972). “Do morphogenetic tissue rearrangements require active cell movements? The reversible inhibition of cell sorting and tissue spreading by cytochalasin B.” J. Cell Biol. 10.1083/jcb.55.3.606 55, 606–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern, C (2004). Gastrulation: from cells to embryo, Cold Spring Harbor Laboratory Press, Cold Spring Harbor, New York. [Google Scholar]
- Thisse, C, and Thisse, B (1999). “Antivin, a novel and divergent member of the TGFbeta superfamily, negatively regulates mesoderm induction.” Development 126, 229–240. [DOI] [PubMed] [Google Scholar]
- Tolic-Norrelykke, S F, Rasmussen, M B, Pavone, F S, Berg-Sorensen, K, and Oddershede, L B (2006). “Stepwise bending of DNA by a single TATA-box binding protein.” Biophys. J. 90, 3694–3703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Townes, P L, and Holtfreter, J (1955). “Directed movements and selective adhesion of embryonic amphibian cells.” J. Exp. Zool. 128, 53–120. [DOI] [PubMed] [Google Scholar]
- Ulrich, F, Concha, M L, Heid, P J, Voss, E, Witzel, S, Roehl, H, Tada, M, Wilson, S W, Adams, R J, Soll, D R, and Heisenberg, C P (2003). “Slb∕Wnt11 controls hypoblast cell migration and morphogenesis at the onset of zebrafish gastrulation.” Development 130, 5375–5384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich, F, Krieg, M, Schotz, E M, Link, V, Castanon, I, Schnabel, V, Taubenberger, A, Mueller, D, Puech, P H, and Heisenberg, C P (2005). “Wnt11 functions in gastrulation by controlling cell cohesion through Rab5c and E-cadherin.” Dev. Cell 9, 555–564. [DOI] [PubMed] [Google Scholar]
- von der Hardt, S, Bakkers, J, Inbal, A, Carvalho, L, Solnica-Krezel, L, Heisenberg, C P, and Hammerschmidt, M (2007). “The Bmp gradient of the zebrafish gastrula guides migrating lateral cells by regulating cell-cell adhesion.” Curr. Biol. 17, 475–487. [DOI] [PubMed] [Google Scholar]
- Warga, R M, and Kimmel, C B (1990). “Cell movements during epiboly and gastrulation in zebrafish.” Development 108, 569–580. [DOI] [PubMed] [Google Scholar]
- Warga, R M, and Nusslein-Volhard, C (1999). “Origin and development of the zebrafish endoderm.” Development 126, 827–838. [DOI] [PubMed] [Google Scholar]
- Winklbauer, R, and Keller, R E (1996). “Fibronectin, mesoderm migration, and gastrulation in Xenopus.” Dev. Biol. 177, 413–426. [DOI] [PubMed] [Google Scholar]
- Wiseman, L L, Steinberg, M S, and Phillips, H M (1972). “Experimental modulation of intercellular cohesiveness: reversal of tissue assembly patterns.” Dev. Biol. 28, 498–517. [DOI] [PubMed] [Google Scholar]