Abstract
The expulsion of material from a cell by fusion of vesicles at the plasma membrane, and the entry of a virus by membrane invagination are complex membrane-associated processes whose control is crucial to cell survival. Our ability to visualize the dynamics of such processes experimentally is limited by spatial resolution and the speed of molecular rearrangements. The increase in computing power of the last few decades enables the construction of computational tools for observing cellular processes in silico. As experiments yield increasing amounts of data on the protein and lipid constituents of the cell, computer simulations parametrized using this data are beginning to allow models of cellular processes to be interrogated in ways unavailable in the laboratory. Mesoscopic simulations retain only those molecular features that are believed to be relevant to the processes of interest. This allows the dynamics of spatially heterogeneous membranes and the crowded cytoplasmic environment to be followed at a modest computational cost. The price for such power is that the atomic detail of the constituents is much lower than in atomistic Molecular Dynamics simulations. We argue that this price is worth paying because mesoscopic simulations can generate new insight into the complex, dynamic life of a cell.
Cells have to manage their functions across a wide range of length and time scales, and cope with thermal and chemical fluctuations in a changing environment. Yet they also have to tightly regulate the spatio-temporal occurrence of processes such as cell division and endo- and exocytosis. Our ability to observe and interrogate a cell to understand how it carries out its myriad functions is limited by experimental resolution, and also by the limits of our intuition, which is largely developed from events in the everyday, macroscopic world. Complementary to experiments, computer simulations provide an integrative language for embodying our understanding of cellular processes that can be probed in ways that are experimentally inaccessible. Although limited by the accuracy of the chosen simulation technique, and by our ability to identify all the relevant details for the system under examination, computer simulations have progressed to the point where they can be used to test hypotheses about biophysical processes in a quantitative manner.
The most accurate, and time consuming, particle-based simulation method is all-atom molecular dynamics (MD). The use of complex, carefully tuned force fields allows MD to capture the atomic interactions between molecules (Allen and Tildesley, 1987), and it is widely used for simulating drug molecules binding to receptors. But the computational resources required for such accuracy are high, and they are limited to processes that occur on scales of tens of nanometers (Ohta-lino et al., 2001; Knecht and Marrink, 2007) and perhaps tens of nanoseconds. At the other extreme, on length scales much larger than the molecular and for times long enough that molecular species can freely diffuse to all parts of a system, sets of ordinary differential equations are used (Kholodenko, 2006) to model biochemical reactions that obey the law of mass action. Partial differential equations (PDEs) can be used to include a degree of spatial dependence, allowing molecules to diffuse around, but are unable to handle small numbers of molecules and complex spatial structure. The cytoplasm is a crowded space that strongly modifies protein behavior from that exhibited in vitro (Takahashi et al., 2005; Ridgway et al., 2006). Many of the cell’s functions take place in or near convoluted, membrane-bound compartments, and involve only a few copies of some molecules whose diffusion times are not negligible compared to their reaction rates. The influence on protein signaling of spatial gradients caused by the slow diffusion of molecules is recognized in recent calculations (Kholodenko et al., 2000; Bhalla, 2004a, 2004b), but is difficult to capture in continuum methods. This has driven the development of a novel class of simulation techniques: so-called mesoscopic simulations.
As their name implies, mesoscopic simulations are designed to model phenomena that occur between the molecular scale of lipids and the micron scale of the cell, and to follow their evolution for milliseconds or longer. They achieve this feat by reducing the degrees of freedom that must be evolved in time, thereby coarse graining the molecular entities in the model, and increasing the time over which the simulation can maintain an accurate portrayal of the system’s dynamics. There is no unique way of coarse graining a molecular model, and various techniques have been developed. These are discussed in detail in several recent reviews of mesoscopic simulations applied to soft matter, and, in particular, amphiphilic membranes (Müller et al., 2006;Venturoli et al., 2006) and vesicle fusion (Shillcock and Lipowsky, 2006). All the methods attempt to keep only those properties of molecules that influence their collective behavior on long length and time scales, for example, the amphiphilic nature of lipids. The methods differ in their representation of these key properties and the degree to which the coarse graining of degrees of freedom is carried.
Coarse-grained MD is most closely derived from atomistic MD, and has been successfully used to study biological problems such as the fusion of small vesicles (Stevens et al., 2003; Marrink and Mark, 2003; Kasson et al., 2006) and the opposite process, their fission (Markvoort et al., 2007). It is typically an explicit-solvent method (but not always, as Reynwar et al. (2007) illustrates) because the water molecules that form the bulk of any biological system are retained, but several molecules or molecular groups are combined into single particles, so that a lipid molecule containing more than 100 atoms is often represented by a computational lipid containing only 11 particles that, at a minimum, consist of only two types: hydrophilic head particles, and hydrophobic tail particles. The particles possess a hard-core repulsive force to prevent their overlap, and this requires a small time step to be used for integrating the equations of motion. It is consequently computationally demanding, and is currently infeasible for system sizes beyond a few tens of nanometers and durations longer than a few microseconds. Dissipative particle dynamics (DPD) is another explicit solvent method (Groot and Warren, 1997), but it goes further in coarse graining the molecular degrees of freedom. It integrates out the small length-scale (<1 nm) bond fluctuations and atomic coordinates within molecules, so that a DPD particle represents a small sphere of material. A water particle may represent three water molecules, and the linear 16-methyl hydrocarbon chains of a dimyristoyl phosphatidylcholine lipid may be represented by only three or four DPD tail particles each. The forces between DPD particles do not possess the hard-core repulsion used in coarse-grained MD, and so a larger time step can be used in the equations of motion that increases the temporal range of the method. Brownian dynamics (BD) can be used to simulate larger length and time scales than explicit-solvent methods because it replaces the solvent particles by implicit forces that mimic the self-assembling property of amphiphilic molecules in water (Noguchi and Takasu, 2001). Eliminating the solvent degrees of freedom means that BD can simulate processes up to seconds and, depending on the number of molecular species being modeled, micron-sized regions of space. The lack of solvent, however, requires complex forces to be used to account for the hydrophobic effect and the propagation of hydrodynamic forces that are mediated by the solvent. Other solvent-free methods also exist, and have recently been used to study the vesiculation of a membrane induced by embedded curvature-inducing inclusions (Reynwar et al., 2007).
Probably the most studied biological application of these techniques is the lipid bilayer membrane. An encouraging result found by Venturoli et al. (2006) on comparing different simulation types is that the properties of the model lipid membranes are quite consistent regardless of the type of mesoscopic simulation method used. This suggests that the models are able to capture the collective properties of the membrane systems relevant to the length and time scales of interest in biology.
The most common cartoon of lipid membranes is drawn from the “fluid mosaic model” of Singer and Nicolson (1972), and appears to show a laterally uniform “sea” of lipids in which float widely separated proteins. Much experimental work since then has revealed that this is an over simplification, and that the plasma membrane is more heterogeneous and crowded than the cartoon suggests (Engelman, 2005). In parallel to this, mesoscopic simulations have progressed from measuring the equilibrium properties of model lipid membranes, containing only one or two species of amphiphile, and are now being used to follow dynamic processes such as vesicle fusion. Significantly, the molecular rearrangements that occur in the simulations when two vesicles, or a vesicle and a planar membrane, fuse appear to be largely independent of the specific simulation type. Similar behavior is seen in coarse-grained molecular dynamics simulations (Marrink and Mark, 2003; Stevens et al., 2003), Monte Carlo simulations (Müller et al., 2003), brownian dynamics (Noguchi and Takasu, 2001), and dissipative particle dynamics (Shillcock and Lipowsky, 2005; Grafmüller et al., 2007). Equally significantly, lipid rearrangements are observed during the formation of a fusion pore in particle-based simulations that cannot be represented in continuum theoretical models that treat membranes as thin elastic sheets (Efrat et al., 2007; Chernomordik and Kozlov, 2003). Two examples are the splayed tails of lipid molecules in which one hydrocarbon chain is embedded in each of the apposed fusing membranes (Ohta-lino et al., 2001), and the observation of a wide distribution of times required for lipid flip-flop from one membrane to the other across the intervening water gap (Grafmüller et al., 2007). Such simulations can test our understanding of the mathematical models constructed to explain biological phenomena. These models are often created using our intuition about the forces or structures that most influence a given process. Because our intuition is largely derived from the macroscopic world, it is not necessarily directly applicable to the world of the cell; a world that possesses properties and forces that are quite different from anything encountered in our everyday life (Jones, 2004). Two examples may help illustrate this.
Although the interior of a cell is very crowded, the lipids, proteins and other molecules all perform an erratic dance throughout the space available to them that is caused by the continual buffeting of surrounding solvent molecules. This is known as Brownian motion, and results from the thermal energy that all molecules possess at physiological temperatures. Many processes in the cell consume energy obtained from the hydrolysis of Adenosine triphosphate (ATP) molecules. Specialized organelles called mitochondria are responsible for producing ATP, but unlike in our world, where fuel has to be packaged and carried to where it is needed, the ATP molecules are simply released into the cytoplasm. Brownian motion then ensures that the molecules rapidly diffuse throughout the cell.
Second, lipids, and other amphiphilic molecules spontaneously self-assemble into complex structures such as two-dimensional membranes; and two proteins can orient and reorient themselves, rapidly probing their mutual interactions until they find their preferred state, and then bind into a unique structure. This ability to explore rapidly many distinct configurations, and to locate the one that minimises their free energy, also derives from Brownian motion, but their self-assembly is a consequence of the molecular nature of the molecules. Lipids are amphiphiles, possessing a water-loving or hydrophilic headgroup chemically bound to water-hating or hydrophobic tails. The oily nature of their tails drives them to segregate themselves from the surrounding solvent, and adopt the typical structures observed: micelles, bilayers and vesicles. Proteins possess surface patches that make them “sticky,” and two proteins can bind weakly or strongly depending on the number of patches that can simultaneously be touching and the degree to which the three-dimensional shapes of their surfaces match.
This combination of continual random motion and self-assembly allows the cell to carry out many functions in ways that would not work at the macroscale. A cell contains many distinct organelles that each have their own purpose. These organelles must be constructed and maintained, and material must be passed from one to another. But the cell does not always control precisely how material is transported, but leaves it to the vagaries of Brownian motion to deliver it where it is needed. It may require many attempts before two proteins bind as they move and reorient about each other. This leads to a temporal uncertainty in the ordering of events that is uncommon in the macroscopic world of cars and planes. (Of course, cells also use directed motion; and molecular motors ensure the efficient delivery of material across micron-sized distances by traversing along actin filaments or microtubules. But this is not the only form of transport available to them.) The chemical reactions that occur in cells sometimes involve many hundreds of molecules, as when biochemical reactions consume ATP molecules that are diffusing through the cytoplasm, but may also include only a few copies of a key molecule, such as a gene transcription molecule. The inevitable fluctuations in the position and concentration of these molecules is another complex feature of the cytoplasmic environment. How a cell regulates its functions in the presence of the stochastic motion of small numbers of molecules is still a mystery. Mesoscopic simulations are already able to shed light on aspects of this puzzle.
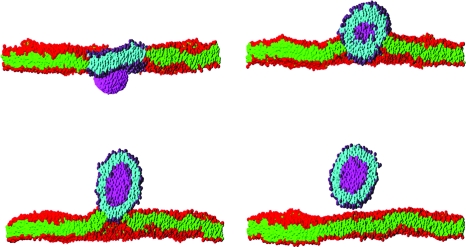
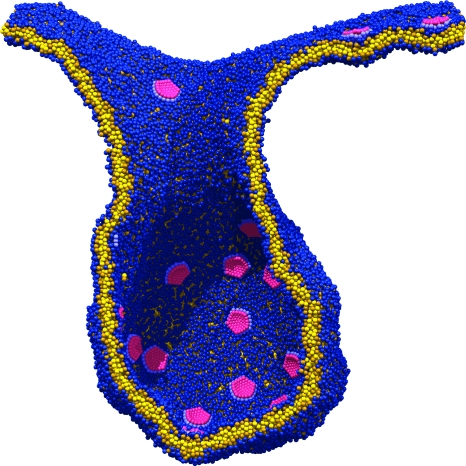
Considerable success has been achieved in the modeling of lipid membranes as discussed in the reviews of Müller et al. (2006), Shillcock and Lipowsky (2006) and Venturoli et al. (2006). The first steps toward including peptides into the models have been taken (Srinivas et al., 2004; Venturoli et al., 2006). A simple model of chemical reactions in DPD is described in Bedau et al. (2006), where the ligation of monomers to form polymers is demonstrated. It is possible to construct a spatially heterogeneous model of regions of a cell via the sculpting of membranes into crypts and invaginations, and to study the interactions of coarse-grained representations of proteins or nanoparticles with membranes (Shillcock and Lipowsky, 2007; Smith et al., 2007). Figure 1 shows four snapshots taken from an explicit-solvent DPD simulation of an elliptical nanoparticle translocating across a lipid membrane. The process is driven by the adhesion energy of the particle binding to the circular patch of lipid within the larger membrane acting together with the line tension around the patch. Such simulations may be useful in exploring the interaction of novel nanoparticles with cell membranes, a process important in determining their toxicity. Rigid, spherical-cap inclusions embedded in a fluid membrane simulated with solvent-free, coarse-grained MD (Reynwar et al., 2007) are able to induce membrane curvature resulting in membrane invagination as shown in Fig. 2, a process that is used by some viruses to infect cells.
Figure 1. Sequence of snapshots of a cross section through a rigid nanoparticle (magenta) translocating across a planar lipid bilayer membrane immersed in solvent (invisible for clarity).
The times of the snapshots are 130 ns, 650 ns, 1.3 μs and 2.8 μs labeled top to bottom by row. The membrane contains 7973 lipids and spans the 50×50 nm2 simulation box. It initially contains a circular patch of 480 molecules of one lipid type (purple headgroups and cyan tails) surrounded by 7493 of the second lipid type (red headgroups and green tails). Both types have identical molecular architecture, but their interactions are chosen so that they phase separate in the membrane. The nanoparticle has approximate dimensions 8×6×6 nm3, and its interactions are chosen so that it prefers to adhere to the patch lipid headgroups rather than the other lipid type. The combination of the adhesion of the nanoparticle to the patch, which induces it to curve, and the line tension of the patch boundary drives the translocation process. The snapshots are taken from a dissipative particle dynamics simulation of the author, and are rendered using the PovRay software (www.povray.org).
Figure 2. A cross section through a membrane invagination driven by the presence of rigid inclusions.
The membrane contains approximately 45,000 lipids and 36 inclusions. The inclusions are spherical caps that induce a local membrane curvature resulting in their aggregation. (Adapted by permission from Macmillan Publishers Limited: Nature447(7143):461–4 (2007), with the permission of M Deserno.)
Physical effects, such as diffusion in confined spaces or in two-dimensional membranes, membrane curvature, and protein crowding are important in biological processes. The self-assembly of syntaxin molecules in the plasma membrane plays a key role in preparing for exocytosis (Sieber et al., 2007; White, 2007), and may be a paradigm for other trans-membrane proteins, such as receptors, that form clusters. The self-assembly of syntaxin clusters and the exchange of freely diffusing molecules between them have been simulated using BD, and are in excellent agreement with fluorescence recovery after photobleaching (FRAP) experiments (Sieber et al., 2007). The simulations also agree with experimental observations that the over-expression of syntaxin leads to more clusters rather than increasing the cluster size, a result that depends on the clustered syntaxin molecules adopting a branch-like structure instead of a linear cylindrical shape. The vesicle-localized SNARE protein synaptotagmin inserts two domains into the target membrane on receipt of a calcium signal, inducing a high positive curvature that bends the membrane toward the vesicle and promotes fusion (Martens et al., 2007). Mesoscopic simulations of vesicle fusion had previously shown that bending two membranes towards each other, and locally raising the tension within the bent region, yielded fusion in a reproducible manner (Shillcock and Lipowsky, 2006). These examples show that biological processes on length scales around 100 nm can be quantitatively explored using simulations. But because different techniques are best suited to different length and time scales, we anticipate that a computational solution that can be scaled up to cellular size requires a combination of techniques to enable it to capture the relevant processes at all intermediate levels. The enormity of this task is made clear by considering a few relevant numbers.
A typical cell has a diameter of the order of 10 μm, cellular processes can take seconds or minutes to occur. Taking 1 nm as a typical molecular length scale, and 1 ns as a typical molecular time scale, the cell contains approximately 1012 volumes of 1 nm3. A 1 s simulation of such a cell that retained atomistic detail would generate 1021 molecular configurations per second. Such enormous data sets are impossible to manage, and even if they could be stored, their analysis would defy comprehension. Mesoscopic simulations reduce the size of these data sets by storing only data in the length and time scales of the process of interest. Up to the scale of 100 nm, explicit solvent methods, such as coarse-grained MD or DPD, capture the solvent-mediated forces relevant to membrane fluctuations and the topology-changing processes of fusion and budding. At longer length scales of 1 μm or so, Brownian Dynamics can be used to model vesicle transport, and at the length scale of the cell, continuous methods using PDEs can be parametrized using data obtained from the lower scales. In this way, a combination of simulation types can propagate data obtained from smaller scales to longer scales.
Limitations of particle-based simulations are apparent in two areas. First, as the modeled systems increase to the length scale of the cell, the memory and CPU time requirements of explicit-solvent methods grow enormously. The DPD and BD simulations described in this article represent systems of 50–100 nm in size, and can be run on a single processor of a Xeon-class personal computer, whereas coarse-grained MD simulations frequently require a small cluster. Future simulations of processes on length scales larger than 100 nm will require more processing power and, almost certainly, parallel implementations of the simulation methods. Second, and more importantly, the insight needed to identify and represent the relevant properties of the molecules involved in a computational model, and the quality of the experimental data used to calibrate the model’s parameters, limit the phenomena that can be accurately simulated. Even a simple lipid-water simulation involving two species of lipid has more than ten interaction parameters whose inter-relationships are important for describing the behavior of the self-assembled membranes (Laradji and Kumar, 2005; Illya et al., 2006). As the number of molecular species grows, the number of such parameters increases as their square, together with more data needed to specify the concentration and distribution of the species. This highlights the need for an interdisciplinary approach to the computational modeling of biological systems; bringing together the biologists with their detailed knowledge of the system of interest and the physicists and computer scientists who have the simulation experience to convert the biological information into a computational model.
Although still in their infancy, simulation tools that can continuously pass time-dependent “measurements” of the cell’s internal state at one length and time scale to a higher-level model that extrapolates it to longer length and time scales will yield insight into cellular processes on many scales from the molecular to the cellular. As well as being used to test hypotheses about cellular function, and to complement theoretical models, such tools can also convey the beauty of cellular behavior, thereby helping to inspire students to explore the overlap of biology, physics and computing. Similar to a well-planned experiment, they can probe our understanding of the interactions between the experimental consituents, lead to further questions about the details of these interactions, and they may reveal unexpected results that lead us onto new paths of research. Carefully designed, multi-scale simulations will provide the cheapest means to interrogate complex biological systems in ways that now seem far fetched, but which will become commonplace in years to come.
ACKNOWLEDGMENTS
The author gratefully acknowledges funding from the Danish Research Foundation, and computer time provided by the Danish Centre for Scientific Computing, and thanks Markus Deserno for providing the image shown in Fig. 2. A critical reading of the manuscript by John Ipsen and Gary Schoenhals is also appreciated. The author is the founder of a start-up company that provides commercial contract research using mesoscopic simulation techniques.
References
- Allen, M P, and Tildesley, D J (1987). Computer Simulation of Liquids, Oxford Science Publications, OUP, Oxford, UK. [Google Scholar]
- Bedau, M A, Buchanan, A, Gazzola, G, Hanczyc, M, Maeke, T, McCaskill, J, Poli, I, and Packard, N H (2006). “Evolutionary design of a DDPD model of ligation.” In Lecture Notes in Computer Science, Talbi E.et al. , (eds), Vol 3871, pp 201–212, Springer, Berlin, Germany. [Google Scholar]
- Bhalla, U (2004a). “Signaling in small subcellular volumes. 1. Stochastic and diffusion effects on individual pathways.” Biophys. J. 10.1529/biophysj.104.040469 87, 733–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhalla, U (2004b). “Signaling in small subcellular volumes. 2. Stochastic and diffusion effects on synaptic network properties.” Biophys. J. 10.1529/biophysj.104.040501 87, 745–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernomordik, L V, and Kozlov, M M (2003). “Protein-lipid interplay in fusion and fission of biological membranes.” Annu. Rev. Biochem. 10.1146/annurev.biochem.72.121801.161504 72, 175–207. [DOI] [PubMed] [Google Scholar]
- Efrat, A, Chernomordik, L V, and Kozlov, M M (2007). “Point-like protrusion as a prestalk intermediate in membrane fusion pathway.” Biophys. J. 10.1529/biophysj.106.103341 92, L61–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelman, D M (2005). “Membranes are more mosaic than fluid.” Nature (London) 10.1038/nature04394 438, 578–580. [DOI] [PubMed] [Google Scholar]
- Grafmüller, A, Shillcock, J C, and Lipowsky, R (2007). “Pathway of membrane fusion with two tension-dependent energy barriers.” Phys. Rev. Lett. 10.1103/PhysRevLett.98.218101 98, 218101(1-4). [DOI] [PubMed] [Google Scholar]
- Groot, R, and Warren, P B (1997). “Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation.” J. Chem. Phys. 10.1063/1.474784 107, 4423–4435. [DOI] [Google Scholar]
- Illya, G, Lipowsky, R, and Shillcock, J C (2006). “Two-component membrane material properties and domain formation from dissipative particle dynamics.” J. Chem. Phys. 10.1063/1.2353114 125, 114710 (1–9). [DOI] [PubMed] [Google Scholar]
- Jones, R AL (2004) Soft Machines: Nanotechnology and Life, OUP, Oxford, UK. [Google Scholar]
- Kasson, P M, Kelley, N W, Singhal, N, Vrljic, M, Brunger, A T, and Pande, V S (2006). “Ensemble molecular dynamics yields submillisecond kinetics and intermediates of membrane fusion.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0601597103 103, 11916–11921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kholodenko, B N (2006). “Cell-signaling dynamics in time and space.” Nat. Rev. Mol. Cell Biol. 7, 165–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kholodenko, B N, Brown, G C, and Hoek, J B (2000). “Diffusion control of protein phosphorylation in signal transduction pathways.” Biochem. J. 10.1042/0264-6021:3500901 350, 901–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knecht, V, and Marrink, S J (2007). “Molecular dynamics simulations of lipid vesicle fusion in atomic detail.” Biophys. J. 10.1529/biophysj.106.103572 92, 4254–4261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laradji, M, and Kumar, P BS (2005). “Domain growth, budding, and fission in phase-separating self-assembled fluid bilayers.” J. Chem. Phys. 10.1063/1.2102894 123, 224902 (1–10). [DOI] [PubMed] [Google Scholar]
- Markvoort, A J, Smeijers, A F, Pieterse, K, van Santen, R A, and Hilbers, P AJ (2007). “Lipid-based mechanisms for vesicle fission.” J. Phys. Chem. B 10.1021/jp068277u 111, 5719–5725. [DOI] [PubMed] [Google Scholar]
- Marrink, S J, and Mark, A E (2003). “The mechanism of vesicle fusion as revealed by molecular dynamics simulations.” JACS 125, 11144–11145. [DOI] [PubMed] [Google Scholar]
- Martens, S, Kozlov, M M, and McMahon, H T (2007). “How synaptotagmin promotes membrane fusion.” Science 10.1126/science.1142614 316, 1205–1208. [DOI] [PubMed] [Google Scholar]
- Müller, M, Katsov, K, and Schick, M (2003). “A new mechanism of model membrane fusion determined from Monte Carlo simulation.” Biophys. J. 85, 1611–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller, M, Katsov, K, and Schick, M (2006). “Biological and synthetic membranes: what can be learned from a coarse-grained description?” Phys. Rep. 10.1016/j.physrep.2006.08.003 434, 113–176. [DOI] [Google Scholar]
- Noguchi, H, and Takasu, M (2001). “Fusion pathways of vesicles: a Brownian dynamics simulation.” J. Chem. Phys. 10.1063/1.1414314 115, 9547–9551. [DOI] [Google Scholar]
- Ohta-lino, S, Pasenkiewicz-Gierula, M, Takaoka, Y, Miyagawa, H, Kitamura, K, and Kusumi, A (2001). “Fast lipid disorientation at the onset of membrane fusion revealed by molecular dynamics simulations.” Biophys. J. 81, 217–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynwar, B J, Illya, G, Harmandaris, V A, Müller, M M, Kremer, K, and Deserno, M (2007). “Aggregation and vesiculation of membrane proteins by curvature-mediated interactions.” Nature (London) 10.1038/nature05840 447, 461–464. [DOI] [PubMed] [Google Scholar]
- Ridgway, D, Broderick, G, and Ellison, M J (2006). “Accommodating space, time and randomness in network simulation.” Curr. Opin. Biotechnol. 10.1016/j.copbio.2006.08.004 17, 493–498. [DOI] [PubMed] [Google Scholar]
- Shillcock, J C, and Lipowsky, R (2005). “Tension-induced fusion of bilayer membranes and vesicles.” Nat. Mater. 10.1038/nmat1333 4, 225–228. [DOI] [PubMed] [Google Scholar]
- Shillcock, J C, and Lipowsky, R (2006). “The computational route from bilayer membranes to vesicle fusion.” J. Phys.: Condens. Matter 10.1088/0953-8984/18/28/S06 18, S1191–S1219. [DOI] [PubMed] [Google Scholar]
- Shillcock, J C, and Lipowsky, R (2007). “Visualizing soft matter: mesoscopic simulations of membranes, vesicles and nanoparticles.” Biophys. Rev. Lett. 2, 33–55. [Google Scholar]
- Sieber, J J, Willig, K I, Kutzner, C, Gerding-Reimers, C, Harke, B, Donnert, G, Rammner, B, Eggeling, C, Hell, S W, Grubmüller, H, and Lang, T (2007). “Anatomy and dynamics of a supramolecular membrane protein cluster.” Science 10.1126/science.1141727 317, 1072–1076. [DOI] [PubMed] [Google Scholar]
- Singer, S J, and Nicolson, G L (1972). “The fluid mosaic model of the structure of cell membranes.” Science 10.1126/science.175.4023.720 175, 720–731. [DOI] [PubMed] [Google Scholar]
- Smith, K, Jasnow, D, and Balazs, A C (2007). “Designing synthetic vesicles that engulf nanoscopic particles.” J. Chem. Phys. 10.1063/1.2766953 127, 084703 (1–10). [DOI] [PubMed] [Google Scholar]
- Srinivas, G, Lopez, C F, and Klein, M L (2004). “Membrane bound hydraphiles facilitate cation translocation.” J. Phys. Chem. B 10.1021/jp036953b108, 4231–4235. [DOI] [Google Scholar]
- Stevens, M J, Hoh, J H, and Woolf, T B (2003). “Insights into the molecular mechanism of membrane fusion from simulation: evidence for the associated of splayed tails.” Phys. Rev. Lett. 10.1103/PhysRevLett.91.188102 91, 188102 (1–4). [DOI] [PubMed] [Google Scholar]
- Takahashi, K, Arjunan, S NV, and Tomita, M (2005). “Space in systems biology of signaling pathways—towards intracellular molecular crowding in silico.” FEBS Lett. 10.1016/j.febslet.2005.01.072 579, 1783–1788. [DOI] [PubMed] [Google Scholar]
- Venturoli, M, Sperotto, M M, Kranenburg, M, and Smit, B (2006). “Mesoscopic models of biological membranes.” Phys. Rep. 10.1016/j.physrep.2006.07.006 437, 1–54. [DOI] [Google Scholar]
- White, S H (2007). “Crowds of syntaxins.” Science 10.1126/science.1148010 317, 1045–1046. [DOI] [PubMed] [Google Scholar]