Functional reorganization in thalamocortical networks: Transition between spindling and delta sleep rhythms

Abstract

Thalamic reticularis, thalamocortical, and cortical cells participate in the 7–14-hz spindling rhythm of early sleep and the slower delta rhythms of deeper sleep, with different firing patterns. In this case study, showing the interactions of intrinsic and synaptic properties, a change in the conductance of one kind of cell effectively rewires the thalamocortical circuit, leading to the transition from the spindling to the delta rhythm. The two rhythms make different uses of the fast (GABA_A) and slow (GABA_B) inhibition generated by the thalamic reticularis cells.

The thalamus is centrally important in the generation of sleep rhythms, such as spindling in early sleep and the delta rhythm in deeper sleep (1–3). It has also been implicated in the generation of other rhythms, as in epilepsy (1, 2), Parkinson tremor (4), and 40 hz oscillations (2, 5). The frequencies involved in these rhythms vary over two orders of magnitude, and their spatial occurrence varies from quite localized to very widespread in the nervous system (5).

Thus, the same body of neurons participates in a variety of rhythms, in addition to their less generalized rhythmic activity during wakefulness. Much has been written about the changes in thalamic cells that accompany the transition between sleep and wakefulness (see refs. 1 and 2 for references). The focus of this paper is on a transition between two rhythmic states, corresponding to two stages of sleep. The larger theme underlying the paper is the “functional reorganization” of a network, allowing the same collection of neurons to exhibit different behaviors. (See refs. 6 and 7 for examples of this theme in the context of invertebrate networks.) In a model we show the different behaviors that are produced as a result of the different uses of inhibition in the system, which itself comes from a change of functional connectivity induced by changes in intrinsic properties of a class of participating neurons.

The behavior we wish to clarify is summarized in ref. 2 as follows: In early sleep, the thalamus exhibits “spindle pockets,” in which 7–14-hz oscillations wax and wane with a duration of 1–3 sec. In deeper sleep, it expresses a more clock-like rhythmicity at the delta frequency of 1–4 hz. [We distinguish this form of the delta rhythm from that produced entirely by the cortex in the absence of thalamic connections (8)]. In these rhythms at least three sets of neurons participate; the thalamic reticular (RE) neurons, the thalamocortical (TC) neurons, and cortical cells. In the two different rhythms (spindling and delta), the behavior of individual cells, as well as the population frequency, is different. During a spindle pocket, an RE cell bursts at 7–14 hz; the TC cells are phase-locked when they fire, but fire only once every several cycles of the population rhythm; thus, the frequency of an individual TC cell is closer to the delta range (though not as regular as during deep sleep). In intact-cortex animals, the initiation of spindle sequences in the thalamus is potentiated by the slow cortical oscillation, at less than 1 hz (8), but spindles can also occur in the absence of cortical input (9). During delta, the population rhythm is very regular. Each TC cell fires a number of times at this population rhythm, then has subthreshold oscillations for a number of cycles, and is periodically revived within the frequency range of the slow rhythm. The RE cells fire less often, at the frequency of and phase-locked to the slow cortical rhythm.

Our model addresses the question of how the same groups of cells might produce these very different rhythms. Through the work of Steriade and others (1, 10), it is known that the TC cells are competent to oscillate in the delta range at appropriate voltage ranges. Nevertheless, there are subtle points associated with the conditions under which these oscillations can synchronize to produce population rhythms in specified ranges. Those conditions involve network properties as well as intrinsic properties of the participating cells. The ideas in this paper build on those of Steriade and colleagues (11, 12) on the role of the cortex in the synchronization of thalamic rhythms, as well as the work of Rinzel and collaborators (13–15) on the role of inhibitory time constants in network behavior.

It is known that the transition from the awake state to drowsiness is accompanied by hyperpolarization of the TC cells due to changes in excitatory inputs (16). This hyperpolarization acts to de-inactivate a low-threshold calcium current and turn on a hyperpolarization-activated mixed-cation inward current (1). These changes are sufficient to turn an isolated TC cell into one that oscillates at a frequency close to delta (1, 10). In the transition from waking to spindling, it is known that there is an increase in leak conductance in both the TC and RE neurons (17). Furthermore, an increase in hyperpolarizing current to a TC cell increases the number of cycles (at delta frequency) that can be elicited in the TC cell by cortical stimulation (10). Together these data suggest that the transition from the spindling rhythm to the delta rhythm might be induced simply by further hyperpolarization of the TC cells (1, 10). Our results suggest that there must be changes in functional network configuration in order for delta rhythm to appear at the network level. The major change is the removal of some of the effects of the inhibitory RE neurons, which act on the TC population to create a rhythm at a higher frequency than the delta rhythm, even when each TC cell is competent to oscillate at the delta frequency.

Synchrony, Clustering, and Sleep Rhythms

In this section we describe the mathematical ideas that underlie the simulations of this paper. The key points concern the role of time constants associated with the onset and offset of inhibition in producing population oscillations in networks of inhibitory cells, or excitatory and inhibitory cells. These ideas apply to the excitatory TC population and the inhibitory RE population.

It is well known that a pair of cells coupled by mutual inhibition can produce oscillations in which the cells are in antiphase (see refs. 15, 18, and 19 for further references). However, inhibition is also capable of synchronizing cells. The analysis of simple models (20, 21) shows that instantaneously acting synapses cannot produce synchrony, but those with finite onset time can do so. Simulations of more biophysically based models (13) reveal that a sufficiently long decay time of the inhibition is also necessary for a stable synchronous solution. Recent analyses of Terman et al. (D.T., N.K., and A.B., unpublished work) confirm and clarify these observations, showing that the onset time of the inhibition governs the size of the basin of attraction of the synchronous solution. Furthermore, in a range of decay times for the inhibition, the decaying inhibition can act to phaselock cells receiving that common inhibition, even though the cells have somewhat different natural dynamics.

The models for two cells that inhibit each other have implications for networks in which some cells inhibit each other, or in which some population receives input from a set of inhibitory cells. In a standard behavior of such networks, seen in simulations (14, 15, 22, 23), the population receiving the inhibition breaks into “clusters” of cells that are out of phase with respect to one another; within a cluster, the cells are synchronous. Clustering can occur robustly and stably when the synchronized solution is unstable or if its domain of attraction is small.

We now consider the relevance of these ideas to the sleep patterns. It is known that the TC cells receive both fast onset/fast offset (GABA_A) and slow onset/slow offset (GABA_B) inhibition from the RE cells. In intact-cortex animals, the TC cells oscillate essentially synchronously (before they damp out) when the cortex is set into action; the frequency of the population is in the range of that of an individual TC cell. By contrast, the population behavior in spindling is that of clustering; individual cells participate once every several cycles, and the population rhythm is several times that of an individual TC cell. (For effects due to local coupling see refs. 24 and 25.)

The ideas outlined above suggest that the spindling rhythm is a consequence of the action of the GABA_A inhibition, which acts to either prevent synchrony of the TC population or make it occur for a very small range of initial conditions (3, 15). They further suggest that the transition to the delta rhythm requires that the effects of this inhibition be removed from the network. This does not require that the inhibition itself be removed, and the model given in the next section demonstrates the transition without making any changes in the inhibitory or excitatory synapses. Rather, changes in intrinsic properties of the RE cells, which receive only excitation in the minimal model, indirectly change the way in which inhibition is used within the network, leading to a situation in which synchrony of the TC cells is possible.

The central idea of this “functional reorganization” is that some alterations of the RE cells can make them insensitive to the cycle by cycle excitation produced by the TC cells. If the RE cells do not respond to that excitation, they are functionally absent from the network, except when input from another area (cortex) causes them to fire (Fig. 1). If the RE cells produce both GABA_A and GABA_B inhibition, then the fast inhibition decays rapidly (within one cycle), leaving only the slow inhibition acting within the network. The absence of the fast inhibition (after the first cycle) creates the preconditions for synchronization, whereas the continuing presence of the slowly decaying inhibition helps to synchronize the cells receiving that inhibition.

Figure 1.

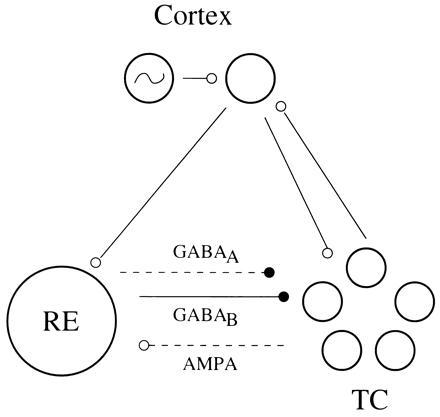
Schematic of the functional connectivity of the network in our model. The TC cells receive fast and slow inhibition from the RE cells and excitation from the cortex; the RE cells receive excitation from the TC cells and the cortex. The broken lines reflect the fact that, when the intrinsic properties of the RE cells are changed to make them less sensitive to excitation, the excitatory TC to RE connection and the fast inhibition to the TC cells are functionally removed (though the synapses are not changed).

A Minimal Network

To demonstrate these ideas, we go to a biophysically and anatomically minimal model of spindling and delta. The simulated network consists of a population of one RE cell, a population of 10 TC cells, and a single oscillator representing cortical output during slow wave activity (see Fig. 1). The lumping of the RE cells into a single entity is motivated by the synchrony of the RE cells in each of the rhythms, though their frequencies and network interactions are different in the two rhythms. Thus, this minimal model focuses on the synchronization properties of the TC cells. The RE cell has excitatory inputs from the TC cells and the cortex. The TC cells have excitatory input from the cortex and inhibitory input from the RE cell. The TC cells are not given connections to one another. The cortex receives input from the TC cells (see Fig. 1).

The RE and TC cells are described by sets of voltage-gated conductance equations, with equations closely related to those introduced by Golomb et al. (14, 15) to study RE–TC interactions in the production of spindling. (See appendix for more details.) In these studies, the RE cells are given ionic conductances for an inward low-threshold calcium current (I_T), a long-lasting outward (AHP) current, and one or two leak currents. The TC cells have the ionic currents I_T, the two leaks, and a hyperpolarization-induced inward current (I_h). These currents are shown (15) to be sufficient to produce a population rhythm in the spindling range. Sustained inhibition is needed to de-inactivate I_T in the TC cells; activation requires a less negative voltage, provided by the inward I_h current.

Our parameters were chosen so that, in the absence of synaptic interactions, neither the RE cells nor the TC cells are oscillators. This is consistent with experiments in a ferret thalamic slice preparation that showed that the network was quiescent if both GABA_A and GABA_B inhibition were blocked, or if the (AMPA) α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid synaptic excitation was blocked (ref. 3 and see also ref. 15). The excitatory connections from TC cells to the RE cell are modeled as in refs. 14 and 15, and both fast and slow inhibition from the RE cell to TC cells have been included as in these studies. (See appendix for details.) To allow heterogeneity in the population the conductances for I_h, and the potassium leak in the TC cells and the I_h activation curve, are allowed to vary over the population. The cortex in our simulation consists of two layers, each lumped into a single unit. One of the units generates a simple relaxation oscillator, while the other relays the output of the first unit to the thalamic cells. The TC cells send their output to the second unit; thus, they do not affect the timing in the first unit.

In this biophysically minimal model, the change in intrinsic currents of the RE cell that induces the transition from spindling to delta is an increase in the potassium leak conductance. We emphasize that in a less reduced model, many changes in currents might have the same network effect; the model is not suggesting which currents must be changed, but rather what the effects of those changed currents must be.

Fig. 2 gives a representative simulation. In the left half, we show the output of the cells of the network when the parameters have been chosen to elicit spindling. For the right half, the potassium leak current is increased in the RE cell. Note that before the change, the RE cell fires at each cycle of the population rhythm, whereas each TC cell fires at only a fraction (one-half) of the population cycles. Each TC cell is firing at a delta frequency, while the population frequency is twice as high (spindling range). At the change, the RE cell stops responding to the excitation from the TC cells. The TC cells continue to oscillate for several more cycles, using the slow inhibition from the last RE burst. Note that in the spindling regime, the TC cells are not synchronous; even when they receive a simultaneous pulse from the cortex, the fast inhibition from the RE cell desynchronizes them immediately. In the delta regime, the RE cell fires only with the cortex, removing the cycle-by-cycle fast inhibition from the TC cells and allowing them to synchronize. (Note that the cortex has additional spikes during delta, which reflect the synchrony of the TC population rhythm.) In our model these spikes do not affect the output of the cortex, and hence the ability of the cortex to create synchrony. Hyperpolarization of the TC cells by injected inhibitory current does not create the transition to the delta rhythm (not shown); instead, the TC population continues to break up into clusters, as in spindling.

Figure 2.

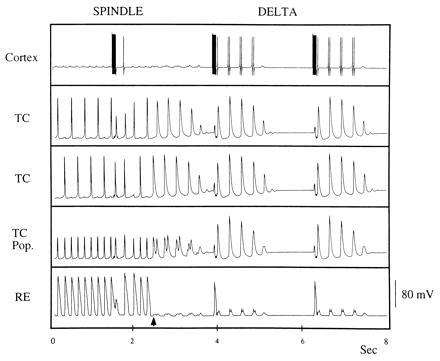
Activity of cortex, two TC cells, the averaged activity of the TC population, and the RE cell in spindling and delta; the change in RE leak conductance from 0.02 to 0.4 is made shortly after 2 sec. The voltage scale is for the TC and RE activity. The number of spikes made by the TC cells during delta can be expanded by increasing the TC leak conductance or decreasing the I_h conductance. Note that during the spindle rhythm, the TC activity is not synchronized and population frequency is spindle frequency, whereas the single cell frequency is much lower. During delta, the TC population is synchronized. The RE cells do not respond to excitation from the TC population, but do respond to the stronger cortical excitation.

Fig. 3 shows a subtle effect of slowly decaying inhibition on a population of TC cells. In this simulation, the 10 TC cells have no interactions with one another, but are provided with common inhibitory input. The TC cells have 10% heterogeneity. (This is important to prevent synchronization during the spindling rhythm due to the common input to the TC cells from the cortex.) The cells are quiescent in the absence of inhibition, so we compare the population behavior with decaying inhibition (Fig. 3A) to that with constant inhibition (Fig. 3B). Because of the heterogeneity, the population getting constant inhibition starts to desynchronize. Decaying inhibition, however, acts to overcome the heterogeneity and keep the population more synchronized. With sufficient heterogeneity, the synchronization can be (approximately) maintained only for a few cycles, even with the cohesive effects of the decaying inhibition, giving a rationale for the damped oscillations seen in the delta rhythm.

Figure 3.

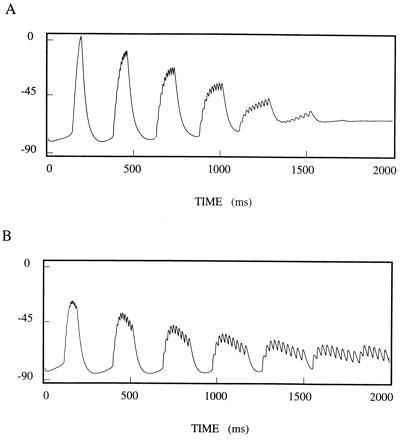
Common inhibitory input can help synchronize unconnected cells if the inhibition decays at appropriate rates. Ten cells with different (but similar) frequencies started synchronously and were allowed to run with (A) common decaying inhibition and (B) common constant inhibition. Traces are voltages averaged over the population. Note that the decaying inhibition keeps the population more synchronous.

In Fig. 4 we have extended the minimal model in two ways and achieved the same results. First, we add a level of complexity in the description of the TC cells to allow them to produce “spindle pockets,” not just ongoing oscillations at the spindle frequency of 7–14 hz. I_h is known to be modulated by many substances (17) that shift its activation curve, providing a different amount of this current at a particular voltage level. I_h is also calcium sensitive (26), with the amount of I_h expressed rising with the concentration of free intracellular calcium. To incorporate waxing and waning in the spindling regime, we follow Destexhe et al. (27), and use the dependence of the conductance on calcium as well as voltage. Because I_T causes a slow increase in the level of calcium over a spindle pocket, influx of calcium increases I_h conductance until the resulting depolarization stops the spindling oscillations by preventing de-inactivation of I_T; a new spindle pocket forms when enough of the calcium has been removed by extrusion or uptake to allow oscillations to start again, and the cortex provides excitation to the RE cells, which in turn provide inhibition to the TC cells (see also refs. 12 and 28). Second, we remove the restriction that all RE cells be synchronous by replacing the single RE cell by three RE cells. (Each TC cell is connected to one RE cell; each RE cell is connected to five TC cells and receives both GABA_A and GABA_B inhibition from the other RE cells.) Note that the TC cells again fire at a fraction of the population cycles, this time with a less precise rhythm.

Figure 4.

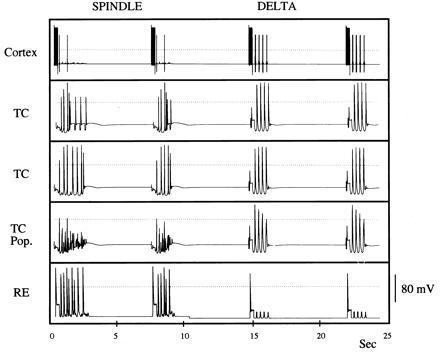
Network with waxing and waning. Larger network with RE cells, each receiving GABA_A and GABA_B inhibition from the other RE cells. As in Fig. 2, the TC cells fire on some cycles during spindling, and synchronously in all cycles during the delta rhythm. The dotted line is zero voltage.

Discussion

Different Roles of Inhibition in the Two Sleep Rhythms.

In the spindling state, the fast inhibition from the RE cell plays two roles: it provides the basis for a rebound for at least one of the TC cells in each cycle and it makes it difficult for the TC cells to synchronize. With a slower rise time in inhibition, the latter can be overcome (data not shown). This is closely related to the phenomenon of synchronization of mutually inhibitory neurons (13, 20, 21). The rebound is unnecessary if the TC cell is itself an oscillator. However, in the presence of the fast (GABA_A) inhibition, the TC oscillators do not synchronize, but form clusters. (For related phenomena, see refs. 14, 15, 22, and 23). During spindling, the slow (GABA_B) inhibition provides long-lasting hyperpolarization of the TC cells, but this is not critical to the spindling phenomenon (15), and simulations (not shown) without GABA_B are qualitatively similar.

In the delta rhythm simulation, the inhibition from the RE is also critical for producing the behavior described in ref. 2, but for an entirely different reason. The slowly decaying GABA_B inhibition is now crucial for allowing the TC cells to oscillate, because those cells do not receive input at each cycle to get a rebound. Removal of the GABA_B input leads the system to stop oscillating (3). Indeed, if the physiological cells require inhibition to oscillate, removal of GABA_B should stop the delta rhythm. The model also predicts that, in the parameter ranges of the delta oscillation, removal of the GABA_A interactions has very little effect. In this model, the increase in the leak conductance of the RE cell makes the latter insensitive to excitatory input from the TC cells, and therefore unable to burst except upon excitation from the cortex; the effects of GABA_A from a cortical volley to RE wear off quickly compared with slow wave period. A key point, however, is that any change in the RE cells that make them unresponsive to excitation will produce the same effect in the network. Thus, in a more complicated and realistic description of the RE cells, various modulations of intrinsic currents could have the same outcome in the network.

Predictions.

The first prediction of this model concerns confirmation of the data shown in refs. 1 and 3 about the behavior of the reticular cells during deeper sleep. The recordings shown in figure 3 of ref. 1 do not correspond to simultaneous recordings of reticular cells and cortical cells; hence, they suggest, but do not demonstrate directly, that the reticular cells fire only as a consequence of the cortical interactions and that they do not respond to excitation from the TC cells. The current model predicts that this must be so if the clustering associated with the spindling rhythm is to be avoided.

The second prediction concerns the role of GABA_B during the delta rhythm. In a regime in which the oscillations in the TC cells damp out between cortical slow waves, the model suggests that the ability of the cortical excitation to renew the waves comes from the GABA_B inhibition to those cells, mediated by the RE cells. Hence a block of GABA_B should abolish that rhythm.

Some Points to Note.

(i) To produce an ongoing spindle rhythm the cortex is not necessary (15, 29). However, unless some TC cells are assumed to be oscillators (27), once a spindle sequence is completed, it requires input to start a new sequence. This comes from the cortex, by way of the RE cells, consistent with Box 1 of ref. 2. (Also consistent with this is the report of ref. 3 that no spontaneously rhythmic TC cells were found in the slice preparation.)

(ii) If the TC cells are sufficiently hyperpolarized to be oscillators without further phasic inhibition, the delta rhythm can be produced without GABA_B inhibition from RE cells. However, the resulting behavior does not have a given cell burst for several cycles and then stop, awaiting cortical input as in ref. 2. We were not able to find any robust parameter ranges in which an isolated TC cell oscillated several times and then damped out. Thus, our simulations suggest that the TC cells oscillate only because the cortex periodically provides sustained (but decaying) inhibition via the RE cells. The number of cycles the TC cells oscillate above threshold can be increased by increasing the leak conductance of the TC cells or decreasing the conductance of I_h. In the spindling rhythm, I_h affects the number of population cycles skipped between jumps of a TC burst (5, 22, 30).

(iii) In the delta rhythm, the cortex also aids in the synchronization by giving the TC cells large synchronous excitation at every slow wave. However, even in the absence of the cortex–TC connection, initial synchronization takes place because of the rebound effect from the fast inhibition after each cortical slow wave. This happens partly because, just prior to the cortical input (after the inhibition to the TC cells has decayed), the TC cells are all close to rest, and hence have similar responses to a simultaneous input. We note that if the TC cells are intrinsic oscillators in delta, then they would not necessarily be close to rest at the onset of a cortical slow wave. In this case, the resulting fast inhibition from the RE cells would tend to desynchronize the TC cells instead of synchronizing them.

Robustness and Key Features.

The explanations given above suggest that the production of the sleep rhythms described in this paper depends on several key features: (i) Neither the TC nor RE cells are intrinsic oscillators in the absence of input. (ii) A TC cell can oscillate at delta frequencies if it has sustained inhibition. It has rebound properties even when not an oscillator. (iii) The ionic currents of the RE cells allow them to respond at spindle frequency if they receive excitation from the TC population at that frequency. When appropriately modulated, the RE cells do not respond to excitation from the TC cells, but can still respond to the longer and more intense excitation from the cortex. (iv) The decay time of the fast (GABA_A) inhibition is critical in the frequency determination of the spindle rhythm, whereas the fast rise time of this synaptic current is critical for desynchronization of the clusters (13, 20–22). (v) The network behavior is very sensitive to the conductances of I_h and I_T, making these currents useful ones to modulate.

Appendix

For Fig. 2 there are 10 TC cells and 1 RE cell. The RE cell satisfies the equation ν′ = −I_T − I_L −I_AHP − I_AMPA −I_CTX. I_T = 1.5 m_∞²h(ν − 90), where m_∞ = 1/(1 + exp(−(ν + 52)/7.4)), h′ = 4.2 (h_∞ − h)/τ_h, h_∞ = 1/(1 + exp((ν + 78)/5)), and τ_h = 100 + 500/(1 + exp(ν + 78)/3). I_L = 0.04(ν + 82.5) + g_KL (ν + 90), where g_KL = 0.02 during spindling and 0.4 during delta. I_AHP = 0.1 m_A(ν + 90), where m′_A = 0.02[CA](1 − m_A) − 0.025 m_A and [CA]′ = −0.01 I_T − 0.08[CA]. I_AMPA = 0.04 ν∑s_j, where the sum is over the TC cells and s_j^′ = 2(1 + exp(−(ν_j + 45)/2))(1 − s_j) − 0.1 s_j.

I_CTX = 0.1 s_Cν, where s_C is defined below.

Each TC cell satisfies the equation ν′ + −I_T − I_L −I_SAG −I_GABAA −I_GABAB −I_CTX. I_T = 2 m_∞²h(ν − 90), where m_∞ = 1/(1 + exp(−(ν + 59)/6.2)), h′ = 4.2 (h_∞ − h)/τ_h, h_∞ = 1/(1 + exp(ν + 81)/4.4), and τ_h = 30 + 220/(1 + exp(ν + 78)/3). I_L = 0.01(ν + 70) + 0.02(ν − v_KL), where v_KL = −97, and I_SAG = g_SAGr(ν + 40), where g_SAG = 0.04, r′ = (r_∞ − r)/τ_r, r_∞ = 1/(1 + exp(−(ν + 75)/5.5)) and τ_r = 20 + 1000/(exp((ν + 71.5)/14.2) + exp(−(ν + 89)/11.6)). I_GABAA = g_As_A(ν + 85), where g_A = 0.2, s′_A = 2x_∞(1 − s_A) −0.08s_A and x_∞ = 1/(1 + exp(−(ν_RT = 45)/2)). I_GABAB = 0.02s_B(ν + 100), where x′_B = 5x_∞(1 −x_B) − 0.01x_B, s′_B = 0.01s_∞(1 − s_B) − 0.005s_B, s_∞ = 1/(1 + exp(−(x_B − 1/e))/0.02). Finally, I_CTX = 0.04s_Cν.

One layer of the cortex satisfies x′ = y + x − x³/3; y′ = −ɛx(1 + 25/(1 + exp(−100x))), where ɛ = 0.0004. The other layer satisfies ν′ = 3ν − ν³ + 1.8 − 2 + 3c_∞ + I_TC; w′ = 0.2(5(1 + tanh(20ν)) −w), where c_∞ = 1/(1 + exp(−100x)) and I_TC = 0.3 ∑s_j; the sum is over the TC cells and each s_j is as before. Finally, s′_C = α(1 − s_C)σ_∞ − βs_C, where σ_∞ = 1/(1 + exp(−100x)).

For Fig. 4, there are 10 TC cells and 3 RE cells. Each RE cell satisfies the above equations with the additional currents I_GABAA and I_GABAB. I_GABAA = 0.1(ν + 75)∑s_Aj/3 and I_GABAB = 0.01(ν + 90)∑s_Bj/3, where the sums are over the RE cells, and s_Aj and s_Bj satisfy the equations for s_A and s_B above. Moreover, I_AMPA = 0.032ν∑s_j/5, where the s_j are as above, and the sum is over five arbitrarily chosen TC cells. The equation for each TC cell is as above, except that s_A = s_Aj and s_B = s_Bj for one arbitrarily chosen RE cell. Moreover, g_SAG = 0.04 + 0.035/ (1 + exp(−([CA] −44)))([CA] −44), where [CA]′ = −0.0415I_T− 0.0007[CA]. Values of the parameters are ν_KL = 100, g_A = 0.17, ɛ = 0.00012, α = 0.5, β = 0.2, g_KL = 0.015 during spindling and g_KL = 0.25 during delta.