Transforming neural computations and representing time

Abstract

Motifs of neural circuitry seem surprisingly conserved over different areas of neocortex or of paleocortex, while performing quite different sensory processing tasks. This apparent paradox may be resolved by the fact that seemingly different problems in sensory information processing are related by transformations (changes of variables) that convert one problem into another. The same basic algorithm that is appropriate to the recognition of a known odor quality, independent of the strength of the odor, can be used to recognize a vocalization (e.g., a spoken syllable), independent of whether it is spoken quickly or slowly. To convert one problem into the other, a new representation of time sequences is needed. The time that has elapsed since a recent event must be represented in neural activity. The electrophysiological hallmarks of cells that are involved in generating such a representation of time are discussed. The anatomical relationships between olfactory and auditory pathways suggest relevant experiments. The neurophysiological mechanism for the psychophysical logarithmic encoding of time duration would be of direct use for interconverting olfactory and auditory processing problems. Such reuse of old algorithms in new settings and representations is related to the way that evolution develops new biochemistry.

Neuroanatomy shows strong evolutionary linkages and conservation of motifs. Pre-piriform (olfactory) cortex appears to be the structural motif on which other parts of old cortex, such as hippocampus, are based (1). The basic structure of neocortex is preserved from primitive mammals to humans. The structure of somato-sensory neocortex is very similar to visual neocortex. One of the paradoxes of neurobiology is how such similar structures can be appropriate to the diverse tasks that they perform.

The way that related molecules and enzymatic pathways evolve to serve varied biochemical functions can be recapitulated in the development of computational abilities in the nervous system. The most common approach to developing a new molecular functionality is by building on a previous solution to a related problem. A useful new molecular functionality is achieved by modifying a previously existing enzyme with a related functionality. Gene duplication allows the old functionality to be preserved in one piece of DNA, while a related new functionality can evolve in the “duplicate” gene (2, 3). In anthropomorphic terms, when an organism is challenged by a new problem at the molecular level, the usual approach in solving the new problem is to modify a mechanism or pathway used to solve a related previous problem.

I argue that one of the ways that the brain evolves to solve new problems and produce new capabilities is by developing (through evolution) transformations that convert new problems into problems that have already been solved. Evolution can proceed by duplication and modification (or in the case of brain, regional specialization) as it has at the molecular level. If this is so, we can look for evidence of appropriate transformations being carried out that would convert the new problem into an older one, even in the absence of understanding how the older problem is solved.

In this paper, I point out that a fundamental problem involved in recognizing time sequences (e.g., spoken syllables) can be transformed so that it is the same computational problem as recognizing the odor of a substance (a very old computation in the history of biology) in an intensity-independent way. This transformation involves representing the time since recent events in terms of neural activity. There are distinct electrophysiological hallmarks of neurons that could carry out such a transformation. What often is dismissed as “adaptation” may, in this context, be responsible for an explicit representation of time itself.

The evolutionary solution of problems by transformation seems to occur at the molecular level, as can be illustrated by the relationship between the glycolytic pathways for fructose and glucose. The fructose glycolytic pathway in present-day bacteria begins:

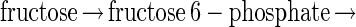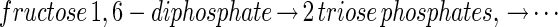where each of the steps indicated by an arrow is catalyzed by a different enzyme. The glucose pathway does not emulate the function of each of these enzymes by a set of new ones. Instead, the problem of using glucose is “solved” by transforming it into the fructose problem at an early step in the cascade. In Escherichia coli, the glucose pathway begins (4):

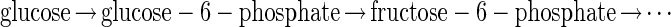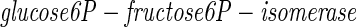The enzyme glucose6P-fructose-6P-isomerase transforms the glucose problem into the fructose problem. A biochemist, knowing the structural relationship between fructose and glucose, could be led by such reasoning to discover this crucial isomerase, even in the absence of understanding the fructose pathway. A neurobiologist, understanding an algorithmic relationship between the computations done indifferent sensory modalities, might similarly seek evidence for a neural transformation converting one problem into another.

The Fundamental Problem of Olfaction

The sense of smell and its aquatic equivalent are ancient and ubiquitous forms of remote sensing. Bacteria, slugs, insects, and vertebrates can all use olfaction to locate, identify, and move with respect to sources of nutrition, mates, and danger. What is the basic computation that must be performed as the basis for the olfactory behavior of animals? Most natural odors consist of mixtures of several molecular species. At some particular strength, a complex odor b can be described by the concentrations N_j^b of its constitutive molecular species. If the stimulus intensity changes, each component increases (or decreases) by the same multiplicative factor. It is convenient to describe the stimulus as a product of two factors, an intensity λ and normalized components n_j^b as:

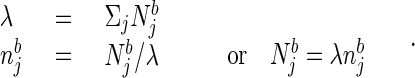1

The n_j^b, are normalized relative concentrations of different molecules, and λ describes the overall odor intensity. Ideally, a given odor quality is described by the pattern of n_j^b, which does not change when the odor intensity λ changes. [In biology, this invariance holds over two or three orders of magnitude of concentration (5).] When a stimulus described by a set {N_j^s} is presented, an ideal odor quality detector answers “yes” to the question “is odor b present?” if and only if for some value of λ:

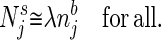2

Appropriate functional criteria for how stringent the approximate equality should be will depend on the biological context. This computation has been called analog match (6).

The identification of the color of a light could be described in similar terms. Ideally, an animal would have thousands of very specific light receptors, each in a different, very narrow, wavelength band. Ideally, the comparison of a new stimulus to a known color would be an analog match problem in thousands of dimensions. Our color vision, however, uses only three broadly tuned receptors. The color comparison that our brains carry out still has the form of an analog match problem, but in only three variables. While we can recognize hundreds of hues, there are also some color analysis errors (or color illusions) because there are so few channels. For example, a mixture of monochromatic yellow light (5500 Å) and monochromatic blue light (4200 Å) is perceived the same as monochromatic green light at an intermediate wavelength.

To understand the algorithm used by higher animals to recognize odor quality, it is similarly necessary to know the representation of odors at the sensory epithelium. Direct studies of vertebrate sensory cells exposed to simple molecular stimuli from behaviorally relevant objects indicate that each molecular species stimulates many different sensory cells, some strongly and others more weakly, while each cell is excited by many different molecular species (7). Mixtures of two unknown odorants are behaviorally perceived as a new odor quality, a different category from either component (8). (Unknown mixtures of known components can be somewhat disentangled by the experienced observer.) Consideration of these diverse facts has led to the view that the pattern of relative excitation across the population of sensory cell classes determines the odor quality in the generalist olfactory system, whether the odorant is a single chemical species or a mixture (7, 9, 10). Molecular biologists have suggested that in mammals, there may be a few hundred different receptor types (11, 12). The compaction of the ideal problem (a receptor for each molecule type) down onto a set of at most a few hundred broadly responsive receptor cell types is similar to the compaction done by the visual system onto three receptor cell classes. However, the olfactory system, having more channels, presumably has fewer illusions. The generalist olfactory systems of higher animals apparently solve the computational problem:

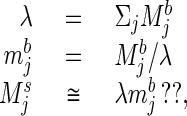3

exactly like that described in Eqs. 1 and 2 except that the index j now refers to the effective channels of input, rather than to molecular types, and the components of M refer to the activity of the various input channels.

A possible mode of carrying out such an algorithm based on phenomena of the olfactory bulb and pre-piriform cortex has been recently described (6), but there may be other neural ways of performing such a computation. For present purposes, we do not need to know how neurobiology achieves this task. The only important point is that the earliest vertebrates must have been able to solve this problem.

Sequence Recognition

The archetypal sequence recognition problem is to identify known syllables or words in connected speech, where the beginnings and ends of words are not necessarily delineated. The same general problem is present in vision (e.g., recognizing a person by the way she walks) and touch. We will use speech for illustration, because so much analysis has been done for engineering purposes.

Speech is a stereotyped sound signal whose power spectrum changes relatively slowly compared with the acoustic frequencies present. The speech sound in a small interval (typically 20 msec) is often classified as belonging to a discrete set of possibilities A, B, C, D, … , so that a speech signal might be represented by a sequence in time as:

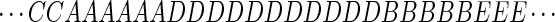A computational system that can reliably recognize known words in connected speech faces three difficulties. First, there are often no delineators at the beginnings and ends of words. Second, the sound of a given syllable in a particular word is not fixed, even for a single speaker. Third, the duration of a syllable or word is not invariant across speakers or for a given speaker. This third difficulty is termed the time warp problem and creates a particularly hard recognition problem in the presence of the other two difficulties. This combination of difficulties has led to the use of computationally intensive and very nonneural “Hidden Markov Model” algorithms for recognizing words (13). Without time warp, template matching would be an adequate solution to the problem.

The initial stage of a “neural” word recognition system, whether biological or artificial, might begin with “units” that recognize particular features A, B, C, etc. A particular feature detector has an output only while its feature is present. Any neural scheme for recognizing a sequence needs some form of short-term memory, since a neuron that is to symbolize (by being active) that a particular syllable has just occurred must receive simultaneously information about the entire prior time span of the utterance, 100–500 msec in the case of a monosyllable. One way to assemble the necessary information is to use a time-delay network (14–16), which slowly propagates signals from unit to unit. A recognition unit can obtain simultaneous information from different relative times in the information stream by making connections at different spatial locations. This amounts to a time-into-space transformation, followed by match to a template.

Syllable lengths vary considerably in normal speech. For example, in a broad spoken digit data base (16), the longest utterance of a particular digit is about twice as long as the shortest utterance of that same word. The following letter strings illustrate the problem created by this fact:

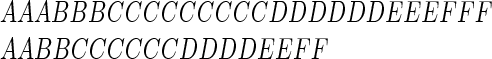These two sequences represent time-warped versions of the same “word.” Clearly, a single rigid template cannot match both strings well, no matter how the template is fashioned or positioned with respect to each of these word strings.

The Occurrence Time Representation

There is an alternate and novel way to represent a symbol string. A string of symbols that have occurred at times earlier than the present time t:

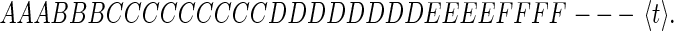4

can be represented by the times of the starts (s) and ends (e) of sequences of repeated symbols. The sequence 4 can thus be represented as:

5

While at first sight, representation 5 seems qualitatively similar to 4, representation 5 leads to a new way to represent the sequence. Considered at time t, string 5 can alternatively be represented by the set of analog time intervals τ[A_s], τ[A_e],τ[B_s],τ[B_e],τ[C_s], … , as illustrated schematically below:

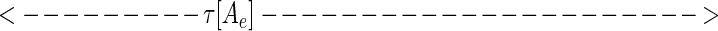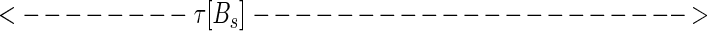6

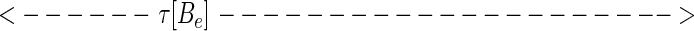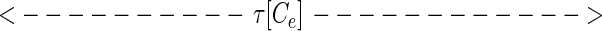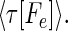In this representation, the sequence that occurs in a finite time window immediately before t is described by a vector τ(t) in a space whose coordinate axes represent the possible symbols A_s,A_e,B_s,B_e, … . Most of the symbols will not occur at all, and their components are zero. The symbols that do occur have components τ[A_s], τ[A_e],τ[B_s], … ; τ(t) implicitly depends on t, since, as time passes, new symbols are constantly occurring (making a previously zero component nonzero), nonzero components of τ are constantly lengthening, and components longer than a cut-off time τ_c are reset to zero.

A known sequence b can also be described by a tableau of times having the appearance of representation 6, with each component describing the time between the occurrence of a symbol like C_e and a time shortly after the end of the sequence when all information about the sequence will have been received. Thus known sequence b can be described as a vector of times τ_b = {τ_b[A_s],τ_b[A_e],τ_b[B_s],τ_b[B_e],τ_b[C_s], … }. This vector does not change with time, since its components represent fixed time intervals.

To determine whether a known sequence b is present in the data stream, the vectors τ_b and τ(t) must be compared. Recognition of the occurrence of sequence b within a uniform time-warp factor λ should take place at the times when:

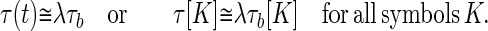7

In this representation, the mathematics of recognizing a given known word has been made equivalent to the problem of finding a match (if any) between the present analog vector τ, representing what has been heard shortly before the present time t and one of the known analog template vectors. The τ[K] in representation 7 are like the N_j^s in 2 or the M_j^s in 3. If the speech has been slowed down or sped up by a factor of λ, then the match which should be sought is the best match with an arbitrary λ, which can of course be different for each word spoken. In this representation, the word recognition problem in the presence of uniform time-warp (within a word) is equivalent to the analog match problem of olfaction.

The Transformation

If the brain solves the sequence recognition problem by transforming it into the analog match problem, it must first produce a transformation of the sequence into the occurrence time representation. This requires a “neural” way to generate signals that represent the time-dependent analog variables τ[A_s],τ[A_e],τ[B_s], … .

Neurons that respond strongly to a particular stimulus, but do not have a sustained response to a sustained stimulus, are common in sensory areas of the brain. Such cells are said to adapt and to detect changing or moving stimuli. Under some circumstances, however, the response of these cells can be described as generating a transformation of representation. Consider a cell that responds to the acoustic feature D in a sequence such as in that in representation 4. A nonadapting neuron would be strongly active while the input sequence sounded like D, as indicated in trace A of Fig. 1. An “adapting” neuron would produce action potentials at a decreasing rate. Suppose the beginning of a sequence of symbols D initiates a stereotyped response of the form shown in trace B. Then the length of each interspike interval is determined by how much time has elapsed since the beginning of the string of D_s (i.e., the time since D_s). The observation of a particular time separation between two successive action potentials uniquely describes the time since D_s. The output of such a cell represents the time-dependent quantity τ[D_s].

Figure 1.

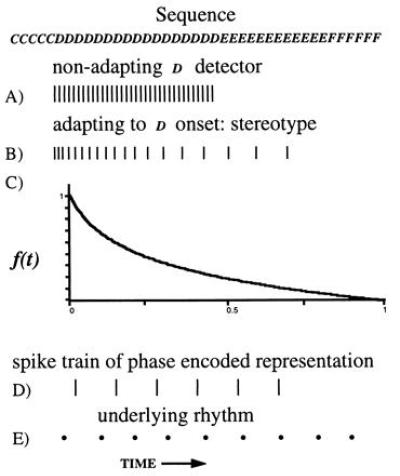
The action potential pattern produced by a nonadapting neuron that detects the feature D in the sequence is shown in trace A. In trace B, the action potential pattern produced by an adapting neuron which recognizes the initiation of a sequence of Ds is shown. Trace C is a representation of trace B in terms of the decay of an instantaneous firing rate. Trace D shows the timing of action potentials conveying information about the elapsed time since the Ds began, by means of phase encoding with respect to an underlying uniform rhythm (trace E).

The functional form of the decay of the firing rate determines exactly how τ[D_s] is represented. This decay is sketched in the figure by a smooth variable, the “instantaneous firing rate” f(t). In the analog match problem, logarithms of quantities like τ[D_s] are particularly useful. The curve sketched in trace C of Fig. 1 is described by:

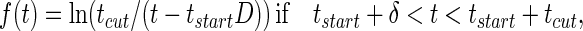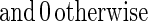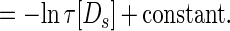Thus, this f(t), a simple decay in trace C of Fig. 1, represents the desired logarithm.

It is essential that neurons responding to inputs from such feature detectors avoid a confusion between the likelihood that a feature was recognized and the time since its recognition. In the representation depicted by trace B of Fig. 1, each particular neuron is involved in an “all-or-none” decision about the recognition of its symbol. If the decision is “yes,” a stereotype time decay is generated. If the decision is “no,” then no action potentials are generated. If there are many neuron recognizers of each symbol, information about the likelihood that a particular symbol occurred is present in the number of recognizers which respond “yes” at the same time, and the time decay of each neuron firing contains independent information about the time since that symbol must have occurred. (Such a scheme also helps solve the problem of what to do if a particular symbol like D_s occurs more than once, for only a subset of detectors need respond to a given occurrence of D_s. This technical issue will be described in a paper dealing specifically with applying these ideas to speech analysis.)

Schemes to represent the transformed information might involve bursting neurons, with the duration or separation of bursts encoding the relevant times or other, more complex modulatory patterns. Some schemes may not even require an all-or-none initial response. The important point is that a population of neurons responding to an event like D_s has a continuing response, supplying the downstream neurons with an interpretable representation of τ[D_s] and also supplying information about the reliability with which D_s was recognized. This is particularly simple to do in the case of phase-encoding neurons, which encode τ[D_s] or lnτ[D_s] by the displacement of the timing of action potentials (Fig. 1, trace D) with respect to an underlying regular rhythm (Fig. 1, trace E; ref. 6). In this case, the outputs of the independent recognizers of a given symbol can simply be summed and analyzed in a time-delay network, without any confusion of the timing information (which conveys τ[D_s] or lnτ[D_s]) and the reliability information, encoded in the number of spikes that occur from different detectors.

Discussion

The fructose–glucose relationship might suggest to a biochemist to look for an isomerase in the glycolytic pathway. Similarly, the mathematical relationship between the analog match problem typified by olfaction and the sequence recognition problems of audition or vision suggests searching for the encoding of the elapsed time since an event in the pattern of action potentials that is induced by the event. The essential transformation necessary to convert “sequence recognition with time warp” into the analog match problem can be carried out by neurons or neural circuits, which might qualitatively be described merely as adapting.

The electrophysiological hallmark of the simplest transformation schemes involve neurons with stereotyped all-or-none responses. These neurons, when excited by an appropriate transient in the stimulus, produce a stereotype pattern of action potentials over an extended period of time. While they are active, the elapsed time since the occurrence of the exciting transient can be evaluated from the present pattern of action potentials. Schemes that do not require an all-or-none response are also possible. The common feature of all such transformations is that the elapsed time since particular past events is encoded in slow cellular variables and in the action potential stream, either on a neuron-by-neuron basis or collectively, by an ensemble of neurons.

Within this framework, the method of storing and representing information about past events is dependent on some of the slow cellular variables of electrophysiology. Indeed, the essential analog information describing the time interval since past events may be quantitatively contained in and represented by the cellular Ca²⁺ level or other slow variables, which is then “read out” and communicated to other cells by its influence on action potential generation. In this regard, Sobel and Tank (17) have recently shown that the Ca²⁺ concentration is used in a cricket neuron as a computational variable relevant to sequence processing. Adapting neurons, adapting synapses, neurons with sustained responses to transients, and neurons with stereotyped responses have all been observed. If an appropriate set of properties is simultaneously present, neurons can carry out the hypothesized transformation.

The ability to judge or match the duration of sounds (or silences) has a fractional accuracy Δτ/τ, which is independent of the duration of sound for time durations over a range of 1000 (18). This Weber–Fechner result is natural to a system that has a neural variable representing the logarithm of a time interval and for which the noise is fixed, independent of the time interval. This fact supports the idea that a logarithmic encoding of time duration, which would be useful for some methods of computing sequence recognition independent of time warp, is employed by the nervous system.

At the anatomical level, the idea presented here suggests that the kind of neural circuitry relevant to recognizing auditory sequences might also be useful in recognizing odors. In this regard, it may be significant that neurons in the medial geniculate nucleus (auditory) of alert cats often respond only to complex tones having a significant time structure, such as a frequency sweep, or even only to ethologically relevant stimuli (19, 20). Many cells in this nucleus are thus capable of recognizing time histories of sounds—i.e., short signal sequences. Deep cells in primary olfactory cortex also project to an olfactory area of the medial dorsal nucleus (MDN) of the thalamus, and lesions of the olfactory thalamic MDN have effects on difficult odor discriminations (21). The medial thalamus might thus usefully perform the same kind of computation on olfactory and on auditory signals. Cats whose lateral olfactory tract (LOT) has been severed still recognize and discriminate odors in spite of the destruction of what is conventionally regarded as the olfactory pathway (21). (Cutting the LOT still leaves intact afferents from the olfactory bulb to the medial half of olfactory cortex.) It would be interesting in this regard to see whether olfactory MDN is particularly important when LOT is severed.

There are other computations that might evolutionarily have spread from one modality to another. For example, the idea that “what moves (or fluctuates) together is an object” seems relevant to problems in olfaction (22), audition (ref. 23; also described in ref. 24), and vision (25, 26). The idea of looking for the evolutionary changes or additions to brain circuits, which permit it to solve problems in one sensory modality by transformation to an earlier solved problem in another modality, is not limited to analog match. If a relatively few neural algorithms can be deployed to solve a wide variety of problems with the help of some simple transformations, there seems less paradox to the limited number of motifs of mammalian neural circuitry.