Attractor models of working memory and their modulation by reward

Abstract

This work reports an empirical examination of two key issues in theoretical neuroscience: distractibility in the context of working memory (WM) and its reward dependence. While these issues have been examined fruitfully in isolation (e.g. Macoveanu et al. in Biol Cybern 96(4): 407-19, 2007), we address them here in tandem, with a focus on how distractibility and reward interact. In particular, we parameterise an observation model that embodies the nonlinear form of such interactions, as described in a recent neuronal network model (Gruber et al. in J Comput Neurosci 20:153-166, 2006). We observe that memory for a target stimulus can be corrupted by distracters in the delay period. Interestingly, in contrast to our theoretical predictions, this corruption was only partial. Distracters do not simply overwrite target; rather, a compromise is reached between target and distracter. Finally, we observed a trend towards a reduced distractibility under conditions of high reward. We discuss the implications of these findings for theoretical formulations of basal and dopamine (DA)-modulated neural bumpattractor networks of working memory.

1 Introduction

The purpose of this work was to test the predictions of a recent computational model of working memory and its modulation by dopaminergic neurotransmission. In what follows, we motivate an experimental protocol and statistical modelling of our data by reviewing working memory and the role of dopamine. We then describe the essential aspects of a recent neuronal (attractor) model of working memory. This model accounts for an interesting psychophysical effect, namely deviance-distraction, and its modulation by dopamine. We use this model as the basis for a psychophysical study and ask whether quantitative deviance-distraction relationships can be accounted for by the model and whether the effects of reward are consistent with the effects of dopamine in the model.

1.1 Working memory

In cognitive psychology, working memory (WM) refers to the capacity for temporarily storing and manipulating information. The concept of working memory has largely replaced or subsumed the older concept of short-term memory, which describes a capacity for passive maintenance. An influential conceptual model of working memory from cognitive psychology (Baddeley and Hitch 1974), motivated primarily from dual-task paradigms, postulates three components of WM; (1) a supervisory (central executive) system, controlling information transfer between (2) a phonological and (3) a visuospatial short-term storage system.

There is a broad, complementary literature examining the anatomical, cellular and neurochemical mechanisms behind these cognitive capacities. Following important early demonstrations of dopamine (DA)-dependent memory (Williams and Goldman-Rakic 1995), it is now clear that DA is implicated in both spatial (e.g. Miyoshi et al. 2002) and phonological (Jacobsen et al. 2006) WM (though, owing to the more substantial literature, our focus will be on visuospatial tasks). Experimental pharmacological lesions of the DA system lead to impaired spatial WM performance (Miyoshi et al. 2002). In contrast, lower doses lead to an enhancement (e.g. Muller et al. 1998). In order to understand the neuroanatomical locations where such drugs influence behaviour, some experimenters have turned to direct application of DA agonists or antagonists (Zahrt et al. 1997). For example, direct application of DA to the prefrontal cortex (PFC) impairs spatial WM (Zahrt et al. 1997).

In a parallel avenue of enquiry, the relation between basal ganglia (BG) activity and WM has been examined in both humans (Lewis et al. 2004) and animal models (Kermadi and Joseph 1995; Kalivas et al. 2001). As in the PFC, these studies have uncovered systematic alterations of BG activity that are specifically related to WM tasks. While these studies have not used direct pharmacological manipulations of DA during WM tasks, it has been noted that striatal neurons are influenced strongly by DA (Nicola et al. 2000). Furthermore, it has long been known from anatomical work that the striatum receives important DA afferents (Lynd-Balta and Haber 1994). It is unclear how modulatory actions of DA in BG interact with the effects of DA in the PFC to influence WM (though see below for one account).

In this work we draw upon computational models in neuroscience. While these inevitably rely on untested heuristics or simplifying assumptions, these models generate predictions at the level of observable variables, which we then exploit in the empirical work reported here.

1.2 The effects of dopamine (DA)

Gruber et al. (2006) use a network model to simulate the interaction of distraction and dopamine on working memory. The model consists of four modules: three associated with PFC and one associated with the BG of the striatum. The model architecture can be seen in Fig. 1. In particular, the model posits a capacity in PFC both for independent transient multimodal stimulus representation (e.g. visual, auditory) and for working memory. The content of working memory at a given time after a sensory stimulus is determined by direct feedforward connections from sensory representations and by the inherent properties of the working memory network itself. Key to the model is the input from the striatum, which is also subject to DA modulation.

Fig. 1.

Model architecture assumed by Gruber et al. (2006)

Visual activity is passed to the PFC working memory network and the striatum. Neurons in the striatum are modelled individually using a biophysically grounded single-compartment model (for details see Gruber et al. 2003). The PFC working memory network is implemented as a line attractor. As well as taking afferents from the sensory areas directly, the PFC memory network receives connections indirectly via the striatum. PFC cells with similar preferences are coupled positively (Gaussian connectivity) in a manner that decreases as their receptive fields become increasingly dissimilar. At close range, these excitatory inputs dominate inhibition by the single inhibitory unit and become self-sustaining. The asymptotic regimes of such a network are well understood (e.g. Brody et al. 2003). In particular, for sufficiently strong input, the network can efficiently encode a stimulus with only a subset of the neurons. Moving between different stimuli (e.g. tones or locations) corresponds to changing the initial states of activity in the network. Importantly, any value of a continuous stimulus parameter finds its own unique asymptotic activity: in other words, the attractor of the network is a continuous line in activity space, which remembers the last stimulus-related input.

Gruber et al. (2006) examined the response of this network to distracting stimuli, which follow a target in time (e.g. after a 1 s interval) and potentially interfere with its representation in working memory. In particular, they present the above network with two stimuli in temporal succession and ask what influence the second (distracter) has on the extant representation of the first (target). For stimuli of fixed intensity and duration the authors derive the relation between distracter distance and the deviance of WM from the true target parameter: the distraction-deviation (DD) curve. Figure 2 illustrates the qualitative form of these DD curves. Characteristically, it adopts a positive slope for a segment about the origin, indicating corruption of working memory. This illustrates that, for distracters in this critical range, memory is pulled towards the distracter. Beyond this critical range the relation rapidly falls off to independence, indicating that the target is retained perfectly in working memory despite the distraction.

Fig. 2.

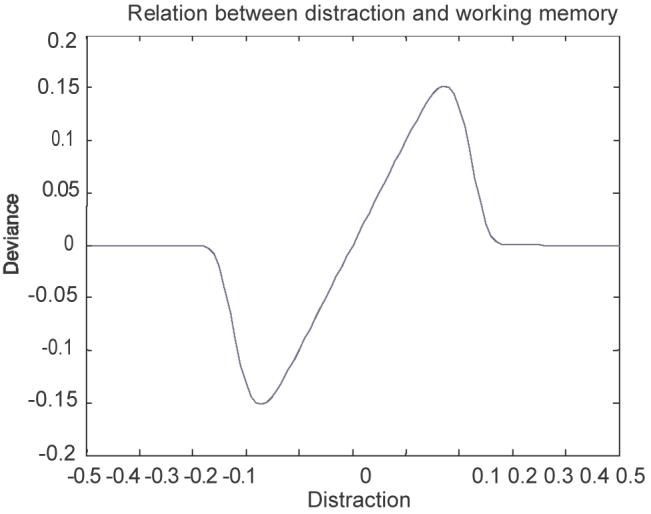
The DD-curve under basal conditions

Finally, Gruber et al. (2006) documents the effect of neuromodulation, principally the induction of cellular bistabiity in the BG (see Gruber et al. 2003), on dynamic properties of the network. A key finding from these simulations is that the nonlinear DD relation is modulated in a nonlinear fashion by DA (see Fig. 3). In particular, while the general form of the relation holds (positive slope around zero and falling off rapidly to independence), the range over which perfect deviation occurs is contracted under high DA. This can be understood intuitively as follows: under high DA, BG cells activated by the target are caught in the up-state and fire consistently. This consistent input by specific units from the BG stabiises the mnemonic PFC activity profile. More importantly, cells not strongly activated by the target are caught in a down-state for the duration of DA-dependent modulation and become insensitive to subsequent distracters.

Fig. 3.

Modulation of the DD-curve. The inner curve has contracted under high DA

In the Gruber et al. (2006) simulations, unity slope of the DD¹ occurs when (1) the PFC network is not modulated by the inputs from the striatum, (2) when only the PRF network is modulated by DA and (3) when the distracters are presented for a sufficiently long time.

1.3 Experimental approach

In this work we examine the predictions of Gruber et al. (2006) empirically. We are interested in the slope of the DD curve over small deviations (is it unity or is WM only partly corrupted by the distracter?) and whether the range of DD is affected by reward. Because the model predictions regard visual working memory for spatial location in isolation, we need a task that engages this and only this system (in isolation from other working and long-term memory systems). With such a task, one might gain information about the nature of WM and its modulation from the shape of the DD-curve.

We hoped to use experimentally controlled visual inputs to reproduce the sensory inputs in the Gruber network and to measure WM status (‘bump location’) via a behavioural response solicited from the subject. As a slight extension of the predictions, we anticipated that definitive effects may be expressed more acutely around the capacity for spatial WM (Macoveanu et al. 2007; Fougnie and Marois 2006).

2 Methods

2.1 Subjects and procedure

Fourteen healthy subjects (eight men, six women) aged between 22 and 37 years were briefed as to the task requirements and familiarised with the task during an introductory training session lasting about 15 min. Subjects were seated 650 mm from a black computer display onto which stimuli were presented sequentially. Subjects initiated each trial by pressing a touch pad. In the testing (but not the training) sessions of individual trials were preceded by a one second cue, indicating the potential value of the trial (1 pound or 0.01 pounds) conditional upon subjects being ‘accurate’ in reporting the location of a target. The task then required fixation on a central cross onto which the mouse cursor was locked for most of the trial. A white ring at three visual degrees surrounded the fixation at all times during a trial. After a 250 ms pause, a set of four stimuli (small filled circles) were presented at random locations around the circumference of the ring for 1 s. We chose to present multiple targets in light of observations in Macoveanu et al. (2007). Following a 3 s interval, a single distracter stimulus, physically identical to those from the target set, was presented close to one of the targets. The distracter was presented at one of nine locations spaced evenly on the interval [−0.4900, 0.4900] radians on either side of the target. After a 1 s pause, the white fixation cross was extinguished, indicating that fixation was no longer necessary and that the mouse cursor was free. Subjects were then required to report the location of the target as accurately as possible with the mouse cursor (the closest target to the distracter). Subjects were able to report any location. For simplicity we analyse their responses in radians (i.e. their response along the perimeter of the unit circle). We did not provide feedback to subjects on a trial-by-trial basis, in the hope that subjects performance would not change systematically during the task, by some feedback-dependent learning mechanism.

Fixation was used to facilitate comparison between this study and others in other literature. Fixation affords the experimenter some control over the retinal coordinates of the stimuli. It also reduces the impact of expectations or creative cognitive strategies used by subjects in order to optimise their task performance. After the training session, we acquired two replications over all conditions (i.e. nine levels of deviances). We randomised (the rows of) the standard form of our design matrix to prevent confounds (e.g. with time-dependent fatigue, etc).

2.2 Pre-processing

Any response greater than one radian in absolute value from the target was excluded before any of the subsequent analyses. This was to exclude trials in which subjects had identified and reported the wrong item from the target set (i.e. an item that was not the closest to the distracter as instructed). As we shall report below, removing these outliers leads to good normality in the within-subject averages.

3 Modelling and results

In this section, we present an analysis of subjects’ responses that rests on a highly nonlinear observation model. This model is parameterised so that we can test hypotheses about formal features of the DD curve, namely the slope at zero deviance and the range over which DD is expressed. Because of its nature, we adopt a Bayesian inversion scheme, using a grid-based approximation to the conditional or posterior density of the models parameters. Although the primary focus of this paper is on the empirical evaluation of the model described above, the analysis of this section represents a demonstration of how to test formal models of psychophysical data in a more general setting.

Due to the intractability of the differential equations in Gruber et al., there is no closed-form theoretical equation for the modulated ‘sleepy-S’ function. We are therefore required to find some convenient proxy for this function that respects both the form of the modulated sleepy-S shaped relation and has interpretable and mechanistically meaningful parameters. Many functions that might be prima facie reasonable do not fully meet these requirements. For example, while the first derivative of a Gaussian has a sleepy-S form, it is not possible to independently parameterise the slope and length of the sleepy-S shape (i.e. these two properties will always be related). Of all possible closed-form functions to model the experimentally measured response deviations, the analytic expression y = xce−γ ^x8+ e is among the simplest (see below). The exponent of x controls how fast the function falls to zero after the peak/trough; the higher the exponent, the sharper the descent. Exponents of 8 or more (i.e. relatively sharp descent), resemble the form of the DD curve predicted by Gruber et al. In the results presented below, we have set the exponent to 8. Results are very similar for other high exponents (e.g. 10, 12). The form of this model can itself be optimised using the model evidence, as discussed later. For positive γ, response deviance y (i.e. distraction) follows the characteristic sleepy-S relationship to the distance x of a distracter from the target (see Fig. 4).

Fig. 4.

Dependence of the DD-curve on parameters

We summarise the influence of other variables by the additive independent Gaussian error e, with unknown variance σ². More formally, our likelihood model for responses can be written

$$\begin{array}{c}p(y\mid \theta )=~NN(yn;\mu n,{\sigma }^2)n=1\hfill \\ \theta =\gamma 1,...,\gamma N,c,\sigma \hfill \\ y=y1,...,yN,\hfill \end{array}$$

where subscripts range over both between- and within-subject replications (N = 497). In this report, we ignore random effects due to subjects and focus on the responses pooled over all trials. The predicted deviance is

$$\mu n=xnce-\gamma nx8{}^{n.}$$

To accommodate our interest in reward-related modulation of γn we define

$$\gamma n(a,b,zn)=\mathrm{e}a+bzn,$$

where z indicates low (0.01 pounds) or high (1 pound) reward for a given trial. As illustrated above, the unknown parameter c defines the slope of the deviating segment of this relation (see Fig. 4). For example, c = 1 implies exact corruption of target by distraction, 0 <c < 1 indicates some compromise between the two, c = 0 corresponds to complete independence between deviance and distraction and 0 > c implies bias in the opposite direction (e.g. overcompensation). The positive scale parameter γ controls the range of deviations and is subordinate to two parameters (a, b), which control the basal range of deviance and any reward-dependent modulation of this range; this means a contraction of this range for 0 <b, and an extension for b <0.

We chose to perform inference within the Bayesian formalism and access a probability distribution over all free model parameters θ = {a, b, c, σ} in light of the data, via Bayes theorem. This formalism requires the careful definition of prior densities p(θ) = p(a)p(b)p(c)p(σ) on the parameter set. {α, β} are ‘nuisance parameters’ which are not of scientific interest to us per se. We therefore integrate uncertainty over their values into our quantities of interest, as described below. We placed an uninformative uniform prior in the positive range.

An informative prior over either one of {a, b} is required to ensure these parameters are jointly identifiable; i.e. under general (bivariate) priors over these parameters, the joint posterior over {a, b} may be improper (fail to integrate to one).² Because of our interest in b, we therefore examined a variety of priors that constrain a. In particular, we examined informative priors that place high probability in the range which yields the sleepy-S functional forms at a plausible scale, as predicted by Gruber et al. (2006) (i.e. a subset of the a domain). We expected that any working memory deviations would occur well within the broad experimental range of one radian. As Fig. 4 (lower panel) illustrates, in the absence of b, this corresponds to constraining log(γ) = a roughly within the range a ≈ 3 to a ≈ 30. Providing most prior mass is in this range, we observed that the posterior on b was relatively insensitive to the precise form of the prior on a. In the results below we constrained a with an informative Gaussian prior of p(a) = N(a; 15, 5).

Due to our interest in hypotheses regarding {b, c}, we specify uninformative uniform priors on these quantities. Any information in the marginal posteriors of these parameters must therefore come from the data.

At a higher level of abstraction one might test the model form itself (in contrast to testing the parameters under an assumed model). A key property of the Bayesian approach adopted in this work is that any alternative analytic model can be compared with a reference model, via a relative evidence measure³ (cf. a Bayes factor or odds ratio). In practice, this entails approximating the model evidence as the sum over the posterior grid array as described below. By formulating our model inversion with the evidence framework, we could exploit model comparison to optimise the form of the model itself (by integrating out dependencies on the parameters of any particular form). This is a more principled approach than cross-validation and obviates the need to assess generalisation errors and the like. We will illustrate this elsewhere; in this work there is no obvious competing alternative model. However, formal hypotheses about the relationship between distraction and deviance can be identified with special settings of our chosen model (e.g. parameter b and/or c is zero). This can be reformulated in term of model selection through optimising the evidence.⁴

Under this model, there is no closed form for the joint posterior

$$p(\theta \mid y).P(y\mid \theta )p\left(\theta \right).$$

We therefore evaluate numerically the posterior at each of 61 × 61 × 61 × 61 points over a regular lattice in the four-dimensional domain (a, b, c, σ). [−30, 30] × [−30, 30]. [−5, 5] × [0, 0.8].

Figure 5 shows the conditional model fit, as specified by the marginal maximum a posteriori (MAP) estimates of θ = {a, b, c, σ} (see below) together with data for high-reward (red) and low reward (blue).

Fig. 5.

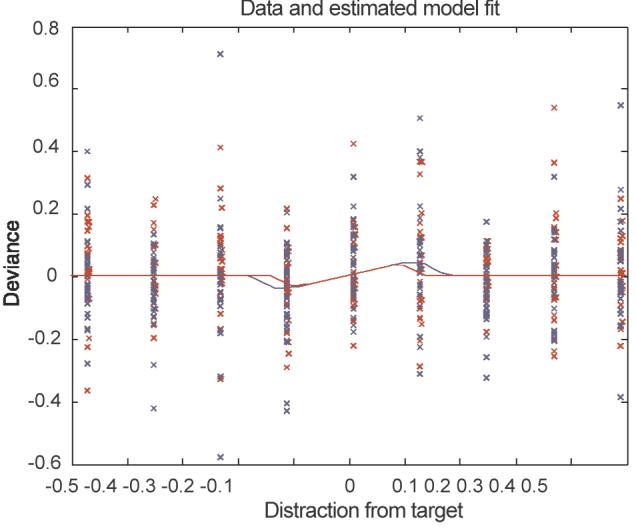
Conditional model fit, as specified by the marginal MAP estimates of the model parameters, together with data. The inner curve describes the high-reward condition

Inference proceeds via the marginal posteriors on the parameters of interest. Figure 6 illustrates the marginal posterior over the slope parameter c. This plot indicates strong evidence (98.9% posterior probability) that behavioural responses to distraction were biased positively in the direction of the target. Interestingly, the maximum a posteriori (MAP) estimate of c is 0.4 and there is a substantial probability (approx. 89.3%) that c < 1.

Fig. 6.

The marginal posterior over the slope parameter c. We see very strong evidence that the slope is greater than zero (i.e. there is a deviance-distracter effect). Interestingly we can be 89.2% certain that this slope is less than one; this is the value predicted by a winner-takes-all mechanism

To assess the predicted effect of reward on the DD curve we evaluated the marginal density of the reward modulation parameter b (Fig. 7). We found moderate evidence (85.5% posterior probability) that behavioural responses to distraction were contracted into a smaller range in trials with high potential reward (1 pound as opposed to 0.01 pounds). This contraction is consistent with the modulatory role of DA in the model reviewed above.

Fig. 7.

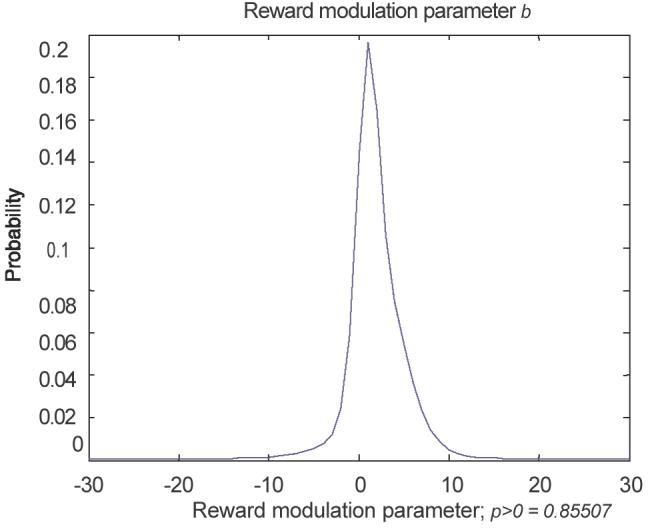
The marginal posterior over the reward modulation parameter b. We see moderate evidence (85.5% posterior probability) that behavioural responses to distraction were contracted into a smaller range in trials with high potential reward (1 pound as opposed to 0.01 pounds)

4 Discussion

We have examined empirical predictions of a theoretical model that portrays working memory as a prefrontal cortex attractor network with additional dopaminergic modulatory inputs from the basal ganglia. The model predicts a specific form for the relation between distracters and deviance in WM from the target. It also predicts a dopaminergic modulation of this relation, as described in Fig. 4. To relate model predictions to real data we assume, largely on the basis of experimental evidence in monkeys and rodents, that more dopamine is released in trials associated with larger reward. In particular, we cued potential reward and the target in sequence and assumed that dopamine is elevated by target presentation per se.⁵ We propose a simple observation model whose parameters can be adjusted to provide a phenomenological fit to the predictions of Gruber et al. (2006). We showed, with high confidence, that responses in a visual working memory task deviate from target in the direction of the distracters, as expected. More interestingly, our results suggest that this distractibility is characterised by a compromise between target and distracter: there is a substantial inductive probability (89.3%) that the target is not simply replaced by the distracter but that information about the target is partially retained. We also observed a trend in the direction of reward-dependent modulation of this distractibility: high potential reward appeared to induce a contraction of the range of distractibility. We anticipate that this effect may be easier to confidently quantify under a higher reward incentive (more that 1 pound) and in tasks with lower motor noise.

We turn now to the interesting observation that memories of the target are, at least partially, robust to distraction, and attempt to reconcile this with the theoretical considerations in the introduction. We examine what properties of modified bump attractors might create this effect, or alternatively whether some hitherto neglected attribute of working memory [e.g. capacity (Fougnie and Marois 2006) or active WM stimulus processing (Baddeley 2000)] might mediate the observed robustness.

Some simple modifications to the standard bump attractor model could account for the sub-unity slope of the DD curve. In the modelling literature, the term line attractor usually refers to attractors in the state space of neuronal firing, where the memory of an item (e.g. position) is encoded in the firing rate of neurons (cf. rate coding). The case considered here is a bump attractor network, where the information is encoded by the position of the activity bump (cf. place coding). The degree to which a bump is pulled from its original position, encoding the target stimulus, depends not only on the distance of the distracter from the bump, but also on the duration of the distracter presentation. With brief distracters, the bump may only be moved partially to the distracter position. This would yield a slope for the DD curve below one. In short, the “stickiness” of the bump could interact with distracter duration to determine DD slope. We are grateful to our reviewers for emphasising that ‘stickiness’ depends on the intrinsic properties of the neuronal units involved. For example, for units with sharper nonlinearity, the bump would be stickier than for graded nonlinearities. Alternatively, short-term plasticity between the synapses inside the bump may automatically decrease the slope. Such plasticity might be expected to occur in real neuronal networks, as it can substantially attenuate random drift that would otherwise corrupt the target encoding.⁶​ Renart et al. (2003), for example, showed that the incorporation of activity-dependent synaptic weights stabilises the bump in the face of threats the attractor’s contour (here biophysical heterogeneities between cells; also see Zhang (1996) in the context of head direction cells).

It should be noted that our model constrained putative reward effects to be expressed in terms of the range over which distractibility occurred (parameter b). In contrast, the slope parameter c is assumed constant, under both high-and low-reward conditions. This form of model precludes any reward-dependent modulation of the curvature of the DD function. This constraint prevents the observation of a dependence of the slope on dopamine, as suggested by extended line attractor models. As noted by one of our reviewers, a DD slope much less than 1 can emerge from line attractor models when inputs to cortex from the basal ganglia are included (see Figs. 4b and 5c in Gruber et al. 2006); thus (modified) line attractor models do not necessarily exhibit strict winner-takes-all properties. The action of the basal ganglia is to break the symmetry of the attractor in a memory and salience (reward)-specific manner. In the context of these observations, it may be that our results are entirely consistent with an extended Gruber et al. model. These issues could be addressed thorough Bayesian model comparison among models in which DA does and does not affect the slope.

Strictly speaking, Gruber et al. (2006) model the case where WM capacity is limited to one item (i.e. one spatial location). Under basal conditions in this scheme, either the target is preserved in WM or the distracter supervenes. In contrast, the large psychological literature on the capacity of WM (Fougnie and Marois 2006; see Owen 2004 for a review) suggests that many items can be retained simultaneously. One could extend the model to include this capacity, for example, using an independent set of networks (each resembling that in Gruber et al. 2006) with some central executive that selects and loads them to capacity. Under these conditions one might imagine that, until capacity is reached, one representation (distracter) would not need to replace another. In contrast, with all networks occupied, the distracter must compete with an extant representation and thus perturb it according to the model predictions.⁷ This is partly why we used four visual targets in this paradigm. Perhaps our observation of a ‘compromise’ memory is more consistent with the idea that multiple items are stored in some inherently co-dependent form. As discussed next, the inclusion of multicapacity in a manner consistent with empirical data may be difficult to reconcile within the attractor network framework.

In general, we expect working memory to perform diverse transformations on a maintained target set. It is unclear exactly what quantities are necessary for the distracted-WM task we report here. For simplicity, the Gruber model (2006) assumes stationarity of the spatial reference frame for representations throughout any one trial (e.g. absolute eye-centred coordinates). Given the functional architecture of working memory (Baddeley 2000), one might envisage that this memory task is completed via functionally diverse processes; for example, the distracter may be encoded relative to the target location (i.e. using a dynamic reference frame). Alternatively, subjects may extract abstract geometrical relations within the target stimuli set (or between that set and some aspect of the subjects perceptual reference frame) to encode them efficiently in a more abstract frame of reference (e.g. the stimuli form the vertices of a diamond, whose geometry might even be verbally encoded cf. the ‘phonological loop’, Baddeley 2000). In debriefing, some subjects did indeed volunteer that they had used such strategies (e.g. visually and/or verbally encoding stimuli as a ‘diamond pattern’). It is unclear whether such capacities can be considered computationally separable from the static representations in Gruber et al. (2006). To the extent that they are, their control in further experiments may result in better isolation of the passive WM described in their model. Alternatively, one might anticipate that it is inherently difficult to separate static representations from the transformations performed on them (see, for example, Machens et al. 2005). Either way, it is plausible that these variables play a role in the robustness of WM.

As we have seen, the predictions of Gruber et al. (2006) depend on a hierarchy of assumptions. At a computational level, it presupposes the bump attractor framework as the mechanism employed by WM. At the functionalist level, it embodies a tacit hypothesis of modularity between the well-documented attributes of WM; namely that the phenomenology of single-item WM generalises to multi-item WM and that passive WM can be described in isolation from dynamic stimulus recoding/transformations. At a cellular level, it specifies the presence/absence of internal noise, short-term plasticity and neuromodulatory factors etc. The WM response to external distracters under basal and rewarded conditions clearly depends on assumptions at all of these levels. Further work is needed before it is clear which level must be developed to accommodate the sub-unity distraction phenomenon observed in our data.