Multiscale Coarse-graining and Structural Correlations: Connections to Liquid State Theory

Abstract

A statistical mechanical framework elucidates the significance of structural correlations between coarse-grained (CG) sites in the multiscale coarse-graining (MS-CG) method [S. Izvekov and G.A. Voth. J. Phys. Chem. B 109 2469 (2005), J. Chem. Phys. 123 134105 (2005)]. If no approximations are made, the MS-CG method yields a many-body multi-dimensional potential of mean force describing the interactions between CG sites. However, numerical applications of the MS-CG method typically employ a set of pair potentials to describe non-bonded interactions. The analogy between coarse-graining and the inverse problem of liquid state theory clarifies the general significance of three-particle correlations for the development of such CG pair potentials. It is demonstrated that the MS-CG methodology incorporates critical three-body correlation effects and that, for isotropic homogeneous systems evolving under a central pair potential, the MS-CG equations are a discretized representation of the well-known Yvon-Born-Green equation. Numerical calculations validate the theory and illustrate the role of these structural correlations in the MS-CG method.

1. Introduction

Although molecular dynamics (MD) simulations provide a powerful tool for investigating complex biomolecular systems,¹ their substantial computational cost limits conventional atomistic MD simulations to investigations on time-scales that are less than microseconds and length-scales that are significantly less than micrometers.^2,3 Such atomistic MD simulations are often inadequate to model biological processes such as protein folding⁴ or signal transduction,⁵ which may occur on significantly larger time- and length- scales. Consequently, there has been growing interest in developing computationally-inexpensive “coarse-grained” (CG) models,^6–18 which can then be simulated over significantly longer time- and length- scales.

In order to reproduce the thermodynamic and structural properties of the original atomistic system, the low-resolution CG structures must be sampled according to the probability distribution function for the fully atomistic representation of the same structures. A formal prescription for designing CG models thus involves the integration over atomistic degrees of freedom to define a reduced description of the system.^2,7 The interactions between CG sites must therefore include not only energetic, but also entropic contributions that result from averaging over eliminated degrees of freedom. In principle, the resulting CG model may require a many-body interaction potential that depends upon the thermodynamic state point.¹³ In practice, though, CG force fields typically model non-bonded interactions with central pair potentials that depend only upon the distance between CG sites.² This effective pair potential represents an approximate decomposition of the many-body interaction obtained from a formal integration over uninteresting degrees of freedom. The procedure for determining this pair potential must appropriately incorporate the effects of many-body correlations in order to reproduce the structure of the original system.

The theory of coarse-grained modeling is similar to the ‘inverse problem’ of liquid state theory.^19–21 Both theories attempt to determine an interaction potential reproducing an observed structure. However, in coarse-grained modeling the target structure is a low-resolution representation of the original structure and the deduced interaction is between the CG sites defining the reduced structure.² The theory of the Yvon-Born-Green (YBG) equation provides a direct solution to this inverse problem,²⁰ under the assumption that such an interaction potential exists. The YBG equation provides an exact relation between a given two-body interaction potential and the n- and (n+1)- particle distribution functions obtained from equilibrium simulations employing the potential. Therefore, a CG pair potential may be determined by inverting the YBG equation for the observed two- and three-particle CG distribution functions. This relationship suggests a role for higher order correlations in deducing a pair potential that will reproduce the observed CG structure.

The multiscale coarse-graining (MS-CG) procedure^16,17 determines CG force fields from atomistic MD simulations by employing a statistical implementation of the Force-Matching (FM) method.^22,23 This MS-CG method has been successful in developing CG models for many complex systems such as ionic liquids,²⁴ mixed lipid bilayers,²⁵ small peptides,²⁶ nano-particles, ²⁷ and even mixed resolution models of trans-membrane proteins in lipid bilayers.²⁸ In the following analysis it is demonstrated that if no approximations in the functional form of the CG force field are made, the MS-CG method determines a many-body multidimensional potential of mean force describing the CG representation of the system. Consequently, simulations employing this many-body MS-CG potential would generate CG structures according to the underlying atomistic distribution function. However, prior numerical applications of the MS-CG method have approximated this many-body interaction potential with a set of bonded and non-bonded pair potentials between CG sites.^{16,17,24–28} The present work demonstrates that the MS-CG equations for this CG pair potential reflect both two- and three-particle correlations between CG sites within a system. Moreover, for homogeneous, isotropic systems the MS-CG equations are equivalent to generalized Yvon-Born-Green (YBG) equations²⁰ for CG sites interacting according to a central pair force field. For such systems the MS-CG methodology explicitly considers the two- and three- particle correlations between CG sites within an atomistic MD simulation, assumes that these distribution functions were generated by a pair-wise decomposable central force field, and then inverts the resulting YBG equation to determine this force field. The YBG theory thus provides a fundamental link between the system structure and the CG force field.

In Section 2.1 the relationship between the MS-CG interaction potential and a multidimensional potential of mean force is derived. The “normal” MS-CG equations are next derived in Section 2.2 by approximating the many-body interaction potential with a central pair-wise decomposable force field. The derivation emphasizes the relationship between the MS-CG equations and the correlations observed between CG sites in atomistic MD simulations. The YBG equation for a CG system is then presented in Section 2.3 and it is shown that for a homogeneous, isotropic system this equation reduces to the MS-CG equations. Numerical illustrations of this analysis are presented in Section 3. In Section 4 the significance of liquid state theory for developing coarse-grained models is considered, especially with regards to the MS-CG and reverse Monte Carlo methods.^2,21,29 These results are reviewed in the Conclusion section, Section 5. Proofs of certain necessary results and generalizations of the theory for a multi-component system are provided in the Appendices. A more detailed discussion of the theory is attached as a Supporting Information section.

2. Theory

2.1. Many-body CG potential of mean force

The multi-scale coarse-graining (MS-CG) method of Izvekov and Voth extends the Force-Matching (FM) method²² to determine coarse-grained (CG) force fields from atomistic molecular dynamics simulations.¹⁷ The CG force field is obtained by minimizing a residual describing the difference between the instantaneous forces defined by the CG force field and the original atomistic force field. This difference is statistically averaged over all CG sites and all configurations sampled from the atomistic MD simulations. As shown below, these configurations must be sampled according to the distribution function for the atomistic Hamiltonian in order to perform the correct averaging. The FM residual for a system described by N_CG identical CG sites may be expressed:

$${\chi }^2=\frac{1}{3N_I{N}_{CG}}{\displaystyle \sum _I^{N_I}{\displaystyle \sum _i^{N_{CG}}{\left|{\stackrel{\rightharpoonup }{F}}_i^{I,AA}-{\stackrel{\rightharpoonup }{F}}_i^{I,CG}\right|}^2}}.$$ (1)

In eq (1) and in the following, Latin subscripts ( i ) indicate particular CG sites and the superscript ( I ) labels configurations sampled during the atomistic MD simulation. Thus, the MS-CG residual compares the total force on a given CG site defined by the atomistic force field for the sampled atomistic configuration, ${\stackrel{\rightharpoonup }{F}}_i^{I,AA},$ with the force on the same site defined by the CG force field for the CG representation of the same configuration, ${\stackrel{\rightharpoonup }{F}}_i^{I,CG}.$

In the limit of adequate sampling, the FM residual may be considered an average over the region of configuration space, D, sampled by an atomistic trajectory and weighted according to the atomistic distribution function, ${\rho }_{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}}),$ defined for the trajectory. The residual may then be expressed as the configurational integral:

$${\chi }^2=\frac{1}{3N_{CG}}{\displaystyle {\int }_{D}d{\stackrel{\rightharpoonup }{r}}^{N_{AA}}{\rho }_{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}}){\displaystyle \sum _i{\left|{\stackrel{\rightharpoonup }{F}}_i^{AA}-{\stackrel{\rightharpoonup }{F}}_i^{CG}\right|}^2}.}$$ (2)

Now, assume that there exists a canonical transformation that partitions the atomistic phase space into a set of coordinates describing the CG sites and a set of residual degrees of freedom: ${\stackrel{\rightharpoonup }{r}}^{N_{AA}}=({\stackrel{\rightharpoonup }{r}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_R}).$ Such a transformation certainly exists, for example, when the CG sites are defined as the centers of mass for groups of atoms. Upon employing this transformation in eq (2), the residual may be considered a functional of the CG force field:

$${\chi }^2\left[{\stackrel{\rightharpoonup }{F}}^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})\right]=\frac{1}{3N_{CG}}{\displaystyle {\int }_{D_{CG}}d{\stackrel{\rightharpoonup }{r}}^{N_{CG}}}{\displaystyle {\int }_{D_R}d{\stackrel{\rightharpoonup }{r}}^{N_R}{\rho }_{AA}\left({\stackrel{\rightharpoonup }{r}}^{N_{AA}}\right){\displaystyle \sum _i{\left|{\stackrel{\rightharpoonup }{F}}_i^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}})-{\stackrel{\rightharpoonup }{F}}_i^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})\right|}^2.}}$$ (3)

The CG force field is defined by minimizing the functional^20,30 according to $\delta {\chi }^2\left[{\stackrel{\rightharpoonup }{F}}^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})\right]/\delta {\stackrel{\rightharpoonup }{F}}_i^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})=0,$ yielding the result:

$${\stackrel{\rightharpoonup }{F}}_i^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})=e^{+\beta V^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})}{\displaystyle {\int }_{D_R}d{\stackrel{\rightharpoonup }{r}}^{N_R}{e}^{-\beta V^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_R})}{\stackrel{\rightharpoonup }{F}}_i^{AA}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_R}\right)}.$$ (4)

Here the canonical ensemble is explicitly considered: ${\rho }_{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}})=e^{-\beta V^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}})/Z(N,V_0,T)}$ where Z(N,V₀,T) is the canonical partition function. The force on CG site i according to the atomistic potential is defined ${\stackrel{\rightharpoonup }{F}}_i^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{AA}})=-\partial V^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_R})/\partial {\stackrel{\rightharpoonup }{r}}_i,$ where the partial derivative is performed with respect to the CG coordinate r⃑_i while holding all remaining atomistic and CG coordinates fixed. In general the force ${\stackrel{\rightharpoonup }{F}}_i^{AA}$ depends upon all N_AA = N_CG + N_R degrees of freedom. The CG force field defined by eq (4) depends upon all N_CG degrees of freedom and may be considered an average of the atomistic force acting on a CG site with the average performed over all sampled atomistic configurations consistent with the fixed CG configuration and weighted according to the atomistic distribution function. The normalization of eq (4) defines a multi-dimensional potential of mean force (pmf) describing the CG sites that may be expressed:

$$e^{-\beta V^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})}={\displaystyle {\int }_{D_R}d{\stackrel{\rightharpoonup }{r}}^{N_R}{e}^{-\beta V^{AA}({\stackrel{\rightharpoonup }{r}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_R})}}.$$ (5)

The CG force field defined in eq (4) is the appropriate gradient of this CG potential:

$${\stackrel{\rightharpoonup }{F}}_i^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})=-{\left(\frac{\partial }{\partial {\stackrel{\rightharpoonup }{r}}_i}{V}^{CG}({\stackrel{\rightharpoonup }{r}}^{N_{CG}})\right)}_{{\stackrel{\rightharpoonup }{r}}^{(N_{CG}-1)}}.$$ (6)

2.2. Force-Matching to a Central Pair Potential

Previous numerical applications of the MS-CG method^{16,17,24–27} have approximated the many-body CG potential of mean force (pmf) derived above in eq (5) with a central pair potential. These applications have determined the optimal CG force field by minimizing the residual in eq (1) under the assumptions that the MS-CG force field is pair-wise additive, such that

$${\stackrel{\rightharpoonup }{F}}_i^{I,CG}={\displaystyle \sum _{j\ne i}{\stackrel{\rightharpoonup }{F}}_{i,j}^{CG}}\left({\stackrel{\rightharpoonup }{r}}_i^I,{\stackrel{\rightharpoonup }{r}}_j^I\right)$$ (7)

and, furthermore, that this force field is central,

$${\stackrel{\rightharpoonup }{F}}_{i,j}^{CG}\left({\stackrel{\rightharpoonup }{r}}_i^I,{\stackrel{\rightharpoonup }{r}}_j^I\right)={\stackrel{\rightharpoonup }{u}}_{i,j}^{I}f\left(r_{i,j}^I\right).$$ (8)

In these definitions r⃑_i represents the Cartesian coordinates of CG site i ; ${\stackrel{\rightharpoonup }{r}}_{i,j}={\stackrel{\rightharpoonup }{r}}_i-{\stackrel{\rightharpoonup }{r}}_j$ represents the vector from the j to the i CG site; ${\stackrel{\rightharpoonup }{r}}_{i,j}=\left|{\stackrel{\rightharpoonup }{r}}_i-{\stackrel{\rightharpoonup }{r}}_j\right|$ represents the magnitude of this vector; ${\stackrel{\rightharpoonup }{u}}_{i,j}={\stackrel{\rightharpoonup }{r}}_{i,j}/{\stackrel{\rightharpoonup }{r}}_{i,j}$ represents the associated unit vector; and f(r )represents the function defining the magnitude of the interaction between CG sites and depends only upon the inter-site distance. The force field, f(r ), minimizing the residual under these constraints is uniquely determined and may be conveniently described by a discrete delta function basis for which δ_D (r) =1 when −Δr / 2 ≤r < Δr / 2 and is 0 otherwise. In this basis the force field may be represented as:

$$f(r)={\displaystyle \sum _d^{N_d}{f}_d{\delta }_D(r-r_d).}$$ (9)

This definition corresponds to tabulating the force field at a discrete set of points, r_d, about which ( r_d − Δr / 2 < r < r_d + Δr / 2 ) the force field is assumed to be constant. Previous applications of the MS-CG method^{16,17,24–27} have typically employed a spline basis for representing the FM force field. However, the basis used in eq (9) is particularly amenable for the following analysis and, in the limit that Δr→0, this representation transparently recovers a continuous representation of the force field.

By minimizing the residual (1) with respect to the elements of the force table, $\partial {\chi }^2/\partial f_d=0,$ and employing the definitions in eq (7)–eq (9), a system of linear algebraic equations is obtained:

$${\displaystyle \sum _{d^{\prime }}{f}_{d^{\prime }}{G}_{d{d}^{\prime }}=b_d,}$$ (10)

in which

$$b_d={\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i}({\stackrel{\rightharpoonup }{F}}_i^{I,AA}·{\stackrel{\rightharpoonup }{u}}_{i,j}^I){\delta }_D(r_{i,j}^I-r_d)}}\rangle }_I$$ (11)

and

$$G_{d{d}^{\prime }}={\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i}{\displaystyle \sum _{k\ne i}({\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I){\delta }_D(r_{i,j}^I-r_d){\delta }_D(r_{i,k}^I-r_{d^{\prime }})}}}\rangle }_I.$$ (12)

The angular brackets denote an average over configurations sampled by the atomistic MD simulation. In the following analysis it will be assumed that this average over configurations is equivalent to the appropriate ensemble average:

$${\langle A(r)\rangle }_I=\frac{1}{N_I}{\displaystyle \sum _I{A}^I(r)={\displaystyle \int d{\stackrel{\rightharpoonup }{x}}^N\rho \left({\stackrel{\rightharpoonup }{x}}^N\right)A(r;{\stackrel{\rightharpoonup }{x}}^N)=\langle A(r)\rangle .}}$$ (13)

The linear system in eq (10) is referred to as the “normal” MS-CG equations because G_dd′ is a symmetric, i.e. normal, matrix. Previous numerical implementations of the MS-CG procedure^{16,17,24–28} have employed an additional block-averaging approximation to solve an equivalent system of over-determined equations for the force field, f_d. It is the purpose of this work to further elucidate the physical significance of the “normal” MS-CG equations and, in particular, to relate them to well-known theories for the liquid state.²⁰

In eq (10) all information regarding the atomistic forces has been packaged into the term b_d. According to eq (11), this information enters as the average projection of the instantaneous total force on each CG site, ${\stackrel{\rightharpoonup }{F}}_i^{I,AA},$ onto the sum of unit vectors from all other CG sites, ${\stackrel{\rightharpoonup }{u}}_{i,j}^I,$ that are a distance r_d from i in the given configuration, I. Thus, the quantity b_d describes the average correlation between the instantaneous net force on each CG site and the local spatial distribution of CG sites a distance r_d away. If this distribution is always instantaneously spherically symmetric, then b_d = 0. Similarly, G_dd′ describes the average instantaneous fluctuations in the local density of CG sites at distances r_d and r_d′ , respectively, from each CG site.

Since the j = k term has not been excluded from the triple sum in eq (12), the quantity G_dd′ includes both two- and three-particle correlations, which may be explicitly separated and analyzed:

$$G_{d{d}^{\prime }}={\delta }_{d{d}^{\prime }}{G}_d^{(2)}+G_{d{d}^{\prime }}^{(3)}$$ (14)

$$G_d^{(2)}={\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i}{\delta }_D}(r_{i,j}^I-r_d)}\rangle }_I$$ (15)

$$G_{d{d}^{\prime }}^{(3)}={\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i,k}{\displaystyle \sum _{k\ne i,j}({\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I){\delta }_D(r_{i,j}^I-r_d){\delta }_D(r_{i,k}^I-r_{d^{\prime }})}}}\rangle }_I.$$ (16)

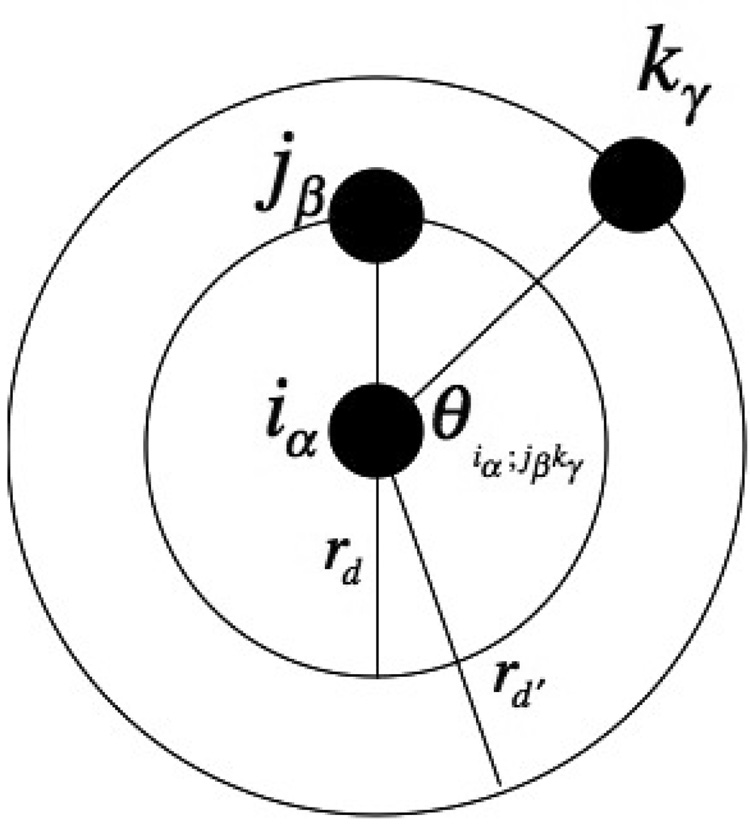
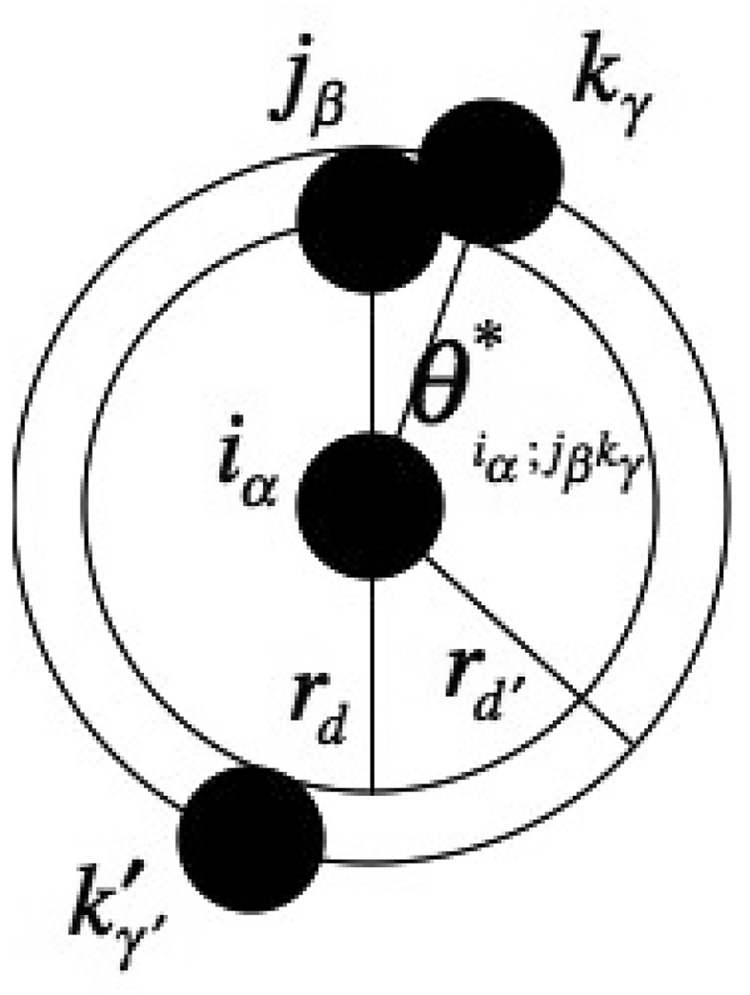
The quantity $G_d^{(2)}$ counts the number of distinct CG sites separated by a distance r_d and is closely related to the radial distribution function for the CG sites. The quantity $G_{d{d}^{\prime }}^{(3)}$ is a direct measure of three-particle correlations between CG sites in atomistic MD simulations. The factor ${\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I=\cos {\theta }_{i;j,k}$ is the cosine of the angle defined between the three CG sites with the site i at the vertex of the angle as illustrated in Figure 1. Thus, $G_{d{d}^{\prime }}^{(3)}$ describes the constrained average value of this quantity for two distinct CG sites, j and k, that are distances r_d and r_d′, respectively, from each CG site, i. Because the three CG sites are distinct, excluded volume effects prevent sites j and k from overlapping. Consequently, for r_d ≈ r_d′, there exists a cone of small angles defined by ${\theta }_{i;j,k}\le {\theta }_{i;j,k}^{*}\approx 0,(\text{such that}{\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I\approx 1,)$ that are never sampled during the MD simulation. Corresponding configurations for which ${\theta }_{i;j,k}\approx \pm \pi (\text{and}{\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I\approx -1)$ are not disfavored and, as a result, the constrained average is negative for distances r_d ≈ r_d′ at which small angle configurations are disfavored. This situation is illustrated in Figure 1b. The form of $G_{d{d}^{\prime }}^{(3)}$ may at first seem somewhat artificial. The dot product factor arises as a consequence of the assumption in eq (8) that the MS-CG force field is directed along the inter-site vector. Moreover, it will be shown that this same factor arises quite naturally in liquid state theories for a central pair potential.

Figure 1.

(a) The geometry of three-particle correlations between CG sites relevant to the MS-CG equations is schematically illustrated. (b) Excluded volume effects define a cone of small angles ${\theta }_{i_{\alpha };j_{\beta }{k}_{\gamma }}\le {\theta }_{i_{\alpha };j_{\beta }{k}_{\gamma }}^{*}$ that is not sampled during MD simulations.

Employing the definitions in eq (14)–eq (16), eq (10) may be re-expressed as:

$$b_d-f_d{G}_d^{(2)}={\displaystyle \sum _{d^{\prime }}{f}_{d^{\prime }}{G}_{d{d}^{\prime }}^{(3)}}.$$ (17)

As mentioned above, all information regarding atomistic forces is contained within b_d. The left hand side of eq (17) depends only upon two-particle information, while the right hand expression reflects three-particle correlations through the term $G_{d{d}^{\prime }}^{(3)},$ which couples the equations for different force table elements. The first term in the left hand expression (i.e., b_d ) describes the average correlation of the total instantaneous force on each CG particle with the spatial distribution of CG particles a distance r_d away. The second term describes the average net force on each CG particle from CG particles a distance r_d away in terms of the MS-CG force field and the average two-particle distribution according to $f_d{G}_d^{(2)}.$ The difference between this average projection of the total force and the average force arising directly from a CG particle at the fixed distance arises from interactions with a third particle. The right hand side of eq (17) then describes how forces from a third particle are correlated with the two-particle structure described in $G_d^{(2)}.$ The quantity $f_{d^{\prime }}{G}_{d{d}^{\prime }}^{(3)}$ describes the average MS-CG force from a distinct third particle, k, a distance r_d′ away from the i CG site, given that the j CG site is a distance r_d away. The dot product in the definition of $G_{d{d}^{\prime }}^{(3)}$ arises because it has been assumed that the interaction between each pair is along the vector connecting them.

Although the numerical MS-CG procedure explicitly employs information regarding the atomistic forces, it is proven in Appendix A that the normal MS-CG equations presented in eq (10) may be recast in a form that is independent of atomistic force information. Under the assumption that the forces on the CG sites measured in MD simulations may be expressed as the gradient of a many-body CG potential energy function generating the observed CG structure, it follows that:

$$\frac{dg(r)}{dr}=\frac{1}{k_{B}T}\left(\frac{1}{4\pi {\rho }^2{V}_0}\right)\frac{1}{r^2}{\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i}({\stackrel{\rightharpoonup }{F}}_i^{I,AA}·{\stackrel{\rightharpoonup }{u}}_{i,j}^I){\delta }_D(r_{i,j}^I-r)}}\rangle }_I,$$ (18)

where

$$g(r)=\left(\frac{1}{4\pi {\rho }^2{V}_0}\right)\frac{1}{r^2}{\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i}{\delta }_D}(r_{i,j}^I-r)}\rangle }_I.$$ (19)

In eq (18) and eq (19) it has been assumed that the average over MD configurations is equivalent to the ensemble average, ρ = N /V₀, and V₀ is the total system volume. Equation (19) defines the radial distribution function for CG sites in an atomistic MD simulation.²⁰ As proven in Appendix A, eq (18) follows immediately from the definition in eq (19).

Multiplying both sides of eq (17) by the factor $1/(4\pi {\rho }^2{V}_0·r_d^2)$ and employing the relations in eq (18) and eq (19), the MS-CG equations for the interaction, f_d, may be expressed as:

$$k_{B}T{\frac{dg}{dr}|}_{r_d}-f_d{g|}_{r_d}={\displaystyle \sum _{d^{\prime }}\left[f_{d^{\prime }}\left(\frac{1}{4\pi {\rho }^2{V}_0}\right)\frac{1}{r_d^2}{G}_{d{d}^{\prime }}^{(3)}\right]}.$$ (20)

Equation (20) contains the same information as eq (17) but has eliminated the explicit dependence upon atomistic forces for an equivalent quantity in terms of the radial distribution function. This equation emphasizes the discrete nature of the MS-CG equations and suggests a continuous representation. The discrete delta function representation defined in eq (9) is particularly convenient for this purpose as, in the limit that Δr→0, eq (20) becomes a one-dimensional linear integral equation

$$k_{B}T\frac{dg(r)}{dr}-f(r)g(r)={\displaystyle \int d{r}^{\prime }f(r^{\prime })M^{FM}(r,r^{\prime }),}$$ (21)

in terms of a FM kernel which describes the effects of three-particle correlations according to

$$\begin{array}{ll}{M}^{FM}(r,r^{\prime })& =\left(\frac{1}{4\pi {\rho }^2{V}_0}\right)\frac{1}{r^2}{G}^{(3)}(r,r^{\prime })\\ & =\left(\frac{1}{4\pi {\rho }^2{V}_0}\right)\frac{1}{r^2}{\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i,k}{\displaystyle \sum _{k\ne i,j}({\stackrel{\rightharpoonup }{u}}_{i,j}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I)\delta (r_{i,j}^I-r)\delta (r_{i,k}^I-r^{\prime })}}}\rangle }_I\end{array}.$$ (22)

Equation (21) re-emphasizes the significance of three-particle correlations in the MS-CG procedure. The left hand side of this equation depends only upon two-particle information and, in the case that the right hand side vanishes, the MS-CG interaction becomes $f(r)=k_{B}Td(\text{ln}g(r))/dr=-w^{\prime }(r),$ where w(r) = −k_BT ln g(r), i.e., the conventional 2-body pmf. Thus the MS-CG pair potential differs significantly from the 2-body pmf because it explicitly considers the effects of three-particle correlations between CG sites in determining a CG force field.

The normal MS-CG equations for a multi-component system are derived in Appendix C. The resulting system of equations for the MS-CG interaction between CG sites of types α and β may be expressed

$$\left(k_{B}T\frac{d}{dr}-f^{\alpha \beta }(r)\right)g_{\alpha \beta }(r)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}^{\prime }\frac{1}{2}\left[M_{\alpha ;\beta \gamma }^{FM}(r,r^{\prime })f^{\alpha \gamma }(r^{\prime })+M_{\beta ;\alpha \gamma }^{FM}(r,r^{\prime })f^{\beta \gamma }(r^{\prime })\right].}}$$ (23)

This equation generalizes eq (21) to consider multiple types of CG particles (labeled with Greek indices), the relevant interactions between them, and also the effect of three-particle correlations centered about the second particle, which is a distinct case for α ≠ β. A more detailed presentation of the derivation is provided in the Supporting Information.

To summarize the preceding analysis, the MS-CG method has been applied to derive a linear integral equation for the MS-CG force field. By assuming that the CG force field is both pair-wise additive and central, according to eq (7) and eq (8), and employing the discrete delta function basis of eq (9), the linear least squares problem defined by the residual in eq (1) has been transformed into a system of linear algebraic equations (10) describing the relationship between the CG force field and the distribution of CG sites. By separating two- and three- particle contributions according to eq (14) and employing the identity in eq (18) to eliminate atomistic force information, the normal MS-CG equations have been recast in a form that depends only upon structural information according to eq (20). Finally, using the discrete basis to pass into the continuum limit, this system of equations has been expressed as the integral equation in eq (21), which generalizes to eq (23) for systems with multiple types of CG sites.

2.3. Yvon-Born-Green Equation

As demonstrated in subsection 2.2, the normal MS-CG equations are a discrete representation of a one-dimensional linear integral equation. For a homogeneous isotropic system, this integral equation is equivalent to the Yvon-Born-Green equation²⁰ describing CG distribution functions resulting from a central pair force field. This result is briefly derived for a one-component system in the present subsection. The general result for multi-component systems is derived in Appendix D. A more detailed presentation is provided as Supporting Information.

Consider a system described by N_CG identical CG sites. The Hamiltonian for this system evolving under an N_CG -particle potential function, V^N_CG, is defined:

$$H({\stackrel{\rightharpoonup }{p}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_{CG}})={\displaystyle \sum _i^{N_{CG}}\frac{1}{2m}{\left|{\stackrel{\rightharpoonup }{p}}_i\right|}^2+V^{N_{CG}}({\stackrel{\rightharpoonup }{r}}^{N_{CG}}).}$$ (24)

Assuming that the total force on each CG site, ${\stackrel{\rightharpoonup }{F}}_i=-\partial V^{N_{CG}}/\partial {\stackrel{\rightharpoonup }{r}}_i,$ arises from a sum of pair interactions,

$${\stackrel{\rightharpoonup }{F}}_i={\displaystyle \sum _j{\stackrel{\rightharpoonup }{F}}_{i,j}}({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j),$$ (25)

then for a homogeneous system with $\rho ({\stackrel{\rightharpoonup }{r}}_i)=\rho =\mathit{\text{const}},$ it follows that the distribution of three arbitrary, but distinct CG particles, i, j, and k may be described according to

$$\left(k_{B}T\frac{\partial }{\partial {\stackrel{\rightharpoonup }{r}}_i}-{\stackrel{\rightharpoonup }{F}}_{i,j}({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j)\right)g^{(2)}({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j)=\rho {\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_k{\stackrel{\rightharpoonup }{F}}_{i,k}}{g}^{(3)}({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j,{\stackrel{\rightharpoonup }{r}}_k).$$ (26)

Equation (26) is the well-known Yvon-Born-Green (YBG) equation²⁰ relating the equilibrium two- and three- CG particle distribution functions to the pair-wise decomposable force field, F⃑_i,j. If the system is also isotropic, the two-particle correlation function is equal to its translational and orientational average:

$$g^{(2)}\left({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j\right)={\displaystyle \int \frac{1}{V_0}d{\stackrel{\rightharpoonup }{r}}_i{\displaystyle \int \frac{1}{4\pi }d{\mathrm{\Omega }}_{j,i}{g}^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i,}{\stackrel{\rightharpoonup }{r}}_j\right)}=}{\hat{\mathrm{P}}}_{\text{RT}}{g}^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i,}{\stackrel{\rightharpoonup }{r}}_j\right)=g\left(r_{i,j}\right).$$ (27)

Equation (27) defines an operator ${\hat{\mathrm{P}}}_{\text{RT}}={\displaystyle \int \frac{1}{V_0}d{\stackrel{\rightharpoonup }{r}}_i{\displaystyle \int \frac{1}{4\pi }d{\mathrm{\Omega }}_{j,i}}}$ which averages over both translation and rotation of the system, where Ω_j,i defines the orientation of the vector r⃑_j,i from the i to the j CG site. For an isotropic homogeneous system the gradient term in eqs (26) may then be simplified as $\partial g^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i,}{\stackrel{\rightharpoonup }{r}}_j\right)/\partial {\stackrel{\rightharpoonup }{r}}_i={\stackrel{\rightharpoonup }{u}}_{i,j}dg\left(r_{i,j}\right)/d{r}_{i,j}.$ Under the additional assumption that the pair interaction between CG sites is central such that,

$${\stackrel{\rightharpoonup }{F}}_{i,j}\left({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j\right)={\stackrel{\rightharpoonup }{u}}_{i,j}f\left(r_{i,j}\right),$$ (28)

eq (26) may be re-expressed to read

$${\stackrel{\rightharpoonup }{u}}_{i,j}\left(k_{B}T\frac{d}{d{r}_{i,j}}-f\left(r_{i,j}\right)\right)g\left(r_{i,j}\right)=\rho {\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_k{\stackrel{\rightharpoonup }{u}}_{i,k}f\left(r_{i,k}\right)g^{(3)}\left({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j,{\stackrel{\rightharpoonup }{r}}_k\right)}.$$ (29)

Projecting this equation onto the vector u⃑_i,j and shifting the integration variable, one obtains the following result:

$$\left(k_{B}T\frac{d}{d{r}_{i,j}}-f\left(r_{i,j}\right)\right)g\left(r_{i,j}\right)=\rho {\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_{k,i}f\left(r_{i,k}\right)\left({\stackrel{\rightharpoonup }{u}}_{i,k}·{\stackrel{\rightharpoonup }{u}}_{i,j}\right)g^{(3)}\left({\stackrel{\rightharpoonup }{r}}_i,{\stackrel{\rightharpoonup }{r}}_j,{\stackrel{\rightharpoonup }{r}}_k\right)}.$$ (30)

Thus the dot product factor arises naturally in an integral equation theory, just as it did in the MS-CG equations. For a system described by a central pair potential without an external field, the average effect of a third particle on two-particle correlations must lie along the two-particle vector.

Because the left hand side of eq (30) depends only on the distance, r_i,j, upon application of the operator P̂_RT eq (30) may be expressed as a one-dimensional integral equation:

$$\left(k_{B}T\frac{d}{d{r}_{i,j}}-f\left(r_{i,j}\right)\right)g\left(r_{i,j}\right)={\displaystyle \int d{r}_{i,k}f\left(r_{i,k}\right)}{M}^{YBG}\left(r_{i,j},r_{i,k}\right).$$ (31)

Equation (31) defines a YBG kernel describing the effects of a third particle on two particle correlations,

$$M^{YBG}\left(r_{i,j},r_{i,k}\right)=\rho r_{i,k}^2{\displaystyle \int d{\mathrm{\Omega }}_{k,i}{\hat{\mathrm{P}}}_{\text{RT}}\left({\stackrel{\rightharpoonup }{u}}_{i,k}·{\stackrel{\rightharpoonup }{u}}_{i,j}\right)}{g}^{(3)}\left({\stackrel{\rightharpoonup }{r}}_{i,}{\stackrel{\rightharpoonup }{r}}_j,{\stackrel{\rightharpoonup }{r}}_k\right).$$ (32)

Moreover, it is shown in Appendix B that

$$M^{YBG}\left(r_{i,j},r_{i,k}\right)=M^{FM}\left(r_{i,j},r_{i,k}\right)=M\left(r_{i,j},r_{i,k}\right).$$ (33)

Therefore, for a homogeneous isotropic system evolving under a central pair potential, the YBG eq (26) may be reduced exactly to the FM equation (21):

$$\left(k_{B}T\frac{d}{dr}-f(r)\right)g(r)={\displaystyle \int d{r}^{\prime }f(r^{\prime })M(r,r^{\prime }).}$$ (34)

Appendix D generalizes the YBG theory for a homogeneous isotropic multi-component CG system. If the system is governed by a set of central pair potentials, the generalized YBG equation reduces to a form that is equivalent to the multi-component MS-CG equations (23):

$$\left(k_{B}T\frac{d}{dr}-f^{\alpha \beta }(r)\right)g_{\alpha \beta }(r)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}^{\prime }\frac{1}{2}\left[f^{\alpha \gamma }(r^{\prime })M_{\alpha ;\beta \gamma }(r,r^{\prime })+f^{\beta \gamma }(r^{\prime })M_{\beta ;\alpha \gamma }(r,r^{\prime })\right].}}$$ (35)

A more detailed derivation is provided in the Supporting Information.

The analysis of section 2 elucidates the general significance of three-particle correlations for deducing CG pair potentials in general and the MS-CG pair force field in particular. Furthermore, the equivalence of eq (23) and eq (35) indicates that the MS-CG method incorporates higher-order correlations in a mechanism that is consistent with the well-known statistical mechanics of the liquid state.²⁰ However, while the analysis of subsection 2.1 and subsection 2.2 and, in particular, the “normal” MS-CG equations presented in eq (17), are generally valid and may be applied to determine a CG force field for any system, the preceding analysis of subsection 2.3, which relates the MS-CG equations to the YBG theory, is strictly valid only for isotropic, homogeneous systems. Moreover, there exists no general proof that the two- and three- CG particle distribution functions measured from atomistic MD simulations may be related to a simple pair potential through a YBG-type equation.^19,31 Rather, as stressed in subsection 2.1, the residual defined by eq (1) is minimized by a many-body CG interaction potential. The MS-CG pair potential investigated in subsection 2.2 is only an approximate decomposition of this interaction potential, albeit one that has physical significance and which incorporates critical three-body correlations as demonstrated in subsection 2.2 and subsection 2.3.

3. Results

The analysis of the previous section demonstrates that the MS-CG equations reflect two- and three-particle correlations between CG sites observed in atomistic MD simulations. The following figures illustrate the effect of these structural correlations on the normal MS-CG equations for coarse-graining a system of 216 Lennard-Jones (LJ) spheres and a system of 216 simple point charge (SPC) water molecules.³² The CG mapping for the LJ system is an identity operation and the resulting MS-CG equations reflect the atomistic structure. The SPC water system is coarse-grained onto two different one-site models: the COM (COG) model maps each SPC molecule onto a single site located at its center-of-mass (geometry). To facilitate comparison between these systems, the LJ sphere system was modeled using the LJ parameters for the oxygen atom in the SPC model. In the following figures, the solid lines correspond to the LJ system, the dashed lines correspond to the SPC system analyzed in terms of the COG, and the dotted lines correspond to the SPC system analyzed in terms of the COM. All MD simulations were performed in the constant NVT ensemble using the GROMACS 3.3.0 software package,³³ with V₀=(1.8602 nm)³ and T = 298K maintained with the Nose-Hoover thermostat.^34,35 All quantities computed from MD simulation were tabulated on a grid with Δr = 0.001nm according to the discrete delta function basis defined in eq (9). Because the grid is so fine, the systems were simulated for 30ns in order to adequately converge all relevant quantities and accurately evaluate necessary numerical derivatives.

Analyzing the MS-CG procedure for the LJ fluid is instructive because the “coarse-graining” for this system is an identity mapping. Clearly there exists a central pair potential that will exactly reproduce the system structure (i.e., the LJ pair potential,) and it is illuminating to investigate the mechanism by which the MS-CG procedure recovers this pair potential from the relevant distribution functions. In contrast, there does not necessarily exist a pair potential for a one-site CG model of water that will reproduce both the two- and three- particle distribution functions measured in atomistic MD simulations.^19,31 The MS-CG procedure determines a central pair potential that would reproduce this structure under the assumption that the CG distribution functions were related by the YBG equation to the assumed central pair potential.

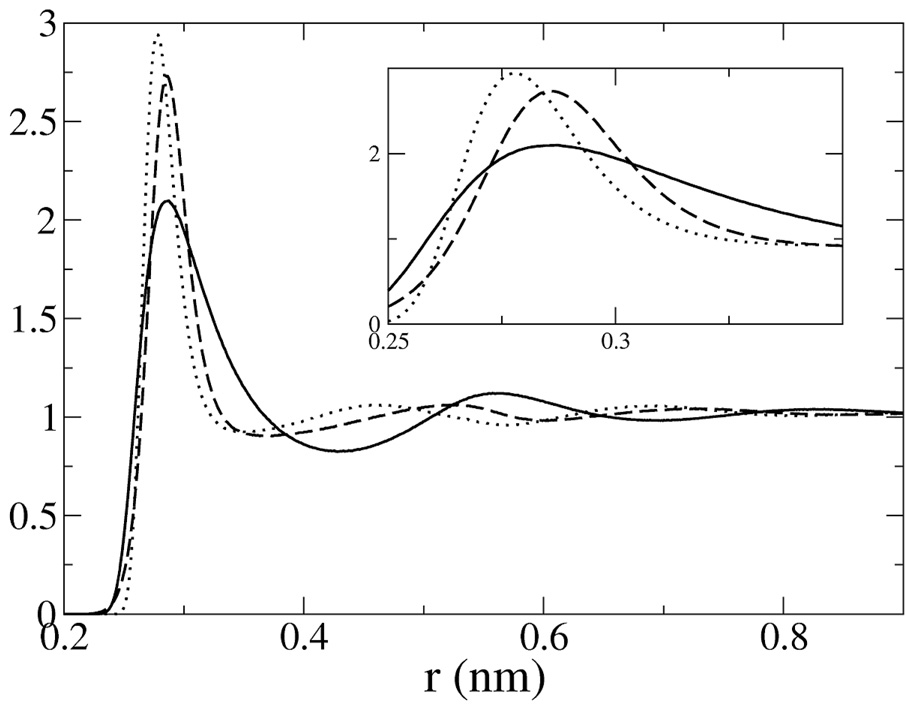
Equation (20) expresses the MS-CG equations in terms of the radial distribution function (rdf), g(r). The rdf’s measured for CG sites in the atomistic simulations are presented in Figure 2. The maxima and minima of the LJ rdf are roughly evenly spaced, corresponding to simple packing. In contrast, the first peak of both SPC rdf’s is much more narrow and the first minima is at shorter range, reflecting the short-range packing effects in water due to the presence of hydrogen atoms. The SPC-COM rdf has a larger and more pronounced hard core region because the CG site roughly corresponds to the oxygen atom of each molecule and the hydrogen atoms that have been integrated out in the CG representation generate a larger excluded volume between the CG sites. In contrast, the SPC-COG model has a less well-defined hard-core region and presents a smaller excluded volume effect. The LJ rdf indicates much longer and more pronounced correlations than either representation of SPC water.

Figure 2.

The radial distribution functions (rdf’s) are presented for atomistic simulations of the LJ (solid), SPC-COG (dashed), and SPC-COM (dotted) systems. The inset provides a detailed comparison of the first peak for each rdf.

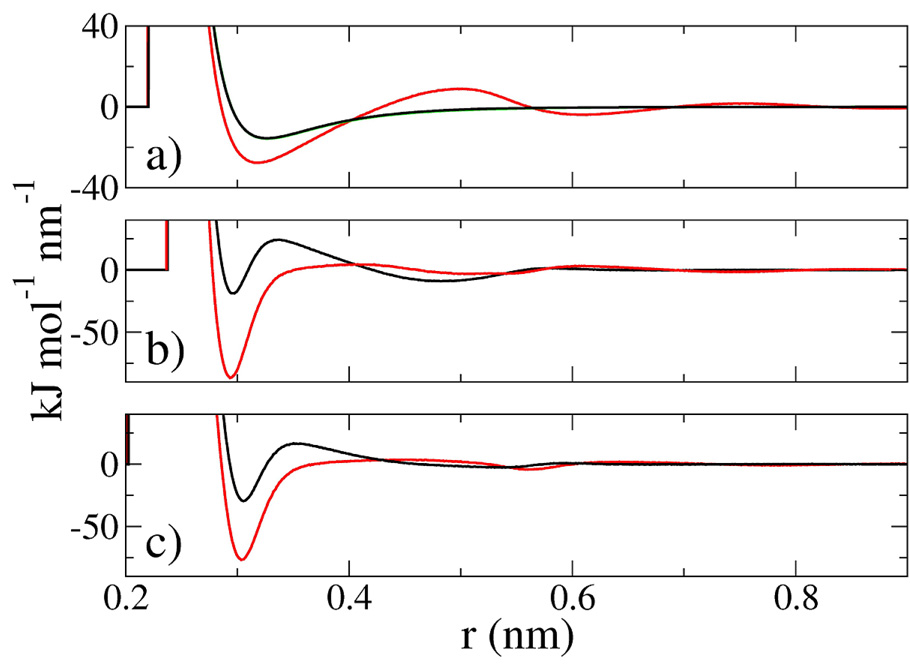
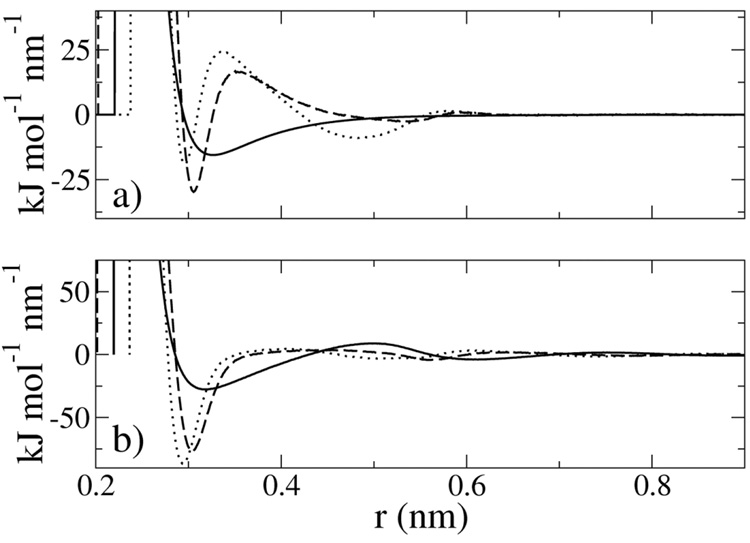
As indicated in section 2.2, if three-particle correlations were not considered in the MS-CG procedure, the resulting CG pair potential would be the conventional two-body pmf. Consequently, the difference between the two-body pmf, w(r), and the MS-CG pair potential may be attributed entirely to the effect of three-particle correlations. Figure 3 directly compares the MS-CG force field, f (r), (black curve) with the mean force, f^mf (r) = −w′ (r), (red curve) for each system. In Figure 3, panel (a) corresponds to the LJ system, while panels (b) and (c) correspond to the SPC-COG and SPC-COM systems, respectively. Figure 4 compares the MS-CG forces (panel a) and the mean forces (panel b) for the different systems. In Figure 4 solid curves describe the LJ system, dashed curves describe the SPC-COG system, and dotted curves describe the SPC-COM system. The mean force is computed from f^mf (r) = k_BTg′ (r) / g(r), where g′ (r) is evaluated using atomistic force information according to eq (18) and the rdf has been smoothed with a running-average over adjacent table elements. The exact LJ force field is also presented as a solid light green line in Figure 3a and it can be seen that the difference between the exact LJ force field and the MS-CG force field for the LJ system is essentially within the thickness of the lines. The mean force for both SPC models vanishes rapidly with increasing r and is relatively featureless after the first attractive well, while the mean force for the LJ model demonstrates longer-range interactions with significant repulsive and attractive regions. The degrees of freedom that have been integrated out in the coarse-grained SPC model screen the mean force between molecules. The MS-CG force field obtained from either representation of the SPC model contains two attractive wells. The first attractive well is deeper and more narrow than the attractive well in the LJ force field. The rapid decay of the mean force after the attractive well in both CG SPC models generates a repulsive barrier in the MS-CG force field at the same distance as the first minimum in the SPC rdf, which corresponds to the presence of hydrogen bonding between each SPC oxygen atom and the second nearest non-bonded hydrogen.³⁶ The barrier between the attractive wells is larger and occurs at shorter range for the SPC-COM model than for the SPC-COG model. The oscillations in the LJ mean force correspond to a smooth monotonic decay of the MS-CG force field.

Figure 3.

The MS-CG force field (black curve) is compared with the mean force (red curve) for the LJ (panel a), SPC-COG (panel b), and SPC-COM (panel c) systems. The difference between the MS-CG force and the mean force arises from the incorporation of three-particle correlations in the MS-CG method according to eq (16). The MS-CG force field for the LJ system is also compared with the exact LJ force field (light green curve) in panel (a) and the difference is seen to be within the thickness of the curve.

Figure 4.

The MS-CG force fields (panel a) and the mean force fields (panel b) are compared for the three different systems. In each panel the LJ results are presented as the solid curve, while the SPC-COG (COM) are presented as the dashed (dotted) curves.

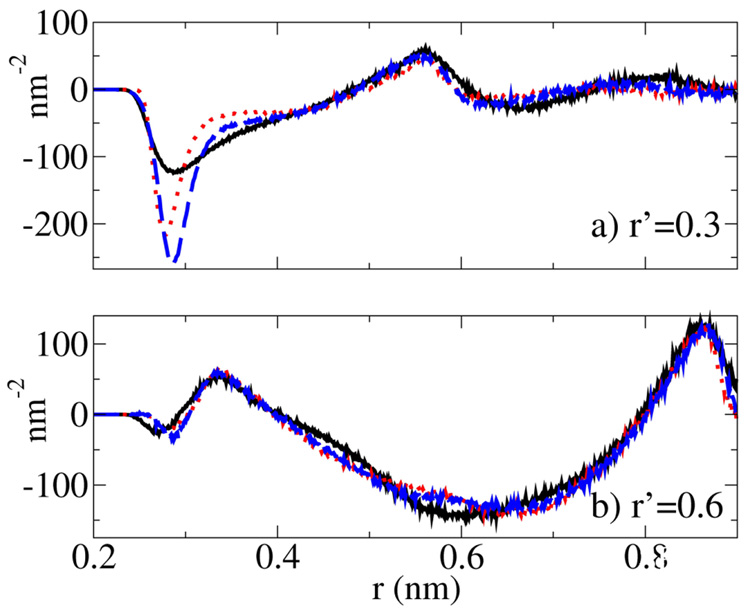
Three-particle correlations enter the MS-CG equations through the quantity $G_{d{d}^{\prime }}^{(3)},$ defined in eq (16), which in the continuum limit may be represented by the symmetric function $G^{(3)}\left(r,r^{\prime }\right)={\langle {\displaystyle \sum _i{\displaystyle \sum _{j\ne i,k}{\displaystyle \sum _{k\ne i,j}\left({\stackrel{\rightharpoonup }{u}}_{i,k}^I·{\stackrel{\rightharpoonup }{u}}_{i,k}^I\right)\delta \left(r_{i,j}^I-r\right)\delta \left(r_{i,k}^I-r^{\prime }\right)}}}\rangle }_I.$ This quantity is plotted in Figure 5 as a function of r for r′ = 0.3 and 0.6 nm . This function reflects the influence of both direct and indirect excluded volume effects on the fluid structure and, ultimately, on the MS-CG interaction potential between CG sites. The three-particle correlations couple the equations for the force field elements, f_d, according to eq (17). Figure 5 has been presented to highlight the fine structure of the three-particle correlations between CG sites within the atomistic system. The range of the coupling, though, is somewhat exaggerated by Figure 5, since the other terms in eq (17) scale as r² due to the statistics of particles on a shell.

Figure 5.

Three-particle correlations between CG sites enter into the MS-CG eq (12) through the quantity G⁽³⁾ (r,r′), which is presented as a function of r for fixed r′ = 0.3 nm (panel a) and r′ = 0.6 nm (panel b). Each panel presents this quantity for the LJ (solid black), SPC-COG (dashed blue), and SPC-COM (dotted red) systems.

For molecular scale coarse-graining (i.e., coarse-graining on length- and time- scales for which molecular excluded volume is relevant), the presence of a fixed third CG particle impacts the distribution of a given pair of CG sites. As illustrated in Figure 1, the geometry of contact between the second and third CG particles defines an excluded volume cone. This cone corresponds to a range of angles θ_i;j,k ≤ θ*_i;j,k ≈ 0 that are not sampled during the MD simulation and, as a result, the spherical average of the cosine of this angle (cos θ_i;j,k = u⃑_i,j · u⃑_i,k) does not vanish. This depletion effect is clearly evident in the calculations of Figure 5, where it can be seen that G⁽³⁾ (r,r′) has a negative peak centered at r ≈ r′. Figure 5 also demonstrates a corresponding density enhancement resulting from the solvation shell of the third CG particle, centered roughly at r ≈ r′ ± 0.3nm. The negative peak of the three-particle correlation function is most pronounced near the first maximum of the rdf. For larger r′, the peak is more diffuse. The SPC water and LJ fluid three-particle correlations are quite similar for r,r′ > 0.3nm and this similarity increases with increasing r,r′. This result is perhaps quite surprising and suggests that, for simple fluids, a reasonable approximation to the three-particle correlation functions important to the MS-CG method might be obtained by appropriately rescaling the LJ three-particle correlation function. This would dramatically reduce the necessary simulation time involved in determining the MS-CG force field, since the three-particle correlation function is clearly the most difficult quantity in the MS-CG equations to converge.

4. Discussion

The analysis of section 2.1 proves that, if no approximations are made in the form of the CG force field, then the MS-CG method determines a multi-dimensional potential of mean force between CG sites according to eq (5). Simulations of CG models employing this many-body interaction potential will sample CG representations of atomistic configurations according to the atomistic distribution function. Such a simulation would reproduce any structural and thermodynamic properties of the atomistic system that may be observed in the CG simulation. However, the calculation and simulation of such a potential are in general not practical. Rather, CG force fields often employ pair potentials to model non-bonded interactions between CG sites. Consequently, it is important to understand the mechanism by which CG pair potentials incorporate many-body effects to approximate this multi-dimensional potential of mean force.

The YBG equation states an exact relationship between the equilibrium two- and three-particle distribution functions resulting from simulations of a given pair potential function.²⁰ If this pair potential depends only upon the inter-particle distance, then, for an isotropic homogeneous system, the YBG equation may be reduced to a one-dimensional integral equation that is equivalent to the MS-CG equations. Thus the MS-CG equations are equivalent in form to a statement of the exact relationship between the two- and three- particle distribution functions that arise from simulations of a homogeneous, isotropic system employing a central pair potential. (However, it should be noted that the converse of the YBG relationship does not necessarily follow. Although, a given pair potential determines a set of resulting correlation functions, a given set of correlation functions does not necessarily determine a pair potential. Thus this relationship does not directly address the general validity of approximating the many-body CG force field with a pairwise additive form.)

The MS-CG procedure may therefore be considered a novel numerical mechanism for solving the ‘inverse’ problem of liquid state theory,¹⁹ i.e., determining an interaction pair potential that generates a given set of distribution functions. If a given set of two- and three-particle distribution functions are generated from a pair interaction, then this interaction may be determined by inverting the generalized YBG equation (26) for F⃑(x⃑_i,x⃑_j). If, moreover, this interaction is central and depends only upon the distance between the two particles, then this pair-wise central force field may be determined by solving the MS-CG equation (23) for f(r_i,j). The MS-CG method takes advantage of atomic force information rather than directly evaluating the numerical derivative of the rdf, which may require extensive sampling.

The Ornstein-Zernicke (OZ) and YBG equations are two of the most well known integral equations for liquid state theory.²⁰ The ‘direct’ solution to either integral equation for the two-particle distribution function requires an (approximate) closure relation that determines a second unknown function in the integral equation. The closure for the OZ equation involves the direct correlation function, c(r), while the closure relation for the YBG equation involves the three-particle distribution function. The OZ equation has been particularly useful for investigating the structure of simple liquids because the direct correlation function is short-ranged and, consequently, more amenable to theoretical and numerical analysis than the YBG equation which depends upon the three-particle correlation function, g⁽³⁾. The OZ equation has also been employed in developing force fields for CG models.¹⁴ However, the YBG equation may be more useful than the OZ equation for solving the inverse problem in developing CG force fields. Although c(r) may be determined by directly inverting the OZ equation, approximate closure relations are necessary to relate the direct correlation function to a CG pair potential. In contrast, the YBG equation for the CG pair potential may be closed by directly computing the relevant distributions of CG sites within an atomistic MD simulation. Inverting the resulting equation provides a force field that will reproduce the correct CG structure, under the assumption that such a force field exists.

It is a fundamental assumption that the CG distribution functions measured in atomistic MD simulations may be generated from a pair-wise central force field. In general, there may not exist such a CG pair potential that will reproduce both the two- and three- particle distribution functions characterizing a given system. Consequently the MS-CG equations presented in eq (21) are not necessarily an exact identity describing the CG structure because the assumed pair potential giving rise to the measured CG two- and three-particle distribution functions may not exist. In fact, recent work has demonstrated that many-body^37–41 and non-central^42,43 interactions may be critical for the coarse-grained modeling of proteins.

The underlying variational principle provides tremendous flexibility in the MS-CG methodology. By minimizing the residual in eq (1), the MS-CG method systematically determines an optimal approximation to the multi-dimensional many-body CG PMF. If no assumptions are made in the form of the CG interaction, the MS-CG procedure determines this many-body PMF, which would reproduce both two- and three-particle structural correlations in CG simulations. Previous numerical implementations of the MS-CG procedure^{16,17,24–28} have determined and employed an optimal central pair decomposition of this CG PMF. However, in principle, the MS-CG procedure may be readily generalized to incorporate both non-central and many-body effects within the CG force field by relaxing the assumptions explicit in eq (7)–eq (8). Many-body interactions may be incorporated into the MS-CG force field either by generalizing the approach of eq (9) and tabulating additional many-body interaction terms on a multidimensional grid or by parameterizing an assumed functional form by minimizing the MS-CG residual. Similarly, non-central interactions may also be incorporated into the CG force field, for instance, by expanding the pair interaction in eq (8) as a series of spherical harmonics.⁴³ However, if the interaction does not depend linearly upon the force field parameters, the minimization procedure for optimizing the MS-CG force field requires a nonlinear regression algorithm.²²

The reverse Monte Carlo (RMC) method has been employed to determine a CG potential that reproduces a given CG rdf when used in CG simulations.^2,29 Chayes and Chayes¹⁹ have proven that there does indeed exist a unique⁴⁴ pair potential that will reproduce an observed rdf.¹⁴ However, this potential is not guaranteed to reproduce higher order distribution functions.³¹ Although by design the RMC method should reproduce CG rdf’s to the desired numerical precision,^2,29 simulations employing this pair potential may not necessarily reproduce the correct three-particle correlations for the system. In particular, using a similar RMC procedure to generate water configurations from known radial distribution functions, Jedlovsky et al.⁴⁵ have demonstrated that three-particle correlations may be inaccurately reproduced although the observed rdf’s are quantitatively accurate. In contrast, Iuchi et al.⁴⁶ have demonstrated that the MS-CG procedure accurately reproduces both the two- and three-particle correlations of a polarizable 4-site water model using a non-polarizable 4-site MS-CG force field.

It is of some interest to briefly compare the MS-CG and RMC methods for developing CG potentials in light of the YBG equation for homogeneous isotropic systems. The MS-CG method implicitly measures the two- and three- particle correlation functions describing CG sites within an atomistic MD simulation and then directly inverts the YBG equation to determine a central CG pair potential that would generate these distribution functions, should such a potential exist. In general such a potential may not exist and, consequently, simulations employing the MS-CG pair potential will not necessarily reproduce either the two- or three-particle correlations exactly. Rather CG simulations employing the MS-CG force field will satisfy a different YBG equation relating the fixed MS-CG force field and the resulting CG distribution functions. Although the MS-CG force field does not necessarily reproduce either the two- or three-particle distribution functions exactly, the method clearly incorporates three-particle correlations. Moreover, because the method does not necessarily reproduce the pair correlation functions, comparison of the relevant rdf’s between atomistic and CG MD simulations is a useful measure of the validity of the CG model.

In contrast, the RMC method only directly considers the two-particle correlation function and attempts to solve the YBG equation for the pair interaction that reproduces the target rdf while allowing the three-particle correlation function to vary as necessary.^2,29 The repeated MC or MD simulations used in iteratively updating the pair potential may be considered a nonlinear regression algorithm that tries to solve the YBG equation for a pair potential reproducing a fixed rdf. If three-particle correlations were not significant in the YBG equation, then the pair potential would be simply the two-body pmf, which is often implemented as an initial condition in the search for the optimal pair potential. With succesive iterations the simulated rdf converges to the target rdf measured from atomistic MD simulations.² The RMC method implicitly incorporates information regarding three-particle correlations by updating the force field to improve agreement between the measured and target rdf, although in successive simulations the three-particle correlations may change. The YBG equation that is implicitly solved through the RMC method incorporates the target rdf and is guaranteed to reproduce this rdf. However, the three-particle correlations in the final YBG equation may be different than those in the original atomistic representation of the system.

In closing, two additional points require brief discussion. The preceding analysis directly addresses non-bonded interactions between CG sites. Bonded interactions may be treated as special cases of non-bonded interactions or by introducing additional terms into the MS-CG potential. In the latter case, the contributions from these interactions should be subtracted from the total forces on CG sites and the preceding analysis still holds for non-bonded interactions. Additionally, it has been mentioned repeatedly that the MS-CG equations are equivalent to the YBG equation for a homogeneous, isotropic system evolving under a central pair potential. In principle, a system described by a central pair potential may be both homogeneous and isotropic. However, these symmetries are not necessarily realized in MD simulations of complex interfacial or biological systems. The presence of a lipid bilayer or a protein in an MD simulation box may break this symmetry. The analysis of Section 2.3, though, requires the additional assumptions of isotropy and homogeneity. Consequently, the FM equations are rigorously equivalent to the YBG equations in eq (35) only for relatively simple systems. However, the analysis of Section 2.2 demonstrates that the FM force field incorporates critical information regarding three-particle correlations for any system. It has been empirically demonstrated that even for highly complex systems the MS-CG method generates a useful and quantitatively accurate model.^{16,17,24–28,46}

5. Conclusions

The present work develops a statistical mechanical framework for understanding the foundations and success of the MS-CG method. It has been shown that the MS-CG method may be used to derive a multi-dimensional pmf for the interactions between CG sites. The “normal” MS-CG equations have been derived for approximating this many-body interaction with central pair potentials. The derivation demonstrates that the MS-CG equations for these potentials reflect not only two-body, but also three-body correlations observed between CG sites during atomistic MD simulations. The generalized YBG equation has been presented for CG systems and it has been proven that this generalized YBG equation is equivalent to the normal MS-CG equations for a homogeneous, isotropic system evolving under a central pair potential. The present analysis provides a connection between the MS-CG method and equilibrium statistical mechanics and also illuminates the general significance of three-particle correlations for deriving CG effective pair potentials.

Supplementary Material

si20061212_110. Supporting Information Available.

A more detailed presentation of the theory is provided as a Supporting Information section. This material is available free of charge via the Internet at http://pubs.acs.org.

Appendices

Appendices A and B involve the properties of Dirac delta functions in spherical polar coordinates. In particular, the derivation of eq (18) and eq (33) employ the following relation⁴⁷

$$\int d\mathrm{\Omega }A(\stackrel{\rightharpoonup }{r}){\delta }^{(3)}(\stackrel{\rightharpoonup }{r}-{\stackrel{\rightharpoonup }{r}}_0)=\frac{1}{r^2}{A}_{SP}(r,{\mathrm{\Omega }}_0)\delta (r-r_0),$$ (36)

which is valid for all r₀ ≠ 0. In eq (36), A_SP (r,Ω₀ ) is the representation of the function A(r⃑) in spherical polar coordinates evaluated in the direction Ω₀ defined by the vector r⃑₀.

Appendix A. Derivation of Equation (18)

Assume that the CG configurations employed in the FM procedure were sampled according to a distribution function, ${\rho }_{CG}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)=\exp \left[-V^{CG}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)/k_{B}T\right]/Z(N,V_0,T),$ where $V^{CG}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)$ is a many-particle CG potential function describing the interactions between CG sites. Selecting two arbitrary CG sites, i and j, and transforming into “sum,” ${\stackrel{\rightharpoonup }{R}}_{ij}=\frac{1}{2}\left({\stackrel{\rightharpoonup }{r}}_i+{\stackrel{\rightharpoonup }{r}}_j\right),$ and “difference,” r⃑_ij = r⃑_i − r⃑_j, variables, then it follows that:

$${\left(\frac{\partial {\rho }_{CG}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)}{\partial r_{ij}}\right)}_{{\stackrel{\rightharpoonup }{R}}_{ij},{\mathrm{\Omega }}_{ij},{\stackrel{\rightharpoonup }{r}}^{(N_{CG}-2)}}=\frac{1}{2k_{B}T}\left(\left({\stackrel{\rightharpoonup }{F}}_i-{\stackrel{\rightharpoonup }{F}}_j\right)·{\stackrel{\rightharpoonup }{u}}_{ij}\right){\rho }_{CG}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right).$$ (37)

The partial derivative is evaluated with respect to the inter-CG site distance (difference variable) r_ij, while holding fixed the relative (difference) orientation Ω_ij, and average position of the two CG sites R⃑_ij as well as the remaining N_CG − 2 sites, ${\stackrel{\rightharpoonup }{r}}^{(N_{CG}-2)}.$

Consider next the quantity G_ij(r) = 〈δ(r − r_ij)〉. Employing the identity in eq (36), it can be proven that

$$\frac{d}{dr}{G}_{ij}(r)=\frac{2}{r}{G}_{ij}(r)+\frac{1}{2k_{B}T}\langle ({\stackrel{\rightharpoonup }{F}}_i-{\stackrel{\rightharpoonup }{F}}_j)·{\stackrel{\rightharpoonup }{u}}_{ij}\delta (r-r_{ij})\rangle .$$ (38)

Let i and j correspond to CG site types α and β, respectively, and define the radial distribution function

$$g_{\alpha \beta }(r)=\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{r^2}\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}{G}_{i_{\alpha }{j}_{\beta }}(r)}}\rangle ,$$ (39)

then

$$\frac{d}{dr}{g}_{\alpha \beta }(r)=\frac{1}{2k_{B}T}\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{r^2}\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}\left({\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}-{\stackrel{\rightharpoonup }{F}}_{j_{\beta }}\right)·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha }j\beta }\delta (r-r_{i_{\alpha }{j}_{\beta }})}}\rangle .$$ (40)

In the case that α = β, the two terms in the summations are equivalent and the result simplifies:

$$\frac{d}{dr}{g}_{\alpha \alpha }(r)=\frac{1}{k_{B}T}\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\alpha }{V}_0}\right)\frac{1}{r^2}\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\alpha }\ne i_{\alpha }}\left({\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha }{j}_{\alpha }}\right)\delta (r-r_{i_{\alpha }{j}_{\alpha }})}}\rangle .$$ (41)

A more detailed derivation is provided in the supporting information section.

Appendix B. Derivation of Equation (33)

Consider the distribution of three distinct CG particles at positions r⃑₁, r⃑₂, and r⃑₃ corresponding to particles i_α, j_β, and kγ in Figure 1. The FM kernel is defined

$$M_{\alpha ;\beta \gamma }^{FM}(r_{12},r_{13})=\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{{r_{12}}^2}{\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha },k_{\gamma }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha },j_{\beta }}({\stackrel{\rightharpoonup }{u}}_{i_a,j_{\beta }}^I·{\stackrel{\rightharpoonup }{u}}_{i_a,k_{\gamma }}^I){\delta }_M(r_{i_a,j_{\beta }}^I-r_{12}){\delta }_M(r_{i_{\alpha },k_{\gamma }}^I-r_{13})}}}\rangle }_I$$ (42)

The YBG kernel is defined:

$$M_{\alpha ;\beta \gamma }^{YBG}(r_{12},r_{13})={\rho }_{\gamma }{r_{13}}^2{\displaystyle \int d{\mathrm{\Omega }}_{31}{\displaystyle \int \frac{1}{4\pi }d{\mathrm{\Omega }}_{21}{\displaystyle \int \frac{1}{V_0}d{\stackrel{\rightharpoonup }{r}}_1({\stackrel{\rightharpoonup }{u}}_{12}·{\stackrel{\rightharpoonup }{u}}_{13})g_{\alpha \beta \gamma }^{(3)}({\stackrel{\rightharpoonup }{r}}_1,{\stackrel{\rightharpoonup }{r}}_2,{\stackrel{\rightharpoonup }{r}}_3)}}}$$ (43)

where Ω_n1 defines the orientation of the unit vector u⃑_n and the three-particle correlation function is defined:

$$g_{\alpha \beta \gamma }^{(3)}({\stackrel{\rightharpoonup }{r}}_1,{\stackrel{\rightharpoonup }{r}}_2,{\stackrel{\rightharpoonup }{r}}_3)=\frac{1}{{\rho }_{\alpha }{\rho }_{\beta }{\rho }_{\gamma }}{\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha },k_{\gamma }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha },j_{\beta }}{\delta }^{(3)}({\stackrel{\rightharpoonup }{r}}_{i_a}^I-{\stackrel{\rightharpoonup }{r}}_1){\delta }^{(3)}({\stackrel{\rightharpoonup }{r}}_{j_{\beta }}^I-{\stackrel{\rightharpoonup }{r}}_2){\delta }^{(3)}({\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}^I-{\stackrel{\rightharpoonup }{r}}_3)}}}\rangle }_I.$$ (44)

The definitions in eq (42) and eq (44) assume that the average over configurations is equivalent to the appropriate ensemble average. After integrating over r⃑₁ in eq (43), the YBG kernel may be expressed

$${\begin{array}{c}M\frac{YGG}{\alpha ;\beta \gamma }(r_{12},r_{13})=\\ \frac{{r_{13}}^2}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{v}_0}\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta \ne i_{\alpha }},{\kappa }_{\gamma }}{\displaystyle \sum _{{\kappa }_{\gamma }\ne i_{\alpha },j_{\beta }}{\displaystyle \int d{\Omega }_{31}{\displaystyle \int d{\Omega }_{21}({\stackrel{\rightharpoonup }{u}}_{12}({\Omega }_{21})·{\stackrel{\rightharpoonup }{u}}_{13}({\mathrm{\Omega }}_{31})){\delta }^{(3)}}({\stackrel{\rightharpoonup }{r}}_{j_{\beta },i_{\alpha }}^I-{\stackrel{\rightharpoonup }{r}}_{21}){\delta }^{(3)}}({\stackrel{\rightharpoonup }{r}}_{{\kappa }_{\gamma },i_{\alpha }}^I-{\stackrel{\rightharpoonup }{r}}_{31})}}}\rangle \end{array}}_I$$ (45)

The integrals over the orientational degrees of freedom may then be evaluated according to the identity in eq (36). Upon performing these integrals within the ensemble average, one obtains the desired result:

$$\begin{array}{ll}{M}_{\alpha ;\beta \gamma }^{YBG}(r_{12},r_{13})& =\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{{r_{12}}^2}{\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha },k_{\gamma }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha },j_{\beta }}({\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}^I)\delta (r_{i_a,j_{\beta }}^I-r_{12})\delta (r_{i_{\alpha },k_{\gamma }}^I-r_{13})}}}\rangle }_I\\ & =M_{\alpha ;\beta \gamma }^{FM}(r_{12},r_{13})\end{array}.$$ (46)

Appendix C. Normal FM equations for a multi-component system

The FM residual for a system with multiple types of CG sites may be expressed:

$${\chi }^2=\frac{1}{3N_I{N}_{CG}}{\displaystyle \sum _I^{N_I}{\displaystyle \sum _{\alpha }^{N_T}{\displaystyle \sum _{i_{\alpha }}^{N_{\alpha }}{\left|{\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}^{I,AA}-{\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}^{I,CG}\right|}^2.}}}$$ (47)

In eq (47) and in the following, Greek indices ( α) represent types of CG sites, Latin subscripts ( i ) represent particular sites of a given CG type, and the superscript ( I ) labels configurations sampled during the atomistic MD simulation. As before it is assumed that the FM force field is pair-wise additive, such that

$${\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}^{I,CG}={\displaystyle \sum _{\beta }{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}{\stackrel{\rightharpoonup }{F}}_{i_{\alpha },j_{\beta }}^{CG}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }}^I,{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}^I\right)}}$$ (48)

and, furthermore, that this force field is central:

$${\stackrel{\rightharpoonup }{F}}_{i_{\alpha },j_{\beta }}^{CG}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }}^I,{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}^I\right)={\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I{f}^{\alpha \beta }\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha },j_{\beta }}^I\right).$$ (49)

Employing the discrete delta function basis of eq (9), a system of linear equations (i.e., the “normal” FM equations for a multi-component system) is obtained by minimizing the residual in eq (47) with respect to each interaction, $f_d^{\alpha \beta }:$

$${\displaystyle \sum _{\gamma }{\displaystyle \sum _{d^{\prime }}\left[\left(1-{\delta }_{\alpha \beta }\right)f_{d^{\prime }}^{\alpha \gamma }{G}_{d{d}^{\prime }}^{\alpha ;\beta \gamma }+f_{d^{\prime }}^{\beta \gamma }{G}_{d{d}^{\prime }}^{\beta ;\alpha \gamma }\right]=\left(1-{\delta }_{\alpha \beta }\right)b_d^{\alpha \beta }+b_d^{\beta \alpha },}}$$ (50)

in which

$$b_d^{\alpha \beta }={\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}\left({\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}^{I,AA}·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I\right)}{\delta }_D\left(r_{i_{\alpha },j_{\beta }}^I-r_d\right)}\rangle }_I,$$ (51)

and

$$G_{d{d}^{\prime }}^{\alpha ;\beta \gamma }={\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha }}\left({\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}^I\right)}{\delta }_D\left(r_{i_{\alpha },j_{\beta }}^I-r_d\right){\delta }_D\left(r_{i_{\alpha },k_{\gamma }}^I-r_{d^{\prime }}\right)}}\rangle }_I.$$ (52)

Equation (50) generalizes eq (10) and employs the symmetry $f_d^{\alpha \beta }=f_d^{\beta \alpha }.$ The quantity defined in eq (52) may be decomposed into two- and three-particle contributions according to:

$$G_{d{d}^{\prime }}^{\alpha ;\beta \gamma }={\delta }_{\beta \gamma }{\delta }_{d{d}^{\prime }}{\left(G^{(2)}\right)}_d^{\alpha \beta }+{\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\alpha ;\beta \gamma },$$ (53)

where

$${\left(G^{(2)}\right)}_d^{\alpha \beta }={\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha }}{\delta }_D\left(r_{i_{\alpha },j_{\beta }}^I-r_d\right)}}\rangle }_I$$ (54)

and

$${\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\alpha ;\beta \gamma }={\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha },k_{\gamma }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha },j_{\beta }}\left({\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}^I\right)}{\delta }_D\left(r_{i_{\alpha },j_{\beta }}^I-r_d\right)}}{\delta }_D\left(r_{i_{\alpha },k_{\gamma }}^I-r_{d^{\prime }}\right)\rangle }_I.$$ (55)

Employing these definitions, eq (50) may then be re-expressed:

$$\begin{array}{l}\left(1-{\delta }_{\alpha \beta }\right)\left[b_d^{\alpha \beta }-f_d^{\alpha \beta }{\left(G^{(2)}\right)}_d^{\alpha \beta }\right]+\left[b_d^{\beta \alpha }-f_d^{\alpha \beta }{\left(G^{(2)}\right)}_d^{\beta \alpha }\right]=\\ \hfill {\displaystyle \sum _{\gamma }{\displaystyle \sum _{d^{\prime }}\left[\left(1-{\delta }_{\alpha \beta }\right)f_{d^{\prime }}^{\alpha \gamma }{\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\alpha ;\beta \gamma }{f}_{d^{\prime }}^{\beta \gamma }{\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\beta ;\alpha \gamma }\right]}}\end{array}$$ (56)

Upon multiplication by the factor 1/(4πρ_αρ_βV₀·r_d²) and application of the definition in eq (39) and the identity in eq (41) from Appendix A, eq (56) may be expressed:

$$k_{B}T{\frac{d{g}_{\alpha \beta }}{dr}|}_d-f_d^{\alpha \beta }{g_{\alpha \beta }|}_d={\displaystyle \sum _{\gamma }{\displaystyle \sum _{d^{\prime }}\frac{1}{2}\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{r_d^2}\left[f_{d^{\prime }}^{\alpha \gamma }{\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\alpha ;\beta \gamma }+f_{d^{\prime }}^{\beta \gamma }{\left(G^{(3)}\right)}_{d{d}^{\prime }}^{\beta ;\alpha \gamma }\right]}}.$$ (57)

Passing into the continuum limit, eq (57) may be represented by a linear one-dimensional integral equation:

$$\left(k_{B}T\frac{d}{dr}-f^{\alpha \beta }(r)\right)g_{\alpha \beta }(r)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}^{\prime }\frac{1}{2}\left[f^{\alpha \gamma }\left(r^{\prime }\right)M_{\alpha ;\beta \gamma }^{FM}(r,r^{\prime })+f^{\beta \gamma }\left(r^{\prime }\right)M_{\beta ;\alpha \gamma }^{FM}(r,r^{\prime })\right]}},$$ (58)

where

$$M_{\alpha ;\beta \gamma }^{FM}\left(r,r^{\prime }\right)=\left(\frac{1}{4\pi {\rho }_{\alpha }{\rho }_{\beta }{V}_0}\right)\frac{1}{r^2}{\langle {\displaystyle \sum _{i_{\alpha }}{\displaystyle \sum _{j_{\beta }\ne i_{\alpha },k_{\gamma }}{\displaystyle \sum _{k_{\gamma }\ne i_{\alpha },j_{\beta }}\left({\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}^I·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}^I\right)}\delta \left(r_{i_{\alpha },j_{\beta }}^I-r\right)}}\delta \left(r_{i_{\alpha },k_{\gamma }}^I-r^{\prime }\right)\rangle }_I,$$ (59)

and, according to Appendix B, $M_{\alpha ;\beta \gamma }^{FM}\left(r,r^{\prime }\right)=M_{\alpha ;\beta \gamma }^{YBG}\left(r,r^{\prime }\right)=M_{\alpha ;\beta \gamma }\left(r,r^{\prime }\right).$

Appendix D. Generalized YBG equation for multi-component CG system

The Hamiltonian for a system with N_α sites of type α and $N_{CG}={\displaystyle \sum _{\alpha }^{N_T}{N}_{\alpha }}$ total CG sites evolving under an N_CG particle potential function, V^N_CG, is defined:

$$H\left({\stackrel{\rightharpoonup }{p}}^{N_{CG}},{\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)={\displaystyle \sum _{\alpha }^{N_T}{\displaystyle \sum _{i_{\alpha }}^{N_{\alpha }}\frac{1}{2m_{\alpha }}{\left|{\stackrel{\rightharpoonup }{p}}_{i_{\alpha }}\right|}^2+V^{N_{CG}}\left({\stackrel{\rightharpoonup }{r}}^{N_{CG}}\right)}.}$$ (60)

Assuming that the total force on each CG site, ${\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}=-\partial V^{N_{CG}}/\partial {\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},$ arises from a sum of pair interactions,

$${\stackrel{\rightharpoonup }{F}}_{i_{\alpha }}={\displaystyle \sum _{\beta }{\displaystyle \sum _{j_{\beta }}{\stackrel{\rightharpoonup }{F}}_{i_{\alpha },j_{\beta }}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)},}$$ (61)

then for a homogeneous system with ρ_α(r⃑_iα) = ρ_α = const, the following relations describe the distribution of three arbitrary but distinct CG particles, i_α, j_β, and kγ :

$$\begin{array}{l}\left(k_{B}T\frac{\partial }{\partial {\stackrel{\rightharpoonup }{r}}_{i_{\alpha }}}-{\stackrel{\rightharpoonup }{F}}_{i_{\alpha },j_{\beta }}\right)g_{\alpha \beta }^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)={\displaystyle \sum _{\gamma }{\rho }_{\gamma }{\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}}}{\stackrel{\rightharpoonup }{F}}_{i_{\alpha },k_{\gamma }}{g}_{\alpha \beta \gamma }^{(3)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }},{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}\right)\\ \left(k_{B}T\frac{\partial }{\partial {\stackrel{\rightharpoonup }{r}}_{j_{\beta }}}-{\stackrel{\rightharpoonup }{F}}_{j_{\beta },i_{\alpha }}\right)g_{\alpha \beta }^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)={\displaystyle \sum _{\gamma }{\rho }_{\gamma }{\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}}}{\stackrel{\rightharpoonup }{F}}_{j_{\beta },k_{\gamma }}{g}_{\alpha \beta \gamma }^{(3)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }},{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}\right)\end{array}.$$ (62)

Equations (62) generalize the Yvon-Born-Green (YBG) equation²⁰ and relate the equilibrium two- and three- CG particle distribution functions to the pair-wise decomposable force field, F⃑_iα·jβ. As before, for an isotropic homogeneous system, the two-particle distribution function is equal to its rotational and translational average, $g_{\alpha \beta }^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)=g_{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right),$ and the gradient terms in eqs (62) may then be simplified: $\partial g_{\alpha \beta }^{(2)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)/\partial {\stackrel{\rightharpoonup }{r}}_{i_{\alpha }}={\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}d{g}_{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)/d{r}_{i_{\alpha },j_{\beta }}.$ Under the additional assumption that the pair interaction between CG sites is central, ${\stackrel{\rightharpoonup }{F}}_{i_{\alpha },j_{\beta }}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }}\right)={\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}{f}^{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right),$ the first equality in eq (62) may be re-expressed:

$${\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}\left(k_{B}T\frac{d}{d{r}_{i_{\alpha },j_{\beta }}}-f^{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)\right)g_{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)={\displaystyle \sum _{\gamma }{\rho }_{\gamma }{\displaystyle \int d{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}{f}^{\alpha \gamma }\left(r_{i_{\alpha },k_{\gamma }}\right)g_{\alpha \beta \gamma }^{(3)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }},{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}\right).}}$$ (63)

Projecting this equation onto the vector u⃑_iα,jβ and shifting the integration variable, one obtains the result:

$$\left(k_{B}T\frac{d}{d{r}_{i_{\alpha },j_{\beta }}}-f^{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)\right)g_{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}_{i_{\alpha },k\gamma }{f}^{\alpha \gamma }\left(r_{i_{\alpha },k_{\gamma }}\right)M_{\alpha ;\beta \gamma }^{YBG}\left(r_{i_{\alpha },j_{\beta }},r_{i_{\alpha },k_{\gamma }}\right),}}$$ (64)

where,

$$M_{\alpha ;\beta \gamma }^{YBG}\left(r_{i_{\alpha },j_{\beta }},r_{i_{\alpha },k_{\gamma }}\right)={\rho }_{\gamma }{\left(r_{i_{\alpha },k_{\gamma }}\right)}^2{\displaystyle \int d{\mathrm{\Omega }}_{k_{\gamma },i_{\alpha }}{\hat{P}}_{\text{RT}}\left({\stackrel{\rightharpoonup }{u}}_{i_{\alpha },k_{\gamma }}·{\stackrel{\rightharpoonup }{u}}_{i_{\alpha },j_{\beta }}\right)g_{\alpha \beta \gamma }^{(3)}\left({\stackrel{\rightharpoonup }{r}}_{i_{\alpha }},{\stackrel{\rightharpoonup }{r}}_{j_{\beta }},{\stackrel{\rightharpoonup }{r}}_{k_{\gamma }}\right)}$$ (65)

and, according to Appendix B, $M_{\alpha ;\beta \gamma }^{YBG}\left(r,r^{\prime }\right)=M_{\alpha ;\beta \gamma }^{FM}\left(r,r^{\prime }\right)=M_{\alpha ;\beta \gamma }\left(r,r^{\prime }\right).$ Similar manipulation of the second relation in eq (62) yields

$$\left(k_{B}T\frac{d}{d{r}_{i_{\alpha },j_{\beta }}}-f^{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)\right)g_{\alpha \beta }\left(r_{i_{\alpha },j_{\beta }}\right)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}_{j_{\beta },k\gamma }{f}^{\beta \gamma }\left(r_{j_{\beta },k_{\gamma }}\right)M_{\beta ;\alpha \gamma }\left(r_{i_{\alpha },j_{\beta }},r_{j_{\alpha },k_{\gamma }}\right).}}$$ (66)

The left hand sides and thus the right hand sides of eq (64) and eq (66) are identical. The two equations may then be averaged to yield the final result, the YBG equation for a homogeneous, isotropic multi-component CG system evolving under a central pair potential:

$$\left(k_{B}T\frac{d}{dr}-f^{\alpha \beta }\left(r\right)\right)g_{\alpha \beta }\left(r\right)={\displaystyle \sum _{\gamma }{\displaystyle \int d{r}^{\prime }\frac{1}{2}\left[f^{\alpha \gamma }\left(r^{\prime }\right)M_{\alpha ;\beta \gamma }\left(r,r^{\prime }\right)+f^{\beta \gamma }\left(r^{\prime }\right)M_{\beta ;\alpha \gamma }\left(r,r^{\prime }\right)\right].}}$$ (67)

Therefore, the generalized YBG equation for a homogeneous and isotropic multi-component CG system evolving under a central pair potential is equivalent to the normal multi-component FM eqs (58).