Abstract
Objective
To evaluate reliability in 3D landmark identification using Cone-Beam CT.
Study Design
Twelve pre-surgery CBCTs were randomly selected from 159 orthognathic surgery patients. Three observers independently repeated three times the identification of 30 landmarks in the sagittal, coronal, and axial slices. A mixed effects ANOVA model estimated the Intraclass Correlations (ICC) and assessed systematic bias.
Results
The ICC was >0.9 for 86% of intra-observer assessments and 66% of inter-observer assessments. Only 1% of intra-observer and 3% of inter-observer coefficients were <0.45. The systematic difference among observers was greater in X and Z than in Y dimensions, but the maximum mean difference was quite small.
Conclusion
Overall, the intra- and inter-observer reliability was excellent. 3D landmark identification using CBCT can offer consistent and reproducible data, if a protocol for operator training and calibration is followed. This is particularly important for landmarks not easily specified in all three planes of space.
Three-dimensional cephalometry has long been proposed as the ideal for orthodontic diagnosis, treatment planning, and follow-up of the patients.1 Diagnosis, treatment planning, and assessment of change over time have been routinely based on landmark based analysis in 2D cephalometry.1
3D landmarks represent an advantage over traditional location of 2D landmarks that may be hindered by rotational, geometric, and head positioning errors. 2, 3 These errors may lead to inaccurate representation of anatomic landmarks, or poor visualization of some structures.4 The use of Cone-Beam CT (CBCT) in dentistry offers great potential for 3D diagnosis and treatment planning compared to CT.5–16 However, the development of three-dimensional landmark-based cephalometric analysis requires definition of 3D landmarks on complex curving structures, which is not a trivial problem. As Bookstein16 noted, there is a lack of literature about suitable operational definitions for the landmarks in the 3 planes of space (coronal, sagittal, and axial). Practical considerations of identification errors, coupled with an essential need for biological relevance and a balanced representation of components of the craniofacial form, limit the number and nature of landmarks available for analysis. Historically landmarks, such as Articulare, were used because of the ease in landmark location on the 2D cephalometric projections, but these projected superimposed structures do not exist in the actual 3D facial structure. For these reasons, the development of 3D landmark-based cephalometric analysis demands suitable operational definitions of the landmark location in each of the 3 planes of space,6 and reproducibility of landmark identification is necessary to take full advantage of the 3D diagnostic power offered by CBCT imaging.17
If 3D landmark identification is reliable and research protocols are carefully planned to avoid bias, then 3D cephalometry has the potential of providing unambiguous information for diagnosis of skeletal asymmetry, longitudinal monitoring of growth, and postsurgical assessment. It’s well known that operator experience has a positive effect on measurement accuracy and reproducibility.17 The purpose of this article was to evaluate intra- and inter-observer reliability in 3D landmark identification using tomographic images generated from CBCT images.
MATERIAL AND METHODS
Pre-surgical CBCT images of 12 patients with varying dentofacial deformities (6 skeletal class II and 6 skeletal class III) were randomly selected to represent the spectrum of diverse facial morphologies from an available pool of 159 patients enrolled in parent study in our Dentofacial Deformities Program. The inclusion criteria for enrollment in the parent study were only individuals with a skeletal deformity severe enough to warrant surgical correction who were between 13 and 50. The exclusion criteria were: 1) presence of a cleft, 2) problems secondary to trauma, 3) degenerative conditions (for example, rheumatoid arthritis), 4) pregnancy at baseline, 5) correction by genioplasty only, and 6) inability to follow written English instructions. Patients were not excluded on the basis of age, gender or ethnicity. Biomedical Institutional Review Board was obtained and informed consent and HIPAA authorization forms were signed by all subjects.
The CBCT scans were obtained using the Dental Volumetric Tomograph NewTom 3G (AFP Imaging, Elmsford, NY). The scanner was operated by a personal computer which used Windows NT operating system (Microsoft Corporation, Redmond, WA). The basis projections were transferred as raw image data to an Expert Workstation where the primary reconstruction was performed using filtered back projection techniques to build the 3D data volume. Secondary reconstruction was equivalent to multiplanar reformatting, allowing the operator to obtain image slices through the 3D volume in any directions.18 The imaging protocol utilized a 12 inch field of view to include the entire facial anatomy. The axial slice thickness was 0.3 mm and the voxels were isotropic. Axial images were saved as 12 bit depth DICOM files. These images were imported in Dolphin 3D (pre-release version 1, Dolphin Imaging & Management Systems, Chatsworth, CA), which utilizes the same procedures as the current version of Dolphin 10 for 3D landmark identification. For each subject, a 3D virtual model was created and used to determine head orientation and standardize the center of the 3D coordinate system. Using axial, coronal and sagittal views of the 3D head rendering, the midsagittal plane of the model was oriented vertically, the transporionic line was oriented horizontally and Frankfort horizontal plane was oriented horizontally. The center of the coordinate system was determined by the intersection of the transporionic line and the midsagittal plane.19
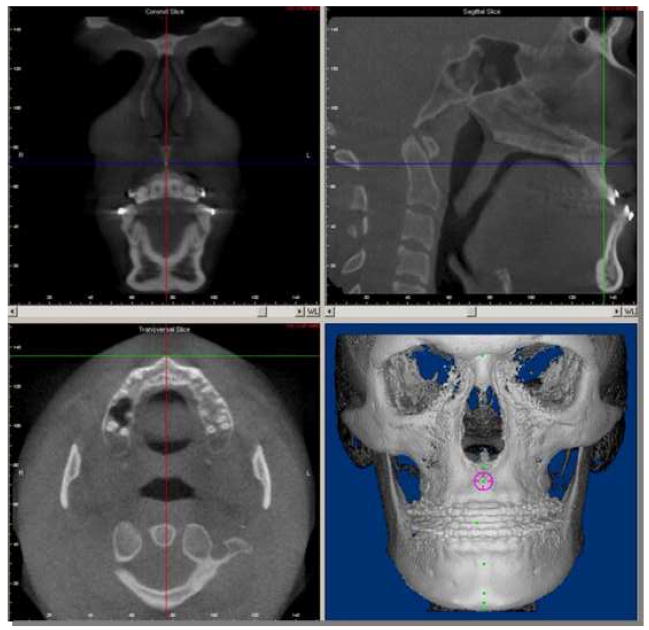
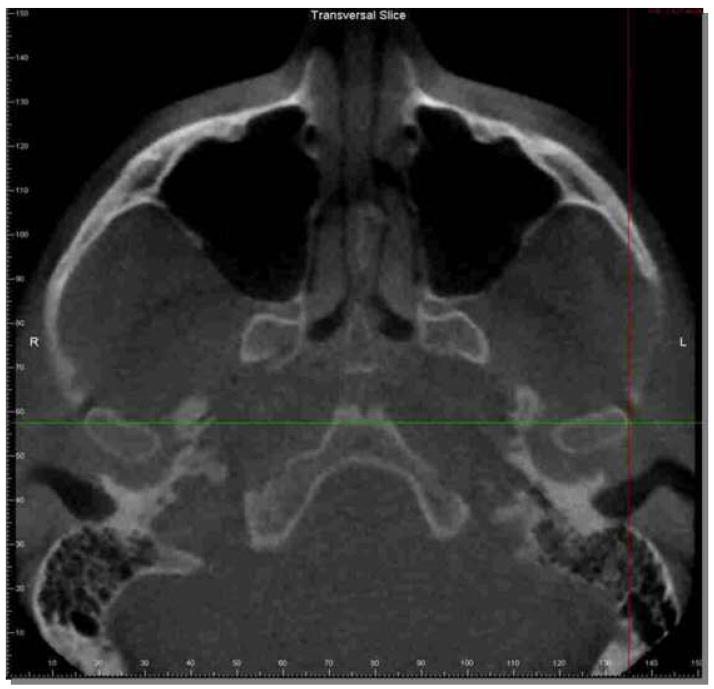
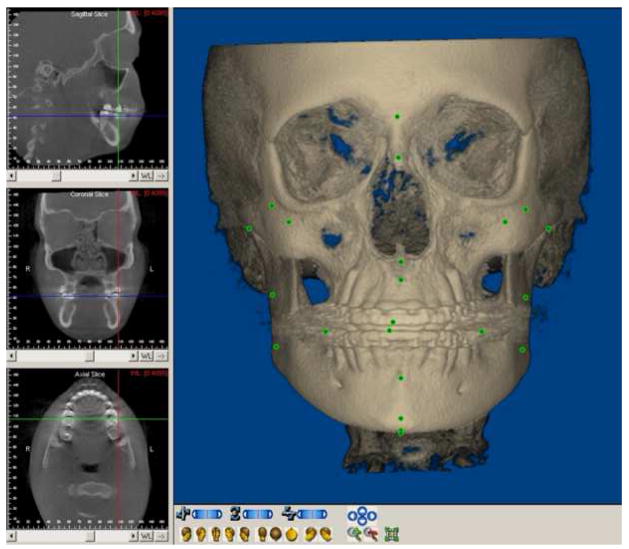
A total of 30 landmarks were selected (Table I), and defined criteria were established for each landmark. The x, y and z coordinates of each landmark were defined to standardize the anatomic identification in the 3 planes of space and to guide the selection of the most appropriate slice in the axial, coronal and sagittal views (Fig. 1 and 2). Besides the cross-sectional slices in the 3 planes of space, the Dolphin software also allows visualization of a 3D virtual rendering. The 3D virtual rendering was used to confirm landmark spatial position, but not for landmark location, because 3D renderings are projected images and not actual surfaces (Figure 3). If the observer had difficulty visualizing any landmark in a specific plane, the software allowed both mutliplanar views or selection of just one single plane in full screen window to zoom and facilitate landmark location (Fig. 3).
Table I.
Landmarks selected for the study.
| Landmark name | Anatomic region | Lateral view | Axial view | Antero-posterior view |
|---|---|---|---|---|
| 1- Sella Turcica (S) | Pituitary fossa of the sphenoidal bone | Middle point of the anteroposterior width of the fossa | Middle point of the anteroposterior and lateral width of the fossa | Middle point of the lateral width of the fossa in the antero- posterior slice determined by the lateral and axial views |
| 2- Nasion (N) | Frontonasal suture | Anterior-most point | Middle-anterior-most point on the anterior contour | Middle point |
| 3- A point (A) | Premaxilla | Posterior-most point on the curve of the maxilla between the anterior nasal spine and supradentale | Middle-anterior-most point on the tip of the premaxilla | Middle point in the antero-posterior slice determined by the lateral and axial views |
| 4- B point (B) | Anterior surface of the mandibular symphysis | Posterior-most point | Middle-anterior-most point on the anterior contour | Middle point in the antero-posterior slice determined by the lateral and axial views |
| 5- Pogonion (Pg) | Contour of the bony chin | Anterior-most point | Middle-anterior-most point on the anterior contour | Middle point in the antero-posterior slice determined by the lateral and axial views |
| 6- Gnathion (Gn) | Contour of the bony chin | Anterior-inferior- most point | Middle-anterior-inferior- most point | Middle-inferior-most point |
| 7- Menton (ME) | Lower border or the mandible | Inferior-most point | Middle-inferior-most point | Inferior-most point |
| 8- Anterior Nasal Spine (ANS) | Median, sharp bony process of the maxilla | Point on the tip | Anterior-most point | Middle point in the antero-posterior slice determined by the lateral and axial views |
| 9- Right mandibular Gonion (rGo) | Angle of the right mandibular body | Middle point along the angle | Posterior-most point | Inferior-most point |
| 10- Left mandibular gonion (lGo) | Angle of the left mandibular body | Middle point along the angle | Posterior-most point | Inferior-most point |
| 11- Right Condylion (rCo) | Right condyle | Superior-most point | Middle point in the axial slice level determined by the lateral and antero-posterior views | Middle Superior-most point |
| 12- Left Condylion (lCo) | Left condyle | Superior-most point | Middle point in the axial slice level determined by the lateral and antero-posterior views | Middle Superior-most point |
| 13- Right Orbitale (rOr) | Latero-inferior contour of the right orbit | Anterior-superior- most point on the edge between the internal and external contours | Anterior-most point | Latero-inferior point most |
| 14- Left Orbitale (lOr) | Latero-inferior contour of the left orbit | Anterior-superior- most point on the edge between the internal and external contours | Anterior-most point | Latero-inferior most point |
| 15-Right Upper Incisal Edge I (rUIE) | Incisal tip of right upper central incisor | Inferior-most point | Middle point of the mesiodistal and buccolingual width | Middle point of the mesiodistal width |
| 16- Right Lower Incisal Edge (rLIE) | Incisal tip of right lower central incisor | Superior-most point | Middle point of the mesiodistal and buccolingual width | Middle point of the mesiodistal width |
| 17- Right Lateral Mandibular Condyle (rLCo) | Lateral contour of the right condyle | Middle point in the lateral slice determined by the axial and antero- posterior views | Middle-lateral-most point on the external surface | Lateral-most point |
| 18- Left Lateral Mandibular Condyle (lLCo) | Lateral contour of the left condyle | Middle point in the lateral slice determined by the axial and antero- posterior views | Middle-lateral-most point on the external surface | Lateral-most point |
| 19- Right Medial Mandibular Condyle (rMCo) | Medial contour of the right condyle | Middle point in the lateral slice determined by the axial and antero- posterior views | Middle-medial-most point on the external surface | Medial-most point |
| 20- Left Medial Mandibular Condyle (lMCo) | Medial contour of the left condyle | Middle point in the lateral slice determined by the axial and antero- posterior views | Middle-medial-most point on the external surface | Medial-most point |
| 21- Right Ramus Point (rRP) | Posterior border of the right mandibular ramus | Middle-posterior- most point between the condylar neck and the angle of the mandibular body | Middle-posterior-most point | Inferior-most point |
| 22- Left Ramus Point (lRP) | Posterior border of the left mandibular ramus | Middle-posterior- most point between the condylar neck and the angle of the mandibular body | Middle-posterior-most point | Inferior-most point |
| 23- Right Upper Molar Point (rUM1) | Distal surface of the molar tube | Middle-posterior- most point | Middle-posterior-most point | Lateral-most point |
| 24- Left Upper Molar Point (lUM1) | Distal surface of the molar tube | Middle-posterior- most point | Middle-posterior-most point | Lateral-most point |
| 25- Right Lower Molar Point (rLM1) | Distal surface of the molar tube | Middle-posterior- most point | Middle-posterior-most point | Lateral-most point |
| 26- Left Lower Molar Point (lLM1) | Distal surface of the molar tube | Middle-posterior- most point | Middle-posterior-most point | Lateral-most point |
| 27- Right Tuberosity (rTb) | Distal contour of the right maxillary tuberosity | Posterior-inferior- most point | Posterior-most point | Inferior-most point |
| 28- Left Tuberosity (lTb) | Distal contour of the left maxillary tuberosity | Posterior-inferior- most point | Posterior-most point | Inferior-most point |
| 29- Right Zygomatic Suture (rZS) | Zygomaticomaxillary suture | Anterior-inferior- most point | Anterior-most point | Lateral-inferior-most point |
| 30- Left Zygomatic Suture (lZS) | Zygomaticomaxillary suture | Anterior-inferior- most point | Anterior-most point | Lateral-inferior-most point |
Figure 1.
Example of identification of A point landmark in the 3 planes of space. The software allows tracking of the cursor with display of all 3 planes of space, and 3D rendering in the same software window to verify landmark location.
Figure 2.
Selection of one plane window display to improve visualization for careful landmark location at each plane at a time. This example displays selection of the axial view in zoom to aid identification of the lateral pole of the left condyle.
Figure 3.
Landmarks displayed in the 3D rendering. Note that landmark locations appear distorted for landmarks located away from the center of the projected rendered view.
Three observers (an orthodontist, a dental radiologist, and a third-year dental student) were trained and calibrated to identify 3D landmarks using the sagittal, coronal, and axial slices using a set of 10 CBCT scans not included in this study. Working independently after calibration, the three observers identified and marked the 30 anatomic landmarks in 12 CBCT exams. Using the sagittal, coronal, and axial views, the position of the landmark was recorded by the Dolphin 3D software as numerical values for the x, y, and z coordinates, respectively. The digitized data were then exported to a Microsoft Excel spreadsheet (Microsoft Corporation, Redmond, WA). The landmark identifications were repeated three times by each observer at intervals of at least three days yielding 36 sets for each observer. A two-way mixed effects ANOVA model with an interaction between observer and patient was fit to each landmark and each coordinate, with observer as a fixed effect (3 levels) and patient as a random effect (12 levels). Intraclass Correlation (ICC) formulas were determined using the table of expected mean squares:20 ICC within observer = (MSpatient + 3MSinteraction − 4MSerror)/(MSpatient + 3MSinteraction +5MSError); ICC between observer = (MSpatient − MSError)/(MSpatient +3MSinteraction +5MSError). A separate repeated measures ANOVA model was fit without the interaction between patient and observer to assess whether bias among the observers existed. To test whether there was systematic bias in the observer estimates of landmark location, that means to test that at least one pair of observers had a mean difference significantly different from zero, or that at least one observer located a landmark consistently differently, an F test was calculated for the X, Y and Z coordinates of each landmark. The level of significance was set at 0.05.
RESULTS
The reliability was estimated by Intraclass Correlations (ICC) for each landmark and each coordinate. Tables of frequencies of the intra and inter-observer reliability summarize the results (Tables II and III). Overall, these tables show that the ICC indicated excellent reliability for both intra and inter-observer assessments.
Table II.
Frequency of the intra-observer reliability estimated by Intraclass Correlation for the X, Y, and Z coordinates.
| Range | Coordinates | Total | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Y | Z | ||||||
| N | % | n | % | n | % | n | % | |
| ICC ≥ 0.90 | 24 | (80.0) | 25 | (83.33) | 28 | (93.33) | 77 | (85.55) |
| 0.75 < ICC < 0.90 | 2 | (6.66) | 3 | (10.0) | 0 | 0 | 5 | (5.55) |
| 0.45 < ICC ≤ 0.75 | 4 | (13.33) | 2 | (6.66) | 1 | (3.33) | 7 | (7.77) |
| ICC ≤ 0.45 | 0 | 0 | 0 | 0 | 1 | (3.33) | 1 | (1.11) |
|
| ||||||||
| Total | 30 | (100.0) | 30 | (100.0) | 30 | (100.0) | 90 | (100.0) |
Table III.
Frequency of the inter-observer reliability estimated by Intraclass Correlations for the X, Y, and Z coordinates.
| Range | Coordinates | Total | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Y | Z | ||||||
| n | % | n | % | N | % | n | % | |
| ICC ≥ 0.90 | 20 | (66.6) | 15 | (50) | 24 | (80.0) | 59 | (65.5) |
| 0.75 < ICC <.0.90 | 4 | (13.3) | 8 | (26.6) | 4 | (13.3) | 16 | (17.7) |
| 0.45 < ICC ≤ 0.75 | 6 | (20.0) | 5 | (16.6) | 1 | (3.3) | 12 | (13.3) |
| ICC ≤ 0.45 | 0 | 0 | 2 | (6.6) | 1 | (3.3) | 3 | (3.3) |
| Total | 30 | (100.0) | 30 | (100.0) | 30 | (100.0) | 90 | (100) |
Table II shows the frequency of the intra-observer reliability estimated by ICC for the coordinates X, Y and Z. The ICC was ≥ 0.9 for 77 (85.55%) of the intra-observer assessments with the greatest frequency in coordinate Z (93.33%). Only 1 (1.1%) of the intra-observer coefficients showed poor reliability (ICC<0.45), which also occurred in the Z coordinate.
The frequency of the inter-observer reliability estimated by ICC for the coordinates X, Y and Z are shown in Table III. The ICC was ≥ 0.9 for 59 (65.55%) of the inter-observer assessments with the greatest frequency in coordinate Z (80.00%). A poor reliability was shown in the Y and Z coordinates as indicated by an ICC <0.45 for 2 (6.66%) cases in the Y coordinate and 1 (3.3%) case in the Z coordinate, totaling only 3 (3.3%) of all inter-observer assessments.
Table IV lists the reliability estimated by ICC for each landmark and each coordinate. Two bilateral landmarks showed low ICC scores indicative of poor reliability: Y coordinate of Right and Left Ramus, and Z coordinate of Right and left Condylion.
Table IV.
Reliability estimated by Intraclass Correlations for each landmark and each coordinate.
| Landmarks | Intra-observer Reliability | Inter-observer Reliability | ||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| Anterior Nasal Spine | 0.98 | 0.99 | 0.99 | 0.89 | 0.83 | 0.99 |
| A point | 0.99 | 0.94 | 1 | 0.91 | 0.7 | 0.99 |
| B point | 0.98 | 0.98 | 1 | 0.94 | 0.9 | 0.99 |
| Gnathion | 0.98 | 0.99 | 1 | 0.96 | 0.92 | 1 |
| Left Condylion | 0.66 | 1 | 0.5 | 0.65 | 0.97 | 0.49 |
| Left mandibular gonion | 0.97 | 0.92 | 0.96 | 0.97 | 0.73 | 0.9 |
| Left Lower Molar Point | 0.98 | 0.98 | 0.93 | 0.97 | 0.82 | 0.87 |
| Left Lateral Mandibular Condyle | 0.98 | 0.98 | 0.99 | 0.98 | 0.94 | 0.97 |
| Left Medial Mandibular Condyle | 0.97 | 0.98 | 1 | 0.97 | 0.95 | 0.99 |
| Left Orbitale | 0.8 | 0.99 | 0.99 | 0.71 | 0.91 | 0.93 |
| Left Upper Molar Point | 0.97 | 0.97 | 1 | 0.94 | 0.81 | 0.95 |
| Left Ramus Point | 0.95 | 0.68 | 1 | 0.94 | 0.44 | 0.98 |
| Left Tuberosity | 0.73 | 0.75 | 0.96 | 0.71 | 0.57 | 0.89 |
| Left Zygomatic Suture | 0.92 | 0.98 | 0.97 | 0.86 | 0.89 | 0.95 |
| Menton | 0.98 | 1 | 1 | 0.95 | 0.92 | 1 |
| Nasion | 0.99 | 1 | 1 | 0.87 | 0.98 | 0.97 |
| Pogonion | 0.98 | 0.99 | 1 | 0.96 | 0.94 | 1 |
| Right Condylion | 0.46 | 0.99 | 0.29 | 0.46 | 0.98 | 0.28 |
| Right mandibular Gonion | 0.99 | 0.89 | 0.93 | 0.96 | 0.71 | 0.91 |
| Right Lower Incisal Edge | 0.99 | 1 | 1 | 0.92 | 0.88 | 0.98 |
| Right Lower Molar Point | 0.96 | 0.96 | 0.93 | 0.94 | 0.87 | 0.88 |
| Right Medial Mandibular Condyle | 0.99 | 0.97 | 0.99 | 0.93 | 0.93 | 0.99 |
| Right Orbitale | 0.81 | 0.99 | 0.98 | 0.65 | 0.96 | 0.95 |
| Right Upper Incisal Edge | 0.98 | 1 | 1 | 0.95 | 0.79 | 0.95 |
| Right Upper Molar Point | 0.97 | 0.93 | 1 | 0.96 | 0.85 | 0.94 |
| Right Lateral Mandibular Condyle | 0.99 | 0.97 | 0.98 | 0.97 | 0.96 | 0.97 |
| Right Ramus Point | 0.98 | 0.51 | 0.99 | 0.95 | 0.29 | 0.99 |
| Right Tuberosity | 0.73 | 0.77 | 0.94 | 0.71 | 0.48 | 0.9 |
| Right Zygomatic Suture | 0.92 | 0.98 | 0.96 | 0.89 | 0.93 | 0.95 |
| Sella Turcica | 0.93 | 1 | 1 | 0.90 | 0.95 | 0.99 |
In order to further examine the inter-observer differences, Table V shows the frequency of differences in mean value on landmark location in the X, Y and Z coordinates. The frequencies were calculated using the range of mean observer scores in each landmark. The summarized results in Table 5 illustrate that 69 (76.6%) of the landmarks had a mean difference quite small of ≤ 1mm and in only 2 (2.22%) cases did the mean difference exceeded 2mm.
Table V.
Frequency of the difference in mean values on location landmark identification in X, Y and Z coordinates.
| Range | Coordinates | Total | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Y | Z | ||||||
| n | % | n | % | N | % | n | % | |
| x ≥ 2 mm | 0 | (0) | 0 | 0 | 2 | (6.6) | 2 | (2.22) |
| 1< x < 2 | 6 | (20.0) | 8 | (26.6) | 5 | (16.6) | 19 | (21.1) |
| 0.5 < x ≤ 1 | 10 | (33.3) | 13 | (43.3) | 10 | (33.3) | 33 | (36.6) |
| x ≤ 0.5 | 14 | (46.6) | 9 | (30.0) | 13 | (43.3) | 36 | (40.0) |
| Total | 30 | (100) | 30 | (100) | 30 | (100) | 90 | (100) |
DISCUSSION
Landmark based analysis using linear and angular measurements are the most popular method of cephalometric analysis among clinicians.1 CBCT potentially provides opportunities for 3D cephalometrics in orthodontic assessment of bony landmarks and air-bounded surfaces such as the facial skin.21 Farman and Scarfe21 have described methods for creating 2D cephalograms from CBCT volumetric data sets so that direct comparisons can be made between existing 2D databases and the future paradigm of 3D analysis. While innumerous 2D cephalometric analysis have been proposed since the introduction of the cephalostat by Broadbent, it appears likely that 3D cephalometry will also lead to new definitions of landmarks and new proposed analyses.2 However, 3D cephalometry requires alterations in paradigms of the 2D radiographic and cephalometric analysis, and demands careful training of residents and clinicians to take full advantage of the potential information offered by 3D imaging.
The development of this study methods required definition of the landmarks in the coronal (antero-posterior) and axial (superior-inferior) plane, in addition to the traditional landmark definitions in the sagittal (lateral) plane. The sources of error in landmark identification in this study can be two fold. First, some landmarks can be easily identified in one or two planes of the space, but landmark identification in the third plane might be difficult. Observers tended to locate the landmark in the planes of easy identification, disregarding the plane of difficult visualization. Second, the selection of the best slice for landmark location in each x, y, z coordinate requires time, calibration training and careful assessment. 3D landmark identification is more time-consuming than conventional 2D cephalograms tracing because it requires identifying landmarks in coronal, sagittal and axial views, and double-checking the visualization in the 3 planes of the space and in the 3D rendering.
Even though the 3 observers in this study had different training backgrounds and one of them had no prior experience with CT or CBCT scans, the observers’ training background had minimal effect on landmark location errors. This minimal effect of prior experience can be explained by careful observer calibration with the definition of landmark location in each of the 3 planes of space before the start of this study, using a set of 10 CBCT scans not included in this study.
In 2D cephalograms, many landmarks are defined as the uppermost or lowermost point of structures. A point on the edge of a structure in a lateral cephalogram may not correspond to the same point in the coronal cephalogram, due to the 2 different x-ray beam projections. This absence of spatial correspondence among the 2D views is a problem in 2D cephalograms. But 3D coordinate points correspond to 3D anatomic truth and pinpoint locations in the exact same anatomic locus.22
Inherent to 3D landmark based cephalometric analysis, even in 3D linear and angular analyses, is the limitation of being unable to assess how entire surfaces changed rather than discreet points. Recent studies have reported the use of 3D CBCT virtual surface models instead of the 3D renderings displayed by commercial softwares such as Dolphin (Dolphin Imaging & Management Systems, Chatsworth, CA) and Invivo (Anatomage, San Jose, CA)) for assessment of treatment changes.6, 15, 23, 24, 25 However, 3D surface models are not available for routine clinical use as these methods are more time-consuming and require computing expertise.
The results of this study showed that it is possible to accomplish landmark identifications in 3D with a high degree of reliability after training. The greatest frequencies of ICC ≥ 0.9 were in the axial view in both intra- and inter-observer analyses, with 93.3% and 80% respectively. But overall, the results were satisfactory in all 3 planes of space. One might have expected greatest reproducibility of landmark location in the sagittal (lateral) plane of space as clinicians are used to landmark identification in 2D lateral cephalograms, but observer calibration and training prior to this study might have aided reproducibility in all 3 planes of space.17 Park et al.4 reported similar results with medical CT, where intraexaminer reliability between two observations found that all 19 landmarks used in their study were reproducible, and there was no significant intraexaminer error.
The accuracy and reproducibility of 3D medical CT has been confirmed by Olszewski et al.26 and Swennen et al.27, 28 but their findings cannot be directly compared to the results in this study because they reported inter- and intra-observer reproducibility of cephalometric measurements not landmark location. Other recent studies described cephalometric analysis based on 3D CT anatomical landmarks to evaluate the craniofacial morphology. 22, 26, 27, 28, 29 But data acquisition with medical CT has some drawbacks: a) higher radiation exposure compared to CBCT; b) horizontal positioning of the patient during record taking falsifies the position of the soft tissue; c) lack of a detailed occlusion due to artifacts; d) limited access for the routine craniofacial patient because of higher cost.3,4, 28, 30 The use of 3D medical CT cephalometric analysis might be limited to those complex orthognathic cases with asymmetry and operable craniofacial syndromes3, 26. The advantages of CBCT over conventional CT include lower radiation dose, lower cost, potentially better access, and high spatial resolution.3 While 3D CBCT analysis for diagnosis and treatment still requires clinical validation, it is expected that CBCT 3D cephalometry will soon be available for routine craniofacial care.28
Although overall, the results of this study were satisfactory in all 3 planes of space, Table IV shows poor reliability of the Y coordinate definition of the Right and Left Ramus points, and the Z coordinate of Right and left Condylion. These findings can be explained by deficient definition criteria of those landmarks in those particular views, and located along the anatomic areas that are not areas of maximum curvature. Therefore, the characteristics of the landmark can influence its reproducibility. The choice of landmarks and the ability to reliably identify determine the usefulness of the 3D cephalometric analysis and have an impact on the accuracy of measurements.31
Inter-observer mean value differences of X, Y and Z coordinates in this study were similar within all 3 planes of space. Sixty-nine (76.6%) of the 90 landmark coordinates had a mean difference quite small of ≤ 1mm and in only 2 (2.22%) Z coordinates the mean difference exceeded 2mm. The clinical significance of the accuracy of the landmark identification error will depend on the level of accuracy required. The acceptable degree of error will depend on the type and complexity of the treatment procedures being planned and the goals of the study. Other factors related to the accuracy and reliability of 3D landmarks will need to be further investigated, such as the effect of slice thickness, use of overlapping slices, scanning time, gantry tilt, and patient head positioning.3 The slice thickness used in this study was 0.3 mm, while CT studies utilize slice thickness of 1 mm or more. Recent studies4,17 emphasize that narrower slices should result in better measurements accuracy decreasing the landmark identification errors.
CONCLUSIONS
Overall, the intra- and inter-observer reliability was excellent. Three dimensional landmark identification from CBCT images can offer consistent and reproducible data, if a protocol for operator training and calibration is followed. Utilization of cross-sectional slices in all 3 views of space take full advantage of the 3D CBCT information, while landmark location on the 3D renderings can lead to errors. This is particularly important for landmarks not easily specified in all three planes of space.
Acknowledgments
This work was supported by NIDCR DE017727, DE005215 and FAPEMA 128/06.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Ana Emilia F. de Oliveira, Professor, Department of Dentistry - I, Universidade Federal do Maranhão, Brazil.
Lucia Helena S. Cevidanes, Assistant Professor, Department of Orthodontics, University of North Carolina.
Ceib Phillips, Professor, Department of Orthodontics, University of North Carolina.
Alexandre Motta, Department of Orthodontics, Universidade do Estado do Rio de Janeiro, Brazil.
Brandon Burke, Fourth-Year DDS Student, University of North Carolina.
Donald Tyndall, Professor, Department of Diagnostic Sciences and General Dentistry, University of North Carolina.
References
- 1.Kumar V, Ludlow JB, Mol A, Cevidanes L. Comparison of conventional and cone beam CT synthesized cephalograms. Dentomaxillofac Radiol. 2007;36:263–9. doi: 10.1259/dmfr/98032356. [DOI] [PubMed] [Google Scholar]
- 2.Halazonetis DJ. From 2-dimensional cephalograms to 3-dimensional computed tomography scans. Am J Orthod Dentofacial Orthop. 2005;127:627–637. doi: 10.1016/j.ajodo.2005.01.004. [DOI] [PubMed] [Google Scholar]
- 3.Lou L, Lagravere MO, Compton S, Major PW, Flores-Mir C. Accuracy of measurements and reliability of landmark identification with computed tomography (CT) techniques in the maxillofacial area: a systematic review. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;104:402–11. doi: 10.1016/j.tripleo.2006.07.015. [DOI] [PubMed] [Google Scholar]
- 4.Park SH, Yu HS, Kim KD, Lee KJ, Baik HS. A proposal for a new analysis of craniofacial morphology by 3-dimensional computed tomography. Am J Orthod Dentofacial Orthop. 2006;129:600, e23–34. doi: 10.1016/j.ajodo.2005.11.032. [DOI] [PubMed] [Google Scholar]
- 5.Scarfe WC, Farman AG, Sukovic P. Clinical applications of cone-beam computed tomography in dental practice. J Can Dent Assoc. 2006;72:75–80. [PubMed] [Google Scholar]
- 6.Cevidanes LH, Styner MA, Proffit WR. Image analysis and superimposition of 3-dimensional cone-beam computed tomography models. Am J Orthod Dentofacial Orthop. 2006;129:611–618. doi: 10.1016/j.ajodo.2005.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hashimoto K, Arai Y, Iwai K, Araki M, Kawashima S, Terakado M. A comparison of a new limited cone beam computed tomography machine for dental use with a multidetector row helical CT machine. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2003;95:371–377. doi: 10.1067/moe.2003.120. [DOI] [PubMed] [Google Scholar]
- 8.Hatcher DC, Aboudara CL. Diagnosis goes digital. Am J Orthod Dentofacial Orthop. 2004;125:512–515. doi: 10.1016/j.ajodo.2003.12.009. [DOI] [PubMed] [Google Scholar]
- 9.Ito K, Yoshinuma N, Goke E, Arai Y, Shinoda K. Clinical application of a new compact computed tomography system for evaluating the outcome of regenerative therapy: a case report. J Periodontol. 2001;72:696–702. doi: 10.1902/jop.2001.72.5.696. [DOI] [PubMed] [Google Scholar]
- 10.Lascala CA, Panella J, Marques MM. Analysis of the accuracy of linear measurements obtained by cone beam computed tomography (CBCT-NewTom) Dentomaxillofac Radiol. 2004;33:291–294. doi: 10.1259/dmfr/25500850. [DOI] [PubMed] [Google Scholar]
- 11.Ludlow JB, Davies-Ludlow LE, Brooks SL. Dosimetry of two extraoral direct digital imaging devices: NewTom cone beam CT and Orthophos Plus DS panoramic unit. Dentomaxillofac Radiol. 2003;32:229–234. doi: 10.1259/dmfr/26310390. [DOI] [PubMed] [Google Scholar]
- 12.Mah JK, Danforth RA, Bumann A, Hatcher D. Radiation absorbed in maxillofacial imaging with a new dental computed tomography device. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2003;96:508–513. doi: 10.1016/s1079-2104(03)00350-0. [DOI] [PubMed] [Google Scholar]
- 13.Mengel R, Candir M, Shiratori K, Flores-de-Jacoby L. Digital volume tomography in the diagnosis of periodontal defects: an in vitro study on native pig and human mandibles. J Periodontol. 2005;76:665–673. doi: 10.1902/jop.2005.76.5.665. [DOI] [PubMed] [Google Scholar]
- 14.Mussig E, Wortche R, Lux CJ. Indications for Digital Volume Tomography in Orthodontics. J Orofac Orthop. 2005;66:241–249. doi: 10.1007/s00056-005-0444-1. [DOI] [PubMed] [Google Scholar]
- 15.Cevidanes LH, Bailey LJ, Tucker SF, Styner MA, Mol A, Phillips CL, Proffit WR, Turvey T. Three-dimensional cone-beam computed tomography for assessment of mandibular changes after orthognathic surgery. Am J Orthod Dentofacial Orthop. 2007;131:44–50. doi: 10.1016/j.ajodo.2005.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bookstein FL. Morphometric tools for landmark data. 1. Cambridge: Cambridge University Press; 1991. p. 435. [Google Scholar]
- 17.Ludlow JB, Laster WS, See M, Bailey LJ, Hershey HG. Accuracy of measurements of mandibular anatomy in cone beam computed tomography images. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2007;103:534–42. doi: 10.1016/j.tripleo.2006.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Parrott QW, Mol A. Master of Science in the Shool of Dentistry. Chapel Hill: 2005. Condylar changes following orthognathic surgery. Thesis submitted to the faculty of the University of North Carolina. [Google Scholar]
- 19.Kumar V, Ludlow J, Cevidanes LHS, Mol A. In vivo comparison of conventional and cone beam CT synthesized cephalograms. Angle Orthodontist. 2008;78(5):873–879. doi: 10.2319/082907-399.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Neter J, Kutner MH, Wasserman W, Nachtsheim CJ. Applied Linear Statistical Models. 4. McGraw Hill/Irwin; 1996. p. 785. [Google Scholar]
- 21.Farman AG, Scarfe WC. Development of imaging selection criteria and procedures should precede cephalometric assessment with cone-beam computed tomography. Am J Orthod Dentofacial Orthop. 2006;130(2):257–65. doi: 10.1016/j.ajodo.2005.10.021. [DOI] [PubMed] [Google Scholar]
- 22.Katsumata A, Fujishita M, Maeda M, Ariji Y, Ariji E, Langlais RP. 3D-CT evaluation of facial asymmetry. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2005;99:212–20. doi: 10.1016/j.tripleo.2004.06.072. [DOI] [PubMed] [Google Scholar]
- 23.Cevidanes LH, Bailey LJ, Tucker GR, Jr, Styner MA, Mol A, Phillips CL, Proffit WR, Turvey T. Superimposition of 3D cone-beam CT models of orthognathic surgery patients. Dentomaxillofac Radiol. 2005;34:369–375. doi: 10.1259/dmfr/17102411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Grauer D, Cevidanes LHS, Phillips C, Mol A, Styner M, Proffit W. Assessment of maxillary surgery outcomes one year post-surgery. J Dent Res. 2006;(Spec Iss A):0813. ( www.dentalresearch.org)
- 25.Lee B, Cevidanes LHS, Phillips C, Mol A, Styner M, Proffit W. 3D assessment of mandibular changes one year after orthognathic surgery. J Dent Res. 2006;(Spec Iss A):1610. ( www.dentalresearch.org)
- 26.Olszewski R, Zech F, Cosnard G, Nicolas V, Macq B, Reychler H. Three-dimensional computed tomography cephalometric craniofacial analysis: experimental validation in vitro. Int J Oral Maxillofac Surg. 2007;36:828–33. doi: 10.1016/j.ijom.2007.05.022. [DOI] [PubMed] [Google Scholar]
- 27.Swennen GR, Schutyser F, Barth EL, De Groeve P, De Mey A. A new method of 3-D cephalometry Part I: the anatomic Cartesian 3-D reference system. J Craniofac Surg. 2006;17:314–25. doi: 10.1097/00001665-200603000-00019. [DOI] [PubMed] [Google Scholar]
- 28.Swennen GR, Schutyser F. Three-dimensional cephalometry: spiral multi-slice vs cone-beam computed tomography. Am J Orthod Dentofacial Orthop. 2006;130:410–6. doi: 10.1016/j.ajodo.2005.11.035. [DOI] [PubMed] [Google Scholar]
- 29.Maeda M, Katsumata A, Ariji Y, Muramatsu A, Yoshida K, Goto S, Kurita K, Ariji E. 3D-CT evaluation of facial asymmetry in patients with maxillofacial deformities. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2006;102:382–90. doi: 10.1016/j.tripleo.2005.10.057. [DOI] [PubMed] [Google Scholar]
- 30.Danforth RA, Dus I, Mah J. 3-D volume imaging for dentistry: a new dimension. J Calif Dent Assoc. 2003;31:817–823. [PubMed] [Google Scholar]
- 31.Baumrind S, Frantz RC. The reliability of head film measurements 1. Landmark identification. Am J Orthod. 1971;60:111–27. doi: 10.1016/0002-9416(71)90028-5. [DOI] [PubMed] [Google Scholar]