EEG source analysis of epileptiform activity using a 1mm anisotropic hexahedra finite element head model

Abstract

The major goal of the evaluation in presurgical epilepsy diagnosis for medically intractable patients is the precise reconstruction of the epileptogenic foci, preferably with non-invasive methods. This paper evaluates whether surface electroencephalography (EEG) source analysis based on a 1mm anisotropic finite element (FE) head model can provide additional guidance for presurgical epilepsy diagnosis and whether it is practically feasible in daily routine. A 1mm hexahedra FE volume conductor model of the patient’s head with special focus on accurately modeling the compartments skull, cerebrospinal fluid (CSF) and the anisotropic conducting brain tissues was constructed using non-linearly co-registered T1-, T2- and diffusion-tensor- magnetic resonance imaging data. The electrodes of intra-cranial EEG (iEEG) measurements were extracted from a co-registered computed tomography image. Goal function scan (GFS), minimum norm least squares (MNLS), standardized low resolution electromagnetic tomography (sLORETA) and spatio-temporal current dipole modeling inverse methods were then applied to the peak of the averaged ictal discharges EEG data. MNLS and sLORETA pointed to a single center of activity. Moving and rotating single dipole fits resulted in an explained variance of more than 97%. The non-invasive EEG source analysis methods localized at the border of the lesion and at the border of the iEEG electrodes which mainly received ictal discharges. Source orientation was towards the epileptogenic tissue. For the reconstructed superficial source, brain conductivity anisotropy and the lesion conductivity had only a minor influence, whereas a correct modeling of the highly conducting CSF compartment and the anisotropic skull was found to be important. The proposed FE forward modeling approach strongly simplifies meshing and reduces run-time (37 Milliseconds for one forward computation in the model with 3.1 Million unknowns), corroborating the practical feasibility of the approach.

1 Introduction

Surgical resection of epileptogenic cortical tissue in pharmaco-resistant epilepsy patients was shown to safely and effectively control seizures, recover function, improve quality of life and even save lives, but epilepsy surgery is still underused in developed countries and non-existent in most developing countries (Wiebe et al., 2001). The precise localization of the epileptogenic foci, preferably with non-invasive methods, is the major goal of the presurgical evaluation (Rosenow and Luders, 2001). In addition to evaluation by video and electroencephalography (EEG) long-term monitoring, magnetic resonance imaging (MRI), single photon emission computed tomography and neuropsychological examination, EEG and magnetoencephalography (MEG) source analysis has risen to a promising tool (Roth et al., 1997; Huiskamp et al., 1997; Waberski et al., 1998; Merlet and Gotman, 1999; Huiskamp et al., 1999; Waberski et al., 2000; Kobayashi et al., 2001; Stefan et al., 2003; Salayev et al., 2006; Plummer et al., 2008). Source analysis results correlated well with results from intracranial recordings (Roth et al., 1997; Merlet and Gotman, 1999; Kobayashi et al., 2001) and epileptogenic subcompartments could well be distinguished using source reconstruction techniques (Roth et al., 1997; Baumgartner et al., 1995; Ebersole, 2000; Lantz et al., 2001). In a large study, source analysis revealed additional localizational information in 35% of the 455 patients and in 10%, it could even considerably contribute to the decision about type, size and eventually necessary prior invasive examinations (Stefan et al., 2003).

The accuracy of source analysis methods depends in part on the volume conductor model used to represent the head. In clinical practice, for EEG, the spherical head model with three homogeneous and isotropically conducting (a single conductivity value) spherical shells representing brain, skull and scalp, and in MEG, the single isotropic compartment sphere model, are still often used. Recent investigations showed that source localization accuracy can be improved through the use of realistically shaped three compartment (brain, skull, scalp, extracted from MRI data) boundary element (BE) or finite element (FE) head models, the current “gold standard” in source analysis (Roth et al., 1997; Huiskamp et al., 1997; Waberski et al., 1998; Huiskamp et al., 1999; Waberski et al., 2000; Fuchs et al., 2007).

However, the cerebrospinal fluid compartment is known to have a much higher conductivity than brain gray and white matter (Baumann et al., 1997) and, because of its three-layeredness into top and bottom compacta and spongiosum, the skull is often considered to be an anisotropic (different conductivity values in different space directions) conductor (Marin et al., 1998; Akhtari et al., 2002; Fuchs et al., 2007). Furthermore, conductivity anisotropy with a ratio of about 1 to 9 (normal to parallel to fibers) has been measured for brain white matter (Nicholson, 1965). The robust and non-invasive direct in-vivo measurement of brain conductivity anisotropy is not possible. However, in (Basser et al., 1994), the assumption was introduced that the conductivity tensor shares the eigenvectors with the water diffusion tensor (DT), which can be measured non-invasively by means of DT-MRI. This assumption was recently used in an effective medium approach which describes a linear relationship between the effective electrical conductivity tensor and the effective water diffusion tensor in brain tissues (Tuch et al., 1999, 2001; Wang et al, 2008). A further positive validation study of this model in a silk yarn phantom was presented by (Oh et al., 2006). The mutual restriction of both the ionic and the water mobility by the geometry of the brain medium builds the basis for the described relationship. The assumption is not, of course, that a fundamental relation exists between the free mobility of ionic and water particles. The claim is rather that the restricted mobilities are related through the geometry.

Besides the finite difference method (FDM) (Hallez et al., 2005), the finite element method (FEM) is able to treat both realistic geometry and inhomogeneous and anisotropic material parameters (Buchner et al., 1997; van den Broek, 1997; Haueisen et al., 2002; Ramon et al., 2004; Wolters et al., 2006; Zhang et al., 2006). Sensitivity studies have been carried out in realistic FE models, supporting the hypothesis that modeling skull and brain conductivity anisotropy has to be taken into account for accurate source reconstruction (van den Broek, 1997; Haueisen et al., 2002; Wolters et al., 2006; Güllmar et al., 2006). It is furthermore known that the high conductivity of the CSF (Ramon et al., 2004; Wolters et al., 2006; Wendel et al., 2008) and local conductivity changes in the vicinity of the primary source as caused by brain lesions or cavities from surgery (van den Broek, 1997; Vatta et al., 2002) or the difference between gray and white matter conductivity (Ramon et al., 2004) have a non-negligible effect on EEG and MEG source analysis. Even if realistic FE models have already successfully been applied to the field of presurgical epilepsy diagnostic, their real potential was not yet exploited since three compartment (brain, skull, scalp) isotropic FE approaches were used (Waberski et al., 1998) or the impact of the highly conducting CSF and the anisotropic conductivity of the brain were ignored (Fuchs et al., 2007). In the past, the difficult construction of the volume discretization and the heavy computational load of the FE method was seen as a drawback, especially when many evaluations of the forward problem are needed, e.g., in source localization schemes (Buchner et al., 1997; van den Broek, 1997; Waberski et al., 1998; Kybic et al., 2005; Plis et al., 2007; Fuchs et al., 2007). As shown in this paper, the generation of regular hexahedra FE meshes takes advantage of the cubic voxel structure which is inherent to MR images so that the meshing step just consists of converting the segmented T1-weighted MRI into a hexahedra mesh with the same resolution, which can be performed in seconds. Due to the excessive computational burden created by previous FEM techniques, evaluation studies often only used sub-optimal numbers of nodes (Buchner et al., 1997; van den Broek, 1997; Waberski et al., 1998). For example, in (Waberski et al., 1998), an FE model with only 10,731 nodes (5mm edge length) was used for the localization of epileptiform activity and it was concluded that, for a general clinical use of FE source analysis, a finer FE discretization and parallel computing is needed. In (Buchner et al., 1997), the setup of a lead field matrix with 8,742 unknown dipole components in a four compartment FE approach with 18,322 nodes took roughly a week of computation time.

In this paper, a 1mm anisotropic hexahedra volume conductor model with about 3.1 Million unknowns will be generated from T1-, T2- and DT-MRI data of a patient who underwent surgery and relapsed. The high-resolution FE model distinguishes the compartments brain white and gray matter, CSF (among others CSF-filled cavity of the first surgery and ventricles), skull and skin. It will be used in goal function scan (Mosher et al., 1992; Knösche, 1997), minimum norm least squares (Hämäläinen and Ilmoniemi, 1984; Knösche, 1997), spatio-temporal current dipole (Scherg and von Cramon, 1985; Mosher et al., 1992; Knösche, 1997) and standardized low resolution electromagnetic tomography (sLORETA) (Pascual-Marqui, 2002; Dannhauer, 2007) EEG inverse source analysis scenarios to localize ictal epileptiform surface EEG (EEG) activity on a high-resolution 2mm 3D influence source space. As we will show, instead of solving “number of sources many FE equation systems” (in the presented study: 517,098), a fast transfer matrix approach allows us to reduce this huge number to a “number of sensors many FE equation systems” (in the presented study: 24). The computational amount of work is thus reduced by more than a factor of 20,000. Any FE-forward computation can then be performed in only 37ms. The presurgical EEG source analysis results are successfully validated by means of postsurgical intracranial EEG (iEEG) measurements. “Postsurgical” is defined throughout this paper as the instant in time after craniotomy and placement of iEEG grids.

2 Methods

2.1 Subject

The patient in this case study is an 11-year-old boy suffering from medically intractable localization-related epilepsy. He had his first seizure in the age of three years and underwent a brain tumor (Dysembryoplastic NeuroEpithelial Tumor, DNET) and epileptic focus resection. After recurrence of seizures 8 years later, the same type of tumor was diagnosed just anterior to the motor area at the cavity from the resection of the first surgery. He was then treated again and went under surgery for tumor resection. The data in this study was acquired during the diagnosis phase for the second tumor resection.

2.2 MRI and CT data acquisition

Presurgical MR imaging of the patient’s head was performed on a 3T SIEMENS TrioTim at the Massachusetts General Hospital. The T1-weighted MRI had an in-plane resolution of 1 × 1mm with a slice thickness of 1mm, 256 slices, a field of view of 256mm and an echo time of 3.37ms. The presurgical DTI scan had 30 directions and 5 B0 sets, 220mm field of view with 1.7 × 1.7mm in-plane resolution and 5mm slice thickness with 20% gap, 23 slices, B-value of 1000, 106ms echo time and 5000ms repetition time. The T2-weighted MRI scan, measured together with the DTI for later DTI to T1-MRI registration purposes, had an in-plane resolution of 0.4 × 0.4mm with a slice thickness of 5mm, 23 slices and a field of view of 173 × 230mm.

A postsurgical CT of the patient, showing the implanted intracranial electrodes, was recorded using a GE Medical System LightSpeed Pro 16. The dataset had an in-plane resolution of 0.5 × 0.5mm with a slice thickness of 0.6mm, 559 slices and a field of view of 250mm.

2.3 FE volume conductor modeling

2.3.1 T1-MRI segmentation

The patient’s T1-MRI dataset was aligned to the AC-PC coordinate system. In a first step, a segmentation into three layers (skin, skull and brain) was performed using a surface model approach (Smith, 2002) implemented in FSL (http://www.fmrib.ox.ac.uk/fsl). The result was manually corrected with Anatomist (http://brainvisa.info). In a second step, the segmented brain compartment was further subdivided into CSF, gray and white matter by an interactive thresholding using the Anatomist software and again manually corrected. Finally, the lesion was manually segmented.

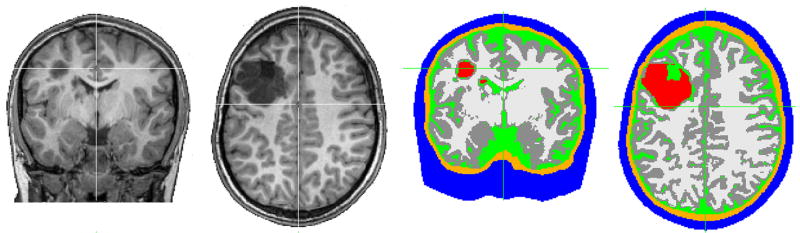
The result of the segmentation process is shown in Figure 1.

Figure 1.

Coronal and axial view of the T1-MRI (left) and the corresponding segmentation (right) with six tissue types: red indicates the lesion, dark gray the gray matter, light gray the white matter, green the CSF, orange the skull and blue indicates the skin.

2.3.2 DTI registration and preprocessing

A proper registration of the DTI data onto the structural T1-MRI is an important step in the setup of an anisotropic FE volume conductor model. Distortions in the DTI due to susceptibility artifacts generally have to be corrected in a non-linear fashion (Thirion, 1998). For non-linear registration methods most often (except for curvature-based non-parametric registration) an initial affine (linear) registration is needed because linear transformations are punished by most non-linear registration smoothing functionals (Modersitzki, 2004). We applied a voxel-similarity based affine registration method without presegmentation using a global optimization of the mutual information cost function between the different modalities (Jenkinson and Smith, 2001) implemented in FSL.

In a first step, the patient’s DTI scans were therefore linearly co-registered with the high resolution axial T2-weighted slices. Subsequently, an affine registration of the T2-MRI onto the 3D T1-weighted volume was performed. Both transformation matrices were combined and the resulting affine transformation was used to register the DTI to the T1 anatomy. The images were then interpolated to 1 mm voxel resolution. Finally, in order to handle the orientation information in the co-registered DT images appropriately, the diffusion gradient direction for each scan was rotated with the transformation matrix to account for the new slice orientation of the diffusion scan.

In a second step, the averaged B0 images of the (linearly co-registered) DTI scan were non-linearly warped to the (linearly co-registered) T2 anatomy following (Thirion, 1998) (for a deeper theoretical insight into the demons registration, see (Modersitzki, 2004, Chapter 11)). The computed correction field was applied to the (linearly co-registered) diffusion weighted scans. The diffusion tensor was then estimated for each voxel using a multivariate linear regression as described in (Basser et al., 1994b).

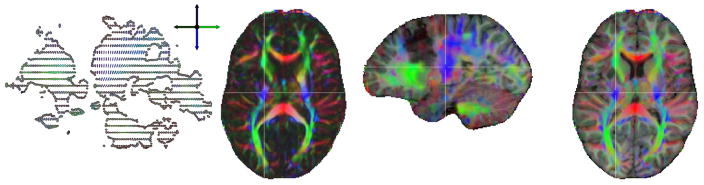
Figure 2 shows a sagittal slice of the original DTI (left), an axial slice of the color coded fractional anisotropy (FA) image after registration to the T1 anatomy (middle left) and an overlay of the color FA image on the T1 image in a sagittal (middle right) and axial (right) view.

Figure 2.

Sagittal slice of the original DTI image (left), axial slice of the color coded fractional anisotropy (FA) image after registration to the T1 anatomy (middle left) and the co-registered color FA image overlaid on the T1-MRI in sagittal (middle right) and axial (right) view. The color indicates the fiber orientation: red is left-right, green is anterior-posterior and blue is superior-inferior.

To correct for non-positive definite tensors, the eigenvalues were checked and thresholded for every voxel. If the second eigenvalue was smaller than 1 · 10⁻⁴ or the third eigenvalue was smaller than 1 · 10⁻⁵, the tensor was removed from the dataset. This was the case for some voxels in the inferior frontal lobe due to distortion artifacts (149 out of 699,280 white matter voxels, i.e., 0.02%, and 2681 out of 675,399 gray matter voxels, i.e., 0.4%). Negative tensor eigenvalues occur due to other measurement errors, e.g. intraventricular CSF pulsation artifacts. The final DTI was masked with the gray and white matter masks for the usage in the head model.

2.3.3 FE mesh generation

The generation of regular hexahedra meshes takes advantage of the cubic voxel structure which is inherent to MR images and thus strongly simplifies FE mesh generation for source analysis (Wolters et al., 2007c). Regular hexahedra have good numerical properties because of their advantageous ratio of inner to outer circumsphere (see, e.g., (Braess, 2007)). However, in comparison to tetrahedra FE approaches like presented in (Buchner et al., 1997; van den Broek, 1997; Wolters et al., 2006; Fuchs et al., 2007), especially high resolutions are necessary to make sure that, e.g., the CSF compartment is appropriately modeled and the skull is a closed compartment even in areas where it is quite thin and to allow simultaneously skull holes where they are realistic. As shown in (Wolters et al., 2007c), hexahedra FE forward modeling inaccuracies measured by means of quasi-analytical formulas in multi-layer sphere studies fast decrease with mesh resolution. In order to avoid those disadvantages of hexahedra meshing, we generated a high-resolution 1 mm hexahedra FE headmodel with 3,098,341 nodes simply by means of a conversion step from the segmented T1-MRI with 1 mm voxel resolution from Section 2.3.1. It will be shown that source analysis based on this accurate high-resolution volume conductor model is still feasible in daily routine when using the methods presented in Section 2.5.

2.3.4 FE conductivity labeling

Table 1 shows the conductivity values ${\sigma }_{\mathit{comp}}^{\mathit{iso}}$ for the head compartments comp that are used for a first isotropic labeling of the finite elements (Ramon et al., 2006). It was not distinguished between hard and soft bone, but the common isotropic value for the conductivity of the compartment skull (Huiskamp et al., 1999; Cuffin, 1996; Buchner et al., 1997; Waberski et al., 1998; Fuchs et al., 2007) was used. In the following, this model will be referred to as 6IsoComp.

Table 1.

Bulk isotropic conductivity ${\sigma }_{\mathit{comp}}^{\mathit{iso}}$ for head compartment comp.

head compartment comp	conductivity ${\sigma }_{\mathit{comp}}^{\mathit{iso}}$ (S/m)
les (lesion)	0.33
wm (white matter)	0.142
gm (gray matter)	0.33
csf (cerebrospinal fluid)	1.538
skull	0.0042
skin	0.43

For the anisotropic tissue compartments brain white and gray matter, the conductivity tensors were computed from the measured diffusion tensors using the effective medium approach presented by (Tuch et al., 1999, 2001). A further positive validation in a silk yarn phantom for this model was recently presented by (Oh et al., 2006). The effective medium approach linearly relates the conductivity tensor σ to the measured diffusion tensor D,

$$\sigma =\text{s}D\text{with}\text{s}:=\frac{{\sigma }_{\text{e}}}{d_{\text{e}}},$$

where σ_e and d_e are the effective extracellular conductivity and diffusivity, respectively. We did not use the empirical scaling $\text{s}=0.736\frac{S·\mathit{sec}}{m{m}^3}$ as in (Tuch et al., 1999; Haueisen et al., 2002), but matched s so that the arithmetic mean over all N_comp conductivity tensor volumes in the brain tissue compartment comp (either wm or gm) optimally matches the volume of the corresponding tensor with the isotropic conductivity ${\sigma }_{\mathit{comp}}^{\mathit{iso}}$ from Table 1, i.e.,

$$\frac{4\pi }{3}{\left({\sigma }_{\mathit{comp}}^{\mathit{iso}}\right)}^3\stackrel{!}{=}\frac{{\displaystyle \sum _{i=1}^{N_{\mathit{comp}}}}\frac{4\pi }{3}{\displaystyle \prod _{j=1}^3}{\sigma }_i^j}{N_{\mathit{comp}}}=\frac{4\pi }{3}·\frac{{\displaystyle \sum _{i=1}^{N_{\mathit{comp}}}}{\displaystyle \prod _{j=1}^3}\text{s}{d}_i^j}{N_{\mathit{comp}}}=\frac{4\pi }{3}{(\text{s}·d_{\mathit{comp}})}^3$$ (1)

with ${\sigma }_i^j$ and $d_i^j$ being the j^th eigenvalue of the i^th conductivity and diffusion tensor of the brain tissue compartment comp, respectively, and

$$d_{\mathit{comp}}:=\sqrt[3]{\frac{{\displaystyle \sum _{i=1}^{N_{\mathit{comp}}}}{\displaystyle \prod _{j=1}^3}{d}_i^j}{N_{\mathit{comp}}}}.$$

For the brain white and gray matter compartments, s can be determined through the least squares fit

$$\text{s}=\frac{d_{wm}{\sigma }_{wm}^{\mathit{iso}}+d_{gm}{\sigma }_{gm}^{\mathit{iso}}}{d_{wm}^2+d_{gm}^2}.$$ (2)

For our data, we found the scaling $\text{s}=0.21\frac{S·\mathit{sec}}{m{m}^3}$.

Table 2 indicates the mean conductivities, i.e., s · d_comp, for white and gray matter resulting from the linear scaling s computed for our dataset using Formula (2) and the one from (Tuch et al., 1999; Haueisen et al., 2002). The latter would result in much higher mean conductivities for brain gray and white matter than compiled in Table 1. For white and gray matter voxels with no measured diffusion tensor (0.02% in wm and 0.4% in gm), the literature isotropic conductivity values from Table 1 were used. In the following, this model will be referred to as 6CompAnisoBrain.

Table 2.

The linear scalings s between the diffusion tensor and the conductivity tensor computed for our dataset using Formula (2) (upper row) and from (Tuch et al., 1999; Haueisen et al., 2002) (lower row) with the resulting mean conductivity s · d_comp for gray and white matter.

s (S · sec/mm3)	Mean conductivity (S/m) for
	gm	wm
0.210	0.211158	0.182963
0.736	0.740057	0.641243

As shown by (van den Broek, 1997; Vatta et al., 2002), brain lesions can present conductivity values that are often quite different from those of surrounding normal tissues and have to be included in head models for accurate neural source reconstruction. Since an accurate determination of the lesion conductivity is a difficult task, the models 6CompAnisoBrainLesCSF and 6CompAnisoBrainLesHalfGM represent two extreme cases, the first being adequate for a highly conductive CSF-filled lesion (lesion conductivity like CSF compartment, see Table 1) and the latter being adequate for a low conductivity like calcified tumor (lesion conductivity like half of the gray matter compartment, see Table 1).

For model 6CompAnisoBrainAnisoSkull, a conductivity anisotropy of 3:1 (tangentially:radially to the skull surface) was assumed for the skull compartment following (Fuchs et al., 2007), who used the measured conductivity values of (Akhtari et al., 2002) for the three skull compartments top and lower compacta and spongiosum.

Finally, for comparisons with the performance of the “gold standard” realistically-shaped three isotropic compartment volume conductor model, in model 3IsoComp the compartments lesion, white matter, gray matter and CSF of model 6IsoComp were homogenized into the isotropic compartment “brain” with a conductivity value of 0.33 S/m.

2.4 EEG and iEEG measurements

The presurgical scalp EEG (EEG) dataset, recorded at 24 electrodes with a sampling frequency of 256Hz, contained one seizure, which had been identified by the Long Term Monitoring (LTM) personnel. The single clinical seizure happened while the patient sat in a chair. The first definite clinical sign was head deviation to the right, a right sided jerking followed by a generalized tonic clonic seizure.

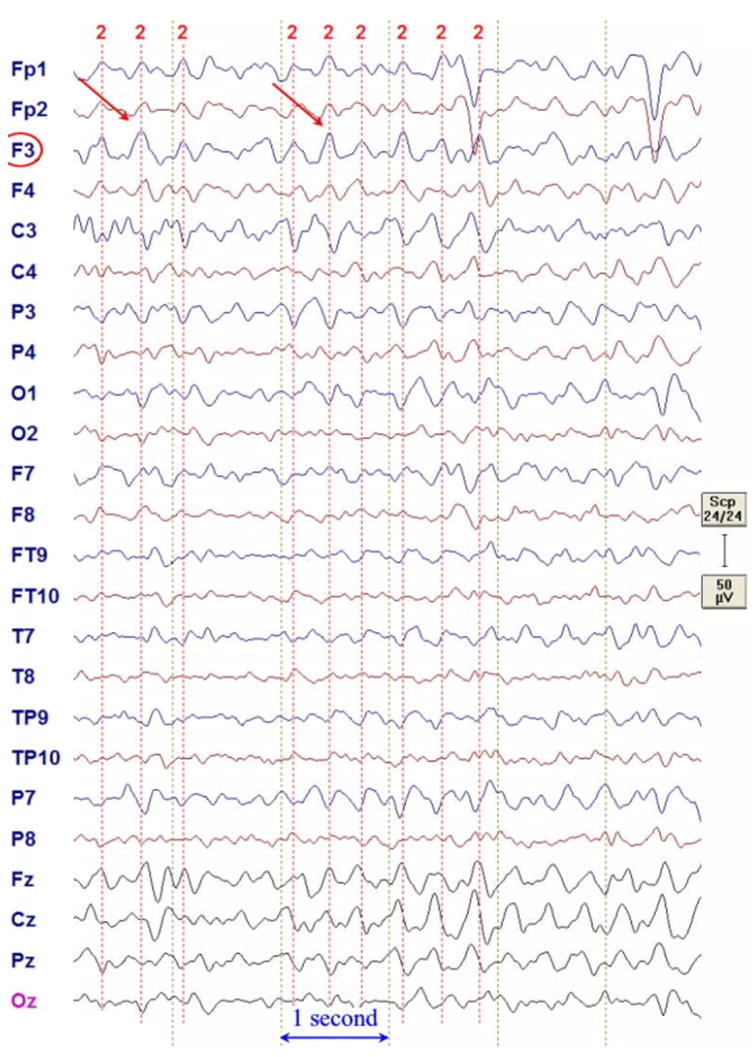
The EEG data was filtered with a 60Hz notch and a 1 to 10Hz band-stop filter using the BESA software package (MEGIS Software GmbH, Germany). As shown in Figure 3, the F3 delta was followed by more midline FZ-CZ delta.

Figure 3.

F3 delta discharges of the presurgical EEG in average reference format.

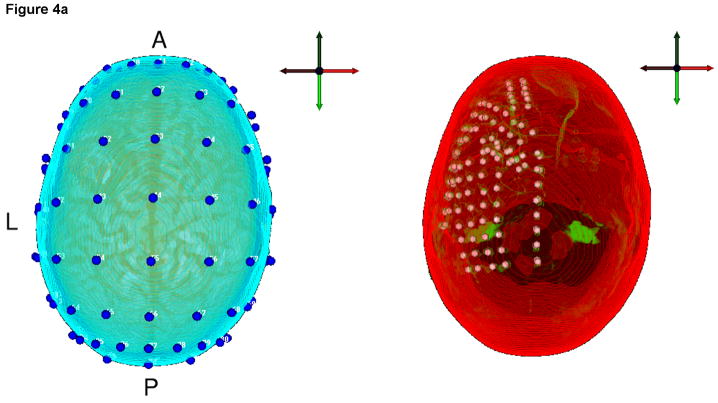
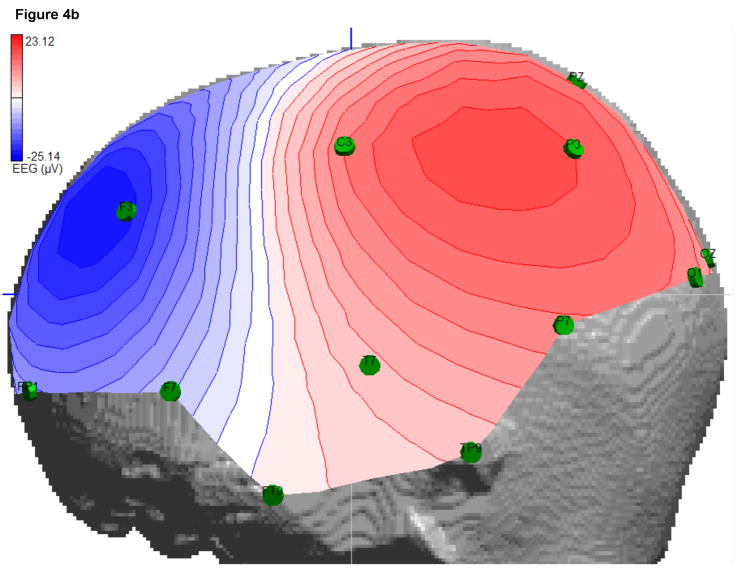
Nine F3 delta bursts were marked by a clinical expert (F.H. Duffy) and averaged to improve data quality for the further source analysis. For the localization, only a short time window of 7.8ms was used (Figure 4b), which included the two samples at the highest signal peak. Besides the labels of the 24 measurement electrodes from a 10-10 standard configuration, no individual EEG electrode locations were available, so that a standard positioning was applied. The software ASA (ANT B.V., Enschede, The Netherlands) contains a file with electrode positions of a 10-10 standard configuration together with four fiducial points (nasion, inion, left and right ear) for a standardized headmodel. The corresponding individual four fiducial points were then marked and the software SCIRun (SCIRun, 2008) (Module “BuildTransform”) was used to determine the affine transformation matrix which best fitted the standardized to the individual fiducial points. This affine transformation was then applied to the standard electrode positions to obtain the individual electrode positions of the 10-10 configuration for our subject. The result is shown in Figure 4a (left). Visualization was carried out using SCIRun. From these positions, the 24 EEG measurement electrodes were identified according to their labels.

Figure 4.

a) Left: The 10-10 standard system EEG electrodes (blue spheres) mapped to the head model of the patient. Right: The outermost layer of the head model (red) and a segmented part of the co-registered CT dataset (green) are shown together with the extracted and mapped iEEG electrode positions. b) EEG interpolated isopotential distribution at the signal peak.

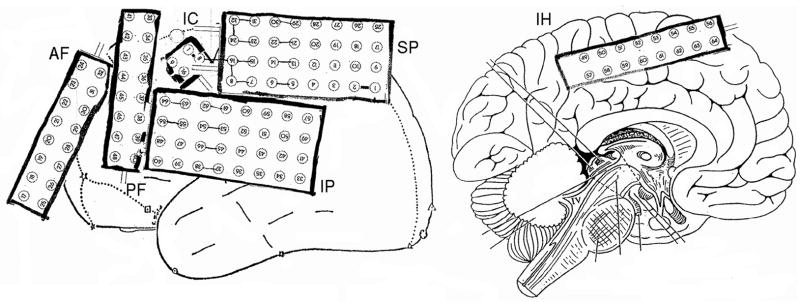
Postsurgically, intracranial long-term video iEEG recordings with 128 electrodes in six grids and a sampling frequency of 256Hz were performed and two datasets were recorded. While the first dataset served for identifying iEEG underlying functional areas, our analysis here uses only the second intracranial dataset for the validation of the presurgical source analysis results. The ictal discharges of the dataset were identified and the 128 intracranial electrode positions were roughly noted during surgery as shown in Figure 5 and scanned in the CT dataset, which was recorded just after the electrode implantation. A registration of the CT to the head model using SCIRun allowed the identification of the iEEG electrode positions with respect to the headmodel, as shown in Figure 4a (right).

Figure 5.

The positions and labels of the iEEG electrodes in the patient’s record. Different stripes are shown, where AF means anterior frontal, PF posterior frontal, IC intra cavity, IP inferior parietal, SP superior parietal and IH interhemisphere.

2.5 Bioelectric forward problem

2.5.1 FEM based forward approach

In the considered low frequency band, the relationship between bioelectric surface potentials and the underlying current sources in the brain can be represented by a quasi-static Maxwell equation with homogeneous Neumann boundary conditions at the head surface (Sarvas, 1987). The primary current sources are generally modeled by mathematical dipoles (Sarvas, 1987; Murakami and Okada, 2006). For a given mathematical dipole and head tissue conductivity distribution, the potential can be uniquely determined (Wolters et al., 2007a) for what is known as the bioelectric forward problem. For the numerical approximation of the bioelectric forward problem, we used the FE method. Three different FE approaches for modeling the mathematical dipole are known from the literature: a subtraction approach (van den Broek, 1997; Wolters et al., 2007a), a Partial Integration direct method (Weinstein et al., 2000), and a Venant direct method (Buchner et al., 1997). In this study we used the Venant FE approach with piecewise linear basis functions based on comparison of the performance of all three in multilayer sphere models, which suggested that for sufficiently regular meshes, it yields suitable accuracy over all realistic source locations (Wolters et al., 2007b,c). Standard variational and FE techniques for the EEG forward problem yield a linear equation system

$$K\underset{\_}{\mathrm{\Phi }}={\underset{\_}{J}}^{\mathit{Ven}}$$ (3)

where K ∈ ℝ^N×N is a sparse symmetric positive definite stiffness matrix, Φ ∈ ℝ^N the coefficient vector for the electric potential and J^V_en ∈ ℝ^N the Venant approach right-hand side vector with N the number of FE nodes (Buchner et al., 1997).

2.5.2 Fast transfer matrix approach

Let us assume that the EEG electrodes directly correspond to FE nodes at the surface of the head model (otherwise, interpolation is needed). It is then easy to determine a restriction matrix R ∈ ℝ^{(s_eeg−1)×N}, which has only one non-zero entry with the value 1 in each row and which maps the potential vector onto the (s_eeg − 1) non-reference EEG electrodes:

$$R\underset{\_}{\mathrm{\Phi }}=:{\underset{\_}{\mathrm{\Phi }}}_{\text{eeg}}.$$ (4)

When defining the following FE transfer matrix for the EEG,

$$T:=R{K}^{-1}\in {\mathbb{R}}^{(s_{\text{eeg}}-1)\times N},$$ (5)

a direct mapping of an FE right-hand side vector onto the unknown electrode potentials is given:

$$T{\underset{\_}{J}}^{\mathit{Ven}}\stackrel{(5)}{=}R{K}^{-1}{\underset{\_}{J}}^{\mathit{Ven}}\stackrel{(3)}{=}R\underset{\_}{\mathrm{\Phi }}\stackrel{(4)}{=}{\underset{\_}{\mathrm{\Phi }}}_{\text{eeg}}.$$ (6)

Note that J^V_en has only C non-zero entries at all neighboring FE nodes to the closest FE node of the considered dipole location (Buchner et al., 1997) (in case of a hexahedra mesh, C = 26), so that TJ^V_en only amounts in 2 · (s_eeg − 1) · C operations.

The inverse FE stiffness matrix K⁻¹ in (5) exists, but its computation is a difficult task, since the sparseness of K will be lost while inverting. By means of multiplying equation (5) with the symmetric matrix K from the right side and transposing both sides, we obtain

$$K{T}^{tr}=R^{tr}.$$ (7)

The FE transfer matrix can thus be computed by means of iteratively solving (s_eeg − 1) large sparse FE linear equation systems. Note that a fast FE transfer matrix approach for the magnetoencephalography (MEG) forward problem can be derived in a similar way (Wolters et al., 2004). For the computation of the EEG transfer matrix T by means of (7), we employ an algebraic multigrid preconditioned conjugate gradient (AMG-CG) method (Wolters et al., 2002). We solve up to a relative error of 10⁻⁶ in the controllable KC⁻¹K-energy norm (with C⁻¹ being one V-cycle of the AMG) (Wolters et al., 2002).

2.6 The bioelectric inverse problem

2.6.1 Discrete source space

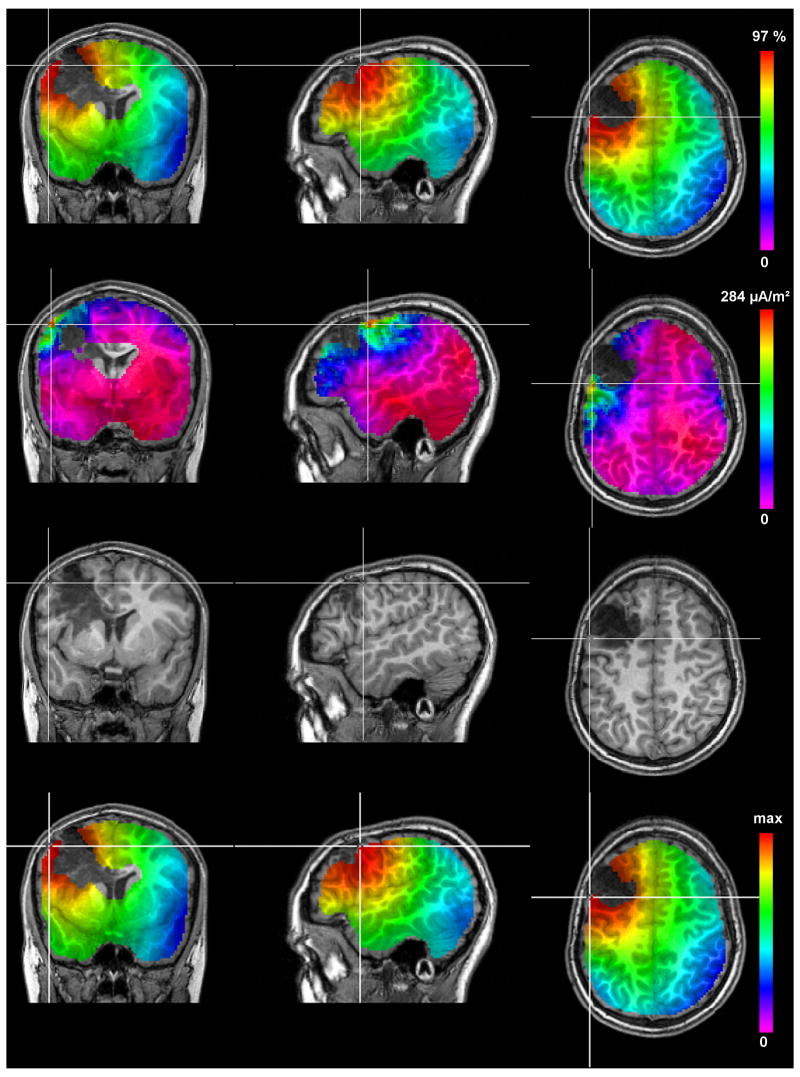
A 3D influence source space that represents the brain compartment in which dipolar source activities might occur was extracted from the segmented T1-MRI for the discrete parameter space source analysis algorithms (GFS, MNLS and sLORETA, see Section 2.6.2). For the brain compartment, a 3mm eroded mask consisting of the gray and white matter compartments was chosen under the assumption that dipole locations (mainly apical dendrites of layer V pyramidal cells (Murakami and Okada, 2006)) are well below the cortical surface. The source space mesh had 172,366 nodes and 157,320 regular hexahedra elements with 2 mm resolution. Dipole sources in the three Cartesian directions were allowed on each mesh node. The source space is implicitly shown in the upper two rows and the last row of Figure 6 as it underlies the discrete parameter space source reconstruction algorithms. It is clearly visible that both the ventricle and the lesion areas were excluded from the source space because no activity is expected from those areas.

Figure 6.

The results of the GFS (top row), MNLS (second row), the rotating dipole fit (third row) and sLORETA (bottom row) using the volume conductor model 6CompAnisoBrain. The crosshairs are located at the amplitude peaks for GFS, MNLS and sLORETA and at the localized position for the rotating dipole fit. An optimized color scale is used for each image with the highest value in red and the lowest in blue-violet.

2.6.2 Inverse methods

The non-uniqueness of the inverse problem implies that assumptions on the source model, as well as anatomical and physiological a-priori knowledge about the source region should be taken into account to obtain a unique solution. Therefore, different inverse approaches for continuous and discrete source parameter space have been proposed (Hämäläinen and Ilmoniemi, 1984; Scherg and von Cramon, 1985; Mosher et al., 1992; Pascual-Marqui, 1994; Fuchs et al., 1999; Knösche, 1997; Pascual-Marqui, 2002).

The first class of approaches that were used here are the classical spatio-temporal dipole modeling approaches, where the number of possible dipoles is restricted to only some few (Scherg and von Cramon, 1985; Mosher et al., 1992; Knösche, 1997). The spatio-temporal focal source models differ in the manner in which they describe the time dependence of the data. Generally, they are grouped into three classes, the unconstrained dipole model (moving dipole), a dipole with temporally fixed location (rotating dipole) and a dipole with fixed location and fixed orientation (fixed dipole) (Mosher et al., 1992). Optimization of the resulting cost function (Mosher et al., 1992) is performed with a Nelder-Mead simplex optimizer which is started from appropriate seed-points and finds the next local minimum of the cost function (Knösche, 1997). The goodness of fit (GOF), often also called “explained variance”, of the spatio-temporal dipole model to the data can then be used as an index of the models quality.

The second class of inverse methods are the scanning methods. From this class, the so-called least-squares scanning or goal function scan (GFS) (Mosher et al., 1992; Knösche, 1997) was used here. The GFS scans systematically position by position of the entire discrete source space defined in Section 2.6.1. At each position, a least squares fit is performed to the chosen data samples, i.e., an optimal rotating dipole is computed for the considered location. As a result, the GOF at each position is displayed as a color map on cross-sections of the source space mesh. The GFS is not subject to pitfalls of non-linear search algorithms, such as being trapped in local minima or slow convergence. Additionally, if the underlying sources have distinct EEG topographies and comparable strength, areas of similar GOF can serve as confidence regions (Knösche, 1997) and GFS results can be used as seed-points for spatio-temporal dipole models. Since a single dipole at each source space mesh node is fitted to the data, this method will naturally work, if there is a single focal source. However, the GFS might fail, e.g., when there are multiple sources which are close to each other, sources that produce overlapping EEG topographies or EEG’s of greatly differing intensities (Mosher et al., 1992).

The last class of inverse approaches that was considered for this study are the current density reconstruction methods. From this class, the minimum norm least squares method (MNLS or Tikhonov-regularization) (Hämäläinen and Ilmoniemi, 1984; Knösche, 1997) and the standardized low resolution electromagnetic tomography (sLORETA) (Pascual-Marqui, 2002; Dannhauer, 2007) were used for our study. The MNLS and sLORETA methods act on a distributed source model, where the restriction to a limited number of focal sources is abolished, i.e., sources are allowed to be simultaneously active on all discrete source space mesh nodes. The non-uniqueness of the resulting problem is compensated by the assumption that the energy of the MNLS should be minimal. The necessary regularization parameter was chosen by means of the L-curve method as described by (Hanke and Hansen, 1993). It is well-known that a regularization without any depth-weighting gives preference to superficial sources (Pascual-Marqui, 1994; Fuchs et al., 1999). Therefore, for the MNLS, a source weighting matrix with L2-norms of the corresponding lead field columns as diagonal entries was chosen (Pascual-Marqui, 1994; Fuchs et al., 1999). As reported in (Pascual-Marqui, 2002), despite of all weighting efforts, linear solutions such as MNLS produced at best images with systematic non-zero localization errors and in a large series of single test source simulations at arbitrary positions and depths in the volume conductor, a standardization of the MNLS as performed in sLORETA was shown to produce zero-localization error.

2.7 Software and computational platform

The SimBio software environment (http://www.simbio.de) was used on a 64bit Linux-PC with an Intel Xeon 5130 processor (2GHz) with 8GB of main memory for all presented FE-based inverse source reconstructions. The SimBio code contains a variety of EEG and MEG inverse source reconstruction algorithms which can be combined with multi-layer sphere, boundary element or finite element forward approaches (Knösche, 1997; Buchner et al., 1997; Zanow, 1997; Wolters et al., 2002, 2004; Güllmar et al., 2006; Wolters et al., 2007a,b,c).

3 Results

3.1 Memory and computation time

When measuring the wall-clock time, it should be distinguished between the setup-computation that only has to be carried out once per head model and computations that have to be carried out hundreds or hundreds of thousands of times depending on the inverse procedure. During the setup, the computation of the transfer matrix T in (5) by means of the AMG-CG solver took about 56min, i.e., about 140s per sensor. The resulting transfer matrix has a size of about 0.6GB (i.e., for 128 electrodes about 3.2GB). Each forward computation in (6), i.e., the right-hand side computation, J^V_en, and the multiplication to the transfer matrix, TJ^V_en, then only took 37ms. The rotating dipole fit, e.g., can then be performed in only 10s of computation time.

3.2 Source analysis results

Five different methods from the presented classes of inverse approaches in Section 2.6.2 were applied to the two time samples at the peak of the averaged ictal F3 delta discharges, namely the GFS, the MNLS, the moving dipole fit followed by the rotating dipole fit and finally sLORETA.

The source analysis results using the volume conductor model 6CompAnisoBrain are presented in Table 3 and Figure 6. In order to get a first overview of the underlying source structure, the GFS was applied, resulting in a single activity peak with a GOF value of 97.03% in the left hemisphere at the posterior lateral border of the lesion, as shown in the upper row of Figure 6. In a second step, the depth-weighted MNLS was used to corroborate the GFS result. The result is shown in the second row of Figure 6, consisting again of a single activity peak at the posterior lateral border of the lesion. Moving and rotating single dipole fits were then started with the GFS localization result as seed-point. With a GOF of about 97.1%, the best fit for both moving and rotating dipole model to the data was achieved slightly (about 2.5mm) outside the pre-defined source space mesh at the posterior lateral border of the lesion at the gyral crown as shown in the third row of Figure 6. The reconstructed dipoles pointed mainly in posterior direction and had amplitudes of about 170nAm.

Table 3.

Localization results of goal function scan (GFS), minimum norm least squares (MNLS), rotating (RotDip) and moving dipole fit (MovDip) and standardized low resolution electromagnetic tomography (sLORETA) in Talairach coordinates and the localization differences between those approaches are presented. GOF denotes the goodness-of-fit. For sLORETA, the indicated GOF is the GOF of the embedded MNLS approach before standardization.

Inverse	Location	Location differences					GOF
method	(in mm)	GFS	MNLS	RotDip	MovDip	sLORETA
		(in mm)
GFS	(−52;4;47)	-	6.6	2.6	2.5;2.3	0	97.02
MNLS	(−50;−1;49) (−50;−1;49)	6.6	-	5.9	6.2;5.8	6.6	99.99 99.99
RotDip	(−53;3;49)	2.6	5.9	-	0.9;1.9	2.6	97.1
MovDip	(−54;3;48) (−52;3;49)	2.5 2.3	6.2 5.8	0.9 1.9	- -	2.5 2.2	97.2 97.1
sLORETA	(−52;4;47) (−52;4;47)	0	6.6	2.6	2.5;2.2	- -	99.99 99.99

Finally, the bottom row of Figure 6 shows the sLORETA result whose peak was at exactly the same position as the GFS peak. For sLORETA, the indicated GOF in Table 3 is the GOF of the embedded MNLS approach before standardization. The crosshairs in Figure 6 are located at the amplitude peaks for GFS, MNLS and sLORETA and at the localized position for the rotating dipole fit.

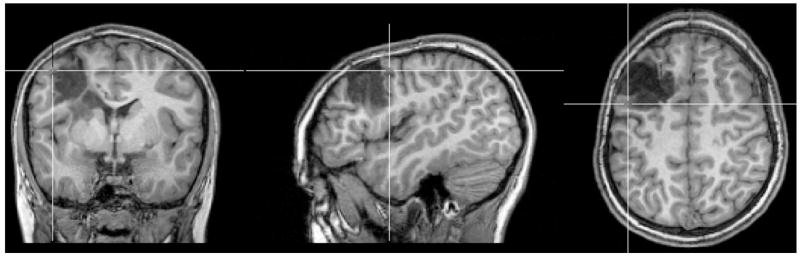
In order to check the sensitivity of source analysis with regard to the impact of the highly conducting CSF compartment, the lesion conductivity and the anisotropic conductivity of the skull and brain tissues, dipole fits and goal function scans were performed in the different 1mm hexahedra FE head models from Section 2.3.4. The differences to the dipole fit results of model 6CompAnisoBrain are shown in Table 4. For the presented specific scenario with a very superficial underlying source, brain conductivity anisotropy as well as possible differences in lesion conductivity (apart from the 29% relative magnitude difference for the CSF-filled lesion case) only have a small influence on dipole fit (see Table 4) and GFS (not shown) source analysis. However, with differences in location of about 9mm, orientation of about 18 degrees and relative magnitude of about 20%, the differences to the dipole fit in the “gold standard” three isotropic compartment realistically-shaped FE model 3IsoComp are distinct as shown in Table 4 and Figure 7. In Figure 7, the cross-hair is again indicating the localized position of the dipole fit. 3:1 skull conductivity anisotropy led to a difference in location of about 5mm, orientation of about 18 degrees and relative magnitude of about 19%. The GFS inverse method corroborated those results (not shown here). With a GOF value of 97.47% of the dipole fit to the measured data, model 6CompAnisoBrainAnisoSkull performed best (see Table 4), even if the GOF is on a high level of about 97% for all examined models.

Table 4.

Differences of dipole fit results in the volume conductor models of Section 2.3.4 and the result using model 6CompAnisoBrain.

Model	Loc.diff.	Orient.diff.	Rel. Mag.diff.	GOF
	(in mm)	(in degree)	(in percent)	97.03
6IsoComp	0.21	4	2.2	97.05
6CompAnisoBrainLesCSF	1.87	8.8	29	97.25
6CompAnisoBrainLesHalfGM	0.62	5.6	5.9	97.12
3IsoComp	8.97	18	19.7	96.59

Figure 7.

The result of the rotating dipole fit in model 3IsoComp. The cross-hair is indicating the localized position.

When summarizing the results, all source analysis methods in the 1mm anisotropic FE model clearly point to a superficial focal epileptic area located in the left hemisphere at the posterior lateral border of the lesion. While the MNLS localized about 6mm more posterior, the location differences between GFS, sLORETA and the spatio-temporal dipole models only differed by maximally 2.6mm. Because the source is very superficial, the modeling of the skull conductivity anisotropy and especially the highly conductive CSF compartment between sensors and source have a significant influence while brain conductivity anisotropy and differences in lesion conductivity were shown to only have a small effect.

3.3 Validation using the iEEG result

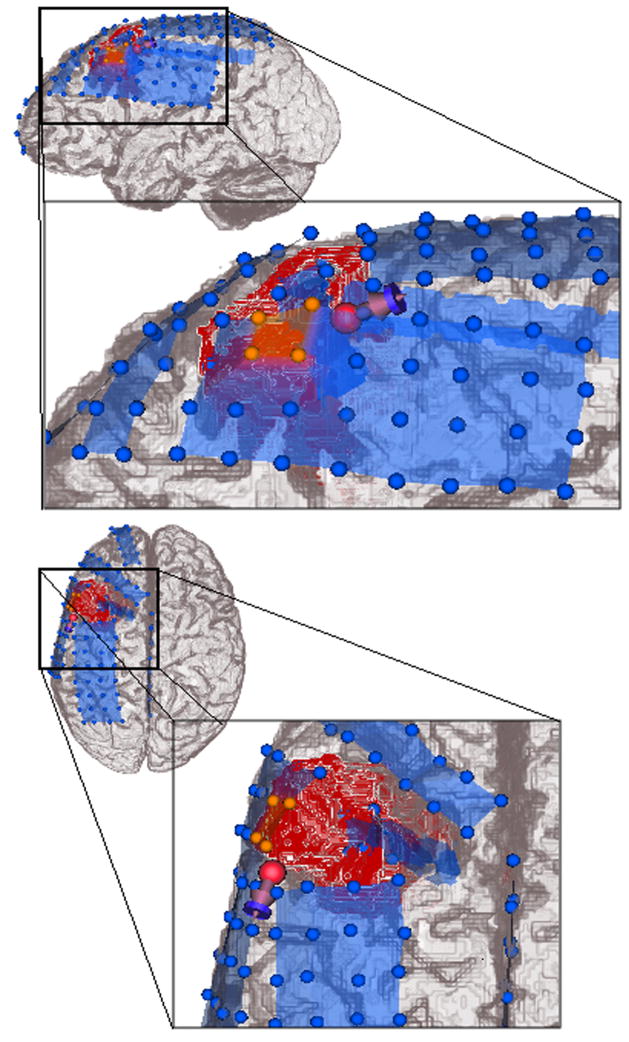
The location of the presurgical rotating dipole fit from Section 3.2 is shown together with the postsurgical iEEG electrodes and stripes in Figure 8. According to the clinical information, the 4 iEEG electrodes which primarily received ictal discharges, are shown in orange. A possible source for the ictal activity might be either located right beneath these electrodes with a mainly radial orientation or it might be located at the posterior lateral border of the electrodes with an increased tangential orientation component so that it only projects one of its poles to the iEEG electrodes. The latter scenario better fits to the presurgical rotating dipole fit result. In summary, the non-invasively localized dipole in model 6CompAnisoBrain is located very close to the intracranial electrodes which primarily received ictal discharges, which validates the source analysis result.

Figure 8.

Presurgical EEG rotating dipole fit result in model 6CompAnisoBrain validated by means of the postsurgical iEEG outcome: The blue spheres represent the postsurgical intracranial grid and stripe electrodes, the four orange spheres are the inferior parietal (IP) grid electrodes, which primarily received ictal discharges. The lesion is marked in red.

4 Discussion

To the best of the authors knowledge, this is the first study using high-resolution (1mm) anisotropic finite element (FE) volume conductor modeling for a non-invasive surface electroencephalography (EEG) based source analysis in presurgical epilepsy diagnosis. The presented EEG FE transfer matrix approach (a similar approach is also possible for the MEG (Wolters et al., 2004)) in combination with the algebraic multigrid preconditioned conjugate gradient (AMG-CG) solver method (Wolters et al., 2002) allowed us to use 1mm edge length leading to about 3.1 Million FE nodes, a resolution, which seemed impossible before (Buchner et al., 1997; van den Broek, 1997; Waberski et al., 1998; Fuchs et al., 2007). A former argument against FE head volume conductor modeling in source analysis was the complexity of the 3D mesh generation (Kybic et al., 2005) and the heavy computational load and thus long waiting time (Buchner et al., 1997; van den Broek, 1997; Waberski et al., 1998; Plis et al., 2007; Fuchs et al., 2007). Because of computational complexity, FE models were restricted to low numbers of nodes such as, e.g., 10,731 (5mm edge length) in a study for the localization of epileptiform activity (Waberski et al., 1998) and 18,322 for the setup of a lead field matrix with 8,742 unknown dipole components which still took roughly a week of computation time (Buchner et al., 1997). Rough restrictions to the number of FE nodes cause unacceptable numerical errors especially for eccentric sources (van den Broek, 1997; Buchner et al., 1997; Marin et al., 1998; Wolters et al., 2007a,b,c) and limit the possibilities of inhomogeneity and anisotropy modeling.

After transfer matrix setup computations in a preprocessing step, which only has to be carried out once per headmodel and which took less than an hour on a standard one-processor Linux machine, an FE forward computation in the 1mm anisotropic hexahedra FE model could be performed in just 37 Milliseconds, which allowed us to setup a lead field matrix with 517,098 unknown dipole components for the discrete inverse methods in only 5 and a half hours. The setup of a lead field matrix with 10,000 unknown dipole components could thus be performed in about 6 Minutes. The generation of the 1mm hexahedra FE mesh is performed in some seconds, the 3D meshing problem is reduced to just a conversion of the segmentation result into the corresponding hexahedra mesh.

Five different inverse source analysis algorithms, a goal function scan (GFS), a minimum norm least squares (MNLS), a moving and a rotating dipole fit and a standardized low resolution electromagnetic tomography (sLORETA) approach were based on the 1mm hexahedra FE model in order to analyse the peak of 9 averaged delta discharges of a recidivous patient suffering from medically-intractable epilepsy. With only small differences in location (a maximal difference of 2.6mm between GFS, sLORETA, moving and rotating dipole fit and 6.6mm between the MNLS and the other approaches), the FE-based EEG inverse algorithms localized a single center of activity at the posterior lateral border of the lesion. While the MNLS localized about 6mm posterior to the other inverse methods, the GFS and the sLORETA localization results were identical. This might corroborate the result of (Pascual-Marqui, 2002), i.e., that, despite of all weighting efforts, former linear solutions such as MNLS produced images with non-zero localization errors, while, in a large series of single test source simulations at arbitrary positions and depths in the volume conductor, sLORETA was shown to produce zero-localization error (Pascual-Marqui, 2002). Source orientation was mainly in posterior direction, i.e., away from the lesion towards the epileptogenic tissue. This source orientation result is in agreement with a recent study which showed that in central and inter-hemispheric spikes, the epileptogenic side cortex was gross surface negative through the sulcal wall to the adjacent gyrus (Salayev et al., 2006).

The presurgical EEG source analysis result was validated with post-surgical intra-cranial EEG (iEEG) measurements and it was found that the reconstructed dipole source was close to the iEEG electrodes which primarily received ictal discharges. The small differences might be due to the deformations of soft brain tissue occurring after craniotomy through the so-called brain shift (Soza, 2005) or through the implantation of the iEEG grids and stripes, the use of standard in contrast to the individual EEG electrode locations, EEG and iEEG data noise, segmentation inaccuracies and the general modeling errors of the bioelectric forward and inverse problem.

The cerebrospinal fluid compartment is known to have a much higher conductivity than brain gray and white matter (Baumann et al., 1997) and, because of its layeredness into compacta and spongiosa, the skull is often represented as an anisotropic conductor (van den Broek, 1997; Marin et al., 1998; Wolters et al., 2006; Fuchs et al., 2007). In agreement with (van den Broek, 1997; Marin et al., 1998; Ramon et al., 2004, 2006; Wolters et al., 2006; Wendel et al., 2008), it was shown in this study that a homogenization of the tissue compartments CSF, gray and white matter into one isotropic compartment as done with “gold standard” realistically-shaped three isotropic compartment boundary element or finite element approaches and the neglect of skull conductivity anisotropy might lead to spurious source reconstructions. Sensitivity studies also showed that brain conductivity anisotropy should be taken into account (Haueisen et al., 2002; Wolters et al., 2006; Güllmar et al., 2006) and that local conductivity changes in the vicinity of the primary source as caused, e.g., by lesions can have a non-negligible effect on source analysis (van den Broek, 1997; Vatta et al., 2002). In (Güllmar et al., 2006) it was found that especially dipole orientation and strength might be significantly influenced by brain anisotropy. As reported in (Pataraia et al., 2005; Salayev et al., 2006), dipole orientations might even be more important than absolute dipole localizations in attributing epileptic activity to subcompartments of the respective brain area. In (Wolters et al., 2006) it was shown that the more the source is surrounded by anisotropic tissue, the more it is important to model the anisotropy. In light of those considerations, the modeling of head tissue conductivity inhomogeneities and anisotropies might be crucial in certain cases of presurgical epilepsy source analysis. However, as shown in this study, the modeling of brain tissue conductivity anisotropy and the inclusion of different lesion conductivities might in other cases be neglected, especially if the source is quite superficial as in the presented study.

The following limitations of the presented work are important. The data of a single case with obviously unilateral and unifocal expression of the epileptiform activity is not representative for all cases of localization-related epilepsy. Further studies including more unselected patients with multifocal epilepsy patterns have to be performed and results of non-invasive source analysis have to be validated with invasive recordings. Electrode positions should be recorded with a digitizer or a photogrammetry device and a larger number of electrodes should be used (Wang and Gotman, 2001). With regard to the skull conductivity modeling, it was recently reported in (Sadleir and Argibay, 2007) that it might not be sufficient to approximate the influence of outer compacta, spongiosa and inner compacta by means of a radial-to-tangential anisotropy as proposed in (Marin et al., 1998; Fuchs et al., 2007) and used in our study. A modeling of the three-layeredness can easily be done in the presented 1mm hexahedra FE approach as long as a segmentation of the spongiosa is available. The location differences between the dipole fit and the GFS and sLORETA inverse approaches can be explained by the chosen procedure for the source space mesh generation. Instead of a 3mm erosion of the mask consisting of the segmented gray and white matter compartments, a 1mm erosion would have been better especially at gyral crown areas. For the presented single source scenario, the MNLS and sLORETA methods were not considered to be very sensitive to the choice of the regularization parameter. However, in other scenarios, this might be different and, since generalized cross-validation was recommended as a method for estimating the sLORETA regularization parameter (Pascual-Marqui, 2002), our chosen L-curve approach might then be suboptimal. To map the diffusion tensors to conductivity tensors, a linear relationship with a scaling of 0.736 was established (Tuch et al., 1999, 2001). In our study, this value would have led to a factor of 3.5 larger mean conductivities of brain tissues than the “gold standard” isotropic approach (see, e.g., (Ramon et al., 2006)). Therefore, we preferred a volume constraint approach that resulted in a scaling of 0.210. This approach certainly minimized the differences between the anisotropic and the corresponding isotropic EEG forward modeling. If we had completely trusted the model and the scaling of (Tuch et al., 1999, 2001) (see also the positive validation of this model in a silk yarn phantom by (Oh et al., 2006)), the increased mean brain tissue conductivity in our study might have been explained by the young age of the patient (with regard to inter- and intra-subject variability of head tissue resistivities, see, e.g., (Haueisen, 1996, Chapter 6.4.1)). Further studies thus have to be performed to validate the scaling parameter, examine its inter- and intra-individual variance and to overall further validate the proposed conductivity tensor imaging method.

In conclusion, the presented study indicates the feasibility of non-invasively localizing an epileptogenic focus by means of surface EEG based inverse source analysis approaches using 1mm anisotropic FE volume conductor modeling. Our result may give new impulse to EEG based source analysis in epilepsy patients and might contribute to clinical presurgical evaluation.