A mathematical model of murine metabolic regulation by leptin: energy balance and defense of a stable body weight

Summary

We have developed a physiologically-based mathematical model, with parameters derived from published experimental data, to simulate the regulatory effects of the leptin pathway on murine energy homeostasis. Model outcomes are consistent with data reported in the literature, and reproduce key characteristics of the energy regulatory system, including compensatory responses that counteract changes in body weight, and the failure of this ability when the leptin pathway is disrupted. Our model revealed the possibility of multiple steady states for body weight. It also provided a unified theoretical framework for two historically antagonistic hypotheses regarding body weight regulation (“set-point” vs. “settling point”). Finally, our model has identified potential avenues for future investigations.

Introduction

Obesity, with its many well-known co-morbidities, has become so prevalent that it is often described as a global epidemic. It is a notoriously obstinate disease – non-surgical treatments directed towards long-term body weight reduction are seldom effective. Energy homeostasis is regulated by centers in the central nervous system (CNS), which receive and integrate information conveyed by signals from peripheral organs (such as fat, gut, and the endocrine pancreas), then send out efferent neural and hormonal signals to regulate food intake and energy expenditure (Morton et al., 2006; Spiegelman and Flier, 2001). Acute changes in an individual's net energy balance are counteracted by opposing changes in food intake and/or energy expenditure which minimize changes in body weight (Leibel et al., 1995; Weigle, 1994). This system is remarkably robust, so that even though energy intake and expenditure can both fluctuate substantially over time, total body weight is maintained within a relatively narrow range.

These observations have led to the “set-point” hypothesis – the idea that in each individual there is an explicit body weight set-point, deviations from which are vigorously opposed by compensatory responses, until the set-point body weight is restored. The nature of this set-point is unknown – no physiological factor representing the set-point has ever been identified. This elusive set-point is believed to have a major genetic component, but some have proposed recently that the set-point may be altered by environmental factors, especially during early development (Levin, 2006). While the difficulty in reversing obesity is often cited as support for the set-point hypothesis, the fact that obesity could develop in the first place is often used to argue against this hypothesis. Opponents of the set-point hypothesis argue that there is little active regulation of body weight, and that the apparent stable body weight is primarily a steady state outcome determined by environmental factors such as diet and life style (the “settling point” hypothesis). In essence, proponents of the set-point hypothesis attribute obesity mostly to intrinsic physiological factors, whereas proponents of the settling point hypothesis believe external environmental factors to be predominant. The debate over which hypothesis is most consistent with experimental and clinical data has lasted several decades, and is still on-going (Kennedy, 1953; Levin, 2005; Levitsky, 2005; Wirtshafter and Davis, 1977).

This controversy underscores the fact that, despite the impressive progress made over the past few decades in unraveling many of the molecular pathways involved in energy regulation, we still have a rather murky understanding of how all the pieces fit together to function as an integrated system. Most previous mathematical models of metabolic energy regulation have not explicitly modeled the neuroendocrine feedback system that maintains energy homeostasis. In order to address this deficiency, we have developed a mathematical model that simulates the physiological system that regulates energy metabolism. This model could complement experimental efforts in answering certain fundamental questions regarding obesity, such as: (i) how different arms of the energy regulatory system interact to produce a stable body weight; (ii) how perturbations such as increased caloric density in food or leptin resistance could affect overall energy balance; and (iii) why there is such wide variation between different individuals subject to similar metabolic environments. We have decided to model the mouse, instead of humans, because mice can be subjected to much more rigorous and invasive experimental investigation, and also because the availability of transgenic mice allows the roles of specific molecular pathways to be studied more thoroughly than is possible in human subjects.

One of the best-characterized arms of the energy regulatory system is the leptin pathway. Leptin is produced by fat cells and secreted into the blood stream. Circulating leptin has effects on some peripheral organs, including muscles and liver, but its most critical effects are in the CNS (particularly the hypothalamus), where a low level of leptin serves as a potent starvation signal, triggering an array of adaptive neuroendocrine responses including hunger/food seeking behavior, efficient metabolism, and suppressed reproduction (Ahima et al., 1996; Badman and Flier, 2007). When the leptin pathway is disrupted by mutations in the gene for leptin or its receptor, the body behaves as if it is constantly starving – resulting in morbid obesity via over-eating and energy hoarding. Although disruptions in the leptin pathway produce very dramatic results, they are also quite rare. Instead, most cases of chronic obesity are characterized by high circulating leptin levels as well as leptin resistance, such that the dose-response towards leptin is diminished compared to leaner individuals.

We have developed this physiologically-based model is to simulate the effects of leptin on the energy regulatory system. The model reproduces key characteristics of this system, such as the ability to counteract changes in environmental factors to minimize variations in body weight, and the failure of this ability when the leptin pathway is disrupted. Variations in specific parameters in the model are able to simulate the wide variations in susceptibility to diet-induced obesity among different in-bred mouse strains (West et al., 1992). Our model revealed that multiple body weight steady states are possible under certain conditions – a potential mechanism contributing to the well-known obstinacy of obesity, with important clinical implications. We also used our model to evaluate the long-standing controversy regarding body weight regulation, and found that a unified model combining aspects of both leading hypotheses (“set-point” vs. “settling point” hypotheses) is most consistent with experimental data.

Methods

We developed a system of ordinary differential equations to describe the effects of leptin on various aspects of energy metabolism (Figure 1 and Supplementary Materials). Detailed derivations of model equations and parameters are available in Supplementary Materials. To evaluate whether a regulatory system based on a body weight set-point is consistent with experimental data, we carried out and compared simulations for two separate systems – with and without control by an explicit set-point. In adherence to established terminology in the field, we will refer to these as the “set-point” and “settling point” models.

Figure 1.

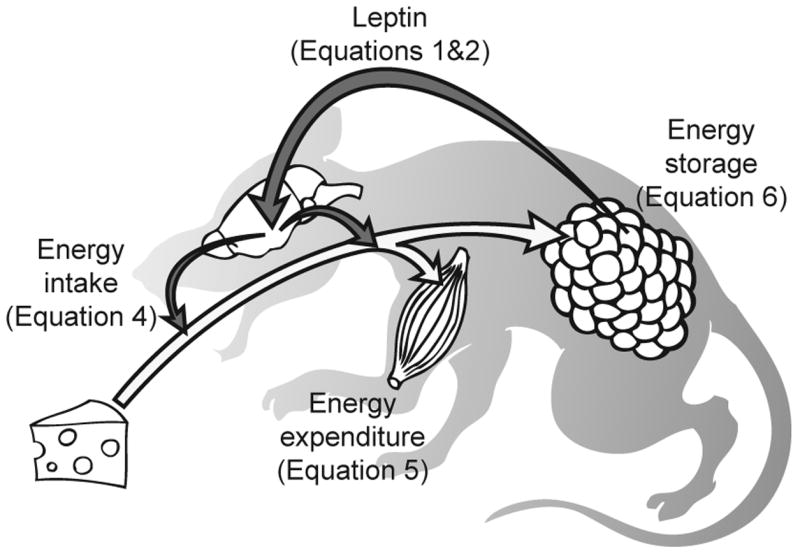
Model of leptin action. White arrow: flow of energy. Dark arrows: flow of information conveyed by neuroendocrine signals. Leptin is produced by fat in proportion to fat mass, it travels to and stimulates the energy regulatory centers in the CNS, which then send out efferent signals to regulate food intake and energy expenditure. The equation numbers refer to equations in the rest of this article that will be used to describe the different components in this system.

Leptin production and transport

We assumed that leptin is produced and secreted by fat cells at a rate roughly linear to total fat tissue mass, and cleared by the kidney by glomerular filtration. This relationship is described as:

$$\frac{d\left({\text{Lep}}_{\text{plasma}}\times \text{BloodVolume}\right)}{dt}=\text{FM}\times R_{\text{syn}}-\text{GFR}\times \text{RenClearance}\times {\text{Lep}}_{\text{plasma}}$$ [Equation 1]

Where Lep_plasma is the plasma concentration of leptin. FM is fat tissue mass. R_syn is the leptin synthesis rate. BloodVolume is the total blood volume. RenClearance is the rate of leptin removal by the kidneys. GFR is the glomerular filtration rate.

Plasma leptin enters the brain both by saturable specific receptors and by nonspecific linear diffusion (Banks et al., 2000; Schwartz et al., 1996). This relationship is represented as an equation taken from Banks et al (Banks et al., 2000):

$${\text{Lep}}_{\text{Brain}}=k_1\frac{{\text{Lep}}_{\text{Plasma}}}{k_2+{\text{Lep}}_{\text{Plasma}}}+k_3({\text{Lep}}_{\text{Plasma}})$$ [Equation 2]

Where Lep_Brain represents whole brain leptin concentration. For the rest of the model, whole brain leptin concentration is assumed to represent the level of leptin exposed to the energy regulatory centers of the brain.

Settling point model

The leptin pathway is arguably the most powerful regulator of food intake. Hyperphagia (over-eating) is a predominant result of disruptions in the leptin pathway. Low leptin levels are a potent initiator of neuroendocrine starvation responses, while administration of exogenous leptin (especially when administered to the brain) reduces food intake (Flynn et al., 1998; Mistry et al., 1997). We used a modified form of the classic Michaelis-Menten equation to represent this relationship, with the maximum (at 0 leptin concentration) scaled by food intake in leptin knock-out animals (Figure S 1A):

$$\text{FoodIntake}=k_4\left(1-\frac{{\text{Lep}}_{\text{Brain}}}{k_5+{\text{Lep}}_{\text{Brain}}}\right)$$ [Equation 3]

Energy intake (E_in) equals to food intake multiplied by its metabolizable energy content (ρ_food):

$$\begin{array}{l}{E}_{\text{in}}={\rho }_{\text{food}}\text{FoodIntake}\\ ={\rho }_{\text{food}}{k}_4\left(1-\frac{{\text{Lep}}_{\text{Brain}}}{k_5+{\text{Lep}}_{\text{Brain}}}\right)\end{array}$$ [Equation 4]

The relationship between energy expenditure and body weight/leptin levels is less clear, with seemingly contradictory reports in the literature (Table S3). Most studies showed that exogenous leptin is most effective at low leptin levels, but at normal, well-fed leptin levels, additional leptin has little effect on energy expenditure. Again we used a modified Michaelis-Menten equation to describe energy expenditure (E_out) as follows:

$$E_{\text{out}}=k_6\text{BM}\left(1+k_7\frac{{\text{Lep}}_{\text{Brain}}}{k_8+{\text{Lep}}_{\text{Brain}}}\right)$$ [Equation 5]

Where BM is the total body weight. When leptin level equals zero, this equation becomes [E_out = k₆BM], and describes the linear relationship between body mass and energy expenditure in leptin knock-out animals (McClintock and Lifson, 1957). The other terms model the additional effect of leptin as a saturable function, so that the energy expenditure-related effects of leptin are most prominent when leptin levels are low, but become roughly constant at higher levels of leptin (Figure S 1B).

Overall energy balance is given by:

$$\begin{array}{l}\frac{dE(t)}{dt}=E_{\text{in}}-E_{\text{out}}\\ ={\rho }_{\text{food}}{k}_4\left(1-\frac{{\text{Lep}}_{\text{Brain}}}{k_5+{\text{Lep}}_{\text{Brain}}}\right)-k_6\text{BM}\left(1+k_7\frac{{\text{Lep}}_{\text{Brain}}}{k_8+{\text{Lep}}_{\text{Brain}}}\right)\end{array}$$ [Equation 6]

Where E(t) denotes the amount of energy stored as fat at time t.

Body weight is the sum of fat mass (FM) and fat-free mass (FFM):

$$\begin{array}{l}\text{BM}=\text{FM}+\text{FFM}\\ =\frac{E(t)}{{\rho }_{\text{fat}}}+\text{FFM}\end{array}$$ [Equation 7]

Where ρ_fat is the energy density of fat. This equation assumes FFM is relatively constant.

Values for each parameter used in this model are listed in Table 1, justifications for these values are included in Supplementary Materials.

Table 1.

Values of model parameters.

Parameter	Value	Units
k1	1.42	ng/g
k2	15.6	ng/ml
k3	0.00272	ml/g
k4	5.6	g/day
k5	0.55	ng/g
k6	244.32	cal/g body weight/day
k7	1	N/A
k8	0.22	ng/g
Rsyn	51.84	ng/g fat tissue/day
GFR	284.4	ml/day
RenClearance	0.25	N/A
ρfood	3.2 (chow diet)	kcal/g
a1	-0.24	g2/ng/day
a2	-288	g2/ng/day2
a3	7.2	cal/ng/day
a4	86.4	kcal/ng/day2

Set-point model

We used proportional-integral controllers to simulate the set-point hypothesis (Supplementary Materials). We assumed that whole brain leptin level is the controlled signal. For the set-point model, food intake and energy expenditure are defined as:

$$\text{FoodIntake}\left(t\right)=a_1\left({\text{Lep}}_{\text{Brain}}\left(t\right)-\text{SetPt}\right)+a_2{\int }_0^t\left({\text{Lep}}_{\text{Brain}}\left(t\right)-\text{SetPt}\right)dt+c_1$$ [Equation 8]

$$E_{\text{Out}}\left(t\right)=\text{BM}\times (a_3\left({\text{Lep}}_{\text{Brain}}\left(t\right)-\text{SetPt}\right)+a_4{\int }_0^t\left({\text{Lep}}_{\text{Brain}}\left(t\right)-\text{SetPt}\right)dt+c_2)$$ [Equation 9]

Where SetPt is the brain leptin set-point. The control action in this model is driven by the difference between brain leptin concentration and the set-point (known as the error signal). For consistency and ease of comparison, we used the steady-state brain leptin level obtained in the settling point model as the set-point. c₁ and c₂ are the amount of food intake and energy expenditure when Lep_Brain equals to the set-point (also known as “bias signals”), again these were set to be the same as the steady-state values of the settling point model (Supplementary Materials).

Other than the food intake and energy expenditure equations, all other equations were kept the same as the settling point model.

Results

Settling point model

Base-line conditions

The equations for the settling point model were solved, assuming fat free mass of 22g (Reed et al., 2007), a standard chow diet (ρ_food ∼ 13.4 kJ/g (Berriel Diaz et al., 2006; Rafael and Herling, 2000)), and an initial fat mass of 2g. Initial leptin concentrations were calculated using equations 1 & 2 (assuming steady state at time 0 for equation 1). The model reached steady-state values of ∼ 6.4 g fat mass, 4.6 ng/ml plasma leptin, and average food intake of 3.6 g/mouse/day. These values are all within the normal range for male C57/B6 mice (Ahima et al., 1996; Collins et al., 2004; McClintock and Lifson, 1957; Reed et al., 2007), and were independent of initial fat mass.

Leptin deficiency

When the leptin pathway was completely disrupted (accomplished in the model by setting the leptin synthesis rate to zero), the model resulted in a mouse with ∼ 73 g body weight at steady state, and the body weight growth curve was in good agreement with experimental data (Figure 2A). Food intake in the simulated leptin knockout (LepKO) mice was higher than wild type (WT) mice (Figure 2B), which is one of the key characteristics of leptin knockout mice. Energy expenditure in the LepKO mice was lower than WT mice at early time points when the LepKO mice still had relatively low body weights, but their energy expenditure increased as body weight increased, eventually overtaking WT mice (Figure 2C), which is consistent with experimental observations (Kaplan and Leveille, 1974; McClintock and Lifson, 1958). When energy expenditure was normalized against body weight, WT mice consistently expended more energy per unit body weight than LepKO mice (Figure 2D). This is a well-documented phenomenon that has been the subject of some debate (Himms-Hagen, 1997).

Figure 2.

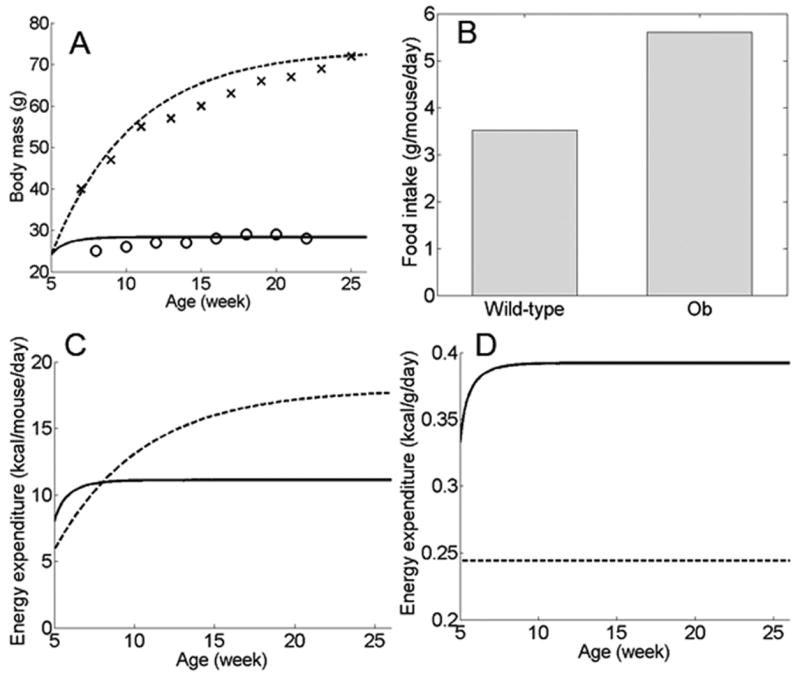
Metabolic consequences of disrupted leptin pathway in the settling point model. (A) Body weight in simulated WT mice (solid line) compared to leptin knockout mice (dotted line). Crosses: body weight of leptin knockout mice of C57Bl6/J background, as reported by the Jackson Laboratory (“Weight gain in B6.V-Lepob/J mice”, http://jaxservices.jax.org/technotes/invivo010906.html). Circles: body weight of WT C57Bl6/J males (J. Tam, unpublished data). Simulation outcomes for both leptin knockout and WT mice are similar to experimental results. (B) Simulated food intake in WT versus leptin knockout mice (ob). (C) Total energy expenditure in WT (solid line) versus leptin knockout (dotted line) mice. (D) Simulated energy expenditure normalized by body weight, in WT (solid line) versus leptin knockout (dotted line) mice.

Haploinsufficiency in leptin or its receptor also causes obesity, albeit not as severe as homozygous knockouts (Chung et al., 1998). In our model, leptin haploinsufficiency can be approximated by halving the rate of leptin synthesis (disregarding compensatory responses, such as up-regulation of leptin receptors, that could lessen the impact of genetic haploinsufficiency in leptin). When leptin synthesis rate was decreased by 50%, percentage body fat increased by about 36% in our model, which is remarkably similar to experimental results showing a roughly 30% increase in percentage body fat in C57Bl/6J mice with haploinsufficiency in leptin or its receptor, after adjusting for age and sex (percentage body fat was 35.2% higher in Lepr^db/+ and 23.5% higher in Lep^Ob/+ mice, no significant difference between the two heterozygotes. Chung et al., 1998).

Compensatory responses to changes in energy balance

The effects of dietary alterations were simulated by setting the metabolizable energy of the diet to ±50% the normal value, respectively. In both cases, the change in diet caused a corresponding change to a new steady-state body weight (Figure 3), and when the dietary energy content returned to normal, body weight quickly returned to pre-diet values (not shown). This behavior is expected of a steady state system subjected to a persistent change in input. The changes in dietary energy content also led to apparent compensatory responses: a decrease in dietary energy content led to increased food intake and decreased energy expenditure, with the combined effect of diminishing the decrease in body weight (Figure 3A); whereas a rise in dietary energy content led to decreased food intake and increased energy expenditure, lessening the increase in body weight (Figure 3B). Similar adaptive responses are seen when energy expenditure is changed (not shown). These compensatory mechanisms that minimize changes in body weight are well-documented in experimental settings (Leibel et al., 1995; Weigle, 1994), and are the core foundation of the set-point hypothesis. In the system depicted in Figure 3 these responses are not corrective attempts to minimize the difference from an explicitly defined reference (which would be the case for a set-point control system), rather they are the products of the leptin dose-response curves for food intake and energy expenditure.

Figure 3.

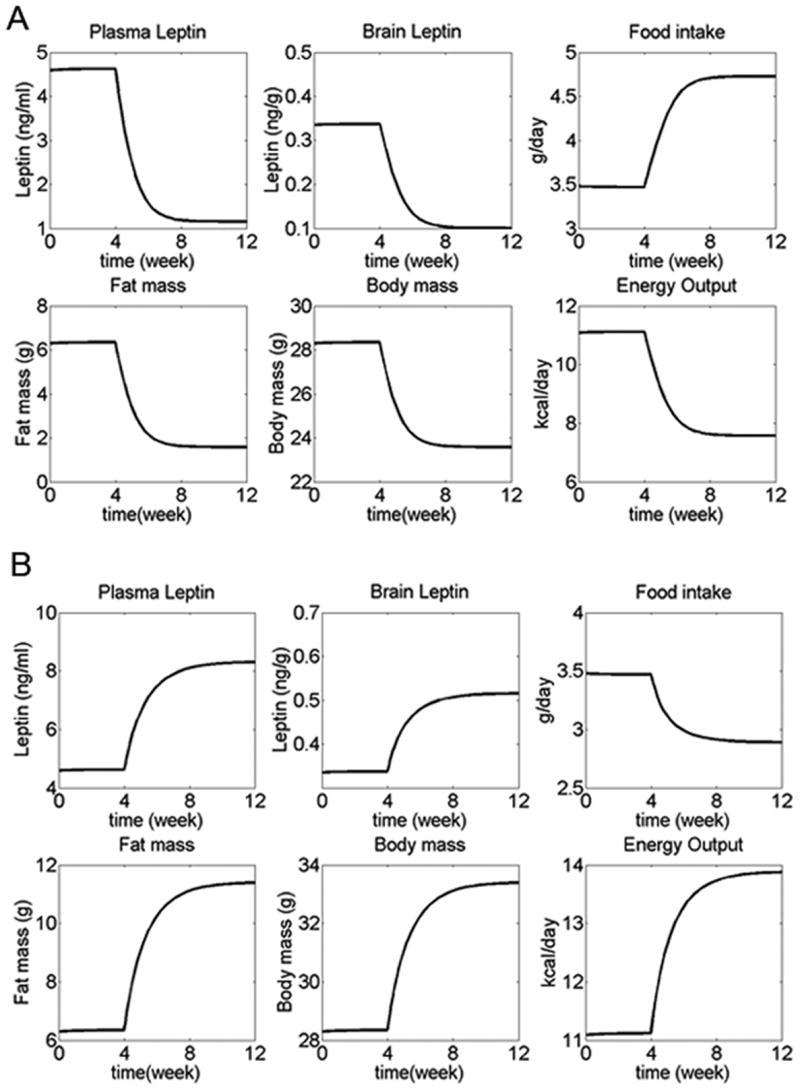
Adaptive changes in response to altered energy intake for the settling point model. Normal diet was eaten during weeks 0-4, while diet energy content was decreased (A), or increased (B) by 50% during weeks 4-12. Plasma and brain leptin levels, fat mass, and total body weight decreased during food restriction and increased during overfeeding, reaching new steady state values. In both cases, food intake and energy expenditure changed in directions that opposed the change in dietary energy content, so that the change in fat mass was diminished.

Sensitivity analysis

To test the sensitivity of this model to the model parameters (k₁-k₈, Rsyn, GFR, and ρ_food), each parameter was varied across its physiological range (see Table S6 for range and justification), and the steady-state model output is obtained across this range (Figure S2).

Results from the sensitivity analysis yielded several intriguing observations. Under normal conditions, body weight is most prominently affected by the parameters that control food intake (k₄) and caloric density in the diet (ρ_food). This implies that normal variability in dietary intake has more pronounced effects on body weight than variability in other factors such as leptin transport rates or energy expenditure.

Note also that despite the lack of an explicit set-point, body weight is maintained within a narrow range, such that even with a diet with very high caloric density, body weight is still relatively low (∼35g, vs. >50g in experimental C57Bl/6J mice (Parekh et al., 1998)). This indicates that change in input (e.g. in dietary caloric content) alone is not sufficient for the development of obesity in the model as currently constructed, with parameters derived using baseline conditions. More severe cases of obesity can only develop if modifications are made to one or more of the model parameters.

Simulation of leptin resistance

Thus far we have assumed that the leptin transport and dose response functions are static, i.e. blood-to-brain leptin transport, food intake and energy expenditure are constants at any given leptin concentration. However, leptin resistance (decreased sensitivity towards leptin) is a hallmark of diet-induced obesity. Transport of leptin across the blood-brain barrier is reduced in the obese (peripheral leptin resistance) (Banks et al., 1999; Van Heek et al., 1997). There is also evidence that sensitivity to leptin in CNS regulatory centers is decreased by obesity (central leptin resistance) – leptin affects food intake and energy expenditure through STAT3 signaling, and obesity causes hypothalamic STAT3 activation to become less responsive to leptin (El-Haschimi et al., 2000). Recent reports have also demonstrated that the neural circuits regulating energy balance are surprisingly flexible even in adulthood (Bouret et al., 2004; Pinto et al., 2004). Given the key role of leptin resistance in obesity, an individual's susceptibility towards leptin resistance is likely to affect that person's propensity to becoming obese.

In our model, peripheral leptin resistance can be simulated by changing the parameters that control blood-to-brain transport of leptin (k₁, k₂, k₃), while central leptin resistance can be simulated by changing the parameters that govern the leptin dose response curves for food intake and energy expenditure (k₄, k₅, k₇, k₈). There is very little quantitative experimental data available on how leptin resistance develops, or how it relates to existing leptin levels. We have arbitrarily chosen to simulate peripheral leptin resistance by increasing k₂ at high leptin concentrations, according to the following ad hoc equation:

$$k_2=k_{2,0}+k_9\left({\text{Lep}}_{\text{plasma}}-k_{10}\right)\times \text{heaviside}\left({\text{Lep}}_{\text{plasma}}-k_{10}\right)$$ [Equation 10]

Where k_2,0 is the original k₂ used in equation 2. k₁₀ is the level of plasma leptin at which peripheral leptin resistance begins to develop. k₉ is a dimensionless factor that scales the increment in k₂ with increasing plasma leptin. The last term is the Heaviside function that causes k₂ to be constantly equal to k_2,0 at plasma leptin levels below k₁₀. Equation 10 simulates leptin resistance by increasing k₂ linearly when plasma leptin levels exceed k₁₀, and assuming that this mode of leptin resistance is fully reversible (Figure 4A,B).

Figure 4.

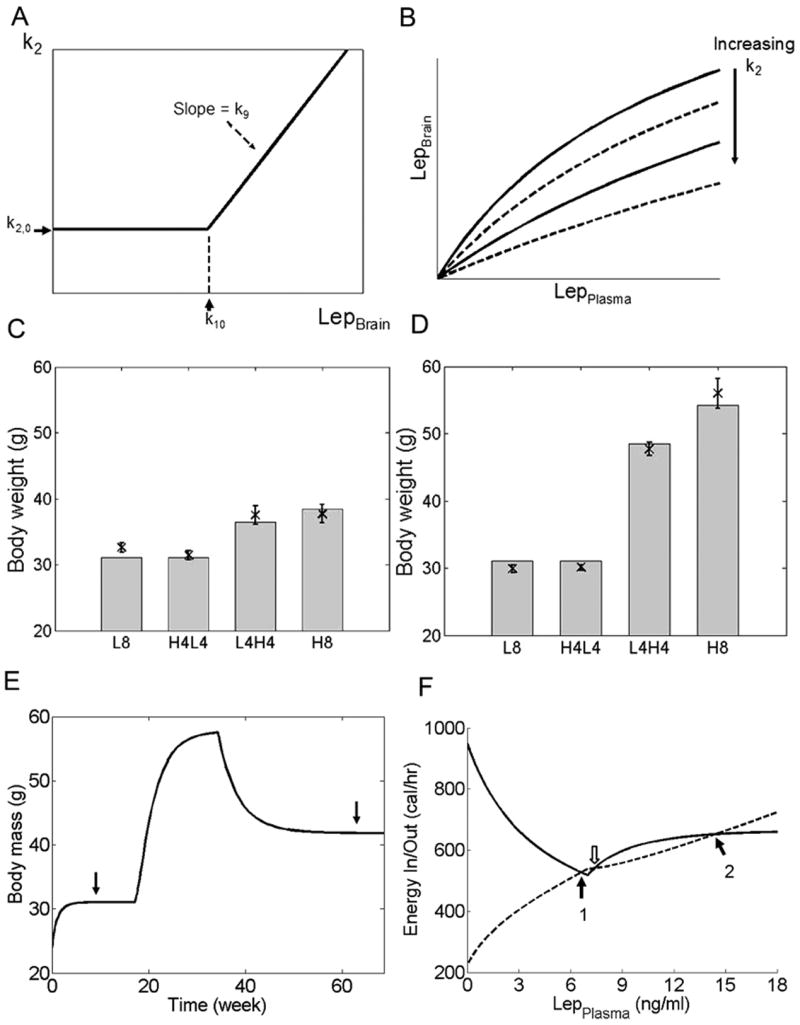
Simulation of peripheral leptin resistance. (A) Modification of k₂ according to Equation 10. k₂ increases at plasma leptin concentrations larger than the threshold level set by k₁₀. k_2,0 = baseline value of k₂. The rate of increase of k₂ is determined by k₉. (B) Blood-to-brain transport of leptin is decreased by increasing values of k₂. Each curve represents the relationship between plasma and brain leptin concentrations at one particular value of k₂. (C,D) Simulation of mice with different susceptibility towards leptin resistance, compared to experimental data from Parekh et al. (Parekh et al., 1998). Mice were given 4 different diet regiments over 8 months: low fat diet all 8 months (L8), high fat diet for 4 months then low fat diet for 4 months (H4L4), low fat diet for 4 months then high fat diet for 4 months (L4H4), or high fat diet for 8 months (H8). Dietary caloric content as reported by Parekh et al. Crosses and error bars represent data reported by Parekh et al., while grey bars represent simulation results. (C) When the value of k₉ is small, the simulated animal is consistent with mouse strains such as A/J that are resistant to diet-induced obesity. (D) When the value of k₉ is large, the simulated animal is consistent with mouse strains such as C57Bl/6J that are susceptible to diet-induced obesity. (E) Multiple steady states are possible when model parameters are permissible. The values of k₉ and k₁₀ in Equation 10 were set to 7 and 9, respectively, then the simulation was repeated with low fat diet for 4 months, high fat diet for 4 months, then returned to low fat diet for 8 months. Even though all other external variables, including the diet, were identical, the steady state body weights (arrows) were different before and after exposure to the high fat diet. (F) Energy intake (solid line) and expenditure (dashed line) are plotted as functions of plasma leptin concentration. Steady state occurs when energy intake equals expenditure (i.e. when the two curves intersect each other). With model parameters used in (E) and a low fat diet, there are two possible stable steady states (black arrows), and a third steady state that is unstable (white arrow). If acute fluctuations (such as a temporary therapeutic intervention or change in diet) in system inputs lead to leptin levels on the left of the point denoted by the white arrow, the system will eventually settle on the lower steady state (arrow 1). When fluctuations lead to leptin levels on the right of this white arrow, the system will settle on the higher steady state (arrow 2) instead.

We then chose values for k₉ and k₁₀ empirically to simulate mice with different susceptibilities towards leptin resistance. The threshold plasma leptin concentration (k₁₀) which leptin resistance begins to develop was assumed to be 10 ng/ml (recall that for our model the baseline steady state plasma leptin concentration was 4.6 ng/ml). When k₉ = 4, the model was resistant to diet-induced obesity, and model outputs were consistent with data from obesity-resistant A/J mice (Figure 4C). When k₉ was increased to 9 (in effect increasing the prominence of leptin resistance), the model became susceptible to diet-induced obesity, and model outputs were consistent with data from C57Bl/6 mice (Figure 4D).

Another interesting observation came from this simulation of leptin resistance. In Figure 4D, the difference between mice fed low fat diet for 4 months then high fat diet for 4 months (L4H4) and the mice fed high fat diet for 8 months (H8) was due to kinetics – the L4H4 group had not reached steady state at the last time point, and if the simulation of the L4H4 group were continued on the high fat diet, eventually their body weight would reach a similar steady state value as the H8 group. However, different combinations of k₉ and k₁₀ could give rise to multiple steady states under identical environmental conditions (Figure 4E,F). Implications of this phenomenon will be discussed below.

Set-point model

Simulation results using the set-point model at base-line (leptin pathway intact, normal chow diet), as well as with disrupted leptin pathway, were similar to experimental data, and comparable to results from the settling point model (Figure 5A). This is expected since we have used steady-state results from the settling point model to define both the set-point and the bias signals of the set-point model, while data from leptin knockouts were used to define the upper and lower bounds for food intake and energy expenditure.

Figure 5.

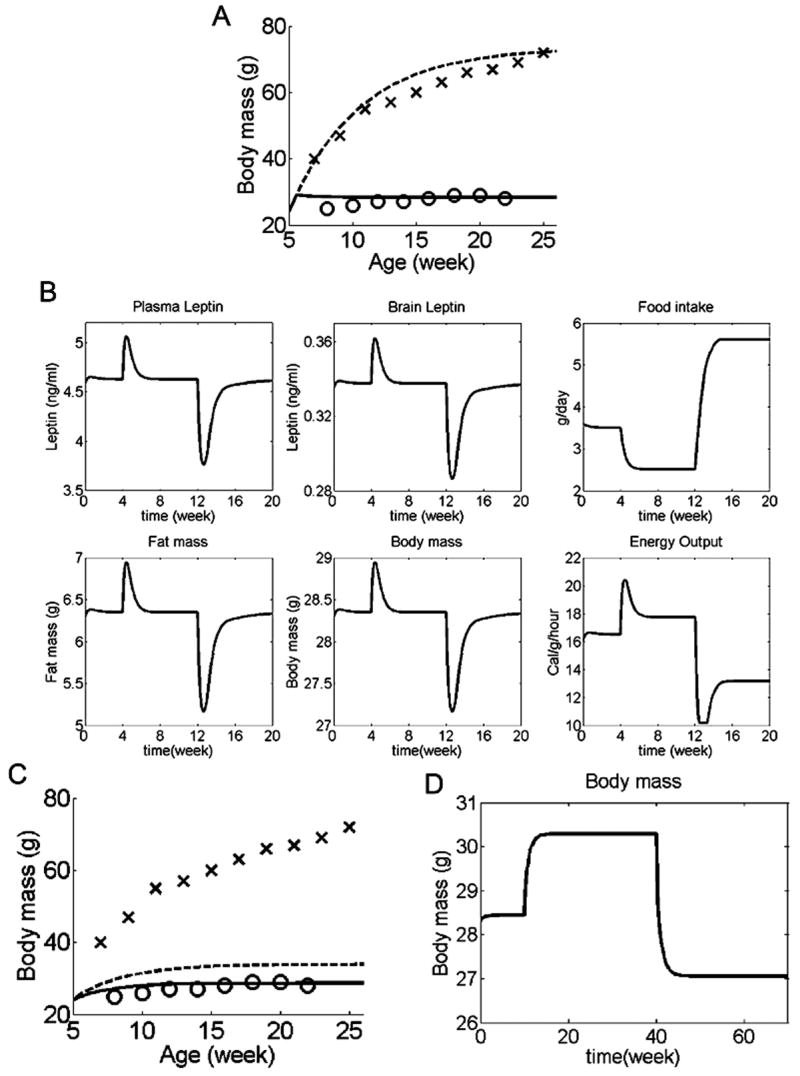
Simulations for set-point model. (A) Body weight in simulated WT mice (solid line) compared to leptin knockout mice (dotted line). Experimental data for body weights of leptin knockout mice (crosses) and WT C57Bl6/J mice (circles) are the same as Figure 2. Simulation outcomes for both leptin knockout and WT mice are similar to experimental data, and comparable to the settling point model. (B) Adaptive changes in response to altered energy intake. Normal diet was eaten during weeks 0-4, while diet energy density 50% above normal during weeks 4-12, and 50% below normal during weeks 12-20. In both cases, compensatory changes in food intake and energy expenditure combined to return body weight to the set-point (body weight at which brain leptin concentration = 0.34 ng/g). (C, D) Set-point system with a set-point that changes in proportion to the error signal, described mathematically by the equation: $\frac{d\left(\text{SetPt}\right)}{dt}=\alpha \left({\text{Lep}}_{\text{Brain}}-\text{SetPt}\right)$, where α = a constant. With this definition of a set-point, the set point reversibly adapts to existing leptin levels. (C) With this changeable set-point, body weight in simulated wildtype mice (solid line) is still similar to experimental data (circles). However, in simulated leptin knockout mice (dotted line) the set-point is continuously lowered so that body weight in these similated mice was much lower than experimental data (crosses). (D) In wildtype mice with an adaptable set-point, the system behaves much more similar to a settling point system than a set-point system (normal diet for weeks 0-10, diet energy density 50% above normal for weeks 10-40, 50% below normal for weeks 40-70).

Response to dietary changes

To evaluate the response of the set-point model to changes in dietary caloric content, we repeated the simulations with varying dietary caloric contents. When dietary caloric content was either increased or decreased by 50%, there was a transient change in body weight and leptin levels, but eventually all these parameters returned to the set-point, despite the persistent change in dietary caloric content (Figure 5B). This result highlights one of the fundamental differences between the settling point and set-point models: whereas a persistent change in input would cause a corresponding shift in steady state output in the settling point model, in the set-point model such a change would eventually be compensated for, upon which the controlled parameter would return to the set-point.

This simulation also illustrates an important fact: diet-induced obesity is incompatible with any set-point regulatory system, such as our set-point model, that is capable of returning the system to the set-point. This is because the controlling actions in such systems are exerted as long as there is a difference between the measured parameter and the set-point, and so the system always returns to the set-point eventually, regardless of variations in extrinsic factors such as dietary caloric content.

In part to circumvent this limitation, proponents of the set-point theory have suggested that perhaps the set-point is mobile, and that an increase in the set-point could explain the development of obesity (Levin, 2005). Since the mechanism by which the set-point could be altered has never been specified, here we will briefly discuss two possible alternatives by which the set-point could change in response to existing leptin concentration.

One suggestion is that perhaps the set-point can be permanently increased (e.g. in obese individuals), but can rarely (if ever) be decreased (Levin, 2005). The difficulty in lowering the set-point would then contribute to the difficulty in losing weight once it is gained. This mode of set-point change could be simulated by a set-point that changes according to the absolute leptin concentration. Since the leptin concentration is always non-negative, this set-point can never decrease. However, a set-point that is permanently increased implies that animals with diet-induced obesity would retain their obese body weights even after returning to a standard diet. This scenario would be analogous to the results shown in Figure 5B, but with a higher body weight set point, which is contrary to results from animal studies showing that diet-induced obesity is reversible when dietary caloric content is returned to normal (Parekh et al., 1998), so a permanently increased set-point change is not compatible with experimental data in rodents.

Another possible mechanism by which the set-point could vary is by changing the set-point in response to the error signal. This would allow the set-point to change reversibly. The first reason this mode of set-point change is unlikely concerns leptin knockouts. Because leptin concentration is constantly zero in leptin knockouts, a set-point that changes in proportion to the error signal would eventually result in a set-point of zero, at which point the leptin knockout animals would eat and expend energy similar to wildtype animals (Figure 5C), which clearly does not happen in experimental animals. This obstacle could be partially circumvented if there were some sort of threshold below which the set-point would not fall. However, even if the leptin knockout scenario was not a problem, this mode of set-point change still requires the overriding of the control mechanisms working to return the system to the original set-point. In other words, this mode of set-point mobility could only become effective if the ability to return the system to its original set-point was lost, resulting in a system much more akin to our previous settling point system than a set-point system (Figure 5D). This limitation also applies to any other model parameters that change in responses to the error signal (e.g. the earlier simulation of leptin resistance by varying k₂ in response to plasma leptin concentration).

For the reasons listed above, even a set-point that is changeable (in response to leptin levels) cannot adequately account for diet-induced obesity. Given that our previous simulation, using a simple steady state system with no set-point, was able to reproduce experimental data of diet-induced obesity with reasonable fidelity, we conclude that body weight regulation in environments of ample dietary energy availability and the development of diet-induced obesity are more consistent with our settling point model than one governed by set-point controllers.

Combination model

While our settling point model is sufficient to simulate the development of diet-induced obesity, there is divergent experimental data when dietary caloric content is reduced below normal. Some animals compensate by increasing the mass of food consumed, and are able to maintain their body weights even at drastically reduced dietary caloric contents, while others are unable to compensate at all (Dalton, 1965; Hirsch et al., 1978; Spiegel, 1973). In general, carnivores (e.g. dogs and cats) and herbivores (e.g. oppossums and rabbits) are less able to compensate for reduced dietary caloric content, while omnivores (e.g. mice, rats and humans) seem to be more effective at sensing and compensating for fluctuations in dietary caloric content, although there are conflicting reports even in rodent and human data. It has been suggested that the ability to appropriately adjust for dietary caloric content may be more important in omnivores due to the wide variety of food they consume, whereas this ability may not be necessary in herbivores and carnivores since they have relatively constant diets in natural settings (Hirsch et al., 1978).

The ability to maintain a constant body weight even in the face of reduced dietary caloric density is more compatible with the set-point model than the settling point model, since the latter could never completely compensate for changes in dietary caloric density. In equations 8 and 9, the integral terms are responsible for the ability to completely eliminate even small errors. Thus in animals that are able to completely compensate for reductions in dietary caloric content, food intake and energy expenditure may be more accurately described by combining aspects of both the set-point and settling point models, as follows:

$$\begin{array}{l}\text{FoodIntake}\\ =k_4\left(1-\frac{{\text{Lep}}_{\text{Brain}}}{k_5+{\text{Lep}}_{\text{Brain}}}\right)+a_2{\int }_0^t\left({\text{Lep}}_{\text{thresh}}-{\text{Lep}}_{\text{Brain}}\left(t\right)\right)dt\times \text{Heaviside}\left({\text{Lep}}_{\text{thresh}}-{\text{Lep}}_{\text{Brain}}\left(t\right)\right)\end{array}$$

$$\begin{array}{l}{E}_{\text{out}}\\ =\text{BM}\times (k_6\left(1+k_7\frac{{\text{Lep}}_{\text{Brain}}}{k_8+{\text{Lep}}_{\text{Brain}}}\right)+a_4{\int }_0^t\left({\text{Lep}}_{\text{thresh}}-{\text{Lep}}_{\text{Brain}}\left(t\right)\right)dt\times \text{Heaviside}\left({\text{Lep}}_{\text{thresh}}-{\text{Lep}}_{\text{Brain}}\left(t\right)\right))\end{array}$$

Where Lep_thresh is the threshold leptin level below which the integral control actions become active. Again, both food intake and energy output are bounded by maximum and minimum values, as described during the derivation of equations 8 and 9. The integral and heaviside terms in these equations allow leptin to function as a safeguard against starvation. At brain leptin concentrations above the threshold, this “steady-state-plus-threshold” system still behaves like the settling point model, where changes in input (e.g. dietary caloric content) would lead to new steady states. However, if brain leptin concentration were to fall below the threshold, the control mechanisms (described by the integral terms in the equations above) would become active, preventing leptin concentration (and by extension, body weight) from falling below the threshold level (Figure 6) by increasing food consumption and reducing energy expenditure. The magnitude of the parameters a₂ and a₄ would determine the strength of this starvation prevention control action. Large values for a₂ and a₄ would confer robust compensatory abilities to counteract decreases in dietary caloric density, while low (or even zero) values for a₂ and a₄ would lead to weak compensatory abilities.

Figure 6.

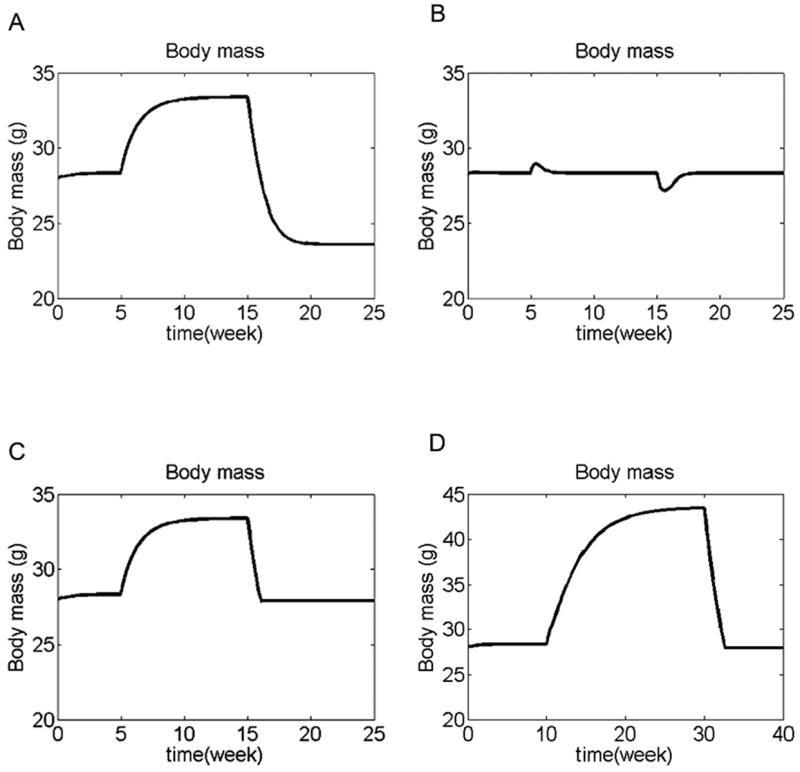
Different responses to altered energy intake by the different simulation models. (A-C) Normal diet was eaten during weeks 0-5. Diet energy density was 50% above normal during weeks 5-15, and 50% below normal during weeks 15-30. (A) Settling point model. This model partially compensates for the change in dietary energy, but the compensation is not complete, leading to a new steady state for each diet. This model is compatible with diet-induced obesity, and animals (such as cats and dogs) that do not compensate well against reduced dietary energy density. (B) Set-point model. This model completely compensates for the change in dietary energy density, so that body weight always returns to the set-point value. This model is incompatible with diet-induced obesity, but the response to reduced dietary energy is consistent with animals (such as rats) that are able to maintain their body weights despite reduced dietary energy density. (C) Steady-state-plus-threshold model. With increased dietary energy density (weeks 5-15), this model behaves like the settling point model, allowing body weight to reach a new steady state. But at reduced dietary energy density (weeks 15-30), the control action becomes active, returning body weight to the threshold level (in this simulation the threshold brain leptin level was set to be 0.32 ng/g, close to the baseline steady state level, so as to be consistent with previous data showing mice given diluted diets maintain their body weights close to those of mice given standard chow ad libitum (Dalton, 1965)). This model allows the development of diet-induced obesity, but also protects more vigorously against starvation. The x- and y-axes are kept constant for graphs A-C for easy comparison. (D) Leptin resistance (as mathematically defined earlier) was included in the steady-state-plus-threshold system. Normal diet was eaten during weeks 0-10. Diet energy density was 50% above normal during weeks 10-30, and 50% below normal during weeks 30-40. The simulated animal developed diet-induced obesity when dietary caloric density was increased, but was able to compensate for below-normal dietary caloric density and prevent its body weight from falling below the threshold level.

Discussion

A number of investigators have used mathematical modeling to study the regulation of energy metabolism and body weight (Abdel-Hamid, 2003; Goldbeter, 2006; Hall, 2006; Kozusko, 2001). However, most of these previous models did not directly address the feedback regulatory mechanisms that regulate food intake and energy expenditure. This may be because most previous models were based on human experiments where food intake was the primary experimental variable, and was determined by the investigator, rather than the subject. Thus the effects of neuroendocrine signals (such as leptin) on feeding were overridden, and therefore such data is not suitable for simulating the regulatory system that controls energy homeostasis under normal, free-feeding conditions.

Here we have developed a mathematical model that explicitly simulates the effects of leptin on energy balance, with parameters derived from published experimental data. Our model reproduces key characteristics of the energy regulatory system – the model produces and defends a stable body weight, the effects of leptin pathway disruption are consistent with experimental results from leptin knockout mice, and varying degrees of susceptibility to leptin resistance (specifically demonstrated for parameter k₂) can result in substantial variations in susceptibility towards diet induced obesity.

Our results showed that an explicit set-point is not required for a stable body weight that is apparently defended against environmental perturbations, and that a settling point model is more consistent with experimental data of diet-induced obesity. On the other hand, our model differs from the prevailing “settling point” concept in that our model includes active regulatory mechanisms (i.e. food intake and energy expenditure both respond to leptin levels), and that intrinsic factors, such as leptin sensitivity, are at least as important as external environmental factors in the development of diet-induced obesity, as we illustrated in our sensitivity analysis and simulation of leptin resistance. We further demonstrated that a hybrid model combining aspects of both set-point and settling point models can more accurately represent animals that are susceptible to diet-induced obesity, yet are still able to compensate for diminished dietary caloric content. This “steady-state-plus-threshold” model is consistent with data showing that low levels of leptin elicits potent anti-starvation responses, while high leptin levels are only partially effective at limiting adiposity (Ahima et al., 1996; Myers et al., 2008). Whether this threshold value could change in response to leptin levels remains to be determined experimentally, but if this threshold value can be raised in response to chronically high leptin levels, it could contribute to the difficulty in losing weight.

Our model predicts that different degrees of susceptibility towards peripheral leptin resistance could account for differences in susceptibility towards diet-induced obesity. One way to test this prediction is by quantifying the change in dose-response towards leptin under conditions of chronic high central leptin levels, and comparing results between mouse strains with different susceptibilities towards diet-induced obesity. Such a study would also be very beneficial towards formulating a more rigorous mathematical description of the development of leptin resistance. In addition, the kinetics for the development of leptin resistance is likely to be quite different than those for energy homeostasis responses. A mathematical model that incorporates both of these kinetic profiles would be very helpful in understanding how these long- and short-term responses towards leptin interact to affect the overall system. Also of note, in the same simulation (depicted in Figure 4C,D), the two strains of mice had very similar body weights on a low fat diet. Thus the propensity for diet-induced obesity in animals more susceptible to leptin resistance was not manifested until exposure to a calorie-rich diet.

When leptin resistance was included in the simulation, multiple stable steady states were possible (given permissible parameter values) under identical external conditions. Systems with multiple steady states are quite common, and detailed explanations for these systems can be found in textbooks on chemistry, thermodynamics or reaction engineering (Fogler, 1999). In Figure 4F, the white arrow marks the unstable steady state, which is also the point of division between the two stable steady states. When transient changes lead to plasma leptin levels to the left of this white arrow, the system will eventually settle at the lower steady state. However if plasma leptin levels were to rise to the right of the white arrow, then the system will settle at the higher steady state. This behavior reveals a potential mechanism contributing to the difficulty in maintaining weight loss – once the system settles into the higher steady state, attempts to changed the body weight will be opposed by the same mechanisms as depicted in Figure 3, and will have no long-term effect unless they are strong enough to force the system back to the left of the white arrow (note that in Figure 4E, after the animal was exposed to high fat diet for 4 months then returned to low fat diet, the new steady state body weight was substantially higher than the previous steady state on low fat diet). Identification of conditions that give rise to multiple steady states could enable the design of therapeutic interventions to “push” an individual's body weight back to a lower, healthy steady state that would persist even after the interventions are withdrawn, as well as the development of therapies that could lower the barrier for transition from the higher to the lower steady state (analogous to the role of catalysts and enzymes in chemical reactions). This finding from our model points to the need for more experimental data to validate whether multiple steady states exist in energy metabolism, and if they do to determine the specific conditions giving rise to the different states.

It should also be noted that while the leptin resistance function we used in this model was fully reversible, it is quite possible that obesity could bring about changes in an individual's physiology that are only partially reversible, or even completely non-reversible (the decision to model leptin resistance as a reversible function was arbitrary – there is currently not enough experimental data to definitively describe the development or “behavior” of leptin resistance). In such cases the permanently altered model parameters could give rise to differences in a formerly-obese individual's metabolic profile that would persist even after the individual returns to a lower body weight.

The validity of outcomes from any mathematical model is critically dependent on the validity of the model's underlying assumptions. The major assumptions made to formulate our current model have been listed in the Supplementary Materials. The following are some future avenues of investigation identified by our model that would enable the relaxation of some of the model assumptions, paving the way for more comprehensive models:

1. More quantitative experimental data on the development of leptin resistance is required to formulate models of leptin resistance based on molecular mechanisms (an ad hoc equation was used in our model due to lack of data). Given the central role of leptin resistance in obesity, such data would also likely yield beneficial insights regarding the treatment of obese patients.

2. Data on how changes in energy balance (including changes in quantity and mode of energy intake/output, e.g. starvation vs. physical activity) lead to changes in fat and fat-free mass over a wide range of experimental conditions (especially during prolonged starvation or muscle-building exercise) would allow the modeling of how energy intake and expenditure affect either the total mass or metabolic profile of fat-free mass.

3. Although leptin is a principal determinant of energy metabolism, it is not the only important signal. Other signals such as insulin and short-term satiety signals have not been explicitly modeled in our simulations. Inclusion of these signals would give a much more comprehensive model. Because of the domineering effects of leptin, experiments must be cautiously designed to isolate the effects of other signals from leptin's confounding effects.

4. The current model only addresses intermediate time scales (days-weeks). Events that occur outside these time intervals were not explicitly modeled due to the paucity of experimental data. More data in these areas would enable the formulation of more powerful models: a model that is accurate to shorter time scales would allow for the evaluation of important factors such as meal patterns, intestinal motility and diurnal variation in hormone and physical activity levels; whereas inclusion of long-term effects would enable the assessment of changes to the metabolic system caused by chronic obesity and aging.

Our present model was constructed for mice. Studies in mice have been crucial in forming our understanding of human obesity – most of the key molecular pathways regulating energy metabolism were originally identified and characterized in mice, and the varying degrees of susceptibility towards diet-induced obesity among different mouse strains is a valuable tool for studying polygenic obesity (which is the norm in humans). However, there are also fundamental differences between human and mouse metabolism. For example, thermogenesis in brown fat represents a significant source of energy expenditure in mice, whereas human adults have very little brown fat. Therefore the same caution that is taken when results from animal experiments are applied to our understanding of human diseases must be taken also with lessons drawn from mathematical models (such as ours) that are based on animal data. Currently the difficulty in obtaining reliable, long-term metabolic data for humans in their natural settings presents a major hindrance against developing a similar model for humans. Ethical concerns have also appropriately excluded human data that require invasive collection techniques. Until technological advances make such data available, the best option may be to develop more sophisticated and accurate models based on experimental animals, and judiciously apply new understandings gained from these models to the human disease. In the meantime, our current model can serve as a unified theoretical framework to interpret existing data regarding body weight regulation, and to identify experiments that need to be done to resolve outstanding controversies.