Complex Dynamic Processes in Sign Tracking With an Omission Contingency (Negative Automaintenance)

Abstract

Hungry pigeons received food periodically, signaled by the onset of a keylight. Key pecks aborted the feeding. Subjects responded for thousands of trials, despite the contingent nonreinforcement, with varying probability as the intertrial interval was varied. Hazard functions showed the dominant tendency to be perseveration in responding and not responding. Once perseveration was accounted for, a linear operator model of associative conditioning further improved predictions. Response rates during trials were correlated with the prior probabilities of a response. Rescaled range analyses showed that the behavioral trajectories were a kind of fractional Brownian motion.

Organisms naturally approach many biologically significant stimuli. These stimuli are called reinforcers, rewards, or goals. This attraction may be inherited by other stimuli that are associated with the primary stimulus; such conditioned attractors act as signposts on paths to the primary reinforcers (Buzsáki, 1982; Killeen, 1989). Pavlov (1955) noted the importance of such attraction in his discussions of the orienting response. Thorndike (1911) made attraction central to the definition of reinforcers, Schnierla (1959) held that attraction and repulsion were the only objective empirical terms applicable to all motivated behavior in all animals, and Hull (1943) emphasized the importance of adience toward positive events and abience from negative ones. Franklin and associates (Franklin & Hearst, 1977; Wasserman, Franklin, & Hearst, 1974) measured regular movements of pigeons toward signs of reinforcement and away from signs of its absence.

The discovery that simple Pavlovian contingencies are adequate to engender directed and easily measurable skeletal activity in a standard chamber led to a new experimental paradigm. Brown and Jenkins (1968) called the arrangement autoshaping, because it could replace the hand shaping that experimenters conducted to establish instrumental responses. Hearst and Jenkins (1974) advocated the more descriptive sign-tracking, but the original term prevailed. A search in PsychLit found over 600 articles that had autoshaping in their title or abstract. The standard autoshaping contingency involves a stimulus that is closely associated in time and space with a primary attractor. The stimulus is usually part of a switch such as a key or an insertable lever that also enables convenient measurement of contact. Other predictors of reinforcement, whether explicit stimuli or background cues, compete with the primary stimulus and slow autoshaping. Locurto, Terrace, and Gibbon (1981) reviewed the first decade of intensive research on the phenomenon. Sign tracking has become a standard procedure for studying the role of Pavlovian contingencies in operant behavior (e.g., Khallad & Moore, 1996) and even provided a basis for the claim that all instrumental conditioning might be best conceived as Pavlovian in nature (e.g., Lajoie & Bindra, 1976; B. W. Moore, 1973).

Sign tracking is a robust survival mechanism but can often lead to behavioral paradoxes. In anomalous scenarios, too strong an attraction to a stimulus can thwart its attainment: Predators charge precipitously, committees close prematurely, lovers stifle with attention. Behavioral experimenters can engineer contingencies so that sign tracking will either abet or thwart attainment of the desired object. If switch contact is arranged to deliver the primary reinforcer, then sign tracking is maintained. This is the common state of nature under which these tendencies evolved. The experimental arrangement is called automaintenance, an instance of instrumental conditioning. If switch closure eliminates delivery of the primary reinforcer on that trial, the arrangement is called negative automaintenance (NA), an instance of omission conditioning. NA is the subject of this article.

Widely held intuitions about the power of instrumental contingencies were violated when Williams and Williams (1969) demonstrated that the omission contingencies in NA did not completely eliminate contact with the signal; responding persisted with fluctuating probability for many sessions. Approach to the external signal was more powerful than approach to behaviors that avoided the signal, even though the latter was regularly paired with reinforcement.

NA provides a convenient dynamic system with which to test theories of conditioning. Whereas autoshaping provides only a few data from each subject in each experiment (viz., the trial numbers and latencies of the first few responses), NA generates behavior that is (dynamically) stable over thousands of trials. Consider the following hypothetical model, which motivated the following experiments: On each trial with a response, approach to the signal undergoes some extinction, and the probability of a key peck therefore decreases. On each trial without a response, approach to some other feature of the environment is conditioned, but so also is the signal; the probability of a response increases as some function of the relative predictiveness of the signal versus other parts of the environment. With different thresholds for initiation and cessation of responding, oscillations of variable periods will occur around some average probability of responding. The experiments to be reported tested this and other models of conditioning.

Method

Two similar experiments were conducted that differ only in details and subjects.

Subjects

Eight pigeons served, 4 in each experiment. Pigeons 5 and 94 were female; the others were presumed male. Pigeon 78 was a White Carneau; the rest were mixed breed. All birds were maintained at 80% to 83% of their ad libitum weights. All had extensive experimental histories of responding for food on various schedules of reinforcement, including in some cases to the same key and keylight color as the one used here. None had experienced autoshaping or omission conditions. Two sessions of extinction before starting these experiments substantially reduced rates of responding, which were quickly reinstated by the first presentations of food.

Apparatus

A standard Lehigh Valley (Allentown, PA) chamber with raised floor measured 30 cm across the work panel, 31 cm deep, and 35 cm high. Three Gerbrands response keys requiring 0.20 N of force for activation were located 20 cm above the floor, centered 8 cm apart. Only the center key was used in these experiments. The hopper aperture measured 6 cm × 5 cm and was centrally located 4 cm above the floor. A 2-W houselight was located 7 cm above the center key.

Procedure

The houselight was kept illuminated throughout the session. White noise was continuous at a level of 71 dB. The primary reinforcer was access to milo grain for 2 s, timed from entry of the pigeon’s head into the hopper. Experimental sessions were conducted 6 days per week.

Experiment 1

The center green key was illuminated with a 2-W bulb for 5 s until food delivery. Measured key pecks extinguished the keylight and initiated the intertrial interval (ITI). Phase 1 consisted of 35 sessions, each session lasting for 150 trials, with a 30 s ITI. Phase 2 consisted of fifteen 100-trial sessions, with ITIs of 10 s (Pigeons 5 and 62) or 50 s (Pigeons 59 and 88). Phase 3 consisted of fifteen 100-trial sessions, with ITI conditions reversed.

Experiment 2

The center green key was illuminated with a 2-W bulb for 5 s until food delivery. Measured key pecks had no effect on the keylight but would abort the feeding scheduled for the end of the signal. Each session lasted until the delivery of 60 reinforcers but no longer than 2 hr. Phase 1 consisted of 20 sessions, with a 40-s ITI. Phase 2 consisted of 15 sessions, with ITIs of 20 s (Pigeons 78 and 91) or 80 s (Pigeons 67 and 94). Phase 3 reversed the ITI conditions. Phase 4 consisted of 15 sessions, with ITIs of 40 s. Phase 5 replaced the fixed 40-s ITI with a random ITI having exponentially distributed intervals with a mean of 40 s; that is a Variable Interval 40 (VI40).

Results

Unconditional Probabilities

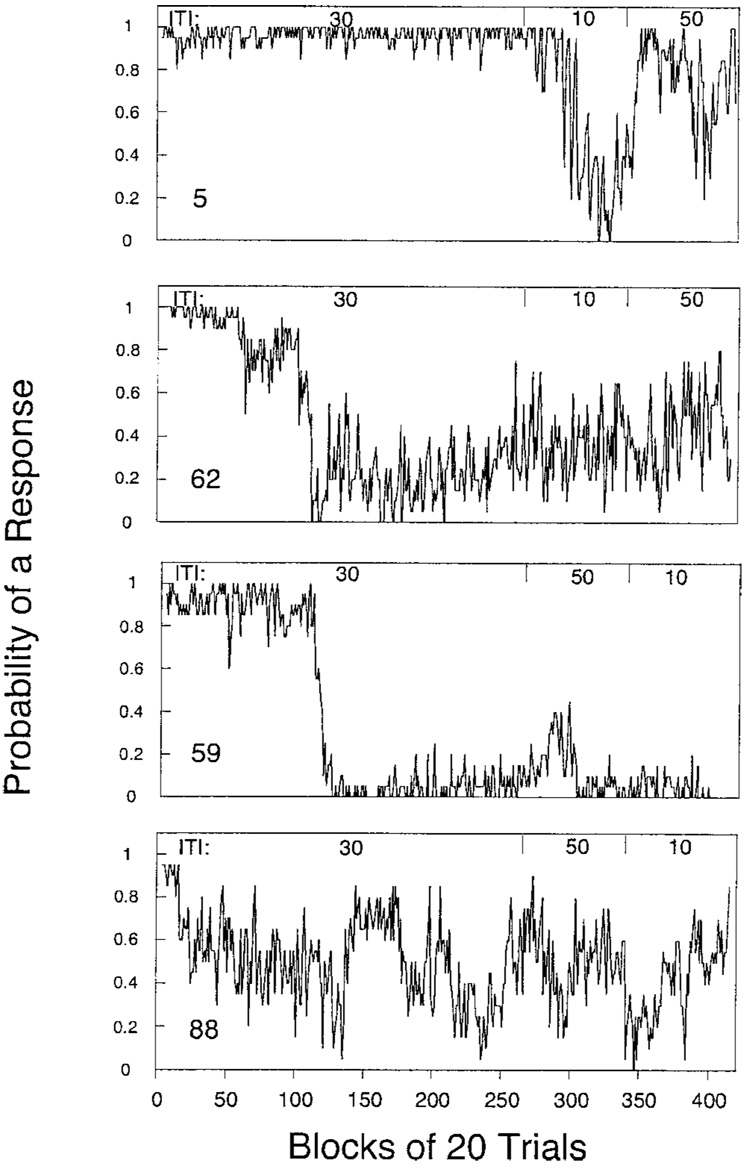
Most pigeons continued to peck the key on some proportion of the trials despite the consistent punishment of such behavior by omission of reinforcement. Figure 1 displays the relative frequency of responding in blocks of 20 trials for each pigeon in Experiment 1. Pigeon 5 pecked on over 95% of the first 6,000 trials. The switch to a 10-s ITI reduced her rate, which recovered under the 50-s ITI. Pigeon 59 showed a transient increase in responding under the 50-s ITI, and Pigeon 88 showed a transient decrease under the 10-s ITI, but there were otherwise no effects of ITI. Pigeon 59 virtually ceased responding after 2,000 trials. For most pigeons, there was substantial variability in the probability of a response from one block to the next.

Figure 1.

The probability of recording a peck over blocks of 20 trials for the 4 pigeons in Experiment 1. Intertrial intervals (ITI) are designated at the top of each graph.

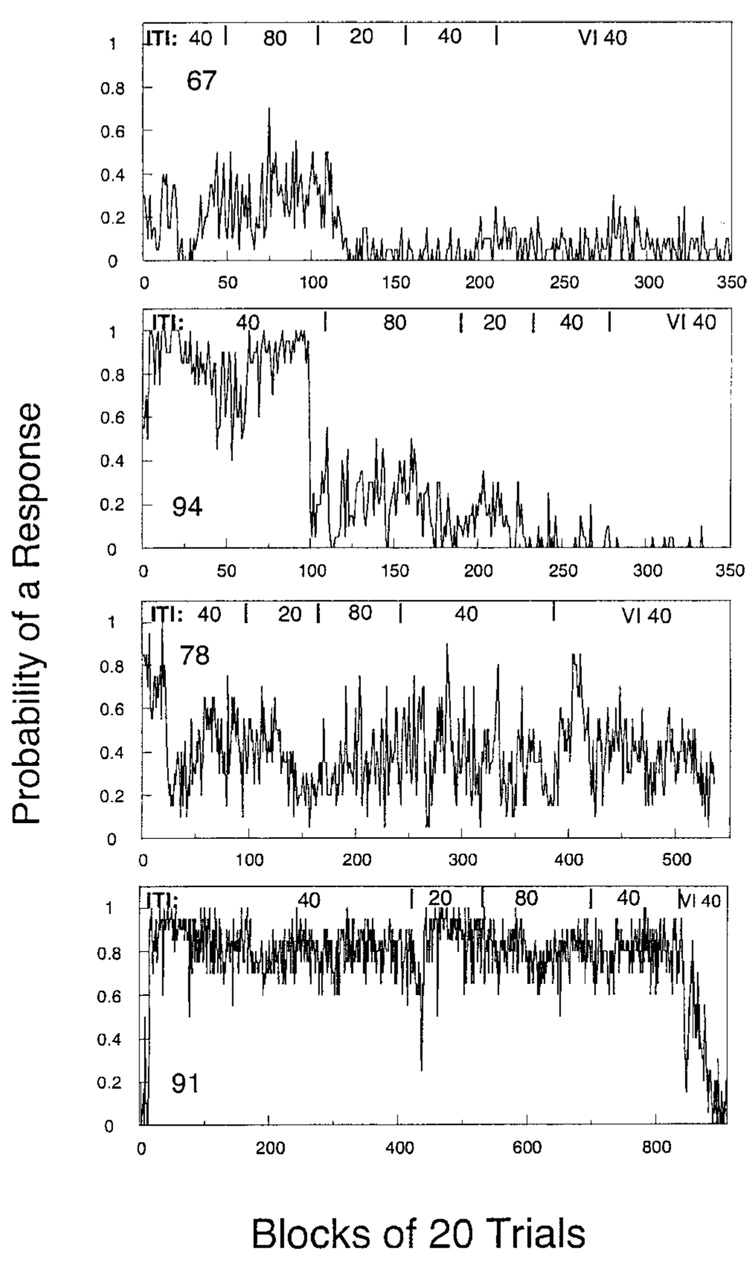
Figure 2 displays the relative frequency of responding in blocks of 20 trials for each pigeon in Experiment 2. There is no obvious difference in performance from that shown in Figure 1, despite the opportunity for multiple responses on each trial in this experiment. Pigeon 91 behaved somewhat like Pigeon 5, pecking on 85% of the first 16,000 trials. Pigeon 78 looked like a blend of Pigeons 62 and 88 from Experiment 1. Pigeons 67 and 94 somewhat resembled Pigeon 59 from Experiment 1. For Pigeon 67, probabilities were higher under the 80-s ITI and fell under the 20-s ITI, never to recover. For Pigeon 94, probabilities fell through the last four sessions of the 40-s ITI, with a slight recovery under the 80-s ITI and possibly a decrease under the 20-s ITI. Observation showed that she had learned to peck the front panel at the bottom of the key aperture, with only occasional slips of responses onto the key. Such a functional drift in elicited responses has been noted before (Lucas, 1975; Myerson, 1974). The remaining pigeons showed no obvious effect of ITI. The shift to a variable ITI did not enhance response rates and was the only manipulation to radically decrease rates for Pigeon 91. In these last sessions, Pigeon 91 cooed at the front panel during the ITI.

Figure 2.

The probability of recording a peck over blocks of 20 trials for the 4 pigeons in Experiment 2. ITI = intertrial interval; VI = variable interval.

Conditional Probabilities

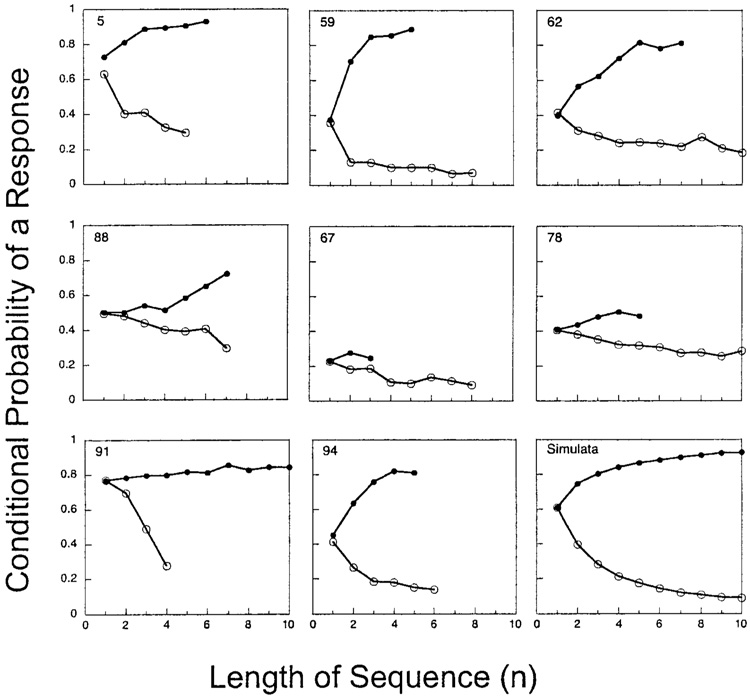
How to proceed beyond the above qualitative analyses? One way to determine the effect of a reinforced (or unreinforced) trial on subsequent behavior is to inspect the probability of a response after a trial with a peck (P) or after a trial with a nonpeck (quiet, Q). The open circles in Figure 3 show the probability of a P after a sequence of n Qs. This is called the hazard function for Ps—the probability that a run of Qs will terminate with a P. It is calculated as the number of sequences of length n divided by the number of sequences of length n or greater. The hazard function for Qs gives the probability that a run of Ps will be terminated by a Q. The filled circles in Figure 3 track the complement of this hazard function for Qs, giving the probability of a P after a sequence of n Ps. Data from all sessions with fixed ITIs were included in these analyses, with graphs carried to the length at which there were fewer than 15 observations. It is clear that the probability of observing a P increases with the number of prior Ps and decreases with the number of prior Qs. The rates of change for both conditional probabilities are correlated, with some pigeons, such as Pigeons 59 and 94, fast in both, and others, such as those in the middle row, slow in both. Pigeon 91 is unique in that the probability of a P was almost independent of the number of prior Ps but decreased quickly with prior Qs.

Figure 3.

The probability of a peck on a trial conditional on the events (peck, P, or quiet, Q) on prior trials. The open circles over 1 show the probability that a single trial with a Q will be followed by a P, the open circles over 2 give the probability that a sequence of two Qs will end with a P, and so on. This curve is the hazard function for Ps. The filled circles over 1 show the probability that a sequence of Ps will last for only one trial, the filled circles over 2 show the probability that it will last for only two trials, and so on. This curve is the complement of the hazard function for Qs. The database for each point decreased geometrically with n; graphing ceased when a condition contained fewer than 15 observations. The last panel shows the hazard functions for simulated data from the perseveration model diagrammed in Figure 4.

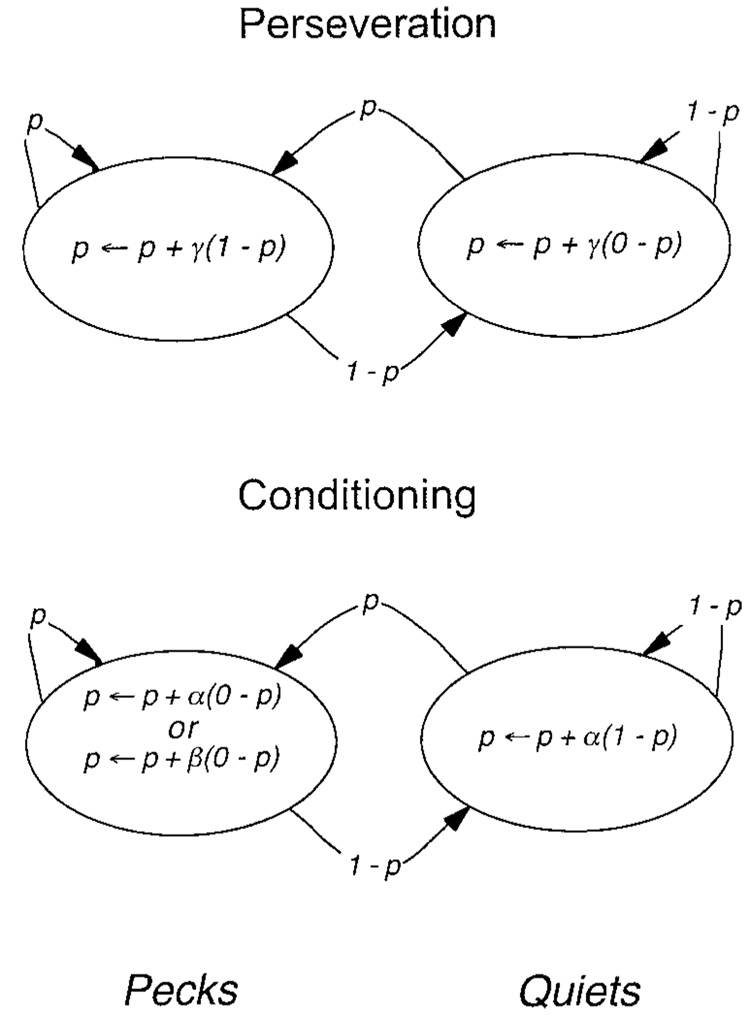
The hazard functions suggest that the pigeons’ tendency is to not just persist in Ps and Qs but to increase the probability of those responses as a function of their immediate history. To validate this inference, I used a simple model of positive feedback (top of Figure 4) to generate simulated data. This model increases the probability (p) of a peck by the fraction γ (gamma) of its distance toward 1 if the prior trial contained a response (that is, if it was a P: the left state in Figure 4). The parameter γ is a measure of persistence of behavior: It indicates the extent to which the base rate is affected by the response on the last trial. The left arrows in Figure 4 indicate that the value of p is replaced by the value on the right with each entry into a state. If the prior trial was a Q (right state in Figure 4), the model decreases the probability of a peck by the fraction γ of its distance toward 0 if a Q occurred on the prior trial (right state). Because the probability of a quiet, q, complements the probability of a peck, a symmetric set of equations govern perseveration of quiets, namely, q ← q + γ (0 − q) in the P state and q ← q + γ (1 − q) in the Q state. Hazard functions from a series of 10,000 simulated responses are shown in the last panel of Figure 3. Varying the perseveration parameter had little effect on the shape of the hazard functions; large values of γ merely hastened the time at which behavior became fixated at 0 or 1. In different runs, the hazard functions lay high in the graph, as for Pigeon 5, or low in the graph, as for Pigeon 67, because of the positive feedback of the perseveration model in combination with the stochastic nature of response selection.

Figure 4.

Top panel: A linear operator model of perseveration. With each trial with a peck (peck state, signified by a left circle) the probability (p) of a peck on the next trial increases by the fraction γ of the distance to 1.0. On each trial without a peck (quiet state, signified by a right circle) the probability of observing a peck on the next trial decreases by the fraction γ of the distance to 0. This constitutes an exponentially weighted moving average of the probability of responding. Bottom panel: A linear operator model of learning to associate the keylight with food and thus approach it. The rate of learning the association is given by the parameter α. On trials without a response, the probability of a response on the next trial increases by the fraction α of the distance to 1.0. On trials with a response there is no food, and the probability decreases by the fraction α of the distance toward 0. In the two-parameter learning model, it decreases by the fraction β, where β is the rate of extinguishing the association.

The hazard functions can be misleading, as they might be misinterpreted as showing a causal relation between prior runs and subsequent behavior. Because baseline probabilities were drifting over the course of these thousands of trials, the hazard functions are in part merely capturing that drift, showing that a peck is more likely to be observed if the trial comes from an epoch of high probability; and the probability that it does come from such an epoch increases with the number of prior trials with a response. This nonrandom selection of data cannot be fixed by parsing the data into epochs with constant probabilities, as those limits would be arbitrary and, with a few exceptions, there is no reason to think that there are any such homogenous epochs to be found in these data. A reality check is possible by determining the probability of a P conditional on two prior trials, in particular QP and PQ. These doublets occur with essentially equal frequency and should be of approximately equal diagnosticity for base probabilities during the epoch from which they are selected. Figure 5 shows that the probability of a P after QP is greater than that after PQ by 3.3 percentage points. Thus, the hazard functions shown in Figure 3 capture a real tendency to persist and are not (only) artifacts of nonrandom sampling. The differential impact of the terminal event in the doublet is washed out after the first subsequent trial.

Figure 5.

The average probability of a key peck for all pigeons conditional on the events—a Q followed by a P (filled circles) or a P followed by a Q (open circles)—on the two prior trials. Data plotted at 1, giving the probability of a response on the trials after the doublets, differ by 3.3 points. Q = quiet; P = peck.

To determine the change in probability expected under the perseveration model, remember that the increment after a P is γ(1 − p) and the increment after a Q is −γp. The probability of the former is p and of the latter is 1 − p. To find the expected changes, integrate:

$$\Delta p|P={\displaystyle {\int }_0^{1}p\gamma (1-p)dp=\gamma /6}$$

and

$$\Delta p|Q=-{\displaystyle {\int }_0^1(1-p)\gamma pdp=-\gamma /6.}$$

The expected changes are of equal magnitude but opposite sign. When p is large, frequent (p) small γ(1 – p) increases are balanced by infrequent (1 – p) large (γp) decreases; when p is small, the reverse happens. The expected value of p does not change. This is a neutral equilibrium, letting the value of p wander over its range without correction. Given a P or a Q, however, the probability of seeing the same outcome on the next trial increases by γ/6, making the process strongly path dependent.

Probability Predicts Rate

In Experiment 2 the keylight remained illuminated for 5 s. This provides an opportunity to study the relationship between the probability of a response and the subsequent latency and rate of responding. To effect this analysis, the perseveration model was applied to the data of each pigeon, and the parameter γ was varied to provide the best prediction of the probability of a response on a trial as a function of the preceding trials. These values are shown in Table 1. The average latency on trials with a response was relatively invariant over this probability, averaging 3.16 s over all subjects and trials, with a standard deviation over subjects of 0.23 s.

Table 1.

Perseveration Parameters (γ), Learning Parameters (α, β), and the Marginal Log₁₀ Likelihood Ratios (LLR) Associated With Each Model

	Perseveration	1-parameter learning model			2-parameter learning model
Pigeon	γ	γ	α	LLRa	γ	α	β	LLRb
5	.028	.085	.0018	26.87	.090	.0082	.0020	1.98
59	.027	.035	.0005	9.30
62	.034	.046	.0012	6.51
88	.028	.032	.0023	4.40
67	.015	.017	.0060	1.25
78	.030	.037	.0029	6.78	.041	.0039	.0079	3.50
91	.020	.021	.0035	3.18
94	.041	.057	.0006	7.98	.060	.0005	.0018	1.57

Note. Models are shown only if the improvements are greater than tenfold.

^af(γ, α) − f(γ), where f(γ, α) is the logarithm of the likelihood of the perseveration and single parameter learning model, and f(γ) is the logarithm of the likelihood of the perseveration model alone.

^bf(γ, α, β) − f(γ, α).

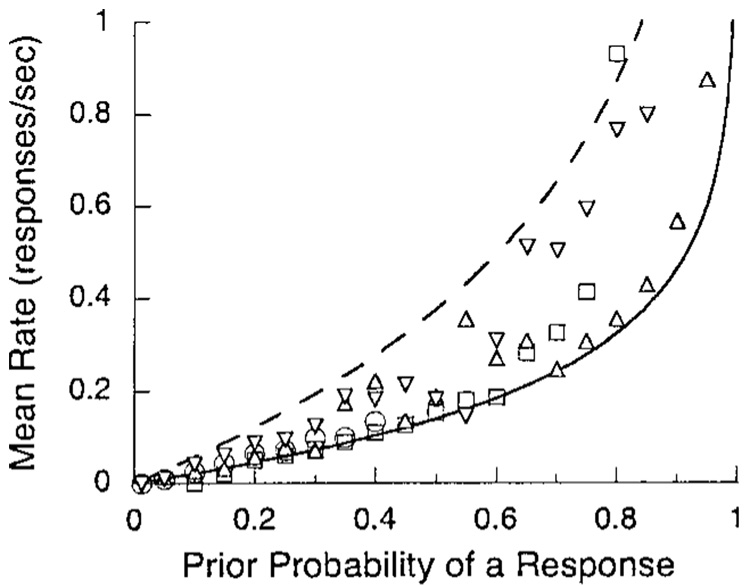
The average response rates are plotted as a function of the estimated response probability in Figure 6. As expected, there is an orderly increase. The solid curve supporting the data is from a map between response rate and probability (Killeen, Hall, Reilly, & Kettle, 2002): If the instantaneous response rate is constant at b, then the probability of witnessing a response in an epoch Δ (delta) is p = 1 − e^−bΔ. Conversely, b = −ln (1 – p)/Δ. In this experiment the observation interval Δ is the trial duration, 5 s. This parameter-free prediction follows the lay of the data systematically below them. The model assumes that response probability is constant throughout the observation interval. If, however, it required 1 s to get to the key, the opportunity for observing a response Δ falls to 4 s, and the curve rises through the center of the data field. The most extreme such assumption would have no responses possible until the average latency (3.16 s) elapsed. The resulting value for Δ generates the dashed line. Thus the range of plausible assumptions for response latency envelopes the data.

Figure 6.

The response rate of all subjects in Experiment 2 on all trials is plotted as a function of the probability of a response predicted by an exponentially weighted moving average of the probabilities on the preceding trials. The parameter of the moving average was γ from the first column of Table 1. The curves are the predicted loci given a constant probability of responding through all of the trial (solid line) or during the postlatency epoch (dashed line).

Uncovering Learning

There is no evidence of learning apparent in Figure 3, which might be manifest as a reversal of the hazard functions after a few trials. Attempts to apply a simple model of learning, such as that shown in the bottom of Figure 4, were overwhelmed by the persistence manifest in the data. There is indirect but strong evidence of learning, however: In simulation with γ = 0.03, the perseveration model almost always fixated at 0 or 1 within 1,000–2,000 trials. But most animals did not become fixated at probabilities of 0 or 1. This provides prima facie evidence for learning or some other force that avoids capture. Two kinds of analyses are explored to find quantitative evidence for that factor. In this section, composite models of learning and perseverance are developed. In a subsequent section a new analytic technique, the rescaled range analysis, is applied.

Composite Models

Likelihood of the data

The perseveration shown in Figure 3 swamps any signal of learning. But if that factor is “covaried out” of the data, evidence for learning may emerge. This is accomplished by fitting the perseveration model shown in Figure 4 to all of the data of each subject. The perseveration model essentially detrends the data, predicting each trial from a moving average of previous trials. First the likelihood of the data is calculated under a default model that predicts the response on each trial from the mean probability of a peck. If that mean is, say, 0.8 and a P occurs, then the likelihood of that outcome given the model is recorded as 0.8. If another P occurs, the probability of those two trials in a row is 0.8 × 0.8. If instead a Q occurs, which has a probability of 0.2, the probability of the PQ doublet is 0.8 × 0.2. This is continued for all of the data. The likelihood of the data under this default model will be very small and is not of intrinsic interest. It provides a base against which the improvement effected by real models may be represented. This strategy is much like calculating the coefficient of determination as the proportion of variance that a model accounts for, using the variance around the mean as the default. The index of merit of a model is the likelihood of the data given the model of interest relative to the likelihood of the data given the default (base rate) model. These are reported as the log likelihood ratios (LLRs), the common logarithm of the ratio of the likelihood of the model in question to that of the alternative model. These numbers tell by how many powers of 10 the predictions are improved by use of the learning model. An advantage of 1 is an improvement by a factor of 10; an advantage of 2 is an improvement by a factor of 100. For a LLR of 5, the probability of the data given the model in the numerator is 100,000 times as likely the probability given the model in the denominator.

The perseveration model

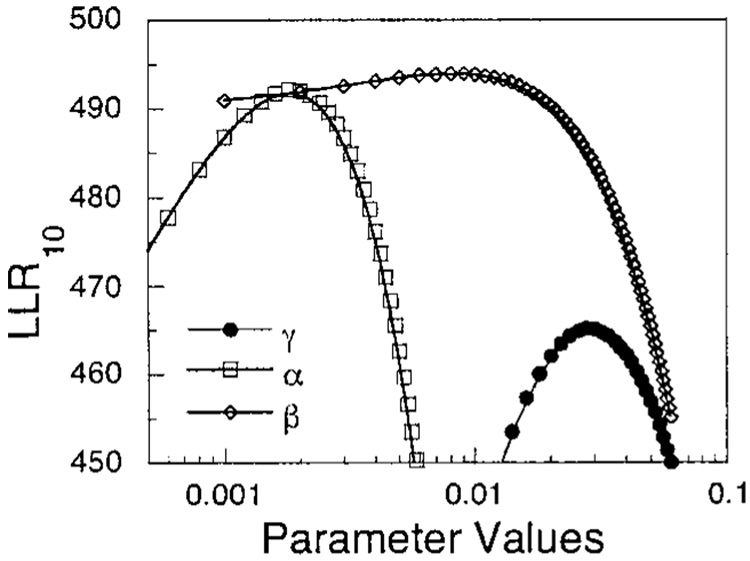
The perseveration model predicts the data on each trial from a weighted average of past performance, with the weights decreasing as the geometric progression: γ, γ(1−γ), γ(1 − γ)², …. The improvement effected by the perseveration model is evaluated by comparing the ratio of the likelihood of the data given the predictions of the perseveration model with the likelihood under the default model, as the value of the parameter γ is increased from 0. This is reported as the LLR. Figure 7 shows the results for Pigeon 5, with the filled circles showing that the perseveration model offers a large advantage in prediction (LLR = 465) over the default, most pronounced when γ = 0.03.

Figure 7.

Filled circles: The log10 likelihood ratio (LLR) of the perseveration model with respect to the predictions afforded by the data from Pigeon 5, as the parameter γ is swept over its range. Squares: the LLR of the learning model in tandem with the perseveration model as α is swept over its range with γ held at its (new) optimal value. The higher maximum indicates a better account of the data. Diamonds: the LLR of the two-parameter learning model as β is swept over its range, with the other parameters held at their optimal values. The marginal advantage of each additional model is the difference in their ordinates at their peaks. These differences are displayed in Table 1.

Learning

Is there any control by reinforcement and its omission to be found in the data after this correction? On each trial after the operation of the perseveration model, the prediction was further adjusted with the learning model shown in the bottom of Figure 4. This model formalizes the idea that on trials without a response (Q, the right state in Figure 4), the keylight is paired with food and becomes associatively conditioned as a sign of food. The tendency to peck consequently increases toward a ceiling of 1, according to a linear operator learning model with a rate parameter of α. On trials with a response, there is no pairing, and so the tendency to peck decreases by αp. The squares in Figure 7 show the additional improvement afforded by that learning model. The data are 10²⁷ times more likely with the composite model than they are with the perseveration model alone.

As the parameter α sweeps up from 0, the optimal value of γ covaries with it. Without the corrective tendency of learning represented in the simple perseveration model, γ takes more conservative values to discharge the responsibilities of the missing parameter α. The best values of these two parameters were determined using an iterative search algorithm that maximized the likelihood of the observed data given the composite model. With an optimal value of 0.002 for α, the optimal value for γ grew to 0.085, where it was held constant to draw the characteristic in Figure 7. The same search algorithm was used to test the marginal efficacy of the learning model for all animals, with results shown in Table 1. In all cases, the observed data are more likely under the hypothesis that learning was occurring in a fashion described by the linear operator model than under the perseveration model alone. The learning model has a median advantage of 5.4. Most simulations with the composite model avoided capture through 10,000 trials, generating trajectories that looked like those of Pigeons 78 and 88.

The linear operator learning model is often elaborated by positing different rates for extinction and conditioning. This is formalized by the model in the bottom of Figure 4, with the rate of extinction of pecking on nonreinforced trials set to β rather than α. For only 3 of the 8 animals did this additional parameter yield more than a tenfold advantage in likelihood. Pigeon 5 was one of those; with α held constant at an optimal value of 0.001, Figure 7 shows that a value of β of 0.009 improved the predictions by a factor of 95.

The reciprocal of the rate parameters tells how many trials are required for the process to move performance halfway to asymptote. For Pigeon 5, the half-life of perseveration, when that was the only predictor, was 35 trials. With the introduction of α, whose half-life was 1/α = 550 trials, half-life of perseveration reduced to 12 trials. With the freeing of β, the rate of decrementing the probability of pecking after a nonreinforcement rose to 1/α = 120 trials and that for incrementing the probability of pecking after reinforcement increased to 1/α = 1,000 trials. Because of these radically different time scales, it is impossible for γ to adjust to an intermediate value to represent all processes. If the times scales are close together, a simple perseveration model may be most parsimonious even if both learning and perseveration are affecting performance; or perseveration plus learning may be most parsimonious even if learning involves different rates of acquisition and extinction. The operation of processes on multiple time scales sets the stage for the following rescaled range analysis.

The linear learning model used here is an elementary version of the classic stochastic learning models of the last century (e.g., Atkinson, Bower, & Crothers, 1965; Bush & Mosteller, 1955). An elegant introduction to them is provided by Wickens (1982). The idea of a geometric increase to an asymptote that depends on the available pool of associative–mnemonic strength is at the core of the Rescorla–Wagner (1972; Miller, Barnet, & Grahame, 1995) model of association, which has been fruitfully applied to autoshaping (e.g., Rescorla, 1982; Rescorla & Coldwell, 1995), as have other associative models involving competition between context and key (see, e.g., Balsam & Tomie, 1985). The success of the associationistic framework (see, e.g., Hall, 1991; Mackintosh, 1983) inspired many variants (e.g., Frey & Sears, 1978; see Pearce & Bouton, 2001, for a current review), all of which may be put to the proof of this reconditioning paradigm. Various versions of these models of conditioning were evaluated with the present data, with none proving uniformly more effective than the composite perseveration–learning model. This may change under the support of a more extensive database.

The Rescaled Range Analysis

The combination of the unstable dynamics of the persistence effect with the stabilizing dynamics of learning occurring on significantly different time scales generates the complex patterns seen in Figure 1 and Figure 2. The dynamics of the resulting trajectories may be elucidated in a theory-free manner with a technique called the rescaled range analysis. This analysis had its origin in a study of the annual deviations in the amount of water that a dam must hold. Hurst (e.g., Hurst, Black, & Simaika, 1965) showed that the amount was typically neither a random (Bernoulli) process, nor was it a random walk (Brownian motion), but something in between, where in between could be characterized by comparing the range between highs and lows over a period (τ) to the length of that period. Hurst and others showed that the normalized range will increase as a power function of the period over which it is measured. In the case of a random process with independent trials, the slope (H) of the power function is close to 0.5. In the case of Brownian motion, H increases to 1.0 (Feder, 1988). In these analyses, the range is normalized (or rescaled) by dividing it by the average standard deviation of the data during the measurement period.

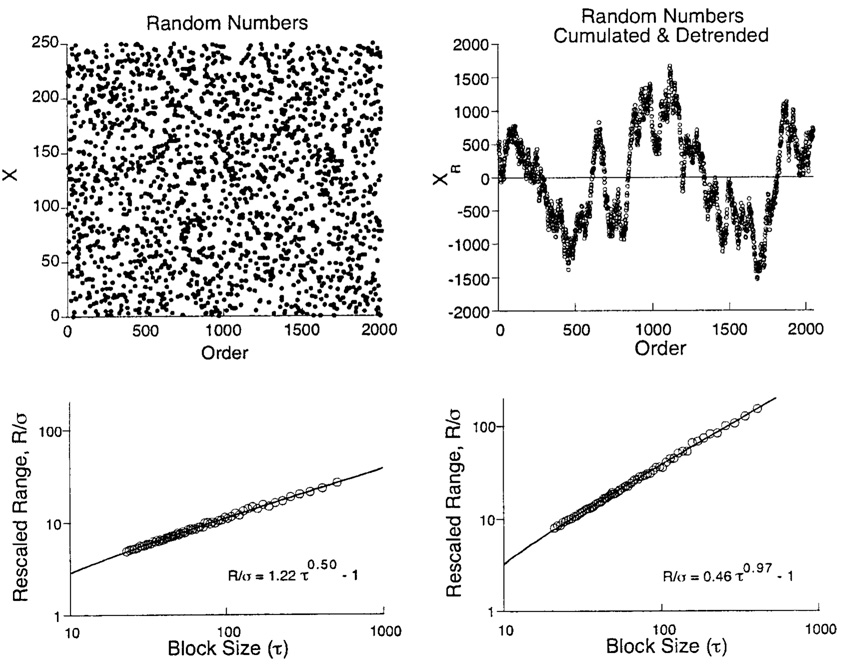
To show how the process works, start with 2,048 truly random integers between X = 0 and X = 250. These numbers are based on the intervals between β-decays of Krypton-85 and were obtained courtesy of John Walker at http://www.fourmilab.ch/hotbits/. They are plotted as a function of their (arbitrary) order in the top left panel of Figure 8. The rescaled range analysis was conducted on the data by dividing the range of the first 20 data by their standard deviation, doing the same for the second 20, the third 20, and so on. The average of these is plotted in the Hurst diagram over an abscissa of 20 in the panel below the original data. The same process was effected with periods of 25, and this average was plotted over τ = 25. The process continued with block sizes of 30, 35, … 500. The resulting power function has a slope close to the predicted value of 0.50. Contrast this with the other extreme in which a succession of random variates are simply added, yielding a random walk. This was done with the data from the first panel. The data were then detrended, with the residuals from that linear regression plotted in the top right panel. This detrending is equivalent to centering the random variates by subtracting 125 from each to achieve 0 average drift. Detrending is a regular part of preprocessing data for this analysis. The rescaled range analyses of these data yield the function shown in the bottom right panel, with H = 0.97. The slopes of power functions in these coordinates are often used as estimates of H. The slopes for these two figures are 0.54 and 1.00.

Figure 8.

Top left panel: 2,048 uniformly distributed integer random variables. Bottom left panel: the Hurst diagram for the variates above it. Top right panel: the variates in the first panel are summed and detrended to generate a random walk around X_R = 0. Bottom right panel: the Hurst diagram for the variates above it. The construction of Hurst diagrams is detailed in the text and Appendix.

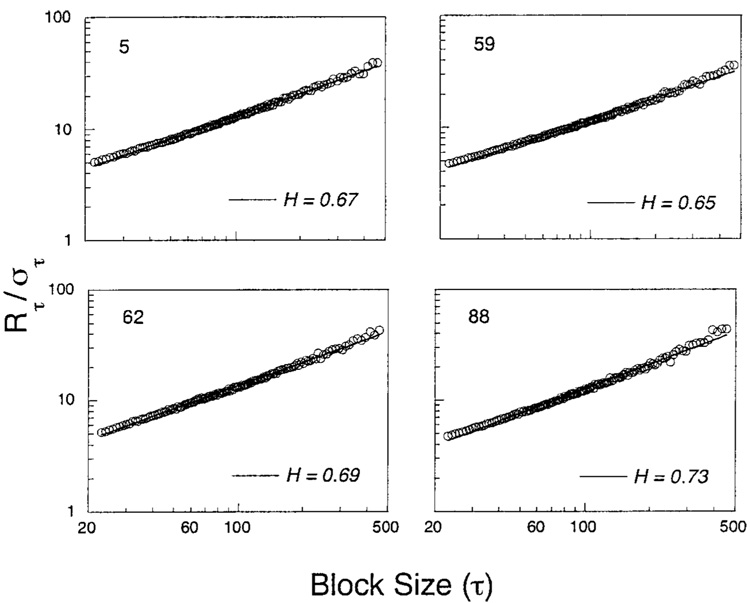
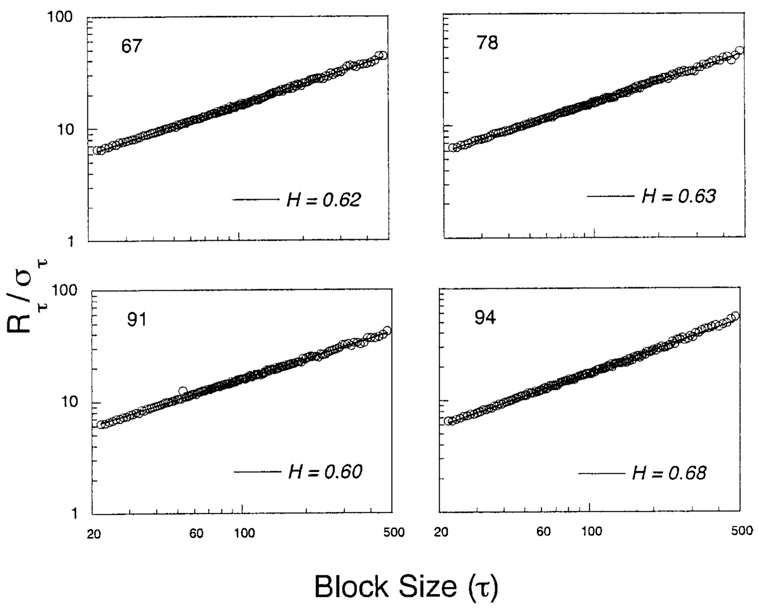
The perseveration in the automaintenance data should cause the Hurst exponents to exceed 0.50. That process was not, however, a pure accumulation of random increments. If p was close to 1, the amount it would increase after a P, γ(1 – p), was less than the amount it would decrease after a Q, (γp). However the expected change was the same except for sign: ±γ(1 − p)p. Learning introduced negative feedback, but it was weaker—had a longer half-life—than the force of perseveration. By itself, such negative feedback will drive slopes lower. Figure 9 and Figure 10 show how those factors play out for the two experiments. The construction of these Hurst diagrams is detailed in the Appendix. The obtained values of H ranged from 0.60 to 0.73, indicating moderate persistence. Some of the functions were slightly concave up. There was a positive correlation between H and γ of r = 0.60 under the simple perseveration model, as would be expected: Greater perseveration as indexed by γ predicts greater persistence as indexed by H.

Figure 9.

Hurst diagrams, in which the rescaled range is plotted as a function of the epoch over which it is calculated, from Experiment 1. Theoretical slopes of these functions can range from 0 through 0.50 (random variates) to 1.00 (random increments, or Brownian motion).

Figure 10.

Hurst diagrams from Experiment 2.

What do the functions shown in Figure 9 and Figure 10 tell us about the behavioral processes? This question is best addressed with simulations. Ten thousand trials were conducted under the basic perseveration model with γ set to 0, and another 10,000 were conducted with γ set to 0.05. The resulting rescaled range analyses are shown in the left panels of Figure 11. In the null condition of the top panel, H was close to 0.50 as expected, and it rose to 0.75 when γ was 0.05. Then the compound model was simulated, with the same values of γ and with α set to a representative value of 0.002. In both cases the negative feedback effected by the learning model lowered the exponent by a few points. Note also the bowing in the bottom two Hurst diagrams, similar to that of some of the behavioral data.

Figure 11.

Hurst diagrams for simulated data. The parameters give the values of γ and α.

The present data frustrated early attempts at analysis with models of associative conditioning. The Hurst diagrams would have immediately indicated a strong preservative component and suggested the use of a persistence model in conjunction with the learning models. Given the results of the log likelihood analyses, the Hurst diagrams now add little to the explicit dynamic models. They remain an excellent descriptive and exploratory analytic technique. They are simple to deploy, yet enjoy a sophisticated mathematical formalism (Mandelbrot, 1982) that may in the future yield deeper insights into associative conditioning.

Variable ITIs

It is a plausible hypothesis that the passage of time through the ITI will predict the appearance of food and compete with the keylight. Animals need not time during the NA procedure, but if they do time accurately, then 35 s past the last feeding in the first phase of Experiment 1 would be as good a predictor of food as the keylight and should compete with it for attention. Accurate timing when food is periodically available might well overshadow extrinsic signs and lead to direct hopper approach. Time discrimination is most accurate for short intervals, and this is consistent with the weaker sign tracking seen with short ITIs. Weakening temporal predictability by use of longer or variable ITIs should enhance tracking to extrinsic signs such as keylights. The failure of pecking to increase when time was made completely uninformative (Figure 1 and Figure 2, VI40 condition) is inconsistent with this hypothesis. Gibbon and associates (Gibbon, Baldock, Locurto, Gold, & Terrace, 1977) found no significant difference in rates of acquisition using variable and fixed ITIs (although the rates were less variable across subjects with variable ITIs). Failure to enhance key pecking could be due to the animals’ ignoring the temporal dimension, or to their attempting to time food onset, not trial onset, and that is aperiodic whenever p > 0 and food is omitted on P trials. Gibbon and Balsam (1981) note that the effects of ITI duration emerge before animals have time to establish fine temporal discriminations and speak of ITI effects being mediated by “a primitive timing sense.” This sense could be the real-time evolution of the learning equations, corresponding to the accumulation and decumulation of associative strength by key and context in real time. But the actual disruption of Pigeon 91’s robust performance (Figure 2) suggests that variable trial onsets not only do not help performance, they may hurt it. Short ITIs apparently undermine the conditioning of key more than context. This is also consistent with a real-time evolution of the learning equations. The equation of the bottom left state in Figure 4 may be written as p_i+1 = (1 − β)p_i. If this is iterated every second, then p_t = (1 − β)^tp₀. This geometric decay of attention to context is concave, so that loss of attention to context at long ITIs will be more than compensated by the heightened attention at short ones, giving the overall advantage to context, not key. Translating these observations into a coherent model with invariant parameters that can treat acquisition and maintenance of behavior is the next challenge.

Discussion

The perseveration found here for Ps (and for Qs) under NA contingencies has precedent in other contexts. If food is presented occasionally but not contingently, pigeons may peck at a low rate indefinitely (Herrnstein, 1966). Pigeon 5 continued pecking at high rates for 40 sessions, despite receiving food only three or four times per session. Pecking in pigeons is a highly prepared response (Burns & Malone, 1992; Killeen, Hanson, & Osborne, 1978). Automaintenance data for rats whose lever-press response is less intimately connected to eating may show a different, more “rational” trend—that is, the learning parameter β may be larger.

When the generating probabilities are not constant, traditional measures of structure in the data such as hazard functions can be misleading. This is compounded by scenarios that provide binary data, which must be aggregated (as in Figure 1 and Figure 2), as the very aggregation tends to obliterate small cumulative changes in underlying probabilities. Different values of α and β will cause the process to find different dynamic equilibria. Changes in response probabilities with changes in trial intervals and ITIs (Balsam & Tomie, 1985; Gibbon & Balsam, 1981; Jenkins, Barnes, & Barrera, 1981) may be associated with changes in those parameters. Pretraining (Killeen, 1984; Linden, Savage, & Overmier, 1997) may play a crucial role by establishing initial values for p. Various other controlling variables in autoshaped performance (e.g., Bowe, Green, & Miller, 1987; Ploog & Zeigler, 1996; Silva, Silva, & Pear, 1992; Steinhauer, 1982) may effect their control through changing system parameters such as those modeled in Figure 4, or in more complicated neural network models (e.g., J. W. Moore & Stickney, 1982).

Figure 6 displayed the close relation between the expected probability of a response and the rate of responding on the subsequent trial. Because response rates have more degrees of freedom than the binary probability of observing a response, their use will increase the power of comparisons between associative theories subjected to such data.

The nonstationary probabilities inherent in the perseveration process generates a path dependency that may be responsible for the metastability found in these and other conditioning paradigms (Killeen, 1978, 1994), with response measures changing to new levels after weeks of apparent stability and remaining stable for additional weeks before changing again. Such path dependency was also seen in the simulations and is consistent with the values of H around 2/3 found in the rescaled range analyses. In the simulations, it sometimes required thousands of trials for the (random) starting values of p to be washed out; not unlike the performance of Pigeons 59, 62, and 94. This is consistent with the implications of Figure 9 and Figure 10 and with the unstable equilibrium of the perseveration process. In fractional Brownian motion—processes with H < 1.0—the correlation of future increments with past increments as a function of the time separating them, t, is C(t) = 2^2H−1 − 1 (Feder, 1988). When H = 1/2, the correlation is 0, as appropriate for random processes. But notice that the interval t does not appear on the right-hand side of this equation: When H ≠ 1/2, increments in the future are correlated with those in the past, and this correlation is independent of the interval separating them. This reflects the extreme path dependency that can occur under conditions where H ≠ 0.5; conditions that may be characteristic of cognition in general (Gilden 2001; Killeen & Taylor, 2000).

Appendix

The Rescaled Range Analysis

Background

Harold Hurst used the centuries of measurements of the depth of the Nile to develop a statistic that would characterize the tendencies for years of drought and years of flood to persist (Hurst et al., 1965). Hurst’s analysis was given a more general treatment as fractional Brownian motion by Mandelbrot and Wallis, whose work is reviewed by Mandelbrot (1982). Feder (1988) provided a good introduction.

The rescaled range statistic, R_τ/σ_τ. The numerator, R_τ, is the difference between the largest and smallest values of the variable during the epoch _τ (the block size or “lag”). Dividing by the standard deviation normalizes this statistic and permits greater generality. One naturally expects the range (and the rescaled range) to increase as the epoch increases in duration. Hurst et al. (1965) and Feller (1951) showed that for random processes, the asymptotic value of the increase is approximately R_τ/σ_τ = kτ^H − 1, where k = (π/2)^H, and H = 1/2.

In application, the prediction, itself an approximation, is often further approximated as kτ^H. In a process with random increments, a random variable is perturbed by some small random displacement after each observation. This is known as a random walk, or Brownian motion, first characterized by Einstein (1905/1998). Although the position of the point during some epoch τ_n depends on its value in the previous epoch τ_{n − 1}, the direction and magnitude of displacement is independent from one epoch to the next. In this case, H = 1. In persistent processes (1/2 < H ≤ 1), deviations from the origin are retained, whereas in antipersistent processes (0 ≤ H < 1/2), they are damped.

Hurst derived the basic square-root relation for random processes, provided ample evidence that many natural processes deviated from this ideal, suggested generative processes that could be present in watersheds, and demonstrated them with simulations using decks of cards. Mandelbrot and Wallis (1969) initiated a study of fractional Brownian motion to address the empirical data of Hurst (Mandelbrot, 1982) and provided a rigorous formalism and extended the empirical observations. Whereas fractional Brownian motion is a model that generates data consistent with many empirical processes, it is mute with respect to the particular mechanisms that might in fact be operative in generating those phenomena. The Hurst exponent is closely related to diffusion processes and to 1/f noise (Schroeder, 1991). Values of H > .50 often reflect the operation of processes occurring on multiple timescales.

Hurst Diagrams

To prepare data for a rescaled range analysis, begin with a series of n observations over units of time t, X(t). In theory the X(t) are continuous random variables, but Bernoulli processes such as the key peck studied in this article suffice: The rescaled range analysis is robust over the form of the data, as long as there are enough of them (Feder, 1988). Significant trends in the data should first be removed by analyzing the residuals from linear or quadratic regressions. Divide the n observations into n/τ blocks, each block containing τ observations. The block size τ is often called the lag. Calculate the mean of X(t) in the first block. For the present data, if τ = 20, this might correspond to the first datum shown in Figure 1, 0.95. Recenter the data by subtracting this mean from each observation in that block. For the sequence 100110 … the recentered sequence would be .05, –.95, –.95, .05, …. Calculate a running sum of these recentered observations: 0.05⁺, −0.90, −1.85−, −1.80, …. Whenever a partial sum is the largest observed, it is flagged with a +, and when it is the smallest, it is flagged with a −. Define R_τ as the difference between the largest positive and negative deviations, to give a range around the mean for this epoch. Calculate the standard deviation of the recentered sample. Divide the former by the latter to find R_τ/σ_τ. In a sample of n = 2,000 observations, there are 100 such epochs of τ = 20 observations. Repeat the above calculations for each epoch and average the statistics to get an estimate of R_20̃/σ_20̃ for all of the data. Because these are ratios, use the geometric mean. Then choose another lag, say 25, and repeat the process for an estimate of R_25̃/σ_25̃ for all of the data. Because these data bases are not independent, neither are the estimates obtained for these two lags. Continue this process ad libitum and plot the rescaled range statistic for each value of lag as a function of the lag. For independent random variables, the result will be a power function with exponent near 1/2, most easily discerned if the data are plotted on double-log coordinates. Truly random data will often have slopes slightly above 0.50. This is because a number of approximations have been made to arrive at the square-root prediction. A more exact approximation, R/σ = (τπ/2)^H – 1, yields the expected slope of 0.50 for the random variates shown in Figure 8.

Many natural and social processes have Hurst exponents greater than 0.5: not only hydrological phenomena but sunspots, tree rings, temperatures, and rainfall. Rivers range from extremely persistent (the Nile, H = 0.8) through more typical ones (H = 0.6 to 0.7) to random ones (the Rhine). The Hurst exponent for the daily yen–dollar exchange rate is 0.64 (Casti, 1994). Gilden (Gilden, 1997; Gilden, Thornton, & Mallon, 1995) has shown that reaction times in many human judgments have a power spectrum of f⁻¹. Such “pink noise” entails a persistence of magnitude similar to those found in the present study.

There is no reason to expect phenomena that are not Brownian to show a power function relating the rescaled range to the lag, unless they were generated from the type of fractional Brownian motion studied by Mandelbrot. That they so often are power functions even when H ≠ 1/2 indicates the presence of positive or negative feedback. When H ≠ 1/2, perturbations are correlated over long times scales, and the process is seriously path dependent, or historical. Deviations from power functions may occur because of (a) data-analytic limitations (lags less than 20 are not reliable) or (b) the correlations are not infinitely extensive. At some large enough lag, the Hurst exponent may shift toward a random process (H = 0.50). This is the case for the stock market, where H = 0.78 out to a lag of about 48 months, whereafter it drops to 0.50 (Casti, 1994).

The rescaled range analysis assumes equal increments and decrements. It is likely to work better with a measure of associative strength (e.g., logit[p]; Killeen, 2001) rather than probability, as the latter suffers floor and ceiling effects that make increments and decrements unequal whenever p ≠ 1/2.