Abstract
Neurons vary greatly in size, shape, and complexity depending on their underlying function. Overall size of neuronal trees affects connectivity, area of influence, and other biophysical properties. Relative distributions of neuronal extent, such as the difference between subtrees at branch points, are also critically related to function and activity. This review covers neuromorphological research that analyzes shape and size to elucidate their functional role for different neuron types. We also introduce a novel morphometric, "caulescence", capturing the extent to which trees exhibit a main path. Neuronal tree types differ vastly in caulescence, suggesting potential neurocomputational correlates of this property.
Keywords: Caulescence, Asymmetry, Morphology, Neuronal function, Neuronal modeling
1. Introduction
Neurons play vital roles in central and peripheral nervous systems, including integration, production, and transmission of electrochemical signals, and establishment of plastic network connectivity. From prenatal development through adulthood, these functions are determined by many interacting factors, such as gene expression, intracellular molecular dynamics, and the type and distribution of ion channels. This review focuses on the most visible, though quite complex traits of neuronal morphology. Morphological properties include a variety of general size characteristics such as length and volume, as well as attributes associated with complexity such as number of branches and asymmetry [1,2]. Each feature has implications for how neurons grow and adapt [3,4], as well as function both locally and in the broader neuronal network [5,6].
1.1. Neuromorphology
Neurons display elongated branching structures stemming from their cell bodies. These trees, called axons and dendrites, respectively send and receive signals to and from other neurons. Axonal and dendritic arbors differ in size and shape both between and within cell classes (Fig 1). Given the complexity and variability of neuronal morphology, computer-aided methods are typically employed to perform comprehensive and quantitative analyses. Many of the previous and current results reviewed here are based on 3D digital reconstructions of neuronal arbors [7]. This process begins with histological slices laid out on slides. The neurons of interest are labeled so they can be captured using a digital camera mounted on a microscope, allowing focusing for acquisition of an entire 3D structure. Specialized software programs, such as Neurolucida [MicroBrightField, Inc., Colchester, VT], Neuron_Morpho [8] (http://www.personal.soton.ac.uk/dales/morpho), or Neuromantic (http://www.rdg.ac.uk/neuromantic) provide tools for visualizing the captured images and/or tracing neuronal branches, outputting 3D coordinates and connectivity of trace points. The end product is a digitized, morphologically realistic neuronal representation that can be loaded into software programs specialized in extracting an extensive array of morphological metrics, such as L-Measure [1] (http://krasnow.gmu.edu/cn3). Digital reconstructions are further imported by software that simulate biophysical properties [9,10], thus providing morphological realism for electrophysiological modeling.
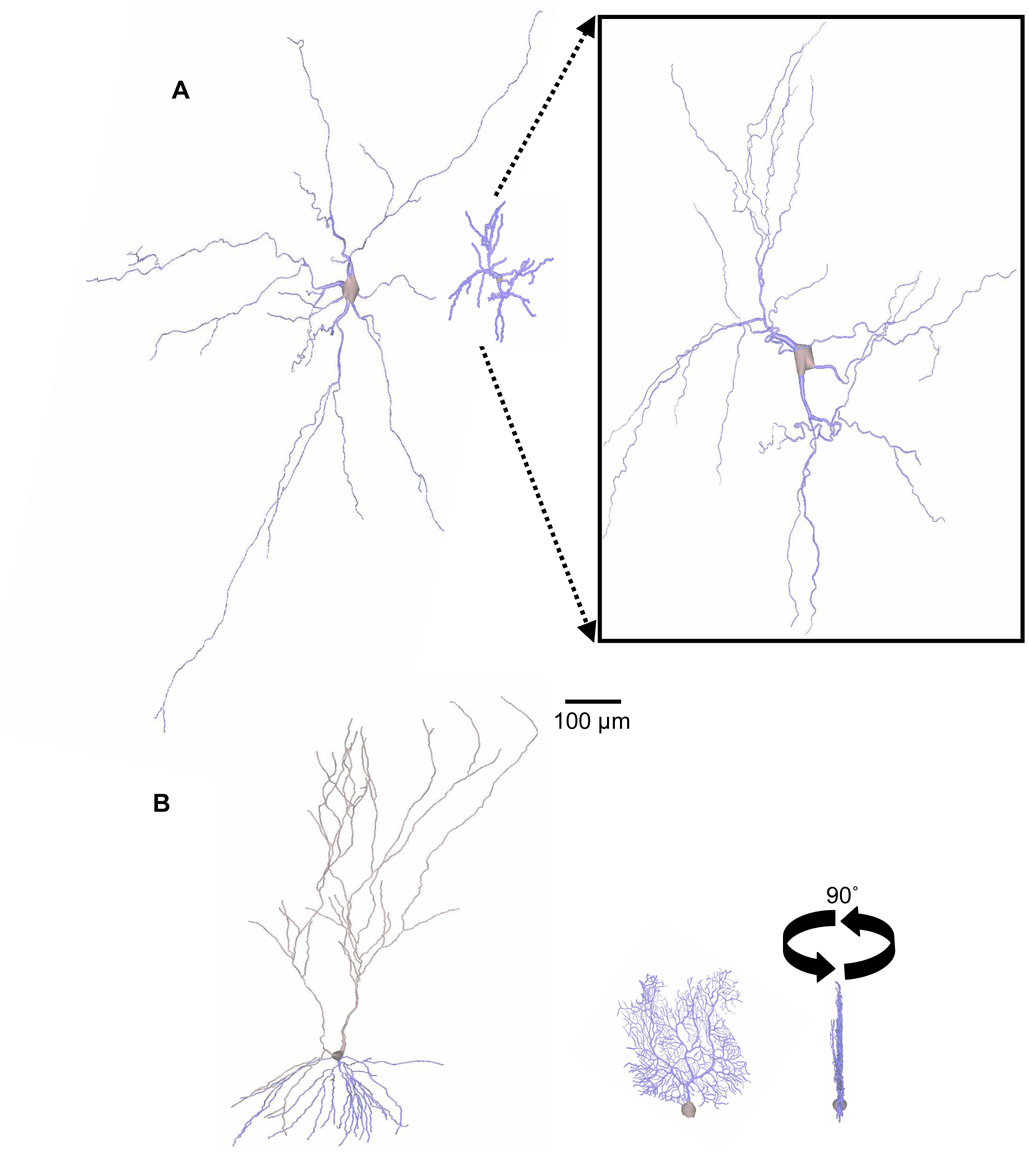
Fig. 1.
Diversity in neuronal size. A. Brainstem motoneuron [72] (left) and cerebrocortical stellate dendritic trees [73] (right) have similar shapes and numbers of branches (53 and 51, respectively) but different total lengths (6298 to 1966 µm). Boxed Inset: Zoomed-in (4×) stellate cell emphasizing morphological similarity to motoneuron besides size. B. Hippocampal CA3 pyramidal [43] (left) and cerebellar Purkinje cell [24] (right) dendritic trees have similar lengths (9670 and 9883 µm) but different numbers of branches (121 and 567). Rotation shows the prototypical Purkinje cell planar shape. All trees (from NeuroMorpho.Org) are to scale.
2. Neuron size and shape
Overall size encompasses an important subset of morphological characteristics of neuronal arbors. Distinct functional aspects of internal neuron size are defined by the total number of terminal branches (the “degree” of the tree) or by continuous morphometrics including total length, surface area, and internal volume [11]. The spatial extent of the neuron can also be described in terms of distance reached from the soma or by the height, width, and depth of a box containing the whole arborization. Greater length often corresponds to greater area of invaded space, and thus greater potential connectivity. For axons this may result in increased divergence (one signal sent to many cells). Total wiring is minimized by increasing length for axons over dendrites [12] when divergence is higher than convergence (more presynaptic than postsynaptic neurons). When convergence is greater than divergence, dendrites have relatively greater length. These predictions were confirmed in retinal, cerebellar, olfactory bulb, and neocortical neurons.
Membrane surface area correlates with number of synapses in dendrites and axon terminals [13,14]. Signal propagation speed linearly increases with diameter, however the metabolic cost also escalates due to the squared relationship between diameter and cross-sectional area [15]. Within the generally large metabolic costs of the brain, synaptic transmission and spike generation are particularly energy intensive due to the high ATP requirements of ionic pumps [16]. The total number of branches (defined as the regions between two bifurcations or between a bifurcation and a termination) is another measure of absolute tree size and varies widely between cell types (Fig 1B). Individual branches may operate in isolation for the separate processing of specific groups of synaptic inputs [17]. Bifurcations also serve as nodes of integration, enhancing dendritic computational power [18].
Each path within a tree, from soma to termination, has its own total number of branches, length, surface area, and volume. For any size metric, the maximum extent among all paths in a tree is also functionally relevant. Greater distance along the path augments passive signal attenuation (i.e. when voltage gated channels are not actively propagating the membrane potential), and thus decreases the influence of distal synapses [19]. Branch order, defined as the number of bifurcations from the cell body (Fig 2A), also influences signals. Computational models and electrophysiological experiments have shown that branch points are prone to failure in active signal propagation [20,21,22]. These failures are due to impedance mismatch between branches, which is in turn affected by differential section areas [23]. A greater density of bifurcations therefore can have a significant impact on passive and active signal propagation both towards and away from the soma. With active propagation, the density of active channels can modulate the effects of morphology and prevent the failure of dendritic spike forward- or back-propagation [24]. Thus, branch points and length can respectively act as digital filters for active signals and continuous filters for passive signals.
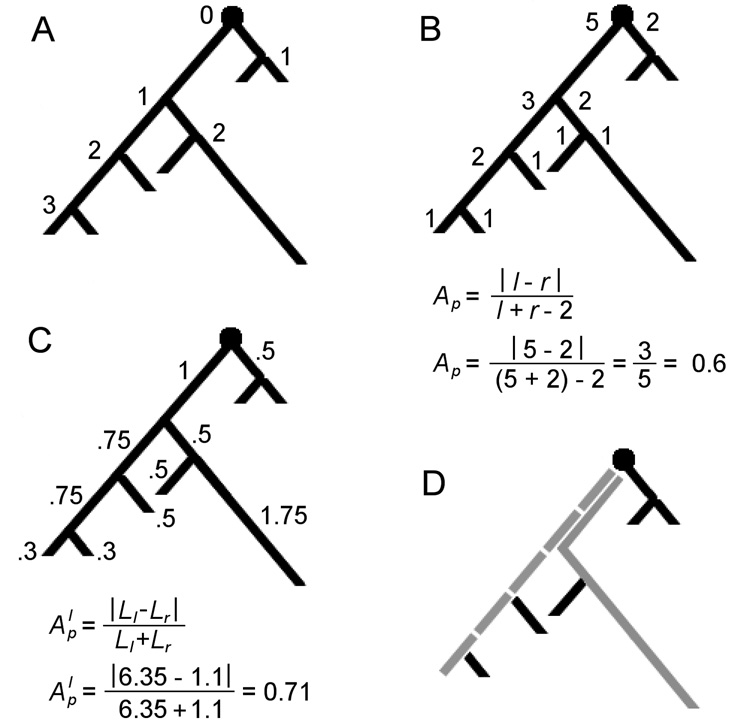
Fig. 2.
Binary tree properties. Branches are the regions between bifurcation or termination nodes. A. Branch (centrifugal) order of each node from the root. B. Terminal degree (number of terminations) of each subtree at each node. The formula for partition asymmetry (Ap) is provided below with calculation for the root of the example tree. C. Lengths of individual segments with length-based partition asymmetry (Alp) for the root. D. Main paths (gray) by degree (dashed) and by length (solid). At the split of the different main paths, the left subtree has a degree of 3 and a length extent of 2.6, while the right subtree has a degree of 2 and a length extent of 2.75.
2.1. Cell growth in development
All the aforementioned morphological properties mature through various developmental stages. Initially, neurons stem several small, undistinguished branches from the cell body. After multiple phases of retraction and elongation, one of the branches becomes differentiated by rapidly elongating and adopting axonal characteristics [25]. The rest of the sprouts eventually assume dendritic properties such as forming spines, small protrusions that synapse with excitatory axons [26]. Axons and dendrites also develop distinct biophysical properties including channel distributions and cytoskeletal makeup [27]. There are numerous molecular agents involved in axonal [28] and dendritic outgrowth [26], though their details are beyond the scope of this review (see also [29]).
2.2. Morphological plasticity
Neurons arborize either from their growth cones located at extending terminal tips or from intermediate segments of existing branches (“interstitial” branching) [30,31]. Branch elongation and arborization allows synapsing with other cell processes, creating a neuronal network. The connectivity of the network must be refined through retraction of underused synapses, testing of others, and stabilization of functionally meaningful ones [32]. This plasticity is driven by dynamic factors, particularly afferent activity, that can impact neurons throughout development and in different ways depending on age and cell type [3,4,5,33]. Dendritic growth mechanisms are sensitive at the population level, producing larger arbors in organisms with enriched environments [34,35] and smaller trees and brain regions in response to stressful environments [36,37,38].
Afferent activity also plays a role in retraction due to competition between inputs. Mitral cells in the olfactory system initially grow dendrites that contact multiple glomeruli, only later to retract from all but one [39]. Multiple cerebellar climbing fiber axons synapse onto individual Purkinje cell dendrites. Upon innervation by parallel fibers onto the Purkinje cell, all climbing fibers retract, except a single one which then expands its dendritic influence [40].
2.3. Extrinsic vs. intrinsic influences
These steps in dendritic and axonal development temporally overlap and interact dynamically. This complex process is mediated by a number of intrinsic (host-cell specific) and extrinsic (cues from neighboring cells, target axons, and surrounding extracellular milieu) factors. The mutual interactions make it difficult to distinguish individual factor roles in dendritic and axonal growth. Models and experiments have each reached differing conclusions on the relative extent of intrinsic and extrinsic influence on neuronal growth.
Samsonovich and Ascoli [41] found that the direction of growth for reconstructed hippocampal dendrites was mostly determined by repulsion from their own soma. Deviations from the orientation leading directly away from the soma were typically followed by corrective deflections based on the segment’s resulting position. The repulsion strength decreased with distance from the soma, yielding the approximately conical shape of hippocampal principal cells.
A stochastic computational growth model could reproduce several morphologically diverse cerebral and cerebellar cortical cell types by modifying only two external cues [42]. Modifying the spatial distribution of simulated ‘neurotrophic particles’ changed both orientation and branch density, whereas modifying the dimensions of the space available for growth changed the gross size and shape of the cell. This study also suggested the requirement of an intrinsic constraint on maximum size to keep larger cells from extending at faster rates than neighboring neurons. Without such a correction, bulkier arbors would increasingly restrict growth particles from reaching smaller trees. The author theorized an alternative extracellular constraint based on distance-dependent concentrations of growth-facilitating cues, possibly related to cortical layers.
3. Qualitative and quantitative neuromorphological features
Tree shape is often the most visually obvious identifier of neuronal arbor and cell types. For example, pyramidal cell dendrites are composed of two polarized arbors, apical and basal (Fig 1B). Both grow away from the cell body in opposite directions, receiving input from different sources. Basal dendrites spread out as they extend from the soma, taking a conical shape with the apex located at the cell body [43]. Apical dendrites also spread out as they grow away from the soma, but they elongate more than basal dendrites, differentiating further as they advance through multiple layers.
Pyramidal cells are the principal neurons in both the cerebral cortex and hippocampus. Although all pyramidal cells share a relatively similar appearance, some differences also exist between regions. The overall size of adult male rat pyramidal dendritic arbors (labeled in vitro) from the NeuroMorpho.Org (http://NeuroMorpho.Org) database [7,44], measured as total number of branches, length, surface area or volume, is approximately 4 to 9 times larger for hippocampal than for cortical pyramidal apical arbors (detailed results not shown) and approximately 3 times larger for hippocampal basal arbors (p < 0.001 for all metrics). There is less difference between cell types when measuring pyramidal dendrites along their principal axis of growth, where cortical pyramidal dendritic arbors (apical and basal combined) are ~70% the size of hippocampal pyramidal dendritic arbors (p < 0.05). Hippocampal neurons are relatively spread out along the other two orthogonal axes compared to cortical pyramidal cells, which appear more elongated. Cortical dendrites may be confined within a more restricted lamella thus appearing flatter. Differences in tissue slice shrinkage leading to greater distortion in one of the cell types may also explain the results.
Cerebellar Purkinje cell dendrites are mostly restricted to growth in two dimensions. They fan out significantly in the rostrocaudal direction, but are nearly flat mediolaterally (Fig 1B, right). Purkinje cells are thus aligned in neat rows correlating with the deep folds (folia) throughout the cerebellar cortex. This architecture may help minimize the length of shared parallel fiber inputs [45]. Some dendritic types, such as in retinal ganglion cells, stop growing upon reaching neighbors of the same type. The resulting ‘retinal tiling’ spatial layout [46] suggests repulsion between neighboring neurons as a shape-constraining mechanism. Other neuronal types such as stellate cells and motoneurons grow away from the soma in many directions (i.e. they are multi-polar) (Fig 1A).
Underlying the shape and physical qualities of dendrites and axons is the cytoskeleton. The cytoskeleton provides and maintains the structural properties of the neuronal trees, mediating intracellular transport [47], and branch diameter [48,49], elongation, and bifurcation [50]. Different cytoskeletal fibers include actin filaments, microtubules, and other intermediate filaments. In dendrites, actin is largely found near the branch surface, where it can give rise to high densities of spines, as well as forming filopodia that sample the extracellular environment to guide direction and growth patterns determining overall shape [51]. Microtubules make up much of the branch core and act as a skeletal backbone maintaining the neuronal tree shape [26]. Microtubules have polarity which determines the direction of resource transport and is an important differentiating factor between axons and dendrites. Axon microtubules only transport distally (towards the plus-ends), while dendritic microtubules face both directions [52]. The loss of function of a motor protein that drags the microtubules into dendrites minus-end first results in elongated dendrites without taper and with an organelle makeup closer to an axon [53].
The size metrics discussed so far relate to many neuronal functions. However, other functional properties depend on more complex shape and size metrics such as branching distributions and patterns [54]. Branching patterns and distributions can be measured in numerous ways providing a challenging choice for the best metrics to explore for a given cell type and features of interest. The following section reviews some common topological measurements including partition asymmetry and modifications thereof.
4. Beyond size: complexity and asymmetry
Considering the shape of neurons beyond their size opens the door to a more extensive set of metrics. Early measures of complexity were restricted to 2D images of neurons. Sholl analysis is a common metric that counts the number of branches at regular distances from the soma [55]. Modified (or Sholl-like) analyses, including 3D variations, were natural extensions once digital 3D reconstructions became available [56,57]. Sholl-like analyses expand size metrics by analyzing their distribution relative to distance measures such as branch order or path distance. As an example, dendritic branches tend to thin as they elongate. Accordingly, numerous computational modeling studies have used distance-dependent diameters to stochastically produce realistic neuron/arbor types [6,58,59,60].
Krichmar et al. [61], loading CA3 pyramidal cell reconstructions into an electrophysiological simulation environment, found that size morphometrics affect firing activity but cannot account for all aspects of electrophysiological behavior. How dendrites are distributed across branch order significantly correlates with aspects of firing patterns. These results suggest that complex morphological properties must be characterized not only by overall size, but how size varies within the given tree.
4.1. Partition asymmetry
Morphological asymmetry reflects the relative balance of branches or size within a tree. Partition asymmetry (Ap) is a relative measure of asymmetry at a bifurcation node based on the distribution of degree (number of terminals) between the node's two subtrees [62]. Figure 2B presents the formula and calculation for a sample tree. The value ranges from 0 (symmetric) to 1 (asymmetric). Since degrees are integers, the number of possible values of Ap depends on the node total degree. The denominator represents the degrees of freedom (total degree minus two, as both left and right subtrees must have at least one terminal).
The number of possible tree shapes increases exponentially with tree size. Even relatively small trees exhibit an exorbitant number of possible branching patterns [62,63]. Given the relatively small number of observations enabled by experimental data acquisition, it is impossible to know if there is only a subset of tree shapes that fully represents a given cell type [64]. It is therefore useful to have an informative scalar morphometric about tree shapes. Van Pelt [62] defined the tree asymmetry index as the average partition asymmetry across a tree, finding this measure sensitive to different tree shapes.
4.2. Asymmetry alternatives
Because partition asymmetry measures the asymmetry of a node given all possible degree distributions, nodes that can only have one possible distribution (i.e. nodes with degree 2 or 3) technically do not have an asymmetry value. Van Pelt et al. [62] choose to give the two possible partitions with degrees < 4 asymmetry values of 0 and 1 for practical purposes, but recognize that these values are arbitrary and mention several alternative methods to measure asymmetry in neuronal trees. Because arbitrary values change the average partition asymmetry for a given tree, we decided to compare asymmetry measures with and without nodes of degree < 4. Measuring partition asymmetry for all axonal and dendritic trees from NeuroMorpho.Org with total degree > 5 (N = 4597), we found that excluding nodes with degrees < 4 resulted in significantly greater standard deviation (0.19 > 0.12, F = 0.39, p < 0.0001) suggesting higher sensitivity to tree shapes. Van Pelt et al. [62] performed a similar comparison for both asymmetry measures for all possible tree shapes with degree ≤ 7 as well as measuring the number of unique values and found analogous results.
Measuring asymmetry at the tree level as opposed to locally provides a different measure that depends on node size. The metric we termed “global asymmetry” accomplishes this by weighting partition asymmetry by degree. Thus, nodes that contribute to a greater part of the entire tree have proportionally greater influence on the measured asymmetry. Since this measure is global in nature, a more absolute partition asymmetry is appropriate. This is achieved by not subtracting 2 in the denominator of the partition asymmetry equation, such that trees with a greater absolute difference in subtree sizes always have greater partition asymmetries.
Asymmetry can also be measured using continuous size metrics such as length, surface area, and volume. Since the branches diverging from a bifurcation have continuous size, even a node with two terminals can be asymmetric. There is therefore no reason for limiting the nodes to be included in such a measure. Additionally, since it is length (or surface area or volume) and not degree being measured, degrees of freedom are not a factor (Fig 2C). Donohue and Ascoli [65] tested the accuracy of growth models in computer simulations using different asymmetry metrics. Basal and apical tree degree asymmetries were accurately produced by different morphometric constraints (diameter and path distance, respectively). Surface area asymmetry however was best determined by path distance for both arbor types. These results suggest that different asymmetry measures may be determined by distinct factors depending on neuron or arbor type.
A novel implementation of partition asymmetry termed “excess asymmetry” was used to measure morphological homeostasis in hippocampal dendritic trees [66]. This metric is based on the idea that if an arbor grows under homeostatic constraints, then larger subtrees will offset smaller subtrees, limiting the size range of the entire tree. Specifically, consider a node with subtrees l and r, where l has subtrees a and b, and r has subtrees c and d. Switching b with either c or d will result in a more symmetric node in case of homeostasis (if a and b are large then c and d are small or vice versa). Excess partition asymmetry then compares the actual partition asymmetry with the swapped partition asymmetries, producing a positive value if there is homeostasis and a value near 0 otherwise. Degree, length, and surface area were all used to determine excess asymmetry. Significantly positive excess asymmetry values were found in several dendritic types of cortical principal cells, suggesting that subtrees grow under homeostatic constraints.
4.3. Asymmetry’s complex relationships
Size metrics have been found to classify arbor and cell types better than some simple asymmetry scalars [67]. However, asymmetry’s relevance may require more targeted methods to fully capture cell type variation. Cuntz et al. [68] modeled a dendritic structure by minimizing total wiring to a sample of potential synaptic sites from a reconstructed fly tangential cell. The resulting virtual dendrite was very different from the corresponding reconstructed cell. It was quite asymmetric and had a clear main path. A second model constrained both total wiring and path distance from synaptic site to soma. Diameter and taper rate were also constrained to minimize the current transfer variability between synapse to soma paths. The result appeared much like the source cell, with several levels of fairly symmetric branching followed by more asymmetric regions. A single asymmetry measure would not be capable of describing the multiple dendritic sub-domains, whereas a set of targeted measures could capture such functionally related patterns.
Neurons abide to many constraints and functions beyond homogeneous synaptic efficacy and minimizing metabolic cost. A more generalized recent model to relate neuronal function and morphology involved an evolutionary algorithm, with “genes” made up of tree growth parameters, and electrophysiological simulations to test virtual neuron fitness [69]. Based on the chosen functional parameters, the model finds optimal dendritic arbors over many generations. Within the resulting set of morphological parameters, those vital to the specified neuronal fitness are more highly conserved.
Asymmetry may correlate with other measurements that more directly reflect the function of the corresponding tree shape feature. The next section introduces “caulescence”, a novel measure that typically correlates with asymmetry, yet often provides a clearer functional consequence. Additionally, we explore analyses suggesting that for certain cell types, larger caulescence appears to cause the high asymmetry values.
5. Caulescence
The term “caulescent” was originally used in botany to describe a plant with a main trunk or stem [70]. As some neurons present tree structures with prominent main paths, including axons and pyramidal cell apical dendrites, we found it appropriate to develop a rule for univocally identifying main paths and a measure to capture their prominence.
The main path of a neuronal tree can be defined as the path from the soma to a termination which at each bifurcation leads to the greatest extent of a given metric (e.g. degree, length, surface area or volume). Degree-based caulescence (CD) follows the path that leads to the higher degree at each bifurcation, while length-based caulescence (CL) takes the path towards the most length (Fig 2D). Caulescence is then defined as the weighted partition asymmetry of nodes along the main path. This choice factors out the influence of secondary subtrees and weights more heavily the bifurcations with the largest extent. Both the partition asymmetry and weighting are based on the same metric used to determine the main path itself. The equation for caulescence is1:
where l and r are the sizes of the two subtrees at each node on the main path. The resulting value represents the overall balance of extent, where high caulescence (close to 1) indicates a very distinct main path and low values reflect a more balanced tree without a clear main path. Figure 3 shows main paths in example neuron types.
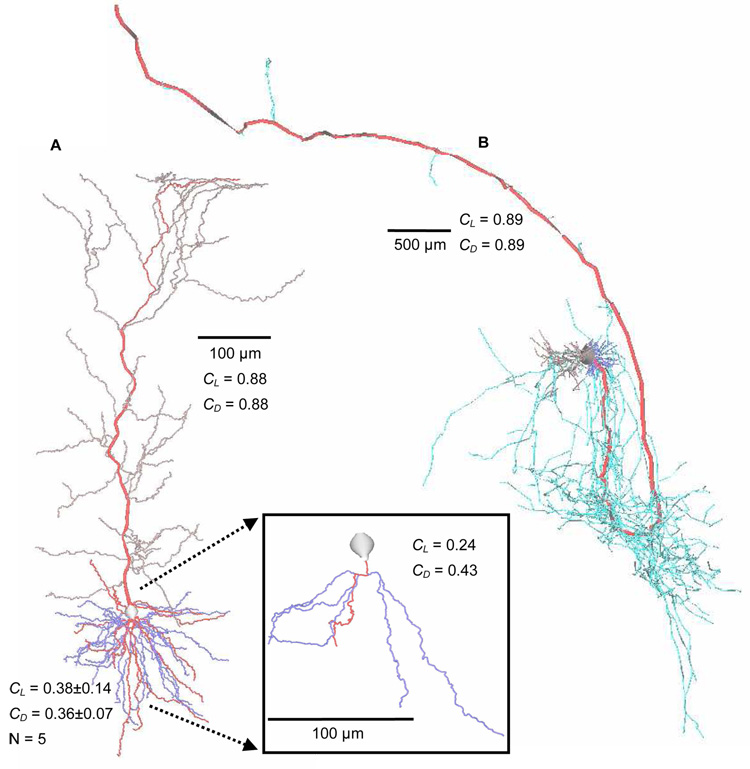
Fig. 3.
Main paths in example neurons from NeuroMorpho.Org. A. Hippocampal subicular pyramidal dendritic arbor [74,75]. Main path (red) is more caulescent in apical (gray, CL = 0.88; CD = 0.88) than basal trees (blue, CL = 0.38±0.14; CD = 0.36±0.07; N = 5). Boxed Inset: Zoomed-in (2×) individual basal tree with main path (red) (CL = 0.24; CD = 0.43). B. Hippocampal CA1 pyramidal cell dendritic (basal: dark blue; apical: gray) and axonal (light blue) arbors [76,77,78]. Axonal main path (thickened red) would not be obvious without color, even though this axonal tree is highly caulescent (CL = 0.89; CD = 0.89). Some branches are thickened for visual clarity. CL = length-based and CD = degree-based caulescence.
The significance of caulescence in neuronal arborizations is revealed in the drastic differences between the values of various cell and arborization types. Using the length metric and NeuroMorpho.Org arbors, pyramidal cell apical dendrites tend to be highly caulescent (0.62 ± 0.17, N=889), while their basal counterparts have much less caulescence (0.37 ± 0.17; N=1779; p < 0.001). As seen in Figure 3A, the main path is more obvious in apical compared to basal dendritic trees. High caulescence by volume or surface area in dendrites can optimize synaptic integration along the main path, analogous to elongating the soma. In fact, surface area (as well as volume, not shown) caulescence is significantly higher than length caulescence for both pyramidal basal (0.39 ± 0.17; p < 0.05) and apical dendrites (0.69 ± 0.16; p < 0.001). This fits with secondary (e.g. oblique) branches having smaller diameter than main branches and therefore high input impedance [23,24,71].
Two groups of NeuroMorpho.Org axons had sample sizes large enough for analysis and varied substantially between types. Cortical basket cell axons had a lower mean caulescence (0.54 ± 0.15; N=57) than uniglomerular projection neuron axons (0.73 ± 0.10; N=233; p < 0.001). As would be expected due to the lack of taper in axons, neither cell class had axons with a significantly different surface area (CS) or volume-based (CV) caulescence compared to CL and CD. The main path in both apical dendrites and axons is acting in part as an efficient way to get from an origin (i.e. soma) to a destination (i.e. apical tuft, axonal terminals), as opposed to sending many branches to neighboring targets.
The adaptation of partition asymmetry in the caulescence definition results in a fairly strong correlation between caulescence and several asymmetry measures, particularly global asymmetry. There are, however, noticeable distinctions. For example, in apical dendrites of rodent hippocampal pyramidal cells, caulescence values below 0.50 are generally lower than, and correlate less with, global asymmetry values (both using the length metric, Fig 4). Caulescence values above 0.50 highly correlate with and fall above global asymmetry. Thus, the ratio of global asymmetry to caulescence is higher at low than at high values (Fig 4 top left inset). This may be due to hippocampal apical dendrites with a major bifurcation near the soma, effectively leading to a second main path. A tree with more than one true main path has lower caulescence due to a highly weighted bifurcation with low partition asymmetry where the second main path begins. The tree's global asymmetry would then be higher than its caulescence because other highly weighted bifurcations on the second main path would contribute a relatively high partition asymmetry. Rodent cortical apical dendrites show no significant difference in correlation above or below caulescence of 0.5 (Fig 4). While rodent hippocampal (0.66 ± 0.21; N=205) and cortical (0.67 ± 0.13; N=258) apical dendrites have similar mean caulescence, primate cortical apical dendrite values (0.57 ± 0.15; N=387) are substantially lower. These results signify important differences between both brain region and species even within a cell and arbor type.
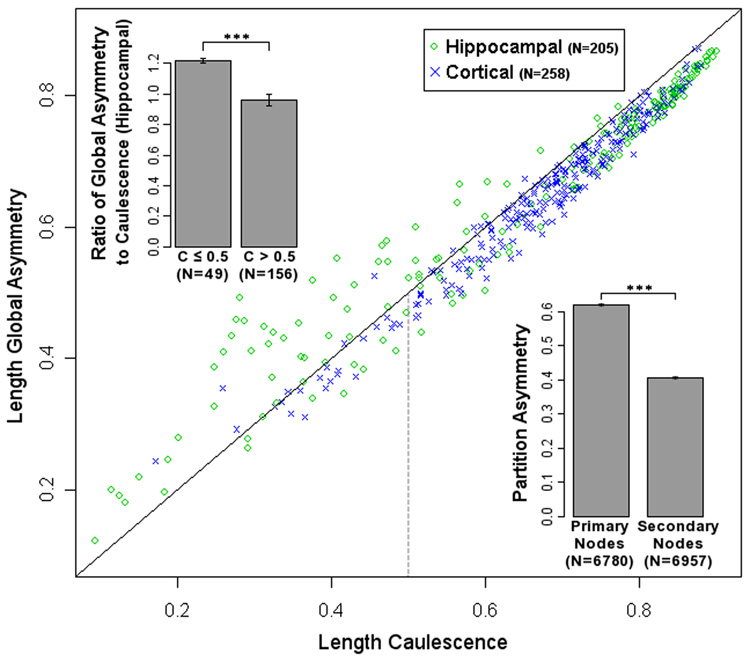
Fig. 4.
Scatter plot of rodent pyramidal cell apical dendrite global asymmetry against caulescence (C), both using the length metric. Green circles represent hippocampal neurons, blue crosses cortical neurons. Solid is the diagonal, where global asymmetry equals caulescence. At C > 0.5, caulescence is greater than global asymmetry, suggesting a difference between bifurcations in the primary and secondary paths. Variability in global asymmetry for hippocampal apical dendrites increases at C < 0.5. This could be explained by dendrites with multiple main paths. Top Left Inset: Mean ratios of global asymmetry to caulescence below and above 0.5 caulescence is significantly different for hippocampal cells (p < 0.0001). Bottom Right Inset: Partition asymmetry analysis of all rodent apical dendrite nodes. Primary path bifurcations have significantly higher partition asymmetry than secondary path bifurcations (p < 0.0001).
Lower global asymmetry may be due to secondary branches. Measuring partition asymmetry separately along the main and secondary paths (Fig 4 bottom right inset) can distinguish the relationship of potentially separate domains. A 2-sample Kolmogorov-Smirnov test rejected that the primary and secondary branch partition asymmetry values could come from the same population (p < 0.001). These results show that main path nodes indeed have significantly higher partition asymmetry than secondary nodes. This means that the asymmetry of apical dendrites is due primarily to the effect of the main path.
For simplicity’s sake, only caulescence defined along a single main path was analyzed. Future incarnations of the metric may be expanded by taking into account the multiple main paths that certain individual trees exhibit, such as some of the low caulescence but high global asymmetry apical dendrites in Figure 4. Additionally, cerebellar climbing fibers and Purkinje cells (Fig 1B) appear to have main paths that split in multiple directions. Another aspect of separating morphological sub-domains is the determination of where a main path ends. Removing acaulescent regions would further differentiate sub-domains. For example, the apical tuft of apical dendrites is more symmetric and thus its exclusion from the main path would likely further increase the high caulescence values of these trees.
6. Conclusion
While many biophysical mechanisms determine cell types throughout the body, such as chemical messengers and metabolic constraints, neuronal characterization would be incomplete without considering morphology. It is both cause and effect of function; a dynamic player in signal propagation, integration, and connectivity. Size morphometrics summed through the trees can characterize fundamental aspects of different cell types. Differential size distributions at branch points serve to quantify less obvious morphological aspects such as asymmetry. All these properties are mediated by function, environment, and metabolic efficiency. Growth and functional models, in conjunction with morphological properties, have the capacity to isolate individual features and increase the understanding of their relationships to one another. One such feature, caulescence, provides a novel tool for characterizing a relatively unexplored aspect of neuromorphology.
Acknowledgements
We thank Dr. John L. Baker, Dr. Duncan E. Donohue, and Ms. Susan Wright for their constructive feedback. This work was supported by NIH grant R01 NS39600 from NINDS, NIMH, and NSF under the Human Brain Project.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Code for measurements including caulescence available at http://mason.gmu.edu/~tgillett/caulescence/
References
- 1.Scorcioni R, Polavaram S, Ascoli GA. L-Measure: a web-accessible tool for the analysis, comparison and search of digital reconstructions of neuronal morphologies. Nat Protoc. 2008;3:866–876. doi: 10.1038/nprot.2008.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Uylings HBM, Van Pelt J. Measures for quantifying dendritic arborizations. Network: Comput Neural Syst. 2002;13:397–414. [PubMed] [Google Scholar]
- 3.Cline HT. Dendritic arbor development and synaptogenesis. Curr Opin Neurobiol. 2001;11:118–126. doi: 10.1016/s0959-4388(00)00182-3. [DOI] [PubMed] [Google Scholar]
- 4.Wong RO, Ghosh A. Activity-dependent regulation of dendritic growth and patterning. Nat Rev Neurosci. 2002;3:803–812. doi: 10.1038/nrn941. [DOI] [PubMed] [Google Scholar]
- 5.Jan YN, Jan LY. The control of dendrite development. Neuron. 2003;40:229–242. doi: 10.1016/s0896-6273(03)00631-7. [DOI] [PubMed] [Google Scholar]
- 6.Ascoli GA. Progress and perspectives in computational neuroanatomy. Anat Rec. 1999;257:195–207. doi: 10.1002/(SICI)1097-0185(19991215)257:6<195::AID-AR5>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 7.Ascoli GA. Mobilizing the base of neuroscience data: the case of neuronal morphologies. Nature Rev Neurosci. 2006;7:318–324. doi: 10.1038/nrn1885. [DOI] [PubMed] [Google Scholar]
- 8.Brown KM, Donohue DE, D'Alessandro G, Ascoli GA. A cross-platform freeware tool for digital reconstruction of neuronal arborizations from image stacks. Neuroinformatics. 2005;3:343–360. doi: 10.1385/NI:3:4:343. [DOI] [PubMed] [Google Scholar]
- 9.Bower JM, Beeman D. The Book of GENESIS: second edition. New York: Springer-Verlag; 1998. [Google Scholar]
- 10.Hines ML, Carnevale NT. NEURON: a tool for neuroscientists. The Neuroscientist. 2001;7:123–135. doi: 10.1177/107385840100700207. [DOI] [PubMed] [Google Scholar]
- 11.Ascoli GA, Alonso L, Anderson S, Barrionuevo G, Benavides-Piccione R, Burkhalter A, et al. Petilla Terminology: Nomenclature of features of GABAergic interneurons of the cerebral cortex. Nature Rev Neurosci. 2008;9:557–568. doi: 10.1038/nrn2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chklovskii DB. Optimal Sizes of Dendritic and Axonal Arbors in a Topographic Projection. J Neurophysiol. 2000;83:2113–2119. doi: 10.1152/jn.2000.83.4.2113. [DOI] [PubMed] [Google Scholar]
- 13.Liu G. Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat Neurosci. 2004;7:373–379. doi: 10.1038/nn1206. [DOI] [PubMed] [Google Scholar]
- 14.Pierce JP, Milner TA. Parallel increases in the synaptic and surface areas of mossy fiber terminals following seizure induction. Synapse. 2001;39:249–256. doi: 10.1002/1098-2396(20010301)39:3<249::AID-SYN1006>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 15.Wang SS, Shultz JR, Burish MJ, Harrison KH, Hof PR, Towns LC, et al. Functional trade-offs in white matter axonal scaling. J Neurosci. 2008;28:4047–4056. doi: 10.1523/JNEUROSCI.5559-05.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laughlin SB, van Steveninck RRR, Anderson JC. The metabolic cost of neural information. Nat Neurosci. 1998;1:36–41. doi: 10.1038/236. [DOI] [PubMed] [Google Scholar]
- 17.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- 18.Mel BW. Information-processing in dendritic trees. Neural Comput. 1994;6:1031–1085. [Google Scholar]
- 19.Pyapali GK, Sik A, Penttonen M, Buzsaki G, Turner DA. Dendritic properties of hippocampal CA1 pyramidal neurons in the rat: Intracellular staining in vivo and in vitro. J Comp Neurol. 1998;391:335–352. doi: 10.1002/(sici)1096-9861(19980216)391:3<335::aid-cne4>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 20.Migliore M. Modeling the attenuation and failure of action potentials in the dendrites of hippocampal neurons. Biophys J. 1996;71:2394–2403. doi: 10.1016/S0006-3495(96)79433-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Williams SR, Stuart GJ. Action potential backpropagation and somato-dendritic distribution of ion channels in thalamocortical neurons. J Neurosci. 2000;20:1307–1317. doi: 10.1523/JNEUROSCI.20-04-01307.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Spruston N, Schiller Y, Stuart G, Sakmann B. Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrites. Science. 1995;268:297–300. doi: 10.1126/science.7716524. [DOI] [PubMed] [Google Scholar]
- 23.Migliore M, Ferrante M, Ascoli GA. Signal propagation in oblique dendrites of CA1 pyramidal cells. J Neurophys. 2005;94:4145–4155. doi: 10.1152/jn.00521.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vetter P, Roth A, Häusser M. Propagation of action potentials in dendrites depends on dendritic morphology. J Neurophysiol. 2001;85:926–937. doi: 10.1152/jn.2001.85.2.926. [DOI] [PubMed] [Google Scholar]
- 25.Dotti CG, Sullivan CA, Banker GA. The establishment of polarity by hippocampal neurons in culture. J Neurosci. 1988;8:1454–1468. doi: 10.1523/JNEUROSCI.08-04-01454.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Scott EK, Luo L. How do dendrites take their shape? Nat Neurosci. 2001;4:359–365. doi: 10.1038/86006.. Comprehensive review of molecular determinants of dendritic shape.
- 27.Fukata Y, Kimura T, Kaibuchi K. Axon specification in hippocampal neurons. Neurosci Res. 2002;43:305–315. doi: 10.1016/s0168-0102(02)00062-7. [DOI] [PubMed] [Google Scholar]
- 28. Yoshimura T, Arimura N, Kaibuchi K. Signaling networks in neuronal polarization. J Neurosci. 2006;26:10626–10630. doi: 10.1523/JNEUROSCI.3824-06.2006.. Comprehensive review of axonal differentiation.
- 29.Donohue DE, Ascoli GA. Models of neuronal outgrowth. In: Koslow SH, Subramaniam S, editors. Databasing the Brain: From Data to Knowledge. New York, NY: Wiley; 2005. pp. 303–323. [Google Scholar]
- 30.Dailey ME, Smith SJ. The Dynamics of Dendritic Structure in Developing Hippocampal Slices. J Neurosci. 1996;16:2983–2994. doi: 10.1523/JNEUROSCI.16-09-02983.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Szebenyi G, Callaway JL, Dent EW, Kalil K. Interstitial branches develop from active regions of the axon demarcated by the primary growth cone during pausing behaviors. J Neurosci. 1998;18:7930–7940. doi: 10.1523/JNEUROSCI.18-19-07930.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Luo L, O'Leary DD. Axon retraction and degeneration in development and disease. Annu Rev Neurosci. 2005;28:127–156. doi: 10.1146/annurev.neuro.28.061604.135632. [DOI] [PubMed] [Google Scholar]
- 33.McAllister AK. Cellular and molecular mechanisms of dendrite growth. Cereb Cortex. 2000;10:963–973. doi: 10.1093/cercor/10.10.963. [DOI] [PubMed] [Google Scholar]
- 34.Fiala BA, Joyce JN, Greenough WT. Environmental complexity modulates growth of granule cell dendrites in developing but not adult hippocampus of rats. Experimental Neurology. 1978;59:372–383. doi: 10.1016/0014-4886(78)90229-7. [DOI] [PubMed] [Google Scholar]
- 35.Nilsson M, Perfilieva E, Johansson U, Orwar O, Eriksson P. Enriched environment increases neurogenesis in the adult rat dentate gyrus and improves spatial memory. J Neurobiol. 1999;39:569–578. doi: 10.1002/(sici)1097-4695(19990615)39:4<569::aid-neu10>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 36.Magariños AM, McEwen BS, Flügge G, Fuchs E. Chronic psychosocial stress causes apical dendritic atrophy of hippocampal CA3 pyramidal neurons in subordinate tree shrews. J Neurosci. 1996;16:3534–3540. doi: 10.1523/JNEUROSCI.16-10-03534.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Radley JJ, Sisti HM, Hao J, Rocher AB, McCall T, Hof PR, et al. Chronic behavioral stress induces apical dendritic reorganization in pyramidal neurons of the medial prefrontal cortex. Neuroscience. 2004;125:1–6. doi: 10.1016/j.neuroscience.2004.01.006. [DOI] [PubMed] [Google Scholar]
- 38.Bremner JD, Randall P, Vermetten E, Staib L, Bronen RA, Mazure C, et al. Magnetic resonance imaging-based measurement of hippocampal volume in posttraumatic stress disorder related to childhood physical and sexual abuse—a preliminary report. Biol Psychiatry. 1997;41:23–32. doi: 10.1016/s0006-3223(96)00162-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Malun D, Brunjes PC. Development of olfactory glomeruli: temporal and spatial interactions between olfactory receptor axons and mitral cells in opossums and rats. J Comp Neurol. 1996;368:1–16. doi: 10.1002/(SICI)1096-9861(19960422)368:1<1::AID-CNE1>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- 40.Scelfo B, Strata P. Correlation between multiple climbing fibre regression and parallel fibre response development in the postnatal mouse cerebellum. Eur J Neurosc. 2005;21:971–978. doi: 10.1111/j.1460-9568.2005.03933.x. [DOI] [PubMed] [Google Scholar]
- 41.Samsonovich AV, Ascoli GA. Statistical morphological analysis of hippocampal principal neurons indicates cell-specific repulsion of dendrites from their own cell. J Neurosci Res. 2003;71:173–187. doi: 10.1002/jnr.10475. [DOI] [PubMed] [Google Scholar]
- 42.Luczak A. Spatial embedding of neuronal trees modeled by diffusive growth. J Neurosci Methods. 2006;157:132–141. doi: 10.1016/j.jneumeth.2006.03.024. [DOI] [PubMed] [Google Scholar]
- 43.Henze DA, Cameron WE, Barrionuevo G. Dendritic morphology and its effects on the amplitude and rise-time of synaptic signals in hippocampal CA3 pyramidal cells. J Comp Neurol. 1996;369:331–344. doi: 10.1002/(SICI)1096-9861(19960603)369:3<331::AID-CNE1>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 44.Ascoli GA, Donohue DE, Halavi M. NeuroMorpho.Org: a central resource for neuronal morphologies. J Neurosci. 2007;27:9247–9251. doi: 10.1523/JNEUROSCI.2055-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Eccles JC, Ito M, Szentagothai J. The Cerebellum as a Neuronal Machine. Heidelberg, Berlin, Gottingen, New York: Springer-Verlag; 1967. [Google Scholar]
- 46.Amthor FR, Oyster CW. Spatial organization of retinal information about the direction of image motion. Proc Natl Acad Sci U S A. 1995;92:4002–4005. doi: 10.1073/pnas.92.9.4002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bhaskar L, Krishnan VS, Thampan RV. Cytoskeletal elements and intracellular transport. J Cell Biochem. 2007;101:1097–1108. doi: 10.1002/jcb.21347. [DOI] [PubMed] [Google Scholar]
- 48.Hillman DE. Neuronal shape parameters and substructures as a basis of neuronal form. In: Schmitt F, editor. The neurosciences, fourth study program. Cambridge, MA: MIT Press; 1979. pp. 477–498. [Google Scholar]
- 49.Hillman DE. Parameters of dendritic shape and substructure: intrinsic and extrinsic determination? In: Lasek RJ, Black MM, editors. Intrinsic determinants of neuronal form and function. New York: Liss; 1988. pp. 83–113. [Google Scholar]
- 50.Dent EW, Tang F, Kalil K. Axon guidance by growth cones and branches: common cytoskeletal and signaling mechanisms. Neuroscientist. 2003;9:343–353. doi: 10.1177/1073858403252683. [DOI] [PubMed] [Google Scholar]
- 51.Fischer M, Kaech S, Knutti D, Matus A. Rapid actin-based plasticity in dendritic spines. Neuron. 1998;20:847–854. doi: 10.1016/s0896-6273(00)80467-5. [DOI] [PubMed] [Google Scholar]
- 52.Baas PW, Deitch JS, Black MM, Banker GA. Polarity Orientation of Microtubules in Hippocampal Neurons: Uniformity in the Axon and Nonuniformity in the Dendrite. Proc Natl Acad Sci USA. 1988;85:8335–8339. doi: 10.1073/pnas.85.21.8335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yu W, Cook C, Sauter C, Kuriyama R, Kaplan PL, Baas PW. Depletion of a Microtubule-Associated Motor Protein Induces the Loss of Dendritic Identity. J Neurosci. 2000;20:5782–5791. doi: 10.1523/JNEUROSCI.20-15-05782.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Schaefer AT, Larkum ME, Sakmann B, Roth A. Coincidence detection in pyramidal neurons is tuned by their dendritic branching pattern. J Neurophysiol. 2003;89:3143–3154. doi: 10.1152/jn.00046.2003. [DOI] [PubMed] [Google Scholar]
- 55. Sholl DA. Dendritic organization in the neurons of the visual and motor cortices of the cat. J Anat. 1953;87:387–406.. Original presentation of Sholl analysis method.
- 56.Caserta F, Eldred WD, Fernandez E, Hausman RE, Stanford LR, Bulderev SV, et al. Determination of fractal dimension of physiologically characterized neurons in two and three dimensions. J Neurosci Methods. 1995;56:133–144. doi: 10.1016/0165-0270(94)00115-w. [DOI] [PubMed] [Google Scholar]
- 57.Ristanović D, Milosević NT, Stulić V. Application of modified Sholl analysis to neuronal dendritic arborization of the cat spinal cord. J Neurosci Methods. 2006;158:212–218. doi: 10.1016/j.jneumeth.2006.05.030. [DOI] [PubMed] [Google Scholar]
- 58.Burke RE, Marks WB, Uhlfhake B. A parsimonious description of motoneuron dendritic morphology using computer simulation. J Neurosci. 1992;12:2403–2416. doi: 10.1523/JNEUROSCI.12-06-02403.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Donohue DE, Ascoli GA. Local diameter fully constrains dendritic size in basal but not apical trees of CA1 pyramidal neurons. J Comput Neurosci. 2005;19:223–238. doi: 10.1007/s10827-005-1850-5. [DOI] [PubMed] [Google Scholar]
- 60.Samsonovich AV, Ascoli GA. Statistical determinates of dendritic morphology in hippocampal pyramidal neurons: a hidden Markov model. Hippocampus. 2005;15:166–183. doi: 10.1002/hipo.20041. [DOI] [PubMed] [Google Scholar]
- 61.Krichmar JL, Nasuto SJ, Scorcioni R, Washington SD, Ascoli GA. Effects of dendritic morphology on CA3 pyramidal cell electrophysiology: a simulation study. Brain Research. 2002;941:11–28. doi: 10.1016/s0006-8993(02)02488-5. [DOI] [PubMed] [Google Scholar]
- 62.Van Pelt J, Uylings HB, Verwer RW, Pentney RJ, Woldenberg MJ. Tree asymmetry--a sensitive and practical measure for binary topological trees. Bull Math Biol. 1992;54:759–784. doi: 10.1007/BF02459929. [DOI] [PubMed] [Google Scholar]
- 63.Harding EF. The Probabilities of Rooted Tree-shapes Generated by Random Bifurcation. J Appl Prob. 1971;3:44–77. [Google Scholar]
- 64.Uemura E, Carriquiry A, Kliemann W, Goodwin J. Mathematical modeling of dendritic growth in vitro. Brain Res. 1995;671:187–194. doi: 10.1016/0006-8993(94)01310-e. [DOI] [PubMed] [Google Scholar]
- 65.Donohue DE, Ascoli GA. A comparative computer simulation of dendritic morphology. PLoS Comput Biol. 2008;4 doi: 10.1371/journal.pcbi.1000089. e1000089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Samsonovich AV, Ascoli GA. Morphological homeostasis in cortical dendrites. Proc Natl Acad Sci USA. 2006;103:1569–1574. doi: 10.1073/pnas.0510057103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Cannon RC, Wheal HV, Turner DA. Dendrites of Classes of Hippocampal Neurons Differ in Structural Complexity and Branching Patterns. J Comp Neurol. 1999;413:619–633. [PubMed] [Google Scholar]
- 68. Cuntz H, Borst A, Segev I. Optimization principles of dendritic structure. Theor Biol Med Model. 2007;4:21. doi: 10.1186/1742-4682-4-21.. Constraints on total wiring, minimum synaptic distance, and diameter/taper for equalized synaptic efficacy resulted in a realistic model of tangential cell dendrite.
- 69. Stiefel KM, Sejnowski TJ. Mapping function onto neuronal morphology. J Neurophysiol. 2007;98:513–526. doi: 10.1152/jn.00865.2006.. Evolutionary algorithm for tree generation, NEURON simulation of virtual dendrites, and “genetic” mutation for determining necessary morphological properties to achieve a neuronal function.
- 70.Martyn T. 2nd ed. London: B and J White; 1796. The language of botany: being a dictionary of the terms made use of in that science, principally by Linneus: with familiar explanations and an attempt to establish significant English terms. [Google Scholar]
- 71.Goldstein SS, Rall W. Changes of action potential shape and velocity for changing core conductor geometry. Biophys J. 1974;14:731–757. doi: 10.1016/S0006-3495(74)85947-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Núñez-Abades PA, He F, Barrionuevo G, Cameron WE. Morphology of developing rat genioglossal motoneurons studied in vitro: changes in length, branching pattern, and spatial distribution of dendrites. J Comp Neurol. 1994;339:401–420. doi: 10.1002/cne.903390308. [DOI] [PubMed] [Google Scholar]
- 73.Staiger JF, Flagmeyer I, Schubert D, Zilles K, Kötter R, Luhmann HJ. Functional diversity of layer IV spiny neurons in rat somatosensory cortex: quantitative morphology of electrophysiologically characterized and biocytin labeled cells. Cereb Cortex. 2004;14:690–701. doi: 10.1093/cercor/bhh029. [DOI] [PubMed] [Google Scholar]
- 74.Golding NL, Kath WL, Spruston N. Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites. J Neurophysiol. 2001;86:2998–3010. doi: 10.1152/jn.2001.86.6.2998. [DOI] [PubMed] [Google Scholar]
- 75.Golding NL, Mickus TJ, Katz Y, Kath WL, Spruston N. Factors mediating powerful voltage attenuation along CA1 pyramidal neuron dendrites. J Physiol. 2005;568:69–82. doi: 10.1113/jphysiol.2005.086793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Tamamaki N, Nojyo Y. Disposition of the slab-like modules formed by axon branches originating from single CA1 pyramidal neurons in the rat hippocampus. J Comp Neurol. 1990;291:509–519. doi: 10.1002/cne.902910403. [DOI] [PubMed] [Google Scholar]
- 77.Tamamaki N, Nojyo Y. Crossing fiber arrays in the rat hippocampus as demonstrated by three-dimensional reconstruction. J Comp Neurol. 1991;303:435–442. doi: 10.1002/cne.903030309. [DOI] [PubMed] [Google Scholar]
- 78.Scorcioni R, Ascoli GA. Algorithmic reconstruction of complete axonal arborizations in rat hippocampal neurons. Neurocomputing. 2005;65–66:15–22. [Google Scholar]