An investigation of EEG dynamics in an animal model of temporal lobe epilepsy using the maximum Lyapunov exponent

Abstract

Analysis of intracranial electroencephalographic (iEEG) recordings in patients with temporal lobe epilepsy (TLE) has revealed characteristic dynamical features that distinguish the interictal, ictal, and postictal states and inter-state transitions. Experimental investigations into the mechanisms underlying these observations require the use of an animal model. A rat TLE model was used to test for differences in iEEG dynamics between well-defined states and to test specific hypotheses: 1) the short-term maximum Lyapunov exponent (STL_max), a measure of signal order, is lowest and closest in value among cortical sites during the ictal state, and highest and most divergent during the postictal state; 2) STL_max values estimated from the stimulated hippocampus are the lowest among all cortical sites; and 3) the transition from the interictal to ictal state is associated with a convergence in STL_max values among cortical sites. iEEGs were recorded from bilateral frontal cortices and hippocampi. STL_max and T-index (a measure of convergence/divergence of STL_max between recorded brain areas) were compared among the four different periods. Statistical tests (ANOVA and multiple comparisons) revealed that ictal STL_max was lower (p < 0.05) than other periods, STL_max values corresponding to the stimulated hippocampus were lower than those estimated from other cortical regions, and T-index values were highest during the postictal period and lowest during the ictal period. Also, the T-index values corresponding to the preictal period were lower than those during the interictal period (p < 0.05). These results indicate that a rat TLE model demonstrates several important dynamical signal characteristics similar to those found in human TLE and support future use of the model to study epileptic state transitions.

Introduction

Spontaneous recurrent seizures are the central feature of epilepsy. Because of the intermittent nature of symptoms, epilepsy has been considered a candidate “dynamical disease” (Mackey and Milton, 1987; Milton et al., 1989; Milton 2003), a term coined to describe disorders in which there are intermittent and recurrent transitions between pathological and more normal states. In epilepsy, three states, the interictal, ictal, and postictal, can be well-defined based on clinical and electrophysiological characteristics. Understanding and characterizing these dynamical states and the transitions between states is a useful way to conceptualize the disorder and its underlying mechanisms and may suggest novel therapeutic approaches based on principles of dynamical control theory.

Using techniques developed for the study of complex nonlinear systems, analyses of intracranial electroencephalographic (iEEG) recordings in patients with medically intractable temporal lobe epilepsy (TLE) have revealed quantifiable dynamical features of the iEEG that distinguished the interictal, ictal, and postictal states in human epilepsy (Iasemidis et al., 1990; Lehnertz and Elger, 1998; Le Van Quyen et al., 2001). For example, the ictal iEEG is characterized by a low value of the short-term maximum Lyapunov exponent (STL_max), a measure quantifying the order (or disorder) of the signal, when compared to the interictal state. Also, STL_max values converge to essentially the same value during the ictal state and diverge in value following a seizure (Sackellares et al., 1997, 2002; Shiau et al., 2000; Iasemidis et al., 1999, 2004). Transitions from the interictal to the ictal state can be characterized by convergence of STL_max values among iEEG channels derived from widespread cortical sites. This convergence occurs over periods on the order of 30-90 min (Iasemidis et al., 2001, 2003a,b) before the ictal onset. These observations led some investigators to postulate that seizures represented the self-organizing behavior characteristic of complex systems (Iasemidis and Sackellares, 1996). That is, the spontaneous generation and resolution of individual seizures may represent the kind of state transitions between an ordered state (seizure) and less ordered behavior (interictal or postictal state) that have been observed in many complex systems (Mackey and Glass, 1977; Nicolis and Prigogine, 1977; Babloyantz and Kaczmarek, 1979; Rapp et al., 1986; Kauffman, 1993).

In order to further investigate the concept of dynamical state transitions in the epileptic brain and, perhaps more importantly, to develop methods for disrupting and controlling the development of seizures, we initiated investigations of the dynamics of the iEEG in a rodent model of TLE (Good et al., 2004; Nair, 2006; Nair et al., 2004, 2006, 2007; Shiau et al., 2005). The continuous hippocampal stimulation model of TLE (Lothman et al., 1990, 1991) was chosen because it manifests many of the features associated with human pharmacoresistant TLE, including similar electrophysiological correlates, pathological changes in the limbic system, and behavioral manifestations of the seizures (Bertram and Lothman, 1993; Quigg et al., 1997, 1998). The seizures in this model are recurrent, spontaneous, and chronic. However, the relevance of this model to understanding the dynamics of human TLE requires that the model have comparable iEEG dynamical characteristics.

In this study, using the continuous hippocampal stimulation model of TLE, we sought to investigate whether dynamical characteristics of the iEEG signal in the rat TLE model during the ictal, interictal, and postictal states, and during transitions into and out of seizures, were similar to those that have been observed in human TLE. The specific objectives of this initial study were to test the hypotheses that, as in human TLE: 1) STL_max values are lowest and closest in value among all cortical sites during the ictal state, and highest and most divergent in value during the immediate postictal state; 2) STL_max values estimated from the stimulated hippocampus are lowest in value among all cortical sites; and 3) the transition from the interictal to the ictal state is associated with a convergence of the values of STL_max among cortical sites comparable to that observed in human studies.

Materials and methods

Animal preparation

Experiments were performed on 2-month old male Sprague Dawley rats (n=4) weighing 210-265 g using protocols and procedures approved by the University of Florida Institutional Animal Care and Use Committee. Anesthesia was initiated with xylazine (10 mg/kg, SQ) and isoflurane (1-3%) in oxygen, animals were placed in a Kopf stereotactic frame, and inhalation anesthesia was continued via a nose mask.

Electrode implantation

The top of the animal's head was shaved and chemically sterilized with iodine. The skull was exposed by a midsagittal incision that began between the eyes and extended caudally to the level of the ears to expose the bregma and lambdoidal suture. A peroxide wash was applied to remove excess soft tissue from the skull. Four 0.8 mm stainless steel screws (Small Parts, Miami Lakes, FL) were placed in the skull to anchor the acrylic headset: 1) two screws were AP 2 mm and bilaterally 2 mm; 2) one screw was AP-3 mm and left 2 mm and served as a ground electrode; and 3) one screw was AP-2 mm to the lambdoidal suture and right 2 mm and served as a reference electrode. Holes were drilled to permit insertion of 2 stainless steel bipolar twist electrodes (1 mm tip separation) into the left and right ventral hippocampi for electrical stimulation and recording (AP-5.3 mm, bilateral 4.9 mm, vertical-5 mm below the dura) and 2 stainless steel monopolar recording electrodes in the bilateral frontal cortices (AP 3.2 mm, bilateral 1 mm, vertical-2.5 mm below the dura). Electrodes were labeled according to their relative positions on the rat's skull as LF/RF (left/right frontal) and LH/RH (left/right hippocampus). Electrode pins were positioned in a plastic strip connector and the entire headset was glued into place using cranioplast cement (Plastics One, Inc., Roanoke, VA). Following surgery, animals were allowed to recover for a week prior to additional procedures.

Induction of seizures

Four animals (A, B, C, and D) underwent hippocampal stimulation one week after surgery to induce status epilepticus. The left ventral hippocampus was stimulated in animals A and C, and the right in animals B and D. During electrical stimulation and iEEG acquisition, animals were housed in specially-made chambers (Bertram et al., 1997). Stimulus trains were delivered for 50-70 min with a duty cycle of 10 s on and 2 s off consisting of biphasic square wave pulses at a frequency of 50 Hz, a pulse duration of 1 ms, and intensities of 300-400 μA. During the stimulus, a normal behavioral response was for the animal to display “wet dog shakes” and increased exploratory activity. After approximately 20-30 min of stimulation, convulsive seizures (up to 1 min in duration) were usually observed about every 10 min. At the end of the stimulus period, continuous iEEG recordings were observed for evidence of slow waves in all recorded channels. If slow waves were not demonstrated, then the stimulus was re-applied for 10-min intervals 1-3 times until continuous slow waves appeared following termination of the stimulus. According to our experience, lack of response to this stimulation protocol was infrequent (<10% of animals) and was attributed, in part, to inaccurate placement of the stimulating electrode in the ventral hippocampus.

Upon termination of continuous hippocampal stimulation, the iEEG continued to demonstrate activity below 5 Hz for 12-24 h and intermittent spontaneous 30-60 s electrographic seizures for 2-4 h. Animals were observed for seizure activity and adequate food and water intake for 12-24 h after stimulation. Following behavioral stabilization, animals were returned to the vivarium for 6 weeks during which time spontaneous seizures developed.

Data acquisition

Each animal was connected by a 6-channel commutator and shielded cable to the recording system, which consisted of an analog amplifier (Grass Telefactor-Model 10), a 12 bit A/D converter (National Instruments, Inc), and recording software (HARMONIE 5.2, Stellate Inc., Montreal). The system was synchronized to a video unit for time-locked monitoring of behavioral changes. Each channel was sampled at a uniform rate of 200 Hz after the signal was filtered using analog high and low pass filters at cutoff frequencies of 0.1 Hz and 70 Hz, respectively. The recording system used a 4-channel referential montage, and the iEEG and video data were then transferred to a 1.4 TB RAID server for subsequent off-line review and analysis.

Data characteristics, seizure detection, and classification

Video-iEEG recordings were reviewed visually for electrographic as well as behavioral seizures. A classification scheme developed by Racine (1972) for kindled seizures was used to grade seizure activity and assign the corresponding “class.” In order to study iEEG dynamics during preictal, ictal, and postictal periods, we used a test seizure data set consisting of a total of 28 iEEG epochs (including preictal, ictal, and postictal periods), each of 2-h duration, from 4 animals with spontaneous seizures (see Table 1). Each epoch contained a single class 5 seizure (i.e., the animal displayed a severe generalized clonic convulsion accompanied by falling down) in the middle of the 2-h period (Table 1). In order to compute interictal dynamical values and compare them to those during the preictal, ictal, and postictal periods, we used an interictal data set consisting of a 24-h seizure-free iEEG block chosen randomly from each animal. We operationally termed the 1-h period before each seizure as the preictal period, and the 1-h period following a seizure as the postictal period. All seizures that occurred within 2 weeks after the start of iEEG data acquisition from each animal were included in the study (rat A had 5 class 5 seizures within the 2 weeks of EEG/video monitoring; rat B had 8; rat C had 7, and rat D had 8; mean seizure frequency = 1 per 2 days). Seizure onset was defined electrographically as the first sustained change in the iEEG that was clearly different than the background activity. Seizure offset was defined as that time when generalized high frequency epileptiform activity ceased abruptly. Seizure offset was followed by a predictable sequence of brief generalized voltage suppression, the appearance of spike and wave discharges (SWDs) at 1-2 Hz, which continued for ~30 s-1 min, and a prolonged generalized voltage suppression across all channels reflective of an actual postictal state. Although postictal SWDs are not typically observed following abrupt truncation of generalized ictal discharges in humans, they do occur in some instances, including the termination phase of status epilepticus. Hence, the SWDs that follow a seizure in this animal model suggest a less abrupt transition from an ictal (most ordered) to a postictal (less ordered) state than that observed for human seizures. All iEEG segments included for analysis were deemed sufficiently artifact-free by review of an electroencephalographer.

Table 1.

Summary of seizure data from iEEG recordings

Rat ID	Number of seizure epochs	Seizure frequency	Seizure duration (s)
			Mean	SD
A	5	1 per 2.8 days	52.8	3.0
B	8	1 per 1.75 days	96.6	20.8
C	7	1 per 2 days	83.7	11.1
D	8	1 per 1.75 days	65.0	11.0
Overall	28	1 per 2 days	78.45	21.8

Seizure numbers and durations are provided for the four animals studied.

iEEG signal analysis methods

Short-term maximum Lyapunov exponent (STL_max)

The Lyapunov exponent provides a measure of the order of a dynamical system and can be calculated from an observable output (in this case, the iEEG signal). Mathematically, it measures the average uncertainty along the local eigenvectors of an attractor in the state space. The short term maximum Lyapunov exponent (STL_max) was calculated from short epochs of iEEG that were reconstructed in a multidimensional space using the method of delays (Takens, 1981). Because the brain is a nonstationary system, it is likely that the signal (EEG), which reflects brain electrical activities, forms a nonstationary time series. Therefore, algorithms used to estimate measures of brain dynamics should be capable of automatically identifying and appropriately weighing existing transients in the signal. The STL_max algorithm adopted in this study was developed specifically for nonstationary EEG data. It was calculated by using a modification of the algorithm proposed by Wolf et al. (1985) for short segments of data (Iasemidis et al., 1990; Iasemidis, 1991). The iEEG datasets were divided into contiguous 10.24-s segments and embedded using an embedding dimension p=7 and a time delay τ= 3, and one STL_max value was obtained for each 10.24-s segment. The selection of these parameters was based on methods described in previous human and animal studies (Iasemidis et al., 1990; Nair et al., 2007). STL_max values were calculated for the iEEG segments sampled from interictal, preictal, ictal, and postictal periods using the algorithm proposed earlier (Iasemidis et al., 1990). We assessed whether there was a reduction in signal order during the ictal state compared to the other periods, i.e., a reduction in STL_max values. To test the hypothesis that STL_max was lowest during the ictal state, STL_max values were calculated as the average value of the 4 simultaneously recorded iEEG channels, and the mean of these calculated values was compared during the preictal, interictal, ictal, and postictal periods. Nested two-way analysis of variance (ANOVA) was applied to test the significance of the “period” effect, in which rats were considered as random blocks and seizures were nested within each rat. When “period” effect was considered to be significant (p<0.05), multiple comparisons testing (Tukey method) was applied to investigate the significance of the difference between each pair of periods.

Low STL_max values have been observed in epileptogenic foci in humans (Sackellares et al., 1995). Thus, we hypothesized that the side of brain that included the stimulated hippocampus, which incurs a slight degree of stimulation-induced injury, was more abnormal than the unstimulated side and therefore would reveal lower STL_max values in this model. To test this hypothesis, mean interictal STL_max values were compared between the 4 channels. Nested two-way analysis of variance (ANOVA) was applied to test the significance of the “channel” effect. When “channel” effect was considered to be significant (p<0.05), multiple comparisons testing (Tukey method) was applied to investigate the significance of the difference between each pair of channels.

Measuring spatial dynamics of STL_max similarity

To test the hypothesis that the rat TLE model exhibits spatiotemporal dynamics between brain regions similar to that observed in human TLE, a T-index (derived from the paired T-statistic) was used to measure the degree of similarity of STL_max between electrode sites over time. The similarity was measured for each 10.24 min (i.e., 60 STL_max points) with a one-point sliding window. The main advantage of utilizing the T-index over a direct mean difference is its ability to incorporate variation among the differences over time points, and thus provide more statistical insights. Mathematically, a (pair-) T index is calculated as the absolute value of mean difference divided by the sample standard deviation of the mean difference (Sackellares et al., 2006). By following the level of T-index values over time, one can observe the convergence (or divergence) transition of STL_max values between two iEEG channels, which could be considered a representation of spatio-temporal dynamics in an epileptic brain.

To test the differences in spatiotemporal interactions between brain areas during the interictal, ictal, preictal, and postictal periods, we compared the mean statistical difference between a hippocampal-frontal channel combination that included the stimulated hippocampus and bilateral frontal cortices, using the average of their T-index values. This selection was based on the premise that complex partial and secondarily generalized seizures occur as a result of the influence of the epileptogenic zone on other regions of the ipsilateral and contralateral cortex. Nested two-way analysis of variance (ANOVA) was applied to test the significance of the “period” effect, in which rats were considered as random blocks and seizures were nested within each rat. When “period” effect was considered to be significant (p<0.05), multiple comparisons testing (Tukey method) was applied to investigate the significance of the difference between each pair of states.

Results

iEEG recordings

The iEEG pattern recorded during interictal periods typically consisted of a mixture of polymorphic delta to beta frequency-range activities of low to moderate amplitude. The iEEG during most seizures was characterized by a low amplitude beta activity that evolved to higher amplitude polyspike waveforms followed by spike-wave theta activity and brief runs of temporally isolated postictal spike-wave and slow wave activity. Fig. 1 shows an iEEG sampled during interictal, ictal, and postictal periods.

Fig. 1.

Samples of 4-channel iEEG recordings of an epileptic rat during (A) interictal (B) ictal and (C) postictal periods. Interictal EEG (A) was sampled one hour before the beginning of the ictal period (B), and the postictal EEG (C) was sampled approximately 10 s after the end of the ictal EEG. LF: Left Frontal Cortex, RF: Right Frontal Cortex, LH: Left Hippocampus, RH: Right Hippocampus. Each of the displayed electrodes is connected to the skull screw reference electrode to generate the corresponding voltage trace.

Analysis of dynamical STL_max profile

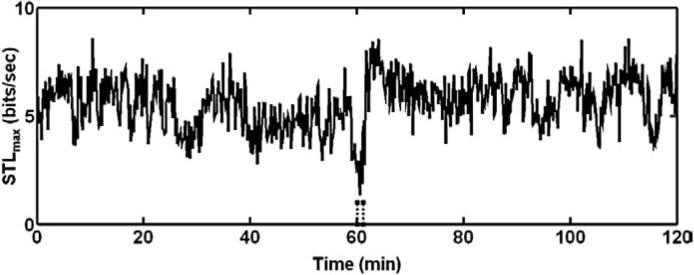
A consistent observation was that the STL_max value was lowest during the ictal period for all seizures analyzed from the 4 animals. Fig. 2 shows a sample STL_max profile derived from a hippocampal iEEG recording before and after a class 5 seizure. The STL_max value decreased to a low value during the seizure and increased at the end of the seizure. It is clear that for each animal, STL_max values were the lowest during the ictal period (Fig. 3). Statistical tests confirmed these observations (“period” effect for STL_max was significant, p<0.01). Multiple comparisons further suggested that: 1) mean STL_max values during interictal and preictal periods were not significantly different (p>0.05) than each other; and 2) mean STL_max values during the ictal period were significantly different (lower, p<0.05) than the other three periods (Fig. 4). The observation of statistically similar STL_max values during the interictal and preictal periods and the significant drop in the values during the ictal period suggested that the transition defined by STL_max values from the interictal to the ictal period was abrupt, and did not precede the ictal event. This observation suggests that the Lyapunov exponents of individual channels by themselves are unable to fully capture the transition from the interictal to a preseizure period, and therefore seems to have limited power to identify a seizure susceptible state, as described in earlier studies with human EEG and simulation models (Lai et al., 2003, 2004). It was also evident that for each animal, STL_max values computed from the stimulated hippocampal channel were the lowest. Statistical tests confirmed these observations (channel effects for STL_max were significant, p<0.01). Multiple comparisons suggested that: 1) mean STL_max values computed from the stimulated hippocampal channel were significantly different (lower, p<0.05) than those from the other three channels.

Fig. 2.

A sample STL_max profile derived from a hippocampal electrode recording. Each value of STL_max (bits/s) was calculated from 10.24 s of iEEG and plotted as a function of time. STL_max values were lowest during the seizure suggesting an increase in system order. Seizure onset and offset are indicated by vertical dashed lines.

Fig. 3.

Comparison of mean STL_max values of the four simultaneously recorded iEEG channels during the interictal, preictal, ictal, and postictal periods. STL_max values are lowest during the ictal period in each of the four animals. Mean STL_max values during interictal and preictal periods were not significantly different (p>0.05) from each other. Mean STL_max values during the ictal period were significantly different (lower, p<0.05) than the other three periods. Postictally, the mean STL_max values are significantly larger (p<0.05) than the other three periods.

Fig. 4.

Comparison of mean interictal STL_max values computed from four recording channels (ipsilateral and contralateral frontal cortex, stimulated and contralateral sides of the hippocampus). STL_max values are lowest in the stimulated side of the hippocampus in each of the 4 animals. Mean STL_max values of the stimulated hippocampal channel were significantly different (lower, p<0.05) than the other three channels.

Analysis of spatial dynamics

T-index was used for the analysis of spatial dynamics of STL_max values among electrode sites, specifically between frontal and stimulated hippocampal regions. Comparison of mean T-index values obtained from preictal, interictal, ictal, and postictal periods revealed that, compared to the interictal state, there was a significant STL_max convergence (p<0.05) between the frontal cortical and hippocampal signals (lower T-index) during the preictal and ictal period, and significant divergence during the postictal period (higher T-index; p<0.05). The mean T-index values generally decreased from interictal to preictal to ictal periods and the T-index values were at their highest values during the postictal period (Fig. 5). Statistical tests of these observations revealed that there was a significant “period” effect on the T-index (of STL_max). Multiple comparisons of mean T-index values revealed that the mean T-index value obtained from each of the four periods was significantly different than the other three periods (p<0.05), with an ascending order from ictal to preictal to interictal to postictal. Contrary to what was observed with individual channel STL_max values, the statistical significance of the difference in T-index values between the interictal and preictal (lower) periods suggested that the transition, defined as the convergence of STL_max values between brain areas, from the interictal to ictal period was not abrupt and preceded the actual onset of the ictal event. This is consistent with the findings and interpretations from studies in human EEGs that spatiotemporal information based on signal dynamics in multi-channel EEGs could offer better insights in identifying the transition(s) from a normal interictal state to a pathological ictal period (Iasemidis et al., 1999; Lai, 2004).

Fig. 5.

Comparison of mean T-index values during interictal, preictal, ictal, and postictal periods. The T-index values were calculated from the differences between STL_max values of the hippocampal and frontal cortical iEEG recordings. T-index values were lowest during the ictal period (high degree of convergence) and highest during the postictal period (high degree of divergence). The mean T-index value obtained from each of the four periods was significantly different than the other three periods (p<0.05), with a descending order from postictal to interictal to preictal to ictal.

Discussion

The main findings of this study were: 1) STL_max was lowest and closest in value among cortical sites during the ictal state, and highest and most divergent during the postictal state; 2) interictal STL_max was lowest in the channel corresponding to the stimulated hippocampus; and 3) the interictal to ictal transition was associated with a convergence of STL_max values among cortical sites as reflected by the drop in T-index values. From a dynamical perspective, these results suggest: (1) the iEEG of the ictal state indicates an increase in spatial-temporal order as compared to the interictal and postictal states; (2) the iEEG of the postictal state indicates less spatiotemporal order than the other states; and (3) during the interictal state, the iEEG of the most critical brain region indicates an increase in signal order. More detailed inspection on the T-index comparisons further revealed that the spatio-temporal order increases from the interictal to preictal period, and continue to increase from the preictal to ictal period. This observation suggests that the transition from the interictal to the ictal state is rather gradual than abrupt.

As in human TLE, transitions from the interictal to the ictal state in the rat TLE model involve a transition from higher to lower values of STL_max. This change has been interpreted to be a transition from a more chaotic (interictal) to a more ordered (ictal) state (Iasemidis and Sackellares, 1996). The average values of STL_max ranged from 4 to 6 during the interictal, preictal, and postictal periods, and from 1.5 to 2.5 during the ictal periods in the animal model, similar to the range of values observed in human TLE. Previous human studies have shown that the lowest values of STL_max were associated with signals recorded from the brain areas in or near the epileptic focus, suggesting that lower STL_max values are associated with more abnormal areas of the brain. The stimulated hippocampal channel in the animal model exhibited the lowest STL_max value among the four recorded brain regions, suggesting that it was more ordered than the other sites. In addition, the decrease in T-index based on convergence of STL_max values derived from multiple sites suggests a diffuse interaction among large areas of the cerebral cortex, involving both cerebral hemispheres; however, the physiological mechanisms underlying this observation remain to be investigated. The mean value of the T-index changes from the interictal to the preictal period, but not in the absolute value of STL_max. This observation suggests that the convergence or divergence between STL_max values (measured by the T-index), rather than the actual STL_max values themselves, may be more useful in detecting a transition between the interictal to the ictal state.

Other investigators have reported measurable characteristics of signal dynamics that distinguish the interictal and ictal states. These include reduction in correlation integrals during the ictal state (Lerner, 1996), changes in signal complexity and synchrony during ictal and postictal periods (Jouny et al., 2005), and decrease in signal complexity during seizures (Dominguez et al., 2008). The dynamics of the transition from the interictal to the ictal state have been investigated in other in vivo and in vitro animal models. Several investigators have used linear or stochastic methods such as power spectrum, wavelet entropy, and Markov chain modeling in their investigations (Khosravani et al., 2005; Paul et al., 2003; Sunderam et al., 2001). The results of these studies suggested detectable dynamical changes before and during seizures. Other studies using nonlinear methodologies based on state-space reconstruction have included application of the correlation dimension to show chaotic activity in rat hippocampal slices (Koch et al., 1992) and have demonstrated evidence of nonlinearity in the EEG (Jung et al., 2003). It should be noted, however, that current analytical methods cannot conclusively prove or disprove the presence of signal nonlinearity (Timmer, 1998; Andrzejak et al., 2001).

In an analysis of dynamics associated with in vitro extracellular recordings of epileptiform activity, Lian et al. (2001) showed a relationship between neuronal excitability and the largest Lyapunov exponent, with the exponent increasing during the onset of low Ca²⁺-induced activity. Another study used unstable periodic orbit and a measure of short-time expansion rate (closely related to the largest Lyapunov exponent) to assess the chaos and determinism in inter-burst interval data in three in vitro hippocampal models of epilepsy (Slutzky et al., 2001). These investigators found statistically significant period-1 or period-2 orbit in 73% of all experiments, which suggested the existence of local determinism, but the global average (Lyapunov estimation) did not offer evidence of determinism, suggesting that the system may be globally stochastic but contains local pockets of determinism.

In contrast to in vitro studies, iEEG recordings performed in in vivo models of acute seizures (Sarnthein et al., 1998), spontaneous seizures (Nair et al., 2004, 2006, 2007), and status epilepticus (Good et al., 2004) showed a reduction in the Lyapunov exponent values during seizures. Sarnthein et al. (1998) also provided additional evidence of low dimensional chaos in the ictal EEG.

One interpretation of the combined results of these in vitro and in vivo studies is that the dynamics of the firing patterns of hippocampal neurons may become more chaotic with increased action potential firing prior to and during the seizure, whereas global dynamics at the level of the EEG become more ordered due to synchronization of neuronal firing over large areas of the cerebral cortex.

The use of the largest Lyapunov exponent to study dynamics of the epileptic brain was initially motivated by the concept of epilepsy as a “dynamical disease”, a term introduced by Mackey and Glass in 1977 (Mackey and Glass, 1977; Mackey and an der Heiden, 1982). This concept was introduced to explain how biological systems can make transitions between normal and pathological states. It was hypothesized that pathological states, such as an epileptic seizure, could result from transitions between normal periodic and chaotic behavior. The bulk of evidence, however, does not support the concept of low-dimensional chaos in iEEGs recorded in patients with TLE (Casdagli, 1992; Theiler et al., 1992; Pritchard et al., 1995; Palus, 1996; Theiler and Rapp 1996). In addition, noisy experimental data have limited the yield of analytical methods (Rapp et al., 1989; Lehnertz et al., 2001; Lai et al., 2003; 2004; Harrison et al., 2005; Iasemidis et al., 2005). Some studies have shown evidence of a deterministic process involved in the occurrence of epileptic seizures (Iasemidis et al., 1994), whereas other studies have used stochastic modeling to explain seizure occurrences (Sunderam et al., 2001).

A qualitative model proposed to explain the results of dynamical investigations of human epilepsy was proposed by Lopes da Silva et al. (2003). Based on this model, the convergence in STL_max values (drop in T-index) may be interpreted as a reflection of the gradual change in an intrinsic control parameter. When the control parameter reaches a critical value, there is an abrupt transition to the ictal state. This qualitative descriptive model also fits well with the dynamical analysis of iEEG recordings in the present study. Convergence of the STL_max values prior to a seizure indicates that some control parameter (s) must be affecting widespread areas of the cortex. It has been proposed that convergence of the Lyapunov exponents among widespread cortical sites reflects increased coupling between the epileptogenic focus and other sites (Iasemidis et al., 2003c, 2004). These studies have demonstrated that changes in coupling strength between chaotic systems can cause abrupt transitions between chaotic and ordered states, providing theoretical support for this idea. If dynamical diseases can be explained on this basis, then it may be possible to use this information to construct optimal therapeutic responses based on manipulation of a control parameter (Rapp et al., 1988) or by external perturbations using techniques developed for the control of chaotic systems (Ditto et al., 1990; Ott et al., 1990; Hunt, 1991; Garfinkel et al., 1992; Roy et al., 1992; Petrov et al., 1993; Rollins et al., 1993; Shinbrot et al., 1993; Schiff et al., 1994). However, the identification of critical control parameters and other essential questions remain unresolved.

An important result of the present study, consistent with observations in human TLE, is that the physiological transitions from the interictal to the ictal state occur over a time scale of minutes. This finding provides important information about the nature of the underlying biological processes and suggests the opportunity for therapeutic intervention on the order of minutes preceding a seizure. The global changes measured by the T-index are on a much longer time scale and appear to precede short duration preictal changes in spiking and bursting activity that have been reported by others (Dichter and Spencer, 1969a,b; Ralston, 1958; Gotman, 1982; Gotman et al., 1982; Katz et al., 1991; Lange et al., 1983; Khosravani et al., 2005). Progress in developing a dynamical theory to explain human epilepsy has been impeded by the difficulties of obtaining sufficient samples of EEG recordings of patients and the many uncontrollable intervening variables that occur in the clinical setting. A valid animal model that exhibits the essential dynamical EEG features of the human condition is clearly necessary. Based on the results of this study, we suggest that the continuous hippocampal stimulation model of TLE provides a useful experimental system from which to develop mathematical dynamical models of epilepsy - a basis for testing the hypothesis that epilepsy is a dynamical disease, and a useful experimental model for identifying and investigating the effects of parameters that control state transitions in epilepsy.