Optimal postnodal lymphatic network structure that maximizes active propulsion of lymph

Abstract

The lymphatic system acts to return lower-pressured interstitial fluid to the higher-pressured veins by a complex network of vessels spanning more than three orders of magnitude in size. Lymphatic vessels consist of lymphangions, segments of vessels between two unidirectional valves, which contain smooth muscle that cyclically pumps lymph against a pressure gradient. Whereas the principles governing the optimal structure of arterial networks have been identified by variations of Murray's law, the principles governing the optimal structure of the lymphatic system have yet to be elucidated, although lymph flow can be identified as a critical parameter. The reason for this deficiency can be identified. Until recently, there has been no algebraic formula, such as Poiseuille's law, that relates lymphangion structure to its function. We therefore employed a recently developed mathematical model, based on the time-varying elastance model conventionally used to describe ventricular function, that was validated by data collected from postnodal bovine mesenteric lymphangions. From this lymphangion model, we developed a model to determine the structure of a lymphatic network that optimizes lymph flow. The model predicted that there is a lymphangion length that optimizes lymph flow and that symmetrical networks optimize lymph flow when the lymphangions downstream of a bifurcation are 1.26 times the length of the lymphangions immediately upstream. Measured lymphangion lengths (1.14 ± 0.5 cm, n = 74) were consistent with the range of predicted optimal lengths (0.1–2.1 cm). This modeling approach was possible, because it allowed a structural parameter, such as length, to be treated as a variable.

the principles governing lymphatic network structure have not been well characterized, in contrast to the advances that have been made in identifying the principles governing the structure of the arterial system (20). Although transport of blood from the heart to the capillaries requires numerous bifurcations to achieve a three-orders-of-magnitude reduction in arterial diameter, most of the radii of an arterial tree can be predicted using Murray's law (20). Analytic methods and mathematical minimization of energy loss at a bifurcation result in a prediction that the cube of a mother vessel radius is equal to the sum of the cube of its daughter vessels. To arrive at this prediction, it was assumed that mean blood flow is governed by Poiseuille's law and conservation of mass governs flow through the bifurcations. This theoretical prediction was subsequently validated by a number of experimental studies (25, 29). Despite significant criticism (21), the finding that arteries adapt to maintain shear stress within a relatively narrow (10–100 dyn/cm²) range (15) eventually provided the missing mechanism giving rise to this theoretical branching rule. The success with which Murray's law predicted the structure of an entire arterial network, however, has yet to be replicated for the lymphatic system.

The central function of the lymphatic system is to transport lymph. The lymphatic system acts to return lower-pressured interstitial fluid to the higher-pressured veins by networks of lymphatic vessels. In contrast to an arterial network with multiple bifurcations that allows passive flow from the aorta to capillaries, lymphatic networks have multiple confluences and must transport lymph against a pressure gradient. Within a mammalian lymphatic system, there is at least a three-orders-of-magnitude difference between radii of initial lymphatic vessels and the radius of the thoracic duct (2). Lymph (interstitial fluid that has entered the lymphatic system) is transported via the small prenodal lymphatic vessels to the lymph nodes. From the lymph nodes, the larger postnodal vessels return lymph to the great veins of the neck. These lymphatic vessels consist of lymphangions, segments of vessels between two unidirectional valves, which contain smooth muscle to pump lymph via phasic contraction (2, 18). Although the structure of lymphatic vessels is similar to that of veins, the function of lymphangions is more similar to that of cardiac ventricles (22).

Heart-arterial interaction provides insight into the characteristics of the lymphatic vessel. The recurring analogies to blood vessels and ventricles were recently leveraged to develop a detailed mathematical model of a lymphangion that integrated the structure and function of both (22, 31). The resulting realistic model included critical phenomena, such as resistance to lymph flow, lymph inertia, and storage of lymph in a lymphangion, based on the ventricular time-varying elastance model (26, 27). All variables varied cyclically. First, the resulting model was used to characterize the transition of lymphangions from pumps to conduits as the axial pressure gradient was reversed (22). Later, the model was extended to explore how coordination of contractions of adjacent lymphangions affects lymph flow (31). This study revealed that the average flow through a lymphatic vessel remained unaffected by the propagation direction of its contractile waves. Although these models were evaluated numerically, they allowed manipulation of parameters, such as length and contractility, that cannot be experimentally controlled (32). The complexity of numerical solutions, however, increases dramatically when an attempt is made to model more than a few lymphangions because of the large number of required parameters. This was also true of the model developed by Reddy et al. (24), who attempted to model the larger vessels of an entire lymphatic network. One of the critical limitations of a detailed large-scale modeling approach is that its complexity is not amenable to the discovery of fundamental optimality principles such as Murray's law. To reduce the complexity inherent in numerically evaluated models, Quick et al. (23) developed an analytic (i.e., algebraic) equation to describe the experimental lymphatic pressure-flow relationships reported by Drake et al. (8, 10). This simple model was validated experimentally, and comparison with a more complex model (22, 31) revealed that it was notably accurate.

Whenever there is a cause-and-effect relationship between two variables, the dependent variable may exhibit an optimum. One such relationship was demonstrated experimentally for the flow from a lymphangion, which exhibited an optimum at a particular distending pressure (17). A number of inferences can be drawn from such functional studies. In this case, it could be inferred that lymph flow is a particularly important variable and that flow optimization is a fundamental principle that governs the structure of lymphangions. However, testing such a hypothesis experimentally is problematic, since structural parameters such as vessel length cannot be made experimental variables. Mathematical modeling, however, allows typically fixed structural parameters to be treated as variables. The purpose of the present work is therefore to apply the algebraic formula describing lymphangion function (23) to determine the structure of a lymphatic network that optimizes lymph flow.

THEORY

Relating Lymphangion Structure to Function: Optimal Length

Stroke volume of a lymphangion.

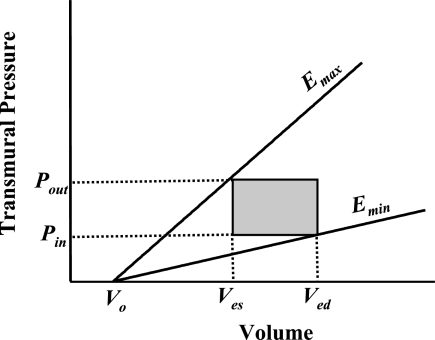
To predict the stroke volume (SV) of a lymphangion analytically, a simple pressure-volume relationship can be assumed that captures the essence of experimentally measured values (Fig. 1, Table 1). Taking this approach, Quick et al. (23) developed a simple model to calculate lymphangion SV as a function of the slope of the end-systolic pressure-volume relationship (E_max), the slope of the end-diastolic pressure-volume relationship (E_min), the inlet pressure (P_in), the outlet pressure (P_out), and the dead volume (i.e., volume at 0 pressure) for the end-diastolic and end-systolic pressure-volume relationships (V₀).

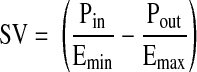(1)

Equation 1 is in the functional form first proposed by Sunagawa et al. (28) to characterize ventricular function. From this ventricular analogy, the value of E_min represents the diastolic tone of a lymphangion, and the value of E_max represents its systolic contractility. The lymphangion model was validated by comparison of results with a detailed, realistic lymphangion model (22, 31) and with experimental data obtained from postnodal bovine mesenteric lymphatic vessels (31). By normalizing E_min and E_max by length (E_min^′ and E_max^′), we can express lymph flow (Q̇) from the lymphangion as a function of end-diastolic cross-sectional area (A_ed), end-systolic cross-sectional area (A_es), length of the lymphangion (l), and frequency of contraction (f)

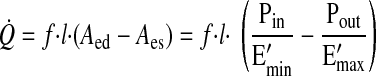(2)

This approximation incorporates the critical assumption that the lymphangion acts as a pump, transporting lymph from a lower pressure to a higher pressure (23).

Fig. 1.

Pressure-volume relationship of a lymphatic segment. Stroke volume, the difference between end-diastolic volume (V_ed) and end-systolic volume (V_es), is determined using inlet pressure (P_in), outlet pressure (P_out), slope of end-systolic pressure-volume relationship (E_max), slope of end-diastolic pressure volume relationship (E_min), and dead volume [i.e., volume at 0 pressure (V₀)].

Table 1.

Parameters and variables that constitute the mathematical model characterized by Eqs. 1–13

Parameter	Definition
Emax	Elastance at end systole
Emin	Elastance at end diastole
V0	Theoretical volume at 0 pressure
E′max	Elastance per unit length at end systole
E′min	Elastance per unit length at end diastole
f	Frequency of lymphangion contractions
Pin	Inlet pressure
Pout	Outlet pressure
SV	Stroke volume
Aed	End-diastolic cross-sectional area
Aes	End-systolic cross-sectional area
Q̇	Flow from lymphangion
l	Length of lymphangion
Ptrans	Transmural pressure
PL	Pressure to transport lymph across a lymphangion
lopt	Optimal lymphangion length
τmax	Maximum endothelial shear stress
red	End-diastolic radius
μ	Lymph viscosity
V	Lymph velocity
EF	Ejection fraction
α	Ratio of endothelial shear stress of lymphangion 1 to lymphangion 2*
δ	Ratio of flow from lymphangion 2 to flow at lymphangion 3*
β	Ratio of EF of lymphangion 1 to EF of lymphangion 2*
φ	Ratio of f of lymphangion 1 to f of lymphangion 2*

^*See Fig. 2.

Lymphangion flow as a function of length.

To determine how the length of a lymphangion affects its ability to pump lymph, we assume that the transmural pressure (P_trans) is constant. P_L characterizes the pressure a lymphangion must generate to transport lymph across its length (l). P_in and P_out can be expressed as a function of l and P_trans

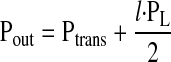(3a)

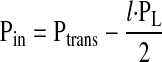(3b)

By substitution of Eq. 3a and Eq. 3b into Eq. 2, Q̇ from the lymphangion can be expressed as a function of l

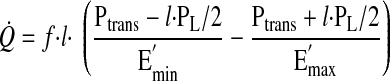(4)

Optimal lymphangion length.

Flow from the lymphangion, represented by Eq. 4, is a parabolic function of length. To obtain the optimal length that produces maximal flow, Eq. 4 was differentiated with respect to length, equated to zero, and solved for length (l_opt).

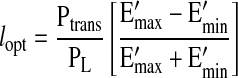(5)

l_opt thus depends on the relative difference between diastolic tone and systolic contractility, as well as P_trans relative to the axial pressure gradient.

Relating Structure to Function: Optimal Confluence

Lymphangion endothelial shear stress.

Endothelial shear stress (τ) in a pumping lymphangion is cyclical. The maximum value (τ_max) occurs at end diastole, when the radius is largest and the velocity of lymph is greatest (7). It can be calculated from end-diastolic radius (r_ed), lymph viscosity (μ), Q̇, and lymph velocity (V) given the same assumptions required for Poiseuille's law (29)

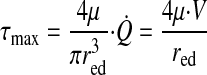(6)

Ejection fraction of a lymphangion.

Ejection fraction (EF), a term commonly used to describe the fraction of blood ejected by the heart in a single contraction, can be applied to lymphangions. The lymphangion EF takes a simple form

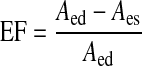(7)

Structure of a lymphangion at a confluence.

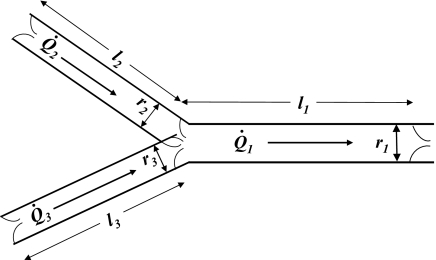
With the assumption of conservation of mass, the sum of flow from the two feeding lymphangions (Q̇₂ and Q̇₃) equals the flow through the downstream lymphangion (Q̇₁; Fig. 2)

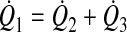(8)

To keep the nomenclature consistent, the parameter values of upstream lymphangions are denoted by subscripts 2 and 3 and those of the downstream lymphangion by the subscript 1.

Fig. 2.

Symmetrical lymphatic vessel structure at a confluence. Flow (Q̇) is governed by conservation of mass, with Q̇₁ = Q̇₂ + Q̇₃. Ratio of lymphangion length (l₁/l₂) and lymphangion radius at end diastole (r₁/r₂) is 1.26, with the assumption of a symmetrical network with constant lymphangion endothelial shear stress and ejection fractions.

Parameters used to describe a lymphangion at a confluence.

Lymphangions at a confluence may not be symmetrical. Three ratios can impact lymphangion function: 1) τ_max of lymphangion 1 is a factor α of lymphangion 2; 2) flow from lymphangion 2 is a factor δ of lymphangion 3; 3) EF of lymphangion 1 is a factor β of lymphangion 2

(9a)

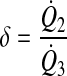(9b)

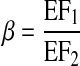(9c)

When the lymphatic network is symmetrical and all input pressures are equal, δ is 1. When α and β equal 1, τ_max and EF are equal among each level of a lymphatic network.

Radius ratio of lymphangions at a confluence.

From Eqs. 6, 8, 9a, and 9b, the ratio of downstream to upstream radii can be expressed as a function of two parameters characterizing the asymmetry in flow and maximal endothelial shear stress

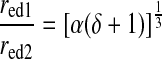(10)

If the network is assumed to be symmetrical (δ = 1) and the endothelial shear stresses are equal (α = 1), the radii of downstream lymphangions are predicted to be larger than those of the feeding upstream lymphangions. From Eq. 10, the ratio of radii at a confluence that optimizes Q̇ in such a network is 1.26, consistent with Murray's law for arterial networks.

Length ratio of the lymphangions at the confluence.

Q̇ can be calculated as a function of V and A_ed

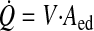(11)

EF, as given in Eq. 7, can then be expressed as a function of endothelial shear stress and r_ed by equating flow in Eqs. 2 and 11, solving for V, and substituting the result into Eq. 6

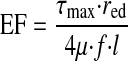(12)

If f₂ and f₃ are assumed to be equal, from Eqs. 9 and 12, the ratio of lengths at a confluence can be expressed in terms of φ, the ratio of upstream to downstream contraction frequencies (f₁/f₂)

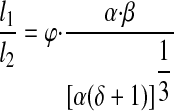(13)

If the network is assumed to be symmetrical and all lymphangion frequency, shear stress, and EF values are assumed to be equal (i.e., α, δ, and φ = 1), the lengths of downstream lymphangions are predicted to be longer than the upstream lymphangions. From Eq. 13, the ratio of lengths at a confluence in such a network is 1.26.

METHODS

Lymphatic Vessel Model Validation

To illustrate validation of the lymphangion model (Eq. 2), data reported by Venugopal et al. (31) were plotted. Briefly, an isobaric preparation was used to study postnodal bovine mesenteric lymphangions (n = 4). The inlet pressure was set at 5.0 mmHg. Outlet pressures were varied from 5.0 to 7.5 mmHg. The outlet pressures in the experiments were set to be higher than the inlet pressure for three reasons. 1) It allowed us to obtain a good estimate of the maximum time-varying elastance without the influence of the conduit-like behavior (22). 2) The vessels under study were likely exposed to pressures in vivo that are higher at the outlet than at the inlet (4). 3) Such an experimental pressure gradient would make the experimental protocol consistent with our mathematical modeling assumptions. After every change in the axial pressure gradient, vessels were allowed to equilibrate for 1 min. Mean flow was plotted as a function of axial pressure gradient. The data were pooled, and results of a linear regression and associated 95% confidence intervals were plotted.

Optimal Lymphangion Length

Consistent with values used in lymphangion models reported by Quick et al. (23) and Venugopal et al. (31), values for E_min and E_max obtained from postnodal bovine mesenteric lymphatic vessels were set at 144.1 and 334.4 cmH₂O/ml, respectively, and V₀ was set to 0.05 ml. Q̇ was then plotted as a function of length normalized by l_opt (Eq. 5). Similarly, Eq. 4 was used to identify l_opt for maximal flow at 0.1 and 2.0 cmH₂O P_trans for 0.5 cmH₂O/cm P_L. The pressure range includes the lowest pressure that prevents collapse up to the value reported by Drake et al. (10). Flow from the lymphangion was calculated for a frequency of five contractions per minute.

Theoretical Radius Change Along the Network of Lymphatic Vessels

To identify the number of confluences in a lymphatic network optimized for flow, it was assumed that the ratios α and δ were equal to 1. The range of radii was assumed to be 3 mm–30 μm (thoracic duct of a human to a lymphatic microvessel). The number of confluences (n) was then predicted using Eq. 10 by repeated scaling of the lymphangion radius by a factor of 1.26.

Length Changes Along the Network of Lymphatic Vessels

To identify how the lymphangion length scales from the thoracic duct to the microvessels in a lymphatic network optimized for Q̇, the ratios α, β, δ, and φ were assumed to be 1. Thoracic duct radius was assumed to be 3 mm. Lengths were calculated from Eq. 13 for the number of confluences (n) in the network. The length of a terminal lymphangion was predicted assuming thoracic duct length and the value of n.

Measured Lengths of Lymphangions

Postnodal bovine mesenteric lymphatic vessels obtained from an abattoir were used to test the theoretical predictions of Eq. 13. Lymphatic vessels were identified by injection of an Evans blue dye-based saline solution into the lymph nodes. After a lymphatic vessel was located, the valves were identified. The distance between the valves was measured using a digital caliper.

RESULTS

Comparison of Algebraic Solution to Data

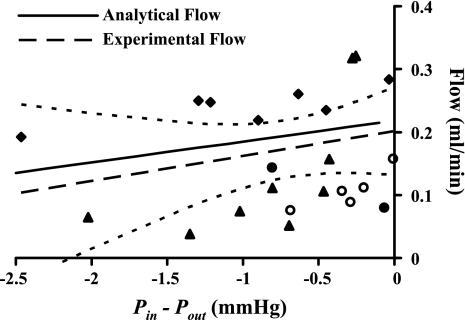
As reported by Quick et al. (23), as outlet pressure was decreased from 7.5 to 5.0 mmHg (n = 4), experimental values of mean flow increased, with a linear regression of the pooled data having a slope of 0.040 ml·min⁻¹·mmHg⁻¹ (Fig. 3). The results of linear regression with 95% confidence intervals are also indicated. The algebraic model, based on parameters specific to a lymphangion reported by Quick et al., yielded results that were well within the 95% confidence interval, even though it was expected that each lymphangion would have different levels of E_max and E_min.

Fig. 3.

Validation of 1st-order (analytic) approximation of lymph flow in a lymphangion (Eq. 4, solid line) (Eq. 2). Experimental data from 4 vessels were used to validate the model first reported by Venugopal et al. (31) for comparison purposes (▴, ⧫, •, and ○). Dashed line, linear regression of pooled data; dashed curves, 95% confidence intervals. Scatter in data represents variation among vessels.

Optimal Lymphangion Length

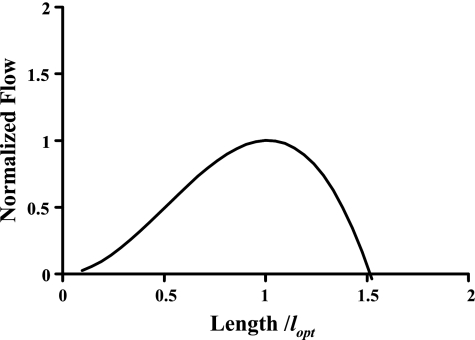
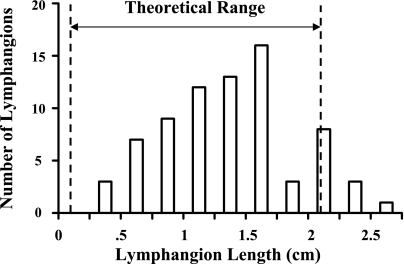
The mathematical model (Eq. 4) indicates that lymphangions exhibit an optimal length that produces maximal flow. The relationship of flow to lymphangion length is illustrated in Fig. 4, with use of the parameter values first reported by Venugopal et al. (31) and the assumption of 2 cmH₂O transmural pressure. With the assumption of 0.1 and 2.0 cmH₂O transmural pressures, the predicted optimum length is 0.1 and 2.1 cm, respectively. This predicted range of optimal lengths is similar to the experimentally measured length (n = 74) of 1.14 ± 0.5 cm (Fig. 5). The optimum can vary considerably depending on P_L used in Eq. 4, with a 9.4% change in the optimum for a 10% change in its value. However, for a given set of parameters, a 10% change in length results in a flow reduction of only 1%, suggesting that flow is not particularly sensitive to length near the optimum. A simple sensitivity analysis is provided in Table 2.

Fig. 4.

Flow from a lymphangion is maximal at optimal length (l_opt). Flow is normalized by its maximum value.

Fig. 5.

Variation of lengths obtained from postnodal bovine mesenteric lymphatic vessel (1.14 ± 0.5 cm, n = 74). Equation 5 was used to predict that optimal lengths can range from 0.1 to 2.1 cm (dashed lines), consistent with data.

Table 2.

Parameters used in sensitivity analysis

Parameter	Values Used in the Model	Change in Optimal Length With 10% Change
Emax	334.4 cmH2O/ml	10.6%
Emin	144.1 cmH2O/ml	9.4%
Ptrans	0.1–2 cmH2O	10.0%
PL	0.5 cmH2O/cm	9.4%

Sensitivity analysis was performed to indicate change in optimal length resulting from 10% change in parameter values using Eq. 5.

Predicting the Number of Bifurcations From Microvessels to Conducting Vessels

Lymphangion radii in an optimal, symmetrical network increase nonlinearly with the confluence number. The number of confluences required for an optimal network of lymphangions with radii ranging from 3 mm to 30 μm is 21.

Predicting Length of a Terminal Lymphangion for a Given Thoracic Duct Length

Using thoracic duct length from previously reported studies (5), we found that, for 21 confluences in a lymphatic network, the lymphangion length of a 30-μm-radius vessel is 294 μm.

DISCUSSION

The present work used a validated, algebraic lymphangion model (23) to predict the structure of a lymphatic network that optimizes lymph flow. Lymphatic vessels are predicted to exhibit an optimum flow when their lymphangions have a particular length. To maintain an optimal flow through a confluence, upstream vessel length must be a simple factor larger than the length of the two feeding upstream vessels. The size of lymphatic vessels is thus predicted to increase progressively from initial lymphatic vessels to the thoracic duct. If the number of lymphangions between bifurcations were proportional to lymphangion length, the resulting lymphatic network structure would be best described as a fractal, since the geometry would be preserved independent of its scale (11). Length predictions were consistent with data collected from bovine mesenteric lymphatic vessels (Fig. 5). This deductive approach to deriving basic teleological principles was possible because the algebraic formula (Eq. 1) allows structural parameters to be treated as variables.

Optimal Length of a Lymphangion

This work predicts a lymphangion length that results in maximal lymph flow (Fig. 4). The observed optimum results from two competing factors: 1) as length increases, SV tends to increase proportionally, and 2) as length increases above the optimum value, the pressure contributed by the lymphatic smooth muscle fails to overcome the axial pressure gradient against which the lymph has to be transported. This fundamental physical limitation suggests two physiological principles. 1) After initial development, lymphangion length cannot adapt as readily as lymphangion frequency, contractility, or tone. Thus it is critical for the lymphangion length to be well chosen. With length optimized, successful adaptation of a lymphangion to acute changes in axial pressure gradient becomes easier. 2) The present work suggests that there is an undiscovered developmental mechanism that places valves in the appropriate place.

Predicting the Value of an Optimal Length

The particular value of an optimal length of a lymphangion depends on a number of parameters. The optimal length (Eq. 5) depends on lymphangion contractility (E_max), tone (E_min), contraction frequency (f), and pressure gradient (P_L). However, the predicted change in optimal lengths resulting from 10% changes in E′_max, E′_min, and P_L is <10.6% (Table 2). However, the optimal length is more sensitive to the assumed operating transmural pressure. For illustrative purposes, transmural pressures were assumed to vary between 0.1 and 2.0 to be consistent with reported values of transmural pressure (2, 10). The resulting predicted range of optimal lymphangion lengths of 0.1–2.1 cm is consistent with the lymphangion length measured from bovine mesenteric lymphangions (1.14 ± 0.5 cm; Fig. 5). The predicted length-to-radius ratio of a lymphatic vessel of 10 was also consistent with reported values (5). The present theoretical work, predicting a length that optimizes flow (for a given transmural pressure), thus complements reported experimental work, illustrating a transmural pressure that optimizes flow (for a given length) (17).

Implications of Lymphangion Length on Basal Frequency

Equation 13 expresses the optimal ratio of upstream and downstream lymphangion lengths as a function of several parameters, including one that represents the ratio of frequencies. The result that the optimal lengths of lymphangions downstream are 1.26 times the lengths of upstream lymphangions explicitly assumes that the contraction frequencies are equal. Previous studies have reported, however, that the resting contractile frequency of lymphangions may vary along the length of the network (4, 17). Given that this small variation in frequency occurs over a significant number of bifurcations, the optimal ratio of lengths at any one bifurcation would not be much smaller than 1.26. Although the present work does not explicitly predict that larger lymphangions contract at a slower rate, it does suggest that, if they do, Eq. 13 has a degree of freedom that allows the length ratio to vary accordingly to maintain optimality.

Scope of the Present Work

Although the equations derived in the present study may apply to prenodal lymphangions or lymphangions from other organ systems, four major factors constrain the scope of the present work. 1) The data used to establish and validate the model were collected from bovine mesenteric vessels. Although lymphangions from other animal models and other organ systems exhibit significant differences in pressure generated and volume ejected (4, 8, 17), they share similar pressure-volume relationships (4, 22). Thus the predicted optimal lengths would be expected to be very different, yet the equations predicting an optimal length (Eqs. 2–5) may still apply. Similarly, the data were obtained from postnodal lymphatic vessels. Because pre- and postnodal lymphangions share a similar structure (14) and exhibit similar indexes of pump function (13, 14) and their flow is governed by the same fundamental physical principles, it is likely that the model equations (Eqs. 2–5) retain their validity for prenodal vessels. 2) The time-varying elastance characterization of the lymphangion pressure-volume relationship (22) assumes that vessels are acting as pumps with developed pressures that are proportional to their end-diastolic volume. This approach is valid for vessels that intrinsically pump, but not for lymph flow, which is governed by extrinsic forces such as cardiac contraction, skeletal muscle contraction, or intestinal peristalsis (2). Although the global significance of lymphatic contractions may be unclear, the equations used to characterize the optimal length are appropriate for pumping lymphangions, such as those that compose mesenteric, cutaneous, cervical, thoracic, and femoral lymphatic vessels (13). 3) Since collapsible vessel behavior requires a completely different set of equations to capture a fundamentally different set of mechanical behaviors (6), lymphangions in the present work are assumed to be inflated with a positive transmural pressure. 4) Although not necessary for the mathematical derivations, the modulation of lymphatic contraction due to spontaneous electrical activity generated by putative pacemaker sites (33) was neglected. To predict the optimal lymphangion length, lymphangion contraction frequency was assumed to be constant and equal to the rate governed by pacemaker cells (33). Although addition of complexities to the model to address these four limiting factors may allow expansion of the scope of the present work, the resulting numerical solutions would not yield the same conceptual clarity apparent from the algebraic formulas represented by Eqs. 1–13.

Dual Pump-Conduit Nature of Lymphangions

One particular assumption basic to all equations in the present work is that lymphatic vessels pump lymph against an axial pressure gradient (i.e., from low to high pressures). Certain conditions, however, can cause the inlet pressure of a lymphangion to rise above its outlet pressure. 1) With interstitial edema, interstitial pressure could rise above central venous pressure (4). 2) With a simple limb elevation, the normal axial pressure gradient can reverse. 3) A pressure gradient can exist across a lymph node (1), suggesting that prenodal vessels might drain into lower-pressure vessels (1, 2). 4) External compression can cause the inlet pressure of a particular lymphangion to be higher than its outlet pressure. When inlet pressure rises above outlet pressure, lymphangions transition from pumps to conduits, as reported by Quick et al. (22). In fact, this axial pressure gradient can favor passive flow, and the valves can be forced open throughout the contraction cycle (22), whether or not a lymphangion exhibits flow-induced relaxation (12). When lymphangions act as passive conduits, the prediction of optimal lymphangion lengths given by Eq. 5 is not valid. Although not incorporated in the present work, the optimal lengths for lymphangions acting as conduits may be similar to equations derived for arterial networks (3, 21, 25), despite the fact that optimality principles governing vessel lengths are typically related to the ability of an arterial tree to be “space filling” (3).

Validity of Basic Assumed Network Properties

Four fundamental assumptions were made to arrive at the final set of equations characterizing optimal lymphatic system structure (Eqs. 5, 10, and 13). 1) The maximum shear stress was calculated using the radius at end diastole. Lymph velocity is not always highest when radius is largest, and peak shear does not always occur at end diastole (7). Although this approximation likely overestimates the value of peak endothelial shear stress, it would not affect the ratio of radii. 2) Lymphangion endothelial shear stresses, contraction frequencies, and EFs at confluences were assumed to be constant. Calculation of endothelial shear stress from the flow data reported for bovine mesenteric lymphangions (22) and rat mesentery lymphangions (7) results in a relatively small range of 3–12 dyn/cm². Similarly, contraction frequencies from initial lymphangions to thoracic duct can change only as much as a factor of 3 (4). Although each lymphangion's frequency varies from initial lymphatic vessels to the thoracic duct, the amount that each varies at a confluence (given the ∼21 confluences) is exceedingly small. Equations 10 and 13 are general, however, and can be used to more accurately predict structure to capture such details. 3) The analytic approximation used to derive an optimal lymphangion length (Eq. 5) required the assumption that lymphangions act as pumps. This approximation fails when the inlet pressure rises above outlet pressures (16, 19), causing lymphangions to act in a manner similar to conduits (22). 4) To arrive at a lymphangion length ratio of 1.26, we assumed that lymphangions at a confluence were symmetrical. Since Eqs. 10 and 13 are general, they can be used to predict a more accurate value for nonsymmetrical networks, although the prediction that lymphatic vessels grow progressively larger from initial lymphatic vessels to the thoracic duct would be maintained in asymmetrical networks. Although some of these assumptions could be made more realistic, the cost to conceptual clarity may be too high, since analytic solutions are necessary to mathematically derive an optimum.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant K25 HL-070608 (C. M. Quick), American Heart Association Grants 0565116Y (C. M. Quick) and 0365127Y (R. H. Stewart), and Centers for Disease Control and Prevention Grant 623086 (G. A. Laine).