Femtosecond observation of benzyne intermediates in a molecular beam: Bergman rearrangement in the isolated molecule

Abstract

In this communication, we report our femtosecond real-time observation of the dynamics for the three didehydrobenzene molecules (p-, m-, and o-benzyne) generated from 1,4-, 1,3-, and 1,2-dibromobenzene, respectively, in a molecular beam, by using femtosecond time-resolved mass spectrometry. The time required for the first and the second C-Br bond breakage is less than 100 fs; the benzyne molecules are produced within 100 fs and then decay with a lifetime of 400 ps or more. Density functional theory and high-level ab initio calculations are also reported herein to elucidate the energetics along the reaction path. We discuss the dynamics and possible reaction mechanisms for the disappearance of benzyne intermediates. Our effort focuses on the isolated molecule dynamics of the three isomers on the femtosecond time scale.

Arynes have presented chemists with structural and synthetic challenges for more than half a century. After the structure proposal for 1,2-didehydrobenzene by Wittig (1) in 1942 and the isotopic labeling experiments of Roberts et al. (ref. 2 and references therein) in 1953, the challenge to understand the behavior and properties of these reactive species has attracted large numbers of chemists and spawned a whole area of inquiry within chemistry (3, 4). Although the greatest effort has been in the study of 1,2-dehydrobenzene, the behavior and properties of the 1,3- and 1,4-isomers have recently been the subject of many studies (refs. 5 and 6; and ref. 7 and references therein). The 1,3-isomer has been characterized recently (5). The 1,4-isomer has gained special prominence because of its propensity to undergo Bergman rearrangement (8) and its relationship to several currently exciting antitumor agents such as neocarzinostatin and dynemicin A.

Materials and Methods

The femtosecond laser and molecular beam apparatus is described in detail elsewhere (ref. 9 and references therein). Briefly, a femtosecond laser system was integrated to a molecular beam apparatus with the capability of measuring time-of-flight mass spectra. The amplified pulses were typically ≈80 fs, and the energy input was ≈150 μJ⋅pulse⁻¹ at 615 nm. For the pump, the 615-nm output was frequency doubled. The probe beam, which ionizes the transient species, was passed to a computer-controlled translation stage for the time delay. Both pump and probe beams were appropriately attenuated to minimize background signals; no ionization was observed when the pump pulse was blocked, and the transients are for the enhanced ionization when both pump and probe pulses are present. 1,4-Dibromobenzene (98%), 1,3-dibromobenzene (97%), and 1,2-dibromobenzene (98%), all from Aldrich, were used without further purification. The mass spectra show their characteristic patterns, as discussed below. The theoretical work reported herein involves density functional theory (DFT) and ab initio methods and will be detailed in the Discussion section.

Results

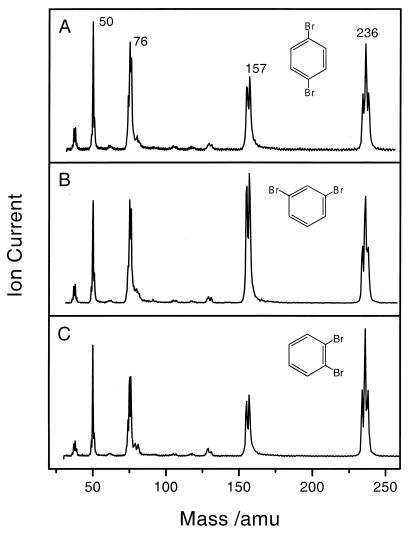
Fig. 1 shows the femtosecond mass spectra of 1,4-dibromobenzene (Fig. 1A), 1,3-dibromobenzene (Fig. 1B), and 1,2-dibromobenzene (Fig. 1C). The mass spectra are similar. The parent signals are characterized by three peaks at 234, 236, and 238 amu, corresponding to the isotopic abundances for bromine (79 and 81 amu). The bromophenyl radicals are observed as the two peaks at 155 and 157 amu, and the benzyne intermediates are found at 76 amu. The mass signals at 75 amu and 50 amu are due to ion fragmentation of the 76 amu species, which correspond to 76 − 1 (hydrogen atom) amu and 76 − 26 (acetylene molecule) amu, respectively. The intensity distribution is consistent with the abundance of the bromine isotopes and with electron-impact findings (10).

Figure 1.

Femtosecond mass spectra of benzyne precursors: 1,4-dibromobenzene (A), 1,3-dibromobenzene (B), and 1,2-dibromobenzene (C). The split peaks are due to bromine isotope composition (see Results). The spectra were obtained at a delay time of ≈50 fs between the pump and probe pulses. The precursors do not absorb a single photon at 307 nm, because the first absorption is typically at 280 nm (26). amu, atomic mass units.

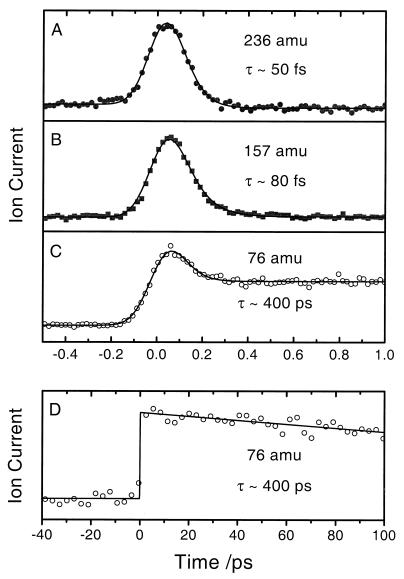
By gating the signal at 236, 157, and 76 amu, we obtained the transient signals for the corresponding species. The results for 1,4-dibromobenzene are shown in Fig. 2. We studied the other two isomers in a similar way. A least-squares fit, with appropriate convolution, gives the decay time of τ ≈ 50 fs for parent (236 amu) and τ ≈ 80 fs for the radical intermediate (157 amu). The transient of the 76 amu contains a fast-decay component, arising from ion fragmentation of the parent and radical species, and a slow one that was persistent on the femtosecond time scale. The lifetime of the 76-amu species was determined by extending the delay time to 100 ps, which gives a decay time constant of ≈400 ps (Fig. 2D), assuming the signal decays to its zero background. Interestingly, the dynamics on both femtosecond and subnanosecond time scales studied from the other two parent molecules (1,3-dibromobenzene and 1,2-dibromobenzene) are essentially the same as those of 1,4-dibromobenzene, within our error, as discussed below.

Figure 2.

Femtosecond transients of p-benzyne and its precursor, 1,4-dibromobenzene, and monobromo intermediate: parent at 236 amu (A), intermediate at 157 amu (B), and intermediate at 76 amu (C). (D) The picosecond transient of the 76-amu species. The symbols are experimental results. The theoretical fits are represented as solid curves giving the decay time (τ) of the parent and the intermediates. Similarly, we examined 1,2- and 1,3-dibromobenzenes.

Discussion

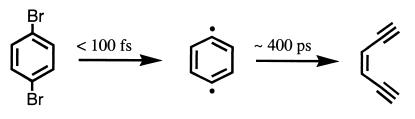
The above observations indicate that two C-Br bonds of the parent species break in less than ≈100 fs and that the intermediate species (76 amu) is formed within 100 fs. The observed ≈400-ps lifetime of the 76-amu species suggests the formation of a p-benzyne molecule, which may undergo ring opening to form Z-hex-3-ene-1,5-diyne via the Bergman rearrangement (Scheme S1).

Scheme 1.

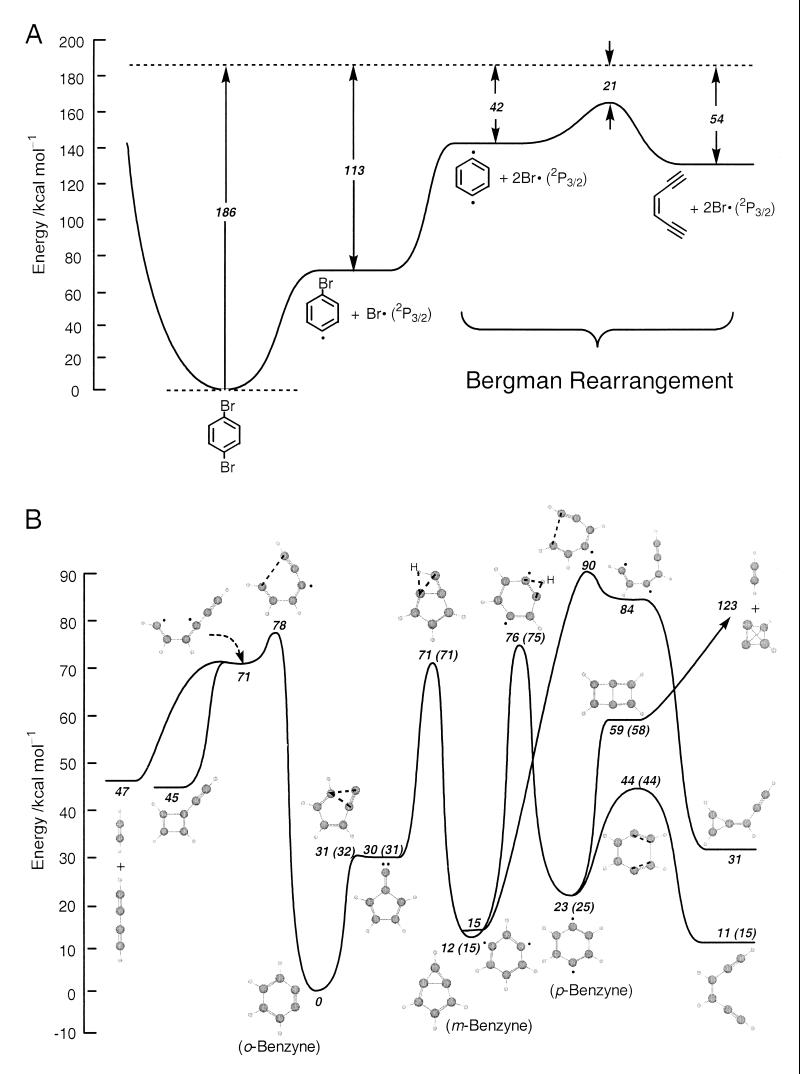
Fig. 3 depicts the reaction pathway of 1,4-dibromobenzene (Fig. 3A) at our excitation energy (186 kcal⋅mol⁻¹) and the ground-state potential energy surface (PES; Fig. 3B), which describes all the benzyne intermediates studied and their related transition states and products. Note that in Fig. 3A, only the reaction paths involving the most stable Br atom (²P_3/2) are shown (see below). The geometry of stationary points was optimized by using the spin-unrestricted DFT method at the B3LYP/6-31G(d) level. As discussed elsewhere (ref. 11; and ref. 12 and references therein), the restricted method was used for all closed-shell species, whereas the unrestricted method was employed for open-shell species. Vibrational frequencies were calculated at the same level of theory to characterize the nature of the stationary points and to determine the zero-point energy correction. To confirm that the transition state is the correct saddle point connecting two local minima, intrinsic reaction-coordinate calculations were performed. The effect of the basis functions for the B3LYP functional was examined by the single-point energy calculations of each species by using the 6-311G(d,p), 6-311+G(2df,p), cc-pVTZ, and aug-cc-pVTZ basis sets. Furthermore, the energies were also calculated at the G2M(RCC6) level of theory (13) for comparison. All calculations were carried out with the gaussian software package (14).

Figure 3.

(On the opposite page.) (A) Ground-state PES showing both primary and secondary C-Br bond-breaking reaction paths for 1,4-dibromobenzene. The energies are calculated at the B3LYP/6-311+G(2df,p)//6–31G(d) level of theory with zero-point energy corrections. The spin-orbit splitting of each Br atom (10.5 kcal⋅mol⁻¹) is taken into account (see Discussion). (B) General ground-state PES for benzynes characterized at the B3LYP/aug-cc-pVTZ//6-31G(d) level of theory with zero-point energy corrections. The values shown in parentheses were calculated by using the gaussian 2 additive scheme at the G2M(RCC6) level. Other reaction pathways, such as those involving diradical and carbene intermediates, have also been considered.

Our DFT/ab initio results indicate two important points. First, based on the PES characterized at the B3LYP/6-31G(d) level, we found the relative energies are decreased by 0–3 kcal⋅mol⁻¹ for most species by using the 6-311G(d,p) basis set. Adding large polarization and diffuse functions or implementing consistent-correlated-valence-polarized triple-zeta basis set does not improve the PES. Second, for most important intermediate species and their corresponding saddle points, the relative energies calculated by using the DFT method are comparable to those obtained at our G2M(RCC6) and other sophisticated ab initio levels (15–17). The full PES calculations for C₆H₄ isomers and their products are shown in Fig. 3B and were obtained by using our DFT calculations at the B3LYP/aug-cc-pVTZ//6-31G(d) level of theory (the values shown in parentheses are from our G2M calculations).

DFT calculations at the B3LYP/6-311G+(2df,p)//6-31G(d) level indicate that the expected first and second C-Br bond energies are 78.2 and 76.0 kcal⋅mol⁻¹, respectively, for 1,4-dibromobenzene; 77.5 and 65.9 kcal⋅mol⁻¹, respectively, for 1,3-dibromobenzene; and 75.6 and 52.8 kcal⋅mol⁻¹, respectively, for 1,2-dibromobenzene. Account must be taken of the strong spin-orbit coupling of bromine atoms, where the energy difference between Br (²P_3/2) and Br (²P_1/2) is 3,685.24 cm⁻¹(≈10.5 kcal⋅mol⁻¹) (18), in predicting the energy available to the benzyne isomers. From energy conservation, with a total energy of 186 kcal⋅mol⁻¹, the maximum available excess energy (assuming formation of ²P_3/2 bromine atoms)† is 42, 53, and 68 kcal⋅mol⁻¹ for p-, m-, and o-benzyne, respectively. We also assume that the kinetic energy of the two bromine atoms is negligible, according to the relative masses in an impulsive (19) ultrafast C-Br bond cleavage.

Under our experimental conditions, the energy available to p-benzyne is sufficient to permit it to undergo Bergman rearrangement only (Fig. 3A). However, for both m- and o-benzyne, the available energies are insufficient for them to surmount any of the reaction barriers shown in Fig. 3B and to form new products. The observed ≈400-ps lifetime, common to the three isomers, suggests that the three isomeric benzyne species may actually interconvert rapidly—most likely as a result of hydrogen tunneling with the ring-opening exit channel as the rate-limiting step. The tunneling probability can be estimated by a hypergeometric function (20) with three parameters (forward barrier height, reverse barrier height, and barrier width) obtained from our DFT calculations to describe a one-dimensional asymmetrical Eckart potential (21, 22). Accordingly, the probability of a hydrogen-atom migration from m-benzyne to p-benzyne is predicted to be 10⁻³ to 10⁻⁴, taking the reaction coordinate frequency from our DFT to be (15 fs)⁻¹. A lifetime is obtained in the range of 10 ps to 100 ps, which is shorter than the observed values, consistent with the interconversion of isomers. For o-benzyne to m-benzyne conversion, the time is even shorter because of the smaller barrier. However, the calculation assumes a one-dimensional coordinate, and also on this time scale, energy redistribution and electronic interconversion (S/T of the diradicals) must be part of a final description of the effective reaction coordinate.

With the force constants obtained from our DFT calculations and the PES shown in Fig. 3, we have made Rice–Ramsperger–Kassel–Marcus calculations for prediction of the unimolecular, microcanonical reaction rate coefficient of the process of Bergman rearrangement. A lifetime of 30 ps was obtained at the aforementioned total available energy of 42 kcal⋅mol⁻¹ for p-benzyne. For the ²P_1/2 channel, the reaction time is much slower (≈100 ns). The difference observed may imply that intramolecular vibrational-energy redistribution is slow and restricted to certain vibrational modes. Examples for such nonstatistical behavior have been found recently, especially for reactions of an ultrafast nature (23, 24), and the formation of benzyne is in this class. The long lifetime of benzynes is consistent with their stability for microwave detection in the gas phase (25).

In summary, the p-benzyne intermediate involved in Bergman rearrangement has been isolated in time and, at the total energy of ≈40 kcal⋅mol⁻¹, has a lifetime consistent with the energetics for the ring opening obtained from our DFT/ab initio calculations. The o- and m-benzynes have similar lifetimes, suggesting the probability of interconversion between isomers before ring opening and/or the vibrational-electronic redistribution in the hot benzyne. This area is rich for further studies, both experimentally and theoretically.

Abbreviations

DFT

density functional theory

amu

atomic mass unit

PES

potential energy surface