Electrostatic effects on funneled landscapes and structural diversity in denatured protein ensembles

Abstract

The denatured state of proteins is heterogeneous and susceptible to general hydrophobic and electrostatic forces, but to what extent does the funneled nature of protein energy landscapes play a role in the unfolded ensemble? We simulate the denatured ensemble of cytochrome c using a series of models. The models pinpoint the efficacy of incorporating energetic funnels toward the native state in contrast with models having no native structure-seeking tendency. These models also contain varying strengths of electrostatic effects and hydrophobic collapse. The simulations based on these models are compared with experimental distributions for the distances between a fluorescent donor and the heme acceptor that were extracted from time-resolved fluorescence energy transfer experiments on cytochrome c. Comparing simulations to detailed experimental data on several labeling sites allows us to quantify the dominant forces in denatured protein ensembles.

The guiding forces of the folding funnel dominate the folding mechanism but are also of key importance in the denatured state. The denatured state is, however, strongly fluctuating and therefore also highly susceptible to weak nonnative electrostatic and hydrophobic interactions. Measurements of the radius of gyration (R_g) suggest that proteins in unfolded states are nearly random coils (1) perhaps modulated by the effects of electrostatic interactions (2–8) or general hydrophobicity (9, 10). Yet a number of techniques, including circular dichroism and NMR, indicate that there can be local helical structure (11–14) and sometimes remnant tertiary structure in chemically denatured ensembles (15). These discrepant views of the denatured ensemble arise from biases inherent to techniques that measure different average properties. Indeed, both experimental (16–23) and theoretical (2, 9, 24) work supports the existence of a multiplicity of populations of unfolded configurations, both compact and extended, in denatured ensembles. Analysis of time-resolved fluorescence energy transfer (TRFET) measurements can reveal composition and structural features of heterogeneous protein ensembles. These experiments have provided distance distributions (P(r)) from dansyl fluorophores to the heme in unfolded iso-1-ferricytochrome c (21–23). In this article we show that models based on funneled (structure-based) energy landscapes (25–30) but additionally incorporating generic hydrophobic collapse and electrostatic interactions lead to heme-fluorophore distance distributions that, in the main, compare quite well with the experimental results. The models correctly predict the effects of salt and pH on the denatured ensemble of cytochrome c (22, 31) and shed new light on the interplay between native structure seeking funneled interactions and electrostatics.

Results

Experimental Data.

We have examined TRFET from a dansyl fluorophore (Dns) to the Fe(III) heme in six variants of Saccharomyces cerevisae iso-1-cytochrome c under GuHCl- and acid-denaturing conditions (21–23). Labeling sites at residues 4, 39, 50, 66, 85, and 99 sample various regions in the protein, permitting comprehensive analysis of the denatured states. The observed nonexponential kinetics reflect distributions of donor (D)–acceptor (A) distances characteristic of the heterogeneous ensembles. The probability distributions of logarithmically spaced rate constants, P(k), were extracted directly from experimental data I(t) (Eq. 1) and then converted to the probability distributions of a range of distances P(r) (Eq. 2). The R₀ value of 39 Å for the dansyl–heme pair limited the D-A distances that can be measured. At longer distances (> 1.5 R₀), the energy transfer efficiency is extremely low and nearly identical rate constants are observed despite the different Dns-heme separation distances. Therefore, single bars at 59 Å in the experimental P(r) distributions represent the structures with r ≥ 59 Å.

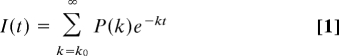Our TRFET data have revealed considerable diversity in both denatured ensembles: there are several distinct populations of different structures, some extended and others compact. A significant population of structures with relatively short D-A distances even under strongly denaturing conditions is evidence for favorable interactions within unfolded polypeptides. Comparison of experimental P(r) distributions for the GuHCl- and the acid-denatured protein suggests that the latter polypeptide ensemble is more compact.

In our simulations we have tracked distances between the heme iron and the C^α atom of each of the six labeled residues. To account for the length of the Dns linker in the experimental data, 6 Å were added to these distances. As was done for TRFET data, all of the structures with r ≥ 59 Å were placed into a single bin. The fluorescence decay curves were calculated from theoretical distributions P(r) according to Eq. 1.

The GuHCl-Denatured Ensemble.

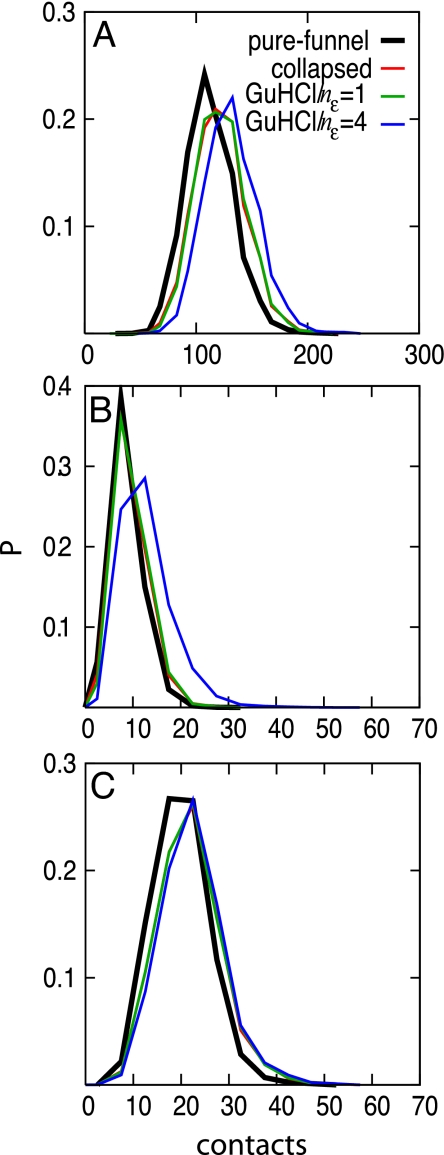
We examined several models that include varying tendencies for nonnative hydrophobic collapse and various strengths of electrostatic forces in addition to forces that are energetically funneled toward the native state (29–30). The potentials were designed such that increasing the magnitude of the electrostatic contribution causes the protein to expand, thereby decreasing the effects of hydrophobic collapse. Electrostatic effects are included using a Coulomb potential with a Debye screening term to account for salt effects (32–33). The electrostatic contribution is scaled by adjusting the parameter n_ε (see Materials and Methods for more information). Simulations using the simple pure-funnel (structure-based) model yield fewer contacts than do models based on funneled landscapes that also include generic collapse (Fig. 1A). A further increase in the number of contacts is seen upon increasing the magnitude of the electrostatic term by changing n_ε from 1 to 4. The increase in the total number of contacts largely reflects an increased number of charge-charge contacts (Fig. 1B). There is no significant change in the number of hydrophobic-hydrophobic contacts due to varying n_ε (Fig. 1C). Despite the corresponding increase in the number of contacts with increased electrostatic contribution, all of the simulations predict a similar radius of gyration (27 ± 3 Å). This value agrees with the value extracted from small-angle X-ray scattering experiments (19).

Fig. 1.

Probability distributions for (A) the number of total contacts, (B) the number of charge-charge contacts, and (C) the number of hydrophobic-hydrophobic contacts. Contacts are defined between those C^αs that are >2 residues apart and that approach closer than 10 Å.

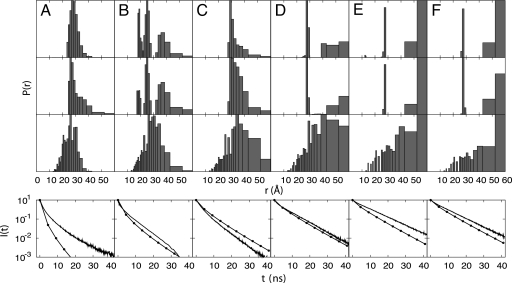
Detailed distance distributions extracted from TRFET data clearly demonstrate the heterogeneity of unfolded ensembles (21–23). Although the pure-funnel model correctly predicts the presence of more extended structures, it fails to predict many of the partially collapsed states. The effects of nonnative hydrophobic collapse and electrostatics are needed to generate the heterogeneous unfolded ensemble observed experimentally. Fig. 2 shows P(r) distributions calculated from a simulation that qualitatively agrees with the experimental data. The fidelity of the simulation to observation is more obvious when the fluorescence decay data are used directly for the comparison than when the inferred distance distributions are compared (Fig. 2).

Fig. 2.

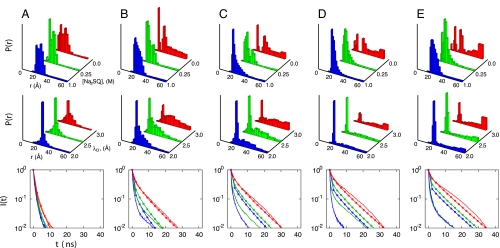
Heme–residue distance probability distributions and the corresponding fluorescence decay curves for the GuHCl-unfolded ensemble involving residues (A) 4, (B) 39, (C) 50, (D) 66, (E) 85, and (F) 99. From top to bottom are: the distributions extracted from TRFET measurements under conditions favoring heme misligation in 3.0 M GuHCl at pH 7 (23), the distributions extracted from TRFET measurements without misligation in 3.0 M GuHCl and 0.15 M imidazole at pH 7 (23), the distributions calculated from simulations based on the GuHCl model with n_ε = 4, and the fluorescence decay curves. The experimental decay curves obtained at 3.0 M GuHCl without misligation are shown in solid lines and the decay curves calculated using the GuHCl model with n_ε = 4 are shown in lines with dots. See Materials and Methods for more information.

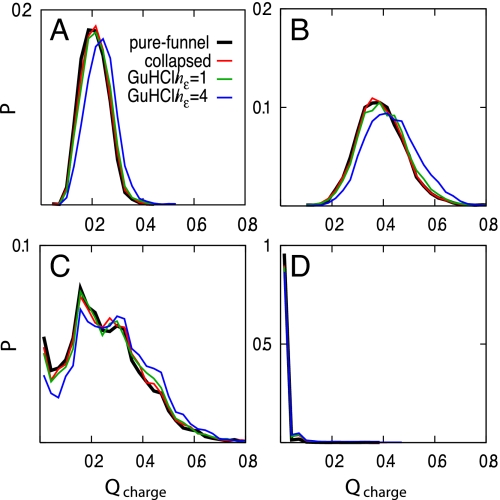
We introduce an order parameter, Q_charge, which is a distance similarity measure restricted only to native charge–charge contacts less than 10 Å. The probability distribution of Q_charge suggests that the electrostatic contributions help steer the denatured ensemble to the native state (Fig. 3). In contrast, generic hydrophobic collapse alone does not increase the similarity of the unfolded ensemble to the native state. However, the electrostatic forces primarily help order the unfolded ensemble for short-range interactions (3≤ i−j <5) but play little role for medium- (5≤ i−j <12) and long-range (i−j ≥12) interactions. It appears that local segments of the protein chain are partially guided by electrostatic forces toward a native-like conformation.

Fig. 3.

Probability distributions of Q_charge for (A) all native contacts, (B) short-range native contacts (3≤ i−j <5), (C) medium-range native contacts (5≤ i−j <12), and (D) long-range native contacts (i−j ≥12).Q_charge is a distance similarity measure of charge-charge contacts that are less than 10 Å in the crystal structure analogous to the folding reaction coordinate Q.

Histidine Misligation in the GuHCl-Denatured Ensemble.

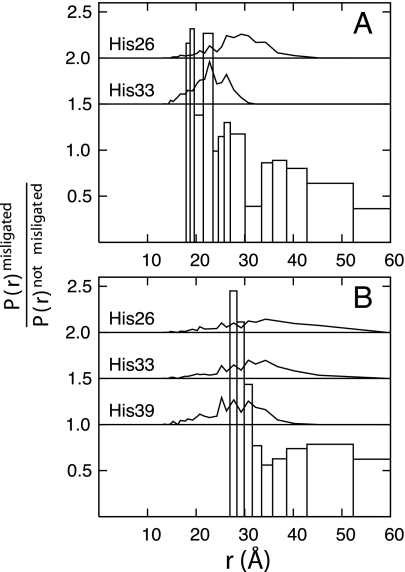
In GuHCl solutions at pH 7, there are three histidine residues in iso-1-ferricytochrome c (His-26, His-33, and His-39) that can bind the heme, replacing the native Met-80 ligand (34). The addition of imidazole inhibits this misligation. We find that most of the heme-residue distance distributions are quite similar for unfolded ensembles with and without misligation (Fig. 2). However, the experimental P(r) distributions between the heme and residue 39 and residue 50 are sensitive to heme ligation and can be compared with simulation. We carried out independent simulations of the three distinct histidine-misligated proteins by introducing a harmonic potential between each of the histidines and the heme. Fig. 4 shows the ratio of the experimental P(r) distributions including misligation effects to the distributions computed without misligation and the P(r) distributions computed for each of the simulated histidine-misligated structures. Experimentally, the misligated unfolded ensemble has an increased probability for short distances between the heme and residue 39 compared with the nonmisligated unfolded ensemble (Fig. 4A). These distances (19 and 24 Å) are most consistent with the maximally probable distance predicted for misligation by His-33 but are less consistent with misligation by His-26. The heme to residue 50 distributions primarily support the existence of misligation by His-39 but do not rule out misligation by His-33. These results are consistent with folding studies of the structurally similar horse heart cytochrome c (a protein that lacks His-39) that have been interpreted in terms of His-33-misligation (35, 36). Moreover, studies of iso-1-ferricytochrome c mutants with single histidine residues suggest that His-26, His-33, and His-39 have comparable heme binding affinities at pH 7 (37, 38). It is likely, then, that the increased population of shorter heme-Dns distances in the presence of misligation (pH 7) can be attributed primarily to binding of His-33 and His-39 to the ferriheme.

Fig. 4.

Ratios of the P(r) distributions extracted from TRFET measurements with misligation to those without misligation are shown by using open bars for (A) the heme to residue 39 pair and (B) the heme to residue 50 pair. The heme-residue P(r) distributions from simulations in which a histidine is permanently misligated to the heme are shown within the plot using black lines. No P(r) distributions for His-39-misligated structures are shown for the heme to residue 39 pair because cysteine mutation and Dns labeling prevent misligation.

Acid-Induced Denatured Ensemble.

The ferricytochrome c energy landscape changes significantly under acidic conditions as the net positive charge on the protein increases from +8 to +23. The TRFET data of the acid-induced unfolded protein (Fig. 5) show that the polypeptide ensemble is composed of a more diverse range of structures under these conditions than found in the GuHCl-induced unfolded state (22). We simulate the salt effects in the acid-induced unfolded ensemble by varying the Debye screening factor. Under high salt conditions (low Debye screening factor) the simulations yield a highly collapsed protein, or molten globule, with P(r) distributions whose peak is close to the native separation. Similar to experiments, simulations show that there is a small population of extended structures in the molten globule ensemble. At low salt concentrations, charge repulsion increases the variety of structures found, as both collapsed and extended conformations become populated. The heme to residue distributions of the simulated acid-induced unfolded ensembles are qualitatively similar to those inferred from experiment (Fig. 5) and the agreement is also apparent in the directly measured fluorescence decay curves (Fig. 5).

Fig. 5.

Heme–residue distance probability distributions and the corresponding fluorescence decay curves for the acid-induced unfolded ensembles for labeling sites at: (A) 4, (B) 39, (C) 50, (D) 66, and (E) 99. From top to bottom are: the distributions extracted from TRFET measurements at pH 2 and different Na₂SO₄ concentrations (22), the distributions calculated from simulations based on the acid/salt model with n_ε = 4 using different Debye screening factors (Å), and the corresponding fluorescence decay curves. The colors of the decay curves correspond to the colors used in the above P(r) distributions with experimental data shown in solid lines and simulation results shown in lines with dots. See Materials and Methods for more information.

Discussion

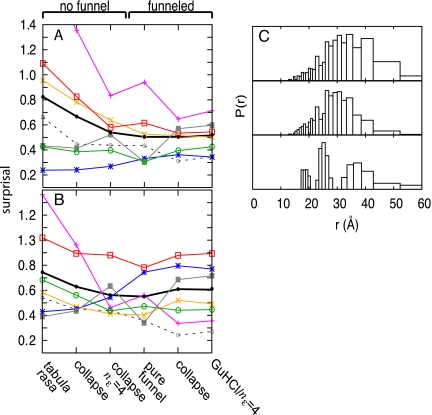
Nonspecific electrostatic effects, hydrophobic collapse, and funneled interactions on the energy landscape synergistically improve the agreement of the P(r) distributions calculated from the simulation with those extracted from TRFET experiments. The effect of adding structure-based potentials to the tabula rasa model is especially clear when comparing some specific distance distributions, such as that for the heme to residue 39 pair. The shorter distance ranges (<30 Å) are not populated to the extent observed in TRFET experiments if the funneling interactions of the folding landscape are not included (Fig. 6). A quantitative assessment of the agreement for all six P(r) distributions is shown using an information theoretic surprisal measure. The surprisal averaged over each heme-residue pair, but restricted to pairs having distances <30 Å, makes clear that funneled energetic terms are necessary to generate appropriately collapsed structures. The surprisal also shows that models based on funneled energy landscapes agree more closely with experiment than do models based on nonfunneled, random polymer chains (Fig. 6 A and B). Furthermore, the models that lack a collapse potential score better for residues in the C-terminal end, particularly the heme to residue 85 distribution. At pH 7, the C-terminal sequence has a high density of polar and charged residues that would not drive hydrophobic collapse. Indeed, increasing the electrostatic contribution, by increasing n_ε, causes the C-terminal end to fray. In contrast, the surprisal measure for the distance of heme to residue 50, which is in a more hydrophobic region of the sequence, decreases for any model in which there is an increase in hydrophobic collapse. Inhomogeneously distributed regions of polar/hydrophobic and positively/negatively charged residues are responsible for the observed heterogeneity of the GuHCl-unfolded ensemble.

Fig. 6.

A surprisal measure is used to compare the results of several models to the distributions determined from TRFET measurements (A) with misligation and (B) without misligation. Surprisal is a measure of the similarity between two distributions, in which small values imply agreement. The surprisal is plotted as lines for each pair distribution involving residues: 4 (*), 39 (×), 50 (+), 66 (□), 85 (■), and 99 (○). The average surprisals of all heme-residue pairs are plotted as black lines. The average surprisals for all pairs, at distances <30 Å, are plotted as dashed lines. See Materials and Methods for further description of the models and of the surprisal calculation. (C) Heme to residue 39 P(r) distributions calculated from simulations based on the nonfunneled, collapse/n_ε = 4 model (Top), the funneled GuHCl/n_ε = 4 model (Middle) and the distribution extracted from TRFET measurements without misligation (Bottom).

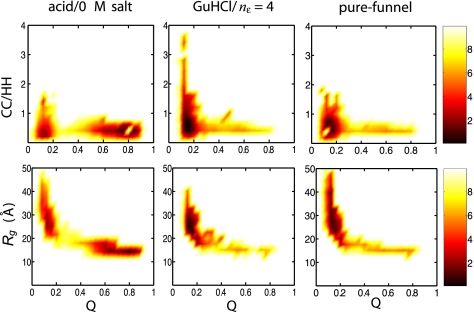
The acid-induced unfolded ensemble exhibits a broader range of structures than the GuHCl-denatured ensemble, suggesting differences in its energy landscape. The driving force for the formation of acid-induced unfolded structures is the chemical frustration caused by increasing the net charge on the protein as a result of protonation. Extended structures arise from like charge repulsion, which causes frustration and opposes the funneled nature of the energy landscape. The differences in unfolded ensembles can be visualized by using free energy surfaces as a function of the folding reaction coordinate Q and other structural measures as seen in Fig. 7. Q is a distance similarity measure that is related to the fraction of native contacts and is close to 1 if the topology of the configuration is similar to that of the native state. The reaction coordinate Q has been used in several studies (25, 27), including one on cytochrome c (29) in which a model with a perfectly funneled energy landscape was shown to predict the same sequential ordering of folding units as inferred by hydrogen exchange (39). The unfolded structures (Q ∼ 0.1) generated using each model are extended and dispersed, as evidenced by their radii of gyration (Fig. 7), and they contract to a near native size at the folding transition state (Q ∼ 0.3). Consistent with small-angle X-ray scattering data, the simulated GuHCl-denatured ensemble is composed of extended structures (R_g > 20 Å), whereas the simulated acid-unfolded ensemble contains both collapsed and extended structures (R_g between 15 and 40 Å) (19, 20). The more compact structures in the acid-unfolded ensemble can have a high fraction of native contacts with Q ranging between 0.5 and 0.9.

Fig. 7.

Free energy surfaces in units of k_BT calculated from simulations based on the acid/0 M salt, GuHCl with n_ε = 4, and pure-funnel models. The free energy surfaces are plotted as a function of the folding reaction coordinate Q (related to the fraction of native contacts)and either the ratio of the number of charge-charge contacts (CC) to hydrophobic-hydrophobic contacts (HH) (Upper) or the radius of gyration (Lower).

The ratio of charge–charge to hydrophobic–hydrophobic contacts shows that the residual structure in the unfolded ensemble generated from the pure-funnel model is mainly due to hydrophobic contacts (Fig. 7). By including electrostatic contributions, the unfolded ensemble reorganizes, owing to an increased number of attractive charge-charge interactions (Fig. 1). Electrostatics affect only local segments of the protein chain because R_g does not change significantly. These electrostatic interactions steer the protein chain as it collapses and they may even drive the preliminary stages of folding as evidenced by Q_charge (Fig. 3). However, because of repulsive electrostatic interactions, the ratio of charge-charge to hydrophobic-hydrophobic contacts is lower in the acid-unfolded ensemble than in the GuHCl-denatured ensemble.

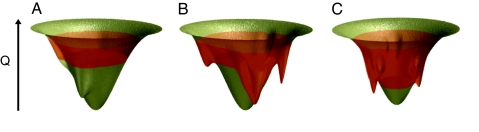
We have demonstrated that there are specific patterns of structures in chemically denatured ensembles of cytochrome c. The heterogeneous distribution of hydrophobic and polar/charged residues results in nonrandom coils with varying amounts of collapse or extension in different regions of the sequence. Denatured ensembles have pockets of local, native-like structure, often guided by electrostatics, but these ensembles are globally unstructured above the folding temperature or at GuHCl concentrations greater than the unfolding midpoint. The destabilizing effects of GuHCl cause the protein to populate higher energy regions of the folding funnel; however, stabilizing nonnative interactions due to misligation can cause rather deep traps (Fig. 8 A and B). Below the folding midpoint or temperature, acidic conditions at low salt concentration can be used to induce unfolding. The structures in the acid-unfolded ensemble are diverse because the funneled energy landscape responsible for folding is opposed by chemically frustrating electrostatic effects from protonation that cause unfolding (Fig. 8). The success of these largely structure-based models in predicting the properties of chemically denatured ensembles suggests that features of a funneled energy landscape are still important even in the unfolded state. The interplay of nonnative hydrophobic and electrostatic effects with the funneled energetics of the landscape determines the properties of unfolded ensembles in agreement with those determined by TRFET experiments.

Fig. 8.

Representations of the folding energy landscapes for cytochrome c. The height corresponds roughly to the structural similarity to the native state, whereas the width corresponds to entropy. In all cases, the folding energy landscape is highly funneled, even in the denatured region. Nevertheless, the region of the funnel that is populated, shown in orange, varies significantly with solvent conditions. (A) The GuHCl-denatured ensemble at pH 7 with imidazole to inhibit misligation. GuHCl acts to destabilize native state contacts causing the ensemble to populate higher regions of the funnel. Electrostatic forces are highly screened and do not cause significant traps, allowing the funnel to be fairly smooth. (B) The GuHCl-denatured ensemble at pH 7 with several large traps due to misligation by histidine residues. These misligated intermediates can be structurally similar to the native state as indicated by the depth of their minima in the funnel. (C) The acid-induced unfolded ensemble with modest traps caused by chemical frustration. These frustrated traps are due to nonnative electrostatic interactions that result from protonation of residues at low pH.

Materials and Methods

To distinguish and quantify the various interaction effects, we simulate several models of the unfolded ensembles of cytochrome c. We start with a perfectly funneled energy landscape Hamiltonian based on the native topology alone. We call this the pure-funnel model and the potential is written as H_{pure−funnel} = V_back + V_contact + V_heme. The backbone potential, V_back, does not contain funneled energetic terms, rather it merely acts to maintain backbone geometry (bond angles and distances) and accounts for excluded volume. The contact potential, V_contact, includes attractive Gaussian well potentials derived from the native X-ray structure summed over all C^αs and C^βs for the protein–protein contacts. In addition, there are explicit interactions between the C^αs and the heme pseudoatoms that model the heme-protein contacts. The native structure stabilizing term, V_contact, is not a simple pair potential but contains 40% nonadditivity (in the native-state conformation). The nonadditivity accounts for cooperative effects that arise from preaveraging over side chain and solvent interactions. The size of the nonadditivity we employ has been shown to account quite well for protein folding barriers and was used in our earlier study of the local unfolding events near the native ensemble (29). The backbone and interaction potentials have been described in detail (29–31). The potential describing the heme, V_heme, includes 8 harmonic constraints and a planarity potential that maintains the square-planar geometry of the five heme pseudoatoms and two harmonic constraints to mimic the covalent bonds. We also study another model that contains, in addition to funneled contact terms, a weak potential that leads to a generic hydrophobic collapse of the protein: V_Rg = 0.01(Rg−Rg^N)² where Rg^N is the radius of gyration of the native state. The Hamiltonian of the hydrophobic collapse model is: H_collapse = H_{pure−funnel} + V_Rg. A long-range electrostatic potential, with charges placed on the C^β atoms, was included to describe denaturation induced by GuHCl and acid which changes the charge-charge interactions:

Ion screening effects are accounted for using a Debye screening term (e^{(−r_ij/λ_D)}). The charge on a residue is +1, −1, or 0, depending on the identity of that residue, r_ij is the distance between C^βs of residues i and j, and γ is the strength of a native contact. Because the funneled energy terms already implicitly contain native electrostatic effects, we chose a dielectric constant so that the long-range and nonnative electrostatics have a more dominant effect in a manner similar to that described (31, 32). The dielectric constant (ε = 30) is chosen to be smaller than that for water but is still significantly larger than the value of 3.5 calculated for ferricytochrome c (33). The long-range electrostatic potential is scaled by the amount of collapse to avoid overcompensating for electrostatics implicitly included in the contact terms that are funneled to the native structure. This model allows for the interplay of electrostatic effects and hydrophobic collapse on the energy landscape of the unfolded ensemble and also allows for a nearly unfrustrated energy landscape near the native ensemble. The Hamiltonian used for the GuHCl unfolded ensemble simulations is given by: H_GuHCl = H_{pure−funnel} + V_Rg + n_ε × V_elec. The Hamiltonian used for the acid/salt unfolded ensemble simulations is: H_acid/salt = H_{pure−funnel} + V_Rg + n_ε × (V_elec + V_prot). The values of λ_D theoretically correspond to the experimental ionic strengths and are set to 1.7 Å for 3.0 M GuHCl and either 2.0, 2.5, or 3.0 Å for 1.0, 0.25, and 0 M Na₂SO₄, respectively. n_ε scales the contribution of electrostatic effects on the ensemble. The protonation potential, V_prot, accounts for the energetic frustration reflected in the destabilization of favorable native contacts due to protonation and is given by:

(31). ε_ij(r_ij) is a unit-depth Gaussian well contact potential between residues i and j. The factor 0.02 was determined by first calculating the electrostatic energy change upon protonation obtained by placing charges on the C^βs in the native conformation. The total destabilization energy distributed among all of the contacts involving protonated residues is then ≈0.02. We also simulated random polymer models that are not based on funneled energy landscapes. The nonfunneled tabula rasa model contains excluded volume and backbone connectivity only: H_tabularasa^n.f.=V_back+V_heme. Models with generic collapse (and no funneling) along with electrostatics are used: H_collapse^n.f.=V_back+V_heme+V_Rg, H_{collapse/elec}^n.f.=V_back+V_heme+V_Rg+n_ε×V_elec.

We chose the temperature for the simulations of the unfolded ensembles to be greater than T_f such that the free energy difference between the folded and unfolded basins is 5 k_BT and the temperature for the simulations of the acid/salt ensembles to be below T_f such that the free energy difference between the high salt molten globule basin and its unfolded basin is −5 k_BT.

The folding order parameter Q measures a structure‘s similarity to the native crystal structure and is given by:

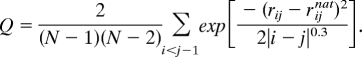The summation runs over all C^α residues, r_ij^nat is the distance between C^αs in the crystal structure, and N refers to the number of residues. The measure Q_charge is analogous to Q but the summation is restricted to charge-charge contacts.

A quantitative comparison of the agreement for the P(r) distributions is shown using an information theoretic surprisal measure:

Surprisal is a measure of the similarity between two distributions and is related to entropy. If two distributions are the same then the surprisal is zero; surprisal increases as the similarity between the two distributions decreases.