Demographic models and IPCC climate projections predict the decline of an emperor penguin population

Abstract

Studies have reported important effects of recent climate change on Antarctic species, but there has been to our knowledge no attempt to explicitly link those results to forecasted population responses to climate change. Antarctic sea ice extent (SIE) is projected to shrink as concentrations of atmospheric greenhouse gases (GHGs) increase, and emperor penguins (Aptenodytes forsteri) are extremely sensitive to these changes because they use sea ice as a breeding, foraging and molting habitat. We project emperor penguin population responses to future sea ice changes, using a stochastic population model that combines a unique long-term demographic dataset (1962–2005) from a colony in Terre Adélie, Antarctica and projections of SIE from General Circulation Models (GCM) of Earth's climate included in the most recent Intergovernmental Panel on Climate Change (IPCC) assessment report. We show that the increased frequency of warm events associated with projected decreases in SIE will reduce the population viability. The probability of quasi-extinction (a decline of 95% or more) is at least 36% by 2100. The median population size is projected to decline from ≈6,000 to ≈400 breeding pairs over this period. To avoid extinction, emperor penguins will have to adapt, migrate or change the timing of their growth stages. However, given the future projected increases in GHGs and its effect on Antarctic climate, evolution or migration seem unlikely for such long lived species at the remote southern end of the Earth.

A major challenge in ecology and conservation is to project the ecological responses of future climate changes (1, 2), using the reported effects of recent climate change on ecological processes. Recently, Thomas et al. (3) predicted that future climate change may cause the extinction of between 15% and 37% of species by 2050, based on species-specific climate envelopes. However, they project 0% species extinction risk for the ice biome, although there is clear evidence of dramatic changes in polar ecosystems related to anthropogenic warming, which may lead to extinctions [e.g., penguins in the Antarctic Peninsula (4), polar bears in the Arctic (5)].

To project a population's response to future climate change one must (i) quantify the effects of climate on vital rates, (ii) project future climate conditions (as we do here with GCM climate models), and (iii) integrate these effects into population models. Most of the literature on population-climate studies has focused on one part of the life cycle [e.g., changing timing of life history in relation to climate conditions (6, 7)], because of the difficulty of measuring climate influences on life history traits over the entire life cycle (8). Few studies have adressed the population response to observed climate change (but see refs. 9–11); even fewer have predicted the population response to future changes (but see ref. 5).

Based on knowledge of the effects of sea ice on the vital rates and population of emperor penguins (12, 13), we develop a stochastic population model to estimate population growth rates and probabilities of quasi-extinction under projections of future ice conditions from climate models used in the latest IPCC Fourth Assessment Report (14).

Emperor penguins reproduce during the harsh Antarctic winter in dense colonies distributed around Antarctica. Sea ice is a key breeding and feeding habitat for emperor penguins. Colonies are formed on sea ice many kilometers from the open sea, and breeding emperors make foraging trips between the colony and areas of open water during the entire incubation and chick rearing periods (15). In years with dense and extensive sea ice cover, foraging trips are longer, energetic costs for adults are higher, and offspring provisioning is lower (16), resulting in lower hatching success (12). Alternatively, absence of, or early break-up of, the winter sea ice holding up the colony may cause low breeding success (17). Sea ice extent during winter also affects the abundance of prey for emperor penguins. Winters with extensive sea ice enhance krill abundance (18), and emperor penguins mainly feed on fish species that depend on krill and other crustaceans (19, 20). In accordance with this, years with reduced sea ice extent coincide with reduced adult survival rates (12). The effects of sea ice on vital rates of the emperor penguin are thus complex (4, 21) and affect the dynamics of its populations.

A dramatic example of such effects, which provides a key element in our analysis, occurred in Terre Adélie between 1972 and 1981. A sudden decrease in winter sea ice extent during several consecutive years, by ≈ 11% on average, coincided with an abrupt decline of the population, by ≈50% (13), and these abrupt changes were attributed to a regime shift (22) (see Fig. S1). Analyses of ice core data (23) suggest a change in meridional atmospheric circulation during the 1970s, bringing more moisture from warm subtropical sources to the Antarctic coast, possibly causing the highest winter air temperature and the lowest winter SIE observed in Terre Adélie during the regime shift (22).

Results and Discussion

We developed a stochastic version of a stage-classified population model (13) (see Materials and Methods) to determine the effects of a fluctuating sea ice environment on the stochastic population growth rate. Following previous studies (see review in ref. 24) we classified the environment into 2 distinct states: outside (1962–1971; 1982–2006) and inside (1972–1981) the regime shift period (see Materials and Methods). We will refer to these as “normal” and “warm” conditions, respectively. The environment follows a 2-state Markov chain that determines the frequency and duration of warm conditions (see Materials and Methods).

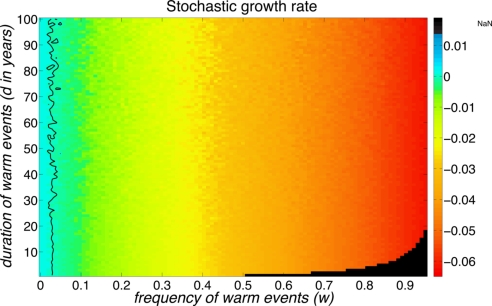
Fig. 1 shows the resulting stochastic growth rate as a function of the frequency and duration of warm events. It decreases dramatically as the frequency increases. The duration (reflecting the autocorrelation of the environment) has little effect, as expected for such long-lived species. A frequency greater than w ≈ 0.03 produces a negative long term growth rate. Thus, if climate change increases the frequency of warm events, it will reduce the population viability of the emperor penguin.

Fig. 1.

Stochastic growth rate (logλ_s) as a function of the frequency w and mean duration d of warm events (in years). It was calculated from a stochastic model with 2 states: normal and warm environmental conditions. The contour denotes logλ_s = 0. The frequency of warm events must satisfy d >

. The dark area indicates impossible combinations of w and d.

Although climate models differ on the sign of Antarctic sea ice trends at the end of the 20th century (25) (see SI Text and Table S1), suggesting a strong influence of natural variability, nearly all models project that sea ice will shrink in future global warming scenarios (26). To project the consequences of this decline, we used a 3-step approach (as in ref. 5), which we will describe first in outline and later in more detail. First, we obtained forecasts of sea ice from a set of IPCC climate models from the CMIP3 archive (see Materials and Methods and SI Text). Second, we classified each year as warm or normal, by comparing the proportional decline in ice in that year to a specified SIE threshold value. The result is a binary sequence of warm and normal years, produced by each climate model, for the rest of the century. These sequences were translated into forecasts of the frequency of warm events, using nonparametric smoothing (5, 27). Finally, the frequencies were used to produce stochastic population projections. Therefore, the analysis depends on the set of climate models, on the sea ice forecasts, and on the SIE threshold defining a warm event.

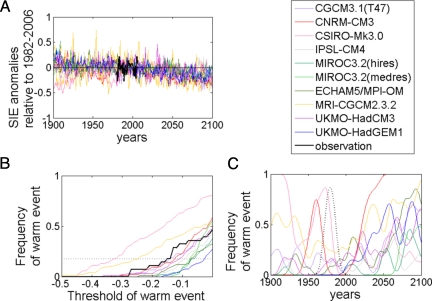
The sea ice forecasts were extracted from the output of a set of 16 IPCC models over the emperor penguin foraging sector (16) in Terre Adélie, i.e., sector 120°E–160°E (see SI Text and Fig. S2). The climate models were forced with the “business as usual” forcing scenario A1B, which describes a future world of very rapid economic growth that depends on fossil and nonfossil energy sources in balanced proportions. Under this scenario, CO₂ levels double from the preindustrial level of 360 parts per million (ppm) to 720 ppm by 2100. We selected 10 of these models, in which the statistical properties of SIE match with those of the satellite observations (28, 25) (see Fig. S3), for analysis. We transformed the SIE from each model to proportional anomalies (SIEa), measured relative to the mean from 1982–2006, as shown in Fig. 2A for each of the 10 models.

Fig. 2.

Sea ice anomolies and warm events. (A) Proportional change in winter sea ice extent anomalies (SIEa) in Terre Adélie (sector 120°E-160°E), measured relative to the mean over the period 1982–2006, produced by 10 coupled IPCC climate models from 1900 to 2100 (for line colors, see legend). (B) Frequency of warm events calculated from the backward projections of SIEa for 10 IPCC climate models from 1900 to 2006 (color lines) and calculated from SIEa satellite observations from 1979 to 2006 (black line) as a function of the threshold defining a warm event. The frequency of warm events experienced by emperor penguin between 1952 and 2006 is 0.18, and is represented by the dotted line. (C) Frequency of warm events from 1900 to 2100 calculated from the SIEa produced by 10 IPCC climate models with the most conservative warm event threshold of −0.15. The dotted black line represent w_t calculated from the sequence of warm and normal events define by the observed regime shift from 1952 to 2006.

We defined a warm event to occur whenever SIEa drops below a specified SIE threshold. Fig. 2B shows the frequency of warm events, as a function of the SIE threshold, for model projections and for observations. To identify an appropriate SIE threshold, we note that the 56-year penguin observation period includes 10 warm events, for a frequency of w̄_o = 10/56 = 0.18 (dotted line of Fig. 2B). Thus, for each climate model, we calculated the SIE threshold that produced a frequency of w̄_o = 0.18 over the observation period; these thresholds range from −0.32 for model IPSL-CM4 to −0.02 for model UKMO-HadGEM1, with 50% of the threshold values falling in the range [−0.14,−0.07]. The same calculation applied to SIE from satellite data yields a threshold of −0.15. Thus, we used a range of SIE threshold values from −0.07 (the most generous) to −0.15 (the most conservative). Each model, and each SIE threshold, generates a binary time series of warm and normal years for the rest of this century. We used nonparametric binary regression (27) to transform the binary time series into probabilities w_t of a warm event (see Fig. 2C for the conservative threshold of −0.15). All 10 climate models predict increased frequencies of warm events by the end of this century.

Finally, using the probabilities w_t, we generated 1000 stochastic population projections for each of the 10 climate models (thus 10000 population trajectories), and calculated the probability of quasi-extinction (defined as a decline by 95%) occurring by 2100.

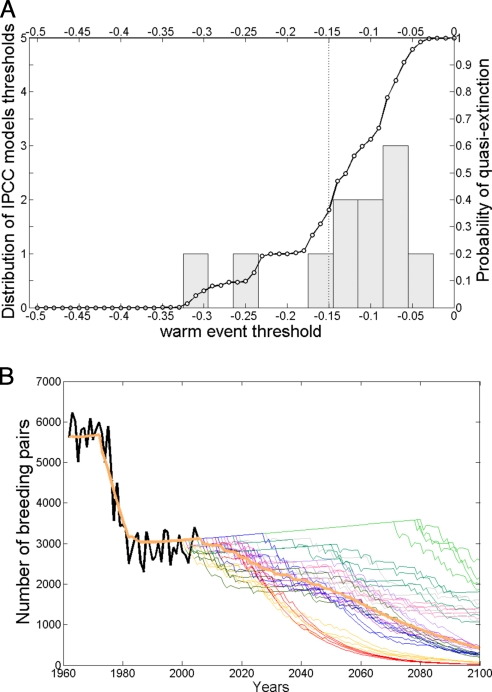
Fig. 3A shows the results. There is a high probability of quasi-extinction by the end of the century (0.36 and 0.84 for thresholds of −0.15 and −0.07, respectively). The median of the 10,000 population projections is nearly constant between 2000 and 2006, which is in good agreement with observed data (Fig. 3B). After 2006 it decreases slowly, and then more rapidly after 2018, to ≈400 breeding pairs by 2100 for the most conservative threshold. This is a decline of 93%. Each stochastic population trajectory shows a different pattern with periods of relative stability, gradual decline, and abrupt decrease. Some decline late [e.g., trajectories from climate model MIROC3.2(medres)] whereas others decline early (e.g., trajectories from climate model CNRM-CM3). By the end of this century, all of the population realizations that had not become quasi-extinct by 2100, were at that point declining strongly.

Fig. 3.

Quasi-extinction and population projection. (A) Probability of quasi-extinction (a decline of 95% or more) of the emperor penguin population in Terre Adélie by 2100, as a function of the warm event thresholds. The distribution of warm event thresholds calculated from Fig. 2B for the 10 IPCC models is represented by the gray bars, and warm event threshold calculated from Fig. 2B for the satellite observation by the vertical dotted line. The probability of quasi-extinction varied from 0.36 to 0.84 over the range of likely thresholds [−0.15; 0.07]. (B) Observations and projections of the emperor penguin population. The thick dark line is the observed number of breeding pairs. The thick orange line from 1962 to 2000 is the projected number of breeding pairs based on the observed sequence of warm events. The thick red line from 2005 to 2100 is the median of 10,000 stochastic projections based on the forecasts of SIEa produced by the 10 IPCC models. To give a sense of the variability in these projections, 30 projections from 2005 to 2100 (three for each climate model) are shown; line colors as in Fig. 2.

These projections are based on a model that includes the entire life cycle and its response to climate (8), integrated with projection of future climate variability. Analyses that include only part of the life cycle (for example, see ref. 29) may reveal some aspects of population response, but cannot predict future trends and variability in a stochastic environment.

Conclusions

We conclude that if winter sea ice extent declines at the rates projected by IPCC models, and continues to influence emperor penguin vital rates as it did in the second half of the 20th century, the emperor penguin population in Terre Adélie will decline dramatically by 2100. Our conclusions are robust for the following reasons. First, our projections of sea ice are based on 10 diverse IPCC climate models. Second, our 2-state environment model assumes that future warm events have no greater impact on penguins than did the warm events during the 1970s. The IPCC models, however, predict that warm years will become warmer; a modified model taking that into account would only increase the probability of quasi-extinction (see SI Text and Fig. S4). Finally, our demographic model is well supported by the data (13). Including other demographic processes, such as density dependence (30), or sex ratio effects, would increase the probability of quasi-extinction.

To avoid extinction, the emperor penguin must adapt by microevolutionary changes or phenotypic plasticity [e.g., by changing timing of their growth stages (2, 31)]. So far, the dates of arrival to the breeding colony and of egg laying have not changed in emperor penguins as they have in other Antarctic seabirds in Terre Adélie (32), suggesting a slow rate of adaptation. Emperor penguins may respond slowly to new selective pressure due to their long generation time (2, 33). The geographical range of Antarctic penguins may shrink following climate warming because the continent limits their movement south. In the Antarctic Peninsula, where warming has been the most pronounced during the second half of the 20th century (34), the northernmost emperor penguin population decreased from 150 breeding pairs in 1950s to only a few breeding pairs today (35). The southernmost emperor penguin populations (≈25% of the world population), in the Ross sea, are currently stable (36) as ice conditions there have slightly increased in recent years (37). As the Antarctic warms, the Ross sea may be the last sanctuary for emperor penguin populations. However, this region too will eventually experience reduced sea ice extent as concentrations of atmospheric GHGs increase further (26).

Materials and Methods

Demographic and climatic time series.

Monitoring of the emperor penguin breeding population and counts of fledged chicks started in 1952 and have been carried out every year since 1962 (12) (see Fig. S1). These data permit calculation of breeding success each year for the entire period. Mark-recapture data collected between 1971 and 1995 permit estimation of other vital rates including adult survival and the proportion of breeders (see ref (13). for more details on the methodology).

The regime shift is defined as a rapid change from one relatively stable state to another. We applied sequential t tests and F tests (38) to the times series of the number of breeding pairs and chicks (see Fig. S1) to detect the regime shift in mean and variance of the signal. Fig. S1 shows the regime shift between 1972–1981.

Data on future sea ice extent were obtained from 16 climate models participating in the IPCC assessment report (26) and averaged over the austral winter (July to September). The data are part of the World Climate Research Program's (WCRP's) Coupled Model Intercomparison Project phase 3 (CMIP3) multimodel dataset, which is available at www.pcmdi.llnl.gov/ipcc/about_ipcc.php. Table S1 summarizes information about these 16 IPCC models.

Stochastic stage-classified model.

The stage-classified model distinguishes breeding adults, nonbreeding adults, and 5 age classes of prebreeders. The demography is described by: n(t + 1) = A_tn(t), where the matrix A_t projects the population vector n from t to t + 1. Estimation of the vital rates and construction of matrices is described in ref. 13. The stochastic population growth rate was calculated by Monte Carlo simulation as:

using T = 50,000. If log λ_s ≤ 0, the population will become extinct. The initial population had the stable age distribution and the number of breeding pairs observed in 1962.

To take into account the effect of warm events such as occurred during the regime shift, we constructed a stochastic model with 2 states: normal and warm environmental conditions. We constructed projection matrices, A_N and A_W, for normal and warm conditions, as averages of annual matrices outside and inside the regime shift, respectively (see Table S2). At each time step, a matrix is selected according to a Markov chain with the transition matrix:

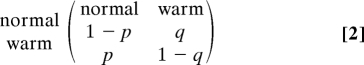where w is the transition probability from normal to warm conditions, and w the transition probability from warm to normal conditions. The long-term frequency and the average duration of warm events are respectively: w = p/(p + q) and d = 1/q.