The Indian Ocean Dipole and malaria risk in the highlands of western Kenya

Abstract

Epidemics of malaria in the East African highlands in the last 2 decades have often been associated with climate variability, particularly the El Niño-Southern Oscillation (ENSO). However, there are other factors associated with malaria risk and there is increased interest in the influences of the Indian Ocean Dipole (IOD), a climate mode of coupled ocean–atmosphere variability, on East African rainfall. This study explores the relationship between IOD and the number of malaria patients in 7 hospitals from 2 districts in the western Kenyan highlands, controlling for the effects of ENSO. We examined temporal patterns (1982–2001) in the number of malaria cases in relation to the dipole mode index (DMI), defined as the difference in sea surface temperature anomaly between the western (10°S-10°N, 50°-70°E) and eastern (10°S-0°, 90°-110°E) tropical Indian Ocean. We used Poisson regression models, adjusted for ENSO index Niño 3 region (NINO3), seasonal and interannual variations. The number of malaria patients per month increased by 3.4%–17.9% for each 0.1 increase above a DMI threshold (3–4 months lag). Malaria cases increased by 1.4%–10.7% per month, for each 10 mm increase in monthly rainfall (2–3 months lag). In 6 of 7 places, there was no evidence of an association between NINO3 and the number of malaria cases after adjusting for the effect of DMI. This study suggests that the number of malaria cases in the western Kenyan highlands increases with high DMI in the months preceding hospital visits.

Malaria is a major human health threat and occurs globally in tropical and subtropical regions. Despite the long history of efforts to control malaria, it remains a major threat to human health. Indeed the threat is increasing, a fact witnessed by an increase in malaria outbreaks in the East African highlands (≈1,500 m above sea level). Malaria outbreaks occurred sporadically in the highlands from the 1920s to the 1950s and became rare thereafter (1, 2). Since the 1980s, however, malaria epidemics have occurred with heightened frequency throughout the Kenyan highlands, causing serious mortality and morbidity (3, 4). Unlike their counterparts in malaria-endemic regions, recent studies have suggested that the residents of highland areas generally lack immunity to Plasmodium falciparum and are particularly vulnerable to malaria infection (5, 6). Possible reasons for the highland malaria include increased drug resistance (7, 8), a change in local malaria transmission resulting from land-use changes (9, 10), increased travel from endemic regions (11), and climate change, including rising temperature (12). These factors might create ideal conditions for a long-term trend for the spread of malaria, but they cannot fully explain interannual variations in the incidence of malaria epidemics.

Climate variability is suspected to be a major factor in the recent resurgence and interannual variations in the incidence of malaria (13, 14). In particular, the El Niño-Southern Oscillation (ENSO), a source of interannual climate variability, was strongly suspected to be related to epidemics in several highland regions in early 1998. ENSO can cause increases in temperature and rainfall, which in turn increase the availability of mosquito breeding grounds and malaria transmission (15, 16). However, factors other than ENSO are also clearly associated with malaria risk in the highlands, because epidemics also occur during weak ENSO periods. Mouchet et al. linked the 1994 malaria epidemic in the highland region of southwest Uganda to heavy rains in the preceding months, but a strong ENSO was not observed during this period (17). The highlands of western Kenya also experienced a malaria epidemic after heavy rains in late 1994 (18).

The Indian Ocean Dipole (IOD), also called the Indian Ocean Zonal Mode, was discovered in the late 90s and is another climate mode as a result of ocean–atmosphere interaction, which causes interannual climate variability in the tropical Indian Ocean (19, 20). The IOD characterizes sea surface temperature (SST) anomalies during this event, with warmer than normal SSTs over the western basin and cooler than usual SSTs in the eastern basin. The East African region receives above normal rainfall during positive IOD events, while rainfall in Indonesia and Australia is reduced, resulting in severe drought (19). Although the extent to which it is independent of ENSO has been debated (21), there is growing evidence that this air–sea interaction process is unique and inherent to the Indian Ocean (22–24). Historical data show that extreme dipole mode events have occurred 8 times in the past 50 years and that the strong ENSO in 1997 coincided with an IOD event (25).

The discovery of this dipole mode has the potential to improve long-term forecasting of rainfall anomalies and potential malaria epidemics in East Africa. Because malaria transmission is closely associated with rainfall, the extreme rainfall caused by the IOD has been suggested to be a cause of malaria epidemics in the East African highlands (26). The purpose of this study was to explore the relationship between the IOD and the incidence of malaria in the western Kenyan highlands, using time-series methodology controlling for the effects of ENSO.

Results

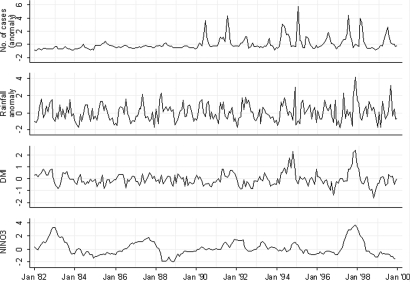
The time series of the number of malaria inpatients per month in the Kapsabet district hospital, the rainfall in Kapsabet, and the DMI and Niño 3 region (NINO3) during the study period are shown in Fig. 1(see Figs. S1 and S2 for other hospitals). Strong IOD events occurred in 1994 and 1997, during which the DMI peaked in August and October, respectively. Strong ENSO events were observed in 1982–83, 1986–87, and 1997–98. The Pearson's correlation coefficient between DMI and NINO3 was 0.36 during the study period. The rainfall in both districts generally showed the well-known bimodal seasonality, with the first peak from March to May (often referred to as the long rains), and the second peak from September to November (the short rains). In 1994 and 1997, exceptionally high rainfall was observed in both districts during the short rains, which preceded a sharp increase in the number of malaria inpatients in the Kapsabet district hospital (Fig. 1). In the Kisii district, an increase in both in- and outpatients after the 1997 short rains was also observed in the district hospital (Fig. S1) and in most of the other hospitals. No obvious increase in the number of hospital patients was observed after the 1994 short rains except in Kapsabet.

Fig. 1.

Time series for the number of malaria inpatients each month in the Kapsabet district hospital, the rainfall in Kapsabet, the dipole mode index (DMI), and the NINO3 SST anomaly (NINO3), 1982–1999. The number of malaria inpatients each month and rainfall are represented by a standardized anomaly relative to the 1982–1999 mean for each variable (The standardized anomaly was calculated only for descriptive analysis and raw data were used for regression analysis).

Relationship with DMI and NINO3.

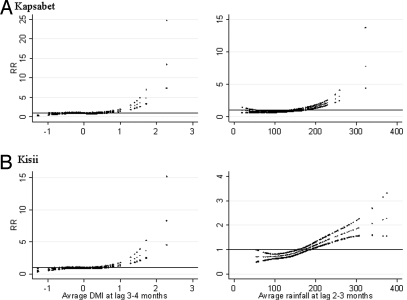
The generalized linear Poisson regression model revealed that an increase in the risk of hospital visits for malaria was associated with high DMI in most hospitals in both districts (Fig. 2, for inpatients in the Kapsabet and Kisii district hospitals; see Fig. S3 for other hospitals). There was no evidence of the association between the number of malaria cases and NINO3 except in Chepterit. The linear threshold model revealed that the number of malaria inpatients in the Kapsabet and Kisii district hospitals increased by 17.9% (95% CI: 13.7–22.4) and 15.0% (95% CI: 10.9–19.4), respectively for a 0.1 increase above the DMI threshold value, with a lag of 3–4 months (Table 1). The effect of DMI varied between locations from 3.4% to 17.9%.

Fig. 2.

Relationships between the relative risk (RR) of malaria scaled to the mean monthly number of inpatients in Kapsabet (A) and Kisii (B) district hospitals and the dipole mode index (DMI) (lag 3–4 months), and the rainfall (lag 2–3 months). The middle line in each graph shows the estimated spline curve, and the top and bottom lines represent 95% confidence limits.

Table 1.

Association between malaria cases and dipole mode index (DMI), NINO3 SST anomaly (NINO3), and rainfall: Effect estimates and thresholds

District	Hospital	In-/outpatient	DMI (lag 3–4 months)		NINO3 (lag 1–2 months)		Rainfall (lag 2–3 months)
			% change (95% CI)a	Threshold (95% CI)	% change (95% CI)a	Threshold (95% CI)	% change (95% CI)a	Threshold (mm) (95% CI)
Nandi	Kapsabet	In	17.9 (13.7, 22.4)	0.7 (0.5, 0.8)	—	—	10.7 (8.2, 13.2)	130 (120, 140)
		Out	9.6 (6.8, 12.4)	0.6 (0.5, 0.4)	—	—	2.9 (2.0, 3.9)	40 (30, 60)
	Mosoriot	Out	3.9 (1.7, 6.1)	−0.4 (−0.5, −0.3)	—	—	6.0 (4.1, 8.0)	100 (90, 110)
	Chepterit	Out	6.6 (3.3, 10.1)	0.5 (0.4, 0.6)	102.7 (34.4, 205.7)	3.5 (3.4, -)	6.1 (4.6, 7.6)	90 (80, 100)
Kisii	Kisii	In	15.0 (10.9, 19.4)	0.7 (0.6, 0.8)	—	—	4.9 (3.6, 6.2)	80 (70, 90)
		Out	17.6 (13.0, 22.4)	1.2 (1.1, 1.3)	—	—	1.4 (0.5, 2.2)	60 (50, 70)
	Keumbu	Out	—	—	—	—	—	—
	Iyabe	Out	3.4 (1.8, 5.0)	L	—	—	2.0 (0.7, 3.4)	L
	Itierio	Out	14.3 (8.0, 20.9)	1.0 (0.9, 1.1)	—	—	3.4 (1.9, 5.0)	120 (100, 130)

L, linear association between exposure and the number of cases.

^aPercent change in the number of malaria cases for each 0.1, 0.1, and 10 mm increase in DMI, NINO3, and rainfall above threshold.

Relationship with Rainfall.

The risk of hospital visits for malaria increased with rainfall in most hospitals in both districts (Fig. 2, for inpatients in the Kapsabet and Kisii district hospitals; see Fig. S4 for other hospitals). There appeared to be an increase in the number of malaria inpatients in the Kapsabet and Kisii district hospitals when the rainfall, with a lag of 2–3 months, was higher than the estimated threshold of 130 mm (95% CI: 120–140) and 80 mm (95% CI: 70–90), respectively. Each 10 mm increase in monthly rainfall above the threshold was associated with an increase in the number of malaria inpatients of 10.7% (95% CI: 8.2–13.2) in Kapsabet and 4.9% (95% CI: 3.6–6.2) in Kisii. The effect of rainfall varied between locations from 1.4% to 10.7%.

Relationship with DMI Adjusted for Rainfall.

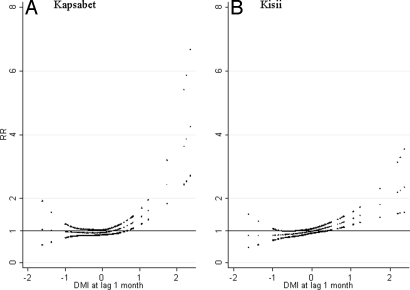
The risk–response relationships between DMI and the number of malaria cases after adjustment for rainfall, and for seasonal and interannual variations and NINO3, are shown in Fig. S5 (for inpatients in Kapsabet and Kisii district hospitals). The positive slope with higher DMI slightly declined after adjustment for rainfall both in Kapsabet and Kisii. After adjustment, we estimated that the effect of DMI on the number of malaria inpatients in Kapsabet and Kisii district hospitals decreased to 13.6% (95% CI: 8.8–18.7) and 12.2% (95% CI: 7.8–16.8), respectively. The effect of DMI on the number of malaria outpatients also decreased in most hospitals in both districts (results not shown). Fig. 3 shows the relationship between DMI and rainfall in Kapsabet and Kisii with a lag of 1 month. There appears to be an increase in rainfall with higher DMI in both districts.

Fig. 3.

Relationships between rainfall scaled as relative risk to the mean monthly rainfall in Kapsabet (1982–1999) (A) and Kisii (1986–2000) (B) and the dipole mode index (DMI) (lag 1 month). The center line in each graph shows the estimated spline curve, and the Upper and Lower lines represent 95% confidence limits.

The model goodness of fit for different climate factors (DMI, NINO3, and rainfall) is shown in terms of Akaike's information criterion (AIC) (Table S1). The AIC of a model including DMI but no NINO3 is smaller than that including NINO3 but no DMI in both Kapsabet and Kisii. The smallest AIC was obtained for the model incorporating DMI, NINO3, and rainfall.

The incorporation of Fourier terms (up to the fifth harmonic adding 1 harmonic at a time) into the model, in place of indicator variables for months, had little effect on the estimates of the effects of DMI, NINO3, and rainfall (results not shown).

Discussion

In the western Kenyan highlands, the number of malaria cases was positively associated with DMI above a threshold level, after adjusting for potential confounding factors such as NINO3, and seasonal and interannual variations. There was no strong evidence of the association between NINO3 and the number of malaria cases after adjusting for the effect of DMI.

Malaria dynamics in the East African highlands have been investigated in relation to climatic factors. Hay et al. showed that mean temperature and rainfall have not changed significantly over the past century at 4 locations in the East African highlands, although the incidence of malaria has increased over the last 2 decades (27). However, Pascual et al., using the same temperature data, found evidence for a significant warming trend (12). Zhou et al. (13) demonstrated that rainfall and temperature play an important role in the variability in monthly numbers of malaria outpatients in the East African highlands, after controlling for seasonal variations and autocorrelation. A recent study of multiyear cycles of malaria outbreaks in a Kenyan highland region showed that both endogenous disease dynamics and rainfall played a role in the temporal dynamics of the disease, over different time scales (14).

The role of ENSO in the interannual variability in East African rainfall has been extensively examined (28, 29). These studies found that ENSO had some influence on equatorial and coastal East African rainfall, with warm events being associated with higher rainfall and cold events with lower rainfall. However, the association was weak, and there was considerable geographic variation. By comparison, the impact of Indian Ocean variability on East African rainfall has received relatively little attention. However, following the discovery of the IOD there has been increased interest in this issue. Black et al. (30) showed that the East African short rains during dipole years were consistently greater than those during nondipole years, regardless of NINO3, and concluded that the link between the short rains and SST in the tropical Pacific was weaker than its link with the IOD. Another study investigated the relationship between East African short rains and DMI and NINO3 using a partial correlation technique, and showed that the influence of the IOD on the short rains was overwhelming, compared with that of the ENSO: the correlation between ENSO and the short rains was not significant when the IOD influence was excluded (31). An atmospheric circulation model also suggests that the Indian Ocean SST exerts a greater influence than the Pacific over the East African short rains (32). Similarly our study found that DMI was positively associated with rainfall in Kapsabet and Kisii.

Our study also found that the 3- to 4-month lag in the positive association between DMI and the number of malaria cases coincided with the sum of the lag between DMI and rainfall (1 month) and the lag between rainfall and the incidence of malaria (2–3 months). Furthermore, the effect of DMI on the number of malaria cases diminished after adjusting for rainfall, suggesting that part of the effect of DMI on the incidence of malaria could be explained by the effect of DMI on rainfall. While these findings do not directly represent a causal connection, when placed in the context of increasing evidence on the effect of positive IOD on the East African short rain (31, 32), they point toward at least 1 hypothesis that may explain the connection. IOD leads to increased rainfall, which would create numerous small water pools that become potential breeding grounds for malaria vectors. The primary malaria vector species in the highlands, Anopheles arabiensis and A. gambiae, mainly breed in sun-lit small temporary pools (10, 33), and their larvae take only 1–2 weeks to grow into adults (34). Thus the increased rainfall by DMI would lead to a rapid increase of vector population in a short period (35), which results in an increased risk of malaria transmission. High humidity associated with rainfall enhances the longevity of malaria vectors, which would also increase the risk of malaria transmission because longer-lived vectors have greater vectorial capacity (more chances for transmission and reproduction) (36). This hypothesis only explains the effect of DMI through rainfall. There are, however, likely to be pathways other than rainfall because the effect of DMI on the number of malaria cases diminished but did not totally disappear after adjusting for rainfall. Investigations into other possible pathways of the IOD–malaria relationship, particularly the role of local weather conditions, are clearly warranted.

Nonclimatic factors could modify the effect of IOD on the incidence of malaria. Local enforcement of eradication measures potentially influences the seasonal and long-term variability of the incidence of malaria. Malaria epidemics were not reported in the highlands of western Kenya after an eradication campaign using residual insecticides in the 1950s (37, 38). Chloroquine could have been effective in the suppression of malaria epidemics until the emergence of resistance (7, 8). Land use change also influences malaria transmission and may influence the effects of IOD by altering microclimatic conditions such as temperature, humidity, and surface runoff (39, 40). Changes in the public health infrastructure may also affect population vulnerability and therefore enhance or reduce the magnitude of the relationship.

The study design used here is time-series regression, comparing monthly counts of patients in the hospitals with exposure measures. The underlying hypothesis is that part of the variance of the monthly distribution of malaria patients is associated with the monthly fluctuations of the exposure indicator, after considering all potential confounding factors. The main advantage of this design is that the population under study serves as its own control, and covariates that vary between subjects but not over time are not potential confounders. Long-term population trends such as changes in the number of the population in an area are not likely to act as confounders because trends in rates are allowed for in the model. Variables that change with time, for example temperature, can confound the relationship of interest if they are correlated with DMI or rainfall, but their effect is partially controlled because seasonal patterns are allowed for in the model. There may be concerns about the immune status of the population at risk changing over time: Infection with Plasmodium parasites increases immunity to reinfection, but population immunity is not likely to change quickly (14). It therefore seems unlikely that this would obscure the short-term (within 6 months) associations between malaria and the factors investigated in this study. Less severe cases would be less likely to be included, but this would not alter the validity of comparisons between time periods, which is the subject of this study. A misdiagnosis of malaria would potentially affect the results of this study, but only if over- (or under-) diagnosis was associated with the climatic factors of interest, and there is no evidence for this.

High correlations between DMI and NINO3 during September–November (the short rain season) have been reported in previous studies (41, 42). Our data also had a high correlation coefficient of 0.70 during the period, but the coefficient was 0.36 with all year data. Because we were interested in data throughout a year for 18 years, the high correlation during the short rain season should not considerably affect our analyses. Although the high correlation may still suggest that NINO3 is also an important factor during the short rain season in the highlands, the influence may be negligible or less than that of DMI because NINO3 showed no significant effect after adjusting for DMI in our regression analysis. Alternatively, an analysis using a subsurface dipole mode index, defined by the difference of the average 20 °C isotherm depth between the western and the eastern tropical Indian Ocean, may provide a clear picture of their influences during the short rain season, because the index shows weak correlation with NINO3 but high correlation with DMI (43). This analysis would possibly disaggregate to a greater degree the effects local to the Indian Ocean basin from those within the Indian Ocean.

Because of the large global burden and climate sensitivity of malaria, the World Health Organization has proposed developing an early warning system for malaria epidemics using climatic parameters (44). Highly accurate, climate-based prediction of malaria epidemics, however, has not yet been developed, especially for highland regions where fluctuations in weather conditions are large (45, 46). A system for forecasting IOD has been developed, and IOD events are predictable 4 months in advance (47). Combined with such a prediction model, the results of this study provide the basis for predicting malaria epidemics in the East African highlands and have the potential to improve disease control. Because geographic variability in rainfall in the East African highlands is high, our results indicate that the role of IOD in the number of malaria cases in other places is also worthy of investigation.

In summary, this study suggests that the number of malaria cases in the western Kenyan highlands increases with high DMI, even after potential confounding by the effect of ENSO is taken into consideration. The association between DMI and the incidence of malaria may be explained, in part, by the effect of DMI on rainfall.

Methods

Malaria and Climate Data.

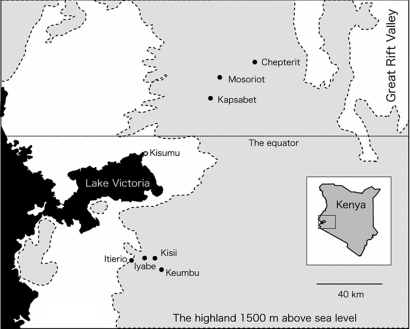
The primary outcome for this study was the monthly number of patients with malaria who visited 7 hospitals in 2 districts (Nandi and Kisii) in the western Kenyan highlands (Fig. 4). For the 2 district hospitals (Kapsabet and Kisii) that have inpatient departments, the number of in- and outpatients for each month was collected. For the remaining 5 hospitals, we just obtained data on outpatients. Detailed information on the locations of the hospitals, number of malaria cases, and climatic conditions is presented in Table 2. Diagnoses of malaria were made by physicians at the hospitals. Not all diagnoses were microscopically confirmed.

Fig. 4.

Locations of the 7 study hospitals in the highlands of western Kenya.

Table 2.

Description of the study sites, monthly numbers of malaria cases, and meteorological data

District	Hospital	Location and elevation	In-/outpatient	Malaria					Annual rainfall, mm
				Period	Mean	SD	Min	Max
Nandi	Kapsabet	(0.12°N, 35.06°E, 2000 m)	In	1982–1999	171	171	14	1152	1520.8
			Out	1983–1999	2024	1045	422	6913
	Mosoriot	(0.19°N, 35.10°E, 2090 m)	Out	1990–1999	806	664	165	4372
	Chepterit	(0.22°N, 35.19°E, 2170 m)	Out	1983–1999	348	325	47	2091
Kisii	Kisii	(0.40°S, 34.46°E, 1670 m)	In	1986–2000	789	640	42	4820	2050.5
			Out	1984–2000	2736	1338	333	12448
	Keumbu	(0.44°S, 34.50°E, 1470 m)	Out	1985–2000	938	412	92	2775
	Iyabe	(0.41°S, 34.40°E, 1470 m)	Out	1984–2000	622	306	19	1698
	Itierio	(0.40°S, 34.43°E, 1650 m)	Out	1985–2000	130	104	6	466

Data on daily rainfall in Kapsabet and Kisii were obtained from the Kenyan Meteorological Department and the total monthly rainfall was calculated from these daily records. The strength of the IOD was measured by the DMI, which is defined as the difference in SST anomaly between the western (10°S-10°N, 50°-70°E) and eastern (10°S-0°, 90°-110°E) tropical Indian Ocean (19). The DMI data were derived from the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) (http://www.jamstec.go.jp/frcgc/research/d1/iod/). The DMI values were calculated using SST data derived from the National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation Sea Surface Temperature data set (48, 49). The base period for calculating anomalies was 1970–2005. The values were standardized to zero mean and unit standard deviation. The strength of the ENSO was measured by SST anomalies in the NINO3 in the Pacific Ocean, which were derived from NOAA Climate Prediction Center data (http://www.cpc.ncep.noaa.gov).

Statistical Analysis.

We used 3 regression models in our analyses. The first model identified the optimal time lags between malaria incidence and each independent variable (DMI, NINO3, and rainfall) through separate regression of malaria incidence on lags of each independent variable. The second model used these identified optimal lags and incorporated DMI and NINO3 in a Poisson generalized linear model (GLM). Based on the GLM findings, a third, linear threshold model was then used to quantify the increase in malaria risk associated with a change in each independent variable.

The question of interest in this study was “Is a change in the DMI in a given month associated with a change in the number of malaria cases n months later?” Temporal associations between climate and disease are confounded by trends and seasonal patterns. To account for seasonality in the incidences of malaria that are not directly because of the IOD, we included indicator variables for months in the model. Indicator variables for the years of the study were also incorporated into the model to allow for long-term trends and other variations among years.

To account for delays in the effect of the IOD on the number of malaria cases, lagged DMI variables were incorporated into the model. We considered lags (delays in effect) of up to 6 months. To identify the optimum lag period, we performed separate regressions for each lag (0, 1, 2, …, 6 months). We separately incorporated DMI variables at each lag into a model comprising indicator variables of months and years (i.e., a model without controlling for mutual confounding between DMI and NINO3). The same procedures were also applied to NINO3 and rainfall to identify the optimum lag for each variable. All lags that showed significant (P < 0.05 level) positive associations are presented in Table 3. In most places, the associations between the number of malaria cases and DMI, NINO3, and rainfall were significantly positive, generally with lags of 3–4, 1–2, and 2–3 months, respectively, which were determined to be the optimum lag period for each exposure variable. The final models of DMI and NINO3 thus contained both of the variables of average DMI at a lag of 3–4 months and average NINO3 at a lag of 1–2 months to control for potential mutual confounding.

Table 3.

Association between malaria cases and dipole mode index (DMI), NINO3 SST anomaly (NINO3), and rainfall: Lags significant at 0.05 level

District	Hospital	In-/outpatient	DMI	NINO3	Rainfall
Nandi	Kapsabet	In	3, 4, 5	0, 1, 2, 3, 4	2, 3
		Out	3, 4	1, 2	2, 3
	Mosoriot	Out	3, 4	0, 1, 2, 3	3
	Chepterit	Out	2, 3, 4	0, 1, 2, 3	2, 3
Kisii	Kisii	In	3, 4	0, 1, 2, 3, 4	2
		Out	3, 4	0, 1, 2, 3	2
	Keumbu	Out	—	—	—
	Iyabe	Out	3	—	2
	Itierio	Out	2, 3, 4	0, 1, 2, 3	2

Numbers indicate the lag number in months. Regression models are adjusted for seasonality (indicator variable of months) and interannual variations (indicator variable of years).

We examined the relationships between the number of malaria cases and DMI, NINO3, and rainfall, using generalized linear Poisson regression models allowing for overdispersion (50). To allow for autocorrelations, an autoregressive term of order 1 was incorporated into the models (51).

Natural cubic splines were used to create graphs of the relationships between the number of malaria cases and DMI (NINO3 and rainfall), where the number of malaria cases was plotted as smoothed functions of DMI (NINO3 and rainfall) (52). This is to assess visually the functional form of the adjusted relationship, thereby identifying whether the relationship was likely to be linear or not across the full range of independent variables. Natural cubic splines have been used in time-series studies of climate–health relationships of which the functional forms were expected to be nonlinear (53, 54). This strategy involved dividing the DMI series into n-tiles and fitting cubic polynomial to the DMI–malaria relationship in each interval. Each interval was joined smoothly by a knot (the boundaries of the intervals) of which the number determines the level of smoothing of the data. The number of knots was decided to be 2 because this number of knots was expected to be sufficient to allow flexibility to fit with the relationship but not too much to obtain a general idea of functional form by exploratory analyses. The choice of 2 knots was not critical to the results, as regressions with up to 5 knots yielded similar relationships (data not shown).

For model diagnostics including the plots of model residuals, predicted and observed time-series plots, and partial autocorrelation function of the residuals, see Figs. S6 and S7; for Akaike's information criterion (AIC) and model deviance, see Table S2.

As the plots of the smoothed relationships between DMI, NINO3, or rainfall and the number of malaria cases suggested log-linear associations above a threshold, we then fitted the data to linear threshold models, i.e., models that assume a log-linear increase in risk above a threshold and no increase in risk below the threshold (53). The choice of the threshold was based on maximum likelihood estimations over a grid of all possible 1-decimal-point values for DMI and NINO3 and every 10 mm for rainfall, within a range indicated on the exposure–malaria graphs. Likelihood profile confidence intervals (CIs) for each threshold were calculated as the thresholds for which deviance of the model was 3.84 more than the minimum. The increase in the number of malaria cases that were associated with a 1-decimal-point increase in a given measure of DMI and NINO3 and a 10-mm increase in a given measure of rainfall above the thresholds, estimated as coefficients from the regression model, was reported as the percentage change.

Finally, the relationship between DMI and the number of malaria cases was estimated, adjusted for rainfall by incorporating the rainfall terms into the model for DMI, to clarify what component of the DMI–malaria association was through factors associated with rainfall.

Although the associations between rainfall and DMI was not the focus of this study, we considered the broad form of the relationship to confirm whether the link between IOD and East African rainfall observed in many previous studies could also be seen in our study sites during the study period (details are in SI Methods). All statistical analyses were carried out using Stata 10.0 (Stata Corporation, College Station, Texas).