Continuous cardiac output and left atrial pressure monitoring by long time interval analysis of the pulmonary artery pressure waveform: proof of concept in dogs

Abstract

We developed a technique to continuously (i.e., automatically) monitor cardiac output (CO) and left atrial pressure (LAP) by mathematical analysis of the pulmonary artery pressure (PAP) waveform. The technique is unique to the few previous related techniques in that it jointly estimates the two hemodynamic variables and analyzes the PAP waveform over time scales greater than a cardiac cycle wherein wave reflections and inertial effects cease to be major factors. First, a 6-min PAP waveform segment is analyzed so as to determine the pure exponential decay and equilibrium pressure that would eventually result if cardiac activity suddenly ceased (i.e., after the confounding wave reflections and inertial effects vanish). Then, the time constant of this exponential decay is computed and assumed to be proportional to the average pulmonary arterial resistance according to a Windkessel model, while the equilibrium pressure is regarded as average LAP. Finally, average proportional CO is determined similar to invoking Ohm's law and readily calibrated with one thermodilution measurement. To evaluate the technique, we performed experiments in five dogs in which the PAP waveform and accurate, but highly invasive, aortic flow probe CO and LAP catheter measurements were simultaneously recorded during common hemodynamic interventions. Our results showed overall calibrated CO and absolute LAP root-mean-squared errors of 15.2% and 1.7 mmHg, respectively. For comparison, the root-mean-squared error of classic end-diastolic PAP estimates of LAP was 4.7 mmHg. On future successful human testing, the technique may potentially be employed for continuous hemodynamic monitoring in critically ill patients with pulmonary artery catheters.

the standard methods for monitoring cardiac output (CO) and left atrial pressure (LAP) in critically ill patients have both involved the use of the pulmonary artery catheter (31, 53). Specifically, CO is estimated with the bolus thermodilution method, while LAP is approximated via the pulmonary capillary wedge pressure (PCWP) method. Despite their clinical use, the thermodilution and PCWP methods have significant limitations. One limitation is that these methods require an operator (to inject the bolus of saline through a proximal catheter port and inflate the balloon at the catheter tip). Consequently, thermodilution and PCWP measurements are often made infrequently. Indeed, in 775 critically ill patients instrumented with pulmonary artery catheters, only 0.83 thermodilution and 0.15 PCWP measurements were made on average per day (11, 39). Another limitation is that several technical problems must be overcome in making valid PCWP measurements. These problems include partial wedging and balloon overinflation (25, 34), dependence of the measurement on the wedge catheter position (14, 19), and proper interpretation of phasic PCWP (10, 17). Even the developers of the PCWP method reported that they could properly measure PCWP only ∼75% of the time in the cardiac catheterization laboratory (41). Similarly, technical problems are also encountered in making thermodilution measurements in which variations in injectate volume, rate, and temperature introduce significant error in the measurement (26, 33, 51). A third limitation is that the injection of fluid and balloon inflation poses risk (e.g., air emoblization) (7, 20, 27). Perhaps due in part to infrequent use (44, 59) and misuse (23, 40, 43, 59) of the PCWP and thermodilution methods, the pulmonary artery catheter has not revealed a clinical benefit [or harm (2)] in the five large randomized, controlled trials that have been performed so far (13, 43, 46, 55, 56), and its usage in the US is declining (60). In other words, the potential benefit of CO and LAP monitoring in guiding clinical decision making may not, in general, be sufficiently attained through the thermodilution and PCWP methods to exceed the upfront risk of using the invasive catheter.

On the other hand, the pulmonary artery catheter also permits continuous (i.e., automated) monitoring of the pulmonary artery pressure (PAP) waveform. Since CO and LAP are both significant determinants of PAP, it may be possible to continuously monitor these two critical hemodynamic variables by mathematical analysis of the PAP waveform. However, we find only five papers in the literature for monitoring CO by PAP waveform analysis (3, 6, 54, 65, 66). This set of papers describes a total of five different techniques that analyzed each individual beat of the PAP waveform to compute CO to within a proportionality constant. However, wave reflections and inertial effects are prominent over the short time scales within a beat (36). Perhaps, as a result, the success of the techniques was, in general, shown to be limited. On the other hand, there is substantial literature on monitoring LAP through the end-diastolic PAP (e.g., Refs. 15, 16). This simple technique is even used in clinical practice (31). However, end-diastolic PAP is not as accurate as PCWP (16) and is considered to be highly unreliable during pulmonary hypertension (15, 31). We find only one paper in the literature describing a more advanced technique to estimate LAP, which specifically involved training a neural network to predict PCWP from the PAP waveform (5). However, this technique did not perform well in subjects whose data were not utilized in training the network. In short, there is a paucity of techniques in the literature for monitoring CO or LAP from the PAP waveform. Moreover, among the few previous techniques, none simultaneously estimate both CO and LAP.

In this study, we developed a new technique to continuously monitor CO and LAP by mathematical analysis of the PAP waveform. The technique is notable in that it 1) analyzes interbeat or beat-to-beat PAP variations in which confounding wave reflections and inertial effects cease to be major factors (36); 2) is not based on training data and may therefore be generally applicable; and 3) jointly estimates CO and LAP. We then performed experiments in five dogs to test the technique with respect to accurate, but highly invasive, reference aortic flow probe CO and LAP catheter measurements during common hemodynamic interventions. A preliminary version of this study has been reported in abbreviated form (61).

The Technique

Our technique for continuous CO and LAP monitoring by PAP waveform analysis represents an extension of a previous technique that we developed for monitoring CO by long time interval analysis of a peripheral arterial blood pressure (ABP) waveform (30, 35). We present the underlying concepts and mathematical steps of the new technique below and then describe its relationship to our initial technique in the discussion.

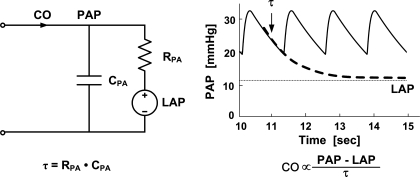
The technique arises from the Windkessel model of the pulmonary circulation shown in Fig. 1, left. This model predicts that PAP should decay like a pure exponential during each diastolic interval with a time constant (τ) equal to the product of the pulmonary arterial resistance (R_PA) and the pulmonary arterial compliance (C_PA). The model further predicts that the exponential pressure decay should equilibrate toward LAP rather than zero pressure. Thus, as illustrated in Fig. 1, right, the Windkessel model suggests that both τ and average LAP may be determined from the PAP waveform by fitting a single exponential plus a constant term to each of its diastolic intervals. Moreover, assuming C_PA is relatively constant within a subject over a monitoring period, proportional CO may then be determined by subtracting LAP from the time average of PAP and dividing this difference by τ (i.e., similar to invoking Ohm's law).

Fig. 1.

A potential technique for continuous cardiac output (CO) and left atrial pressure (LAP) monitoring by intra-beat analysis of the pulmonary artery pressure (PAP) waveform. The Windkessel model of the pulmonary circulation (left) suggests that a time constant τ, which is equal to the product of the pulmonary arterial compliance (C_PA) and the pulmonary arterial resistance (R_PA), and average LAP may be determined from the PAP waveform by fitting an exponential plus a constant term to each of its diastolic intervals (right, wherein the displayed PAP waveform was simulated by a Windkessel model). Moreover, assuming C_PA is relatively constant, proportional CO may then be determined similar to invoking Ohm's law (right). However, this technique should not be very accurate, as pure exponential diastolic decays are usually obscured in experimental PAP waveforms by faster wave reflections and inertial effects (see Fig. 3 and discussion).

However, pure exponential diastolic decays are generally not apparent in experimental PAP waveforms (54; see Fig. 3) due to wave reflections and inertial effects in the pulmonary circulation (36). On the other hand, such phenomena may only complicate the PAP waveform over short time scales (i.e., high frequencies; Refs. 30, 35, 36). For example, as the time scale increases (i.e., the frequency decreases), the wavelengths of the propagating waves become larger with respect to the dimension of the pulmonary circulation such that the circulation appears more lumped, and inertial effects, which are proportional to the time derivative of the flow rate, become more attenuated. Thus the Windkessel model of Fig. 1 may be a more valid representation of the long time scale or beat-to-beat (i.e., low frequency) dynamics of the PAP waveform. So, for example, if pulsatile activity abruptly ceased, then PAP may eventually decay like a pure exponential and equilibrate to LAP once the faster confounding dynamics vanish.

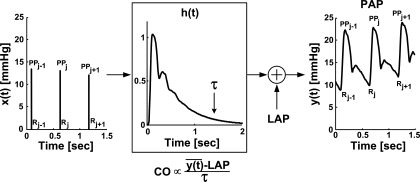
Our technique therefore analyzes the PAP waveform over long time intervals (seconds to minutes) to determine the pure exponential decay and equilibrium pressure that would eventually result if pulsatile activity suddenly ceased. More specifically, average LAP and the PAP-LAP response to a single, solitary cardiac contraction [see h(t), where t indicates discrete time, in Fig. 2] are simultaneously estimated by optimal fitting or prediction of a 6-min segment of the PAP waveform sampled to 90 Hz. Then τ is determined by fitting a single exponential to the tail end of h(t) once the faster wave and inertial effects have vanished (see Fig. 2; Refs. 30, 35). Finally, average proportional CO is computed similar to invoking Ohm's law (see Fig. 2) and conveniently calibrated to absolute CO with a thermodilution measurement.

Fig. 2.

Novel technique for continuous CO and LAP monitoring by long time interval analysis of the PAP waveform. First, a cardiac contractions signal [x(t)] is constructed from a 6-min PAP waveform segment [y(t)] based on the impulse ejection model. (PP_j and R_j are, respectively, the pulse pressure and the onset time of PAP upstroke of the jth beat.) Second, y(t) is fitted according to the sum of a constant term with the convolution between x(t) and an impulse response [h(t)]. That is, the constant term and h(t) are estimated so as to optimally fit y(t). The estimated constant term represents average LAP, while the estimated h(t) represents the PAP-LAP response to a single cardiac contraction. Next, the time constant τ of the Windkessel model of Fig. 1 is determined by fitting an exponential to the tail end of h(t) once the faster wave reflections and inertial effects vanish. Finally, average proportional CO is determined similar to invoking Ohm's law and conveniently calibrated with a thermodilution measurement.

Figure 2 indicates that the single contraction PAP-LAP response and average LAP are estimated in two steps. First, a signal representing the cardiac contractions [x(t)] is derived from the measured PAP waveform segment [y(t)] based on the well-known impulse ejection model (9, 32). That is, x(t) is formed as an impulse train in which each impulse is located at the time of end-diastolic PAP (R) and has an area equal to the subsequent pulse pressure (PP).

Second, y(t) is fitted according to the sum of an unknown constant term with the convolution between the known x(t) and an unknown impulse response [h(t)]. That is, the constant term and h(t) are estimated so as to permit the best fit or prediction of y(t) in the least squares sense. The estimated constant term represents the average LAP, while, by mathematical definition, the estimated h(t) represents the PAP-LAP response to a single cardiac contraction. The impulse response h(t) and average LAP are specifically estimated with the following autoregressive exogenous input (ARX) structure with constant term a₀:

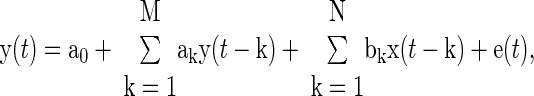(1)

where e(t) is the unmeasured residual error, a_k and b_k are sets of unknown parameters, and M and N represent the unknown model order limiting the number of parameters (28). For a fixed model order, the parameters are estimated from x(t) and y(t) through regularized least squares minimization of e(t). This optimization is achieved in closed form using linear least squares estimation with Tikonov regularization (28). The model order is determined by minimizing the minimum description length criterion (28) over a range of 1 ≤ M,N ≤ 15. With the estimated parameters, average LAP and h(t) are computed as follows:

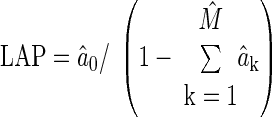(2)

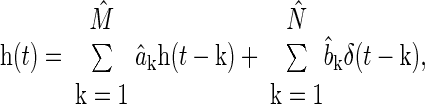(3)

where hat (circumflex ^) indicates estimated parameters, and δ(t) is the unit impulse function. In principle, reliable estimation of average LAP and subsequent determination of τ are achieved by virtue of accurately fitting the long time scale or beat-to-beat variations in the PAP waveform segment.

METHODS

We conducted canine experiments to evaluate the long time interval PAP waveform analysis technique as well as to compare it to competing intrabeat analysis techniques. We outline our methods for data collection and analysis below.

Data Collection

Experiments were performed in five normal adult dogs (10–26 kg), either beagles or mongrels. Each dog was studied on two separate days under a protocol approved by the MSU All-University Committee on Animal Use and Care.

On the first experimental day, chronic instrumentation was installed in the dog for data recording using a sterile procedure as follows. General anesthesia was induced with an intravenous injection of propofol (2.2–6.6 mg/kg) and maintained with inhaled isoflorane (1.5–2.5%), and mechanical ventilation was instituted. A left lateral thoracotomy was performed. An ultrasonic flow probe was placed around the ascending aorta for reference CO (A-series, Transonic Systems, Ithaca, NY). {After chronic implantation of this flow probe to ensure acoustic coupling, the error in measuring relative CO changes, which is all that is needed to evaluate the new technique for estimating proportional CO, is reported to be 2% (57, 58). One source of this error is changes to coronary blood flow [4–5% of the CO (12)], which is not captured by the flow probe.} A tygon catheter was directly inserted through the left atrial appendage for reference LAP (Norton, Akron, OH). The chest was evacuated and closed in layers, with the cable and catheter tunneled subcutaneously and exteriorized between the scapulae. The dog was then allowed 10–14 days for recovery, during which the catheter was irrigated daily with a heparinized saline solution.

On the second experimental day, additional transient instrumentation was achieved as follows. General anesthesia was induced and maintained as previously described. Mechanical ventilation was instituted at a rate of 12 breaths/min and a tidal volume of 20–25 ml/kg (in 3 of the dogs). A micromanometer-tipped catheter was inserted into a jugular vein and positioned under fluoroscopic guidance in the main pulmonary artery for the PAP waveform (Millar Instruments, Houston, TX). Another micromanometer-tipped catheter was similarly inserted and positioned for the right ventricular pressure (RVP) waveform (in 4 of the dogs). A third micromanometer-tipped catheter was placed in the descending thoracic aorta via femoral artery access in conjunction with fluoroscopic guidance for an ABP waveform (in 3 of the dogs). A catheter was inserted into a cephalic vein for drug and isotonic fluid administration, and surface electrodes were positioned for two frontal ECG leads. All of the analog transducer outputs were interfaced to a personal computer through an analog-to-digital conversion system (DataQ Instruments, Akron, OH). The cardiovascular measurements were then recorded in each dog at a sampling rate of 500–1,000 Hz over the course of 100–230 min during a subset of the following common hemodynamic interventions: infusions of dobutamine, isoproterenol, esmolol, phenylephrine, nitroglycerin, and volume as well as hemorrhage. Various infusion rates were employed followed by recovery periods.

Data Analysis

Technique evaluation.

The technique was applied offline to 6-min nonoverlapping segments of the PAP waveforms so as to estimate proportional CO and absolute LAP trends for each dog. (When the 6-min segment included a step PAP change due to bolus drug infusion, the technique was applied to the longest steady interval of the waveform within the segment.) The corresponding absolute reference CO and LAP trends were established by averaging the aortic flow probe and LAP catheter measurements over the identical time segments. To compare an estimated proportional CO trend with the absolute reference CO trend, the former trend was first scaled to have the same mean value as the latter trend in each dog. The estimated, calibrated CO and absolute LAP trends were then evaluated against their corresponding reference trends through: 1) classic regression analysis to comprehensively illustrate the estimated values versus the reference values and provide the correlation coefficient (ρ) between these values; 2) Bland-Altman analysis (1) (which has become the standard for comparing two clinical measurement methods) to comprehensively illustrate the estimation errors versus the highly accurate reference values (rather than the average of the estimated and reference values) and indicate the bias μ and precision σ of the estimation errors; and 3) the root mean square of the estimation errors (RMSE = 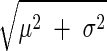) to succinctly indicate the overall error size. Both absolute and relative estimation errors were assessed, with relative CO estimation errors in units of percent and absolute LAP estimation errors in units of millimeters of mercury emphasized for congruence with previous, related studies (e.g., Ref. 4). [Note that the CO RMSE here, when expressed in percent, is equivalent to the CO root-mean-squared normalized error (RMSNE) that we reported in previous studies (30, 35, 52).] In addition, the changes in the estimated, calibrated CO and absolute LAP trends with respect to their mean values in each dog were evaluated against the corresponding changes in the reference trends for some of the hemodynamic interventions through Bland-Altman analysis.

Comparison to intra-beat analysis techniques.

For comparison, three competing intra-beat analysis techniques were also applied to the measured PAP waveforms. The first technique was the classic end-diastolic PAP estimate of LAP. The second technique, which is illustrated in Fig. 1, involved fitting a single exponential and constant term to each diastolic interval (approximated as the downstroke from peak systolic pressure to end-diastolic pressure) of the PAP waveform so as to estimate τ and LAP and then computing proportional CO by subtracting LAP from the time average of PAP and dividing this difference by τ. The third technique involved 1) fitting multiple complex exponentials and a constant term to each diastolic interval of the PAP waveform (via a numerical search) to account for confounding wave reflections and inertial effects in addition to τ and LAP; 2) extrapolating the exponentials to low pressure and fitting a single exponential to the extrapolated values so as to determine τ; and 3) likewise computing proportional CO with the estimated LAP and τ. These single and multiple exponential fitting techniques may have neither been tested nor proposed before. However, the two techniques do represent adaptations to a technique previously proposed by Engelberg et al. (8) in which τ is estimated by directly fitting a single exponential to each diastolic interval of the PAP waveform minus the LAP waveform.

To make a fair comparison, the beat-to-beat τ and LAP estimated by the intra-beat analysis techniques were averaged over the same 6-min time segments analyzed by the long time interval analysis technique so as to compute analogous proportional CO and absolute LAP trends. The LAP trends estimated by the classic end-diastolic PAP technique were then comprehensively evaluated as described for the long time interval analysis technique, whereas the proportional CO and absolute LAP trends estimated by the two new exponential fitting techniques were assessed only through the RMSE for the sake of brevity.

RESULTS

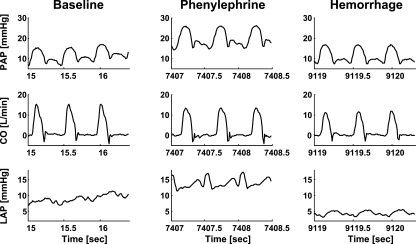
Figure 3 illustrates sample segments of the PAP waveform as well as the measured aortic flow (CO) and LAP waveforms from one of the dogs during baseline and the phenylephrine and hemorrhage interventions. Relative to baseline, CO decreased and LAP increased during phenylephrine due to enhanced cardiac afterload, while CO and LAP both decreased during hemorrhage due to diminished venous return. Table 1 provides a summary of the average baseline hemodynamic values of the dogs and the average effect of each of the employed interventions on these values. As exemplified in Fig. 3, pure exponential diastolic decays were generally not apparent in the measured PAP waveforms throughout the experiments.

Fig. 3.

Sample segments of the PAP waveform and the measured aortic flow (CO) and LAP waveforms from dog 5 during baseline, phenylephrine, and hemorrhage conditions. Note that pure exponential diastolic decays are not apparent in the PAP waveform segments.

Table 1.

Summary of the average baseline hemodynamic values of the dogs and the average effect of each of the employed interventions on these values

Condition	CO	LAP	Mean PAP	Mean ABP	RVSP	RVDP	HR
Baseline	2.76±0.85	7.1±1.4	13.7±2.7	88.3±10.8	25.1±6.4	2.6±1.8	134±8
Dobutamine	40.1±17.9	14.0±23.0	42.4±19.6	27.7	46.9±14.9	51.3±116.7	8.1±4.3
Isoproterenol	103.4	−20.7	46.2	−23.2	N/A	N/A	18.3
Esmolol	−0.1±20.5	52.1±40.3	24.8±9.5	−1.3±25.4	9.0±21.6	470.2±259.0	−7.4±3.6
Phenylephrine	−9.8±12.5	98.0±60.0	61.8±40.4	64.7±12.2	31.1±27.7	113.4±118.7	−4.0±4.1
Nitroglycerin	5.7±14.1	37.6±49.1	21.2±29.2	−15.8	4.9±10.9	87.9±148.1	−0.1±1.2
Volume	40.4	57.4	26.1	−24.3	29.4	585.8	−3.2
Hemorrhage	−7.3	−17.6	18.9	N/A	N/A	N/A	7.4

Values are given as means ± SE over the dogs (unless only one dog was available). Baseline values are expressed in physical units of l/min for CO, mmHg for pressures, and beats/min for HR, whereas intervention values are presented as percent changes relative to the baseline values. CO, cardiac output; LAP, left atrial pressure; PAP, pulmonary artery pressure; ABP, arterial blood pressure; RVSP, right ventricular systolic pressure; RVDP, right ventricular diastolic pressure; HR, heart rate.

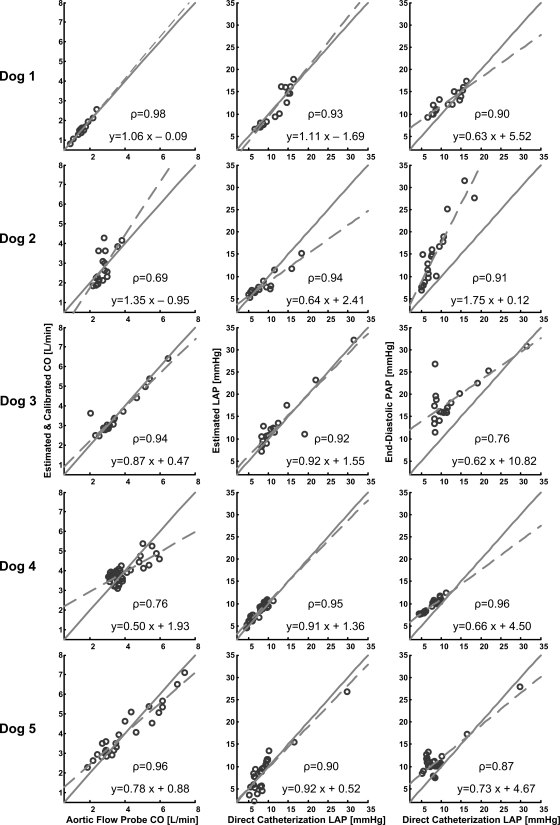
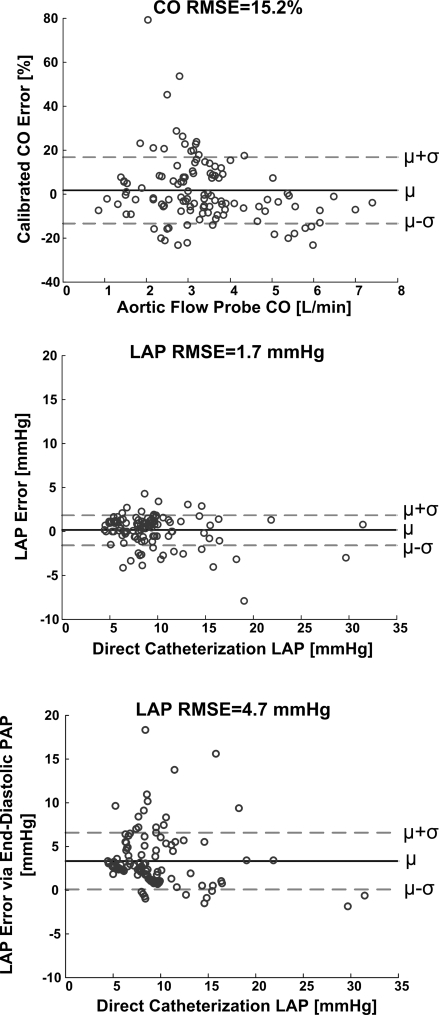
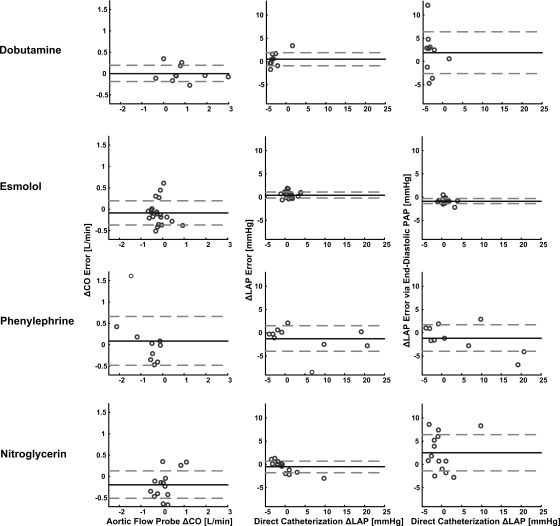
Table 2 and Figs. 4–6 show the results of applying the new long time interval analysis technique as well as the classic end-diastolic PAP technique to the measured PAP waveforms. In particular, Table 2 lists the hemodynamic range and calibrated CO and absolute LAP RMSEs for each dog. Figure 4 illustrates regression plots of the calibrated CO and absolute LAP estimates for each dog, while Fig. 5 shows Bland-Altman plots of these estimates pooled over all five dogs. Figure 6 illustrates Bland-Altman plots of the changes in the calibrated CO and absolute LAP estimates (with respect to their mean values in each dog) for the dobutamine, esmolol, phenylephrine, and nitroglycerin interventions pooled over all five dogs. (Note that similar plots for the other employed interventions included significantly fewer data points and therefore did not provide as interesting of an assessment.)

Table 2.

Summary of hemodynamic range and results of the technique of Fig. 2 as well as the classic end-diastolic PAP technique for each dog

Dog	CO Range, l/min	LAP Range, mmHg	Mean PAP Range, mmHg	Mean ABP Range, mmHg	HR Range, beats/min	CO RMSE, % (l/min)	LAP RMSE, mmHg (%)	LAP via End-Diastolic PAP RMSE, mmHg (%)
1	0.9–2.4	6.6–16.4	17.4–26.1	N/A	101–139	5.6 (0.09)	1.5 (12.2)	2.0 (23.8)
2	2.2–3.8	5.0–18.3	12.7–32.9	N/A	131–168	21.6 (0.58)	1.7 (15.4)	7.5 (83.7)
3	2.0–6.5	8.2–31.5	15.1–36.3	75–170	115–155	18.7 (0.40)	2.4 (18.2)	7.3 (80.1)
4	3.1–6.0	4.5–11.2	10.2–15.6	67–95	129–148	13.0 (0.53)	0.9 (13.7)	2.0 (34.6)
5	1.9–7.4	5.1–29.7	11.3–30.9	58–165	117–164	13.5 (0.50)	2.2 (27.3)	3.2 (48.3)
Total	0.9–7.4	4.5–31.5	10.2–36.3	58–170	101–168	15.2 (0.47)	1.7 (18.3)	4.7 (56.0)

RMSE is root-mean-squared error.

Fig. 4.

Results of the technique of Fig. 2 as well as the classic end-diastolic PAP technique in terms of regression plots of the calibrated CO and absolute LAP estimates vs. their corresponding reference aortic flow probe CO and LAP catheter values for each dog. The parameter ρ represents the correlation coefficient between the estimated and reference values.

Fig. 5.

Results of the technique of Fig. 2 as well as the classic end-diastolic PAP technique in terms of Bland-Altman plots of the calibrated CO and absolute LAP errors vs. the reference aortic flow probe CO and LAP catheter values pooled over all five dogs. The parameter μ indicates the bias error; σ, the precision error; and RMSE the root-mean-squared error (i.e.,).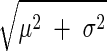

Fig. 6.

Results of the technique of Fig. 2 as well as the classic end-diastolic PAP technique in terms of Bland-Altman plots of the changes in the calibrated CO and absolute LAP estimates (with respect to their mean values in each dog) vs. the corresponding changes in their reference values for the dobutamine, esmolol, phenylephrine, and nitroglycerin interventions pooled over all 5 dogs.

CO ranged from ∼75 to 200% of its baseline value on average in each dog, whereas LAP generally ranged from ∼4.5 to 17 mmHg in the dogs and briefly reached higher values up to 31.5 mmHg. Mean PAP varied by 15 mmHg on average in each dog, while mean ABP changed over a much larger range of up to 106 mmHg in one dog. Heart rate (HR) varied over a range of ∼70 beats/min over all the dogs but did not reach values <100 beats/min.

The correlation coefficient ρ between the estimated and reference CO values was 0.87 ± 0.06 (mean ± SE) over all the dogs and ranged from 0.69 to 0.98 for each dog, while the calibrated CO RMSE was 15.2% (0.47 l/min) over all the dogs and ranged from 5.6% (0.09 l/min) to 21.6% (0.58 l/min) for each dog. Among the three large calibrated CO error outliers (>40%; see Fig. 5), two were obtained between interventions (recovery period) from dog 2 and the other was obtained during the phenyleprhine intervention in dog 3. If these outliers were ignored, the overall calibrated CO RMSE would reduce to 11.8%. The calibrated CO RMSE was due almost entirely to precision error merely as a result of the manner in which the proportional CO estimates were calibrated. The calibrated CO errors showed a mild, negative correlation with the reference CO values (ρ = −0.26), with the calibrated CO estimates being systematically underestimated at high reference CO values (>4.5 l/min). This underestimation occurred only when HR and stroke volume were both high (results not shown). However, the absolute value of the calibrated CO errors was virtually uncorrelated with the reference CO values (ρ = −0.07). The errors in the changes in the calibrated CO estimates appeared roughly of the same magnitude for the four illustrated interventions (if the single large positive outlier in the phenylephrine intervention were ignored).

The correlation coefficient ρ between the LAP values estimated by the new technique and the reference LAP values was 0.93 ± 0.01 over all the dogs and ranged from 0.90 to 0.95 for each dog, while the LAP RMSE was 1.7 mmHg (18.3%) over all the dogs and ranged from 0.9 mmHg (12.2%) to 2.4 mmHg (27.3%) for each dog. The overall RMSE of the estimated LAP, which was uncalibrated, had essentially no bias error component and was thus mostly a result of precision error. The LAP errors and their absolute values were likewise only modestly related to the reference LAP values (ρ = −0.22 and 0.31), with no obvious systematic overestimation or underestimation over any reference LAP range. Similarly, the errors in the changes in the LAP estimates appeared approximately of the same magnitude for the four illustrated interventions (if the single large negative outlier in the phenylephrine intervention were ignored).

The correlation coefficient ρ between the LAP values estimated by the classic end-diastolic PAP technique and the reference LAP values was 0.88 ± 0.03 over all the dogs and ranged from 0.76 to 0.96 for each dog, while the overall LAP RMSE was 4.7 mmHg (56.0%) over all the dogs and ranged from 2.0 mmHg (23.8%) to 7.5 mmHg (83.7%) for each dog. This overall LAP RMSE was due to a bias error of 3.3 mmHg and a precision error of 3.5 mmHg. The LAP errors and their absolute values were also hardly correlated to the reference LAP values (ρ = −0.12 and −0.04). Finally, the errors in the changes in these LAP estimates were about the same as the changes in the LAP values estimated by the new technique for the esmolol and phenyleprhine interventions but much larger for the dobutamine and nitroglycerin interventions.

As further comparison, the overall calibrated CO and absolute LAP RMSEs were 20.2% (0.58 l/min) and 4.5 mmHg (53.7%) for the single exponential fitting technique and 18.0% (0.58 l/min) and 2.8 mmHg (31.9%) for the multiple exponential fitting technique employing three complex exponentials (detailed results not shown in the tables or figures). Note that we were unable to reduce the latter RMSEs by using more exponentials or performing the fit over the actual diastolic intervals as established with the simultaneously measured RVP waveforms.

DISCUSSION

Previously, we developed and validated a technique to monitor relative changes in CO by novel long time interval analysis of a peripheral ABP waveform (30, 35). That technique effectively fits a Windkessel model of the systemic arterial tree accounting for the total peripheral resistance (R_A) and the nearly constant arterial capacitance or compliance (C_A) to the ABP variations occurring over time scales greater than a cardiac cycle wherein wave reflections cease to be a major factor. More specifically, first, a cardiac contractions signal is constructed from a 6-min ABP waveform segment via the impulse ejection model [analogous to x(t) in Fig. 2]. Then, an impulse response is estimated, which when convolved with the cardiac contractions signal, optimally fits the ABP waveform segment. Next, the Windkessel time constant (R_AC_A) is determined by fitting an exponential to the tail end of the impulse response once the faster wave reflections vanish (similar to Fig. 2). Finally, average proportional CO is computed by dividing the time average of ABP with the Windkessel time constant.

Here, we extended that technique to the PAP waveform so as to monitor LAP in addition to CO. The extension amounts to the inclusion of a constant term in the analysis to account for average LAP (see Figs. 1 and 2 and eq. 1). That is, an additive constant term is estimated along with the impulse response so as to optimally fit the PAP waveform segment. Note that this extension is actually necessary for reliable fitting, as LAP is a major determinant of PAP due to the small R_PA. Then, the Windkessel time constant of the pulmonary arterial tree (τ = R_PAC_PA) is similarly determined from the tail end of the impulse response, and average proportional CO is computed by subtracting average LAP from the time average of PAP and dividing this difference by τ (thereby implicitly assuming a linear R_PA and constant C_PA). In principle, this extension may likewise be applied to an ABP waveform so as to monitor venous pressure as well as proportional CO. However, venous pressure is usually much smaller than ABP due to the large R_A and may therefore be neglected (as with our original technique) or difficult to estimate. While our original technique may permit continuous and minimally invasive or even noninvasive monitoring of relative changes in CO, the more invasive technique here should be preferred when LAP monitoring is also indicated. Furthermore, its proportional CO estimates may be conveniently calibrated to absolute CO with a thermodilution measurement.

The extended technique is unique to the few previous, related PAP waveform analysis techniques (see introduction) in that it analyzes PAP variations over time scales greater than a cardiac cycle in which wave reflections and inertial effects are attenuated and jointly estimates CO and LAP. We initially presented the technique in abbreviated form in Ref. 29. In that article, we also described testing of the technique with respect to an existing dataset comprising a small number of thermodilution CO and PCWP measurements from critically ill patients in which the reference measurements did not vary much within each patient. The purpose of the present animal study was to demonstrate the validity of the technique with respect to a larger number of highly accurate, reference aortic flow probe CO and LAP catheter measurements during a more interesting hemodynamic range. The new contributions of this full paper include: 1) presentation of the complete study results; 2) comprehensive description of the technique and background; and 3) comparison of the technique to intra-beat analysis techniques.

The results of this study indicate that our new technique agreed well with reference aortic flow probe CO and LAP catheter measurements from five dogs during commonly employed hemodynamic interventions (see Tables 1–2 and Figs. 3–6). That is, the overall calibrated CO and absolute LAP RMSEs of the technique were 15.2% and 1.7 mmHg, respectively. These RMSEs compare favorably to the 17% error reported for clinical thermodilution measurements (18, 51) and the 1–2 mmHg error found in valid PCWP measurements (16, 24). (Note that larger PCWP errors may be expected in clinical practice, as PCWP measurements are often made incorrectly as discussed above.) The calibrated CO RMSE here is also similar to that obtained with our original long time interval analysis technique in six swine (35). The study results also show that the new technique was in better agreement with the reference methods than three competing intra-beat analysis techniques, namely the classic end-diastolic PAP technique and the two exponential fitting techniques proposed herein. In particular, the long time interval analysis technique estimated LAP with hardly any bias, unlike the end-diastolic PAP technique, and less than half the precision error of this classic technique. The multiple exponential fitting technique did provide lower calibrated CO and absolute LAP RMSEs than the other two intra-beat analysis techniques by accounting for the wave reflections and inertial effects with complex exponentials. However, these RMSEs, especially pertaining to LAP, were still larger than those of the long time interval analysis technique, which captured information embedded in the beat-to-beat PAP variations. Thus the results of this study of five chronically instrumented dogs demonstrate proof of concept of the new technique. If similar results were to hold over a large population of human patients, then our technique may be able to replace the standard operator-required thermodilution and PCWP methods in clinical practice.

We were not able to achieve a HR lower than 100 beats/min in our canine experiments with the employed interventions. Thus our study is limited in that it does not address the validity of the technique over this lower HR range. However, theoretically, our technique should perform more accurately as HR decreases, because the Windkessel model of Fig. 1 becomes a more valid representation of the PAP waveform with decreasing frequency. For example, if the HR were sufficiently low, a pure exponential decay may be visually apparent toward the end of the longer diastolic interval (i.e., the fast confounding dynamics will have had enough time to vanish).

An assumption of our new technique is that C_PA is constant within a subject over a monitoring period. This assumption is specifically needed to be able to estimate relative changes in CO. (The estimation of absolute LAP is not at all reliant on this assumption.) However, some previous studies suggest that C_PA may, on the contrary, decrease with increasing pressure (22, 42, 47, 49). If C_PA varied widely within each of our dogs, then the estimation of proportional CO would be unreliable, with the CO error showing substantial, positive correlation to mean PAP. However, proportional CO was well estimated as we have discussed, and the CO error was only modestly correlated with mean PAP (ρ = 0.20). Thus C_PA may have been at least approximately constant over a mean PAP range of up to 21 mmHg within a dog here. The relative constancy of C_PA that we observed here contradicts the aforesaid studies but is consistent with other studies (21, 50). The contrasting results could be due to differences in the technique for estimating C_PA and the experimental conditions (e.g., mean PAP range). While larger changes in mean PAP within a given subject could certainly elicit more significant changes in C_PA, in such circumstances, the proportional CO estimates could always be recalibrated to the new C_PA value with a readily available thermodilution measurement. Note that the small changes in C_PA that likely occurred in our experiments do represent a source of the CO error of the technique.

Another potential source of the errors is that the technique did not account for all of the major mechanisms of respiratory variability in the PAP waveform. That is, the external reference pressure of the pulmonary circulation is in actuality intrathoracic pressure rather than the zero pressure indicated by the Windkessel model of Fig. 1. Thus the technique cannot account for respiratory-induced changes in intrathoracic pressure that are directly transmitted to PAP. However, note that the technique is able to account for the respiratory-induced variations in intrathoracic pressure that modulate venous return to the right heart and the respiratory sinus arrhythmia phenomenon (48) through the cardiac contractions signal.

On the other hand, nonlinearity of R_PA due to recruitment and distension phenomena probably did not represent a major source of the errors here. Since the dogs were in the supine posture and average LAP was never <4.5 mmHg (see Table 2), all of the collapsible pulmonary capillaries may have been open (i.e., zone 3 pulmonary blood flow) throughout the study (12, 37). Thus R_PA may have always been operating in its linear regimen. However, note that even when some of the pulmonary capillaries are collapsed (i.e., zone 1 pulmonary blood flow) and some are exhibiting the vascular waterfall effect (i.e., zone 2 pulmonary blood flow) (Refs. 12, 37), the linear R_PA assumption may not be grossly violated as R_PA is specifically assumed to be linear only over each 6-min segment of analysis (i.e., piece-wise linear).

Like intra-beat analysis techniques, the long time interval analysis technique can be implemented in real time on a home personal computer. However, its main disadvantage with respect to the conventional techniques is that it cannot identify very rapid CO and LAP changes. However, we believe that the temporal resolution afforded by our long time interval analysis technique (on the order of a few minutes) will be sufficient to successfully guide many therapeutic interventions as well as detect most deleterious hemodynamic events, with rapid catastrophic events (e.g., ventricular arrhythmias) being easily detected with standard modalities (e.g., surface ECG leads). Another disadvantage of the long time interval analysis technique is that PAP waveform artifact observed in the critical care setting may be a more significant problem. That is, the new technique requires a contiguous segment of relatively artifact-free PAP waveform on order of minutes for analysis, while the conventional techniques require just a beat. However, note that PAP waveform artifact was a nonfactor in the present controlled laboratory experiments.

It should be noted that the continuous thermodilution method, which was introduced sometime after the standard bolus thermodilution method and is gaining popularity (38, 62–64), is also able to provide continuous CO monitoring with a temporal resolution on order of minutes through use of the pulmonary artery catheter (with a thermal filament proximal to the catheter end for automatic heating of blood). However, the signal-to-noise ratio of this method is small compared with standard thermodilution (7), which may render the continuous method to be less accurate (67). Moreover, in contrast to the PAP waveform analysis technique here, the continuous thermodilution method is unable to provide continuous LAP monitoring.

There are several other methods currently available for measuring CO (see Ref. 7). Ultrasound methods are perhaps the most notable, as they are noninvasive and also provide measurements of left atrial dimensions. However, a major disadvantage of these methods is that they require a well-trained operator to make each measurement. Another important disadvantage is that left atrial dimensions, unlike LAP, do not permit tracking of pulmonary edema and differentiation between cardiac dysfunction and hypovolemia (40). Our technique would therefore be preferred when the invasiveness of the pulmonary artery catheter is permissible.

Upon future successful testing in humans over a wide hemodynamic range (including a lower HR range than that studied herein), our new PAP waveform analysis technique may ultimately be employed for continuous CO and LAP monitoring in critically ill patients instrumented with pulmonary artery catheters. Such continuous monitoring capabilities would offer considerable advantages over the standard, operator-required thermodilution and PCWP methods. These advantages include: 1) circumventing the infrequent use, misuse, and added risk of the standard methods (see introduction); 2) saving precious time in the busy critical care environment (7); 3) obtaining an early indication of deleterious hemodynamic events so as to provide enough time for successful therapy; 4) being able to assess in real time the effects of fluid and drug interventions for optimal therapy (e.g., targeting diuretic dosage in heart failure patients to minimize LAP without significantly compromising CO); and 5) permitting remote critical care monitoring (45). We therefore believe that the new technique, in conjunction with specific pulmonary artery catheter management protocols as called for in recent editorials (2, 23, 40, 44), may ultimately allow the pulmonary artery catheter to reveal a clinical benefit in a wide variety of critically ill patient populations.

GRANTS

This work was supported by grants from the National Institutes of Health (HL-080568) and the National Science Foundation (CAREER 0643477).