Models of Brainstem Responses to Bilateral Electrical Stimulation

Abstract

A simple, biophysically specified cell model is used to predict responses of binaurally sensitive neurons to patterns of input spikes that represent stimulation by acoustic and electric waveforms. Specifically, the effects of changes in parameters of input spike trains on model responses to interaural time difference (ITD) were studied for low-frequency periodic stimuli, with or without amplitude modulation. Simulations were limited to purely excitatory, bilaterally driven cell models with basic ionic currents and multiple input fibers. Parameters explored include average firing rate, synchrony index, modulation frequency, and latency dispersion of the input trains as well as the excitatory conductance and time constant of individual synapses in the cell model. Results are compared to physiological recordings from the inferior colliculus (IC) and discussed in terms of ITD-discrimination abilities of listeners with cochlear implants. Several empirically observed aspects of ITD sensitivity were simulated without evoking complex neural processing. Specifically, our results show saturation effects in rate–ITD curves, the absence of sustained responses to high-rate unmodulated pulse trains, the renewal of sensitivity to ITD in high-rate trains when inputs are amplitude-modulated, and interactions between envelope and fine-structure delays for some modulation frequencies.

Introduction

Bilateral cochlear implants (CI) are growing in importance as a clinical solution for people who are deaf or have severe to profound hearing loss in both ears. Compared with a single cochlear implant, bilateral implants provide patients with improvements in sound localization and in speech reception in complex environments (van Hoesel and Tyler 2003; Schoen et al. 2005; Ricketts et al. 2006). There is widespread belief, however, that bilateral processing possibilities are not being fully realized. Despite the fact that electrical stimulation provides robust responses and more precise phase locking of firings on the auditory nerve (AN) than does acoustic stimulation (Moxon 1967; Kiang and Moxon 1972; Hartmann et al. 1984; Dynes and Delgutte 1992; Shepherd and Javel 1997), interaural timing cues appear to be less useful for bilateral CI users than for normal binaural acoustic processing. In particular, human psychophysical measurements show poorer performance in localization and in ITD discrimination for CI users than for acoustic processing by normal listeners (Poon 2006; Tyler et al. 2006; van Hoesel 2007; Grantham et al. 2008).

Physiological recordings in the inferior colliculus (IC) of the cat in response to electric stimulation of AN fibers show good sensitivity to interaural time delay (ITD) for many stimuli (Smith and Delgutte 2008). Specifically, these results show that electric ITD-tuning with low-rate unmodulated pulse trains was as sharp as normal acoustic tuning to broadband noise at some intensities; however, the sharpness and shape of the rate–ITD curves depend strongly on overall intensity, with dynamic ranges for ITD sensitivity as low as 1 dB for some units. Observed sensitivity was also dependent on the rate of the periodic pulse trains: sensitivity is best below 100 pulses per second (pps) and decreases with pulse rate so that, at rates above 150 pps, most neurons gave only onset responses [consistent with monaural results reported by Snyder and colleagues 2000]. Measurements with amplitude-modulated pulse trains (Smith and Delgutte 2008) show ITD sensitivity for both envelope and fine-structure delays. In particular, when a 1,000-pps carrier is sinusoidally amplitude-modulated at 40-Hz, IC neurons show good sensitivity to fine-structure ITD; as modulation frequencies increase above 100 pps and as carrier frequencies increase above 1,000 pps, sensitivity decreases.

As physiological data become available, opportunities arise for modeling the relationships among the response patterns observed at different levels. In the present study, brainstem models developed to describe responses to acoustic stimuli are applied to electric stimuli. Specifically, responses generated by a simplified variation of the medial superior olive (MSO) model of Zhou et al. (2005) are compared to measured peak-type IC responses for biphasic current pulse stimuli, both modulated and unmodulated. The parameters of the input model stage are varied to explore the effects of higher synchronization, higher rates, and amplitude modulation in response to electrical stimulation. Although the model is fundamentally an MSO model, whereas the comparison data are from the IC, one can think of this as a simplified model for the inputs to the IC with the assumption that the IC inherits its sensitivity (or lack of sensitivity) to ITD from the MSO level. Thus, the parameter range reported here, for example, the relatively fast temporal dynamics that are required in this model for the observed ITD sensitivity, would be seen at the MSO level but not necessarily at the IC level.

Methods

Modeling results presented here were simulated in the NEURON environment (Hines and Carnevale 1997, 2000) and in the EARLAB simulation environment (Mountain et al. 2005). Both the input description and the MSO model are closely related to those used in a previous study (Zhou et al. 2005) with three modifications: (1) the input model includes a wider range of parameter values so that it can describe peripheral responses to both electrical and acoustic stimulations; (2) the cell model has only a soma compartment; and (3) the effect of inhibition is excluded so that the model neuron’s ITD sensitivity depends only on the excitatory inputs. Also, for convenience, the best ITD was chosen to be zero for all model cells. These modifications reduced model complexity and rendered results that are less dependent on specific assumptions.

Cell model

The cell model has one compartment with the ionic channels that were measured and described by Rothman and Manis (2003) in studies of neurons in ventral cochlear nucleus (VCN). We implemented the channel parameters of their Type-II VCN neurons. The maximum conductances of the sodium (Na), low-threshold potassium (KLT), high-threshold potassium (KHT), hyperpolarization-activated inward currents (I_h), and leak currents were specified as follows: G_Na = 1,000 nS, G_LTK = 200 nS, G_KHT = 150 nS, G_h = 20 nS, G_L = 2 nS, and the corresponding reversal potentials were E_Na = 55 mV, E_k = −70 mV, E_h = −43 mV, E_L = −65 mV. For all simulations, the resting membrane potential was −63.6 mV, the capacitance was 12 pF, and the criterion threshold for counting action potentials was −10 mV. Twenty excitatory synapses (ten per side) provided independent synaptic conductance changes. For each synapse, a conductance increment was generated in response to each action potential of its input model. The synaptic conductance increment was simulated by an alpha function with a time constant τ_e of 0.1 ms and with the peak conductance G_e, which was varied in our simulations. The resting membrane time constant was 0.9 ms, and with τ_e equal to 0.1 ms, the resulting half-width of the unitary postsynaptic potential was 0.7 ms. The effects of changes in the synaptic time constant on ITD sensitivity (for τ_e equal to 0.05, 0.1, and 0.25 ms) were also explored.

Based on previous MSO model studies (Colburn et al. 1990; Han and Colburn 1993; Dasika et al. 2005), the ITD sensitivity of a model cell depends on the coincidences between arrivals of subthreshold monaural inputs from the two ears. For the present study, we expected that the results would be affected by, among other parameters, the strength of the monaural inputs; this was explored in part by using different values of peak conductance G_e of individual synaptic inputs in the simulations. For each simulation, when the value of G_e was set, this value of G_e was used for all synapses. In particular, representative values of G_e were chosen to cover the range from 1.4 to 12 nS. For example, in the simulations with amplitude-modulated current pulses, one value of G_e (G_e = 4 nS) was chosen such that summed excitatory activities due to inputs from one ear would be above threshold, and another value (G_e = 1.4 nS) was chosen to be just below threshold. The larger value (G_e = 4 nS) generated a response from synchronized pulses on the ten inputs on one side with 100% probability; the smaller value (G_e = 1.4 nS) never generated a response in unilateral test runs, but generated responses to synchronized bilateral inputs. It should be noted that values of G_e required for threshold response depend on the rest of the cell model, including the location of the synapse (cell body or dendrites, if any) and the kinetics of ionic currents in the voltage-dependent channels, and so the values provided in results are specific to the present model.

The parameter values described above result in model cell behavior that is generally consistent with physiological observations. The membrane of the model cell contains I_KLT and I_Na channels, which have been shown to enhance coincidence detection in MSO cells; in addition, the model contains I_h channels, also found in MSO cells, which depolarize the resting membrane sufficiently to partially inactivate I_Na and activate I_KLT (Svirskis et al. 2004; Scott et al. 2005). The activation of I_KHT and I_KLT contributes to membrane repolarization during an action potential, and the activation of the low-threshold potassium conductance (gKLT) produces faster membrane time constants near resting potential. For example, in the VCN (Manis and Marx 1991), type II neurons (with KLT channels) have faster time constants than type I neurons (without KLT channels). In our model cell, the membrane time constant at rest of 0.9 ms at 38°C is slower than a measured membrane time constant of 0.3 ms during hyperpolarizing current pulses in MSO cells of mature gerbils at 35°C (Scott et al. 2005). The half width of EPSPs of 0.7 ms in our model cells is comparable to 0.4–0.5 ms found in mature MSO cells (Scott et al. 2005). Modulated by KLT activities, the brief EPSPs shorten the coincidence window of MSO cells for detecting ITDs.

Input model

Input synaptic events to the MSO cell model, all excitatory, were generated by ten statistically independent random processes for each side. These inputs describe the firing patterns of bushy cells in the anteroventral cochlear nucleus (AVCN) to acoustic stimuli or to electrical current-pulse stimulation of the AN fibers, with and without amplitude modulation. Probabilities of responses were specified independently for each current pulse or acoustic stimulus cycle. The input models and associated parameters are described separately (below) for unmodulated stimuli, including acoustic tones and unmodulated current-pulse trains, and for amplitude-modulated current-pulse trains.

For tonal acoustic stimuli and for periodic (unmodulated) electrical pulse trains, we assumed, for each input fiber that there was at most one event per period and that input events were generated by a two-stage process for each period: first, the occurrence (or not) of an input was determined with a fixed probability p, and second, the temporal location T_k within the period was determined. This input description is the same as used in Zhou et al. (2005). For these unmodulated cases, input patterns were characterized with three main parameters: the period T of the input stimulus, the average input rate R_ave, and the input synchrony index SI. The parameters R_ave and SI independently control the rate and the temporal aspects of input discharge trains. For tonal stimuli, the period T is the inverse of the tone frequency f_in, and for unmodulated electrical pulse trains, the period T is the inverse of the rate of pulses per second (pps). More specifically, the probability p of an input within a period is a constant (necessarily less than or equal to unity) so that R_ave is equal to p/T. The temporal location T_k within the period was drawn from a Gaussian distribution with mean T/2, and standard deviation T/(2F), i.e., 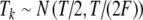. Note that the spike train is delayed by a half period (or by π phase) relative to the start of the period at kT for k equal to zero and positive integers. The parameter F corresponds to the inverse of the coefficient of variation of the jitter distribution and determines the strength of phase-locking. The value of F that provides a desired value of the synchrony index SI can be calculated from the formula 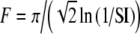. For the case of electrical current-pulse stimuli, in the basic model with τ_e = 0.1 ms, simulations showed that the shape of the summed conductance change is approximately independent of SI when its value exceeds 0.95, a characteristic of electrical stimulation. Thus, in simulations, further increases in the value of SI made no distinctive differences in model response to pulse-train stimuli with pulse rates of 500 pps or higher, which were used in the large majority of our simulations. For each input train, an absolute refractory period, 0.5 ms, was imposed after each input event, during which the arrival of a consequent input event was eliminated. Consequently, reduction in R_ave could occur if the SI value were not sufficiently high. For high SI values, this effect is negligible (e.g., for SI = 0.8 and f_in = 500 Hz, the reduction due to refractoriness is less than 1%).

The simulations reported here for unmodulated pulse-train stimuli explore a range of parameter values, chosen to include values that are appropriate for both acoustic and electric stimuli. Average rates vary from 120 to 350 spikes/s, and values of SI range from 0.8 to 0.99. Our most important goal is to understand the interactions of the input parameters and the cell-model parameters, with the general notion that values of the average rate and synchronization index are likely to be higher for electrical stimuli, especially considering the narrow dynamic range for electrical responses. Since excitatory inputs to the MSO are from spherical bushy cells in the AVCN, these neurons serve as the natural comparison. The lower value of input synchrony (SI = 0.8) in our simplified input model for acoustic inputs is slightly above the lowest maximum values (SI_max = 0.75) observed in individual AVCN projections in the trapezoid body with characteristic frequencies (CFs) in the 300- to 700-Hz range (Joris et al. 1994). Also, while the synchrony in individual low-frequency neurons in the AVCN can be very high (i.e., the majority of values of SI_max are equal to or greater than 0.9 for CFs below 700 Hz), differences in the latencies of multiple MSO-input neurons may lower the effective synchrony of the grouped inputs to an MSO neuron. High SI values, up to 0.99 or even unity, were included to reflect the high synchrony indices observed with electrical stimulation at low frequencies.

Another factor explored here addresses possible differences between electrical and acoustic cases in the distribution of the latencies of the multiple inputs from a single side to brainstem neurons. Latency differences may arise from the timing of excitation of AN fibers or from propagation delays along the ascending pathways to the ITD-sensitive cells. Since the basic computation at the MSO is coincidence detection and since scattered arrival latencies of monaural inputs decrease their effective synchrony, monaural differences in arrival times or phases affect ITD sensitivity. Since electrical stimulation eliminates (or at least complicates) the cochlear traveling wave delay of acoustic stimulation, it could well be that electrical stimulation results in a different time delay distribution over nerve fibers. It is not a priori clear whether this would increase or decrease phase variations at the coincidence cells because of possible latency variations at the excitation point and propagation delays between the excitation point and the coincidence cells. The simplest assumption is that electrical stimulation results in better synchronization at the coincidence detectors. Alternatively, any significant traveling wave delays could be compensated in the normal auditory system, so that electrical excitation would have more variation at the cell. The investigations reported here explore the effects of latency differences between the monaural excitatory inputs of the MSO cell, without specifying the source of the differences in latency (e.g., from the auditory-nerve excitation or from the innervation pathway). We refer to the collective existence of input latency differences as “temporal input dispersion,” and for convenience, we describe the latencies in terms of the stimulus period, i.e., in terms of phase delays. Specifically, we define a phase-dispersion parameter PD as the width (in cycles of the stimulus period) of a rectangular distribution of input phase delays for the monaural inputs to the model MSO cell. Thus, a PD value of zero would mean no added phase delay for any input, and a PD value of unity would mean that the phases of the inputs were uniformly distributed from zero to one full period, therefore collectively carrying essentially no useful phase information about the stimulus for ITD processing. Both random-phase selection from the uniform distribution and uniformly spaced, fixed phases (uniformly spaced over the range of the distribution) were used in the simulations. Results are presented only for the fixed-distribution case since there were minimal differences between fixed and random cases when there are ten inputs per side to the MSO, as assumed here. This PD parameter was explored only for nonmodulated pulse train cases.

For the amplitude-modulated pulse trains stimulating the AN, we assumed that the probability of the occurrence of an input event at the MSO cell is controlled by the amplitude of the electrical pulse and thus varies due to the modulation. Specifically, input excitation is represented by trains of input pulses with Gaussian-distributed amplitudes, defined such that the mean and SD of the pulse height are both proportional to the amplitude of the external stimulus pulse. An action potential input to the model MSO cell occurs when the input pulse exceeds a constant threshold A_th. The temporal location of an input pulse T_k is specified in the same way as in the unmodulated case. Except for the random occurrences of the pulses, there is no significant temporal jitter in the pulse times (SI = 0.99), based on the empirical observation that neural responses at the AN can reach near-perfect synchronization to electrical pulse stimulation below 500 pps (van den Honert and Stypulkowski 1987; Babalian et al. 2003). Thus, the probability of a response to each pulse increases with the amplitude of the electrical current pulse. For an amplitude-modulated pulse train, we assumed the amplitude function A(t), given by 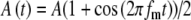, where A is a random variable with mean unity and SD equal to 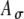, and the pulses occur at multiples of the interpulse interval T, again shifted by a half period T/2 as above. For a particular t, the expected value of A(t) is equal to 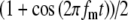, and the SD of A(t) is equal to this expected value scaled by the factor 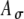, resulting in . Given the threshold A_th, the probability p(t) of an input to the model cell for a pulse occurring at time t is simply calculated as the probability that the Gaussian variable with mean 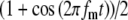and SD 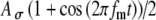exceeds A_th. Samples of the random amplitude A were assumed to be statistically independent from pulse to pulse, so that there is no refractoriness in the input process beyond the limit of one input per pulse for a single input fiber. Since no more than one input pulse was assumed to occur within the interval of length T, and pulses occur (or not) at times 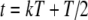, the expected number of inputs in the kth stimulus period is equal to p(kT + T/2), the probability of an event at time kT + T/2. The average input rate during the kth interval, r(kT), is equal to p(kT + T/2)/T with T in seconds. Thus, the expected number of inputs from a single fiber over the total duration NT is 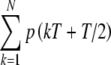, so that the average input rate R_ave is given by 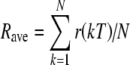. In later sections, when the time dependence of the input rate is plotted, we plot the average rate for interval k as a function of the pulse time; that is, p(kT + T/2)/T is plotted as a function of kT + T/2. Even though k and therefore kT +  T/2 are not continuous, it is convenient to plot with linear interpolation between sequential rates.

The input model for unmodulated pulse trains, described above, can also be formulated in terms of the probability of threshold crossing by a random-amplitude pulse train. Of course, the probability is constant for each pulse, and the implicit assumption is that the synchronization index is within the saturated range of large values, also described above.

In both unmodulated and modulated cases, we tested model responses to variations in the fine-structure ITD (ITD_fine), which is defined as the time difference between the arrivals of individual stimulus pulses from the two sides. A positive ITD_fine indicates the delay of the ipsilateral pulse train by ITD_fine, resulting in pulse times at kT + T/2 + ITD_fine. In the amplitude-modulated pulse-train case, the envelope ITD (ITD_env) is specified separately from the fine structure delay. A positive ITD_env indicates the delay of the ipsilateral envelope function by ITD_env, A(t − ITD_env). Most simulations have an ITD_env value of zero while ITD_fine is varied, although some simulations have other fixed envelope delays. Another possibility is to vary the whole-waveform delay, in which case the fine structure and envelope delays are equal. Cases in which the envelope delay ITD_env is varied separately from fine-structure delay, ITD_fine can be compared to empirical results for acoustic (Sterbing et al. 2003; D’Angelo et al. 2003) and electric (Smith and Delgutte 2008) stimuli.

Results I. Unmodulated, periodic pulse trains

Simulations with unmodulated, periodic pulse-train inputs were run to explore the effects of input parameters for several levels of synaptic strength. Specifically, the input average rate R_ave, the input synchronization index SI, and the range of the input phase distribution PD, were varied for several levels of synaptic strength G_e. For unmodulated pulse trains, simulated inputs for a given pulse rate (in pps) correspond to acoustic inputs at the corresponding frequency (in Hertz), so that the parameter values of R_ave and SI determine the appropriateness of the simulation for acoustic or electric cases. In general, one expects that electric stimulation results in higher values of SI, higher maximum average rates, narrower dynamic ranges, and unspecified changes in PD. As noted above, the effective synchronization of the inputs is determined by the combination of SI and PD. It can be verified that an increase in PD has an effect on the rate–ITD function comparable to a decrease in SI. (A quantitative description of this trading relation has not been undertaken.) The range of SI values explored spans the range from 0.7 to 1.00, the range of average input rates R_ave extends from 120 to 350 spikes/s, and the values of synaptic strength G_e vary from 5 to 9 nS in these unmodulated cases. Within the context of varying R_ave, G_e, and SI, the effects of the excitatory synaptic time constant (τ_e) were also explored, and interactions between 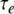and KLT activity were noted.

Effects of input parameters

In the first series of simulations, combinations of input average rate, synchronization index, latency dispersion, and synaptic time constant in the input model were explored with moderate and strong synaptic strengths of 5 and 9 nS.

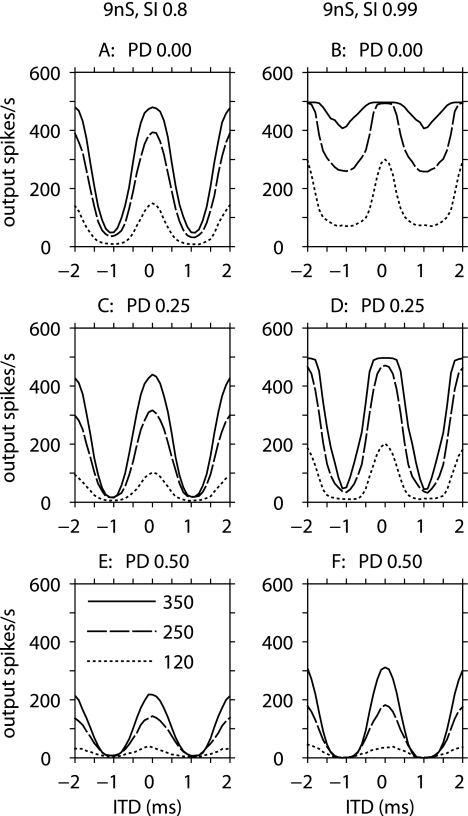
Consider first the strong synaptic strength (G_e = 9 nS) with SI = 0.8 and no phase dispersion, as shown in the top-left panel of Figure 1. Three different input stimulus rates (120, 250, and 350 spikes/s) result in three rate–ITD curves, in which the output rates increase with input rate as expected, and the shapes of the curves are generally maintained. That is, the rate–ITD curves all show good modulation with ITD and therefore good ITD sensitivity. Note that the lowest input rate (120 spikes/s) in combination with the other parameters results in a rate–ITD curve that is similar in response rates and width of ITD-tuning to published peak-type acoustic rate–ITD responses, which have a single maximum per period, as recorded from MSO (Goldberg and Brown 1969; Yin and Chan 1990; Spitzer and Semple 1995) and from IC neurons (Fitzpatrick et al. 2002).

FIG. 1.

Rate–ITD functions from a model MSO cell with strong synaptic strength (9 nS). Left column: results for inputs with SI = 0.8, characteristic of acoustic stimuli. Right column: results for inputs with SI = 0.99, characteristic of electric stimuli. In each row, the input phase dispersion (PD) was set to a different value: A, B PD = 0 (top row); C, D PD = 0.25 stimulus periods (middle row); E, F PD = 0.5 stimulus periods (bottom row). The legend shown in panel E applies to all panels, with the numbers in the legend denoting the average input spike rates (in spike/s) for each of the 20 inputs.

If the input synchronization SI is increased to 0.99 for the inputs to this model cell, with other parameters kept fixed, the output rate increases significantly, as shown in the top-right panel of Figure 1. Most importantly for ITD sensitivity, the increase in input SI produces a large increase in response rate when the bilateral inputs are out of phase, especially for the higher input rates. These responses at unpreferred ITDs (ITD = −1 ms, ITD = 1 ms) are due to substantial “monaural coincidences” (Han and Colburn 1993; Batra and Yin 2004). In combination with the fact that the maximum firing rate saturates at the stimulus rate, the increased out-of-phase response leads to reduced modulation depth and poor ITD sensitivity. When the input rate is 350 spikes/s, the modulation depth is reduced to below 20%, and ITD sensitivity would be expected to be dramatically reduced.

The lower panels of Figure 1 show the effects of latency dispersion (all other parameter values are the same as in the top panels). The phase dispersion PD increases to 0.25 in the second row and to 0.5 in the third row. For the lower value of synchronization (SI = 0.8) in the left panels, an increase in PD from 0 to 0.25 has a relatively small effect, presumably because the additional input dispersion is not significant relative to spread of input times for this value of SI. Increasing the value of PD to 0.5 has a larger effect on rate, but the shapes of the rate–ITD curves are not affected much. For the higher value of synchronization (SI = 0.99) in the right panels, the latency dispersion generally improves the modulation depth by reducing saturation and lowering monaural coincidences. These results are consistent with the general expectation that increases in PD are equivalent to reductions in SI, although the net effect of changes in these parameters depends on their starting values.

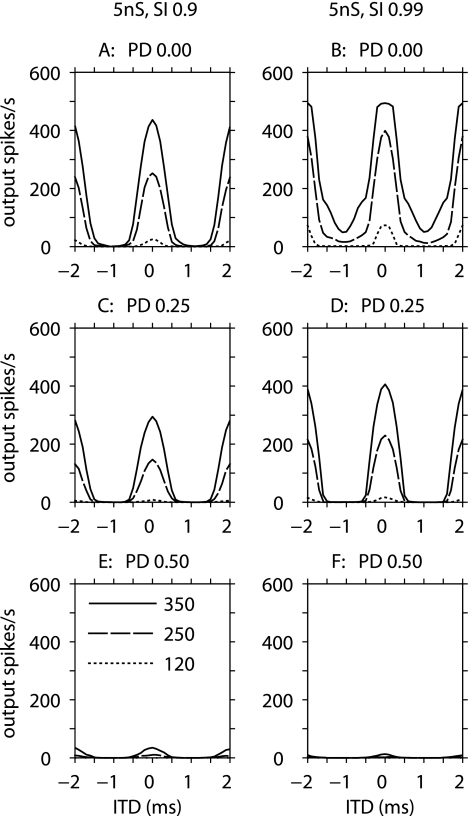
Figure 2 shows results for a cell with a moderate synaptic strength (G_e = 5 nS) when the same parameters are varied. Note that, even though the synchronization index is increased to 0.9 in the left column, the lower synaptic strength with the same number of inputs is not adequate to generate many responses with the 120 spikes/s input rate in either column. On the other hand, the high rates and high synchronization cases do not lead to high rates of monaural coincidences at bad phase nor to saturated rates at good phase. Again, the interaction of parameters, particularly the tradeoff between latency dispersion across fibers and synchronization for single fibers, is clearly observed in these data.

FIG. 2.

Rate–ITD functions from a model MSO cell with moderate synaptic strength (5 nS). Left column: results for inputs with SI = 0.9, characteristic of acoustic stimuli. Right column: results for inputs with SI = 0.99, characteristic of electric stimuli. In each row, the input phase dispersion (PD) was set to a different value: A, B PD = 0 (top row); C, D PD = 0.25 stimulus periods (middle row); E, F PD = 0.5 stimulus periods (bottom row). The legend shown (E) applies to all panels, with the numbers in the legend denoting the average input spike rates in spikes/s for each of the 20 inputs.

Effects of the synaptic time constant

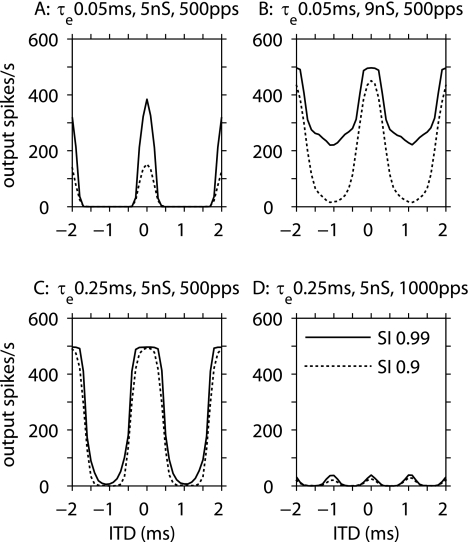
With the exception of the simulations described in these few paragraphs, the excitatory synaptic time constant (τ_e) was maintained at τ_e = 0.1 ms, and the study focused on other aspects of the models. The value τ_e = 0.1 ms was selected because it produced ITD responses that were not overly susceptible to high discharge rates at unpreferred ITD, and that showed robust ITD sensitivity for input frequencies of 500 and 1 kHz. This τ_e value produces a compromise between faster synaptic models that help maintain ITD sensitivity at higher input frequencies, but are more sensitive to input synchrony, and slower synaptic models that are less sensitive to input synchrony, but contribute to a rapid loss of ITD sensitivity with increasing input frequency. Our observations of the effect of the synaptic time constant are summarized in Figure 3, in which the top panels show results for τ_e = 0.05, and the lower panels for τ_e = 0.25 ms. Each panel compares the ITD sensitivity at two levels of input synchrony, with examples of two synaptic strengths and two input frequencies in different panels. The data shown are for average input spike rates of 350 spikes/s per input and zero phase dispersion. For the faster time constant, τ_e = 0.05 ms, there were relatively weak responses for moderate synaptic strengths (5 nS) and moderately high input SI (0.9; panel 3A), and relatively high response rates at unpreferred ITD with higher synaptic strengths (9 nS) and high input SI (0.99; panel 3B), resulting in compromised ITD sensitivity in both conditions. For the slower time constant, τ_e = 0.25 ms, and moderate synaptic strength (5 nS), good ITD sensitivity is provided at both SI values for the stimulus frequency 500 Hz (Panel 3C), but very weak responses occur at all ITD values at both SI values for the stimulus at 1,000 Hz (Panel 3D). In addition, with τ_e = 0.25 ms and 1,000-Hz inputs, responses were similarly weak for input spike rates up to 1,000 spikes/s (not shown). In contrast, for τ_e = 0.05 ms and for τ_e = 0.1 ms, at the same moderate synaptic strength (5 nS) and input synchrony (SI = 0.9 and 0.99), responses to 1,000-pps inputs became strong with increasing input spike rates and maintained well-modulated ITD sensitivity (neither the results for τ_e = 0.05 ms, nor the results for τ_e = 0.1 ms, are shown).

FIG. 3.

Rate–ITD functions in three model MSO cells, showing the effects of synaptic time constants (τ_e), in relation to input synchrony, synaptic strength, and input frequency f_in. Model cells with faster synaptic time constants are more sensitive to input synchrony, whereas those with slower synapses are more sensitive to input frequency. Aτ_e = 0.05 ms, G_e = 5 nS, f_in = 500 Hz; Bτ_e = 0.05 ms, G_e = 9 nS, f_in = 500 Hz; Cτ_e = 0.25 ms, G_e = 5 nS, f_in = 500 Hz; Dτ_e = 0.25 ms, G_e = 5 nS, f_in = 1,000 Hz. The legend showing the input SI values (0.9 and 0.99) in (D) applies to all panels. The average input spike rate of 350 spikes/s for each of the 20 inputs was maintained for every condition shown in this figure.

The reduction of response for τ_e = 0.25 ms is surprising, since larger τ_e values effectively increase overall excitation. Additional simulations (not shown) reveal the reasons for this reduction, namely, that the suppressive effects of the low-threshold potassium conductance (effects described later in connection with Figure 5) are stronger in the presence of prolonged, cumulative synaptic potentials. The membrane factors that reduce the responses across all ITDs at 1,000-Hz also reduce primarily the out-of-phase response at 500-Hz, thus improving ITD sensitivity for the lower frequency input.

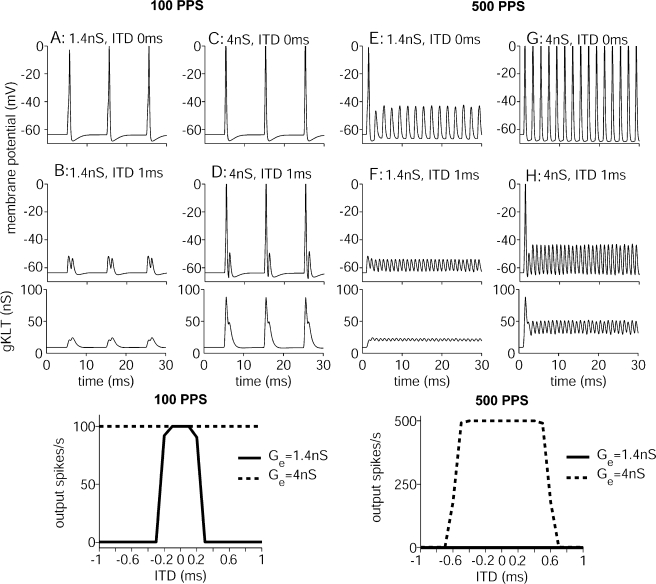
FIG. 5.

Membrane responses of model cells to different ITD values. A, B Membrane potentials for bilateral inputs at 100 pps with zero and 1-ms ITD with G_e = 1.4 nS. C, D Membrane potentials for bilateral inputs at 100 pps with zero and 1-ms ITD with G_e = 4 nS. E, F Membrane potentials for bilateral inputs at 500 pps with zero and 1-ms ITD with G_e = 1.4 nS. G, H Membrane potentials for bilateral inputs at 500 pps with zero and 1-ms ITD with G_e = 4 nS. The conductance of the low-threshold potassium channel (gKLT) for the 1-ms ITD conditions is plotted under the membrane potential traces in B, D, F, and H. The bottom panels show rate–ITD responses for 100 and 500 pps inputs with G_e values of 1.4 and 4 nS.

Summed excitatory conductance functions

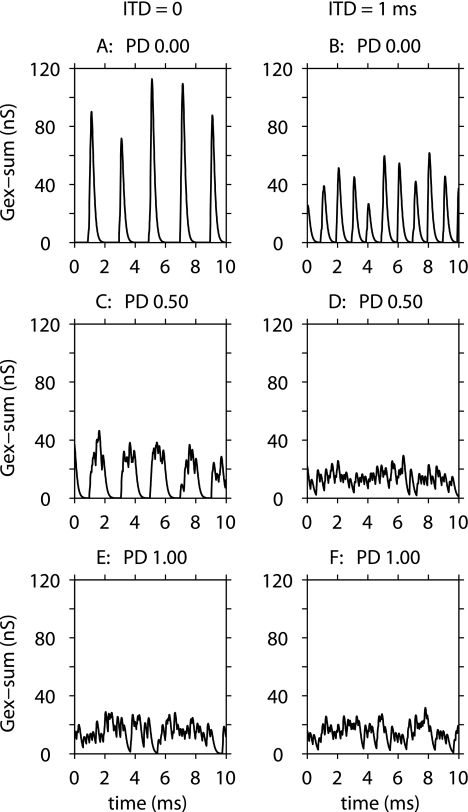
The influences of ITD and input phase-dispersion on G_ex-sum, the summed excitatory conductance from all input fibers in the model MSO cell, are illustrated in Figure 4 for G_e = 9 nS, where G_ex-sum is plotted as a function of time. As in other simulations in this paper, there are ten excitatory inputs from each side. For every condition shown in Figure 4, the stimulus period is 500 Hz, and each input fiber has a discharge rate of 250 spikes/s and an SI equal to 0.99. The overall synchrony of the ensemble of inputs is reduced as PD between the inputs is increased. The summed-conductance function captures the combined effect of inputs on the model cell because left and right inputs are not distinguished in this single-compartment model. In each panel, the summed conductance function G_ex-sum is plotted over a 10-ms interval for conditions that include some of those shown in Figure 1 (right column). Specifically, in Figure 4, time is measured from the start of an arbitrary time point, 1.48 s after the onset of the 500-pps stimulus. The six panels show G_ex-sum for two ITD values (the ITD is zero in the left column, and 1 ms in the right column) and three values of PD as indicated. In panel A, the zero ITD contributes to synchronous, sharply peaked increases in G_ex-sum during each stimulus period, and to the entrainment of output discharges to the stimulus. In panel B with ITD = 1 ms, G_ex-sum exhibits two smaller synchronous and sharply peaked increases per stimulus period, resulting in a discharge rate of just under 300 spikes/s (see Fig. 1, panel B for the rate–ITD function). In the middle row, added phase delays between inputs ranging from 0 to 0.5 stimulus periods were introduced (same condition as the middle, dashed curve in the bottom-right panel of Fig. 1). In panel C with ITD = 0, synchronous increases in G_ex-sum still occur every stimulus period. Although the phase differences between the inputs decrease the amplitude and increase the duration of the conductance increase, the output discharge rate is slightly less than 200 spikes/s by means of the alternation from zero G_ex-sum (producing a lower membrane voltage and relatively inactivated potassium channels in the model) to a high value of G_ex-sum sufficient for rapid membrane depolarization and an action potential. In panel D with ITD = 1 ms, the combined inputs from both sides are evenly distributed across the entire stimulus period, and no periodic behavior can be seen in G_ex-sum. Mean G_ex-sum is similar to that for zero ITD, but the relatively steady G_ex-sum values contribute to a higher baseline membrane potential and the activation of the model’s low-threshold potassium channels. The activated potassium channels suppress further depolarization, resulting in a very low output discharge rate. In panels E and F, the added phase delays between inputs were equally spaced from 0 to 1 stimulus period, producing a lack of periodic increases in G_ex-sum for ITD = 0 and 1 ms, resulting in very low output discharge rates for all values of ITD.

FIG. 4.

The sum of excitatory conductances (G_ex-sum) as a function of time in the model MSO cell with strong synaptic strength (9 nS). In all panels, the stimulus period is 2 ms, and each individual input fiber has a discharge rate of 250 spikes/s and an SI of 0.99. The overall synchrony of the ensemble of inputs is reduced as the phase dispersion (PD) between the inputs is increased. Left column: results for zero ITD. Right column: results for 1-ms ITD. In each row, the input phase dispersion (PD) was set to a different value: A, B PD = 0 (top row); C, D PD = 0.5 stimulus periods (middle row); E, F PD=1.0 stimulus periods (bottom row). The 10-ms sample shown ran from 1.480 to 1.490 s after the onset of the 3-s stimulus. The pulse rates are 500 pps.

Effects of membrane activity on rate–ITD tuning at higher pulse rates

Since responses of IC neurons to electrical stimulation (Smith and Delgutte 2007) show minimal sustained responses for higher pulse rates, the interaction of input pulse rate and membrane activity were explored in our model cell. Figure 5 shows results for unmodulated pulse trains with two synaptic strengths (1.4 and 4 nS) and two pulse rates (100 and 500 pps). In the top two rows of panels in Figure 5, the membrane potential of a model MSO cell is shown in response to bilateral unmodulated pulse-train stimuli at 100 and 500 pps with 0 ms (top row) and 1 ms (second row) ITDs. The conductance of the KLT channel (gKLT) is shown in the third row of panels, for the 1-ms-ITD condition only. The rate–ITD curves are plotted in the bottom panels of the figure for ITDs in the range from −1 to +1 ms. For the conditions illustrated in Figure 5, the spike rate of each input was set equal to the input pulse rate (100 or 500 pps), i.e., the MSO model cell received 20 inputs with a constant rate of 100 or 500 spikes/s. The SI value was equal to 0.99 for all input fibers, and no additional latencies between inputs were introduced (PD = 0). These configurations reveal effects of the input pulse rate and minimize effects of amplitude and timing jitters of inputs on model responses.

For the 100-pps condition with G_e = 1.4 nS (Figs. 5A and B), membrane potentials at zero ITD exceed the threshold with a 100% probability as seen by the action potentials that occur at every multiple of ten milliseconds. When the ITD is 1 ms, there are no action potentials. When the synaptic strength increases to 4 nS (Figs. 5C and D), membrane potentials for both ITD values exceed the threshold with 100% probability. For the 500-pps condition, the same synaptic strengths induce very different membrane activities. The ongoing membrane potential remains in the subthreshold regime at both zero and 1 ms ITD for G_e = 1.4 nS (Fig. 5, panels E and F), even though individual pulses at zero ITD can trigger an action potential as shown in the 100-pps condition (and seen in the onset spike in panel 5E). At the higher synaptic level with G_e = 4 nS (Figs. 5G and H), the membrane potential crosses threshold at every input cycle (every 2 ms) with zero-ITD inputs and remains unresponsive after onset with a 1-ms ITD (i.e., out-of-phase input for 500 pps). In the model, the failure to discharge to high-frequency suprathreshold inputs is correlated with the shunting effect of the low-threshold potassium channel. As shown for the 1-ms-ITD condition in the third row of panels, a sustained upward shift in the membrane potential inducing significant accumulations of gKLT occurs for the 500-pps inputs, but not for the 100-pps inputs.

The above results indicate that the ITD tuning is governed by both the synaptic input strength and the membrane properties such as thresholding, saturation, and shunting behavior. As shown in the bottom panels, ITD sensitivity shows opposite dependences on synaptic input strength at the 100- and 500-pps conditions. For the 100-pps condition, better ITD-tuning results from the low synaptic level (G_e = 1.4 nS) because this low synaptic strength yields suprathreshold inputs at zero ITD but subthreshold inputs at 1-ms ITD. On the other hand, the moderate synaptic level (G_e = 4 nS) yields supra-threshold inputs at both 0 and 1-ms ITDs, resulting in saturated ITD tuning within this ITD range. For the 500-pps inputs, in contrast, spike generation at both 0- and 1-ms ITDs is suppressed by the active channels, notably the low-threshold potassium channel, so that responses are absent at the lower synaptic level. At the moderate synaptic level, responses at zero ITD overcome the shunting effect of active channels more than those at 1-ms ITD, such that ITD-tuning is improved due to the reduced responses at 1-ms ITD. These observations indicate that ionic channel activities could either improve or worsen ITD tuning through suppressing responses at the out-of-phase (Fig. 5H) or in-phase conditions (Fig. 5E), respectively, and that membrane shunting behavior exerts greater influences on model ITD sensitivity to high-rate pulses than to low-rate pulses.

Summary of results with unmodulated pulse trains

When the MSO model cell was stimulated by low-rate, moderately phase-locked, input action potentials, a range of ITD patterns was observed, depending on the degree of synchronization and the average input rate in relation to the synaptic strength of the excitatory synapses. In general, when the average input rate and the synaptic strength are adequate to generate responses, the output firing rate of this simple coincidence cell varies with the ITD; however, if the phase locking of the input fiber responses, as measured by the synchronization index SI, is very strong, and the latency dispersion across input fibers (as measured by the phase-dispersion parameter, PD) is small, then the combined input firings to the cell may excite the cell strongly for every ITD, such that the cell shows a saturated response with minimal ITD dependence. In order to achieve good ITD sensitivity, the combined stimulation must be strong enough to stimulate the cell at its preferred ITD (fixed at zero ITD in the simulations here) and not so strong as to stimulate the cell at the un-preferred ITD (a half-period of delay causing out-of-phase inputs). The responses for out-of-phase inputs at low frequencies are usually generated by “monaural coincidences” which must be minimized to achieve good ITD sensitivity.

Our simulations indicate that inputs of higher synchronization are well suited to weaker synapses and smaller ranges of latencies across monaural inputs, and further that, with this matching, sharply tuned ITD sensitivity can be achieved. Results also indicate that inputs of lower synchronization typically associated with acoustically driven inputs are well suited to stronger synapses, and that with this matching, ITD sensitivity can be maintained over a wide dynamic range of input rates even in combination with considerable differences in the latencies across monaural inputs. Inputs and cell parameters that are “mismatched” lead to saturated output rates or minimal output rates, in both cases leading to reduced sensitivity to ITD in the model cell response.

In addition to the effects of the synaptic strength and input synchrony, the time constant of the excitatory synaptic conductance (τ_e) has effects on the model that interact with activity of the low-threshold potassium channel. While the model results cannot reveal the actual values of τ_e in MSO cells, they suggest that a favorable range of τ_e may exist in the MSO for maintaining good ITD sensitivity at various input conditions; however, a loss of ITD sensitivity may still occur when the input rates and synchrony are increased to levels consistent with stimulation by cochlear implants.

Membrane activity also affects ITD tuning in ways that directly interact with input rate. When the model cell is stimulated by high-rate pulses, illustrated here by 500-pps pulse trains in Figure 5, the model responses can be suppressed with a sustained subthreshold depolarization of the cell. This behavior, which is determined in part by the low-threshold potassium channels in the cell model, is manifested by the absence of sustained responses (Figs. 5E, F, and H) and is observed when the combined input rate is relatively stable (constant over time), strong enough to maintain the activation of the low-threshold potassium channels, but not strong enough to activate the sodium channels to generate an action potential. Together, simulations of unmodulated pulse-train stimuli suggest that the decreases in ITD sensitivity in CI experiments may result from two different neural mechanisms at the MSO level: (1) firing-rate saturations with strong synaptic strength in combination with increases in synchronization as shown for a wide range of input rates; (2) shunting effects of ionic channel activities as shown to high pulse-rate inputs. Of course, similar factors may also be present in more peripheral neurons. In the following section, we focus on reestablishing rate–ITD tuning of an MSO model in high pulse-rate conditions via amplitude modulation.

Results II. Amplitude-modulated stimuli

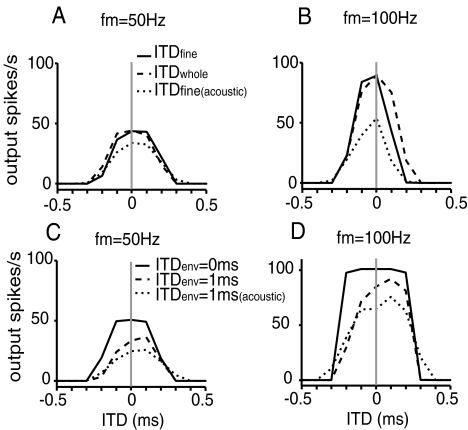
Rate–ITD tuning for delays in the fine structure for sinusoidally amplitude-modulated (SAM) pulse trains are presented in the following subsections. Particular attention is paid to input rate and to modulation frequency for the case when only fine-structure ITD is varied (the envelope ITD is zero). Then, cases are considered in which the ITD of the envelope is not zero and the fine-structure delay and the envelope delay are varied separately; these cases result in ITD functions that are asymmetric around the “best ITD,” which is zero in all of our simulations.

Effects of amplitude modulation and fine-structure delay on input patterns to the MSO

Input patterns to the MSO cells are the result of neural processing at the AVCN in response to acoustic or electric stimulation at the auditory periphery. In Figure 6, the effects of the two input parameters, the discharge threshold A_th and the modulation-amplitude jitter 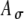, on the input-rate function are explored. As described in the “Methods” section, an input event occurs in response to a stimulus pulse when the random amplitude of the pulse exceeds the threshold A_th. 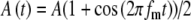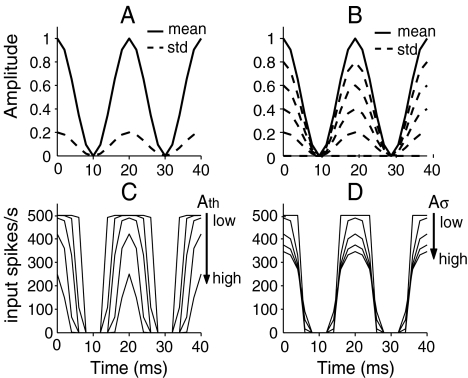The random amplitude is described by the envelope function A(t), where , and A is a Gaussian random variable with a mean of unity and a SD of 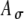. Figure 6 shows the mean and SD of the SAM envelope function of the electrical signal A(t) (panels 6A and 6B) and the corresponding input-rate function r(t) (panels 6C and 6D) calculated for values of t spaced every 2 ms, for specified values of A_th and 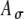(see caption), and with linearly interpolated values in between. Increasing A_th decreases the strength and narrows the width of r(t) for a given 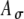(Fig. 6C). If the variability is increased (by increasing ) with A_th fixed, the peak strength of r(t) is decreased, but the width of r(t) is relatively unchanged (Fig. 6D). These observations emphasize that the shape of an input rate-function to the MSO cells may differ from the envelope function of electrical pulse trains due to neural processing preceding the MSO. In simulations, combinations of A_th and 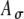values were chosen to yield different input patterns to the model MSO cell; however, the differential effects of A_th and 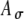were not explored explicitly in this study.

FIG. 6.

Model parameters of SAM stimuli affect the input rate to the MSO model. A The mean 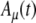and SD 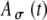of the stimulus envelope A(t) = A(1 + cos(2πf_mt))/2, where A is a Gaussian variable with N(1,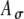), , 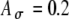and f_m = 50 Hz. B Same functions as shown in (A) with additional examples of 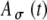, including a range of 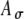values from 0 to 0.8 with an increment of 0.2. C The input rate (calculated at times kT + T/2 and linearly interpolated) using the stimulus in (A) with different threshold values A_th, which range from 0.2 to 1 with an increment of 0.2, and 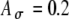. D The input rate using the stimulus in (B) with different 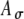values (0 to 0.8 with an increment of 0.2) and with A_th fixed at 0.6.

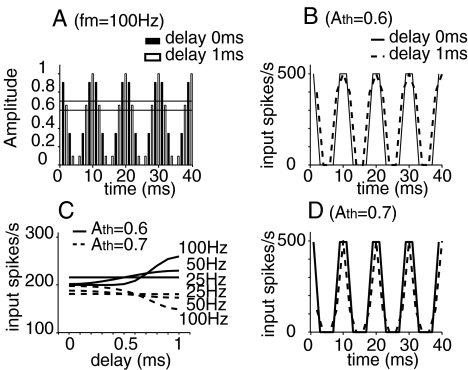
In simulations using SAM stimuli, fine-structure and envelope delays (ITD_fine and ITD_env) were varied independently. For instance, when individual pulses on one side were delayed by D, but the envelopes were not delayed (so that ITD_fine = D and ITD_env = 0), the left or right periodic pulse train was shifted in time according to ITD_fine, and although both pulse trains sampled a common envelope waveform characterized by the equation A(t), each pulse train sampled the envelope at the times of its individual pulses. Figure 7 shows the effects of fine-structure delay ITD_fine on the interpolated form of the input-rate function r(t) for a 500-pps train (pulse period T = 2 ms) modulated at 100 Hz. In Figure 7A, two modulated pulse trains with fine-structure delays of 0 and 1 ms (filled and open bars, respectively) are plotted, both modulated by the same envelope waveform A(t) with f_m equal to 100 Hz. Since the locations of the kth input pulse is centered at kT + T/2 + D with little jitter (see details in the “Methods” section), the parameter T/2 of 1 ms causes pulses in the pulse train with delay D of 1 ms (open bars) to align with the peak of A(t), whereas pulses in the train without the added delay D do not. As shown in Figure 7A, the two pulse trains have different pulse amplitude profiles, even though they sample the same A(t) function. As a result, the shape of the instantaneous input-rate function r(t) varies with the fine-structure delay as well as the threshold value applied to A(t) for postsynaptic events. This effect is substantial when, as in the case shown here, the modulation frequency is within a factor of four or five of the carrier frequency. Two example thresholds (at 0.6 and 0.7) are marked with horizontal lines on Figure 7A. With A_th = 0.6 (and with 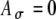), three pulses for the 1-ms delay and two pulses for the zero delay exceed the threshold per input cycle. In comparison, with A_th = 0.7, only one pulse crosses the threshold for 1-ms delays (and still two cross for a 0-ms delay). The corresponding r(t) functions (with 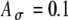) at 1-ms delays exhibit different widths for the two threshold values used—a broader r(t) with A_th = 0.6 (Figure 7B) and a narrower r(t) with A_th = 0.7 (Figure 7D) than the r(t) for zero delays.

FIG. 7.

The influences of fine-structure delays on the input-rate function. A Pulse trains with delays of 0 and 1 ms sample the envelope of the SAM waveform at different points. For purposes of illustration, no amplitude variation is added 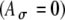; the pulse rate is 500 pps and f_m is equal to 100 Hz. B, D Different fine-structure delays lead to different shapes of input-rate functions r(t), illustrated here for two threshold values, 0.6 and 0.7, and with 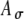fixed at 0.1 and f_m = 100 Hz. C Variations of R_ave with fine-structure delays are stronger for 100-Hz modulated inputs than 25-Hz and 50-Hz inputs. In the average-input-rate plots, parameter values are 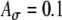and A_th = 0.6 for solid lines and are 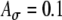and A_th = 0.7 for dashed lines.

Due to these differences in r(t), the average input rate R_ave, as indicated by the area under the interpolated r(t) function, changes with fine-structure delay and A_th. Figure 7C compares variations of R_ave as a function of fine-structure delay at two different threshold levels for 500-pps trains modulated at three different modulation frequencies. Significant variations of R_ave are observed for inputs with 100-Hz modulations, but not with 25 and 50-Hz modulations, between 0- and 1-ms delays (0 to π for the 500-pps trains) because changes in the number of threshold crossings are greater when fewer pulses are contained within one modulation period of SAM stimuli as in the case for higher modulation frequencies. Variations of R_ave also depend on A_th. Here, the two threshold levels result in opposite trends of R_ave with increasing fine-structure delay, correlated with the width difference between the two r(t) functions as shown in Figures 7B and D. Three additional observations, not shown in Figure 7, were made: (1) Due to the periodic nature of the inputs, R_ave changes cyclically with the period equal to that of the input pulse train, and the values of R_ave for delays between 1 and 2 ms (π to 2π for the 500-pps trains) have even symmetry around the 1-ms point. (2) The value of 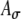affects the trend of variations in R_ave and the shape of r(t). (3) Variations in R_ave depend on the ratio between the carrier rate and modulation frequency, not their individual values. For example, significant changes were also observed for a 1,000-pps carrier with a modulation frequency of 200 Hz, but not 100 Hz. Overall, unlike the cases using unmodulated inputs (which have a flat input-rate function and therefore constant R_ave values at all ITDs), results in Figure 7 reveal that substantial variations in R_ave and in the shape of r(t) could be induced across different delays, depending on the modulation frequency of the envelope. Thus, rate–ITD responses to modulated inputs could be affected by not only the instantaneous timing difference but also the instantaneous rate differences between two input-rate functions. These input effects are described below.

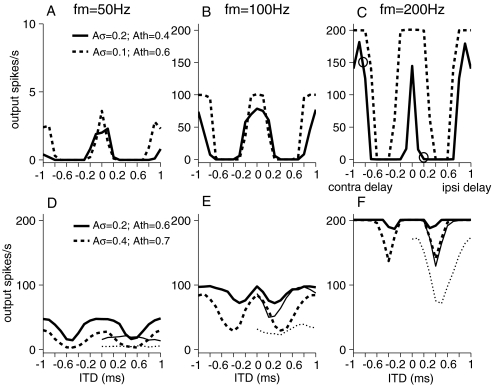
Rate–ITD tuning to SAM inputs: effects of input rate and modulation frequency

In the unmodulated input condition (Fig. 5), membrane shunting behavior confounds neural ITD sensitivity by reducing responses to supra-threshold bilateral inputs at 500-pps. Consequently, these rate–ITD responses do not manifest the input-timing sensitivity of the MSO cell. In the following simulations, amplitude-modulation decreases the effective synaptic input strength (and therefore neural firing) during half of the modulation cycle, thereby reducing the effects of shunting of the membrane for subsequent inputs. Owing to the cyclic input-rate function (Fig. 6), a model cell recovers from the shunting effect of ionic channel activities during the trough of a SAM waveform and tends to discharge along the rising slope of a SAM waveform. Two carrier rates 500 and 1,000 pps were used to investigate the effects of amplitude modulation on fine-structure ITD sensitivity of model cells.

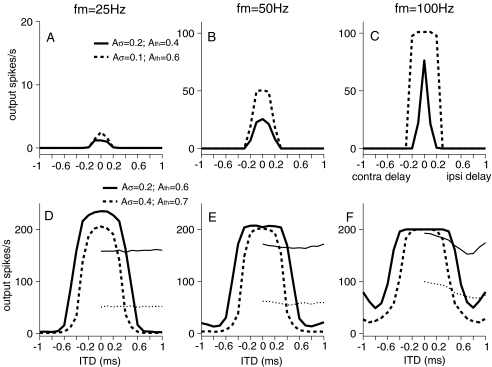
Figure 8 shows the rate–ITD functions for SAM-pulse-train stimuli for a 500-pps carrier with modulation frequencies f_m of 25, 50, and 100 Hz. Two sets of A_th and 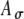values were used to generate inputs with different input-rate profiles and different average input rates R_ave (as described in the “Methods” section and illustrated in Fig. 7). Results depicted with solid lines have higher R_ave values than those depicted with dashed lines. Similar to the unmodulated condition (Fig. 5 bottom panels), responses were tested at low and moderate synaptic strengths (upper and lower rows, respectively). When results in Figures 5 and 8 are compared, one can observe that responses are restored, and ITD tuning is improved by amplitude modulation even though the average input rate is reduced by the modulation. For the low synaptic strength condition when G_e = 1.4 nS (Figs. 8A,B and C), ITD sensitivity is restored when responses are restored. Notably, inputs with lower R_ave values (dashed lines with A_th = 0.6) can lead to even more responses than those with higher R_ave values (solid lines with A_th = 0.4). The increase in responses is not caused by the decrease in R_ave per se, but by the difference in the shape of input-rate function r(t), which can occur when different threshold values are imposed. As discussed below in connection with Figures 9 and 10, changes in the shape of r(t) affect the interplay of depolarization and shunting effects. Both of these factors contribute to the results shown in Figure 8.

FIG. 8.

Rate–ITD responses to 500-pps SAM stimuli at three different modulation rates (three columns) and two input parameter sets (given in the legends and shown by solid and dashed lines). Simulation results using low and moderate synaptic levels (G_e = 1.4 and 4 nS) are shown in the upper and lower panels, respectively. To generate an ITD, only the carrier pulse train (i.e., the fine structure) is delayed, not the envelope. In comparison to the unmodulated case (Fig. 5, 500 pps), model responses showed improved ITD sensitivity to SAM stimuli for both sets of 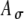and A_th values. At the low synaptic level (A, B, and C), the average input rates R_ave for 25-, 50-, and 100-Hz modulations with zero fine-structure delay are in turn 275, 283, and 242 spikes/s (for the parameter case with solid lines) and 215, 201, and 199 spikes/s (for the parameter case with dashed lines). At the moderate synaptic level (D, E, and F), the corresponding input rates are 206, 202, and 190 spikes/s (solid lines) and 153, 153, and 143 spikes/s (dashed lines). Monaural responses as a function of fine-structure delays between 0 and 1 ms are shown as fine lines in the panels for the moderate synaptic levels.

FIG. 9.

Rate–ITD responses to 1,000-pps SAM stimuli at three different modulation rates (three columns). Simulation results using low and moderate synaptic levels (G_e = 1.4 and 4 nS) were shown in the upper and lower panels, respectively. At the low synaptic level (A, B, and C), the average input rates for 50-, 100-, and 200-Hz modulations with zero fine-structure delay are in turn 553, 566, and 485 spikes/s (for the parameter case with solid lines) and 431, 403, and 399 spikes/s (for the parameter case with dashed lines). At the moderate synaptic level (D, E, and F), the corresponding input rates are 412, 404 and 381 spikes/s (solid lines) and 307, 307, and 287 spikes/s (dashed lines). Monaural responses as a function of fine-structure delays between 0 and 1 ms are shown as fine lines in the panels for the moderate synaptic levels; monaural responses are absent for the low synaptic level.

FIG. 10.

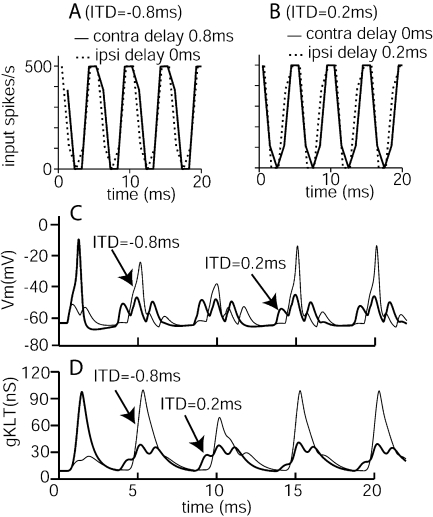
Interpolated input-rate functions, membrane potentials, and low-threshold potassium conductances gKLT for several cases. A, B The input-rate functions for ipsilateral (ipsi) and contralateral (contra) inputs with ITDs of −0.8 ms (contra delay of 0.8 ms) and 0.2 ms (ipsi delay of 0.2 ms), respectively, for the conditions marked by circles in Figure 9c (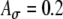, A_th = 0.6, and G_e = 1.4 nS). C, D The membrane potential and gKLT for the same two ITDs. The weaker responses at 0.2-ms ITD are due to the earlier arrivals of ipsilateral inputs, which activate gKLT and reduce the spike generation.

For the moderate synaptic strength (G_e = 4 nS) case (Figs. 8D, E and F), SAM stimuli again result in better rate–ITD tuning than unmodulated stimuli (cf., the dashed curve in Fig. 5). By using SAM stimuli, responses at ITDs near the in-phase condition were decreased by reducing input strength (smaller R_ave), resulting in output rates near 200 spikes/s instead of 500 spikes/s; responses at ITDs near the out-of-phase condition were increased somewhat relative to the unmodulated case by releasing membrane from the shunting state with the SAM stimuli. Between the two input-threshold values used, the height and width of r(t) are significantly reduced for inputs with A_th = 0.7 (dashed lines) and thus the corresponding rate–ITD responses are lower at most ITDs than those to inputs with A_th = 0.6 (solid lines). Altogether, the overall ITD-tuning is narrower in responses to SAM inputs than to unmodulated inputs.

Another aspect of the results shown in Figure 8 is the effect of modulation frequency f_m on ITD sensitivity (cf., the different columns in Fig. 8). We observed at two synaptic strengths that the rate of modulation exerts different influences on ITD tuning. For the lower synaptic strength (upper row), faster modulation leads to greater release from the shunting effect of the membrane and sharper ITD-tuning; for the moderate synaptic strength (lower row), ITD-tuning remains relatively insensitive to the modulation frequency. Such a dependence of model responses on f_m is caused by the interaction between activities of the ionic channels and the dynamics of stimulus amplitude. Recall that the average input rate R_ave and the shape of the input-rate functions vary with fine-structure delays (cf., Fig. 7), depending on the modulation frequency. It is likely that the ITD responses shown in Figure 8 originate from the delay-dependent r(t), as well as the sensitivity of the model cell to ITDs. To reveal the underlying input strength at different ITDs, monaural response rates as a function of fine-structure delays are plotted along with the rate–ITD responses at the moderate synaptic strength condition (thin lines in Figs. 8D, E, and F). (No monaural responses were elicited at the low synaptic strength conditions.). Because the discharge rate of the model cell is affected by both R_ave and the amplitudes of individual pulses within one modulation period, monaural rate may not exhibit the same dependence on delays as R_ave does, as reflected in the nonmonotonic dependence of monaural rate on delay (Fig. 8F) in contrast to the monotonic changes in the average input rate over the same range as seen in Figure 7C. It is observed that monaural rates at modulation frequencies of 25 and 50 Hz remain fairly constant with delays, as expected from results in Figure 7C. With a modulation frequency of 100 Hz, the monaural rate is not constant over delay and varies similarly to the binaural responses in Figure 8F. Thus, the rate–ITD responses at modulation frequencies of 25 and 50 Hz, but not 100 Hz, reflect more of the actual ITD-sensitivity of the model cell. The observed dependence of monaural responses on fine-structure ITD (when envelope ITD is fixed) would be difficult to use to judge relative delays or to make other behavioral judgments because this dependence varies with the individual neuron. In the model here, changes in threshold change this dependence as seen in Figure 7C, so that one would expect a distribution of parameters over the population of cells; thus, sensitivity to these changes would require knowledge of population distributions, overall levels, etc. This seems unlikely to be useful for monolateral CI users.

Figure 9 shows the rate–ITD functions for SAM-pulse-train stimuli for a 1,000-pps carrier with modulation frequencies f_m of 50, 100, and 200 Hz. All other model parameters remain the same as those in simulations for the 500-pps carrier rate. The same effects of input rate and modulation frequency occur at both synaptic levels; these effects are described above in connection with Figure 8. Variation in the delay-dependent monaural rates at the moderate synaptic level are clearly seen (fine lines in panels D–F) when modulation frequencies of 100 and 200 Hz were used. One interesting property seen in the results of Figure 9 (where two fine-structure periods are shown) is that responses between 0- and 0.5-ms ITDs (ipsilateral inputs delayed) and those between –1 and –0.5-ms ITDs (contralateral inputs delayed) are not identical for some input conditions, even though these ITD values correspond to the same interaural phase differences (IPD), 0 to π, due to the cyclic nature of the inputs. A notable instance is marked by circles at ITDs of −0.8 and +0.2 ms in Figure 9C corresponding to the 200-Hz modulation frequency. As illustrated in Figure 10, this result can be understood by the dependence of the shape of the input-rate function on the fine-structure delay r(t). Delaying the contralateral inputs by 0.8 ms (solid line in Fig. 10A) does not lead to a same r(t) function as delaying ipsilateral inputs by 0.2 ms (dashed line in Fig. 10B). Because the alignment in the strength of r(t) between ipsilateral and contralateral inputs affects model ITD responses, the model cell discharges significantly more at the ITD of −0.8 ms than at the ITD of 0.2 ms, as shown in both Figures 9C and 10C. A close examination of responses at an ITD of 0.2 ms reveals that the early arrival of ipsilateral inputs (dashed line, Fig. 10B) activates the low-threshold potassium channel (Fig. 10D), which reduces the membrane depolarization and firings to subsequent inputs (Fig. 10C), compared to the condition with an ITD of −0.8 ms. This observation indicates that when the envelope modulation frequency is relatively high, and fine-structure and envelope ITDs are independently varied, model responses to ITD_fine around the secondary peaks (ITD = ±1 ms at 1,000 pps or IPD = ±2π) may not replicate those at the zero ITD and that the rate–ITD curve may not be symmetric around an IPD of π.

Rate–ITD tuning to SAM inputs: effects of asymmetric inputs and envelope delays

Model ITD responses presented here so far were simulated under the assumption that bilaterally identical electrical stimulation of AN fibers generates statistically identical ipsilateral and contralateral inputs to an MSO cell. This assumption was realized by applying the same A_th and 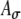values to SAM inputs from the two sides. However, the neural processing between the AN and MSO may not be identical between two sides. For example, different monaural response rates to ipsilateral and contralateral inputs are often reported in the MSO (Goldberg and Brown 1969; Yin and Chan 1990; Spitzer and Semple 1995). In addition, similar to many physiological studies, ITD sensitivity in this model study is based on responses to fine-structure delays; the envelope function A(t) does not shift with ITD_fine (i.e., ITD_env = 0 for all ITD_fine). In normal sound fields, however, sounds that reach the two ears have envelope ITDs (approximately) matched to fine-structure ITDs (i.e., ITD_env = ITD_fine). Thus, bilateral electrical stimulations with unmatched ITD_env and ITD_fine may lead to unnatural outcomes of binaural processing. In the simulations of this section, effects on rate–ITD functions caused by interaurally different input patterns and/or envelope delays were explored. The interaurally asymmetric effect was simulated by using different A_th values for inputs to the MSO model from the two sides in response to the same SAM waveform. This manipulation leads to differences in the magnitude and width of the input-rate functions for ipsilateral and contralateral inputs (denoted by r_ipsi(t) and r_contra(t), respectively), as illustrated in Figure 6C. The effects of ITD_env were simulated by time-shifting the envelope function A(t) prior to amplitude-modulating the periodic pulse trains. To assert that the effects of asymmetric input patterns and envelope delays do not rely on the high synchronization of the electrical pulse trains (SI = 0.99 is used), we also simulated model responses to acoustic SAM stimuli by reducing response synchrony to the low-frequency tones. For the acoustic condition, SI = 0.9 is used based on the empirical measurements from fibers of the trapezoid body (Joris et al. 1994).

Figure 11 shows rate–ITD_fine responses to 500-pps SAM stimuli with f_m equal to 50 and 100 Hz and with manipulations in either ipsilateral or contralateral input levels (via A_th) or envelope ITD, ITD_env. Synapses with low strengths, G_e = 1.4 and 1.6 nS, were used for electric and “acoustic” simulations, respectively. When different A_th values were used (see caption for panels A and B), for the condition in which ITD_fine = ITD_env, rate–ITD tuning was reasonably symmetric around zero ITD (as shown by the ITD_whole response in dashed lines), indicating that responses of model cells are sensitive to the absolute time delay between r_ipsi(t) and r_contra(t), and less sensitive to the direction of the delay (i.e., positive or negative ITDs) and to the relatively small difference in strength between r_ipsi(t) and r_contra(t). In contrast, for the condition in which ITD_fine and ITD_env are inconsistent, the response dependence on fine-structure delays ITD_fine (with ITD_env = 0) is not symmetrical around zero (cf., solid curves in Figs. 11A and B). This is primarily due to variations in the amplitude profiles of r_ipsi(t) and r_contra(t) with fine-structure input delays when the envelope delays are fixed. As shown in Figure 7, depending on the threshold value used, opposite trends of changes in the width and R_ave of the input functions with input delay can occur, resulting in the condition that r_ipsi(t) leading r_contra(t) produces significantly different effects than r_contra(t) leading r_ipsi(t). The disparity in the shape and strength of bilateral input functions can be strong enough to elicit different subthreshold membrane activity associated with gKLT, similar to results shown in Figures 10C and D, and thus different discharge rates of model cells at symmetric ITDs. Such input-rate effects on ITD tuning are more apparent in responses to the 100-Hz f_m, which shows more abrupt changes in r(t) with delays (Fig. 7). Moreover, reduced synchronization in the fine-structure of inputs, as in the “acoustic” stimulation case, reduces the response rates, but does not eliminate the asymmetries in the shape of the ITD function (dotted lines). Thus, bilateral differences such as those in the threshold may effectively introduce asymmetry in ITD tuning to SAM stimuli for a variety of conditions.

FIG. 11.

Effects of interaural differences in input-rate functions on rate–ITD tuning. Differences due to interaural differences in threshold A_th (A and B) and in envelope delay ITD_env (C and D) are shown. The pulse rate is 500 pps and f_m is equal to 50 Hz in A and C and 100 Hz in B and D. The low level of synaptic strength (G_e = 1.4 nS) was used for all simulations except for conditions marked (‘acoustic’) where G_e = 1.6 nS and SI = 0.9. (All other conditions have SI = 0.99 as in Figs. 5–10.) A, B Input functions r(t) with different profiles between ipsilateral and contralateral stimuli lead to asymmetric rate–ITD_fine tuning when ITD_env is zero, but not for whole-waveform delays (when ITD_whole = ITD_fine = ITD_env). The different r(t) shapes were generated by using different A_th values for the two bilateral inputs. In A, A_th is equal to 0.6 and 0.7 for contralateral and ipsilateral stimuli, respectively; 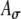equal to 0.1 for both. In (B), the corresponding values for A_th are 0.6 and 0.4 for contralateral and ipsilateral stimuli with 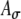equal to 0.2 for both. C, D Input functions r(t) with different envelope delays ITD_env also lead to asymmetric rate–ITD_fine tunings. The response rate also decreases as a result of desynchronized rate profiles between ipsilateral and contralateral stimuli; here A_th = 0.6 and 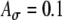were used for the pulse trains on both sides.

In panels C and D of Figure 11, the interaural envelope delays are varied, while the values of A_th and all other parameters are the same on both sides. By introducing nonzero ITD_env, the ipsilateral and contralateral pulse trains sample different envelope waveforms at zero ITD_fine, resulting in different r_ipsi(t) and r_contra(t) functions, similar to the case using different thresholds (Figs. 11A and B). As expected, introducing nonzero ITD_env moves the peak responses to a different ITD, as illustrated by the 0.1-ms shift in panels C and D, and leads to an asymmetrical ITD_fine function around zero ITD. In addition, less synchronization in the fine structure (“acoustic case”) changes the rate, but not the shape of responses (dotted lines). In comparison, responses are stronger and symmetric around zero when an ITD_env of zero was used. Together, results in Figure 11 indicate that the ITD_fine values with the maximal responses reflect input configurations that tend to match the best ITD (zero here) and that promote good recovery from the membrane shunting state.

Summary of results for modulated inputs

By modulating the input waveform, the neuron is stimulated anew in each modulation cycle, and sustained (periodic) responses return when the modulation frequency is low. The sensitivity to modulation seen here depends on the voltage-sensitive channels of the model-cell membrane; there are no inhibitory inputs. Modulating the envelopes of inputs also affects ITD sensitivity. A tuned rate–ITD_fine function is achieved for some combinations of input rate, synaptic strength, and modulation frequency. In our simulation, the interaction between membrane activity and input patterns dominates the ITD sensitivity of model cells. The observed ITD tuning to SAM stimuli, therefore, depends on the characteristics of ionic channels applied and would presumably be absent in responses of model cells that do not implement an active cell membrane, such as models that use a simple cross-correlation between bilateral inputs to describe the MSO activity. Responses of model cells also reveal differential sensitivity to and interactive effects with envelope and fine-structure ITDs. When the modulation frequency is a significant fraction of the carrier pulse rate, there is an undersampling of the envelope, so that inputs with different input phases (fine-structure ITDs) have different shapes of instantaneous rate functions r(t). These effects led to asymmetries in the fine-structure of ITD dependence around an IPD of π, even when the basic model structure was symmetric. Introducing unequal input thresholds or a nonzero envelope delay enlarges further the difference between r_ipsi(t) and r_contra(t) at individual ITDs, which leads to asymmetric rate–ITD curves for fine-structure ITD around the preferred ITD (zero here). This observation suggests that peak ITD in response to electrical stimulation is not necessarily determined by the delay difference between the input pulse trains when bilateral excitatory inputs have mismatched envelope and fine-structure waveforms (ITD_fine ≠ ITD_env) or when there are differences in the neural discharge threshold (A_th) between the two sides at more peripheral levels. This latter factor may be thought of as an intrinsic level difference between two sides, which is manifested by different monaural response rates in the majority of MSO units (Goldberg and Brown 1969; Yin and Chan 1990; Spitzer and Semple 1995).

Discussion

A simplified MSO cell model was used to explore responses of binaurally sensitive neurons to patterns of input spikes that represent stimulation by acoustic or electric waveforms. In general, although the model is very simplified, it captures aspects of available midbrain data and suggests issues that may be important for understanding psychophysical results. In this section, we compare observations from the model to physiological recordings and relate our study to reported sensitivity of CI listeners to ITD.

Relation to physiological responses

The behavior of the simple model analyzed here is compared to physiological observations from the inferior colliculus (IC) in response to bilateral electrical stimulation of acutely deafened animals. Since simulation results are generated by a simplified MSO model (with only excitatory inputs), comparisons are made with the peak-type responses of IC neurons. We assume that the ITD sensitivity of these IC neurons is to a large extent inherited from those of the MSO outputs. In the binaural coincidence-detector neurons of the MSO, fast synapses and specific membrane responses (e.g., shunting behavior of KLT channels) are used to detect submillisecond input delays. These membrane properties may be unnecessary for IC neurons with inherited ITD sensitivity.

One of the observations of Smith and Delgutte (2007) is that rate–ITD functions of single IC neurons in response to electrical stimuli are comparable to those of acoustic stimulation for limited current ranges. Although we have not quantified the degree of synchrony, width of tuning, nor the frequency dependence of these measures, model outputs are generally consistent with their observations. The primary difference between electrical and acoustic cases in the modeling is the lack of robustness to variations in the model parameters when the input patterns to the comparator cell are highly synchronized, as one would expect for electrical stimulation cases. Our modeling efforts focus on the tendency toward saturation of output rate with a resulting lack of sensitivity to ITD. This is explored explicitly in the behavior of the simple MSO model in response to unmodulated bilateral excitatory inputs under various combinations of synaptic and input parameters (Figs. 1 and 2). Saturated behavior around the preferred ITDs is seen in both the model and empirical data. Two factors appear to contribute to this behavior: (1) the limited dynamic range of the auditory nerve response to electrical currents; and (2) the tendency of the binaural cells to saturate for highly synchronized, high-rate inputs. Another important factor influencing model responses to high-rate inputs is the shunting effect of ion channels so that model cells only respond at stimulus onset (Fig. 5E and H).

Similarities between model behavior and empirical data are also seen for the modulated conditions. Consistent with neural data (Smith and Delgutte 2008), model responses show improvements in ITD sensitivity when SAM pulse trains are used (Figs. 8 and 9). The presence of modulation allows sensitivity to the fine structure of a waveform, even when the pulse rate is too high to get sustained responses to unmodulated trains. Consistently shown at multiple modulation frequencies, more (fewer) ITD responses are elicited at the low (moderate) synaptic level to modulated inputs than to the unmodulated. Interestingly, model results with and without modulation resemble physiological results in an acoustic IC study by Kuwada and colleagues (D’Angelo et al. 2003; Sterbing et al. 2003). They found that neurons show either enhanced or suppressed responses to SAM stimuli with low-frequency carriers and that neurons with lower response rates to unmodulated stimuli tend to have greater enhancement effects of modulation (cf. Figs. 5 and 6 in Sterbing et al. 2003). Notably, our simple model does not involve differences in adaptation between ascending excitation and inhibition as proposed by others (D’Angelo et al. 2003) in discussing the above phenomena; rather, this behavior results from the interaction between the pulse strength and the release from shunting of the membrane due to KLT channels at the initial stage of bilateral interaction.

It is clear that a more complex model will be needed to capture the complexity of IC cells and their innervation, especially those with nonpeak-type patterns of ITD sensitivity. Simple models, like the one explored here, provide initial information about what aspects of available data can be understood with basic mechanisms. Starting with a simple model, the effects of added attributes, such as inhibitory inputs or a more complex array of ion channels, can be evaluated in the context of the differences relative to the simple models. The fewer the parameters of a model, the clearer the role of each parameter, so there are advantages to starting simple. In the case of the simple MSO model used here, it is informative that saturation effects are so clearly prominent and that improvements in sensitivity to fine-structure ITD are provided by envelope modulation.

Relation to psychophysical abilities of CI users

Smith and Delgutte (2007) have pointed out an apparent conflict in that IC neurons are consistently well-tuned to ITD (when the stimulus is appropriately chosen for the neuron), whereas human listeners’ sensitivities to ITD with bilateral CIs are much poorer than with normal acoustic hearing. To address this issue, it is necessary to specify the information that is available for judgments based on the population of neural responses. In comparisons between ITD sensitivity in electric hearing and acoustic hearing, the population point of view is critical because differences in the populations imply both differences in information available and changes in the selection process of which neurons provide useful information as circumstances change. Changes in the selection process may require a period of learning and adaptation to the changed distribution of information over the population.

Both the model explored here and empirical results from the IC show good ITD sensitivity for single neurons, but only for a narrow range of stimulus parameters. Thus, for a fixed stimulus, the population of MSO cells may be predominately cells that were stimulated to saturation (with no dependence on ITD) or not adequately stimulated to exhibit ITD discrimination. From the overall psychophysical point of view, the quality of ITD discrimination performance would depend on the ability of the processing to focus on the ITD-sensitive cells and to ignore the larger number of ITD-insensitive cells. This may require modified central processing, significantly different from the normal processing of ITDs for acoustic inputs.

Simulation results in this study suggest that performance in discriminating ITDs would improve if the configuration of the inputs or the cell parameters such as synaptic strength could be adjusted. Our modeling results also suggest that an important difference between electric and acoustic hearing may be the difference in the distribution of latencies over the auditory-nerve fiber population, a factor that influences ITD sensitivity. It would be interesting to know whether such artificially induced changes in temporal dispersions at the MSO can be beneficially adjusted with restored synaptic functions as observed in the cochlear nucleus of congenitally deaf animals under electrical stimulation (Ryugo et al. 2005). As revealed in various animal models (Keuroghlian and Knudsen 2007), many aspects of sound processing including binaural hearing can be modified by experience in both young and adult animals through neural plasticity and this may apply to ITD sensitivity in long-term implant patients.

Some of these results may also be relevant to the encoding of the stimulus envelope (Shannon et al. 1995). For simple stimuli, it has been argued that to represent the envelope information in SAM pulse stimuli, the carrier rate f_c should be at least four to five times the modulation rate f_m to avoid the undersampling problem (Wilson 1997). For ITD sensitivity, this ratio f_c/f_m may have to be even higher because the input rate varies significantly with input delay when f_c/f_m equals five in our simulation, causing different responses at the main and side peaks of ITD curves. Additionally, a slight imbalance between bilateral inputs significantly altered ITD responses (cf., results for f_m of 100 Hz in Fig. 11). In this context, recall that McKay et al. (1994) reported that in the low f_c/f_m ratio range, the detection of modulation rate can be disrupted when the carrier and modulation rates are not harmonically related. Although only harmonic carrier and modulation rates were used in the model results presented here, other results (not presented) showed that for inharmonic conditions, input rate profiles are not identical across modulation cycles and, rate–ITD responses show even more complex patterns. Overall, our results imply that in electrical hearing the extraction of fine-structure ITDs and therefore spatial information may be greatly influenced by the complex stimulus envelopes that carry speech information. One of the implications of this work is that envelope information is better preserved when the envelope delay and the fine structure delays are synchronized or when the ratio f_c/f_m is large. Also, studies that simultaneously explore representations of speech signals and source locations are suggested by this modeling.

Overall, we simulated several observed aspects of ITD sensitivity without evoking complex neural processing. Encouraged by the results with this simple model, we plan to develop a more complete model that predicts more complex aspects of IC responses, e.g., the model of Cai et al. (1998), and that includes explicit descriptions of the stages of peripheral processing. Ultimately, a more complete model would allow the testing of alternative stimulation and coding strategies with respect to detailed binaural information.