Abstract
Accurate prediction of B-cell epitopes has remained a challenging task in computational immunology despite several decades of research. Only 10% of the known B-cell epitopes are estimated to be continuous, yet they are often the targets of predictors because a solved tertiary structure is not required and they are integral to the development of peptide vaccines and engineering therapeutic proteins. In this article, we present COBEpro, a novel two-step system for predicting continuous B-cell epitopes. COBEpro is capable of assigning epitopic propensity scores to both standalone peptide fragments and residues within an antigen sequence. COBEpro first uses a support vector machine to make predictions on short peptide fragments within the query antigen sequence and then calculates an epitopic propensity score for each residue based on the fragment predictions. Secondary structure and solvent accessibility information (either predicted or exact) can be incorporated to improve performance. COBEpro achieved a cross-validated area under the curve (AUC) of the receiver operating characteristic up to 0.829 on the fragment epitopic propensity scoring task and an AUC up to 0.628 on the residue epitopic propensity scoring task. COBEpro is incorporated into the SCRATCH prediction suite at http://scratch.proteomics.ics.uci.edu.
Keywords: B-cell, continuous, epitope, prediction, SVM
Introduction
B-cell epitopes are the portions of antigens that are recognized by the variable regions of B-cell antibodies. Researchers can use knowledge about epitopes to design diagnostic tests (Schellekens et al., 2000), develop synthetic vaccines (Tam and Lu, 1989; Hughes and Gilleland, 1995) and engineer therapeutic proteins (Chirino et al., 2004). In contrast to T-cell epitope prediction, B-cell epitope prediction has yet to reach a high level of accuracy and remains a very challenging task in computational immunology.
Historically, researchers have differentiated continuous epitopes (epitopes that consist of a linear sequence of residues) from discontinuous epitopes (epitopes that consist of a non-linear collection of residues). It is estimated that only 10% of the B-cell epitopes are continuous (Pellequer et al., 1991). However, van Regenmortel (van Regenmortel, 2006) pointed out that many discontinuous epitopes consist of several groups of linearly continuous residues and that continuous epitopes have a tertiary structure. Thus, it is worthwhile to develop continuous epitope predictors since systems trained only on continuous epitopes could be useful to identify both continuous and discontinuous epitopes.
Initial attempts at predicting epitopes involved propensity scales combined with various local averaging techniques (Hopp and Woods, 1981; Parker et al., 1986; Pellequer et al., 1991; Pellequer et al., 1993). On small datasets, these methods appeared to be quite useful. However, Blythe and Flower (Blythe and Flower, 2005) showed that on a larger dataset, no simple propensity scale and averaging technique could do much better than random.
Recently, there have been two general approaches for continuous epitope prediction. One approach is to assign an antigenic propensity score to each residue in the query protein. This approach is followed by Larsen et al. (Larsen et al., 2006) and Söllner and Mayer (Söllner and Mayer, 2006). Another approach to epitope prediction is to classify sequence fragments as an epitope or a non-epitope. This approach is followed by Saha and Raghava (Saha and Raghava, 2006), Chen et al. (Chen et al., 2007) and El-Manzalawy et al. (El-Manzalawy et al., 2008).
In this article, we present COBEpro, a two-step system for the prediction of continuous B-cell epitopes. In the first step, COBEpro assigns a fragment epitopic propensity score to protein sequence fragments using a support vector machine (SVM) with a unique set of input features. While most previous methods use an artificially fixed length fragment, COBEpro is capable of using sequence fragments of any length. In addition, COBEpro can incorporate predicted or true secondary structure and solvent accessibility into the SVM. In the second step, COBEpro calculates an epitopic propensity score for each residue based on the SVM scores of the peptide fragments in the antigen sequence. In this article, we show that COBEpro achieves high levels of performance on several publicly available datasets relative to previously published methods. Moreover, COBEpro addresses both the problem of distinguishing epitope peptide fragments from non-epitope peptide fragments and the problem of assigning an epitopic propensity score to residues within an antigen sequence. In addition to benchmarking COBEpro on several common continuous B-cell epitope datasets, we also benchmark COBEpro on a discontinuous B-cell epitope dataset and make blind predictions for the top 10 antigens recently identified in the pathogen Francisella tularensis (Sundaresh et al., 2007).
Methods
Datasets and preparation
In this article, we used several different datasets to train and benchmark COBEpro. These datasets were derived from several different previously published sources: BciPep (Saha et al., 2005), Pellequer (Pellequer et al., 1993) and HIV (Korber et al., 2003). The BciPep datasets consist of epitope/non-epitope sequence fragments. The Pellequer and HIV datasets consist of whole antigen proteins annotated with precise epitope boundaries.
The BciPep database was originally curated by Saha et al. (Saha et al., 2005) and subsequently used for deriving datasets and training predictors by Saha and Raghava (Saha and Raghava, 2006), Chen et al. (Chen et al., 2007) and El-Manzalawy et al. (El-Manzalawy et al., 2008). The dataset curated in Chen et al. (Chen et al., 2007) consists of 872 epitope sequence fragments and an equal number of assumed non-epitope fragments randomly selected from the SWISS-PROT database. In this article, we refer to the fragment dataset curated by Chen et al. as ChenFrag. Although the epitopes in the BciPep database are of varying length, Chen et al. applied a truncation-and-extension method to create fragments 20 residues in length. Additionally, no attempt was made by Chen et al. to remove possible homologous antigen sequences.
The redundancy-reduced dataset curated by El-Manzalawy et al. (El-Manzalawy et al., 2008) consists of 701 epitope sequence fragments and an equal number of assumed non-epitope fragments randomly selected from the SWISS-PROT database. In this article, we refer to the fragment dataset curated by El-Manzalawy et al. as BCPREDFrag. The truncation-and-extension method was also applied by El-Manzalawy et al. to curate the BCPREDFrag dataset. Additionally, El-Manzalawy et al. reduced redundancy in the BCPREDFrag dataset at an 80% sequence identity threshold.
One concern with the method of randomly selecting non-epitope fragments from the SWISS-PROT database used by Chen et al. in the creation of the ChenFrag dataset and by El-Manzalawy et al. in the creation of the BCPREDFrag dataset, is that the predictors could learn to discern antigen sequence from non-antigen sequence as opposed to epitope fragment/non-epitope fragment classification. We therefore curated four additional epitope/non-epitope fragment datasets to evaluate COBEpro's binary classification performance using the HIV and Pellequer databases.
The HIV database was originally curated by Korber et al. (Korber et al., 2003) and a training dataset was subsequently curated by Larsen et al. (Larsen et al., 2006). This dataset consists of 10 antigenic proteins and 103 different epitope fragments. Approximately, 38% of the residues in this dataset are annotated as belonging to at least one epitope. The Pellequer database was originally curated by Pellequer et al. (Pellequer et al., 1993) and a training dataset was subsequently curated by Larsen et al. (Larsen et al., 2006). This dataset consists of 14 antigens and 83 different epitope fragments. Approximately 34% of the residues in this dataset are annotated as belonging to at least one epitope.
From these whole sequence datasets, we extracted both fixed length and variable length fragments. We randomly selected non-epitope fragments from the non-epitope annotated regions of the antigen sequences. This is in contrast to the method used by Chen et al. (Chen et al., 2007) and El-Manzalawy et al. (El-Manzalawy et al., 2008) of randomly selecting non-epitope fragments from SWISS-PROT. We were able to select non-epitope fragments from antigens in the datasets because the proteins in the datasets were well studied and it was likely that most of the epitopes have been annotated. Our motivation for selecting non-epitope fragments from the same sequence, as opposed to selecting them randomly from SWISS-PROT, was to ensure that we were evaluating COBEpro's ability to discern epitope from non-epitope fragments, rather than antigen from non-antigen.
For each epitope fragment in the variable length fragment datasets, PellFragVL and HIVFragVL, 10 non-epitope fragments of the same length were selected. Non-epitope fragments were defined as any peptide fragment not overlapping with any annotated epitopes. The non-epitope fragments were randomly selected from the same antigen as the corresponding epitope fragment.
In addition to the variable length fragment datasets, we curated two fixed length fragment datasets for the HIV and Pellequer datasets, HIVFragFL and PellFragFL. Based on results from Chen et al. (Chen et al., 2007) and El-Manzalawy et al. (El-Manzalawy et al., 2008), we used a fixed length of 20 residues. For each epitope in the HIV and Pellequer datasets that is less than 20 residues in length, we added the epitope fragment padded on each side as symmetrically as possible with neighboring residues to the fragment dataset. For each epitope in the HIV and Pellequer datasets greater than 20 residues in length, we added all 20 residue fragments within the epitope to the fragment dataset. For each positive epitope fragment within the fragment datasets, we added 10 non-epitope fragments, randomly selected from the same antigen sequence, 20 residues in length not overlapping with any annotated epitopes.
With the availability of the entire antigenic protein sequence in the HIV and Pellequer datasets, we were able to predict the secondary structure and relative solvent accessibility using the SSpro and ACCpro predictors from the SCRATCH protein structure prediction suite (Pollastri et al., 2002a, 2002b; Cheng et al., 2005). These predictors achieve accuracy levels of about 79 and 77%, respectively. Secondary structure propensity scales and solvent accessibility scales have been previously used for epitope prediction (Pellequer et al., 1991; Alix, 1999; Odorico and Pellequer, 2003), but the propensity scales are far less accurate than SSpro and ACCpro. For each of the four fragment datasets derived from the HIV and Pellequer datasets, we curated an additional dataset augmented with the predicted protein structural features. These datasets are named HIVFragFLstruct, HIVFragVLstruct, PellFragFLstruct and PellFragVLstruct.
To benchmark COBEpro's ability to assign residue epitopic propensity scores, we curated two whole sequence datasets, PellWholestruct and HIVWholestruct. These datasets include secondary structure and solvent accessibility predictions. In these datasets, residues within annotated epitopes were considered epitopic and residues not within any annotated epitopes were considered non-epitopic.
In addition to the various continuous B-cell epitope datasets, we benchmarked COBEpro on the discontinuous B-cell epitope dataset used by Discotope (Haste Andersen et al., 2006) and BEpro (Sweredoski and Baldi, 2008) (formerly known as PEPITO). In evaluating COBEpro on this dataset, we assumed that the tertiary structure is unknown and the secondary structure and relative solvent accessibility were predicted from the sequence alone. We also made blind predictions for the top 10 antigens recently identified in the pathogen F. tularensis (Sundaresh et al., 2007). This pathogen causes tularemia, which is a highly virulent and lethal disease.
Fragment epitopic propensity score predictor
COBEpro uses a SVM, as implemented by svmlight (Joachims, 1999), to assign an epitopic propensity score to peptide fragments. The input to the SVM for each peptide fragment is a vector of similarities to the positive epitope fragments in the training library. Several similarity measures were considered, but the total number of identical substrings was found to be most effective. This similarity measure is the number of amino acids present in both sequences plus the number of amino acid dimers present in both sequences plus the number of amino acid trimers present in both sequences and so on. The length of the input vector to the SVM is dependent on the number of positive epitope fragments in the training library. For example, if ‘ABACD’ were the peptide fragment to be classified and the positive epitopes in the training library were ‘ABAD’, ‘BADD’ and ‘ABAB’, then the input to the SVM would be [6, 4, 4] (the number of identical substrings between the query peptide and the first positive epitope fragment is 6 (‘A’, ‘B’, ‘D’, ‘AB’, ‘BA’, ‘ABA’), the number of identical substrings between the query peptide and the second positive epitope fragment is 4 (‘A’, ‘B’, ‘D’, ‘BA’) and the number of identical substrings between the query peptide and the third positive epitope fragment is 4 (‘A’, ‘B’, ‘AB’, ‘BA’)). The same similarity metric is used for comparing the secondary structure and solvent accessibility of the peptide fragments using the respective three-letter secondary structure alphabet (‘H’, ‘E’, ‘C’) and the two-letter relative solvent accessibility alphabet (‘E’, ‘B’).
We also explored including the similarity scores of the non-epitope fragments in the training library when calculating the input vector, but found that the predictor's performance actually decreased. It is suspected that the decrease in performance comes from the different feature space created within the SVM. With our novel set of inputs, COBEpro can make predictions for fragments of different lengths and COBEpro can include secondary structure and solvent accessibility by using three input values for each epitope in the training library (one for sequence similarity, one for secondary structure similarity and one for solvent accessibility similarity).
For the evaluation of COBEpro on the ChenFrag and BCPREDFrag datasets, we used a 10-fold cross validation scheme, where 8 of the folds were used in the training set, 1-fold was used for tuning parameters in the SVM such as the kernel type (e.g. linear or Gaussian) and kernel parameters (e.g. the width s of the Gaussian kernel), and the final fold was used for evaluation. The default value for the regularization parameter was used for all training. Other settings were tried, but they did not improve performance.
For the evaluation of COBEpro on the HIV and Pellequer fragment datasets, we alternated using one of the datasets for training the SVM and the other for testing. With the availability of the secondary structure and solvent accessibility predictions for the HIV and Pellequer datasets, we explored how their incorporation affects COBEpro's performance. In evaluating these two datasets, we used the optimal parameters found in evaluating the ChenFrag dataset.
Residue epitopic propensity score predictor
COBEpro uses a novel method for combining the fragment epitopic propensity scores to produce an epitopic propensity score for each residue. COBEpro first obtains the epitopic propensity score of every possible peptide fragment between 5 and 18 residues in length within the query protein. We selected the range of 5–18 residues because 95% of the epitope fragments in our datasets are in this range.
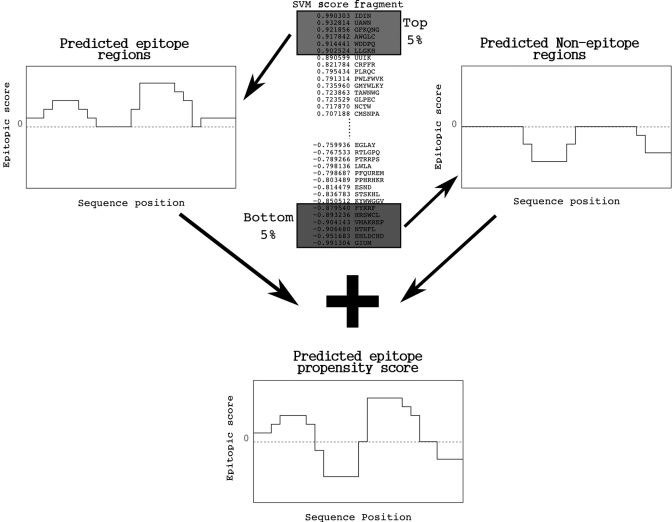
The second step in COBEpro is to combine these fragment predictions into a single score for each residue. Several schemes for combining the predictions were explored in the course of benchmarking our prediction. One simple scheme would be to sum the raw SVM scores of each peptide fragment overlapping with a given residue. Another possible scheme would be to assume the highest scoring fragments are epitopes. In this scheme, a residue would get a positive ‘vote’ for each epitope fragment containing the residue. A third scheme would assume the lowest scoring fragments are non-epitopes and a residue would get a negative ‘vote’ for each non-epitope fragment containing the residue. In the course of benchmarking COBEpro, we found that combining the most and least likely peptide fragments worked well and using the top 5% and bottom 5% scoring fragments yielded the optimal performance. In this scheme, the positive and negative votes are summed for each residue (Fig. 1).
Fig. 1.
Schemes for predicting residue epitopic propensity scores. One scheme for predicting residue epitopic propensity scores could sum the raw SVM scores for each fragment that covers a residue. Another scheme could use the top 5% most likely fragments as positive votes (top left). Yet another scheme could use the 5% least likely fragments as negative votes (top right). The optimal scheme for combining the fragment epitopic propensity scores sums the votes for both the 5% most likely and 5% least likely fragments to produce a residue epitopic propensity score (bottom center).
Performance measures
To evaluate COBEpro, we used several different metrics. The primary metric used was the area under the curve (AUC) of the receiver operating characteristic (ROC). This metric was preferred because of its ability to measure the performance of the predictor independent of the threshold used for classification and it is not dependent on the number of positive and negative test cases. In addition, AUC was the metric recommended for benchmarking epitope prediction performance at a workshop organized by the National Institute of Allergy and Infectious Disease in 2006 (Greenbaum et al., 2007). Intuitively, the AUC is the probability that a randomly chosen positive test case will have a score greater than a randomly chosen negative test case. An AUC of 1.0 corresponds to a perfect score and an AUC of 0.5 corresponds to a random predictor. In addition, we use several threshold-dependent metrics including accuracy, sensitivity (also known as recall), specificity, precision and F1 measure (Baldi et al., 2000). The 95% confidence intervals were determined using 100 000 bootstrap samples.
Results
Performance on the ChenFrag dataset
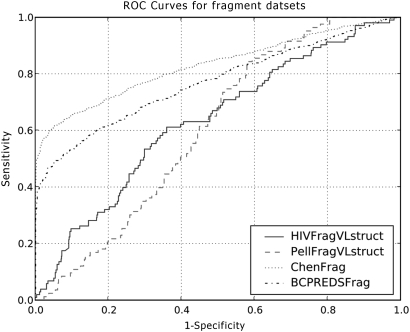
We first benchmarked COBEpro's performance on the ChenFrag dataset. Using the 10-fold cross-validation scheme as described previously with a linear kernel, we achieved an AUC of 0.685. The best cross-validated performance was obtained using a Gaussian kernel with a width of 0.001. Using these settings, COBEpro achieved an AUC of 0.829 and an accuracy of 78.0%. Additional performance measures for a variety of kernel widths are given in Table I. The thresholds used for the various performance measures were selected to maximize the accuracy on the parameter-tuning fold. The ROC curves for the ChenFrag dataset as well as the other fragment datasets are displayed in Fig. 2. It is worthwhile to note that the ROC curve of the performance on the ChenFrag dataset is higher than the ROC curve of the performance on the BCPREDFrag dataset. This is most likely due to the homologous proteins in the ChenFrag dataset and the redundancy reduction performed on the BCPREDFrag dataset.
Table I.
Cross-validated performance on the ChenFrag fragment dataset
| Linear kernel | Gaussian kernel, 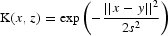 |
||||
|---|---|---|---|---|---|
| s = 0.01 | s = 0.001 | s = 0.0001 | s = 0.00001 | ||
| AUC | 0.685 | 0.521 | 0.829 | 0.820 | 0.806 |
| CV Threshold | −1.65 | −0.18 | −0.03 | −1.04 | −1.03 |
| Accuracy (%) | 64.7 | 50.4 | 78.0 | 77.4 | 75.9 |
| Sensitivity (%) | 43.6 | 40.7 | 60.9 | 62.4 | 58.0 |
| Specificity (%) | 85.8 | 60.1 | 95.1 | 92.4 | 93.8 |
| Precision (%) | 75.4 | 50.5 | 92.5 | 89.2 | 90.4 |
| F-measure (%) | 55.3 | 45.1 | 73.4 | 73.4 | 70.7 |
The cutoff for calculating the threshold-dependent performance measures is selected to maximize accuracy on the parameter-tuning fold. Bold values indicate the highest AUC ROC performance.
Fig. 2.
ROC curves for the fragment datasets. The ChenFrag and BCPREDFrag datasets contain only fixed length primary sequence fragments and non-epitope fragments are randomly selected from SWISS-PROT. The ChenFrag datasets contain homologous proteins, whereas the BCPREDFrag datasets are redundancy reduced. The PellFragFLstruct and HIVFragVLstruct datasets contain variable length epitopes fragments with primary sequence information as well as predicted secondary structure and solvent accessibility. Both the PellFragFLstruct and HIVFragVLstruct datasets are redundancy-reduced and non-epitope fragments are drawn from portions of antigenic sequences not annotated as being in an epitope.
Performance on the BCPREDFrag dataset
On the recently curated BCPREDFrag dataset, COBEpro achieved an AUC (0.768) higher than any previous predictor. Additional performance measures are recorded in Table II. As noted previously, the most likely explanation for the discrepancy in AUC performance between the BCPREDFrag dataset and the ChenFrag dataset is the presence of homologous proteins in the ChenFrag dataset and absence of homologous proteins in the BCPREDFrag dataset.
Table II.
Cross-validated performance on the BCPREDFrag fragment dataset
| Linear kernel | Gaussian kernel, 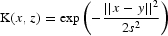 |
||||
|---|---|---|---|---|---|
| s = 0.01 | s = 0.001 | s = 0.0001 | s = 0.00001 | ||
| AUC | 0.592 | 0.527 | 0.768 | 0.727 | 0.592 |
| Accuracy (%) | 56.2 | 50.0 | 71.4 | 71.3 | 69.1 |
| Sensitivity (%) | 35.9 | 29.5 | 55.4 | 47.1 | 48.8 |
| Specificity (%) | 76.5 | 70.5 | 87.4 | 95.6 | 89.4 |
| Precision (%) | 60.4 | 50.0 | 81.5 | 91.1 | 82.2 |
| F-measure (%) | 45.0 | 37.1 | 66.0 | 62.1 | 60.8 |
The cutoff for calculating the threshold-dependent performance measures is selected to maximize accuracy on the parameter-tuning fold. Bold values indicate the highest AUC ROC performance.
Performance on the HIV and Pellequer fragment datasets
We analyzed the performance of COBEpro on the Pellequer and HIV fragment datasets using the optimal kernel parameters found while benchmarking COBEpro on the ChenFrag dataset. In our analysis, we explore the usage of either a fixed length or varying length window and the usage of the amino acid sequence alone or in combination with the secondary structure and solvent accessibility. The results from our benchmarking are reported in Tables III and IV. Without a validation dataset, the threshold for the performance measures is set to predict the same frequency of epitopes in the test dataset (CV threshold).
Table III.
Performance on Pellequer fragment datasets (trained on HIV datasets)
| PellFragFL | PellFragFLstruct | PellFragVL | PellFragVLstruct | |
|---|---|---|---|---|
| AUC | 0.485 | 0.536 | 0.504 | 0.606 |
| Accuracy (%) | 72.3 | 84.0 | 20.4 | 82.9 |
| Sensitivity (%) | 7.2 | 12.0 | 92.7 | 8.4 |
| Specificity (%) | 83.5 | 91.2 | 7.9 | 90.3 |
| Precision (%) | 7.1 | 12.0 | 14.8 | 8.1 |
| F-measure (%) | 7.1 | 12.0 | 25.5 | 8.2 |
The cutoff for calculating the threshold-dependent performance measures was selected to ensure that the same percentage of epitopes was predicted as in the test dataset. Bold values indicate the highest AUC ROC performance.
Table IV.
Performance on HIV fragment datasets (trained on Pellequer datasets)
| HIVFragFL | HIVFragFLstruct | HIVFragVL | HIVFragVLstruct | |
|---|---|---|---|---|
| AUC | 0.494 | 0.558 | 0.418 | 0.632 |
| Accuracy (%) | 82.9 | 83.3 | 29.0 | 84.0 |
| Sensitivity (%) | 12.2 | 10.7 | 56.4 | 18.4 |
| Specificity (%) | 90.5 | 90.8 | 26.1 | 90.8 |
| Precision (%) | 12.2 | 10.7 | 7.6 | 17.1 |
| F-measure (%) | 12.2 | 10.7 | 13.4 | 17.7 |
The cutoff for calculating the threshold-dependent performance measures was selected to ensure that the same percentage of epitopes was predicted as in the test dataset. Bold values indicate the highest AUC ROC performance.
While the SVMs trained with the PellFragFL and HIVFragFL datasets failed to achieve an AUC much higher than random, the SVMs trained with the PellFragVL and HIVFragVL datasets performed significantly better. While the incorporation of the secondary structure and solvent accessibility in the PellFragFLstruct and HIVFragFLstruct datasets did not increase performance, the structural feature predictions had a positive impact on the PellFragVLstruct and HIVFragVLstruct datasets; with increases in the AUC of 0.102 and 0.214, respectively, over the datasets not incorporating secondary structure and relative solvent accessibility. Using the PellFragVLstruct dataset for training the SVMs, COBEpro achieved an AUC of 0.632 on the HIVFragVLstruct dataset. Using the HIVFragVLstruct dataset for training the SVMs, COBEpro achieved an AUC of 0.606 on the PellFragVLstruct dataset.
Performance on HIV and Pellequer whole sequence datasets
COBEpro's residue epitopic propensity performance on the HIV and Pellequer datasets was benchmarked by alternately using one dataset for training the SVM and the other for evaluation. The results from the different prediction schemes are in Table V. In both datasets, by combining the predictions of the most likely epitope and non-epitope fragments, COBEpro was able to achieve an AUC of 0.628 with a 95% confidence interval of (0.559, 0.698) on the Pellequer dataset and an AUC of 0.605 with a 95% confidence interval of (0.557, 0.656) on the HIV datasets.
Table V.
Residue epitopic propensity performance (AUC) on Pellequer and HIV datasets
| Test dataset | Raw SVM score | Top 5% | Bottom 5% | Top and bottom 5% |
|---|---|---|---|---|
| PellWholestruct | 0.589 | 0.605 | 0.603 | 0.628 |
| HIVWholestruct | 0.547 | 0.588 | 0.578 | 0.605 |
The PellWholestruct dataset was evaluated using an SVM trained on the HIVFragVLstruct dataset. The HIVWholestruct dataset was evaluated using an SVM trained on the PellFragVLstruct dataset.
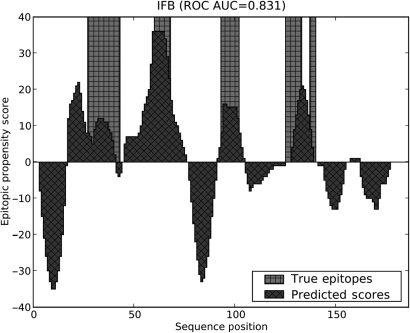
As an example of the performance of COBEpro for making predictions on whole sequences, we highlight one protein from the Pellequer dataset, IFB (Fig. 3). COBEpro was able to achieve an AUC of 0.831 with regard to the residue epitopic propensity scoring on this sample protein. It is worthwhile to note that the number of residues with a positive epitopic propensity score will be roughly equal to the number of residues with a negative epitopic propensity scores because of the voting-based prediction scheme. Since there are typically fewer epitopic residues than non-epitopic residues, there will inherently be more false positives than false negatives. This is tolerable since the primary goal of COBEpro is to assign epitopic propensity scores that rank the residues from most epitopic to least epitopic, not make a binary classification. While not all proteins were predicted at as high a performance level, IFB clearly demonstrates the power of COBEpro to identify the most likely and least likely regions of antigenic activity.
Fig. 3.
Residue epitopic propensity score predictions for pellequer protein IFB. The areas filled with diagonal hash marks represent the predicted propensity scores and the columns denoted by vertical and horizontal hash marks represent the true epitope locations.
Performance at Discotope residue epitopic propensity scoring
In addition to the continuous B-cell epitope datasets, we also benchmarked COBEpro on the discontinuous dataset curated for Discotope (Haste Andersen et al., 2006) and subsequently used in BEpro (Sweredoski and Baldi, 2008) (formerly PEPITO). We chose to benchmark COBEpro on this dataset to attempt to determine whether continuous B-cell predictors could be used to predict discontinuous B-cell epitopes accurately. On this dataset, COBEpro achieved an average AUC of 0.591 with a 95% confidence interval of (0.582, 0.601). This is in contrast to the AUC of 0.726 and 0.754 achieved by Discotope and BEpro, respectively. While COBEpro's AUC is considerably lower than previous predictors, it should be noted that these predictors are trained on discontinuous epitopes and they take an antigen tertiary structure as input, in contrast to COBEpro, which is trained only on continuous epitopes and uses only the antigen primary sequence as input. COBEpro achieved an average recall of 77.5% with an average precision of 11.9%.
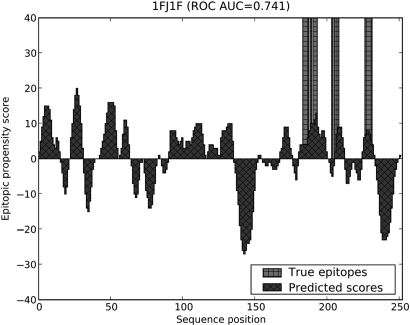
In Fig. 4, we see the predicted residue epitopic propensity scores for a typical Discotope protein 1FJ1F, which is a known Lyme disease antigen. Note that COBEpro was able to identify the discontinuous epitope even though all the linear segments within the discontinuous epitope are less than six residues in length.
Fig. 4.
Residue epitopic propensity score predictions for discotope protein 1FJ1F. The areas filled with diagonal hash marks represent the predicted propensity scores and the columns denoted by vertical and horizontal hash marks represent the true epitope locations. While there are several false positive regions, COBEpro has identified the three major epitopic regions within the discontinuous epitope with fairly tight bounds.
Assessing the statistical significance of COBEpro
One way to assess the statistical significance of COBEpro is to compare it to a random predictor. Several rigorous statistical tests were performed to determine the significance level at which COBEpro's performance is better than a random predictor's performance for epitopic propensity prediction at both the residue level and fragment level. The AUC is the performance metric used in the statistical tests. In each statistical test, the null hypothesis is that a random predictor performs at least as well as COBEpro and the alternate hypothesis is that COBEpro performs better than a random predictor. For the purposes of the statistical tests, a random predictor is defined as a predictor that outputs a random epitopic propensity score from the uniform distribution between zero and one for any input. Other models for random predictors were considered (such as providing a shuffled sequence as input to COBEpro); however, they were discarded because they were not applicable in all of the statistical tests performed or did not make truly random predictions. The uniform distribution between zero and one is acceptable for calculating the AUC because the AUC is both scale and shift invariant. More generally, the AUC is only dependent on the ordering of the predictions.
Estimating the standard deviation of the performance and P-value
A bootstrap procedure was used to estimate the standard deviation of the performance of each predictor and the P-value of the null hypothesis (Efron and Tibshirani, 1993). In the estimation of the standard deviation of the performance of COBEpro (SDPRED), the actual predicted values for each residue or fragment were used. In the estimation of the standard deviation of the performance of a random predictor (SDRND), random predictions were obtained for each residue or fragment from the distribution as described previously. The exact number of bootstrap samples in each statistical test (100 000) was selected because it provides a good balance between attainable precision and computation time. For the fragment datasets (including ChenFrag, BCPREDFrag, HIVFragVLstruct and PellFragVLstruct), bootstrap samples were created by randomly selecting with replacement fragments from the datasets. For the whole sequence datasets (including HIVWholestruct, PellWholestruct and Discotope), bootstrap samples were created by randomly selecting with replacement sequences from the datasets. The bootstrap estimate of the P-value is the number of times the random predictor performed at least as well as COBEpro in the 100 000 bootstrap samples divided by 100 000.
Statistical test results
The results of the statistical tests are provided in Tables VI and VII. The z-score is defined as 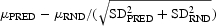 , where μRND = 0.5 and μPRED are the observed performance of COBEpro, which is an unbiased estimate of the true performance. Given these statistical results, it is clear that one can safely reject all the null hypotheses that a random predictor performs as well as COBEpro with confidences ranging from 99 to 99.999%.
, where μRND = 0.5 and μPRED are the observed performance of COBEpro, which is an unbiased estimate of the true performance. Given these statistical results, it is clear that one can safely reject all the null hypotheses that a random predictor performs as well as COBEpro with confidences ranging from 99 to 99.999%.
Table VI.
Statistical tests of COBEpro on fragment epitopic propensity scoring
| Data set | μCOBEpro | SDCOBEpro | SDRND | z-score | P-value |
|---|---|---|---|---|---|
| ChenFrag | 0.829 | 9.97E−03 | 1.38E−02 | 1.93E + 01 | <1.E−05 |
| BCPREDFrag | 0.768 | 1.27E−02 | 1.54E−02 | 1.34E + 01 | <1.E−05 |
| HIVFragVLstruct | 0.632 | 2.86E−02 | 3.00E−02 | 3.18E + 00 | 8.4E−04 |
| PellFragVLstruct | 0.606 | 2.57E−02 | 3.34E−02 | 2.52E + 00 | 6.01E−03 |
Table VII.
Statistical tests of COBEpro on residue epitopic propensity scoring
| Dataset | μCOBEpro | SDCOBEpro | SDRND | z-score | P-value |
|---|---|---|---|---|---|
| HIVWholestruct | 0.605 | 2.53E−02 | 1.58E−02 | 3.52E + 00 | 1.9E−04 |
| PellWholestruct | 0.628 | 3.54E−02 | 1.22E−02 | 3.39E + 00 | 2.6E−04 |
| Discotope | 0.591 | 4.72E−03 | 1.37E−02 | 6.26E + 00 | <1.E−05 |
Discussion
In comparing the results from COBEpro with other predictors, one concludes that COBEpro is at least as well as all other predictors on each continuous B-cell epitope dataset. On the ChenFrag dataset, COBEpro achieved a higher accuracy than the accuracy reported by Chen et al. (Chen et al., 2007) (78.0 versus 73.71). On the BCPREDFrag dataset, COBEpro achieved a higher AUC than the AUC reported by El-Manzalawy et al. (El-Manzalawy et al., 2008) (0.768 versus 0.758). On the PellWholestruct and HIVWholestruct datasets, COBEpro achieved a mean AUC half a percentage point higher than the mean AUC reported by Larsen et al. (Larsen et al., 2006) (0.605 versus 0.600). COBEpro also performed quite well on the discontinuous Discotope epitope dataset, with a mean AUC of 0.591.
There are several features in COBEpro that are novel to B-cell epitope prediction. In COBEpro's first step, one unique feature is the novel input vector to the SVM. Whereas most predictors use simple protein property scales and amino acid compositions for input, COBEpro uses a vector of similarities to other epitope fragments. While COBEpro's SVM input may somewhat obfuscate simple sequence motifs, we believe that this representation combined with the ability of SVMs to handle high dimensional data allows COBEpro to identify complex patterns that may be found in B-cell epitopes. COBEpro's second step differs significantly from other approaches in how the fragment epitopic propensity scores are used. Most systems simply assign to the middle residue in the peptide fragment the same epitopic propensity score as the fragment. COBEpro considers the fragment epitopic propensity score equally relative to each residue in the fragment when calculating the residue epitopic propensity scores, as there is no reason to believe that the fragment epitopic propensity score is more relevant to the middle residue than the outer residues in the peptide fragment.
One may wonder why fragment epitopic propensity scores are calculated before residue epitopic propensity scores in a top-down approach, where fragment predictions are made before residue predictions, as the reverse, bottom-up approach might seem more natural. However, the first step of assigning the fragment epitopic propensity scores can be viewed as a course grained prediction and the second step of assigning the residue epitopic propensity scores can be viewed as a fine grain prediction. It may be possible that this top-down approach could be applied to other prediction tasks such as protein secondary structure prediction.
A large discrepancy is seen in Fig. 2 between the AUC on the datasets derived from the BciPep database (∼0.8) and the AUC on the datasets derived from the HIV and Pellequer databases (∼0.6). This division corresponds to different methods used for selecting non-epitope fragments. While there could be several explanations for this observation, we hypothesize that the models trained on datasets containing non-epitope fragments randomly sampled from SWISS-PROT were actually learning to discern antigen sequences from non-antigen sequences.
To test this hypothesis, we curate a dataset consisting of the positive fixed-length epitope fragments from the HIVFragFL dataset and an equal number of non-epitope fragments randomly selected from SWISS-PROT. When we evaluate the performance of the SVM using 10-fold cross validation on this dataset, we record an AUC of 0.919. This performance level is considerably higher than the chance level AUC of 0.494, we record in our unbiased benchmarking where both epitope and non-epitope fragments are derived from the same antigenic sequences. When we perform the same test using the PellFragFL dataset, we record an AUC of 0.713. Again, this is much higher than the AUC previously recorded in our unbiased benchmarking of 0.485.
From these results, we can see considerable differences in performance between methods for selecting non-epitope fragments and that selecting non-epitopes randomly from SWISS-PROT appears to produce biased performance measures. All the available evidence suggests that predictors trained on datasets containing non-epitope fragments randomly sampled from SWISS-PROT are, in part, learning to discern antigen source species from non-antigen source species and that it is necessary to construct training datasets using only antigenic sequences to prevent biased models and biased benchmarking. Considering this, we use the PellFragVLstruct dataset to train the SVM in the online version of COBEpro since this dataset contains only antigenic sequences and the dataset contains a larger training library of antigens than the HIVFragVLstruct dataset.
In conclusion, we have demonstrated how COBEpro can bridge the two approaches for predicting epitopes. Through careful and unbiased benchmarking, we have demonstrated that COBEpro achieves a level of performance at least comparable to other methods. COBEpro achieves this high performance by incorporating a unique set of input features, including protein structural features when available. Additionally, we provide evidence that non-epitope fragments should be drawn from antigenic sequences to ensure unbiased measurement of epitope prediction performance. Access to COBEpro is provided online through the SCRATCH prediction suite.
COBEpro and BEpro can be used to determine the putative epitopic regions in antigens identified using new high-throughput protein chips that can identify antigen proteins in a variety of pathogens. These high-throughput protein chips, where all of the proteins from an infectious agent are printed onto a microarray chip and the chip is probed for antibody reactivity with each possible antigen, have been previously described in Davies et al. (Davies et al., 2005) and Sundaresh et al. (Sundaresh et al., 2006). As a proof of concept, we ran COBEpro on the antigens recently identified in the pathogen F. tularensis using high-throughput protein chips (Sundaresh et al., 2007) and the predicted epitopes are available in the Supplementary data available at PEDS online. These predictions are left for future experimental laboratories to confirm. In time, it is hoped that this combination of high throughput technology for identifying antigens with computational methods for identifying epitopes, such as BEpro and COBEpro, may help improve our ability to develop synthetic peptide vaccines. Additionally, COBEpro could be used to improve the effectiveness of therapeutic proteins by identifying epitopes and then testing in silico which mutations would reduce the immunogenicity of the epitopic regions. In each of these examples, COBEpro and BEpro are not relied upon to give a 100% accurate prediction nor are they used to distinguish antigen from non-antigen. Rather, they are most effective in combination with laboratories using high-throughput technologies. In this setting, false positives can be tolerated and COBEpro and BEpro can be used to reduce the search space to a more manageable size.
Funding
This work was supported by the National Institutes of Health [LM-07443-01]; the National Science Foundation [EIA-0321390]; and a Microsoft Faculty Research Award to P.B.
Supplementary Material
Footnotes
Edited by Jim Houston
References
- Alix A. Vaccine. 1999;18:311–314. doi: 10.1016/s0264-410x(99)00329-1. (314). [DOI] [PubMed] [Google Scholar]
- Baldi P., Brunak S., Chauvin Y., Andersen C.A., Nielsen H. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
- Blythe M., Flower D. Protein Sci. 2005;14:246–248. doi: 10.1110/ps.041059505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Liu H., Yang J., Chou C. Amino Acids. 2007;33:423–428. doi: 10.1007/s00726-006-0485-9. [DOI] [PubMed] [Google Scholar]
- Cheng J., Randall A.Z., Sweredoski M.J., Baldi P. Nucleic Acids Res. 2005;33:W72–W76. doi: 10.1093/nar/gki396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chirino A.J., Ary M.L., Marshall S.A. Drug Discov. Today. 2004;9:82–90. doi: 10.1016/S1359-6446(03)02953-2. [DOI] [PubMed] [Google Scholar]
- Davies D.H., et al. Proc. Natl Acad. Sci. USA. 2005;102:547–552. doi: 10.1073/pnas.0408782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B., Tibshirani R. An Introduction to the Bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- El-Manzalawy Y., Dobbs D., Honavar V. J. Mol. Recognit. 2008;21:243–255. doi: 10.1002/jmr.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenbaum J.A., et al. J. Mol. Recognit. 2007;20:75–82. doi: 10.1002/jmr.815. [DOI] [PubMed] [Google Scholar]
- Haste Andersen P., Nielsen M., Lund O. Protein Sci. 2006;15:2558–2567. doi: 10.1110/ps.062405906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopp T., Woods K. Proc. Natl Acad. Sci. USA. 1981;78:3824–3828. doi: 10.1073/pnas.78.6.3824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes E., Gilleland H.J. Vaccine. 1995;13:1750–1753. doi: 10.1016/0264-410x(95)00166-x. [DOI] [PubMed] [Google Scholar]
- Joachims T. Making large-Scale SVM Learning Practical. In: Schölkopf B., Burges C., Smola A., editors. Advances in Kernel Methods—Support Vector Learning. MIT Press; 1999. [Google Scholar]
- Korber B., Brander C., Haynes B., Koup R., Moore J., Walker B., Watkins D. HIV Immunology and HIV/SIV Vaccine Databases 2003. Los Alamos, New Mexico: Los Alamos National Laboratory, Theoretical Biology and Biophysics; 2003. [Google Scholar]
- Larsen J., Lund O., Nielsen M. Immunome Res. 2006;2:2. doi: 10.1186/1745-7580-2-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odorico M., Pellequer J. J. Mol. Recognit. 2003;16:20–22. doi: 10.1002/jmr.602. [DOI] [PubMed] [Google Scholar]
- Parker J., Guo D., Hodges R. Biochemistry. 1986;25:5425–5432. doi: 10.1021/bi00367a013. [DOI] [PubMed] [Google Scholar]
- Pellequer J., Westhof E., Van Regenmortel M. Methods Enzymol. 1991;203:176–201. doi: 10.1016/0076-6879(91)03010-e. [DOI] [PubMed] [Google Scholar]
- Pellequer J., Westhof E., Van Regenmortel M. Immunol. Lett. 1993;36:83–99. doi: 10.1016/0165-2478(93)90072-a. [DOI] [PubMed] [Google Scholar]
- Pollastri G., Baldi P., Fariselli P., Casadio R. Proteins. 2002;a 47:142–153. doi: 10.1002/prot.10069. [DOI] [PubMed] [Google Scholar]
- Pollastri G., Przybylski D., Rost B., Baldi P. Proteins. 2002;b 47:228–235. doi: 10.1002/prot.10082. [DOI] [PubMed] [Google Scholar]
- Saha S., Raghava G.P. Proteins. 2006;65:40–48. doi: 10.1002/prot.21078. [DOI] [PubMed] [Google Scholar]
- Saha S., Bahsin M., Raghava G.P. BMC Genomics. 2005;6:79. doi: 10.1186/1471-2164-6-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schellekens G., Visser H., de Jong B., van den Hoogen F., Hazes J., Breedveld F., van Venrooij W. Arthritis Rheum. 2000;43:155–163. doi: 10.1002/1529-0131(200001)43:1<155::AID-ANR20>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Söllner J., Mayer B. J. Mol. Recognit. 2006;19:200–208. doi: 10.1002/jmr.771. [DOI] [PubMed] [Google Scholar]
- Sundaresh S., Doolan D.L., Hirst S., Mu Y., Unal B., Davies D.H., Felgner P.L., Baldi P. Bioinformatics. 2006;22:1760–1766. doi: 10.1093/bioinformatics/btl162. [DOI] [PubMed] [Google Scholar]
- Sundaresh S., et al. Bioinformatics. 2007;23:i508–i518. doi: 10.1093/bioinformatics/btm207. [DOI] [PubMed] [Google Scholar]
- Sweredoski M.J., Baldi P. Bioinformatics. 2008;24:1459–1460. doi: 10.1093/bioinformatics/btn199. [DOI] [PubMed] [Google Scholar]
- Tam J.P., Lu Y.A. Proc. Natl Acad. Sci. USA. 1989;86:9084–9088. doi: 10.1073/pnas.86.23.9084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Regenmortel M.H. J. Mol. Recognit. 2006;19:183–187. doi: 10.1002/jmr.768. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.