Scale-based scatter correction for computer-aided polyp detection in CT colonography

Abstract

CT colonography (CTC) is a feasible and minimally invasive method for the detection of colorectal polyps and cancer screening. Computer-aided detection (CAD) of polyps can improve consistency and sensitivity of virtual colonoscopy interpretation and reduce interpretation burden. However, high-density orally administered contrast agents have scatter effects on neighboring tissues. The scattering manifests itself as an artificial elevation in the observed CT attenuation values of the neighboring tissues. This pseudoenhancement phenomenon presents a problem for the application of computer-aided polyp detection, especially when polyps are submerged in the contrast agents. The authors have developed a scale-based correction method that minimizes scatter effects in CTC data by subtraction of the estimated scatter components from observed CT attenuations. By bringing a locally adaptive structure, object scale, into the correction framework, the region of neighboring tissues affected by contrast agents is automatically specified and adaptively changed in different parts of the image. The method was developed as one preprocessing step in the authors’ CAD system and was tested by using leave-one-patient-out evaluation on 56 clinical CTC scans (supine or prone) from 28 patients. There were 50 colonoscopy-confirmed polyps measuring 6–9 mm. Visual evaluation indicated that the method reduced CT attenuation of pseudoenhanced polyps to the usual polyp Hounsfield unit range without affecting luminal air regions. For polyps submerged in contrast agents, the sensitivity of CAD with correction is increased 24% at a rate of ten false-positive detections per scan. For all polyps within 6–9 mm, the sensitivity of the authors’ CAD with scatter correction is increased 8% at a rate of ten false-positive detections per scan. The authors’ results indicated that CAD with this correction method as a preprocessing step can yield a high sensitivity and a relatively low FP rate in CTC.

INTRODUCTION

Motivation

Colon cancer is one of the most common, yet most treatable forms of cancer. Early detection of colon polyps (small round growths in the colon lining) is the best way to approach treatment. Therefore, a quick, simple, nonintrusive detection method is very important. CT colonography (CTC) is a feasible and minimally invasive method for the detection of colorectal polyps and cancer screening.¹ Computer-aided detection (CAD) of polyps in CTC can improve consistency and sensitivity of virtual colonoscopy interpretation and reduce interpretation burden. Typically, a CAD system is used to analyze CTC data automatically by use of image analysis and pattern recognition algorithms, and the locations of detected abnormalities are reported to physicians.

In CTC, proper bowel preparation is considered essential for confident detection of colorectal lesions.² Residual solid and liquid materials may reduce the sensitivity of CTC by obscuring polyps, and solid pieces of stool may reduce the specificity of CTC by imitating polyps. In fecal-tagging CTC, orally administered tagging agents are used to opacify residual fluid and stool to facilitate the differentiation of polyps from residual materials. However, the tagging agents have a high radiodensity, and thus, the high-density orally administered contrast agents have scatter effects on neighboring tissues. The scattering manifests itself as an artificial elevation in the observed CT attenuation values of the soft-tissue regions and air that are located next to tagged regions.³ CT attenuation values of pseudoenhanced regions vary differently with respect to the amount, distribution, and density of tagging agents. One example is shown in Fig. 1. The mean of CT attenuation of a polyp without pseudoenhancement (patient in prone scan and the polyp is surrounded by luminal air) is around 72 HU [Fig. 1a], while the mean of CT attenuation of the same pseudoenhanced polyp (the same patient in supine scan while the same polyp is submerged in contrast agents) is artificially elevated to around 160 HU [Fig. 1b].

Figure 1.

The mean of CT attenuation of a polyp: (a) Polyp without pseudoenhancement (patient in prone scan and the polyp is surrounded by luminal air) and (b) polyp is pseudoenhanced (the same patient in supine scan while the same polyp is submerged in contrast agents).

This pseudoenhancement phenomenon presents technical challenges for the application of computer-aided polyp detection, especially when polyps are submerged in the contrast agents. First, CAD may misclassify pseudoenhanced polyps to false-positive (FP) detections because the classification features that are extracted by CAD on pseudoenhanced polyps can be severely distorted due to their observed similar radiodensity with tagged materials. Second, the pseudoenhancement phenomenon varies greatly according to the amount, distribution, and density of tagging agents, and they can be quite different even between different regions of the same colon. Therefore, the motivation in the present study is to propose a scatter correction method to reduce scatter effects on computer-aided polyp detection in CT colonography.

Related work

Projection-based convolution-subtraction methods for correcting scatter effects are usually used in computed tomography images. Scatter effects are estimated directly in each projection, then the resulting scatter effects estimates are subtracted from each projection to yield an estimate of the corrected images for reconstruction.^{4, 5, 6, 7} If the projection data have been stored in the backup media, these scatter correction techniques can be retrospectively applied on the acquired image. However, in some facilities, only the reconstructed image is stored in the backup media and projection data are not available. Therefore, many researchers are interested in image-based correction methods which need only the scatter-uncorrected image. Ulmer and Kaissl⁸ developed a deconvolution procedure to remove scatter effects. The assumption in this method is the scatter-affected image I₀ is the convolution of scatter-unaffected image I_t and a scatter kernel K. Thus, scatter corrected image ${\widehat{I}}_t$ is the deconvolution of acquired image I₀ and the kernel K. The problems of this method are deconvolution is computationally expensive and the parameters of K need to be determined carefully to avoid oscillations. Shidahara et al.⁹ developed a practical image-based scatter correction method for brain perfusion single-photon emission computed tomography images. In this method, the scatter component image was initially estimated by convolving uncorrected image I₀ with a spatially invariant scatter function SF. The estimated scatter image was then subtracted from the uncorrected image I₀ and the corrected image ${\widehat{I}}_t$ was used for the next iterative calculation until the convergence limit. In this method,⁹ the scatter function SF was spatially invariant and fixed for the entire image. It has some limitations in precisely modeling the complicated scatter effects. Therefore, the authors are thinking to combine image structure information to generate a spatially variant and adaptive scatter function for SF scatter correction.

Purpose and outline of paper

In this paper, a scale-based correction method that minimizes scatter effects in CTC data for computer-aided polyp detection is proposed. The object scale proposed by Saha and Udupa¹⁰ is a fundamental, well-established concept in image processing. This concept has been successfully applied in segmentation,^{11, 12, 13} filtering,¹⁰ and registration.¹⁴ The premise behind the concept of scale is to consider the local size of the object in carrying out local operations on the image. This local size is determined at every image element. More specifically, local scale at any location c is defined as the radius of the largest hyperball with center c, which is fully contained in the object. Although scatter is generally considered as a global effect, the rationale for the proposed local concept scale-based method relies on two facts: First, for the authors’ specific application, computer-aided polyp detection, especially small polyps, it is reasonable to consider that locally tagging agents have much more scatter effects on submerged polyps than the global high-density bones or metal objects. Second, the scatter effect varies according to the amount, distribution, and density of locally tagging agents, thus it makes sense to consider local object scale in the correction method. With this as the central theme, the method described in this paper differs from previous work as follows: (1) By bringing a locally adaptive structure, object scale, into the correction framework, the scatter function is adaptive and spatially variant. That is, the region of neighboring tissues affected by contrast agents is automatically specified and adaptively changed in different parts of the image. (2) By developing this method as one preprocessing step in the authors’ CAD system for the detection of polyps, the scatter correction is only applied to the neighborhood of contrast agents; polyps surrounded by luminal air will not be corrected.

The complete methodology of the approach presented in this paper is described in Sec. 2. The effectiveness of the approach, both visually and quantitatively, is demonstrated in Sec. 3 and concluding remarks are presented in Sec. 4.

METHODS

Method overview

The method consists of three phases: (1) computation of object scale for a given CTC image, (2) estimation of scatter components, and (3) subtraction of estimated scatter components from observed CT attenuations.

Computation of object scale for a given CTC image

The scale at every voxel c, K(c), is defined as the radius of the largest hyperball centered at the voxel c such that all voxels within the ball satisfied a predefined image intensity homogeneity criterion. First, for any voxel c in a given image, a digital ball of radius r centered at c is the set of voxels,

$$B_r\left(c\right)=\left\{d\right|\Vert d-c\Vert ⩽r\},$$ (1)

where ‖d−c‖ denotes the distance between c and d. Then, a homogeneity fraction, FO_r(c), is defined, which indicates the fraction of the ball boundary occupied by a region that is sufficiently homogeneous with c by

$$F{O}_r\left(c\right)=\frac{{\sum }_{d∊B_r\left(c\right)}W(f\left(c\right)-f\left(d\right))}{|B_r\left(c\right)-B_{r-1}\left(c\right)|},$$ (2)

where |B_r(c)−B_r−1(c)| is the number of voxels in (i.e., volume of) B_r(c)−B_r−1(c), f(c) is the intensity of voxel c, and W(x) is a homogeneity function defined by

$$W\left(x\right)=e^{-x^2∕2}.$$ (3)

The algorithm of scale computation initializes K(c) at every voxel c as 1. Then it iteratively increases the ball radius r by 1, and checks for the fraction of the object FO_r(c) containing c that is contained in the ball. The first time this fraction falls below a predefined constant, the authors consider that the ball contains an object region different from that to which c belongs and set K(c) as r. Further details can be found in Ref. 10.

In the first phase, scale is computed at every voxel of a given CTC image. Under this definition, the locally adaptive scale has a small value in the region close to boundary, and has high value in the region far away from boundary (Fig. 2). This local information could be used to define an adaptive scatter function in the next step. Actually, this local concept of scale has been shown to be useful in inhomogeneity correction in MR images.¹⁵

Figure 2.

Illustration of local structure size or scale. (a) Volume of interest (VOI) of a slice CTC image. Note that the scale is usually small in the vicinity of boundaries. (b) The corresponding VOI of scale image. In this image, intensity at a location is proportional to the scale value at that location.

Estimation of scatter components

The distribution of scatter components I_s is estimated by convolving the observed CTC image I₀ with an adaptive symmetric scatter function SF(c):

$$I_s=I_0\otimes \mathrm{SF}\left(c\right),$$ (4)

$$\mathrm{SF}\left(c\right)={\left(\frac{1}{\sqrt{\pi }\sigma }\right)}^2{e}^{-({(x-u)}^2+{(y-v)}^2)∕{\sigma }^2}.$$ (5)

The parameters of the scatter function, u and σ, are adaptively set as the transformed scale values derived from the first phase:

$$u=v=0.5(S_c-K\left(c\right)),$$ (6)

$$\sigma =S_c-K\left(c\right),$$ (7)

where S_c is a parameter of maximum scale value which is set in the scale computation algorithm. Since scale value at every voxel c is computed independently, scatter function SF(c) is adaptive and spatially variant according to the density and distribution of contrast agents. That is, transformed scale is used to adaptively describe the region∕extent of scatter effects of soft tissue introduced by the neighboring contrast agents. The nearby contrast agents have more scatter effects on surrounding polyps than the farther away agents have.

In the specific polyp detection application presented here, scatter correction is only applied to the region nearby contrast agents instead of the whole image, which is determined by the segmentation of the colon in the authors’ CAD system.¹⁶

Subtraction of scatter components

Finally, the CT attenuation values are corrected by subtraction of the estimated scatter component I_s from the observed CT attenuation at each voxel c:

$${\widehat{I}}_t=I_0-I_s.$$ (8)

The corrected image ${\widehat{I}}_t$ could be iteratively corrected by repeating this procedure (Secs. 2B, 2C, 2D. However, the authors did not find significant improvement when the iteration was increased and all results in this paper were from the procedure without iteration.

Implementation in CTC CAD

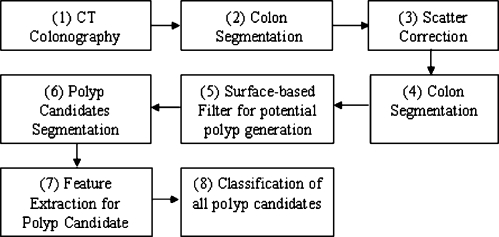
The authors implemented the scale-based scatter correction method as a preprocessing step in the CTC CAD system presented in this paper. The main stages of implementation of scatter correction in the CAD system presented here (Fig. 3) include the following: (1) CT colonography is performed on patients following a cathartic bowel preparation that includes the administration of oral contrast agents. (2) The colon is segmented by a region growing algorithm to identify the air- and contrast-filled colonic lumen.¹⁷ (3) Scatter correction is applied to the image voxels within and adjacent to contrast agents. (4) Colon segmentation is repeated since CT values of the scatter affected regions were changed by scatter correction. (5) A surface-based filter is used for potential polyp generation. First, the colon surface is extracted based on colon segmentation and iso-surface techniques.^{16, 18} Next, for each point on the surface, geometric and local volumetric properties are analyzed and filtered.¹⁶ The filtered surface vertices are then clustered based on connectivity. The clusters are potential polyp candidates. (6) The centroid of each cluster is used as a seed for more accurate polyp candidate segmentation by a 3D deformable model segmentation algorithm.¹⁹ (7) Characteristic features, such as intensity, shape and texture, are calculated from the segmented detection and its surrounding regions.²⁰ (8) The candidate pool is a large set, including true positive (TP) and FP detections. Finally, a decision of true polyp or false positive is made by a support vector machine (SVM) classifier.²⁰

Figure 3.

Implementation of scatter correction in the authors’ CAD system.

RESULTS

The following demonstrates both qualitatively, through image display, and quantitatively, through evaluation experiments, the performance of our scale-based scatter correction method on computer-aided polyp detection in CTC.

Data

Patients underwent a 24 h clear-liquid diet colonic preparation that included orally administered laxatives (90 mL of sodium phosphate and 10 mg of bisacodyl) and oral contrast agents in divided doses (500 mL of barium sulfate and 120 mL diatrizoate meglumine and diatrizoate sodium). CT scanning was performed in both the supine and prone positions during a single breath hold following patient-controlled insufflation of the colon with room air via a small flexible rectal catheter. The CT scanning parameters were 1.25 to 2.5 mm collimation, a table speed of 15 mm∕s, a reconstruction interval of 1 mm, tube current and voltage of 100 mA s and 120 kV_p on a four- or eight-channel CT scanner (Light Speed or LightSpeed Ultra, General Electric Medical Systems).

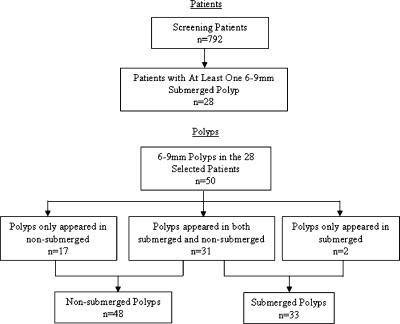
For performance evaluation of the scale-based correction method presented here, 28 patients were selected according to the following rule: All patients had to have at least one submerged polyp in the 6 to 9 mm size range. These 28 patients (56 CTC scans) had 50 colonoscopy-confirmed polyps measuring 6–9 mm. Polyps were grouped by whether they were submerged in oral contrast material on the CTC images. Thirty-one polyps were submerged on one CTC scan (supine or prone) and nonsubmerged on the other, 17 polyps were only nonsubmerged, and the remaining 2 polyps were only submerged. Finally, 33 (31+2) submerged and 48 (17+31) nonsubmerged polyps are included in the evaluation experiment. Figure 4 summarized the patient and polyp selection.

Figure 4.

Patient and polyp flowchart.

Qualitative display

For visual evaluation, we viewed the regions of polyps and computed the mean CT attenuation within the regions before and after the application of the scatter correction. Figure 5 shows several examples of correction. The CT attenuation of pseudoenhanced polyps (surrounded by contrast agents) was reduced to the usual polyp Hounsfield range with the application of scatter correction, and the polyps surrounded by luminal air were not affected by the correction. The mean and standard deviation of HU differences for submerged and nonsubmerged polyps before and after correction are 78±21 and 30±12, respectively (n=31, p=0.01). Some true positive (TP), false negative (FN), and false positive (FP) polyps are demonstrated in Fig. 6.

Figure 5.

The mean of CT attenuation of polyps without pseudoenhancement (the first column, patient in supine∕prone scan and the polyp is surrounded by luminal air), pseudoenhanced polyps (the second column, the same patient in prone∕supine scan while the same polyp is submerged in contrast agents), and corrected polyps (the third column).

Figure 6.

Examples of TP, FN, and FP detections. The first row shows the 2D and 3D displays of one TP detection (an 8 mm polyp) in CAD with scatter correction which is FN in CAD without scatter correction. The second row shows one FN detection (a 9 mm polyp) in CAD with and without scatter correction. This polyp is at the air–fluid boundary and scatter effects are low. The third row shows one FP detection on a haustral fold in CAD with and without scatter correction.

Quantitative analysis

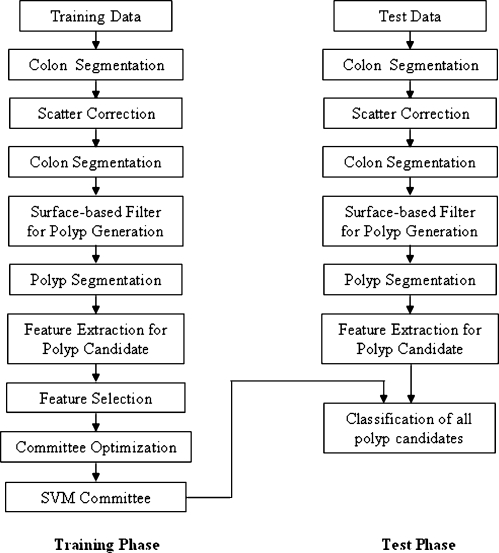
Quantitative evaluation included two phases: training phase and test phase. Performance of the authors’ CAD system without and with scatter correction was compared based on leave-one-patient-out evaluation. The evaluation flowchart of the authors’ CAD system with scatter correction is illustrated in Fig. 7. In the training phase, colon segmentation, scatter correction, identification of suspected polyps, and polyp segmentation are applied to the training data. After that, quantitative features are then computed for each suspected polyp. A progressive feature selection is run to select three pertinent features for one SVM. Then a committee optimization process is performed to form a committee of seven SVMs.²⁰ Leave-one-patient-out analysis is applied in this training phase. In the application phase, given the test data, the same segmentation, scatter correction, and feature computation process is carried out to obtain potential polyp detections and their features. The detections and features are then fed into the SVM committee formed in the training phase to determine whether they are true polyps or false detections.²⁰

Figure 7.

Flowchart of quantitative evaluation.

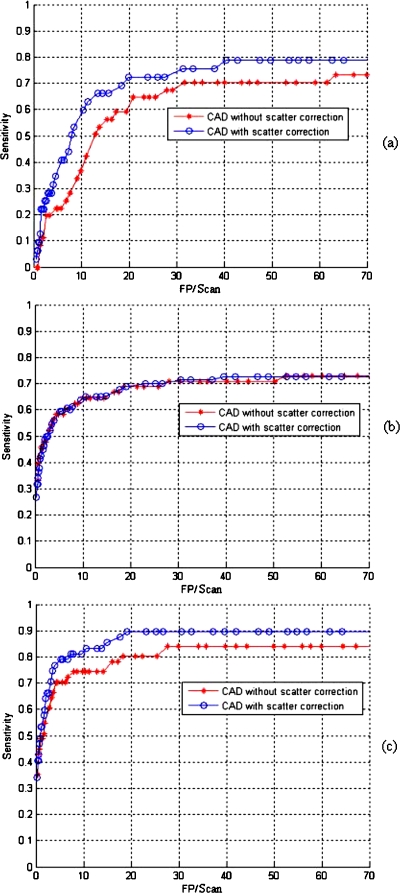
The free response receiving operation characteristic (FROC) curves with and without scatter correction are compared (Fig. 8). For those pseudoenhanced polyps, the sensitivity with correction was increased 24% at a rate of ten false-positive detections per scan [Fig. 8a]. The correction method did not affect the polyps surrounded by luminal air [Fig. 8b]. For all polyps (polyps adjacent contrast agents and polyps surrounded by luminal air) within 6–9 mm, the sensitivity with correction was increased 8% at a rate of ten false-positive detections per scan [Fig. 8c]. Figure 8 also showed that (1) the authors’ CAD system without scatter correction reported lower detection sensitivity for the polyps submerged in contrast agents and (2) polyps above fluid and polyps below fluid are now found almost equally well in the authors’ CAD system with scatter correction. The quantitative results are summarized in Table 1. The authors note that for polyps under fluid the sensitivity is increased from 36% (12∕33) to 60% (20∕33).

Figure 8.

FROC curves of our CAD system without and with the application of correction: (a) 6–9 mm polyps submerged in contrast agents; (b) 6–9 mm polyps surrounded by luminal air; (c) all polyps measuring 6–9 mm. The curves show the benefits of the scatter correction for submerged polyps. Polyps that are surrounded by luminal air are unaffected by the correction.

Table 1.

Comparing sensitivity at ten FP per scan for CAD without and with scatter correction. The sensitivity is significantly increased for polyps under fluid with scatter correction. There is no significant increase for all polyps. P values are obtained using the Fisher exact test.

Sensitivity	CAD without scatter correction	CAD with scatter correction	P value
Under fluid polyps	36% (12∕33)	60% (20∕33)	0.04
Above fluid polyps	64% (31∕48)	64% (31∕48)	1
All polyps	74% (37∕50)	82% (41∕50)	0.4

The correction method is implemented in C language as a preprocessing step of the authors’ CAD system. The mean computation time over 56 scans was around 2 min on a PC with a 3.2 GHz CPU.

DISCUSSION

High-density orally administered contrast agents have scatter effects on neighboring tissues by artificially elevating the observed CT attenuation values of the neighboring tissues. This pseudoenhancement phenomenon presents a problem for the application of computer-aided polyp detection, especially when polyps are submerged in the contrast agents. The authors developed a scale-based correction method that minimizes scatter effects in CTC data by subtraction of the estimated scatter components from observed CT attenuations. The method was developed as one preprocessing step in the authors’ CAD system and was tested by using leave-one-patient-out evaluation on 56 clinical CTC scans. For polyps submerged in contrast agents, the sensitivity of CAD with correction is increased 24% at a rate of ten false-positive detections per scan. For all polyps within 6–9 mm, the sensitivity of the authors’ CAD with scatter correction is increased 8% at a rate of ten false-positive detections per scan. The authors’ results indicated that CAD with this correction method as a preprocessing step can yield a high sensitivity and a relatively low FP rate in CTC. Particularly for 6–9 mm those are clinically important but were difficult for radiologists to locate without CAD. The corrected sensitivity is near that of expert radiologists.

In the authors’ experiment, initially (before classification of all polyp candidates), 43 true positive (TP) and 6553 false positive (FP) are detected by the CAD system without scatter correction. With scatter correction 45 TP and 6521 FP are detected by the CAD. This result indicated that the authors’ scatter correction impacts the final classification rather than the initial polyp detection. The initial polyp detection is mainly based on shape features such as curvatures, while the scatter correction process mainly adjusts the density features of the detections. Since density features are major features in the classifier, correcting them can greatly improve the classification. Before the correction, the pseudoenhanced polyps may be misclassified to FP detections because the density features are severely distorted due to their observed similar radiodensity with tagged materials.

The present work has some similarities to the adaptive correction method of Nappi and Yoshida.²¹ In that work, pseudoenhancement phenomena were modeled as a cumulative energy field originating from high CT attenuation values and were corrected by subtraction of the accumulated local energy estimated from the CT attenuation of each voxel. First, both methods are not physics-based but image-based correction methods; the projection data are not required. Second, the assumptions of both methods are the same. That is, pseudoenhancement is additive and CT attenuation values are corrected by subtraction of the estimated scatter component∕pseudoenhanced energy from the observed CT attenuation at each voxel. Finally, for the application of computer-aided polyp detection, both methods are only applied in the neighborhood of contrast agents; polyps surrounded by luminal air will not be corrected. However, the present scale-based correction method differs from their work in three essential ways: (1) The scatter component is estimated as a convolution between the observed CT image and an adaptive scatter spread function in the authors’ scale-based correction method while the pseudoenhanced energy in Ref. 21 is iteratively estimated from contrast agents as an expanding wave front with decreasing energy. (2) In the authors’ scale-based method, a local adaptive structure, object scale, is applied to the correction framework to compensate the varying scattering effects according to the amount, distribution, and density of locally tagging agents. The region of neighboring tissues affected by contrast agents is automatically specified and adaptively changed in different parts of the image. (3) The scale-based method is a convolution-subtraction scatter correction method which is closer to the fundamental physics model. Local structure (by scale) and density of contrast agents (by convolution) are simultaneously considered into this convolution-subtraction correction method.

One of the limitations of the present study is that only scatter effects from oral contrast agent are considered. Pseudoenhancement phenomenon caused by high density bones or metal objects in a body section is not discussed in our specific application, polyp detection. The second limitation is that the correction method is based on the segmentation of colon, especially the contrast agent segmentation. Therefore, the accuracy of segmentation will affect the performance of the present scatter correction.

In summary, a scale-based scatter correction method that efficiently compensates for pseudoenhancement has been presented. The method markedly improves (by 8%–24%) the sensitivity for detecting the important class of polyps 6–9 mm in size.