Coalescence Times and F_ST Under a Skewed Offspring Distribution Among Individuals in a Population

Abstract

Estimates of gene flow between subpopulations based on F_ST (or N_ST) are shown to be confounded by the reproduction parameters of a model of skewed offspring distribution. Genetic evidence of population subdivision can be observed even when gene flow is very high, if the offspring distribution is skewed. A skewed offspring distribution arises when individuals can have very many offspring with some probability. This leads to high probability of identity by descent within subpopulations and results in genetic heterogeneity between subpopulations even when Nm is very large. Thus, we consider a limiting model in which the rates of coalescence and migration can be much higher than for a Wright–Fisher population. We derive the densities of pairwise coalescence times and expressions for F_ST and other statistics under both the finite island model and a many-demes limit model. The results can explain the observed genetic heterogeneity among subpopulations of certain marine organisms despite substantial gene flow.

NATURAL populations of organisms are often subdivided by geography. Individuals may or may not migrate between these subpopulations. Modeling gene flow between subpopulations can be traced back to Wright (1931), whose island model describes a population subdivided into discrete, local subpopulations by geography, with limited migration between individual subpopulations. With the advent of techniques to characterize genetic variation, several measures of population subdivision have been proposed on the basis of probabilities of identity (see Rousset 2002 for a review). These include Wright's (1951) F_ST, Nei's (1982) γ_ST, and Lynch and Crease's (1990) N_ST.

The quantity F_ST can, under the assumption of equilibrium, be used to estimate levels of gene flow from allozyme data (Wright 1951). The quantity γ_ST can be calculated from DNA sequence data and is equivalent to F_ST if the mutation rate is very low (Slatkin 1991). Levels of gene flow between subpopulations can thus also be estimated from DNA sequence data. However, Slatkin (1991) argues that F_ST is appropriate for allozyme data, whereas the gene genealogy-based method of Slatkin and Maddison (1989) is appropriate for DNA sequence data. As F_ST continues to be used in investigations of population structure and, recently, as a tool for identifying loci under selection (e.g., Murray and Hare 2006), we are concerned with F_ST and related measures below.

We derive expressions for F_ST and N_ST under the island model of population subdivision with symmetric migration (Nagylaki 1980; Strobeck 1987) and skewed offspring distribution among individuals in a population. When the offspring distribution is skewed, individuals have some nonnegligible probability of having very many offspring. The population model of skewed offspring distribution we adopt in this work can result in an ancestral process with asynchronous multiple mergers (Eldon and Wakeley 2006). An ancestral process with asynchronous multiple mergers, or Λ-coalescent, was introduced by Pitman (1999) and also derived by Sagitov (1999) from a Cannings (1974) model. In a Λ-coalescent, any number of ancestral lines can coalesce at once to a single ancestor. In contrast, the Kingman coalescent (Kingman 1982a,b) allows only two lines to coalesce each time. For a single population, the ancestral process obtained from the population model of Eldon and Wakeley (2006), and employed in this work, is a special case of the Λ-coalescent of Pitman (1999) and Sagitov (1999).

Type III survivorship curve, and high fecundity, characterize a diverse group of organisms (e.g., many plants and marine animals). A prime example are marine species with broadcast spawning, including Atlantic cod (Gadus morhua; Árnason 2004), Pacific oysters (Crassostrea gigas; Beckenbach 1994; Hedgecock 1994a), and red drum (Sciaenops ocellatus; Turner et al. 2002). A model of skewed offspring distribution, in which individuals can have very many offspring with a nonnegligible probability, may therefore better apply in such cases than the Wright–Fisher (Fisher 1930; Wright 1931) or the Moran (Moran 1958, 1962) models.

Genetic observations from these species also argue against the standard population models. Genetic diversity is observed to be much lower than expected on the basis of population size for some marine populations (Hedgecock et al. 1982; Nei and Graur 1984; Avise et al. 1988; Avise 1994). In particular, low effective to actual population size ratios have been reported for Atlantic cod (Árnason 2004), red drum (Turner et al. 2002), and the Pacific oyster (Hedgecock 1994a), and this has been explained by high variance in offspring distribution (Crow and Kimura 1970; Hedrick 2005). Second, models of skewed offspring distribution predict a large number of singleton variants (Eldon and Wakeley 2006; Sargsyan and Wakeley 2008), a feature observed, for example, in Pacific oysters (Boom et al. 1994), Atlantic cod (Árnason 2004), and some hydrothermal vent taxa (Won et al. 2003; Hurtado et al. 2004; Johnson et al. 2006; Young et al. 2008).

Genetic heterogeneity on a small spatial scale has been observed for many marine populations, including the purple sea urchin (Strongylocentrotus purpuratus; Edmands et al. 1996), even though planktonic larvae disperse over wide-ranging habitats (Johnson and Black 1984; Watts et al. 1990; Hedgecock 1994b; David et al. 1997). A range of explanations has been proposed for the observed heterogeneity (see Burton 1983; Palumbi 1994). Our aim is to address, by analytic methods, the problem concerning the genetic population structure of a highly fecund species with potentially highly skewed offspring distribution, like the Atlantic cod (Árnason et al. 2000).

We obtain the probability distributions of pairwise coalescence times, and expressions for F_ST, for both the finite island and a many-demes limit model. Our main result is that evidence of population subdivision can be observed in genetic data even if the usual migration rate Nm is very large. In essence, a skewed offspring distribution leads to high probabilities of identity by descent within subpopulations and thus high F_ST. Therefore, patterns in genetic data indicating population subdivision cannot be taken to indicate low levels of gene flow in a population with a skewed offspring distribution. In fact, estimates of migration rate based on F_ST (or N_ST) are confounded by the reproduction parameters of our model of skewed offspring distribution. These results may explain the genetic heterogeneity among subpopulations of some marine species like the purple sea urchin (S. purpuratus; Edmands et al. 1996), despite the potential for wide dispersal of long-lived planktotrophic larvae (Burton 1983; Palumbi 1994).

METHODS AND RESULTS

Throughout we are concerned with neutral genetic diversity at a single nonrecombining locus in a haploid population. As usual, N is the population size. The results should hold for a diploid population with gametic migration if we replace N with 2N. The population model we consider is a modification of the well-known Moran model of reproduction (Moran 1958, 1962). In the Moran model, a single randomly chosen individual reproduces each time step. To keep the population size constant a randomly chosen individual, but not the offspring, dies to make room for the offspring.

In our model, which was first presented in Eldon and Wakeley (2006), a single randomly chosen individual (the parent) reproduces each time step. With probability 1 – ɛ the parent has one offspring. Alternatively, with probability ɛ the parent has ψN – 1 offspring (a large reproduction event) with 0 < ψ < 1. To keep population size constant when a large reproduction event occurs, a total of ψN – 1 individuals die to make room for the new offspring. In our model the parent always persists. The parameter ψ represents the fraction of the population that is replaced by the offspring of the parent. Eldon and Wakeley (2006) show that this modified Moran model of overlapping generations gives rise to a coalescent process that allows for asynchronous multiple mergers of ancestral lines, i.e., is of the same type as the ancestral process considered by Pitman (1999) and Sagitov (1999).

For ease of presentation, we define the following quantities: N_γ, c_N, λ_γ, and I_A. The quantity N_γ is the coalescence timescale in our model. The coalescence timescale is proportional to the number of time steps, on average, it takes for two individuals to coalesce (in a single population). It depends on the value of ɛ that we assume has the form ɛ ≡ 2φ/N^γ for some constants φ and γ with 0 < φ, γ < ∞. In our model, the coalescence timescale is N^γ/2 time steps when 0 < γ < 2. In the usual Moran model, the timescale is N²/2 time steps, which is also the value of N_γ when γ ≥ 2.

For a single population, Eldon and Wakeley (2006) show that different coalescent processes result depending on γ. Multiple mergers of ancestral lines are allowed in the coalescent process when 0 < γ ≤ 2, while Kingman's coalescent (Kingman 1982a,b) results when γ > 2. The probability that two individuals do coalesce in a single time step is denoted by c_N and depends on ɛ. The rate λ_γ of coalescence of two individuals is obtained from c_N by “speeding up” time by a factor of N_γ. When 0 < γ ≤ 2, λ_γ depends on the reproduction parameters φ and ψ. In mathematical notation, N_γ is expressed as 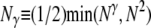, and the coalescence probability c_N is

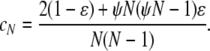(1)

For notational convenience, we also define the indicator function I_A as

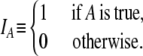For example, I_γ<2 = 1 if γ < 2, and zero otherwise. In our model a large reproduction event occurs when the number of offspring of the parent equals ψN – 1. These events occur with probability ɛ. Our choice of ɛ = 2φ/N^γ results in the coalescence timescale being N_γ. The rate λ_γ of coalescence is then

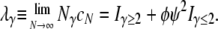(2)

The coalescence rate λ_γ is a key quantity in nearly all of our results below.

Model of subdivision:

We now consider the finite island model of population subdivision with the simplifying assumption that migration does not change the sizes of the subpopulations (Nagylaki 1980; Strobeck 1987; Herbots 1997). Reproduction in all the subpopulations follows the modified Moran model described above. The discrete-time ancestral process for a sample of size 2 is a Markov chain with transition probabilities given in Equation A1 in the appendix.

We are concerned with small migration rates, specifically those on the order of 1/N_γ time steps. This means that a single individual resides in the same subpopulation for 2N_γ time steps, on average, before migrating to a different subpopulation. When 0 < γ < 2, each individual resides in the same subpopulation for only N^γ time steps, on average. This time can be much shorter (when 0 < γ < 1) than the usual average of N time steps assumed in Wright–Fisher populations. In other words, a large number of individuals migrate during N time steps when 0 < γ < 1. We let m denote the probability that a single individual resided in a different subpopulation in the previous time step and model m as m = m_γ ≡ κ/(2N_γ) in which κ is a finite constant (0 < κ < ∞).

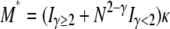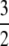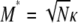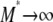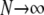To illustrate the difference between our migration rate κ and the usual migration rate Nm let M* ≡ N²m_γ denote a migration rate scaled in units of N² time steps (or N generations). This corresponds to the usual “Nm” in the Wright–Fisher model. Substituting for m_γ gives . If, for example, γ = , then . When γ < 2 the migration rate M* is very high; i.e., as since κ is finite. However, in our modified model of reproduction coalescence also occurs on the timescale of N^3/2 time steps (or 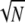generations when γ = 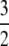) and thus “counteracts” the effects of high migration rate.

The main results of this work concern expected coalescence times (Equations 3 and 5) and F_ST-like measures (Equations 10–12). We also derive the densities of the coalescence times (see appendix). The densities are used to derive distribution functions for the number of segregating sites between two sequences (see the appendix), which in turn yield expressions for F_ST-like measures including mutation (Equations 13 and 14).

The distributions of the coalescence times are functions of λ_γ:

DNA sequences differ because they have accumulated mutations from the time of their most recent common ancestor until they are sampled. By assuming a very low mutation rate, Slatkin (1991) derived an expression for F_ST in terms of expected values of coalescence times. The time until two genes coalesce is therefore a fundamental quantity in theoretical work on structured populations. Given two genes sampled from a structured population, two different coalescence times arise that are of interest: the time T₀ until two genes sampled from the same subpopulation coalesce and time T₁ until two genes sampled from different subpopulations reach a common ancestor. The densities of T₀ and T₁ were previously derived under the structured coalescent by Takahata (1988) and Nath and Griffiths (1993) in the case of two subpopulations and by Herbots (1997) for any finite number of subpopulations.

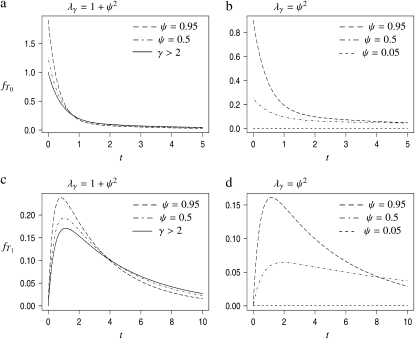
Given the transition rates in Equation A2, we can obtain the distributions of the coalescence times T₀ and T₁ (see the appendix). Figure 1 shows the distributions of T₀ and T₁, respectively, as functions of time for different values of ψ (the fraction of the population replaced by the offspring of a single individual). As ψ increases (i.e., tends to 1), the coalescence times T₀ and T₁ become very short.

Figure 1.—

The densities 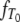and 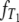of times to coalescence for two genes sampled from the same (T₀), or different (T₁), subpopulations as functions of time for different values of ψ when the number of subpopulations D = 3 and φ = κ = 1. The coalescence timescale is N²/2 in a and c and N^γ/2 with 0 < γ < 2 in b and d. The solid lines in a and c are the densities obtained under the standard coalescent (i.e., γ > 2).

The expected value and variance of T₀ are both less than the corresponding quantities for T₁. Specifically,

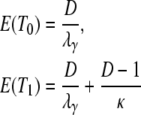(3)

and

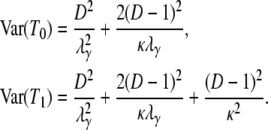(4)

Equation 3 holds a key result, namely that E(T₀) is always less than E(T₁).

The significance of the result in Equation 3 is best understood by an example. When γ < 2, say 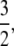then the timescale is N_γ = N^3/2, and λ_γ = ψ² (assuming φ = 1). Our migration parameter is then κ = m_γN_γ = m_γN^3/2. Migration is scaled in units of N² time steps in a standard Moran population. If we let M* ≡ N²m_γ be a scaled migration rate in units of N² time steps, then if m_γ is of order 1/N^3/2 as above, M* becomes very high in a large population. 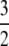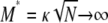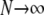Specifically, since γ = , we have (as ), since κ is a constant. The result in Equation 3 says that even when 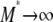one will still see evidence of population structure in DNA sequence data, since coalescence occurs on a timescale of 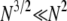time steps (in a large population) when γ = 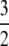. In fact, 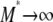as 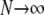whenever 0 < γ < 2.

Similarly, 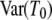is always less than 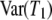. In addition, the expected value and variance of T₀ are inversely proportional to λ_γ and thus will be small when the probability of large reproduction events is close to one. The expressions for E(T₀) and E(T₁) (Equation 3) obtained under the usual reproduction models (Nei and Feldman 1972; Li 1976; Griffiths 1981) can be recovered by assuming that large reproduction events occur on a longer timescale (γ > 2) than usual (e.g., Wright–Fisher) sampling, in which case λ_γ = 1. The variances of T₀ and T₁ were first derived by Hey (1991) under the structured coalescent and can be recovered in the same way from Equation 4.

A many-demes limit:

The structured coalescent simplifies under certain migration mechanisms when the number of subpopulations is taken to be much greater than the sample size of DNA sequences (Wakeley 1998). The convergence of the ancestral process under a many-demes limit (i.e., when 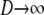) follows from the work of Möhle (1998), which shows how events in a stochastic process that occur on different timescales can be separated (see the appendix for a more detailed description). We consider the ancestral process in the limit 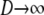and 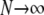. Switching the order of the limits leads to the same coalescent process (see the appendix).

The limit process of two genes sampled from a population subdivided into very many subpopulations (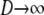), each of which is very large (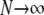), is of the form P*e^tG* in which P* and G* are given by Equations A16 and A19, respectively. The form of P* tells us that the ancestral process immediately enters the continuous-time process if the two genes are sampled from two different demes. If the two genes are sampled from the same subpopulation, they coalesce with probability 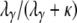or enter the continuous-time process by moving to different subpopulations with probability 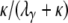. In the continuous-time process the two lines wait with exponential time with rate 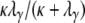on a timescale of DN_γ time steps until they coalesce. The ancestral process under the many-demes limit model (Equation A19) differs from the limit process obtained when the number of subpopulations is finite (Equation A2), in that G* has a zero entry for the transition where the two alleles enter the same subpopulation, after having been separated. When D < ∞, the corresponding rate is κ/(D – 1) (Equation A2). Ancestral lines can coalesce, however, only if they reside in the same subpopulation. The matrix B* (Equation A18) ensures that the two lines do arrive in the same subpopulation.

Again we are interested in the coalescence times T₀ and T₁ of two genes sampled from the same, or different, subpopulations, respectively. The distribution of T₀ is a mixture distribution (see appendix), and we obtain

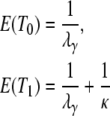(5)

and

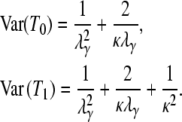(6)

The expressions for the expected value and variance of T₀ and T₁ obtained under the many-demes limit model (Equations 5 and 6) are functions of λ_γ and κ in the same way as the corresponding expected values and variances (Equations 3 and 4) obtained for a finite number of subpopulations. In particular, we always expect a shorter coalescence time for two ancestral lines sampled from the same subpopulation than if they were sampled from different subpopulations.

Deriving F_ST and N_ST:

The quantity F_ST is commonly used to assess levels of population subdivision. The inbreeding coefficient of an individual relative to a collection of subpopulations, F_IT, can be attributed to nonrandom mating within a subpopulation (F_IS) and to differences among subpopulations (F_ST; Wright 1951). Two sequences are identical by descent if they have not experienced mutation from the time of their most recent common ancestral sequence until they are sampled. If we let f₀ and f denote the probability of identity by descent of two genes sampled from the same subpopulation (f₀) and at random from the collection of subpopulations (f), we can express F_ST as

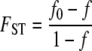(7)

(Nei 1973). By the definition of F_ST in terms of inbreeding coefficients (as in Equation 7), F_ST depends on the mutation rate (μ). By forcing μ to be very low Slatkin (1991) derived an approximation of F_ST that is a function of expectation of coalescence times and is given by

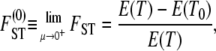(8)

in which T is the coalescence time of two lines randomly sampled from the collection of subpopulations, T₀ is the time to coalescence of two lines from the same subpopulation, and μ is the mutation rate.

To obtain an expression of 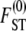in terms of coalescence times under skewed offspring distribution, we can proceed by first obtaining the expected coalescence time E(T) of two genes randomly sampled from the collection of subpopulations, which is readily obtained from Equations 3 and A10 and is given by

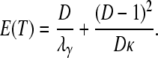(9)

When the number of subpopulations D is finite, the general form of 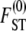is

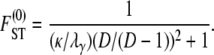(10)

For example, when 0 < γ < 2, the rate of coalescence is λ_γ = ψ² (with φ = 1) and Equation 10 gives 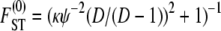. The expression for 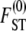in Equation 10 has the same form as the one derived by Slatkin (1991) under the standard coalescent. The key difference is that, under skewed offspring distribution, F_ST is a function of the rate λ_γ (Equation 2) of coalescence and thus a function of the reproduction parameters φ and ψ. The result that Slatkin (1991) obtained can be recovered from Equation 10 by taking γ > 2, in which case λ_γ = 1 (recall that the probability of large reproduction events ∝ 1/N_γ).

When the number of subpopulations 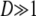, we obtain from Equation 10

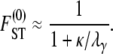(11)

In Equation 11 we have taken two limits: 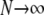and 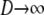. Switching the order of the limits gives the same limit result for F_ST in Equation 11.

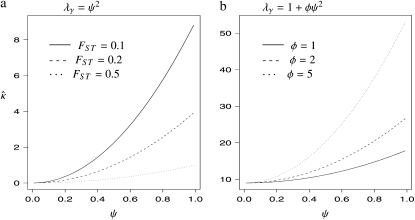
Following Wright (1951), the value of F_ST has often been used to estimate levels of gene flow. Figure 2 shows 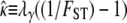, obtained from Equation 11, as a function of ψ for different values of F_ST (Figure 2a) and φ (Figure 2b) and for two different values of λ_γ. Since F_ST is a function of ψ and φ, so is any estimate of gene flow based on F_ST, as Figure 2 clearly shows.

Figure 2.—

The estimate 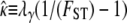of migration rate from Equation 11 as a function of ψ. (a) 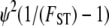when F_ST = 0.1 (solid line), F_ST = 0.2 (dashed line), and F_ST = 0.5 (dotted line). (b) 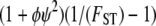with F_ST = 0.1 and φ = 1 (solid line), φ = 2 (dashed line), and φ = 5 (dotted line).

Lynch and Crease (1990) used the number of pairwise sequence differences of DNA sequences to estimate levels of genetic heterogeneity. In that context, Lynch and Crease (1990) introduced the quantity N_ST that has the form 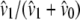in which 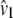and 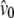are the average number of pairwise differences between sequences sampled from different, or the same, subpopulations, respectively. If mutation rate is constant and mutations occur according to the infinite-sites model (Watterson 1975), then N_ST estimates 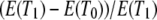(Slatkin 1993). Using the results obtained for expected coalescence times (Equation 3), we obtain as in Equation 11 for the many-demes limit model of population subdivision and

(12)

when D < ∞. The effect of skewed offspring distribution is the same on N_ST as it is on F_ST. Under the infinite-sites mutation model we do not need an assumption of small mutation rate to obtain an expression of N_ST in terms of coalescence times, unlike the case for F_ST. As N_ST is defined, the mutation parameter cancels out (Slatkin 1993).

Number of segregating sites between pairs of sequences:

By the definition of F_ST in terms of probabilities of identity by descent (Equation 7), F_ST depends on mutation. Eldon and Wakeley (2006) show that the limit process (as 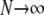) of our model of skewed offspring distribution predicts nonzero levels of genetic variation only when γ > 1. If we (as in Eldon and Wakeley 2006) let μ denote the probability of mutation for each offspring in a single time step, we define the mutation rate θ as 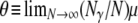(and γ > 1). We can include mutation in an expression for F_ST by first obtaining the probability distributions of the number of segregating sites, under the infinite-sites model (Watterson 1975), between two genes given a model of population subdivision with migration. Let K₀ denote the number of segregating sites between two genes sampled from the same subpopulation and K denote the number of segregating sites between two genes sampled randomly from the collection of subpopulations. The distributions of K₀ and K are derived in the appendix, along with the distribution of the number of segregating sites K₁ between two genes sampled from different subpopulations. Then by the definition of F_ST given in Equation 7 we obtain

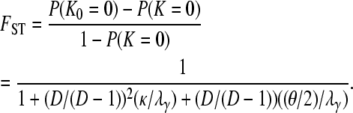(13)

When ,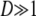

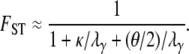(14)

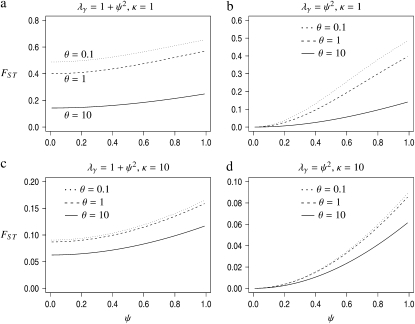
From Equation 14 we conclude that mutation can affect F_ST only if θ is large relative to λ_γ. The expression for F_ST in Equation 14 has the same form as the one derived by Wilkinson-Herbots (1998) and by Nei (1975) and Takahata (1983) by other methods, under the Wright–Fisher model, including mutation. In Figure 3, F_ST from Equation 14 is graphed as a function of ψ for different values of θ and κ. The interpretation of Figure 3 is that F_ST, as a function of ψ, can vary considerably when the timescale of coalescence (and migration) is in units of N^γ/2 generations with 1 < γ < 2 (Figure 3, b and d).

Figure 3.—

The quantity F_ST from Equation 14 as a function of ψ (with φ = 1) for different values of θ, κ, and rate of coalescence (λ_γ). Solid lines, θ = 10; dashed lines, θ = 1; dotted lines, θ = 0.1.

Nei's genetic distance d:

Not all indicators of separation between populations depend on λ_γ. Nei's (1972) genetic distance is more appropriate for estimating divergence time between species, and F_ST-like quantities are more suitable for inferring population structure within species (Slatkin 1991). Nei's (1972) genetic distance measure is given by 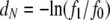in which f₀ and f₁ are the probabilities of identity by descent of two genes sampled from the same or different subpopulations, respectively, and we add the subscript N to remind us that time is discrete. If we now assume that 0 < μE(t_i) < 1 for i = 0, 1, then using the Maclaurin series expansion of the logarithmic function 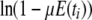we obtain 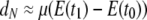(previously obtained by Slatkin 1991) in which t₀ and t₁ are the coalescence times for two genes sampled from the same, or different, subpopulations, respectively. To obtain an expression of d for continuous time, we assume that the product 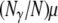converges to a constant θ as 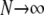(and γ > 1). Rewriting the approximation for d_N gives

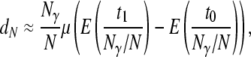(15)

which has the continuous-time limit

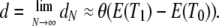(16)

However, using the expressions for E(T₁) and E(T₀) (Equation 3), we obtain 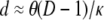and so Nei's (1972) genetic distance is independent of λ_γ. Another way of deriving an expression for d is to note that the probability of identity by descent of two genes is the same as the probability that no mutations occur from the time they are sampled until they reach a common ancestor. Thus f_i = P(K_i = 0) for i = 0, 1. We can therefore write

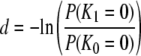(17)

for any model of population subdivision. For the many-demes limit model under consideration,

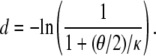Using either the limit approach (Equation 16) or the substitution approach (Equation 17) in the many-demes limit model, and assuming small θ/κ (i.e., 0 < θ/κ < 1), d is of the form θ/κ. The same result is obtained for a finite number of subpopulations. Indeed, when D is finite, we obtain from Equations A28 and A29

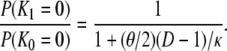(18)

Thus, if 0 < (θ/2)(D – 1)/κ < 1, we have from Equations 17 and 18

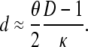(19)

Even if (θ/2)(D – 1)/κ > 1, we have from Equations 17 and 18 that d is not a function of λ_γ. Thus Nei's (1972) genetic distance can be used to estimate divergence times of species even if one or both species have skewed offspring distribution, since d is proportional to the time of separation of two populations (Nei 1972; Slatkin 1991).

DISCUSSION

Some organisms, for example Pacific oysters (Beckenbach 1994; Hedgecock 1994a) and Atlantic cod (Bekkevold et al. 2002; Árnason 2004), may exhibit skewed offspring distribution among individuals in a population. Both Beckenbach (1994) and Hedgecock (1994a) describe the reproductive mode of oysters, for example, as a lottery, in which only the offspring of a few lucky females survive. Oyster and cod females have very high reproductive potential, as they may produce millions of eggs in a single spawning (May 1967; Strathmann 1987; Chambers and Waiwood 1996; Kjesbu et al. 1996). The Wright–Fisher model does not capture the skewed offspring distribution possibly exhibited by organisms with high fecundities and high early mortality. The models of Pitman (1999) and Sagitov (1999), and later of Eldon and Wakeley (2006) and Sargsyan and Wakeley (2008) for overlapping generations in a single population, incorporate the skewness and may thus better apply to organisms with highly fecund individuals and sweepstakes-style recruitment. By deriving distributions of coalescence times for two genes sampled from a subdivided population, we show how skewed offspring distribution confounds estimates of migration rate between subpopulations when based on F_ST-like measures of population subdivision.

An important result of this work is that F_ST depends not only on the migration rate κ but also on the parameters (ψ and φ) of our model of large offspring numbers. Demographic processes such as population size fluctuations, founder effects, or skewed offspring distribution have been thought to increase genetic differentiation among subpopulations. As defined and calculated from genetic data, common indicators of population subdivision then take on high values, thus suggesting low levels of migration (Boileau et al. 1992; Whitlock 1992; Slatkin 1993; Hedgecock 1994a). Our main conclusions are twofold. First, F_ST is shown to depend on the parameters controlling the size (ψ) and frequency (φ) of large reproduction events (the probability that the offspring of a single individual replace a fraction ψ of the population is ɛ = 2φ/N^γ) and can thus indicate high or low levels of genetic heterogeneity depending on ψ and φ. To illustrate, consider the expression for F_ST derived under the many-demes limit model without mutation (Equation 11), and let the timescale of coalescence occur on N^γ/2 time steps (i.e., 0 < γ < 2). In that case the rate of coalescence λ_γ = ψ² (by taking φ = 1), and the rate of large reproduction events is high. By fixing κ, we see that F_ST ranges from very low (when ψ is low), to ≈1/(1 + κ), when ψ ≈ 1. Second, to the extent that F_ST (or N_ST) is used in estimating levels of gene flow, these estimates are confounded by λ_γ and thus by φ and ψ. Also, migration in our model is not the usual Nm quantity, but is given by κ = m_γN_γ. This means that even when Nm is very large, we may still observe genetic heterogeneity, since the rate of large reproduction events is also large. In a population where individuals can have very many offspring, gene flow is not the only demographic force that influences genetic heterogeneity.

The coalescence times T₀ and T₁ (for genes sampled from the same or different subpopulations, respectively) are fundamental quantities of the ancestral process of genes in subdivided populations. The time during which DNA sequences accumulate mutations is determined by T₀ and T₁. As we have shown, the coalescence times depend on the skewness of the offspring distribution through the rate λ_γ (Equation 2) of coalescence. By deriving the distributions of T₀ and T₁ for two genes in a structured population, we have obtained insight into how skewed offspring distribution shapes the genetics of structured populations. Since T₀ and T₁ are functions of φ and ψ through the rate of coalescence λ_γ, all the quantities of interest in regard to investigation of the genetics of structured populations, including expected values, number of segregating sites, and indicators of population subdivision, are functions of λ_γ.

One such insight is that genetic heterogeneity can be observed in genetic data even if gene flow is very high by the usual standard (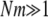). Edmands et al. (1996) found significant genetic heterogeneity among subpopulations of the purple sea urchin S. purpuratus sampled along the coast of California and Baja California. The ecology and physiology of S. purpuratus indicate the capacity for highly skewed offspring distribution: external fertilization and very high fecundity. Despite a planktonic larval period of several weeks (Strathmann 1978), and thus a potential for high dispersal, both allozyme and mtDNA sequence data revealed genetic differentiation, even over short distances (Edmands et al. 1996). We have shown that, regardless of the timescale of migration, E(T₀) < E(T₁). Genetic heterogeneity can, therefore, be observed in DNA sequence data even if gene flow is very high, in a population with skewed offspring distribution. Population turnover in a metapopulation model when demes that become extinct are recolonized by one or a few individuals can also lead to increased F_ST (Wade and McCauley 1988; Whitlock and McCauley 1990; Pannell 2003). Indeed, a model of metapopulation structure that allows only one founder for every deme that is recolonized necessarily results in a coalescent process with multiple mergers, if the founder can have many offspring.

In summary, we consider the coalescence times of a subdivided population following a sweepstakes-style recruitment. The expected coalescence time for two genes sampled from the same subpopulation is always less than the expected coalescence time for two genes sampled from different subpopulations, even when migration occurs on a very short timescale. Estimates of migration rate based on F_ST are confounded by the rate λ_γ of coalescence, since F_ST-like measures of genetic heterogeneity are a function of the reproduction parameters of our model of skewed offspring distribution. These results underscore the importance of choosing an appropriate limit process for the population under consideration.

APPENDIX

The discrete-time transition matrix:

The probability transition matrix Π_N (Equation A1) for the ancestral process over one time step for the case of arbitrary fixed number D ≥ 2 of subpopulations has three states: (1) two lines in the same deme but not coalesced, (2) two lines in different demes, and (3) the two lines have coalesced. We do not distinguish between subpopulations. The transition probabilities in Π_N are derived under the assumption that migration does not alter the subpopulation sizes (Nagylaki 1980; Strobeck 1987; Herbots 1997). We let m denote the single backward migration fraction. The matrix Π_N is

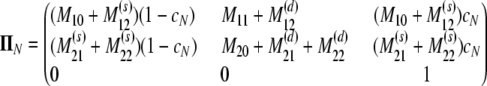(A1)

in which c_N is the coalescence probability and

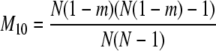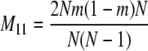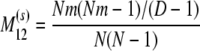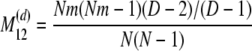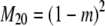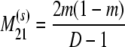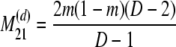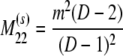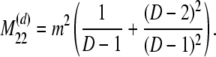The matrix in Equation A1 is a generalization of the matrix for the same migration mechanism (cf. Wakeley 2008) obtained under the usual Wright–Fisher model of reproduction. In Equation A1, the probability of coalescence is c_N, instead of the usual 1/N, as is the case for the haploid Wright–Fisher model. The corresponding continuous-time process has rate matrix G given by

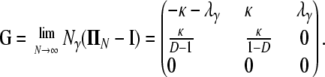(A2)

Distribution functions of the coalescence times when D is finite:

In this section we derive the distribution functions for the coalescence times T₀ and T₁ when the number of subpopulations is finite. Given the distributions of T₀ and T₁ we can determine the distribution of the coalescence time T of two genes sampled at random from the collection of subpopulations. The distributions of these coalescence times allow us to derive expressions for F_ST with or without mutation.

We can use the rate matrix (Equation A2) to obtain the density functions for T₀ and T₁. Using Laplace transforms (see Herbots 1997) we obtain

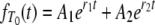(A3)

in which

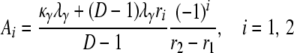(A4)

and

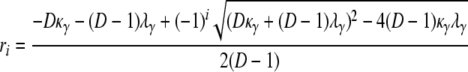(A5)

for i = 1, 2. To obtain the density function of T₁, we note that T₁ can be represented as a sum of two independent random variables, T₁ = Y₁ + T₀, where Y₁ is an exponential random variable with rate κ_γ/(D – 1). By direct calculation,

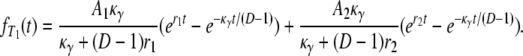(A6)

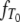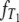The form of the continuous functions and (Equations A3 and A6) immediately yields the cumulative densities 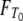and 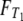for T₀ and T₁, respectively. Namely, writing λ_i = –r_i for i = 1, 2,

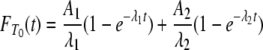(A7)

and

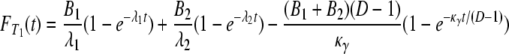(A8)

in which

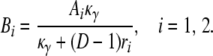Let T denote the time to coalescence for two genes sampled at random from the collection of subpopulations. Then, with probability 1/D the two genes are sampled from the same subpopulation, and with probability 1 – 1/D they are sampled from different subpopulations. The cumulative density function (c.d.f.) F_T of T is then given by

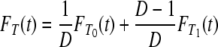(A9)

in which 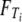denotes the c.d.f. of T_i for i = 0, 1. The expected value of T is

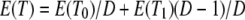(A10)

in which E(T₀) and E(T₁) are given by Equation 3 and the variance of T is

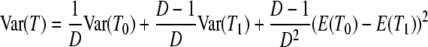(A11)

in which Var(T₀) and Var(T₁) are given by Equation 4. Note that although the expected value of T lies between E(T₀) and E(T₁), Equation A11 tells us that the variance of T may not lie between the variance of T₀ and T₁. If 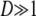, then Var(T) > Var(T₁).

A many-demes limit model:

In this section we derive the ancestral process for two genes in the many-demes limit (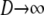) and as 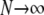. Since now 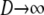, the single-generation backward transition matrix, following Möhle (1998), can be written

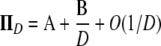(A12)

in which the matrices A and B are given below. The matrix A describes the probabilities of the transitions that occur on a timescale of time steps. The matrix B/D describes transitions that occur on a timescale of D time steps, thus forming the continuous-time part of the ancestral process. The limit process (as 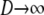) is then given by Π(t) = Pe^tPBP in which 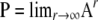describes the equilibrium process of the events that occur on the timescale of time steps (Möhle 1998). The ancestral history of a sample is first adjusted by an instantaneous process described by P and then enters a continuous-time process described by the rate matrix PBP. Given the ancestral process, we can derive the distributions of T₀ and T₁.

The instantaneous matrix A is

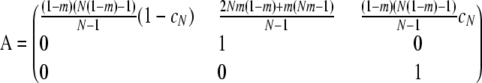(A13)

with eigenvalues λ₁ = λ₂ = 1 and

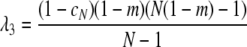and we observe that 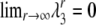. By calculating the corresponding eigenvectors (not shown) we obtain the limit matrix P by diagonalizing A,

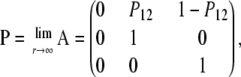(A14)

in which

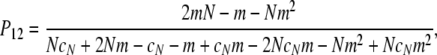(A15)

and in the limit 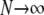we obtain

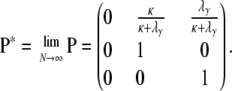(A16)

When 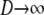but holding N finite, the ancestral process is given by Pe^tPBP, in which the matrix B is given by

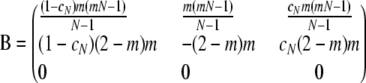(A17)

and we obtain

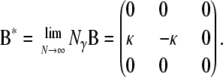(A18)

The rate matrix G* = P*B*P* then takes the general format

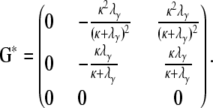(A19)

The ancestral process in the limit 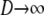and 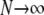is P*e^tG* and immediately yields the density functions for T₀ and T₁ as follows. The time T₁ to coalescence for two lines sampled from different demes follows in each case (γ > 2, γ = 2, and 0 < γ < 2) an exponential distribution with rate 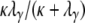. Now consider the time T₀ to coalescence for two lines sampled from the same subpopulation. Going back in time, two lines in the same subpopulation can either coalesce with probability 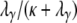or they enter the continuous-time process with probability 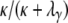, in which case one of the two lines migrates to a different subpopulation. Thus T₀ follows a mixture distribution with cumulative density function

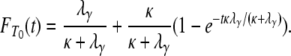(A20)

Order of limits irrelevant in the many-demes limit model:

In this section we show that the same ancestral process is obtained irrespective of the order of the limits 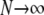and 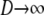. We have already derived the process when first 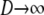and then 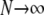. Now we show that the same ancestral process is obtained when first 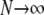and then .

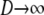As 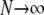, we obtain the ancestral process described by the rate matrix

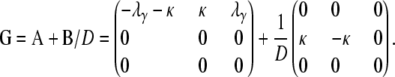(A21)

We remark that Aⁿ = (–κ – λ_γ)ⁿ⁻¹A for n ≥ 1. Since A is a rate matrix, we have, with a = κ + λ_γ,

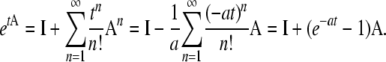(A22)

Equation A22 immediately gives us the instantaneous matrix

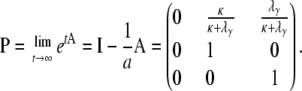(A23)

Equations A21 and A23 then give us the rate matrix G = PBP after first taking the limit 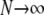and then .

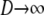By similar arguments we can show that the ancestral process does indeed result in coalescence regardless of initial state. Indeed,

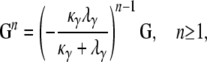(A24)

which gives, writing b = κλ_γ/(κ + λ_γ),

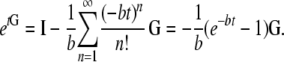(A25)

The equilibrium distribution (as 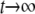) is then

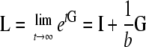(A26)

and we obtain that two genes do reach a common ancestor regardless of initial state—i.e.,

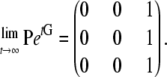(A27)

Number of segregating sites:

We now consider the number of segregating sites, under the infinite-sites model (Watterson 1975), between two genes in the two models of population subdivision discussed previously. First, consider the model of finite number of subpopulations. Let K₀ and K₁ denote the number of segregating sites for two genes sampled from the same or different subpopulations, respectively. We let θ denote the scaled mutation rate and note that, given a specific length of time t, the number of segregating sites is Poisson distributed with rate θt/2. The probability distribution for the number of segregating sites for two genes sampled from the same subpopulation is

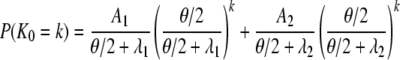(A28)

in which A₁ and A₂ are given in Equation A4, and λ_i = –r_i from Equation A5.

The probability distribution for the number of segregating sites between two genes sampled from different subpopulations is

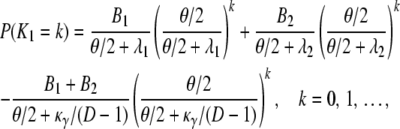(A29)

in which B_i = A_iκ/(κ + (D – 1)r_i) for i = 1, 2. The expected value and variance of K₀ are both less than the corresponding quantities for K₁. Indeed,

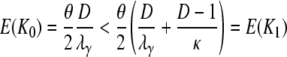(A30)

and

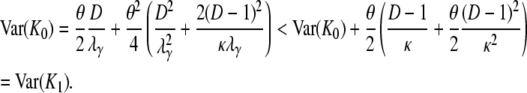(A31)

The probability mass distribution of the number of segregating sites K for two genes sampled at random from the collection of subpopulations is

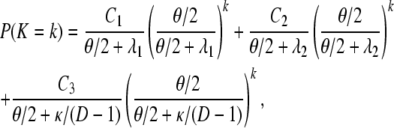(A32)

in which C_i = A_i/D + (D – 1)B_i/D for i = 1, 2 and 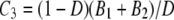. One can write K ∼ (1/D)K₀ + (1 – 1/D)K₁; i.e., K is a mixture distribution. In fact, K is distributed as K₀ with probability 1/D and as K₁ with probability 1 – 1/D. Hence,

(A33)

and so E(K₀) < E(K) < E(K₁). However, the variance of K (Equation A34), which can be obtained in the same way as the variance of the time to coalescence of two genes sampled at random from the collection of subpopulations (Equation A11), may not lie between the variance of K₀ and K₁. The variance of K is

(A34)

Number of segregating sites under the many-demes limit model:

Under the many-demes limit model of population subdivision, the probability mass distribution for the number of segregating sites K₁ between two genes sampled from different subpopulations is

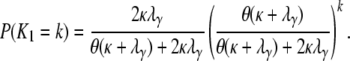(A35)

The expected number and the variance of the number of segregating sites between two genes sampled from different subpopulations is then

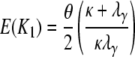(A36)

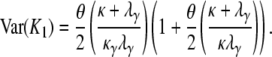(A37)

The probability mass function for K₀, the number of segregating sites between two genes sampled from the same subpopulation, is (k = 0, 1, …)

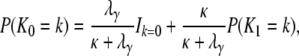(A38)

which gives expected value

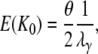(A39)

and the variance of K₀ is

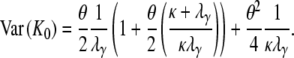(A40)